Komputasi untuk Sains dan Teknik -Menggunakan Matlab-

(1)

Komputasi untuk Sains dan Teknik

-Menggunakan

Matlab-Supriyanto Suparno

( Website: http://supriyanto.fisika.ui.ac.id )

( Email: supriyanto@sci.ui.ac.id atau supri92@gmail.com )

Edisi IV

Revisi terakhir tgl: 1 Maret 2013

Departemen Fisika-FMIPA, Univeristas Indonesia Dipublikasikan pertama kali pada September 2007

(2)

(3)

Muflih Syamil Hasan Azmi Farah Raihanah Nina Marliyani

(4)

(5)

Kata Pengantar

Perubahan adalah suatu keniscayaan. Aksioma itu berlaku juga pada buku ini — yang mulai ditulis pada tahun 2005. Mulai 24 juli 2010, edisi ke-4 ini diluncurkan dalam rangka mengubah sasaran tujuan dari buku edisi ke-3.

Penekanan penulisan edisi ke-3 adalah ingin memperkenalkan sebanyak mungkin metode numerik kepada mahasiswa tingkat sarjana di Departemen Fisika, Universitas Indonesia. Ha-sil evaluasi proses perkuliahan menunjukkan bahwa diskusi matematis terlalu dominan diban-dingkan diskusi aplikasi metode numerik pada masalah ﬁsika. Oleh karena itu saya memutusk-an untuk memperbesar porsi pembahasmemutusk-an aplikasi metode numerik sehingga beberapa metode numerik yang diulas pada edisi ke-3 dengan sengaja dihilangkan dalam edisi ke-4 ini.

Rujukan utama buku edisi-4 ini tetap bersumber pada buku teks standar yang sangat populer di dunia komputasi, yaitu buku yang ditulis oleh Richard L. Burden dan J. Douglas Faires dengan judul Numerical Analysis edisi ke-7, diterbitkan oleh Penerbit Brooks/Cole, Thomson Learning Academic Resource Center. Namun demikian, buku ini telah dilengkapi dengan sejumlah contoh aplikasi komputasi pada upaya penyelesaian problem-problem ﬁsika.

Walaupun buku ini masih jauh dari sempurna, namun semoga ia dapat menyumbangkan kontribusi yang berarti untuk kebangkitan ilmu pengetahuan pada diri anak bangsa Indonesia yang saat ini sedang terpuruk. Saya wariskan buku ini untuk siswa dan mahasiswa Indonesia dimanapun mereka berada. Anda berhak memanfaatkan buku ini. Saya izinkan anda untuk meng-copy dan menggunakan buku ini selama itu ditujukan untuk belajar dan bukan untuk tujuan komersial. Bagi yang ingin berdiskusi, memberikan masukan, kritikan dan saran, silakan dikirimkan ke email: supri92@gmail.com

Akhirnya saya ingin mengucapkan rasa terima kasih yang tak terhingga kepada Dede Dju-hana yang telah berkenan memberikan format LA_{TEX-nya sehingga tampilan tulisan pada buku}

ini benar-benar layaknya sebuah buku yang siap dicetak. Tak lupa, saya pun berterima kasih kepada seluruh mahasiswa yang telah mengambil mata kuliah Komputasi Fisika dan Anaisis Nu-merik di Departemen Fisika, FMIPA, Universitas Indonesia atas diskusi yang berlangsung selama kuliah. Kepada seluruh mahasiswa dari berbagai universitas di Timur dan di Barat Indonesia juga saya ungkapkan terima kasih atas pertanyaan-pertanyaan yang turut memperkaya isi buku ini.

Depok, 24 Juli 2010 Supriyanto Suparno

(6)

(7)

Daftar Isi

Lembar Persembahan i

Kata Pengantar iii

Daftar Isi iii

Daftar Gambar ix

Daftar Tabel xiii

1 Pendahuluan 1

1.1 Inisialisasi variabel . . . 1

1.2 Perhitungan yang berulang . . . 2

1.3 Mengenal cara membuat graﬁk . . . 3

1.4 Baris-baris pembuka . . . 5

1.5 Membuat 2 graﬁk dalam satu gambar . . . 5

1.6 Latihan . . . 10

2 Matrik dan Komputasi 15 2.1 Mengenal matrik . . . 15

2.2 Vektor-baris dan vektor-kolom . . . 16

2.3 Inisialisasi matrik dalam memori komputer . . . 16

2.4 Macam-macam matrik . . . 17 2.4.1 Matrik transpose . . . 17 2.4.2 Matrik bujursangkar . . . 18 2.4.3 Matrik simetrik . . . 18 2.4.4 Matrik diagonal . . . 18 2.4.5 Matrik identitas . . . 18 2.4.6 Matrik upper-triangular . . . 19 2.4.7 Matrik lower-triangular . . . 19 2.4.8 Matrik tridiagonal . . . 19

2.4.9 Matrik diagonal dominan . . . 19

2.4.10 Matrik positive-definite . . . . 20

2.5 Operasi matematika . . . 20

2.5.1 Penjumlahan matrik . . . 20

2.5.2 Komputasi penjumlahan matrik . . . 21

2.5.3 Perkalian matrik . . . 24

2.5.4 Komputasi perkalian matrik . . . 27 v

(8)

2.5.5 Perkalian matrik dan vektor-kolom . . . 35

2.5.6 Komputasi perkalian matrik dan vektor-kolom . . . 36

2.6 Penutup . . . 39

2.7 Latihan . . . 40

3 Fungsi 41 3.1 Fungsi internal . . . 41

3.2 Fungsi eksternal . . . 42

3.3 Fungsi eksternal pada operasi matrik . . . 44

3.4 Fungsi eksternal penjumlahan matrik . . . 46

3.5 Fungsi eksternal perkalian matrik . . . 47

3.6 Fungsi eksternal perkalian matrik dan vektor-kolom . . . 49

3.7 Penutup . . . 51

3.8 Latihan . . . 52

4 Aplikasi dalam Sains 55 4.1 Fungsi internal . . . 55

5 Integral Numerik 63 5.1 Metode Trapezoida . . . 63

5.2 Metode Simpson . . . 64

5.3 Peran faktor pembagi, n . . . 66

5.3.1 Source code metode integrasi . . . 66

5.4 Metode Composite-Simpson . . . 67 5.5 Adaptive Quardrature . . . 69 5.6 Gaussian Quadrature . . . 69 5.6.1 Contoh . . . 70 5.6.2 Latihan . . . 70 6 Diferensial Numerik 73 6.1 Metode Euler . . . 73

6.2 Metode Runge Kutta . . . 79

6.2.1 Aplikasi: Pengisian muatan pada kapasitor . . . 82

6.3 Latihan I . . . 87

6.4 Metode Finite Difference . . . . 90

6.4.1 Aplikasi . . . 96

6.5 Latihan II . . . 97

6.6 Persamaan Diferensial Parsial . . . 98

6.7 PDP eliptik . . . 98

6.7.1 Contoh pertama . . . 100

6.7.2 Script Matlab untuk PDP Elliptik . . . 103

6.7.3 Contoh kedua . . . 106

(9)

6.8.1 Metode Forward-difference . . . 107

6.8.2 Contoh ketiga: One dimensional heat equation . . . 108

6.8.3 Metode Backward-difference . . . 113 6.8.4 Metode Crank-Nicolson . . . 116 6.9 PDP Hiperbolik . . . 119 6.9.1 Contoh . . . 122 6.10 Latihan . . . 122 7 Metode Iterasi 125 7.1 Kelebihan Vektor-kolom . . . 125 7.2 Pengertian Norm . . . 126

7.2.1 Script perhitungan norm dua . . . 126

7.2.2 Script perhitungan norm tak hingga . . . 127

7.2.3 Perhitungan norm-selisih . . . 127

7.3 Iterasi Jacobi . . . 128

7.3.1 Script metode iterasi Jacobi . . . 130

7.3.2 Stopping criteria . . . 139

7.3.3 Fungsi eksternal iterasi Jacobi . . . 141

7.4 Iterasi Gauss-Seidel . . . 142

7.4.1 Script iterasi Gauss-Seidel . . . 143

7.4.2 Algoritma . . . 150

7.4.3 Script iterasi Gauss-Seidel dalam Fortran . . . 150

7.5 Iterasi dengan Relaksasi . . . 152

7.5.1 Algoritma Iterasi Relaksasi . . . 153

8 Metode Eliminasi Gauss 155 8.1 Sistem persamaan linear . . . 155

8.2 Teknik penyederhanaan . . . 156

8.2.1 Cara menghilangkan sebuah variabel . . . 157

8.2.2 Permainan indeks . . . 157

8.3 Triangularisasi dan Substitusi Mundur . . . 158

8.3.1 Contoh pertama . . . 158

8.3.2 Contoh kedua . . . 160

8.4 Matrik dan Eliminasi Gauss . . . 161

8.4.1 Matrik Augmentasi . . . 161

8.4.2 Penerapan pada contoh pertama . . . 162

8.4.3 Source-code dasar . . . 165

8.4.4 Optimasi source code . . . 167

8.4.5 Pentingnya nilai n . . . 174

8.4.6 Jangan puas dulu.. . . 175

8.4.7 Pivoting . . . 175

(10)

8.6 Contoh aplikasi . . . 178

8.6.1 Menghitung arus listrik . . . 178

8.6.2 Mencari invers matrik . . . 180

8.7 Penutup . . . 187

9 Aplikasi Eliminasi Gauss pada Masalah Inversi 189 9.1 Inversi Model Garis . . . 189

9.1.1 Script matlab inversi model garis . . . 192

9.2 Inversi Model Parabola . . . 193

9.2.1 Script matlab inversi model parabola . . . 197

9.3 Inversi Model Bidang . . . 198

9.4 Contoh aplikasi . . . 200

9.4.1 Menghitung gravitasi di planet X . . . 200

10 MetodeLU Decomposition 207 10.1 Faktorisasi matrik . . . 207

10.2 Algoritma . . . 211

11 Interpolasi 217 11.1 Interpolasi Lagrange . . . 217

11.2 Interpolasi Cubic Spline . . . 220

12 Metode Newton 231 12.1 Deﬁnisi akar . . . 231

12.2 Metode Newton . . . 232

12.3 Script metode Newton . . . 235

12.4 Fungsi ber-input vektor . . . 237

12.5 Fungsi ber-output vektor . . . 238

12.6 Fungsi ber-output matrik . . . 239

12.7 Metode Newton untuk sistem persamaan . . . 239

12.8 Aplikasi: Mencari sumber sinyal . . . 241

12.9 Aplikasi: Mencari pusat gempa . . . 245

13 Metode Monte Carlo 247 13.1 Penyederhanaan . . . 247

14 Inversi 251 14.1 Inversi Linear . . . 251

14.2 Inversi Non-Linear . . . 254

15 Lampiran 257 15.1 Script Iterasi Jacobi, jcb.m . . . 257

(11)

(12)

(13)

Daftar Gambar

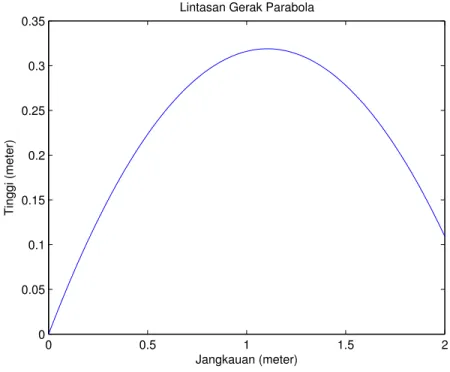
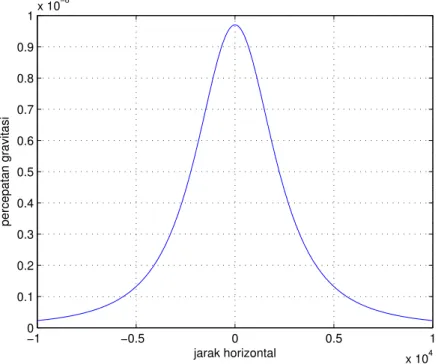
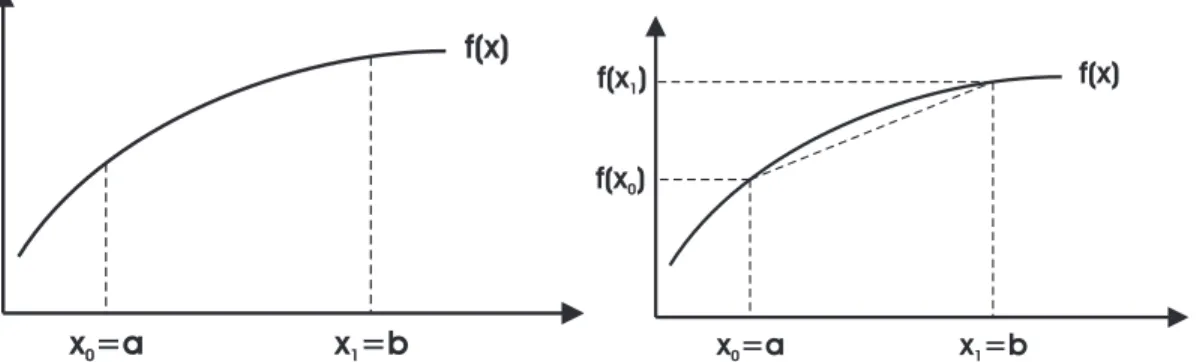
1.1 Data perubahan kecepatan terhadap waktu . . . 4 1.2 Data perubahan kecepatan terhadap waktu dengan keterangan gambar . . . 4 1.3 Grafik gelombang berfrekuensi 5 Hz . . . 6 1.4 Grafik yang dilengkapi dengan keterangan sumbu-x dan sumbu-y serta judul . . . 7 1.5 Grafik yang dilengkapi dengan font judul 14pt . . . 7 1.6 Dua buah grafik dalam sebuah gambar . . . 8 1.7 Tiga buah grafik dalam sebuah gambar . . . 9 3.1 Kurva lintasan gerak parabola yang dihasilkan oleh fungsi eksternal parabol() . . 43 4.1 Variasi nilai percepatan gravitasi terhadap perubahan jarak horizontal . . . 61 5.1 Metode Trapezoida. Gambar sebelah kiri menunjukkan kurva fungsif (x) dengan batas

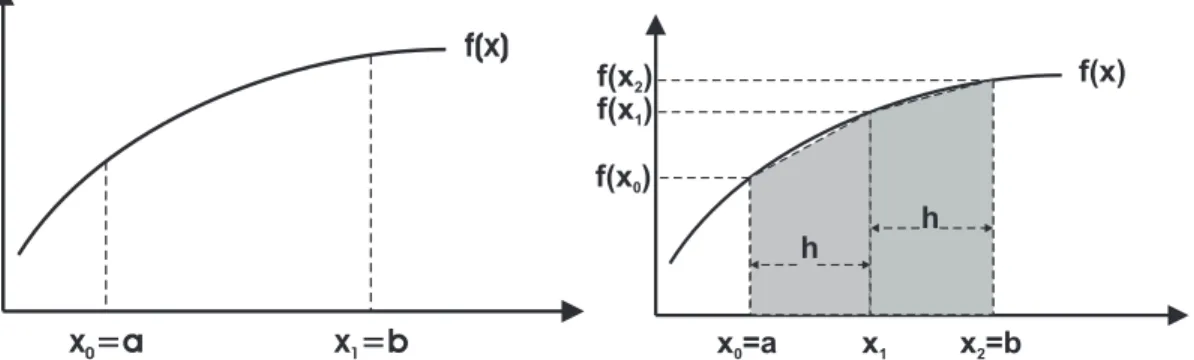
bawah integral adalaha dan batas atas b. Gambar sebelah kanan menunjukan cara meto-de Trapesoida menghitung integral meto-dengan cara menghitung luas area integrasi, dimana luas area integrasi sama dengan luas trapesium di bawah kurvaf (x) dalam batas-batas a danb. Jika anda perhatikan dengan teliti, ada area kecil dibawah garis kurva dan diatas garis miring yang berada diluar bidang trapesium. Metode Trapesoida tidak menghitung luas area kecil tersebut. Disinilah letak kelemahan metode trapezoida.. . . 64 5.2 Metode Simpson. Gambar sebelah kiri menunjukkan kurva fungsi f (x) dengan batas

bawah integral adalaha dan batas atas b. Gambar sebelah kanan menunjukan cara me-tode Simpson menghitung luas area integrasi, dimana area integrasi di bawah kurvaf (x) dibagi 2 dalam batas intervala − x1danx1− b dengan lebar masing-masing adalah h. . 65 5.3 Metode Composite Simpson. Kurva fungsi f (x) dengan batas bawah integral adalah a

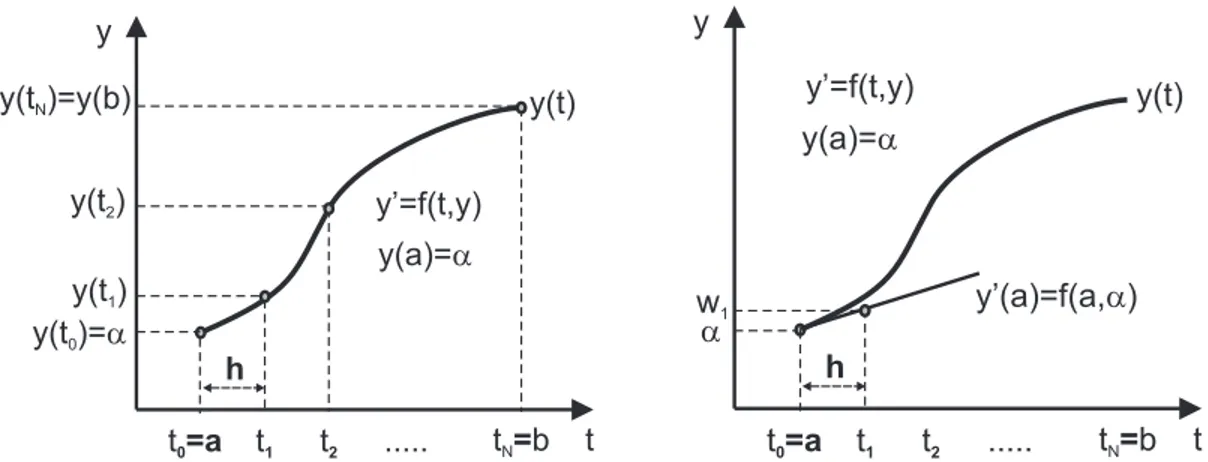
dan batas atasb. Luas area integrasi dipecah menjadi 8 area kecil dengan lebar masing-masing adalahh. . . 68 6.1 Kiri: Kurvay(t) dengan pasangan titik absis dan ordinat dimana jarak titik absis sebesar

h. Pasangan t₁adalahy(t₁), pasangan t₂adalahy(t₂), begitu seterusnya. Kanan: Garis singgung yang menyinggung kurvay(t) pada t=a, kemudian berdasarkan garis singgung tersebut, ditentukan pasangant₁ sebagaiw₁. Perhatikan gambar itu sekali lagi! w₁dan y(t₁) beda tipis alias tidak sama persis. . . 74 6.2 Kurva biru adalah solusi exact, dimana lingkaran-lingkaran kecil warna biru pada kurva

menunjukkan posisi pasangan absis t dan ordinat y(t) yang dihitung oleh Persamaan (6.9). Sedangkan titik-titik merah mengacu pada hasil perhitungan metode euler, yaitu nilaiwi. . . 78

(14)

6.3 Kurva biru adalah solusi exact, dimana lingkaran-lingkaran kecil warna biru pada kurva menunjukkan posisi pasangan absis t dan ordinat y(t) yang dihitung oleh Persamaan (6.9). Sedangkan titik-titik merah mengacu pada hasil perhitungan metode Runge Kutta

orde 4, yaitu nilaiwi. . . 82

6.4 Rangkaian RC . . . 83

6.5 Kurva pengisian muatanq (charging) terhadap waktu t . . . . 88

6.6 Kurva suatu fungsif (x) yang dibagi sama besar berjarak h. Evaluasi kurva yang dilakukan Finite-Difference dimulai dari batas bawah x0 = a hingga batas atas x6 = b . . . 90

6.7 . . . 95

6.8 Skema grid lines dan mesh points pada aplikasi metode Finite-Difference . . . . 99

6.9 Susunan grid lines dan mesh points untuk mensimulasikan distribusi temperatur pada lempeng logam sesuai contoh satu . . . 101

6.10 Sebatang logam dengan posisi titik-titik simulasi (mesh-points) distribusi temperatur. Ja-rak antar titik ditentukan sebesarh = 0, 1. . . 108

6.11 Interval mesh-points dengan jarakh = 0, 1 dalam interval waktu k = 0, 0005 . . . 108

6.12 Posisi mesh-points. Arahx menunjukkan posisi titik-titik yang dihitung dengan forward-difference, sedangkan araht menunjukkan perubahan waktu yg makin meningkat . . . . 109

9.1 Sebaran data observasi antara suhu dan kedalaman . . . 190

9.2 Kurva hasil inversi data observasi antara suhu dan kedalaman . . . 193

9.3 Kurva hasil inversi data observasi antara suhu dan kedalaman . . . 198

9.4 Graﬁk data pengukuran gerak batu . . . 202

9.5 Graﬁk hasil inversi parabola . . . 204

11.1 Sejumlah titik terdistribusi pada koordinat kartesian. Masing-masing titik memi-liki pasangan koordinat(x, y) . . . 220

11.2 Kurva interpolasi cubic spline yang menghubungkan semua titik . . . 221

11.3 Sejumlah polinomial cubic yaituS0, S1, S2... dan seterusnya yang saling sambung-menyambung sehingga mampu menghubungkan seluruh titik . . . 221

11.4 Proﬁl suatu object . . . 227

11.5 Sampling titik data . . . 227

11.6 Hasil interpolasi cubic spline . . . 228

11.7 Hasil interpolasi lagrange . . . 228

12.1 Fungsi dengan dua akar yang ditandai oleh lingkaran kecil berwarna merah, yaitu pada_{x = −2 dan x = 2 . . . 231}

12.2 Fungsi dengan satu akar yang ditandai oleh lingkaran kecil berwarna merah, ya-itu pada_{x = −1, 2599 . . . 232}

12.3 Koordinat sumber sinyal berada pada_{x = −4 dan y = −8 . . . 241}

13.1 Lingkaran dan bujursangkar . . . 247

(15)

(16)

(17)

Daftar Tabel

5.1 Polinomial Legendre untukn=2,3,4 dan 5 . . . 70

6.1 Solusi yang ditawarkan oleh metode eulerwi dan solusi exacty(ti) serta selisih antara keduanya . . . 77

6.2 Solusi yang ditawarkan oleh metode Runge Kutta orde 4 (wi) dan solusi exact y(ti) serta selisih antara keduanya . . . 82

6.3 Perbandingan antara hasil perhitungan numerik lewat metode Runge Kutta dan hasil perhitungan dari solusi exact, yaitu persamaan (6.16) . . . 87

6.4 Hasil simulasi distribusi panas bergantung waktu dalam 1-dimensi. Kolom ke-2 adalah solusi analitik/exact, kolom ke-3 dan ke-5 adalah solusi numerik forward-difference. Ko-lom ke-4 dan ke-6 adalah selisih antara solusi analitik dan numerik . . . 112

6.5 Hasil simulasi distribusi panas bergantung waktu dalam 1-dimensi dengan metode backward-differencedimanak = 0, 01 . . . 116

6.6 Hasil simulasi distribusi panas bergantung waktu (t) dalam 1-dimensi dengan metode backward-difference dan Crank-Nicolson . . . 120

7.1 Hasil akhir elemen-elemen vektor x hingga iterasi ke-10 . . . 138

7.2 Hasil perhitungan norm2-selisih hingga iterasi ke-10 . . . 139

7.3 Hasil Iterasi Gauss-Seidel . . . 143

7.4 Hasil perhitungan iterasi Gauss-Seidel . . . 153

7.5 Hasil perhitungan iterasi Relaksasi denganω = 1, 25 . . . 153

9.1 Data suhu bawah permukaan tanah terhadap kedalaman . . . 189

9.2 Data suhu bawah permukaan tanah terhadap kedalaman . . . 194

9.3 Data ketinggian terhadap waktu dari planet X . . . 201

12.1 Koordinat Sumber Sinyal dan Waktu Tempuh Sinyal . . . 241

12.2 Data Gempa . . . 246

(18)

(19)

Pendahuluan

✍ Objektif :

⊲ Mengenal cara inisialisasi variabel. ⊲ Mengenal operasi matematika. ⊲ Mengenal fungsi-fungsi dasar. ⊲ Mengenal cara membuat grafik.

1.1 Inisialisasi variabel

Salah satu perbedaan utama antara komputer dan kalkulator adalah pemanfaatan variabel da-lam proses perhitungan. Kebanyakan kalkulator tidak menggunakan variabel dada-lam proses per-hitungan; sebaliknya, komputer sangat memanfaatkan variable dalam proses perhitungan.

Misalnya kita ingin mengalikan 2 dengan 3. Dengan kalkulator, langkah pertama yang ak-an kita lakukak-an adalah menekak-an tombol ak-angka 2, kemudiak-an diikuti menekak-an tombol _{×, lalu} menekan tombol angka 3, dan diakhiri dengan menekan tombol =; maka keluarlah hasilnya berupa angka 6. Kalau di komputer, proses perhitungan seperti ini dapat dilakukan dengan me-manfaatkan variabel. Pertama-tama kita munculkan sebuah variabel yang diinisialisasi1 _dengan

angka 2, misalnya A = 2. Kemudian kita munculkan variabel lain yang diinisialisasi dengan angka 3, misalnya_{B = 3. Setelah itu kita ketikkan A ∗ B; maka pada layar monitor akan tampil} angka 6. Bahkan kalau mau, hasil perhitungannya dapat disimpan dalam variabel yang lain lagi, misalnya kita ketiikan _{C = A ∗ B; maka hasil perhitungan, yaitu angka 6 akan disimpan} da-lam variableC. Script2matlab untuk melakukan proses perhitungan seperti itu adalah sebagai berikut

A = 2; B = 3; C = A * B

1_{inisialisasi adalah proses memberi nilai awal pada suatu variabel}

2_Script_{adalah daftar baris-baris perintah yang akan dikerjakan (di-eksekusi) oleh komputer}

(20)

Nama suatu variabel tidak harus hanya satu huruf, melainkan dapat berupa sebuah kata. Misalnya kita ingin menyatakan hukum Newton kedua, yaituF = ma, dimana m adalah massa, a adalah percepatan dan F adalah gaya. Maka, script matlab dapat ditulis seperti berikut ini

massa = 2; percepatan = 3;

gaya = massa * percepatan

Atau bisa jadi kita memerlukan variabel yang terdiri atas dua patah kata. Dalam hal ini, kedua kata tadi mesti dihubungkan dengan tanda underscore. Misalnya begini

besar_arus = 2; beda_potensial = 3;

nilai_hambatan = beda_potensial / besar_arus

Semua contoh di atas memperlihatkan perbedaan yang begitu jelas antara penggunaan kom-puter dan kalkulator dalam menyelesaikan suatu perhitungan. Saya akan tunjukkan perbedaan yang lebih tegas lagi pada bagian berikut ini.

1.2 Perhitungan yang berulang

Di dalam matlab, suatu variabel dapat diinisialisasi dengan urutan angka. Misalnya jika variabel t hendak diinisialisasi dengan sejumlah angka yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 dan 10, caranya sangat mudah, cukup dengan mengetikkan

t = 0:10;

Angka 0 pada script di atas merupakan nilai awal; sedangkan angka 10 adalah nilai akhir. Contoh lainnya, jika anda hanya menginginkan bilangan genap-nya saja, cukup ketikkan

t = 0:2:10;

Disini, angka 2 bertindak sebagai nilai interval dari 0 sampai 10. Sehingga angka-angka yg mun-cul hanyalah 0, 2, 4, 6, 8 dan 10. Andaikata anda menginginkan urutan angka yang terbalik, maka yang perlu anda lakukan adalah

t = 10:-2:0;

sehinggan angka yang muncul adalah 10, 8, 6, 4, 2 dan 0. Adakalanya proses perhitungan meminta kita untuk memulainya dari angka kurang dari nol, misalnya

t = -10:3:4;

maka angka-angka yang tersimpan pada variabel t adalah -10, -7, -4, -1 dan 2.

Dengan adanya kemampuan dan sekaligus kemudahan inisialisasi urutan angka seperti ini, maka memudahkan kita melakukan perhitungan yang berulang. Sebagai contoh, kita ingin mensimulasikan perubahan kecepatan mobil balap yang punya kemampuan akselerasi 2 m/dt2_.

Rumus gerak lurus berubah beraturan sangat memadai untuk maksud tersebut

(21)

Jika kita hendak mengamati perubahan kecepatan mobil balap dari detik pertama disaat sedang diam hingga detik ke-5, kita dapat menghitung perubahan tersebut setiap satu detik, yaitu

pada t = 1 _⇒ v1 = (0) + (2)(1) ⇒ 2m/dt

pada t = 2 _⇒ v2 = (0) + (2)(2) ⇒ 4m/dt

pada t = 3 _⇒ v3 = (0) + (2)(3) ⇒ 6m/dt

pada t = 4 _⇒ v4 = (0) + (2)(4) ⇒ 8m/dt

pada t = 5 _⇒ v5 = (0) + (2)(5) ⇒ 10m/dt

Script matlab untuk tujuan di atas adalah

a = 2; t = 1:5; vo = 0; v = vo + a * t

Jarak tempuh mobil juga dapat ditentukan oleh persamaan berikut s = vot +

1 2at

2 _(1.2)

Untuk menentukan perubahan jarak tempuh tersebut, script sebelumnya mesti ditambah satu baris lagi

1 a = 2;

2 t = 1:5;

3 vo = 0;

4 s = vo * t + 1/2 * a * t.^2

Ada hal penting yang perlu diperhatikan pada baris ke-4 di atas, yaitu penempatan tanda titik pada t.ˆ2. Maksud dari tanda titik adalah setiap angka yang tersimpan pada variabelt harus di-kuadratkan. Jika anda lupa menempatkan tanda titik, sehingga tertulis tˆ2, maka script tersebut tidak akan bekerja.

1.3 Mengenal cara membuat grafik

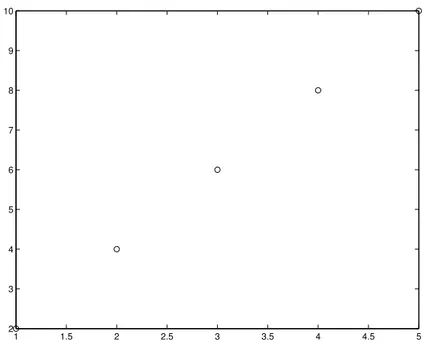
Seringkali suatu informasi lebih mudah dianalisis setelah informasi tersebut ditampilkan dalam bentuk graﬁk. Pada contoh mobil balap tadi, kita bisa menggambar data perubahan kecepatan mobil terhadap waktu dengan menambahkan satu baris lagi seperti ditunjukkan oleh script dibawah ini 1 a = 2; 2 t = 1:5; 3 vo = 0; 4 v = vo + a * t 5 plot(t,v,’o’)

Jika script tersebut di-run, akan muncul Gambar 1.1. Untuk melengkapi keterangan gambar, beberapa baris perlu ditambahkan

(22)

1 1.5 2 2.5 3 3.5 4 4.5 5 2 3 4 5 6 7 8 9 10

Gambar 1.1: Data perubahan kecepatan terhadap waktu

1 a = 2; 2 t = 1:5; 3 vo = 0; 4 v = vo + a * t; 5 plot(t,v,’o’); 6 xlabel(’Waktu (dt)’); 7 ylabel(’Kecepatan (m/dt)’)

8 title(’Data Kecepatan vs Waktu’)

1 1.5 2 2.5 3 3.5 4 4.5 5 2 3 4 5 6 7 8 9 10 Waktu (dt) Kecepatan (m/dt)

Data Kecepatan vs Waktu

(23)

1.4 Baris-baris pembuka

Ketika anda membuat script di komputer, anda mesti menyadari bahwa script yang sedang anda buat akan memodiﬁkasi isi memory komputer. Oleh karena itu saya menyarankan agar sebelum kalkulasi anda bekerja, maka anda harus pastikan bahwa memory komputer dalam keadaan bersih. Cara membersihkannya, di dalam matlab, adalah dengan menuliskan perintah clear. Alasan yang sama diperlukan untuk membersihkan gambar dari layar monitor. Untuk maksud ini, cukup dengan menuliskan perintah close. Sedangkan untuk membersihkan teks atau tulisan di layar monitor, tambahkan saja perintah clc. Saya biasa meletakkan ketiga perintah tersebut pada baris-baris awal sebagai pembukaan bagi suatu script matlab. Inilah contohnya,

1 clear 2 close 3 clc 4 5 a = 2; 6 t = 1:5; 7 vo = 0; 8 v = vo + a * t; 9 plot(t,v,’o’); 10 xlabel(’Waktu (dt)’); 11 ylabel(’Kecepatan (m/dt)’)

12 title(’Data Kecepatan vs Waktu’)

1.5 Membuat 2 grafik dalam satu gambar

Misalnya, sebuah gelombang dinyatakan oleh persamaan y = A sin(2πf t + θ)

dimana A = amplitudo; f = frekuensi; t = waktu; θ = sudut fase gelombang. Jika suatu gelombang beramplitudo 1 memiliki frekuensi tunggal 5 Hz dan sudut fase-nya nol, maka script untuk membuat graﬁk gelombang tersebut adalah

1 clc 2 clear 3 close 4 5 A = 1; % amplitudo 6 f = 5; % frekuensi

7 theta = 0; % sudut fase gelombang

8 t = 0:0.001:1; % t_awal = 0; t_akhir = 1; interval = 0.001

9 y = A * sin(2*pi*f*t + theta); % persamaan gelombang

10

11 plot(t,y) % menggambar grafik persamaan gelombang

Grafik di atas muncul karena ada fungsi plot(t,y) yang diletakkan dibaris paling akhir pada script. Modifikasi script perlu dilakukan untuk memberi penjelasan makna dari sumbu-x dan sumbu-y serta memberikan judul grafik

(24)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1

Gambar 1.3: Graﬁk gelombang berfrekuensi 5 Hz

1 clc 2 clear 3 close 4 5 A = 1; % amplitudo 6 f = 5; % frekuensi

7 theta = 0; % sudut fase gelombang

9 y = A * sin(2*pi*f*t + theta); % persamaan gelombang

10

11 plot(t,y) % menggambar grafik persamaan gelombang

12 xlabel(’Waktu, t (detik)’); % melabel sumbu-x

13 ylabel(’Amplitudo’); % melabel sumbu-y

14 title(’Gelombang berfrekuensi 5 Hz’); % judul grafik

Untuk memperbesar font judul graﬁk, tambahkan kata fontsize(14) pada title(), contohnya

title(’\fontsize{14} Gelombang berfrekuensi 5 Hz’); % judul grafik

Bila kita perlu menggambar dua buah graﬁk, contoh script berikut ini bisa digunakan

1 clc

2 clear

3 close

4

6

7 A1 = 1; % amplitudo gelombang 1

8 f1 = 5; % frekuensi gelombang 1

9 theta1 = 0; % sudut fase gelombang 1

10 y1 = A1 * sin(2*pi*f1*t + theta1); % persamaan gelombang 1

11

(25)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Waktu, t (detik) Amplitudo Gelombang berfrekuensi 5 Hz

Gambar 1.4: Graﬁk yang dilengkapi dengan keterangan sumbu-x dan sumbu-y serta judul

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 −1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1 Waktu, t (detik) Amplitudo Gelombang berfrekuensi 5 Hz

(26)

14 theta2 = pi/4; % sudut fase gelombang 2

16

17 figure

18

19 subplot(2,1,1)

20 plot(t,y1) % menggambar grafik persamaan gelombang 1

21 xlabel(’Waktu, t (detik)’);

22 ylabel(’Amplitudo’);

23 title(’\fontsize{14} Gelombang berfrekuensi 5 Hz’);

24

25 subplot(2,1,2)

29 title(’\fontsize{14} Gelombang berfrekuensi 3 Hz, fase pi/4’);

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 −1 −0.5 0 0.5 1 Waktu, t (detik) Amplitudo Gelombang berfrekuensi 5 Hz 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 −1 −0.5 0 0.5 1 Waktu, t (detik) Amplitudo

Gelombang berfrekuensi 3 Hz, fase pi/4

Gambar 1.6: Dua buah graﬁk dalam sebuah gambar

Sekarang, jika kita ingin melihat tampilan superposisi kedua gelombang di atas, maka script berikut ini bisa digunakan

1 clc

2 clear

3 close

4

6

9 theta1 = 0; % sudut fase gelombang 1

11

14 theta2 = pi/4; % sudut fase gelombang 2

(27)

16

17 y3 = y1 + y2; % superposisi gelombang

18

19 figure

20

21 subplot(3,1,1)

25 title(’\fontsize{14} Gelombang berfrekuensi 5 Hz’);

26

27 subplot(3,1,2)

31 title(’\fontsize{14} Gelombang berfrekuensi 3 Hz, fase pi/4’);

32

33 subplot(3,1,3)

34 plot(t,y3) % menggambar grafik superposisi gelombang

37 title(’\fontsize{14} Superposisi gelombang 5 Hz dan 3 Hz’);

0 0.2 0.4 0.6 0.8 1 −1 0 1 Waktu, t (detik) Amplitudo

Gelombang berfrekuensi 5 Hz

Gelombang berfrekuensi 3 Hz, fase pi/4

Superposisi gelombang 5 Hz dan 3 Hz

(28)

1.6 Latihan

1. Jarak tempuh mobil balap yang bergerak dengan percepatan 2 m/dt2 dari posisi diam ditentukan oleh rumus berikut

s = vot +

1 2at

2

Buatlah script untuk menggambarkan graﬁk jarak tempuh terhadap waktu dimulai dari t = 0 hingga t = 20 dt.

2. Sebuah elektron memasuki area yang dipengaruhi oleh medan listrik seperti gambar beri-kut dimana diketahui besar muatan elektron = 1,6_×10−19C, massa elektron = 9,11_×10−31

kg, kecepatan_{v = 3×10}6 _{m/dt, kuat medan listrik} _{E = 200 N/C , dan panjang plat ℓ =}

0,1 meter. Posisi koordinat elektron memenuhi persamaan

x = vt _{y = −}1 2 eE m t 2 _{dimana percepatan} _{a =} eE m

Buatlah script untuk menentukan variasi posisi elektron (x, y) terhadap waktu (t), mulai dari_{t = 0 detik hingga t = 3,33×10}−8_{detik dengan interval waktu 3,33}_×10−10_detik.

3. Berkali-kali bola ditendang dari depan gawang ke tengah lapangan oleh penjaga gawang yang sedang berlatih. Misalnya bola ditendang sedemikian rupa sehingga bola selalu ber-gerak dengan kecepatan awal 5 m/dt. Diketahui konstanta gravitasi adalah 9,8 m/dt2.

(a) Plot variasi ketinggian maksimum bola bila sudut tendangan bervariasi dari 30o

hing-ga 60odengan interval 5o. Persamaan untuk menghitung ketinggian maksimum ada-lah

hmaks=

v2 osin2α

2g (1.3)

(b) Plot variasi jangkauan maksimum bola bila sudut tendangan bervariasi dari 30o

hing-ga 60odengan interval 5o. Persamaan untuk menghitung jangkauan maksimum ada-lah

xmaks=

v2_osin 2α

g (1.4)

(29)

4. Sebuah bola konduktor pejal memiliki jari-jari sebesar 0,75 meter. Kuat medan listrik yang terukur pada permukaan kulit bola diketahui sebesar 890 N/C dan mengarah ke pusat bola. Dengan memanfaatkan hukum Gauss, tentukan:

(a) Tuliskan script matlab untuk menggambarkan kurva kuat medan listrik vs jarak, mulai dari 0 meter hingga 10 meter.

(b) Plot gambar kurva-nya

5. Tuliskan sebuah script untuk menggambar superposisi gelombang yang terbentuk dari 9 gelombang berfrekuensi 9 Hz, 18 Hz, 27 Hz, 35 Hz, 47 Hz, 57 Hz, 65 Hz, 74 Hz dan 82 Hz.

6. Sebuah kapasitor 8µF dan sebuah induktor sebesar 25 mH, masing-masing dihubungkan ke sumber tegangan bolak-balik 150 Volt dengan frekuensi 60 Hz.

(a) Tentukan nilai reaktansi kapasitif pada rangkaian (a); dan reaktansi induktif pada rangkaian (b).

(b) Tuliskan script matlab untuk menggambarkan kurva arus dan tegangan pada rangka-ian (a); kemudrangka-ian plot gambar kurva-nya.

(c) Tuliskan script matlab untuk menggambarkan kurva arus dan tegangan pada rangka-ian (b); kemudrangka-ian plot gambar kurva-nya.

7. Muatan Q1 sebesar 4µC terletak pada x = -1; sementara Q2 = 4µC terletak pada x = 1.

Buatlah script matlab untuk tujuan:

(a) menghitung medan listrik pada x = -2

(b) menghitung medan listrik pada x = 0 (cek: dititik ini, medannya harus NOL)

(c) menghitung medan listrik pada x = 2 (cek: besar medan harus sesuai dengan point pertanyaan (a))

(d) menghitung medan listrik pada -1< x < 1 dengan interval 0.1

(e) plot kurva perhitungan di atas. (cek: nilai medan terkecil ada di x = 0; dan nilai medan meningkat ketika mendekati x = -1 atau x = 1)

(30)

(g) plot kurva perhitungan di atas. (cek: nilai medan harus meningkat ketika mendekati x = -1)

(h) menghitung medan listrik pada 1< x < 10 dengan interval 0.1

(i) plot kurva perhitungan di atas. (cek: nilai medan harus meningkat ketika mendekati x = 1)

(j) plot kurva medan listrik dari x = -10 hingga x = 10 dengan interval 0.1

(a) plot kurva medan listrik dari x = -10 hingga x = 10 dengan interval 0.1

(b) menghitung medan listrik pada x = 0 (cek: dititik ini, medannya TIDAK NOL; dima-nakah posisi yang medannya NOL ?)

(c) mencari titik x yang medan-nya nol pada -1< x < 1 (d) mencari titik-titik x yang medannya bernilai 20000

(a) menghitung potensial listrik pada x = -2 (b) menghitung potensial listrik pada x = 0

(c) menghitung potensial listrik pada x = 2 (cek: besar potensial harus sama dengan point pertanyaan (a))

(d) menghitung medan listrik pada -1< x < 1 dengan interval 0.1

(e) plot kurva perhitungan di atas. (cek: nilai potensial listrik terkecil ada di x = 0; dan nilai potensial listrik meningkat ketika mendekati x = -1 atau x = 1)

(f) menghitung potensial listrik pada -10< x < -1 dengan interval 0.1

(g) plot kurva perhitungan di atas. (cek: nilai potensial listrik harus meningkat ketika mendekati x = -1)

(h) menghitung potensial listrik pada 1< x < 10 dengan interval 0.1

(i) plot kurva perhitungan di atas. (cek: nilai potensial harus meningkat ketika mende-kati x = 1)

(j) plot kurva potensial listrik dari x = -10 hingga x = 10 dengan interval 0.1

10. Muatan Q1 sebesar 4µC terletak pada x = -1; sementara Q2 = -20µC terletak pada x = 1.

(a) plot kurva potensial listrik dari x = -10 hingga x = 10 dengan interval 0.1 (b) menghitung potensial listrik pada x = 0

(31)

11. Sebuah bola pejal memiliki jari-jari sebesar 0,75 meter. Kuat medan listrik yang terukur pada permukaan bola diketahui sebesar 890 N/C dan mengarah keluar bola. Dengan memanfaatkan hukum Gauss, tentukan:

(a) Total muatan yang terdapat pada kulit bola (b) Apakah muatan-nya positif atau negatif ?

(c) Kuat medan listrik pada jarak 1 meter dari pusat bola (d) Kuat medan listrik pada jarak 0,5 meter dari pusat bola

(e) Buatlah script matlab untuk menggambarkan kurva kuat medan listrik terhadap jarak mulai dari pusat bola sampai ke jarak 3 meter

(32)

(33)

Matrik dan Komputasi

✍ Objektif :

⊲ Mengenalkan matrik, vektor dan jenis-jenis matrik.

⊲ Mendeklarasikan elemen-elemen matrik ke dalam memori komputer. ⊲ Mengenalkan operasi penjumlahan dan perkalian matrik.

⊲ Membuat script operasi matrik.

2.1 Mengenal matrik

Notasi suatu matrik berukuran n x m ditulis dengan huruf besar dan dicetak tebal, misalnya An×m. Hurufn menyatakan jumlah baris, dan huruf m jumlah kolom. Suatu matrik tersusun

atas elemen-elemen yang dinyatakan dengan huruf kecil lalu diikuti oleh angka-angka indeks, misalnya aij. Indeks i menunjukkan posisi baris ke-i dan indeks j menentukan posisi kolom

ke-j. A= (aij) =       a11 a12 . . . a1m a21 a22 . . . a2m .. . ... ... an1 an2 . . . anm       (2.1)

Pada matrik ini,a11,a12, ...,a1madalah elemen-elemen yang menempati baris pertama.

Semen-taraa12,a22, ...,an2adalah elemen-elemen yang menempati kolom kedua.

Contoh 1: Matrik A2×3 A= " 3 8 5 6 4 7 #

dimana masing-masing elemennya adalah a11 = 3, a12 = 8, a13 = 5, a21 = 6, a22 = 4, dan

a23= 7.

(34)

Contoh 2: Matrik B3×2 B=    1 3 5 9 2 4   

dimana masing-masing elemennya adalah b11 = 1, b12 = 3, b21 = 5, b22 = 9, b31 = 2, dan

b32= 4.

2.2 Vektor-baris dan vektor-kolom

Notasi vektor biasanya dinyatakan dengan huruf kecil dan dicetak tebal. Suatu matrik dina-makan vektor-baris berukuranm, bila hanya memiliki satu baris dan m kolom, yang dinyatakan sebagai berikut a=ha11 a12 . . . a1m i =ha1 a2 . . . am i (2.2) Sedangkan suatu matrik dinamakan vektor-kolom berukurann, bila hanya memiliki satu kolom dann baris, yang dinyatakan sebagai berikut

a=       a11 a21 .. . an1       =       a1 a2 .. . an       (2.3)

2.3 Inisialisasi matrik dalam memori komputer

Sebelum dilanjutkan, saya sarankan agar anda mencari tahu sendiri bagaimana cara membuat

m-filedi Matlab dan bagaimana cara menjalankannya. Karena semua source code yang terdapat dalam buku ini ditulis dalam m-file. Walaupun sangat mudah untuk melakukan copy-paste, namun dalam upaya membiasakan diri menulis source code di m-file, saya anjurkan anda menulis ulang semuanya.

Dalam Matlab terdapat 3 cara inisialisasi matrik. Cara pertama1_{, sesuai dengan Contoh 1,}

adalah 1 clear all 2 clc 3 4 A(1,1) = 3; 5 A(1,2) = 8; 6 A(1,3) = 5; 7 A(2,1) = 6; 8 A(2,2) = 4; 9 A(2,3) = 7; 10 A

Sedangkan untuk matrik B3×2, sesuai Contoh 2 adalah

1_{Cara ini bisa diterapkan pada bahasa C, Fortran, Pascal, Delphi, Java, Basic, dll. Sementara cara kedua dan cara}

(35)

1 clear all 2 clc 3 4 B(1,1) = 1; 5 B(1,2) = 3; 6 B(2,1) = 5; 7 B(2,2) = 9; 8 B(3,1) = 2; 9 B(3,2) = 4; 10 B

Cara kedua relatif lebih mudah dan benar-benar merepresentasikan dimensi matriknya, dimana jumlah baris dan jumlah kolom terlihat dengan jelas.

1 clear all 2 clc 3 4 A=[ 3 8 5 5 6 4 7 ]; 6 7 B=[ 1 3 8 5 9 9 2 4 ];

Cara ketiga jauh lebih singkat, namun tidak menunjukkan dimensi matrik lantaran ditulis hanya dalam satu baris.

1 clear all 2 clc 3 4 A=[ 3 8 5 ; 6 4 7 ]; 5 B=[ 1 3 ; 5 9 ; 2 4]; 2.4 Macam-macam matrik 2.4.1 Matrik transpose

Operasi transpose terhadap suatu matrik akan menukar elemen kolom menjadi elemen-elemen baris. Notasi matrik tranpose adalah AT atau At.

Contoh 3: Operasi transpose terhadap matrik A

A= " 3 8 5 6 4 7 # AT =    3 6 8 4 5 7   

Dengan Matlab, operasi transpose cukup dilakukan dengan menambahkan tanda petik tunggal di depan nama matriknya

1 clear all

(36)

3 4 A=[ 3 8 5 5 6 4 7 ]; 6 7 AT = A’; 2.4.2 Matrik bujursangkar

Matrik bujursangkar adalah matrik yang jumlah baris dan jumlah kolomnya sama.

Contoh 4: Matrik bujursangkar berukuran 3x3 atau sering juga disebut matrik bujursangkar orde 3 A=    1 3 8 5 9 7 2 4 6    2.4.3 Matrik simetrik

Matrik simetrik adalah matrik bujursangkar yang elemen-elemen matrik transpose-nya bernilai sama dengan matrik asli-nya.

Contoh 5: Matrik simetrik

A=       2 _{−3 7} 1 −3 5 _{6 −2} 7 6 9 8 1 _{−2 8 10}       AT =       2 _{−3 7} 1 −3 5 _{6 −2} 7 6 9 8 1 _{−2 8 10}       2.4.4 Matrik diagonal

Matrik diagonal adalah matrik bujursangkar yang seluruh elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonalnya.

Contoh 6: Matrik diagonal orde 3

A=    11 0 0 0 29 0 0 0 61    2.4.5 Matrik identitas

Matrik identitas adalah matrik bujursangkar yang semua elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonal yang seluruhnya bernilai 1.

Contoh 7: Matrik identitas orde 3

I=    1 0 0 0 1 0 0 0 1   

(37)

2.4.6 Matrik upper-triangular

Matrik upper-tringular adalah matrik bujursangkar yang seluruh elemen dibawah elemen dia-gonal bernilai 0 (nol).

Contoh 8: Matrik upper-triangular

A=       3 6 2 1 0 4 1 5 0 0 8 7 0 0 0 9       2.4.7 Matrik lower-triangular

Matrik lower-tringular adalah matrik bujursangkar yang seluruh elemen diatas elemen diagonal bernilai 0 (nol).

Contoh 9: Matrik lower-triangular

A=       12 0 0 0 32 ₋₂ 0 0 8 7 11 0 −5 10 6 9       2.4.8 Matrik tridiagonal

Matrik tridiagonal adalah matrik bujursangkar yang seluruh elemen bukan 0 (nol) berada dise-kitar elemen diagonal, sementara elemen lainnya bernilai 0 (nol).

Contoh 10: Matrik tridiagonal

A=       3 6 0 0 2 −4 1 0 0 5 _{8 −7} 0 0 3 9      

2.4.9 Matrik diagonal dominan

Matrik diagonal dominan adalah matrik bujursangkar yang memenuhi

|aii| > n

X

j=1,j6=i

|aij| (2.4)

dimanai=1,2,3,..n. Coba perhatikan matrik-matrik berikut ini

A=    7 2 0 3 5 −1 0 5 −6    B=    6 4 ₋₃ 4 ₋₂ 0 −3 0 1   

(38)

Pada elemen diagonalaii matrik A,|7| > |2| + |0|, lalu |5| > |3| + | − 1|, dan | − 6| > |5| + |0|.

Maka matrik A disebut matrik diagonal dominan. Sekarang perhatikan elemen diagonal matrik B,_{|6| < |4| + | − 3|, | − 2| < |4| + |0|, dan |1| < | − 3| + |0|. Dengan demikian, matrik B bukan} matrik diagonal dominan.

2.4.10 Matrik positive-definite

Suatu matrik dikatakan positive-definite bila matrik tersebut simetrik dan memenuhi

xTAx> 0 (2.5)

Contoh 11: Diketahui matrik simetrik berikut

A=    2 ₋₁ 0 −1 2 ₋₁ 0 ₋₁ 2    untuk menguji apakah matrik A bersifat positive-definite, maka

xTAx = hx1 x2 x3 i    2 ₋₁ 0 −1 2 ₋₁ 0 ₋₁ 2       x1 x2 x3    = hx1 x2 x3 i    2x1− x2 −x1+ 2x2− x3 −x2+ 2x3    = 2x2₁_{− 2x}1x2+ 2x22− 2x2x3+ 2x23 = x2₁+ (x2₁_{− 2x}1x2+ x22) + (x22− 2x2x3+ x23) + x23 = x2₁+ (x1− x2)2+ (x2− x3)2+ x23

Dari sini dapat disimpulkan bahwa matrik A bersifat positive-definite, karena memenuhi x2₁+ (x1− x2)2+ (x2− x3)2+ x23 > 0

kecuali jikax1=x2=x3=0.

2.5 Operasi matematika

2.5.1 Penjumlahan matrik

Operasi penjumlahan pada dua buah matrik hanya bisa dilakukan bila kedua matrik tersebut berukuran sama. Misalnya matrik C2×3

C= "

9 5 3 7 2 1 #

(39)

dijumlahkan dengan matrik A2×3, lalu hasilnya (misalnya) dinamakan matrik D2×3 D= A + C D = " 3 8 5 6 4 7 # + " 9 5 3 7 2 1 # = " 3 + 9 8 + 5 5 + 3 6 + 7 4 + 2 7 + 1 # = " 12 13 8 13 6 8 #

Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi penjumlahan antara matrik A2×3 dan C2×3, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik

tersebut, yaitu " d11 d12 d13 d21 d22 d23 # = " a11+ c11 a12+ c12 a13+ c13 a21+ c21 a22+ c22 a23+ c23 #

Dijabarkan satu persatu sebagai berikut

d11= a11+ c11 d12= a12+ c12 d13= a13+ c13 (2.6) d21= a21+ c21 d22= a22+ c22 d23= a23+ c23

Dari sini dapat diturunkan sebuah rumus umum penjumlahan dua buah matrik

dij = aij+ cij (2.7)

dimanai=1,2 dan j=1,2,3. Perhatikan baik-baik! Batas i hanya sampai angka 2 sementara batasj sampai angka 3. Kemampuan anda dalam menentukan batas indeks sangat penting dalam dunia programming.

2.5.2 Komputasi penjumlahan matrik

Berdasarkan contoh operasi penjumlahan di atas, indeks j pada persamaan (2.7) lebih cepat berubah dibanding indeksi sebagaimana ditulis pada 3 baris pertama dari Persamaan (2.6),

d11= a11+ c11

d12= a12+ c12

(40)

Jelas terlihat, ketika indeks i masih bernilai 1, indeks j sudah berubah dari nilai 1 sampai 3. Hal ini membawa konsekuensi pada script pemrograman, dimana looping untuk indeksj harus diletakkan di dalam looping indeksi. Aturan mainnya adalah yang looping-nya paling cepat harus diletakkan paling dalam; sebaliknya, looping terluar adalah looping yang indeksnya paling jarang berubah.

Bila anda masih belum paham terhadap kalimat yang dicetak tebal, saya akan berikan contoh

source codedasar yang nantinya akan kita optimasi selangkah demi selangkah. OK, kita mulai dari source code paling mentah berikut ini.

1 clear all

2 clc

3

4 A=[3 8 5; 6 4 7]; % inisialisasi matrik A

5

6 C=[9 5 3; 7 2 1]; % inisialisasi matrik B

7

8 % ---proses penjumlahan

matrik----9 D(1,1)=A(1,1)+C(1,1); 10 D(1,2)=A(1,2)+C(1,2); 11 D(1,3)=A(1,3)+C(1,3); 12 D(2,1)=A(2,1)+C(2,1); 13 D(2,2)=A(2,2)+C(2,2); 14 D(2,3)=A(2,3)+C(2,3); 15

16 % ---menampilkan matrik A, C dan

D----17 A

18 C

19 D

Tanda % berfungsi untuk memberikan komentar atau keterangan. Komentar atau keterangan tidak akan diproses oleh Matlab. Saya yakin anda paham dengan logika yang ada pada bagian % —proses penjumlahan matrik—- dalam source code di atas. Misalnya pada baris ke-9, elemen d11adalah hasil penjumlahan antara elemena11danc11, sesuai dengan baris pertama Persamaan

2.6.

Tahap pertama penyederhanaan source code dilakukan dengan menerapkan perintah for

-enduntuk proses looping. Source code tersebut berubah menjadi 1 clear all

2 clc

3

5

7

matrik----9 for j=1:3 10 D(1,j)=A(1,j)+C(1,j); 11 end 12 13 for j=1:3 14 D(2,j)=A(2,j)+C(2,j); 15 end

(41)

16

D----18 A

19 C

20 D

Pada baris ke-9 dan ke-13, saya mengambil hurufj sebagai nama indeks dimana j bergerak dari 1 sampai 3. Coba anda pikirkan, mengapaj hanya bergerak dari 1 sampai 3?

Modiﬁkasi tahap kedua adalah sebagai berikut 1 clear all

2 clc

3

5

7

matrik----9 i=1 10 for j=1:3 11 D(i,j)=A(i,j)+C(i,j); 12 end 13 14 i=2 15 for j=1:3 16 D(i,j)=A(i,j)+C(i,j); 17 end 18

D----20 A

21 C

22 D

Saya gunakan indeks i pada baris ke-9 dan ke-14 yang masing-masing berisi angka 1 dan 2. Dengan begitu indeks i bisa menggantikan angka 1 dan 2 yang semula ada di baris ke-11 dan ke-16. Nah sekarang coba anda perhatikan, statemen pada baris ke-10, ke-11 dan ke-12 sama persis dengan statemen pada baris ke-15, ke-16 dan ke-17, sehingga mereka bisa disatukan kedalam sebuah looping yang baru dimanai menjadi nama indeksnya.

1 clear all

2 clc

3

5

7

matrik----9 for i=1:2 10 for j=1:3 11 D(i,j)=A(i,j)+C(i,j); 12 end 13 end 14

(42)

17 C

18 D

Coba anda pahami dari baris ke-9, mengapa indeksi hanya bergerak dari 1 sampai 2?

Source code di atas memang sudah tidak perlu dimodiﬁkasi lagi, namun ada sedikit saran untuk penulisan looping bertingkat dimana sebaiknya looping terdalam ditulis agak menjorok kedalam seperti berikut ini

1 clear all

2 clc

3

5

7

matrik----9 for i=1:2 10 for j=1:3 11 D(i,j)=A(i,j)+C(i,j); 12 end 13 end 14

D----16 A

17 C

18 D

Sekarang anda lihat bahwa looping indeksj ditulis lebih masuk kedalam dibandingkan looping indeksi. Semoga contoh ini bisa memperjelas aturan umum pemrograman dimana yang lo-oping-nya paling cepat harus diletakkan paling dalam; sebaliknya, looping terluar adalah

loopingyang indeksnya paling jarang berubah. Dalam contoh ini looping indeks j bergerak lebih cepat dibanding looping indeksi.

2.5.3 Perkalian matrik

Operasi perkalian dua buah matrik hanya bisa dilakukan bila jumlah kolom matrik pertama sama dengan jumlah baris matrik kedua. Jadi kedua matrik tersebut tidak harus berukuran sama seperti pada penjumlahan dua matrik. Misalnya matrik A2×3 dikalikan dengan matrik

B3×2, lalu hasilnya (misalnya) dinamakan matrik E2×2

(43)

E = " 3 8 5 6 4 7 #    1 3 5 9 2 4    = " 3.1 + 8.5 + 5.2 3.3 + 8.9 + 5.4 6.1 + 4.5 + 7.2 6.3 + 4.9 + 7.4 # = " 53 101 40 82 #

Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi perkalian antara ma-trik A2×3dan B3×2, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik

terse-but, yaitu " e11 e12 e21 e22 # = " a11.b11+ a12.b21+ a13.b31 a11.b12+ a12.b22+ a13.b32 a21.b11+ a22.b21+ a23.b31 a21.b12+ a22.b22+ a23.b32 #

Bila dijabarkan, maka elemen-elemen matrik E2×2adalah

e11= a11.b11+ a12.b21+ a13.b31 (2.8)

e12= a11.b12+ a12.b22+ a13.b32 (2.9)

e21= a21.b11+ a22.b21+ a23.b31 (2.10)

e22= a21.b12+ a22.b22+ a23.b32 (2.11)

Sejenak, mari kita amati perubahan pasangan angka-angka indeks yang mengiringi elemene, elemena dan elemen b mulai dari persamaan (2.8) sampai persamaan (2.11). Perhatikan peru-bahan angka-indeks-pertama pada elemene seperti berikut ini

e1.. = ..

e2.. = ..

Pola perubahan yang sama akan kita dapati pada angka-indeks-pertama dari elemena e1.. = a1...b...+ a1...b...+ a1...b...

e1.. = a1...b...+ a1...b...+ a1...b...

e2.. = a2...b...+ a2...b...+ a2...b...

(44)

polanya sama

ei.. = ai...b...+ ai...b...+ ai...b...

dimana i bergerak mulai dari angka 1 hingga angka 2, atau kita nyatakan i=1,2. Selanjut-nya, masih dari persamaan (2.8) sampai persamaan (2.11), marilah kita perhatikan perubahan angka-indeks-kedua pada elemene dan elemen b,

ei1= ai...b..1+ ai...b..1+ ai...b..1

ei2= ai...b..2+ ai...b..2+ ai...b..2

ei1= ai...b..1+ ai...b..1+ ai...b..1

ei2= ai...b..2+ ai...b..2+ ai...b..2

Dengan demikian kita bisa mencantumkan hurufj sebagai pengganti angka-angka indeks yang polanya sama

eij = ai...b..j+ ai...b..j+ ai...b..j

dimana j bergerak mulai dari angka 1 hingga angka 2, atau kita nyatakan j=1,2. Selanjut-nya, masih dari persamaan (2.8) sampai persamaan (2.11), mari kita perhatikan perubahan angka-indeks-kedua elemen a dan angka-indeks-pertama elemen b, dimana kita akan dapati pola sebagai berikut

eij = ai1.b1j + ai2.b2j+ ai3.b3j

(45)

dimanak bergerak mulai dari angka 1 hingga angka 3, atau kita nyatakan k=1,2,3. eij = aik.bkj+ aik.bkj+ aik.bkj

eij = aik.bkj+ aik.bkj+ aik.bkj

Kemudian secara sederhana dapat ditulis sebagai berikut

eij = aik.bkj+ aik.bkj+ aik.bkj (2.12)

Selanjutnya dapat ditulis pula formula berikut

eij = 3

X

k=1

aikbkj (2.13)

dimanai=1,2; j=1,2; dan k=1,2,3.

Berdasarkan contoh ini, maka secara umum bila ada matrik An×myang dikalikan dengan matrik

Bm×p, akan didapatkan matrik En×p dimana elemen-elemen matrik E memenuhi

eij = m

X

k=1

aikbkj (2.14)

dengani=1,2,. . . ,n; j=1,2. . . ,p; dan k=1,2. . . ,m.

2.5.4 Komputasi perkalian matrik

Mari kita mulai lagi dari source code paling dasar dari operasi perkalian matrik sesuai dengan contoh di atas. 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 B = [1 3; 5 9; 2 4]; % inisialisasi matrik B 6

7 % ---proses perkalian

matrik----8 E(1,1)=A(1,1)*B(1,1)+A(1,2)*B(2,1)+A(1,3)*B(3,1);

9 E(1,2)=A(1,1)*B(1,2)+A(1,2)*B(2,2)+A(1,3)*B(3,2);

10 E(2,1)=A(2,1)*B(1,1)+A(2,2)*B(2,1)+A(2,3)*B(3,1);

11 E(2,2)=A(2,1)*B(1,2)+A(2,2)*B(2,2)+A(2,3)*B(3,2);

12

13 % ---menampilkan matrik A, B dan

E----14 A

15 B

(46)

Sejenak, mari kita amati dengan cermat statemen dari baris ke-9 sampai ke-12 sambil dikaitkan dengan bentuk umum penulisan indeks pada perkalian matrik yaitu

eij = aik.bkj+ aik.bkj+ aik.bkj (2.15)

Dari sana ada 4 point yang perlu dicatat:

• elemene memiliki indeks i dan indeks j dimana indeks j lebih cepat berubah dibanding indeksi.

• pada baris statemen ke-8 sampai ke-11 ada tiga kali operasi perkalian dan dua kali operasi penjumlahan yang semuanya melibatkan indeksi, indeks j dan indeks k. Namun indeks k selalu berubah pada masing-masing perkalian. Jadi indeksk paling cepat berubah diban-ding indeksi dan indeks j.

• elemena memiliki indeks i dan indeks k dimana indeks k lebih cepat berubah dibanding indeksi.

• elemenb memiliki indeks k dan indeks j dimana indeks k lebih cepat berubah dibanding indeksj.

Tahapan modiﬁkasi source code perkalian matrik tidak semudah penjumlahan matrik. Dan mengajarkan logika dibalik source code perkalian matrik jauh lebih sulit daripada sekedar me-modiﬁkasi source code tersebut. Tapi akan saya coba semampu saya lewat tulisan ini walau harus perlahan-lahan. Mudah-mudahan mudah untuk dipahami.

Saya mulai dengan memecah operasi pada statemen baris ke-8 yang bertujuan menghitung nilaiE(1, 1) 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 B = [1 3; 5 9; 2 4]; % inisialisasi matrik B 6

matrik----8 % ---E(1,1) dihitung 3 kali

9 E(1,1)=A(1,1)*B(1,1);

10 E(1,1)=E(1,1)+A(1,2)*B(2,1);

11 E(1,1)=E(1,1)+A(1,3)*B(3,1);

12

13 % ---E(1,2); E(2,1); dan E(2,2) masih seperti semula

14 E(1,2)=A(1,1)*B(1,2)+A(1,2)*B(2,2)+A(1,3)*B(3,2);

15 E(2,1)=A(2,1)*B(1,1)+A(2,2)*B(2,1)+A(2,3)*B(3,1);

16 E(2,2)=A(2,1)*B(1,2)+A(2,2)*B(2,2)+A(2,3)*B(3,2);

17

E----19 A

20 B

21 E

Agar baris ke-9 memiliki pola yang sama dengan baris ke-11 dan ke-12, upaya yang dilakukan adalah

(47)

1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 B = [1 3; 5 9; 2 4]; % inisialisasi matrik B 6

matrik----8 % ---E(1,1) dihitung 3 kali

9 E(1,1)=0;

10 E(1,1)=E(1,1)+A(1,1)*B(1,1);

11 E(1,1)=E(1,1)+A(1,2)*B(2,1);

12 E(1,1)=E(1,1)+A(1,3)*B(3,1);

13

15 E(1,2)=A(1,1)*B(1,2)+A(1,2)*B(2,2)+A(1,3)*B(3,2);

16 E(2,1)=A(2,1)*B(1,1)+A(2,2)*B(2,1)+A(2,3)*B(3,1);

17 E(2,2)=A(2,1)*B(1,2)+A(2,2)*B(2,2)+A(2,3)*B(3,2);

18

E----20 A

21 B

22 E

Dari sini kita bisa munculkan indeksk 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 B = [1 3; 5 9; 2 4]; % inisialisasi matrik B 6

matrik----8 E(1,1)=0;

9 for k=1:3 % k bergerak dari 1 sampai 3

10 E(1,1)=E(1,1)+A(1,k)*B(k,1);

11 end

12

14 E(1,2)=A(1,1)*B(1,2)+A(1,2)*B(2,2)+A(1,3)*B(3,2);

15 E(2,1)=A(2,1)*B(1,1)+A(2,2)*B(2,1)+A(2,3)*B(3,1);

16 E(2,2)=A(2,1)*B(1,2)+A(2,2)*B(2,2)+A(2,3)*B(3,2);

17

E----19 A

20 B

21 E

Kemudian cara yang sama dilakukan padaE(1, 2), E(2, 1), dan E(2, 2). Anda mesti cermat dan hati-hati dalam menulis angka-angka indeks!!!

(48)

7 % ---proses perkalian matrik----8 E(1,1)=0; 9 for k=1:3 10 E(1,1)=E(1,1)+A(1,k)*B(k,1); 11 end 12 13 E(1,2)=0; 14 for k=1:3 15 E(1,2)=E(1,2)+A(1,k)*B(k,2); 16 end 17 18 E(2,1)=0; 19 for k=1:3 20 E(2,1)=E(2,1)+A(2,k)*B(k,1); 21 end 22 23 E(2,2)=0; 24 for k=1:3 25 E(2,2)=E(2,2)+A(2,k)*B(k,2); 26 end 27

E----29 A

30 B

31 E

Inisialisasi elemen-elemen matrik E dengan angka nol, bisa dilakukan diawal proses perkalian yang sekaligus memunculkan indeksi dan j untuk elemen E

matrik----8 for i=1:2 % i bergerak dari 1 sampai 2

9 for j=1:2 % j bergerak dari 1 sampai 2

10 E(i,j)=0; 11 end 12 end 13 14 for k=1:3 15 E(1,1)=E(1,1)+A(1,k)*B(k,1); 16 end 17 18 for k=1:3 19 E(1,2)=E(1,2)+A(1,k)*B(k,2); 20 end 21 22 for k=1:3 23 E(2,1)=E(2,1)+A(2,k)*B(k,1); 24 end 25 26 for k=1:3 27 E(2,2)=E(2,2)+A(2,k)*B(k,2); 28 end 29

(49)

E----31 A

32 B

33 E

Sekarang coba anda perhatikan statemen pada baris ke-15 dan ke-19, lalu bandingkan indeks i dan indeks j pada elemen E. Indeks mana yang berubah? Ya. Jawabannya adalah indeks j. Dengan demikian kita bisa munculkan indeksj

10 E(i,j)=0; 11 end 12 end 13 14 j=1; 15 for k=1:3 16 E(1,j)=E(1,j)+A(1,k)*B(k,j); 17 end 18 19 j=2; 20 for k=1:3 21 E(1,j)=E(1,j)+A(1,k)*B(k,j); 22 end 23 24 for k=1:3 25 E(2,1)=E(2,1)+A(2,k)*B(k,1); 26 end 27 28 for k=1:3 29 E(2,2)=E(2,2)+A(2,k)*B(k,2); 30 end 31

E----33 A

34 B

35 E

Lihatlah, statemen dari baris ke-15 sampai ke-17 memiliki pola yang sama dengan statemen dari baris ke-20 sampai ke-22, sehingga mereka bisa disatukan kedalam looping indeksj 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 B = [1 3; 5 9; 2 4]; % inisialisasi matrik B 6

(50)

9 for j=1:2 % j bergerak dari 1 sampai 2 10 E(i,j)=0; 11 end 12 end 13 14 for j=1:2 15 for k=1:3 16 E(1,j)=E(1,j)+A(1,k)*B(k,j); 17 end 18 end 19 20 for k=1:3 21 E(2,1)=E(2,1)+A(2,k)*B(k,1); 22 end 23 24 for k=1:3 25 E(2,2)=E(2,2)+A(2,k)*B(k,2); 26 end 27

E----29 A

30 B

31 E

Sekarang coba sekali lagi anda perhatikan statemen pada baris ke-21 dan ke-25, lalu bandingkan indeksi dan indeks j pada elemen E. Indeks mana yang berubah? Ya. Jawabannya tetap indeks j. Dengan demikian kita bisa munculkan juga indeks j disana

10 E(i,j)=0; 11 end 12 end 13 14 for j=1:2 15 for k=1:3 16 E(1,j)=E(1,j)+A(1,k)*B(k,j); 17 end 18 end 19 20 j=1; 21 for k=1:3 22 E(2,j)=E(2,j)+A(2,k)*B(k,j); 23 end 24 25 j=2; 26 for k=1:3 27 E(2,j)=E(2,j)+A(2,k)*B(k,j); 28 end 29

(51)

E----31 A

32 B

33 E

Cermatilah, statemen dari baris ke-21 sampai ke-23 memiliki pola yang sama dengan statemen dari baris ke-25 sampai ke-27, sehingga mereka pun bisa disatukan kedalam looping indeksj

10 E(i,j)=0; 11 end 12 end 13 14 for j=1:2 15 for k=1:3 16 E(1,j)=E(1,j)+A(1,k)*B(k,j); 17 end 18 end 19 20 for j=1:2 21 for k=1:3 22 E(2,j)=E(2,j)+A(2,k)*B(k,j); 23 end 24 end 25

E----27 A

28 B

29 E

Akhirnya kita sampai pada bagian akhir tahapan modiﬁkasi. Perhatikan baris ke-16 dan ke-22. Indeksi pada elemen E dan A bergerak dari 1 ke 2, sehingga indeks i bisa dimunculkan

10 E(i,j)=0; 11 end 12 end 13 14 i=1; 15 for j=1:2

(52)

16 for k=1:3 17 E(i,j)=E(i,j)+A(i,k)*B(k,j); 18 end 19 end 20 21 i=2; 22 for j=1:2 23 for k=1:3 24 E(i,j)=E(i,j)+A(i,k)*B(k,j); 25 end 26 end 27

E----29 A

30 B

31 E

Sekarang, statemen dari baris ke-15 sampai ke-19 memiliki pola yang sama dengan statemen dari baris ke-22 sampai ke-26. Mereka bisa disatukan oleh looping indeksi

matrik----8 for i=1:2 9 for j=1:2 10 E(i,j)=0; 11 end 12 end 13 14 for i=1:2 15 for j=1:2 16 for k=1:3 17 E(i,j)=E(i,j)+A(i,k)*B(k,j); 18 end 19 end 20 end 21

E----23 A

24 B

25 E

Inilah hasil akhir dari tahapan-tahapan modiﬁkasi yang selanjutnya saya sebut sebagai proses optimasi. Upaya yang baru saja saya perlihatkan, sebenarnya penuh dengan jebakan-jebakan kesalahan, terutama jika anda kurang cermat membaca indeks dan pola. Upaya seperti itu memerlukan konsentrasi dan perhatian yang tidak sebentar. Upaya semacam itu tidak semudah meng-copy hasil akhir optimasi. Walaupun bisa di-copy, namun saya menyarankan agar anda mencoba melakukan proses optimasi itu sekali lagi di komputer tanpa melihat catatan ini dan tanpa bantuan orang lain. Kalau anda gagal, cobalah berﬁkir lebih keras untuk mencari jalan keluarnya. Jika masih tetap gagal, silakan lihat catatan ini sebentar saja sekedar untuk mencari

(53)

tahu dimana letak kesalahannya. Hanya dengan cara begitu ilmu programming ini akan bisa menyatu pada diri anda.

2.5.5 Perkalian matrik dan vektor-kolom

Operasi perkalian antara matrik dan vektor-kolom sebenarnya sama saja dengan perkalian an-tara dua matrik. Hanya saja ukuran vektor-kolom boleh dibilang spesial yaitum x 1, dimana m merupakan jumlah baris sementara jumlah kolomnya hanya satu. Misalnya matrik A, pada con-toh 1, dikalikan dengan vektor-kolom x yang berukuran3 x 1 atau disingkat dengan mengatakan vektor-kolom x berukuran3, lalu hasilnya (misalnya) dinamakan vektor-kolom y

y= Ax y = " 3 8 5 6 4 7 #    2 3 4    = " 3.2 + 8.3 + 5.4 6.2 + 4.3 + 7.4 # = " 50 52 #

Sekali lagi, tanpa mempedulikan nilai elemen-elemen masing-masing, operasi perkalian antara matrik A dan vektor-kolom x, bisa juga dinyatakan dalam indeksnya masing-masing, yaitu

" y1 y2 # = " a11.x1+ a12.x2+ a13.x3 a21.x1+ a22.x2+ a23.x3 #

Bila dijabarkan, maka elemen-elemen vektor-kolom y adalah y1 = a11.x1+ a12.x2+ a13.x3

y2 = a21.x1+ a22.x2+ a23.x3

kemudian secara sederhana dapat diwakili oleh rumus berikut

yi= 3 X j=1 aijxj dimanai=1,2.

Berdasarkan contoh tersebut, secara umum bila ada matrik A berukurann x m yang dikalikan dengan vektor-kolom x berukuranm, maka akan didapatkan vektor-kolom y berukuran n x 1

(54)

dimana elemen-elemen vektor-kolom y memenuhi yi= m X j=1 aijxj (2.16) dengani=1,2,. . . ,n.

2.5.6 Komputasi perkalian matrik dan vektor-kolom

Mari kita mulai lagi dari source code paling dasar dari operasi perkalian antara matrik dan vektor-kolom sesuai dengan contoh di atas

1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 x = [2; 3; 4]; % inisialisasi vektor x 6

7 % ---proses perkalian matrik dan

vektor----8 y(1,1)=A(1,1)*x(1,1)+A(1,2)*x(2,1)+A(1,3)*x(3,1);

9 y(2,1)=A(2,1)*x(1,1)+A(2,2)*x(2,1)+A(2,3)*x(3,1);

10

E----12 A

13 x

14 y

Sejenak, mari kita amati dengan cermat statemen dari baris ke-8 dan ke-9 sambil dikaitkan dengan bentuk umum penulisan indeks pada perkalian antara matrik dan vektor-kolom yaitu

yi1= aij.xj1+ aij.xj1+ aij.xj1 (2.17)

Dari sana ada 3 point yang perlu dicatat:

• elemeny dan elemen x sama-sama memiliki indeks i yang berpasangan dengan angka 1. • pada baris statemen ke-8 dan ke-9 ada tiga kali operasi perkalian dan dua kali operasi

penjumlahan yang semuanya melibatkan indeks i dan indeks j. Namun indeks j sela-lu berubah pada masing-masing perkalian. Jadi indeks j lebih cepat berubah dibanding indeksi.

• elemena memiliki indeks i dan indeks j dimana indeks j lebih cepat berubah dibanding indeksi.

Kita mulai dengan memecah operasi pada statemen baris ke-8 yang bertujuan menghitung nilaiy(1, 1)

1 clear all

2 clc

(55)

4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A

5 x = [2; 3; 4]; % inisialisasi vektor x

6

vektor----8 y(1,1)=A(1,1)*x(1,1); 9 y(1,1)=y(1,1)+A(1,2)*x(2,1); 10 y(1,1)=y(1,1)+A(1,3)*x(3,1); 11 12 y(2,1)=A(2,1)*x(1,1)+A(2,2)*x(2,1)+A(2,3)*x(3,1); 13

E----15 A

16 x

17 y

Agar baris ke-8 memiliki pola yang sama dengan baris ke-9 dan ke-10, upaya yang dilakukan adalah 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 x = [2; 3; 4]; % inisialisasi vektor x 6

vektor----8 y(1,1)=0; 9 y(1,1)=y(1,1)+A(1,1)*x(1,1); 10 y(1,1)=y(1,1)+A(1,2)*x(2,1); 11 y(1,1)=y(1,1)+A(1,3)*x(3,1); 12 13 y(2,1)=A(2,1)*x(1,1)+A(2,2)*x(2,1)+A(2,3)*x(3,1); 14

E----16 A

17 x

18 y

Dari sini kita bisa munculkan indeksj 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 x = [2; 3; 4]; % inisialisasi vektor x 6

vektor----8 y(1,1)=0; 9 for j=1:3 10 y(1,1)=y(1,1)+A(1,j)*x(j,1); 11 end 12 13 y(2,1)=A(2,1)*x(1,1)+A(2,2)*x(2,1)+A(2,3)*x(3,1); 14

E----16 A

17 x

(56)

Dengan cara yang sama, baris ke-13 dimodiﬁkasi menjadi 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 x = [2; 3; 4]; % inisialisasi vektor x 6

vektor----8 y(1,1)=0; 9 for j=1:3 10 y(1,1)=y(1,1)+A(1,j)*x(j,1); 11 end 12 13 y(2,1)=0; 14 for j=1:3 15 y(2,1)=y(2,1)+A(2,j)*x(j,1); 16 end 17

E----19 A

20 x

21 y

Inisialisasi vektor y dengan angka nol dapat dilakukan diawal proses perkalian, sekaligus me-munculkan indeksi 1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 x = [2; 3; 4]; % inisialisasi vektor x 6

vektor----8 for i=1:2 9 y(i,1)=0; 10 end 11 12 for j=1:3 13 y(1,1)=y(1,1)+A(1,j)*x(j,1); 14 end 15 16 for j=1:3 17 y(2,1)=y(2,1)+A(2,j)*x(j,1); 18 end 19

E----21 A

22 x

23 y

Kemudian, untuk menyamakan pola statemen baris ke-13 dan ke-17, indeksi kembali dimun-culkan

1 clear all

(57)

3

4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A

5 x = [2; 3; 4]; % inisialisasi vektor x

6

vektor----8 for i=1:2 9 y(i,1)=0; 10 end 11 12 i=1; 13 for j=1:3 14 y(i,1)=y(i,1)+A(i,j)*x(j,1); 15 end 16 17 i=2; 18 for j=1:3 19 y(i,1)=y(i,1)+A(i,j)*x(j,1); 20 end 21

E----23 A

24 x

25 y

Akhir dari proses optimasi adalah sebagai berikut

1 clear all 2 clc 3 4 A = [3 8 5; 6 4 7]; % inisialisasi matrik A 5 x = [2; 3; 4]; % inisialisasi vektor x 6

vektor----8 for i=1:2 9 y(i,1)=0; 10 end 11 12 for i=1:2 13 for j=1:3 14 y(i,1)=y(i,1)+A(i,j)*x(j,1); 15 end 16 end 17

E----19 A

20 x

21 y

2.6 Penutup

Demikianlah catatan singkat dan sederhana mengenai jenis-jenis matrik dasar dan operasi pen-jumlahan dan perkalian yang seringkali dijumpai dalam pengolahan data secara numerik. Se-muanya akan dijadikan acuan atau referensi pada pembahasan topik-topik numerik yang akan datang.

(58)

2.7 Latihan

1. Diketahui matrik A, matrik B, dan vektor x sebagai berikut

A=       1 3 ₋₆ ₋₂ 5 9 7 5.6 2 4 8 ₋₁ 2.3 1.4 0.8 −2.3       B=       8 1 4 21 3 10 5 0.1 7 ₋₂ 9 ₋₅ 2.7 −12 −8.9 5.7       x=       0.4178 −2.9587 56.3069 8.1       (a) Buatlah script untuk menyelesaikan penjumlahan matrik A dan matrik B. (b) Buatlah script untuk menyelesaikan perkalian matrik A dan matrik B. (c) Buatlah script untuk menyelesaikan perkalian matrik A dan vektor x. (d) Buatlah script untuk menyelesaikan perkalian matrik B dan vektor x.

(59)

Fungsi

✍ Objektif :

⊲ Mengenalkan fungsi internal. ⊲ Membuat fungsi ekstenal.

⊲ Membuat fungsi ekternal untuk penjumlahan matrik. ⊲ Membuat fungsi ekternal untuk perkalian matrik.

3.1 Fungsi internal

Fungsi internal adalah fungsi bawaan yang sudah tersedia di dalam Matlab; contohnya: sqrt(),

sind()dan log10(). Ketika kita hendak mencari akar kuadrat dari angka 49, maka cukup dengan mengetikkan

>> sqrt(49)

ans =

7

Untuk mencari nilai sinus dari 30◦_C >> sind(30)

ans =

0.5000

dan untuk mendapatkan nilai logaritma berbasis 10 dari angka 10000

>> log10(10000)

ans =

4

Selain sqrt(), sind() dan log10(), masih banyak lagi fungsi internal yang dimiliki Matlab. Adanya fungsi internal sangat memudahkan kita dalam membuat script dengan Matlab.