TINJAUAN PERSAMAAN LAPLACE DIMENSI DUA DENGAN SYARAT BATAS DIRICHLET DAN ROBIN
SKRIPSI
Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta
untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana Sains
Oleh: Rini Widya Astuti
12305144042
PROGRAM STUDI MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
v MOTTO
Mahasuci Allah yang menguasai (segala) kerajaan, dan Dia Mahakuasa atas segala sesuatu. (QS. Al Mulk:1)
Allah tidak akan membebani seseorang melainkan sesuai dengan kesanggupannya. (QS. Al Baqarah:286)
HALAMAN PERSEMBAHAN
Karya yang sederhana ini dipersembahkan untuk
Kedua orang tua, Bapak Eriyono dan Ibu Sriati Ambarwati yang telah banyak berkorban demi kebahagiaanku.
Saudara terbaikku, Kak Handoko, Mbak Fetty , dan juga adik mungilku kesha yang selalu memberikan perhatian, maupun pengertiannya.
Bulek Widati dan Om Pur yang sudah aku anggap seperti orang tua kedua. Terimakasih atas kasih sayang dan bantuan yang kalian berikan.
Sahabatku, Mohammad Ahzaul Umam yang selalu ada disaat-saat terbaik maupun terburuk. Terimakasih atas kasih sayang sederhana dan kesabaranmu menghadapiku. Sahabat sekamar, Septiana Dwi Hapsari. Terimakasih telah menjadi ojek tangguhku. Sahabat Edelweizem, Ninik, Tika, kunita, Mbak Pipit, Mbak Evi, Mbak Nur, Jupe,
dan Nurhayati yang telah menjadi keluarga di perantauan. Terimakasih atas segalanya.
Sahabat ingkung, Anita, Ratih, Mada, Isas, Zen, dan Lela. Terimakasih atas semangat, perhatian, dan pengalaman yang kalian berikan.
Teman seperbimbingan, Ahmadi dan Agus Supratama. Terimakasih atas bantuan dan semangatnya.
vii
TINJAUAN PERSAMAAN LAPLACE DIMENSI DUA DENGAN SYARAT BATAS DIRICHLET DAN ROBIN
Oleh Rini Widya Astuti NIM. 12305144042
ABSTRAK
Tugas akhir ini bertujuan untuk mengetahui pemodelan persamaan Laplace dimensi dua dan membahas tentang penyelesaian persamaan Laplace dimensi dua pada koordinat kartesius dan koordinat polar. Syarat batas yang digunakan yaitu syarat batas Dirichlet dan syarat batas Robin.
Tahapan yang dilakukan dalam memodelkan persamaan Laplace dimensi dua yaitu mengambil sebuah bidang berbentuk persegi panjang dengan panjang dan lebar . Kemudian dihubungkan dengan sumber potensial ( ). Bidang tersebut dipartisi menjadi subpartisi yang sangat kecil. Berdasarkan hukum fisika yang menjelaskan hubungan laju aliran potensial (fluks) terhadap perbedaan potensial, maka diperoleh persamaan gradien potensial untuk bidang subpartisi tersebut. Dengan melibatkan penjumlahan fluks pada subpartisi, diperoleh model persamaan Laplace dimensi dua + = 0 dengan dan menggambarkan domain posisi yang terletak diantara 0 sampai dan diantara 0 sampai . Dalam hal ini menunjukkan potensial pada posisi dan .
Setelah diperoleh model persamaan Laplace dimensi dua, berikutnya akan dibahas penyelesaian persamaan Laplace dimensi dua pada koordinat kartesius dan koordinat polar. Menentukan penyelesaian permasalahan syarat batas Dirichlet dan syarat batas Robin pada bidang persegi panjang. Kemudian akan dilakukan simulasi distribusi suhu untuk kedua permasalahan tersebut dengan mengambil tinjauan lempengan logam berbentuk persegi panjang. Selanjutnya menentukan penyelesaian permasalahan syarat batas Dirichlet pada suatu daerah dalam cakram. Pada kasus ini simulasi distribusi suhu dilakukan dengan mengambil tinjauan lempengan logam berbentuk lingkaran. Simulasi distribusi suhu berupa simulasi untuk grafik dua dimensi maupun tiga dimensi. Dalam mencari penyelesaian masalah syarat batas tersebut digunakan metode separasi variabel.
DAFTAR ISI
TUDUL ... i
PERSETUTUAN ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERNYATAAN ... iv
MOTTO ... v
HALAMAN PERSEMBAHAN ... vi
ABSTRAK ... vii
KATA PENGANTAR ... viii
DAFTAR ISI ... x
DAFTAR TABEL ... xii
DAFTAR GAMBAR ... xiii
DAFTAR LAMPIRAN ... xiv
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Batasan Masalah... 4
C. Rumusan Masalah ... 5
D. Tujuan Penulisan ... 5
E. Manfaat Penulisan ... 6
BAB II KATIAN TEORI ... 7
A. Limit ... 7
B. Turunan……….. .. ... 9
C. Turunan Fungsi Trigonometri dan Hiperbolik ... .. 11
D. Aturan Rantai pada Turunan ... 13
E. Turunan Parsial ... 18
F. Persamaan Diferensial ... 20
G. Masalah Nilai Awal dan Syarat Batas ... 27
xi
I. Persamaan Karakteristik ... 31
J. Deret Fourier ... 33
K. Metode Separasi Variabel ... 45
L. Keadaan Steady-State ... 53
BAB III PEMBAHASAN ... 55
A. Pemodelan Persamaan Laplace ... 55
B. Penyelesaian Masalah Syarat Batas Persamaan Laplace pada Koordinat Kartesius dan Polar ... 63
1. Permasalahan Syarat Batas Dirichlet pada Bidang Persegi Panjang ... ... 63
2. Permasalahan Syarat Batas Robin pada Bidang Persegi Panjang ... 85
3. Permasalahan Syarat Batas Dirichlet pada Daerah dalam Cakram ... 97
C. Tinjauan Hasil Simulasi ... 117
BAB IV PENUTUP ... 122
A. Kesimpulan ... 122
B. Saran ... 123
DAFTAR PUSTAKA ... 124
DAFTAR TABEL
xiii
DAFTAR GAMBAR
Gambar 2. 1 Ilustrasi Konsep Turunan ... 9
Gambar 3. 1 Bidang Persegi Panjang dengan Sumber Potensial ... 56
Gambar 3. 2 Aliran Fluks ( ) pada Bidang Partisi ... 58
Gambar 3. 3 Syarat Batas Dirichlet pada Bidang Persegi Panjang ... 63
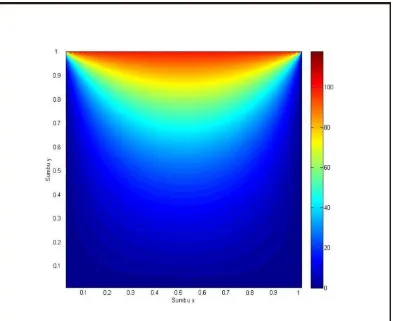
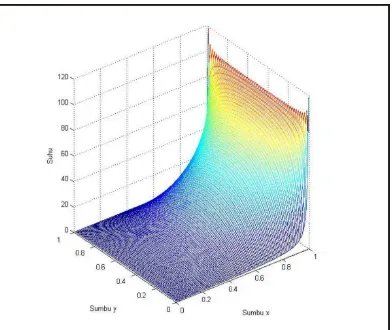
Gambar 3. 4 Distribusi Suhu pada Persamaan (3.45) ... 72
Gambar 3. 5 Grafik 2D Distribusi Suhu pada Persamaan (3.45) ... 73
Gambar 3. 6 Distribusi Suhu pada Persamaan (3.45a)... 77
Gambar 3. 7 Grafik 2D Distribusi Suhu pada Persamaan (3.45a) ... 78
Gambar 3. 8 Distribusi Suhu pada Persamaan (3.45b) ... 82
Gambar 3. 9 Grafik 2D Distribusi Suhu pada Persamaan (3.45b) ... 83
Gambar 3.10 Syarat Batas Robin pada Bidang Persegi Panjang ... 85
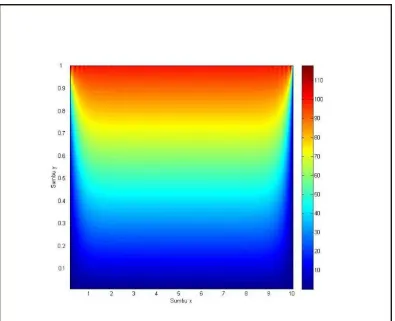
Gambar 3.11 Distribusi Suhu pada Persamaan (3.77) ... 95
Gambar 3.12 Grafik 2D Distribusi Suhu pada Persamaan (3.77) ... 96
Gambar 3.13 Syarat Batas Dirichlet pada Daerah dalam Cakram ... 102
Gambar 3.14 Distribusi Suhu pada Persamaan (3.125) ... 112
DAFTAR LAMPIRAN
Lampiran 1 M-Scdipt untuk distribusi suhu Persamaan (3.45) pada Gambar (3.4).
Lampiran 2 M-Scdipt untuk distribusi suhu Persamaan (3.45) pada Gambar (3.5).
Lampiran 3 M-Scdipt untuk distribusi suhu Persamaan (3.45a) pada Gambar (3.6).
Lampiran 4 M-Scdipt untuk distribusi suhu Persamaan (3.45a) pada Gambar (3.7).
Lampiran 5 M-Scdipt untuk distribusi suhu Persamaan (3.45b) pada Gambar (3.8).
Lampiran 6 M-Scdipt untuk distribusi suhu Persamaan (3.45b) pada Gambar (3.9).
Lampiran 7 M-Scdipt untuk distribusi suhu Persamaan (3.77) pada Gambar (3.11).
Lampiran 8 M-Scdipt untuk distribusi suhu Persamaan (3.77) pada Gambar (3.12).
Lampiran 9 M-Scdipt untuk distribusi suhu Persamaan (3.125) pada Gambar (3.14).
1 BABBIB PENDAHULUANB
B
A. LatarBBelakangBMasalahB
Matematika merupakan salah satu ilmu pengetahuan yang sering menjadi pedoman untuk menyelesaikan permasalahan sehari-hari dan juga untuk menunjang perkembangan ilmu pengetahuan dan teknologi. Sebagai sarana berfikir dalam memecahkan masalah secara logis, sistematis, obyektif, kritis, dan juga rasional, matematika dapat diterapkan dalam berbagai disiplin ilmu. Permasalahan-permasalahan dalam disiplin ilmu sains maupun teknik telah banyak ditransformasi ke dalam persamaan matematika melalui proses pemodelan matematika. Melalui pemodelan matematika permasalahan yang ada menjadi lebih sederhana dan lebih mudah dicari penyelesaiannya. Salah satu model matematika yang banyak digunakan adalah persamaan diferensial.
2
Salah satu persamaan diferensial parsial yang merupakan contoh klasik dari persamaan elliptik yaitu persamaan Laplace. Persamaan Laplace merupakan persamaan dasar dari teori potensial dan memegang peranan penting pada ilmu fisika maupun teknik. Persamaan ini dapat digunakan untuk mendeskripsikan perilaku potensial listrik, potensial gravitasi, potensial fluida, maupun suatu aliran suhu yang tidak bergantung pada waktu (Arfken, 1985). Tidak ada nilai awal yang menyertai persamaan Laplace, karena persamaan tersebut tidak bergantung pada waktu atau steady state (Duffy, 2003). Berbeda dengan persamaaan diferensial parsial yang berhubungan dengan waktu seperti persamaan panas dan persamaan gelombang. Meskipun demikian, persamaan ini diikuti dengan syarat batas tertentu.
Penyelesaian masalah persamaan diferensial parsial pada tugas akhir ini menggunakan metode separasi variabel. Pemilihan metode tersebut dikarenakan persamaan Laplace merupakan persamaan yang separabel pada koordinat kartesius, polar, maupun silinder (Greenberg, 1998). Ide dasar metode separasi variabel yaitu transformasi suatu persamaan diferensial parsial kedalam persamaan diferensial biasa, setelah diperoleh persamaan diferensial biasa kemudian diselesaikan sehingga diperoleh penyelesaian dari persamaan diferensial parsial. Dalam penyelesaian persamaan diferensial parsial akan diperoleh penyelesaian secara umum. Untuk memperoleh penyelesaian secara khusus, diperlukan adanya nilai awal dan syarat batas.
3
Penerapan Persamaan Laplace dalam Menyelesaikan Masalah iilai Batas pada
Koordinat Polar. Penelitian tersebut membahas tentang penerapan fungsi
harmonik digunakan untuk menyelesaikan permasalahan nilai batas Dirichlet pada koordinat polar dalam domain yang berbeda, dimana fungsi harmonik merupakan penyelesaian dari persamaan Laplace. Namun, pada penelitian tersebut lebih menekankan pada perhitungan penyelesaian persamaan Laplace dalam koordinat polar dalam beberapa domain secara matematis.
Salah satu topik pada tugas akhir ini sudah pernah dibahas dalam buku yang berjudul “Boundary Value Problems and Partial Differential Equations” oleh Mayer Humi, namun pada buku tersebut lebih menekankan perhitungan secara matematis. Hal yang serupa juga terlihat dalam buku yang berjudul “Advanced Engineering Mathematics (Second Edition)” oleh Greenberg. Oleh karena itu, tugas akhir ini membahas persamaan Laplace dimensi dua yang lebih menekankan tentang implementasi secara riil dengan syarat batas yang berbeda. Implementasi secara riil yang dimaksud yaitu aplikasi persamaan Laplace pada proses perambatan panas.
4
berubah terhadap perubahan waktu secara langsung. Perubahan panas hanya terjadi karena adanya sumber panas yang diletakkan pada batas lempengan logam dan perubahannya hanya tergantung kepada posisi. Sehingga berdasarkan kondisi diatas, permasalahan ini bisa dikaji dengan menggunakan persamaan Laplace.
Kajian yang dimaksud pada penelitian ini meliputi pemodelan persamaan Laplace serta penentuan penyelesaian untuk permasalahan syarat batas dengan metode separasi variabel. Syarat batas yang digunakan yaitu syarat batas Dirichlet dan syarat batas Robin. Simulasi proses perambatan panas dilakukan pada lempengan logam dua dimensi, sehingga akan melibatkan persamaan Laplace yang berdimensi dua pula. Terdapat dua sistem koordinat yang bersesuaian dengan persamaan diferensial yang berdimensi dua yaitu sistem koordinat kartesius dan koordinat polar. Dalam hal ini bidang dua dimensi berbentuk persegi panjang untuk sistem koordinat kartesius dan berupa cakram untuk sistem koordinat polar.
B. BatasanBMasalahB
Beberapa pembatasan ruang lingkup permasalahan yang perlu diperhatikan dalam tugas akhir ini yaitu sebagai berikut.
1. Persamaan Laplace dimensi dua dengan syarat batas Dirichlet dan Robin. 2. Penyelesaian persamaan Laplace dimensi dua menggunakan metode separasi
5 C. RumusanBMasalahB
Berdasarkan latar belakang yang telah dipaparkan di atas, sehingga dapat diperoleh rumusan masalah sebagai berikut.
1. Bagaimana model persamaan Laplace dimensi dua?.B
2. Bagaimana penyelesaian persamaan Laplace dimensi dua dengan syarat batas Dirichlet pada bidang persegi panjang?B
3. Bagaimana penyelesaian persamaan Laplace dimensi dua dengan syarat batas Robin pada bidang persegi panjang?B
4. Bagaimana penyelesaian persamaan Laplace dimensi dua dengan syarat batas Dirichlet pada daerah dalam cakram?B
B
D. TujuanBPenulisanB
Berdasarkan rumusan masalah di atas, tujuan penulisan tugas akhir ini adalah sebagai berikut.
1. Menjelaskan model persamaan Laplace dimensi dua.
2. Menjelaskan penyelesaian persamaan Laplace dimensi dua dengan syarat batas Dirichlet pada bidang persegi panjang.B
3. Menjelaskan penyelesaian persamaan Laplace dimensi dua dengan syarat batas Robin pada bidang persegi panjang.B
4. Menjelaskan penyelesaian persamaan Laplace dimensi dua dengan syarat batas Dirichlet pada daerah dalam cakram.B
6 E. ManfaatBPenulisanB
Manfaat dari penulisan tugas akhir ini adalah sebagai berikut
1. Bagi Mahasiswa, menambah pengetahuan tentang model persamaan Laplace dimensi dua, mampu menyelesaikan persamaan Laplace dimensi dua sehingga dapat diperoleh penyelesaian dari persamaan Laplace dimensi dua dengan syarat batas Dirichlet maupun syarat batas Robin.
2. Bagi Universitas, mampu memberikan tulisan yang berkualitas tentang persamaan Laplace dimensi dua dan beberapa kasus persamaan Laplace dimensi dua.
BAB II
KAJIAN TEORI
Pada bab ini akan dibahas beberapa hal yang digunakan sebagai landasan
pada penulisan bab III. Materi yang diuraikan berisi tentang definisi, teorema, dan
beberapa kajian matematika, antara lain tentang Limit, Turunan, Turunan Fungsi
Trigonometri dan Fungsi Hiperbolik, Aturan Rantai pada Turunan, Turunan
Parsial, Persamaan Diferensial, Persamaan Diferensial Biasa, Persamaan
Diferensial Parsial, Masalah Nilai Awal dan Syarat Batas, Masalah
Sturm-Liouville dan Fungsi Eigen, Deret Fourier, Metode Separasi Variabel, dan
Keadaan Steady State.
A. Limit
Pemikiran tentang limit yang menyatakan bahwa berarti
bahwa selisih antara dan dapat dibuat sekecil mungkin dengan
mensyaratkan bahwa cukup dekat, tetapi tidak sama dengan (Purcell, 2010).
Definisi 2.1 Limit (Dale Varberg & Edwin J Purcell, 2010)
Diberikan yang artinya untuk setiap yang nilainya sangat
kecil, terdapat sedemikian sehingga dengan syarat
atau dengan kata lain
Contoh 2.2 Akan dibuktikan bahwa
Analisis Pendahuluan:
Akan ditentukan nilai dari , sebagai berikut
sehingga
Berdasarkan Persamaan (2.1) diperoleh nilai dari
Bukti baku:
Andaikan nilai dari , dan dipilih nilai dari , sehingga didapatkan
B. Turunan
Konsep dasar dari turunan adalah perubahan suatu fungsi dalam sesaat.
Gambar (2.1) berikut diilustrasikan tentang konsep dari turunan. Misalkan
terdapat , dan dimana , serta .
Gambar (2.1) Ilustrasi Konsep Turunan
Berdasarkan Gambar (2.1) diperoleh
Apabila nilai diperkecil mendekati nol, sehingga Persamaan (2.2) menjadi
Jika nilai limit ini ada, maka nilai limit tersebut disebut dengan turunan
(perubahan nilai suatu fungsi sesaat) dari di .
Definisi 2.3 Turunan (Dale Varberg & Edwin J Purcell, 2010)
Turunan pertama fungsi dinotasikan dengan yang nilainya pada
sebarang adalah
dengan syarat nilai limit dari f(x) ada.
Notasi dari turunan disimbolkan dengan notasi Leibniz
atau notasi
prima atau bisa dinotasikan sebagai atau
.
Sebagai ilustrasi dari definisi turunan tersebut, perhatikan contoh berikut
ini.
Contoh 2.4 Akan ditentukan turunan pertama dari .
Menurut Definisi (2.3), sehingga
C. Turunan Fungsi Trigonometri dan Hiperbolik
Adapun aturan-aturan atau teorema pencarian turunan fungsi trigonometri
adalah sebagai berikut.
Teorema 2.5 Turunan Fungsi Sin (Dale Varberg & Edwin J Purcell, 2010)
Jika , maka .
Bukti:
Berdasarkan Definisi (2.3), sehingga
Terbukti.
Teorema 2.6 Turunan Fungsi Cos (Dale Varberg & Edwin J Purcell, 2010)
Jika , maka .
Bukti:
Berdasarkan Definisi (2.3), sehingga
Terbukti.
Aturan-aturan atau teorema pencarian turunan fungsi hiperbolik adalah
sebagai berikut.
Bentuk lain dari , sementara .
Teorema 2.7 Turunan Fungsi Sinh (Dale Varberg & Edwin J Purcell, 2010)
Jika , maka .
Bukti:
Karena bentuk lain dari adalah , sehingga
Terbukti.
Teorema 2.8 Turunan Fungsi Cosh (Dale Varberg & Edwin J Purcell, 2010)
Jika , maka
Bukti:
Karena bentuk lain dari adalah , sehingga
Terbukti.
D. Aturan Rantai pada Turunan
Sebelum membahas teorema aturan rantai pada turunan, perlu diketahui
sifat dasar dari suatu turunan. Dalam hal ini akan ditunjukkan hubungan antara
keberadaan turunan suatu fungsi pada titik terhadap kekontinuan suatu fungsi
tersebut pada titik .
Teorema 2.9 Kekontinuan Fungsi (Bartle, 2000)
Bukti:
Diberikan interval , dan berlaku . Akan dibuktikan bahwa
kontinu pada dengan menunjukkan bahwa mendekati ketika
. Untuk setiap , sedangkan , sedemikian sehingga
Karena ada, maka nilai limitnya ada. Sehingga diperoleh
Karena selisih mendekati 0 ketika , dapat disumpulkan bahwa
. Sehingga kontinu pada .
Terbukti.
Pernyataan-pernyataan berikut merupakan ringkasan dari hubungan antara
kekontinuan dan turunan.
(i) Jika suatu fungsi memiliki turunan pada , maka fungsi tersebut
(ii) Ada kemungkinan suatu fungsi kontinu pada , tetapi tidak
memiliki turunan pada . Sehingga, kekontinuan tidak menjamin
adanya turunan.
Sebagai ilustrasi dari teorema kekontinuan tersebut, perhatikan contoh berikut ini.
Contoh 2.10 Diberikan fungsi
1. untuk
Merupakan fungsi yang memiliki turunan pada , sehingga fungsi
tersebut kontinu pada . Karena jika diambil diperoleh
.
2. untuk .
Merupakan fungsi yang kontinu, tetapi tidak punya turunan pada .
Karena untuk diperoleh,
untuk dan
untuk . Namun untuk nilai limitnya tidak
terdefinisi. Sehingga fungsi tersebut tidak punya turunan pada .
Aturan rantai dapat digunakan untuk mempermudah penurunan suatu
fungsi komposit. Fungsi komposit merupakan suatu fungsi yang variabel
Teorema 2.11 Aturan Rantai pada Turunan (Dale Varberg & Edwin J
Purcell, 2010)
Misalkan dan . Jika g terdiferensiasikan di dan
terdiferensiasikan di , maka fungsi komposit , yang didefinisikan
oleh adalah terdiferensiasikan di dan
yakni
atau
Bukti:
Misalkan bahwa dan , bahwa terdiferensiasikan di dan
bahwa terdiferensiasikan di Ketika diberikan pertambahan ,
terdapat pertambahan yang berkorespondensi dalam dan yang diberikan oleh
Jadi,
Berdasarkan Teorema (2.9) yang menyatakan bahwa jika punya turunan di ,
maka kontinu di , sehingga . Hal tersebut mengakibatkan ,
mengingat merupakan fungsi atas . Oleh karena itu,
Terbukti.
Pada penulisan bab III, aturan rantai digunakan dalam proses pengubahan
persamaan Laplace dari koordinat kartesius ke dalam koordinat polar. Sebagai
ilustrasi dari teorema mengenai aturan rantai pada turunan tersebut, perhatikan
contoh berikut ini.
Contoh 2.12 Diberikan fungsi
.
Akan ditentukan turunan pertama dari fungsi sebagai berikut.
Fungsi dapat dinyatakan sebagai dengan dan
. Karena dan
sehingga
Apabila menggunakan notasi Leibnitz, maka turunan dapat ditentukan sebagai
berikut.
Jika dimisalkan , dengan , maka
dan . Sehingga
E. Turunan Parsial
Turunan parsial merupakan turunan dari sebuah fungsi dari beberapa
variabel terhadap salah satu variabel bebasnya, dengan menganggap semua
variabel bebas yang lainnya konstan (Spiegel, 1992).
Definisi 2.13 Turunan Parsial (Spiegel, 1992)
Misalkan suatu fungsi merupakan fungsi dari dua variabel dan , turunan
parsial dari terhadap dan berturut-turut dinyatakan oleh
dan , dengan definisi: serta
Andaikan bahwa adalah suatu fungsi dua variabel dan , dengan
menganggap konstan, maka adalah fungsi satu variabel .
Turunan fungsi di disebut turunan parsial terhadap di dan
dinyatakan oleh . Jadi
Dengan cara yang sama, turunan parsial terhadap di dinyatakan
dengan dan diberikan oleh
Sebagai ilustrasi dari definisi turunan parsial tersebut, perhatikan contoh berikut
ini.
Contoh 2.14 Akan ditentukan
dan
dari fungsi
Menurut Definisi (2.13) sehingga diperoleh
dan
F. Persamaan Diferensial
Dalam bagian ini akan dijelaskan tentang persamaan diferensial.
Definisi 2.15 Persamaan Diferensial (Ross, 1984)
Persamaan diferensial adalah persamaan yang memuat turunan dari satu atau
Berdasarkan banyaknya variabel bebas, persamaan diferensial dapat
diklasifikasikan menjadi dua yaitu persamaan diferensial biasa dan persamaan
diferensial parsial. Berikut diberikan definisi persamaan diferensial biasa dan
persamaan diferensial parsial.
Definisi 2.16 Persamaan Diferensial Biasa (Ross, 1984)
Persamaan diferensial biasa adalah persamaan diferensial yang memuat turunan
dari satu atau lebih variabel tak bebas terhadap satu variabel bebas.
Definisi 2.17 Persamaan Diferensial Parsial (Ross, 1984)
Persamaan diferensial parsial adalah persamaan diferensial yang memuat
turunan dari satu atau lebih variabel tak bebas terhadap lebih dari satu variabel
bebas.
Persamaan diferensial biasa (PDB) dinotasikan dengan notasi Leibniz
atau notasi prima , atau bisa juga
dinotasikan dengan . Persamaan diferensial parsial (PDP)
dinotasikan dengan
untuk turunan pertama fungsi atas variabel tak bebas
terhadap variabel bebas . Untuk turunan parsial kedua, ketiga dan seterusnya
sampai turunan ke berturut-turut dinotasikan sebagai
.
Persamaan diferensial parsial juga bisa dinotasikan dengan untuk
turunan kedua fungsi atas variabel tak bebas terhadap variabel bebas .
Definisi 2.18 Order Persamaan Diferensial (Ross, 1984)
Order persamaan diferensial adalah order tertinggi dari semua turunan yang
terdapat pada persamaan diferensial tersebut.
Definisi 2.19 Derajat Persamaan Diferensial (Ross, 1984)
Derajat persamaan diferensial adalah pangkat tertinggi dari order tertinggi dari
semua turunan pada persamaan diferensial.
Sebagai ilustrasi dari definisi order dan derajat persamaan diferensial parsial
tersebut, perhatikan contoh berikut ini.
Contoh 2.20 Berikut ini contoh persamaan diferensial
(1)
, merupakan persamaan diferensial biasa berorder 2 dan
berderajat 1.
(2)
, merupakan persamaan diferensial parsial
berorder 2 dan berderajat 2.
Berdasarkan hubungan antara variabel tak bebas dan turunan-turunannya,
persamaan diferensial order dibagi menjadi dua yaitu persamaan diferensial
linear dan persamaan diferensial non linear.
Definisi 2.21 Persamaan Diferensial Linear (Ross, 1984)
Persamaan diferensial linear order dengan variabel bebas dan variabel tak
dengan .
Persamaan diferensial dikatakan muncul dalam bentuk linear jika memenuhi
syarat-syarat berikut ini:
(i) derajat dari variabel tak bebas dan turunan-turunannya adalah satu
(ii) tidak ada perkalian antara variabel tak bebas dengan turunan-turunannya
dan perkalian antara turunan dengan turunannya
(iii) tidak ada fungsi transenden dari variabel-variabel tak bebas.
Persamaan diferensial yang tidak memenuhi syarat-syarat tersebut disebut
persamaan diferensial non linear.
Diberikan persamaan diferensial parsial linear order dengan satu
variabel tak bebas dan dua variabel bebas dan yang terdefinisi pada domain
didefinisikan sebagai berikut:
dengan , dan fungsi dan konstanta yang
diberikan dalam variabel dan .
Definisi 2.22 Persamaan Diferensial Homogen (Humi, 1992)
Contoh 2.23 Berikut ini contoh-contoh persamaan diferensial
(1)
(2)
(3)
(4)
Contoh 2.23 (1) merupakan persamaan diferensial biasa, berorder enam,
berderajat satu, linear, dan homogen.
Contoh 2.23 (2) merupakan persamaan diferensial biasa, berorder tiga, berderajat
dua, non linear, dan non homogen
Contoh 2.23 (3) merupakan persamaan diferensial parsial, berorder tiga,
berderajat satu, linear, dan homogen,
Contoh 2.23 (4) merupakan persamaan diferensial biasa, berorder dua dan
berderajat satu, non linear, dan homogen,
Selanjutnya akan diberikan teorema mengenai prinsip superposisi yang
berlaku untuk persamaan diferensial homogen berorder .
Teorema 2.24 Prinsip Superposisi (Dennis G Zill, 2005)
Jika adalah penyelesaian dari persamaan diferensial homogen
berorde dari Persamaan (2.3) pada interval I, maka kombinasi linearnya
dengan untuk adalah konstanta, juga penyelesaian dalam
interval I.
Bukti:
Misalkan didefinisikan sebagai operator diferensial dan
adalah penyelesaian dari persamaan diferensial
homogen, sehingga Jika didefinisikan
, maka linearitas dari adalah
karena nilai dari maka
Terbukti.
Persamaan diferensial parsial linear order dua dengan variabel tak bebas
dan variabel bebas dan , yang terdefinisi pada domain mempunyai bentuk
umum sebagai berikut
Definisi 2.25 Klasifikasi Persamaan Diferensial Parsial (Humi, 1992)
Persamaan diferensial (2.4) disebut
(i) elliptik jika untuk semua
(ii) parabolik jika untuk semua
(iii) hiperbolik jika untuk semua
Sebagai ilustrasi dari definisi klasifikasi persamaan diferensial parsial linear order
dua tersebut, perhatikan contoh berikut ini.
Contoh 2.26 Persamaan diferensial
(1) Laplace
merupakan persamaan diferensial elliptik,
karena
(2) Panas
merupakan persamaan diferensial parabolik, karena
(3) Gelombang
merupakan persamaan diferensial
hiperbolik, karena
G. Masalah Nilai Awal dan Syarat Batas
Pada bagian ini akan dibahas mengenai pengertian Nilai Awal, Syarat
Batas serta Masalah Nilai Awal dan Syarat Batas yang menyertai suatu persamaan
diferensial parsial. Mengingat apabila persamaan diferensial diselesaikan, maka
akan diperoleh suatu penyelesaian umum. Namun untuk memperoleh
penyelesaian khusus diperlukan adanya nilai awal dan syarat batas.
Menurut (Humi, 1992) yang dimaksud dengan nilai awal adalah kondisi
yang harus dipenuhi pada awal waktu tertentu . Dalam hal ini persamaan
Laplace merupakan persamaan yang tidak disertai dengan nilai awal, karena
persamaan Laplace tidak bergantung pada waktu. Sebagai contoh dari pengertian
nilai awal tersebut, diberikan suatu persamaan panas dengan nilai awal
. Nilai awal menyatakan bahwa suhu pada posisi
saat waktu adalah
Syarat Batas adalah suatu syarat atau kondisi yang harus dipenuhi pada
batas-batas domain terkait dengan ruang (Humi, 1992). Sebagai ilustrasi,
diberikan suatu persamaan panas dengan syarat batas dan .
Syarat batas menunjukkan bahwa suhu pada posisi saat waktu
dipertahankan sebesar nol derajat, sedangkan
menunjukkan bahwa
perubahan suhu terhadap posisi saat waktu dipertahankan nol derajat.
Selanjutnya akan diuraikan mengenai jenis-jenis syarat batas untuk
persamaan diferensial parsial order dua. Diberikan domain dengan dan
dan
dengan
sebarang konstanta. Dalam (Humi, 1992) syarat batas dikatakan
(i) Dirichlet jika syarat batasnya memberikan nilai dari sebarang fungsi
pada atau dapat ditulis dan
dengan dan fungsi dalam variabel .
(ii) Neumann jika syarat batasnya memberikan nilai turunan terhadap
pada atau dapat ditulis
dan
dengan dan fungsi dalam variabel .
(iii) Robin jika syarat batasnya memberikan relasi linear antara dengan
pada atau dapat ditulis
dan
dengan sebarang konstanta serta dan fungsi dalam variabel .
Sebagai ilustrasi mengenai jenis-jenis syarat batas tersebut, perhatikan
contoh berikut ini.
Contoh 2.27 Diberikan persamaan diferensial
.
Syarat batas
(1) merupakan Syarat Batas Dirichlet.
(2)
merupakan Syarat Batas Neumann.
(3)
Selanjutnya akan diuraikan mengenai Masalah Nilai Awal dan Syarat
Batas atau disingkat MNASB. Masalah yang bersesuaian dengan persamaan
diferensial parsial akan rumit jika jumlah penyelesaian independen untuk
persamaan tersebut adalah tak terbatas (Humi, 1992). Sehingga formulasi lengkap
dari sistem fisik dalam hal persamaan diferensial parsial membutuhkan perhatian
tidak hanya untuk persamaan yang mengatur sistem tetapi juga untuk perumusan
yang benar dari kondisi batas maupun kondisi awal. Masalah nilai awal dan syarat
batas adalah masalah yang terdiri dari suatu persamaan diferensial yang
dilengkapi dengan nilai awal dan syarat batas. Kemudian jika masalah nilai awal
dan syarat batas tersebut diselesaikan maka akan diperoleh penyelesaian khusus.
Sebagai ilustrasi mengenai pengertian masalah nilai awal dan syarat batas
tersebut, perhatikan contoh berikut ini.
Contoh 2.28 Diberikan sebuah senar dengan panjang yang diikat pada kedua
ujungnya. Kemudian senar tersebut dipetik. Pergerakan senar pertama kali (saat
) mempunyai fungsi posisi untuk , sehingga diperoleh nilai
awal . Setelah dipetik, pergerakan di kedua ujung senar yang
terikat pada dan dipertahankan nol untuk . Sehingga diperoleh
syarat batas dan
Jadi diperoleh Masalah Nilai Awal dan Syarat Batas sebagai berikut
dan syarat batas
H. Masalah Sturm-Liouville dan Fungsi Eigen
Definisi 2.29 Masalah Sturm-Liouville (Dean G. Duffy, 2003)
Diberikan persamaan diferensial linear berorde 2 berikut ini
dengan syarat batas
Dalam hal ini nilai dari dan merupakan fungsi bilangan real
atas sedangkan adalah suatu parameter. Nilai dari merupakan
suatu konstanta real, sedangkan nilai dari dan merupakan suatu fungsi
yang kontinu dan positif yang terletak pada interval Persamaan (2.5)
disebut sebagai persamaan Sturm-Liouville dan bersama-sama dengan syarat
batas pada Persamaan (2.6) dan (2.7), membentuk suatu Masalah
Sturm-Liouville.
Jika diperhatikan pada Persamaan (2.5), masalah tersebut mempunyai
penyelesaian untuk setiap nilai yaitu , . Penyelesaian
tersebut dinamakan dengan penyelesaian trivial. Tetapi akan diperoleh
tersebut dinamakan penyelesaian non trivial. Nilai yang bersesuaian dinamakan
nilai eigen dan fungsinya disebut sebagai fungsi eigen.
I. Persamaan Karakteristik
Diberikan persamaan diferensial homogen berorder dua dengan variabel
tak bebas dan variabel bebas yang terdefinisi pada domain sebagai berikut
dengan dan merupakan suatu konstanta. Untuk memudahkan mencari
penyelesaian Persamaan (2.8) diperlukan suatu persamaan karakteristik yang
sepadan dengan persamaan tersebut. Persamaan karakteristik dapat diperoleh
dengan melakukan subtitusi
dan berturut-turut oleh dan .
Sehingga dalam hal ini persamaan karakteristik yang sepadan dengan Persamaan
(2.8) adalah
Persamaan karakteristik yang diperoleh berupa persamaan pangkat biasa
yang dapat diselesaikan dengan melakukan pemfaktoran sehingga diperoleh
akar-akar karakteristik. Secara umum, akar-akar-akar-akar karakteristik dari suatu persamaan
diferensial linear homogen orde 2 menurut (Ross, 1984) dibedakan menjadi tiga,
yaitu
1. Akar-akar karakteristik riil berbeda.
Misalkan akar dari persamaan karakteristik pada Persamaan (2.9) adalah
dan dengan , maka penyelesaian umum dari Persamaan (2.9)
2. Akar-akar karakteristik riil kembar.
Misalkan akar dari persamaan karakteristik pada Persamaan (2.9) suatu akar
riil kembar yaitu , maka penyelesaian umum dari Persamaan (2.9) adalah
3. Akar-akar karakteristik bilangan kompleks.
Misalkan akar dari persamaan karakteristik pada Persamaan (2.9) adalah
dan , maka penyelesaian umum dari Persamaan (2.9)
adalah
Sebagai ilustrasi dari definisi persamaan karakteristik dan akar-akar karakteristik
tersebut, perhatikan contoh berikut ini.
Contoh 2.30
1. Akan ditentukan penyelesaian umum dari
Persamaan karakteristik yang sepadan dengan Persamaan (2.13) adalah
dan
Karena diperoleh akar-akar karakteristik riil berbeda, sehingga berdasarkan
Persamaan (2.10) diperoleh penyelesaian umum Persamaan (2.13) sebagai berikut
2. Akan ditentukan penyelesaian umum dari
Persamaan karakteristik yang sepadan dengan Persamaan (2.14) adalah
.
Karena diperoleh akar-akar karakteristik riil kembar, sehingga berdasarkan
Persamaan (2.11) diperoleh penyelesaian umum Persamaan (2.13) sebagai berikut
J. Deret Fourier
Pada bagian ini akan dibahas mengenai Deret Fourier.
Definisi 2.31 Fungsi Periodik (Humi, 1992)
Diberikan fungsi yang terdefinisi untuk setiap . Fungsi dikatakan
periodik dengan periode jika , dengan
Contoh 2.32
(1) Fungsi adalah fungsi yang periodik dengan periode 2 . Sebab
.
(2) Fungsi adalah fungsi yang periodik dengan periode .
Sebab
Definisi 2.33 Deret Fourier (Humi, 1992)
Diberikan fungsi yang terdefinisi pada interval . Deret Fourier
fungsi tersebut adalah
dengan
dan
Contoh 2.34 Akan ditentukan Deret Fourier dari
Berdasarkan Definisi (2.33) tentang Deret Fourier, sehingga diperoleh nilai dari
Jadi, Deret Fourier dari adalah
(Mayer Humi & William B. Miller, 1992).
Kemudian diberikan definisi fungsi genap dan fungsi ganjil.
Definisi 2.35 Fungsi Genap dan Fungsi Ganjil (Humi, 1992)
Diberikan fungsi terdefinisi pada interval . Fungsi
dikatakan sebagai fungsi genap jika pada interval dan
Contoh 2.36
1. Fungsi merupakan fungsi ganjil, karena
untuk setiap pada interval .
2. Fungsi merupakan fungsi genap, karena
untuk setiap pada interval .
3. Fungsi bukan merupakan fungsi genap maupun fungsi ganjil
karena
Kemudian dibahas mengenai Deret Fourier sinus dan Deret Fourier
cosinus.
Teorema 2.37 Deret Fourier Sinus (Humi, 1992)
Diberikan fungsi terdefinisi pada interval dan dapat diperluas
sebagai fungsi ganjil pada interval Jika Deret Fourier dari ada,
maka Deret Fourier tersebut berbentuk
dengan
Bukti:
Diketahui fungsi terdefinisi pada interval dan dapat diperluas
sebagai fungsi ganjil pada interval Deret Fourier dari ada,
sehingga Deret Fourier tersebut adalah
dengan
Dimisalkan , sehingga diperoleh
Karena merupakan fungsi ganjil dan merupakan fungsi
genap, sehingga diperoleh
dan
Karena merupakan fungsi ganjil dan merupakan fungsi
ganjil, diperoleh
Jadi terbukti bahwa Deret Fourier untuk adalah
dengan
Deret Fourier ini disebut Deret Fourier sinus fungsi .
Contoh 2.38 Diberikan fungsi
Akan ditentukan Deret Fourier sinus untuk fungsi tersebut.
Berdasarkan Teorema 2.37 maka Deret Fourier sinus dari fungsi adalah
dengan
Jadi, Deret Fourier dari adalah
Teorema 2.39 Deret Fourier Cosinus (Humi, 1992)
Diberikan fungsi terdefinisi pada interval dan dapat diperluas
sebagai fungsi genap pada interval Jika Deret Fourier dari ada,
maka Deret Fourier tersebut berbentuk
dengan
Bukti :
Diketahui fungsi terdefinisi pada interval dan dapat diperluas sebagai
fungsi genap pada interval Deret Fourier dari ada, sehingga Deret
Fourier tersebut adalah
dengan
Dimisalkan , sehingga diperoleh
karena merupakan fungsi genap, maka
Karena dan merupakan fungsi genap, sehingga diperoleh
Jadi terbukti bahwa Deret Fourier untuk adalah
dengan
Torema 2.39 disebut juga deret Fourier cosinus.
Contoh 2.40 Diberikan fungsi
Akan ditentukan Deret Fourier cosinus untuk fungsi tersebut.
Berdasarkan Teorema 2.39 maka Deret Fourier cosinus dari fungsi adalah
dengan
dan
Jadi Deret Fourier cosinus dari fungsi adalah
K. Metode Separasi Variabel
Metode Separasi Variabel adalah metode untuk mencari penyelesaian
persamaan diferensial dengan cara mengasumsikan penyelesaian tersebut
merupakan perkalian dari fungsi-fungsi variabel bebas yang ada pada persamaan
diferensial tersebut. Metode separasi variabel bertujuan untuk mereduksi
persamaan diferensial parsial yang diberikan menjadi bentuk persamaan
diferensial biasa. Dengan demikian persamaan diferensial parsial tersebut lebih
Diberikan persamaan diferensial linear homogen dengan variabel bebas
dan , serta variabel tak bebas yang dilengkapi dengan syarat batas tertentu.
Diasumsikan penyelesaian dari persamaan diferensial tersebut adalah
Langkah-langkah penyelesaian persamaan diferensial tersebut dengan
metode separasi variabel yaitu sebagai berikut (Humi, 1992):
1. Persamaan disubstitusi ke persamaan diferensial.
2. Hasil dari langkah (1) dibagi dengan .
3. Jika hasil dari langkah (2) dapat dinyatakan sebagai jumlahan suku-suku
yang hanya tergantung dari dan suku-suku yang hanya tergantung dari ,
maka dengan konstanta pemisah atau akan didapat sistem dua
persamaan diferensial biasa.
4. Gunakan syarat batas yang diberikan untuk menentukan syarat batas untuk
persamaan diferensial biasa dari langkah (3).
5. Selesaikan persamaan diferensial (Masalah syarat Batas) hasil dari langkah
(3) dan langkah (4).
6. Diperoleh , yang merupakan penyelesaian dari
persamaan diferensial di atas. Kemudian dengan prinsip superposisi
ditentukan penyelesaian umumnya.
7. Gunakan nilai awal yang diberikan, kemudian ditentukan penyelesaian
Masalah Nilai Awal dan Syarat Batas.
Contoh 2.41 Diberikan persamaan diferensial parsial
dengan syarat batas
dan nilai awal
Masalah Nilai Awal dan Syarat Batas (2.15) sampai (2.17) akan diselesaikan
dengan menggunakan metode Separasi Variabel. Jika diasumsikan
adalah penyelesaian dari MNASB di atas maka langkah-langkah
penyelesaiannya sebagai berikut:
1. Persamaan disubstitusikan ke Persamaan (2.15)
sehingga diperoleh
2. Persamaan (2.18) dibagi dengan sehingga diperoleh
atau
3. Untuk mendapatkan dua persamaan diferensial biasa dari Persamaan (2.19),
digunakan konstanta pemisah – sehingga
dan
4. Jika digunakan syarat batas (2.16) yaitu dengan
pada persamaan maka diperoleh
dan
Berdasarkan Persamaan (2.20) disyaratkan , sehingga
.
5. Diperoleh Masalah Sturm-Liouville sebagai berikut
Selanjutnya dicari penyelesaian non trivial dari Masalah
Sturm-Liouville (2.22a) dan (2.22b) yang dapat ditinjau menjadi tiga
kemungkinan yaitu untuk dan .
Kemungkinan 1 :
Dari persamaan (2.22a) didapat , penyelesaiannya
adalah , dengan A dan B konstanta sebarang. Jika
digunakan syarat batas (2.22b) yaitu , maka diperoleh
. Jadi untuk Masalah Syarat Batas (2.22a) dan (2.22b)
Kemungkinan 2 :
Persamaan (2.22a) mempunyai persamaan karakteristik
Karena diketahui , persamaan karakteristiknya
menjadi , dan akar-akar karakteristiknya adalah dan – yang
bernilai real. Penyelesaian Persamaan (2.22a) adalah
dengan dan konstanta sebarang. Jika digunakan syarat batas
(2.22b) yaitu , maka diperoleh
dan
Karena , sehingga . Penyelesaian Masalah
Sturm-Liouville (2.22a) dan (2.22b) adalah penyelesaian trivial .
Jadi untuk Masalah Syarat Batas (2.22a) dan (2.22b)
mempunyai penyelesaian trivial.
Persamaan (2.22a) mempunyai persamaan karakteristik
. Karena diketahui , persamaan karakteristiknya menjadi
, dan akar-akar karakteristiknya adalah bilangan kompleks
dan – . Penyelesaian Persamaan (2.22a) adalah
dengan dan konstanta sebarang. Jika digunakan syarat batas
(2.16b) yaitu , maka diperoleh
dan
Agar mempunyai penyelesaian non trivial diambil sehingga
diperoleh
Jadi untuk Masalah Sturm-Liouville (2.22a) dan (2.22b) mempunyai
penyelesaian non trivial dengan Nilai Eigen
dan konstanta sebarang,
Jadi penyelesaian Masalah Sturm-Liouville (2.22a) dan (2.22b) adalah
dengan Nilai Eigen dan konstanta sebarang,
Kemudian dicari penyelesaian untuk persamaan (2.21a).
Telah diketahui bahwa sehingga diperoleh
Persamaan (2.24) diintegralkan terhadap , sehingga diperoleh
6. Persamaan (2.23) dan (2.25) disubstitusi ke persamaan ,
sehingga diperoleh
atau
dengan
Kemudian dengan menggunakan prinsip superposisi, diperoleh
penyelesaian dari Masalah Syarat Batas tersebut yaitu
7. Berdasarkan nilai awal (2.17) yaitu , sehingga Persamaan
(2.27) menjadi
Kalikan Persamaan (2.28) dengan fungsi yang orthogonal dengan
yaitu , sehingga diperoleh
Bentuk orthogonal yang berada di ruas kanan pada Persamaan (2.30)
nilainya akan sama dengan nol, kecuali jika , sehingga Persamaan
(2.30) menjadi
Jadi, penyelesaian Masalah Nilai Awal dan Syarat Batas (2.15) sampai
(2.17) adalah
dengan
I. Keadaan Steady State
Keadaan steady state merupakan kondisi dimana sifat-sifat suatu sistem
tidak berubah dengan berjalannya waktu (Freedman, 2008). Jika dimisalkan
ini berarti untuk setiap nilai dari sistem tersebut, turunan parsial terhadap waktu
adalah nol.
Keadaan ini dapat diekspresikan pada sebuah lempengan logam berbentuk
persegi panjang ataupun berbentuk lingkaran yang diberi sumber panas pada
sisi-sisinya. Sebelum mencapai steady state, suhu pada lempengan logam tersebut
akan merambat dan mengalami perubahan. Perubahan suhu yang terjadi disebut
keadaan transien. Pada hal ini perambatan suhu merupakan jenis perambatan dua
dimensi, dimana perambatan yang terjadi bergantung pada posisi atau
. Proses perambatan ini terjadi karena pada masing-masing sisi telah diberi
BAB III
PEMBAHASAN
A. Pemodelan Persamaan Laplace
Pemodelan persamaan ini akan diilustrasikan untuk sistem dimensi dua.
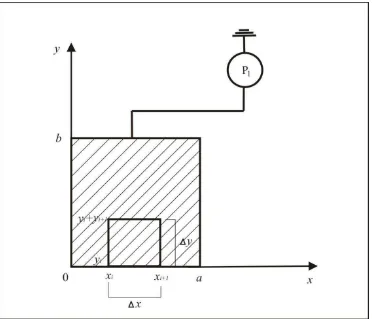
Diberikan sebuah bidang berbentuk persegi panjang dengan panjang dan lebar
direntangkan sepanjang sumbu dan sumbu seperti pada Gambar (3.1). Bidang
persegi panjang tersebut bisa berupa bidang yang terbuat dari suatu perantara
listrik konduktif, atau penampang aliran fluida, atau dapat juga terbuat dari
penampang konduktor suhu. Jika bidang tersebut dihubungkan dengan sumber
potensial , maka akan ada aliran potensial yang melewatinya. Dalam kasus
ini, diasumsikan bahwa
1. Material yang membentuk bidang persegi panjang memiliki sifat murni
dissipatif konstan per satuan panjang, yang berarti bahwa bidang
tersebut merupakan bidang yang tidak dapat menyimpan energi.
2. Bidang persegi panjang terhubung dengan sumber potensial pada
salah satu titik.
3. Aliran potensial yang mengalir pada bidang hanya mengalir dari
potensial tinggi menuju ke potensial rendah.
Gambar (3.1) Bidang Persegi Panjang dengan Sumber Potensial
Berdasarkan Gambar (3.1) diketahui bidang persegi panjang dengan
panjang dan lebar direntangkan sepanjang sumbu dan sumbu , kemudian
bidang tersebut dipartisi menjadi sangat banyak sehingga setiap bidang partisi
berukuran sangat kecil. Selanjutnya akan dipilih partisi interval . Misalkan
terletak pada interval dengan kata lain kemudian pada interval
dipartisi sebesar dengan untuk setiap .
Banyak partisi pada interval adalah dengan menuju tak berhingga. Hal
tersebut berakibat jarak antar ke nilainya mendekati nol sehingga .
[image:70.595.129.501.83.402.2]kemudian pada interval dipartisi sebesar dengan untuk
setiap . Banyak partisi pada interval adalah dengan
menuju tak berhingga. Hal tersebut berakibat jarak antar ke nilainya
mendekati nol sehingga .
Karena bidang persegi panjang terhubung dengan sumber potensial, yaitu
sehingga akan melibatkan suatu aliran potensial yang dapat memicu
terjadinya perbedaan potensial. Aliran potensial pada bidang persegi panjang
dalam kasus ini merupakan fungsi dari posisi . Laju aliran potensial yang
melewati bidang tidak dapat diukur secara langsung. Akan tetapi konsepnya
mempunyai arti fisik karena berhubungan dengan kuantitas skalar yang dapat
diukur yaitu potensial. Besarnya laju aliran potensial yang menembus luasan
bidang disebut fluks . Aliran potensial pada suatu bidang partisi dengan laju
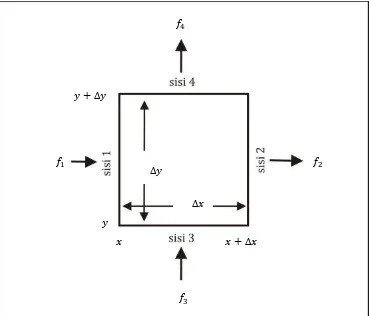
Gambar (3.2) Aliran fluks pada suatu Bidang Partisi
Berdasarkan Gambar (3.2) diketahui bahwa dan merupakan fluks
yang masuk pada sisi 1 dan sisi 3, sedangkan dan merupakan fluks yang
keluar dari sisi 2 dan 4 pada suatu bidang partisi. Laju aliran potensial pada
bidang partisi tersebut dapat dihitung berdasarkan hukum fisika yang menjelaskan
hubungan laju aliran potensial dengan perbedaan potensial . Perbedaan
potensial antara dua ujung bidang partisi berbanding lurus dengan ketahanan
bidang per satuan panjang, fluks yang melewati bidang partisi, dan panjang
bidang partisi (Vemuri, 1981). Secara matematis perbedaan potensial tersebut
dapat dinyatakan sebagai
[image:72.595.129.500.84.400.2]
dengan indeks 1 menunjukkan perbedaan potensial pada sisi 1. Tanda negatif
menunjukkan bahwa fluks mengalir dari potensial tinggi menuju potensial rendah.
Persamaan (3.1) dapat ditulis menjadi
Karena sehingga Persamaan (3.2) menjadi
Persamaan (3.3) merupakan persamaan gradien potensial untuk sisi pertama.
Analog untuk mencari gradien potensial pada ketiga sisi lainnya,
kemudian diperoleh gradien potensial pada keempat sisi elemen bidang partisi
adalah
Perhatikan bahwa untuk menyederhanakan Persamaan (3.4a) sampai dengan
Persamaan (3.4d) digunakan definisi turunan parsial karena terdapat lebih dari
Penyelesaian untuk komponen fluks sebagai berikut
Berdasarkan hukum konservasi yang menyatakan bahwa fluks yang masuk
berbanding lurus dengan fluks yang keluar (Vemuri, 1981), maka
Substitusi Persamaan (3.5a) sampai dengan Persamaan (3.5d) ke Persamaan (3.6)
diperoleh
Apabila Persamaan (3.7) dikalikan dengan
sehingga diperoleh
atau dapat ditulis
Karena dan , sehingga Persamaan (3.8) menjadi
karena
maka Persamaan (3.9) menjadi
Kasus di atas dilakukan pada bidang persegi panjang dengan sumber
, maka diperoleh syarat batas . Karena bidang persegi
panjang ketiga sisinya terbatas pada dan , sedangkan
potensial pada ketiga sisi tersebut dipertahankan sebesar nol sehingga diperoleh
syarat batas . Dari Persamaan (3.13) dan syarat
batas yang telah diketahui, didapatkan Masalah Syarat Batas sebagai berikut:
Persamaan (3.10) merupakan Persamaan Laplace dimensi dua, dengan
menunjukkan potensial secara umum. Sedangkan potensial secara khususnya
bergantung pada area fisika yang akan dikaji, dalam (Vemuri, 1981) beberapa
[image:76.595.223.507.223.372.2]area fisika yang dimaksud dapat dilihat pada tabel berikut
Tabel 1: Potensial dan Fluks dalam Beberapa Area Fisika
No Area Fisika Variabel p (Potensial) Variabel f (Fluks)
1 Elektrodinamika Tegangan Arus Listrik
2 Elektrostatis Potensial Listrik Fluks
3 Mekanika Fluida Tekanan Laju Aliran
B. Penyelesaian Masalah Syarat Batas Persamaan Laplace pada Koordinat
Kartesius dan Koordinat Polar
1. Permasalahan Syarat Batas Dirichlet pada Bidang Persegi Panjang
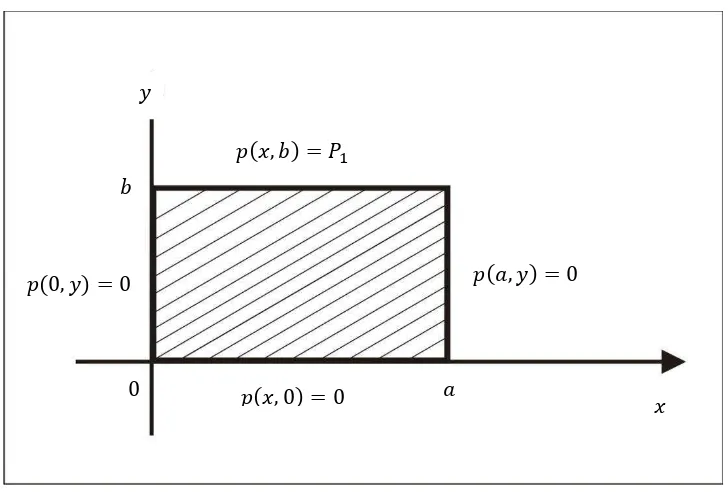
Syarat batas pada bidang persegi panjang berdasarkan Persamaan (3.12)
sampai dengan Persamaan (3.15) dapat diilustrasikan dalam bentuk koordinat
kartesius seperti gambar berikut
Gambar (3.3) Syarat Batas Dirichlet pada Bidang Persegi Panjang
Masalah persamaan Laplace pada bidang persegi panjang dengan panjang
dan lebar , kemudian diasumsikan bahwa sumber potensial . Masalah tersebut dapat disajikan secara matematis sebagai berikut:
dengan syarat batas
[image:77.595.131.495.245.494.2]
Akan ditentukan penyelesaian dari Persamaan (3.16) dengan
menggunakan metode separasi variabel. Misalkan sehingga
Apabila Persamaan (3.18) dan (3.19) disubstitusikan ke Persamaan (3.16), maka
diperoleh
Persamaan (3.20) dibagi dengan sehingga diperoleh
dengan mengambil variabel pemisah negatif , sehingga Persamaan (3.21)
menjadi
dan
Dalam kasus ini digunakan syarat batas , dengan
pada persamaan maka diperoleh
dan
Berdasarkan Persamaan (3.21) disyaratkan , sehingga
, dan diperoleh Masalah Nilai Eigen Sturm-Liouville sebagai berikut
Selanjutnya ditentukan penyelesaian non trivial dari Persamaan (3.25) dan
(3.26) yang dapat ditinjau menjadi tiga kemungkinan yaitu dan
.
Kemungkinan 1: untuk nilai , sehingga Persamaan (3.25) menjadi
dengan syarat batas . Penyelesaian umum dari P