PENERAPAN PEMBELAJARAN BERBASIS MASALAH UNTUK MENINGKATKAN KEMAMPUAN BERPIKIR KRITIS MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA.

(1)

SKRIPSI

Diajukan untuk Memenuhi Sebagian dari Syarat Memperoleh Gelar Sarjana Pendidikan Jurusan Pendidikan Matematika

Disusun Oleh

Cytra Dewi Purnamasari 1009052

JURUSAN PENDIDIKAN MATEMATIKA

FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUANALAM UNIVERSITAS PENDIDIKAN INDONESIA

(2)

MENINGKATKAN KEMAMPUAN BERPIKIR KRITIS MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA

Oleh

Cytra Dewi Purnamasari

Sebuah skripsi yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Sarjana pada Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam

Juli 2014

Hak Cipta dilindungi undang-undang.

(3)

CYTRA DEWI PURNAMASARI

PENERAPAN PEMBELAJARAN BERBASIS MASALAH UNTUK MENINGKATKAN KEMAMPUAN BERPIKIR KRITIS MATEMATIS SISWA

SEKOLAH MENENGAH PERTAMA

Disetujuidandisahkanolehpembimbing: Pembimbing I

Dr. H. SufyaniPrabawanto, M.Ed NIP. 196008301986031003

Pembimbing II

Drs. Nar Herrhyanto, M.Pd NIP.196106181987031001

Mengetahui,

KetuaJurusanPendidikanMatematika

(4)

v DAFTAR ISI

Halaman

ABSTRAK ...i

KATA PENGANTAR ...iii

UCAPAN TERIMA KASIH ...iv

DAFTAR ISI ...v

DAFTAR TABEL...viii

DAFTAR GAMBAR ... ix

DAFTAR LAMPIRAN ... ..x

BAB I PENDAHULUAN A. Latar Belakang Masalah ... 1

B. Rumusan Masalah ... 4

C. Tujuanpenelitian ...5

D. Manfaat Penelitian ...5

E. Definisi Operasional ... 6

BAB II TINJAUAN PUSTAKA A. Kemampaun Berpikir Kritis Matematis ... 8

B.Pembelajaran Berbasis Masalah ...11

C. Pembelajaran Matematika ...15

D.Pembelajaran Konvesional ...17

E.Sikap Siswa terhadap Pembelajaran Matematika ...20

F. Keterkaitan Pembelajaran Berbasis Masalah terhadap Peningkatan Kemampuan Berpikir Kritis ...21

G.Penelitian yang Terkait ...23

H.Kerangka Pemikiran ...24

(5)

BAB III METODOLOGI PENELITIAN

A. Metode dan Desain Penelitian...26

B. Populasi dan sampel ...27

C. Perangkat Pembelajaran...27

1. Rencana Pelaksanaan Pembelajaran ...27

2. Bahan Ajar Berupa Lembar Kerja Kelompok ...27

D. Instrumen Penelitian ...28

1. Instrumen Tes ...28

2. Instrumen Non-Tes ...36

E. Prosedur Pelaksanaan Penelitian ...37

F. Teknik Analisis Data ...38

1. Analisis Data Kuantitatif ...39

a. Analisis Kemampuan Berpikir Kritis Matematis Awal...39

b. Analisis Kemampuan Berpikir Kritis Matematis Akhir ...41

c. Analisis Peningkatan Kemampuan Berpikir Kritis Matematis ...43

d. Analisis Kualitas Peningkatan Kemampuan Berpikir Kritis Matematis ...46

a. Data Angket ...48

b. Pengolahan Data Observasi ...48

c. Analisis Jurnal Harian Siswa ...49

BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Hasil Penelitian ...50

2. Analisis Data Kualitatif ...60

B. Pembahasan ...67

1. Peningkatan Kemampuan Berpikir Kritis Matematis Siswa...68

(6)

BAB V KESIMPULAN DAN SARAN

A. Kesimpulan ...74 B. Saran ...74

DAFTAR PUSTAKA ...75

LAMPIRAN

(7)

ABSTRAK

Cytra Dewi Purnamasari (1009052)Penerapan Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Berpikir Kritis Matematis Siswa Sekolah Menengah Pertama

Penelitian ini dilatarbelakangi oleh rendahnya kemampuan berpikir kritis matematis siswa Sekolah Menengah Pertama. Tujuan penelitian ini adalah: 1) untuk mengetahui apakah peningkatan kemampuan berpikir kritis matematis siswa yang mendapatkan pembelajaran dengan pembelajaran berbasis masalah lebih baik daripada siswa yang mendapatkan pembelajaran dengan pembelajaran konvesional dan 2) mengetahui sikap siswa terhadap pembelajaran matematika dengan menggunakan pembelajaran berbasis masalah.Penelitian ini menggunakan metode kuasi eksperimen dengan desain penelitian berbentuk desain kelompok kontrol non-ekuivalen. Populasi dalam penelitian ini adalah seluruh siswa kelas VII SMPN 15 Bandung. Adapun sampel sebanyak 2 kelas dari 10 kelas yang dipilih secara tidak acak.Hasil analisis menunjukkan bahwa: (1) peningkatan Kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran berbasis masalah lebih baik daripada peningkatan kemampuan berpikir kritis matematis yang mendapat pembelajaran konvesional dan (2) siswa menunjukkan sikap yang positif terhadap pembelajaran berbasis masalah dan terhadap pelajaran matematika.

(8)

ii

ABSTRACT

Cytra Dewi Purnamasari (1009052) Application of problem bases learning to

increase mathematic critical thinking ability of junior high school students

This research is backgrouned by the lack of mathematic critical thinking of junior high school students. The purpose of this research are: 1) to know does the increasing of students’ mathematic critical thinking ability which taught by the learning method of problem bases learning will be better than the students which taught by conventional learning method and 2) to know students’ attitude of mathematical learning method that used study cases. This research used quasi experiment method with research design that was non equivalen control group. The objects of this research is all 7�ℎ_{grade student of SMPN 15 Bandung. While} the samples are two classes from SMPN 15 Bandung that was not randomly taken.The result of this research are 1) the increasing of students’ mathematic critical learning ability which taught by the learning method of problem bases learning will be better than the students which taught by conventional learning method and 2) the students show a good attitude to mathematical learning method and the study cases.

(9)

BAB 1

PENDAHULUAN

A. Latar Belakang Masalah

Matematika sebagai salah satu mata pelajaran di sekolah yang dinilai sangat memegang peranan penting karena matematika dapat meningkatkan pengetahuan siswa dalam berpikir secara logis, rasional, kritis dan cermat sehingga siswa dapat memiliki kemampuan memperoleh, menganalisis, menyimpulkan dan memanfaatkan informasi. Dalam matematika, gagasan

dihubungkan dan dibangun satu dengan lainnya sehingga pemahaman dan pengetahuan siswa makin mendalam dan kemampuan siswa untuk menerapkan matematika juga makin meluas. Dengan demikian siswa dapat mempersiapkan diri untuk memecahkan masalah dalam berbagai situasi, termasuk di sekolah, di rumah, dan di tempat kerja.

Dalam Standar Isi Permendiknas no. 22 tahun 2006, mata pelajaran matematika bertujuan agar peserta didik memiliki kemampuan sebagai berikut:

1. Memahami konsep matematika, menjelaskan keterkaitan antar konsep dan mengaplikasikan konsep atau algoritma, secara luwes, akurat, efisien, dan tepat, dalam pemecahan masalah.

2. Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika dalam membuat generalisasi, menyusun bukti, atau menjelaskan gagasan dan pernyataan matematika.

3. Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh.

4. Mengomunikasikan gagasan dengan simbol, tabel, diagram, atau media lain untuk memperjelas keadaan atau masalah.

5. Memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu memiliki rasa ingin tahu, perhatian, dan minat dalam mempelajari matematika, serta sikap ulet dan percaya diri dalam pemecahan masalah.

Kemudian National Council of Teacher Mathematic (NCTM, 2000)

(10)

(connection); (4) komunikasi (communication); serta (5) representasi (representation) (Fauzi, 2011:3).

Berdasarkan tujuan diatas tampak bahwa salah satu arah atau orientasi pembelajaran matematika adalah kemampuan penalaran. Berpikir kritis merupakan bagian dari penalaran, sesuai dengan pernyataan Krulik Rudnik (Rohayati, 2005:1), bahwa penalaran mencangkup berpikir dasar, berpikir kritis, dan berpikir kreatif.

Cabera (Fachrurazi, 2011:77) mengemukakan bahwa pentingnya mengembangkan kemampuan berpikir kritis harus dipandang sebagai sesuatu yang urgen dan tidak bisa disepelekan lagi. Penguasaan kemampuan berpikir kritis tidak cukup dijadikan sebagai tujuan pendidikan semata, tetapi juga sebagai proses fundamental yang memungkinkan siswa untuk mengatasi ketidaktentuan masa mendatang.

Namun untuk mencapai kemampuan berpikir kritis tersebut bukanlah pekerjaan yang mudah. Jaworski (Depdiknas, 2006) menyatakan bahwa penyelenggaraan pembelajaran matematika tidaklah mudah karena fakta menunjukkan para siswa mengalami kesulitan dalam mempelajari matematika. Hal tersebut sejalan dengan pendapat Rohaeti (2008:2) menyatakan bahwa para siswa cenderung hanya menghapalkan sejumlah rumus, perhitungan dan langkah-langkah penyelesaian soal yang telah dikerjakan guru atau yang ada dalam buku teks, sehingga menyebabkan kemampuan berpikir kritis dan kreatif siswa tidak berkembang secara optimal.

Berpikir kritis matematis siswa-siswa Indonesia khususnya siswa

SMP masih belum memuaskan. Hal ini dapat dilihat pada rendahnya persentase jawaban benar siswa kita dalam Trends in International Mathematics and Science Study (TIMSS) 1999 dan 2003 (Sutame, 2011:309). Pada studi TIMSS terungkap bahwa siswa Indonesia lemah

(11)

data-data atau fakta yang diberikan (Noer, 2009:474). Berdasarkan fakta tersebut, dapat dikatakan bahwa kemampuan pemecahan masalah, kemampuan berpikir kritis, kreatif, dan reflektif siswa pada umumnya masih rendah.

Kemudian penelitian Karim (Nurningsih, 2013:4) menunjukkan bahwa rata-rata kemampuan berpikir kritis siswa SMP berada pada kualifikasi kurang dan Tim Survey IMSTEP-JICA pada tahun 1999 (Fachrurazi, 2011:77) menemukan sejumlah kegiatan yang dianggap sulit oleh siswa dalam mempelajarinya dan cara guru dalam mengajarkannya di

kota Bandung. Adapun kegiatan yang dianggap sulit tersebut adalah pembuktiandalam pemecahan masalah yang memerlukan penalaran matematis, menemukan generalisasi atau konjektur, dan menemukan hubungan antara data atau fakta yang diberikan. Kalau diperhatikan kegiatan tersebut merupakan kegiatan yang menuntut kemampuan berpikir kritis. Dengan demikian dapat disimpulkan bahwa hasil survei tersebut menemukan bahwa siswa mengalami kesulitan jika dihadapkan kepada persoalan yang memerlukan kemampuan berpikir kritis. Kemudian hasil studi pendahuluan melalui wawancara dengan seorang guru matematika kelas VII disalah satu SMPN Bandung, diperoleh bahwa kebanyakan siswa masih belum bisa memecahkan masalahmatematika yang mengakibatkan kemampuan berpikir kritis siswa rendah.

Sikap siswa terhadap pembelajaran matematika merupakan hal yang penting untuk di perhatikan. Banyak siswa di setiap jenjang pendidikan menganggap bahwa matematika merupakan mata pelajaran yang sulit, menakutkan, membosankan atau tidak terlalu berguna dalam kehidupan

sehari-hari sehingga sikap siswa terhadap pembelajaran matematika kurang dan mengakibatkan adanya sikap negatif dari siswa terhadap pembelajaran matematika.Menurut Hart (Malik, 2011:77) terdapat korelasi yang signifikan antar sikap dan prestasi belajar matematika. Kurang dari 20%_{sikap dapat dianggap berasal prestasi belajar matematika. Oleh karena}

(12)

harus menyenangkan, mudah dipahami, tidak menakutkan, dan ditunjukkan kegunaanya (Russeffendi, 1988:233).

Sehubungan dengan permasalahan di atas, maka dapat ditegaskan bahwa usaha perbaikan proses pembelajaran melalui upaya pemilihan model pembelajaran yang tepat dan inovatif dalam pembelajaran matematika di sekolah merupakan suatu kebutuhan yang sangat penting untuk dilakukan. Salah satu model pembelajaran yang diduga dapat digunakan untuk memperbaiki kualitas proses dan hasil belajar adalah model Pembelajaran Berbasis Masalah (PBM). Menurut Tan (Amir,

2009:22) pembelajaran berbasis masalah memiliki ciri-ciri seperti pembelajaran dimulai dengan pemberian masalah, masalah memiliki konteks dengan dunia nyata, siswa secara berkelompok aktif merumuskan masalah dan mengidentifikasi kesenjangan pengetahuan mereka, mempelajari dan mencari sendiri materi yang terkait dengan masalah dan melaporkan solusi dari masalah. Sementara guru lebih banyak memfasilitasi. Dengan demikian dalam PBM guru tidak menyajikan konsep matematika dalam bentuk yang sudah jadi, namun melalui kegiatan pemecahan masalah siswa digiring ke arah menemukan konsep sendiri (reinvention) sehingga dapat meningkatkan kemampuan berpikir kritis siswa.

Dengan demikian berdasarkan latar belakang yang telah dipaparkan di atas, maka penulis tertarik untuk meneliti “Penerapan Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Berpikir Kritis Matematis Siswa Sekolah Menengah Pertama”.

B. Rumusan Masalah

Berdasarkan latar belakang yang telah diuraikan sebelumnya, maka rumusan masalahnya adalah:

(13)

2. Bagaimana sikap siswa terhadap pelaksanaan pembelajaran matematika dengan menggunakan pembelajaran berbasis masalah?

C. Tujuan Penelitian

Berdasarkan rumusan masalah, maka tujuan penelitian ini adalah sebagai berikut:

1. Untuk mengetahui apakah peningkatan kemampuan berpikir kritis matematis siswa yang mendapatkan pembelajaran dengan pembelajaran berbasis masalah lebih besar daripada siswa yang mendapatkan

pembelajaran dengan pembelajaran konvesional.

2. Mengetahui sikap siswa terhadap pembelajaran matematika dengan menggunakan pembelajaran berbasis masalah.

D. Manfaat Penelitian

Penelitian ini diharapkan memberikan manfaat kepada banyak pihak, diantaranya sebagai berikut :

1. Bagi sekolah, dapat dijadikan masukan untuk menentukan kebijakan, khusunya bagi pengembang kurikulum dalam rangka meningkatkan kualitas pembelajaran matematika.

2. Bagi guru matematika, diharapkan pembelajaran matematika menggunakan model pembelajaran berbasis masalah dapat dijadikan sebagai salah satu alternatif dalam pembelajaran matematika menuju ke arah perbaikan kualitas pembelajaran matematika di sekolah.

3. Bagi siswa, diharapkan pembelajaran berbasis masalah ini dapat meningkatkan semangat untuk belajar dan memberikan pengalaman

belajar yang berbeda dari biasanya sehingga diharapkan dapat meningkatkan prestasi belajar matematika siswa.

(14)

E. Definisi Operasional

Agar tidak terjadi salah penafsiran, ada beberapa istilah yang perlu didefinisikan yaitu:

1. Kemampuan Berpikir Kritis Matematis

Kemampuan berpikir kritis matematis adalah sebuah proses dimana seseorang membuat keputusan yang masuk akal dalam mengenali, mengidentifikasi, dan memahami persoalan serta menemukan solusinya dalam masalah matematika. Indikator

kemampuan berpikir kritis yang digunakan dalam penelitian ini adalah 1) Focus (fokus) yaitu hal pertama yang harus dilakukan untuk mengetahui informasi. Untuk fokus terhadap permasalahan, diperlukan pengetahuan. Semakin banyak pengetahuan yang dimiliki akan semakin mudah mengenali informasi; 2) Reason (alasan) yaitu mencari kebenaran dari pernyataan yang akan dikemukakan; 3) Inference (penyimpulan) yaitu langkah dari alasan menjadi kesimpulan; 4) Situation (situasi) yaitu kebenaran dari peryataan tergantung situasi yang terjadi; 5) Clarity (kejelasan) yaitu siswa mampu membedakan beberapa hal dengan jelas (tidak menimbulkan makna ganda); dan 6) Overview (tinjauan) yaitu melihat kembali sebuah proses dalam matematika kebenaran peryataan dalam situasi yang ada sehingga bisa menentukan keterkaitan dengan situasi lainnya.

2. Pembelajaran Berbasis Masalah

Pembelajaran berbasis masalah adalah model pembelajaran yang melibatkan siswa untuk memecahkan suatu masalah matematika yang

(15)

Mengembangkan dan mempresentasikan hasil; 5) Menganalisis dan mengevaluasi proses mengatasi masalah.

3. Pembelajaran Konvesional

Pembelajaran konvesional adalah pembelajaran yang biasa dilakukan dengan cara sebagai berikut: (1) guru mengajar kepada sekelompok siswa dalam suatu kelas dengan memandang siswa memiliki kemampuan yang tidak berbeda, sehingga setiap siswa diberi pelayanan yang sama; (2) guru memberikan informasi kemudian menerangkan suatu konsep; (3) siswa diberikan kesempatan untuk

bertanya kepada guru dan mengemukakan pendapatnya sehingga interaksi dalam proses belajar mengajar terjadi; (4) guru memberikan contoh soal dan selanjutnya meminta siswa mengerjakannya di papan tulis serta memberikan pekerjaan rumah.

4. Sikap Terhadap Pembelajaran Matematika

(16)

BAB III

METODOLOGI PENELITIAN

A. Metode dan Desain Penelitian

Penelitian ini bertujuan untuk melihat apakah peningkatan kemampuan berpikir kritismatematis siswa yang memperoleh pembelajaran dengan model pembelajaranberbasis masalah lebih baik daripada siswa yang memperoleh pembelajaran konvensional. Pada penelitian ini, variabel bebasnya adalah model pembelajaranberbasis

masalah dan variabel terikatnya adalah kemampuan berpikir kritis matematis.Metode yang digunakan dalam penelitian ini adalah metode kuasi eksperimen, sehingga sampel yang digunakan sebagai kelas eksperimen dan kelas kontrol tidak dipilih secara acak/random.

Adapun desain yang digunakan dalam penelitian ini adalah desain kelompok kontrol non-ekuivalen. Kelas eksperimen pada penelitian ini adalah kelompok siswa yang mendapatkan pembelajaran dengan model pembelajaran berbasis masalah, sedangkan kelas kontrol pada penelitian ini adalah kelompok siswa yang mendapatkan pembelajaran dengan pembelajaran konvensional. Sebelum diberikan perlakuan, kedua kelas ini diberikan pretest untuk mengetahui kemampuan awal siswa. Kemudian, setelah diberikan perlakuan kedua kelas diberikan posttest.Adapun desain eksperimen pada penelitian ini digambarkan sebagai berikut (Ruseffendi, 2010:53):

O

X

O

O O

Keterangan:

O = Pretest/Posttest berupa tes kemampuan berpikir kritis matematis X = Pembelajaran matematika dengan model pembelajaran berbasis

masalah

(17)

B. Populasi dan Sampel

Populasi dalam penelitian ini adalah seluruh siswa kelas VII SMP Negeri 15 Bandung tahun ajaran 2013/2014. Sampel yang dipilih sebanyak dua kelas dari sepuluh kelas. Dari kedua kelas tersebut, satu kelas digunakan sebagai kelas eksperimen dan satu kelas lagi digunakan sebagai kelas kontrol. Berdasarkan informasi dari guru mata pelajaranmatematika bahwa sepuluh kelas dari kelas VII memiliki karakteristik yang relatif sama. Oleh karena itu, dari kesepuluh kelas tersebut dipilih satu kelas yaitu kelas VII C sebagai kelas eksperimen yang mendapat pembelajaran

matematika dengan model pembelajaran berbasis masalah dan satu kelasyaitu kelas VII E sebagai kelas kontrol yang mendapat pembelajaran matematika dengan pembelajaran konvensional.

C. Perangkat Pembelajaran

Dalam suatu pembelajaran dibutuhkan beberapa perangkat pembelajaran sebagai pendukung guna tercapainya tujuan dari pembelajaran tersebut. Beberapa perangkat yang digunakan dalam penelitian ini, adalah:

1. Rencana Pelakasanaan Pembelajaran (RPP)

Menurut tim sosialisasi KTSP dalam website Dikti, Rencana Pelaksanaan Pembelajaran (RPP) adalah rencana yang menggambarkan prosedur dan pengorganisasian pembelajaran untuk mencapai satu kompetensi dasar yang ditetapkan dalam Standar Isi dan telah dijabarkan dalam silabus. Pada penelitian ini, RPP yang gunakan untuk kelas eksperimen disesuaikan dengan model Pembelajaran Berbasis

Masalah dan pada kelas kontrol disesuaikan dengan model pembelajaran konvesional.

2. Bahan Ajar Berupa Lembar Kerja Kelompok (LKK)

(18)

(LKK) adalah lembaran-lembaran yang berisi tugas yang harus dikerjakan oleh peserta didik secara kelompok.Pada penelitian ini, LKK diberikan kepada kelas eksperimen disusun menyesuaikan dengan langkah-langkah model pembelajaran berbasis masalah dan indikator kemampuan berpikir kritis, sedangkan kelas kontrol tidak menggunakan LKK tetapi hanya menggunakan buku sumber.

D. Instrumen Penelitian

Instrumen tes adalah suatu alat pengumpulan data untuk mengevaluasi

kemampuan kognitif, afektif, dan psikomotor siswa. Instrumen yang digunakan dalam penelitian ini terdiri dari instrumen tes dan non-tes. Instrumen tes berupa tes kemampuan berpikir kritis matematis dan instrumen non-tes berupa lembar observasi angket dan jurnal.

1. Intrumen Tes

Intrumen Tesyang digunakan dalam penelitian ini adalah tes kemampuan berpikir kritis matematis. Pada penelitian ini akan dilaksanakan dua kali tes, yaitu pretest untuk mengetahui kemampuan berpikir kritis awal siswa sebelum mendapatkan perlakuan dan posttestt untuk mengetahui kemampuan berpikir kritis matematis siswa setelah mendapat perlakuan.

Jenis tes yang digunakan dalam penelitian ini adalah tes tertulis dengan bentuk uraian. Tes uraian dipilih karena tes uraian akan terlihat sejauhmana siswa dapat mencapai setiap indikator kemampuan berpikir kritis matematis siswa.

Pemberian skor tes kemampuan berpikir kritis matematis

(19)

Tabel 3.1

Kriteria Skor Kemampuan Berpikir Kritis Matematis Siswa

Skala Kriteria

0

Lembar jawaban hanya terdapat satu dari kriteria berikut: 1. Lembar jawaban kosong sama sekali

2. Data dalam permasalahan sudah disebutkan , tapi tidak ada yang dilakukan atau sedikit perlakuan tapi tidak sesuai dengan msalah

3. Ada jawaban tapi salah dan tidak ada usaha lain yang terlihat

1

Lembar jawaban hanya terdapat satu dari kriteria berikut:

1. Ada sedikit pekerjaan yang memperlihatkan pemahaman terhadap masalah dibanding hanya menyalin data yang tersedia, tetapi pendekatan yang digunakan tidak akan sampai pada penyelesaian yang benar.

2. Sebuah strategi yang tidak tepat sudah dimulai namun tidak dilanjutkan, dan tidak ada tanda-tanda siswa akan memulai strategi lain. Dapat dilihat, bahwa siswa mencoba satu pendekatan yang tidak berfungsi lalu menyerah.

3. Siswa mencoba untuk mencapai tujuan sampingan tapi tidak berhasil.

2

1. Siswa menggunakan strategi yang tidak sesuai dan mendapatkan jawaban yang tidak benar. Tapi, pekerjaan itu menunjukkan pemahaman terhadap masalah. 2. Strategi yang tepat digunakan, tetapi

a) Tidak dilanjutkan cukup jauh sampai mencapai penyelesaian. Contoh: hanya ada dua masukan dalam sebuah daftar terorganisir

b) Digunakan secara tidak tepat dan sampai pada “ tidak ada jawaban” atau jawaban yang salah.

3. Siswa sampai pada tujuan sampingan tapi tidak dilanjutkan. 4. Penyelesaian yang benar terlihat, tetapi

a) Proses penyelesaian tidak dapat dimengerti b) Tidak ada proses penyelesaian

3

1. Siswa telah mengimplementasikan strategi penyelesaian yang menuju pada jawaban yang benar, tapi terdapat bagian yang salah mengerti pada bagian masalah atau ada beberapa syarat yang terbengkalai.

2. Strategi penyelesaian yang tepat sudah teraplikasi, tetapi

a) Siswa menjawab permasalahan secara tidak tepat tanpa alasan jelas

b) Bagian numerikal yang benar pada jawaban telah diberikan tapi jawaban tidak dilabeli atau dilabeli secara salah

c) Tidak ada jawaban.

3. Jawaban yang benar telah diberikan dan beberapa tanda bahwa strategi penyelesaian yang tepat telah dipilih, tetapi penggunaan strategi tidak begitu jelas.

4

1. Siswa melakukan kesalahan dalam menyampaikan strategi penyelesaian. Tetapi, kesalahan tidak menunjukkan ketidakpahaman pada permasalahan atau pelaksanaan strategi. Tetapi, lebih pada kesalahan penulisan dan penyalinan. 2. Pemilihan dan pelaksanaan strategi penyelesaian tepat dan jawaban yang benar

(20)

Sebelumdigunakan dalam penelitian, terlebih dahulu soal tes tersebut diujicobakan pada siswa diluar sampel penelitian yang sudah mempelajari materi yang akan diujikan. Pengujian soal tes tersebut digunakan untuk mengetahui validitas butir soal, realibilitas tes, daya pembeda, dan indeks kesukaran butir soal. Data yang diperoleh dari hasil uji coba kemudian diolah dengan menggunakan bantuan Software AnatesV 4.0.7 tipe uraian.Berikut ini akan dijelaskan penentuan kualitas maupun kelayakan intrumen tes tersebut:

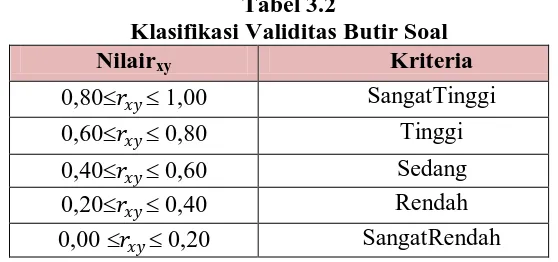
a. Validitas Butir Soal

Menurut Suherman (1990: 135) suatu alat evaluasi disebut valid (absah atau sahih), apabila alat tersebut mampu mengevaluasi apa yang seharusnya dievaluasi. Oleh karena itu keabsahannya bergantung pada sejauhmana ketepatan alat evaluasi itu dalam melaksanakan fungsinya, dengan demikian suatu alat evaluasi disebut valid jika ia dapat mengevaluasi dengan tepat sesuatu yang dievaluasi itu. Untuk mengetahui validitas butir soal dari suatu tes dapat menggunakan teknik korelasi product momen. Besarnya koefisien kolerasi tersebut dapat ditentukan dengan rumus (Suherman, 1990:154).

  

(21)

menurut Guilford (Suherman, 1990:147). Adapun klasifikasi koefisien

Hasil validitas diatas perlu diuji keberartiannya, dengan perumusan hipotesis :

H0 : validitas tiap butir soal tidak berarti H1 : validitas tiap butir soal berarti

Statistik ujinya sebagai berikut (Sugiyono , 2002:215).

= −2

1− 2

Keterangan :

r : validitas setiap butir soal n : banyaknya subjek

Berikut adalah perhitungan validitas pada instrumen tes yang diujicobakan pada siswa kelas VIII-4 SMP Negeri 9 Bandung sebanyak 31 siswa menggunakan Software AnatesV 4.0.7 dan diperoleh analisis validitas tiap butir soal instrumen pada tabel 3.3. Berdasarkan Tabel 3.3, validitas untuk soal no 1,2, 3, 4 dan 5 tergolong sedang artinya soal

(22)

menyebabkan H0ditolak, maka dapat disimpulkan bahwa setiap butir soal berarti. Hasil perhitungan selengkapnya dapat dilihat pada lampiran C.2.

Tabel 3.3

Hasil Analisis Validitas Butir Soal Instrumen Tes No

soal

Validitas Keberartian validitas butir soal

� Kriteria _� _�� Kesimpulan

1 0,52 Sedang 3,29 2,04 Validitas berarti 2 0,59 Sedang 3,96 2,04 Validitas berarti 3 0,58 Sedang 3,85 2,04 Validitas berarti 4 0,41 Sedang 2,41 2,04 Validitas berarti 5 0,51 Sedang 3,18 2,04 Validitas berarti

b. Reliabilitas Tes

Suherman (1990:167) menyatakan bahwa reliabilitassuatu alat ukur atau alat evaluasi dimaksudkan sebagai suatu alat yang memberikan hasil yang tetap sama (konsisten), hasil pengukuran itu harus tetap sama (relatif sama) jika pengukurannya diberikan pada subjek yang sama meskipun dilakukan orang, waktu dan tempat yang berbeda, tidak terpengaruh oleh pelaku, situasi dan kondisi. Untuk mencari koefisien reliabilitas soal tipe uraian (secara manual) dapat dihitung dengan menggunakan rumus Cronbach Alpha, yaitu :

11 = −₁ (1−

2

2 )

Keterangan:

11

r = koefisien reliabilitas perangkat tes

n = banyak butir soal (item)

s_i2 = jumlah varians skor tiap item

(23)

Dengan rumus varians:

2₌ 2

− ( )2

Keterangan :

= �ℎ

2 ₌ _�ℎ

2 ₌ _{� �}

n = jumlah subjek

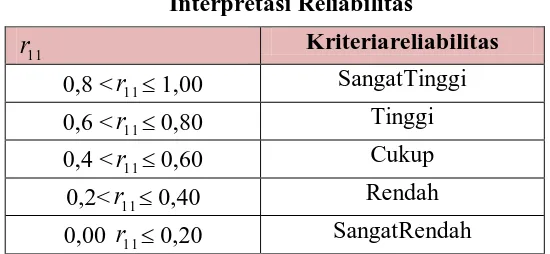
Guilford (Suherman, 1990:177) menyatakan bahwa kriteria untuk menginterpretasikan koefisien reliabilitas adalah:

Tabel 3.4

Interpretasi Reliabilitas

Perhitungan derajat realibititas pada instrumen tes yang diujicobakan pada siswa kelas VIII-4 SMP Negeri 9 Bandung sebanyak 31 siswa menggunakan Software Anates dan diperoleh koefisien reliabilitasnya sebesar 0,43. Hal ini menunjukkan bahwa soal yang dibuat mempuyai koefisien reliabilitasnya cukup,artinya instrumen tes akan mendapat hasil yang tetap sama (konsisten) meskipun dilakukan oleh orang, waktu dan tempat yang berbeda, tidak terpengaruh oleh pelaku, situasi dan kondisi .

11

r Kriteriareliabilitas

(24)

c. Daya Pembeda

Menurut Suherman (1990:199) daya pembeda dari sebuah butir soal menyatakan seberapa jauh kemampuan butir soal tersebut mampumembedakan antara testi yang mengetahui jawabannya dengan benar dengan testi yang tidak dapat menjawab soal tersebut (atau testi yang menjawab salah). Untuk menentukan daya pembeda tipe uraian menggunakan rumus (dalam Suherman, 1990:201).

��= � − �

��

Keterangan:

��= daya pembeda satu butir soal tertentu

� = rata-rata skor tiap butir soal dari siswa kelompok atas

� = rata-rata skor tiap butir soal dari siswa kelompok bawah

��= skor maksimal ideal (bobot)

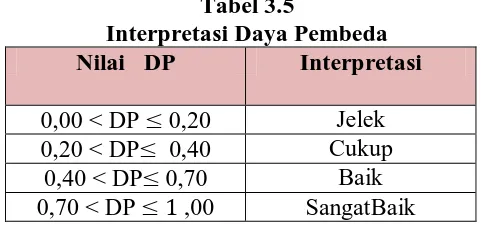
Kriteria yang

digunakanuntukmenginterpretasikandayapembedaadalahseperti pada (Suherman, 1990:202).

Tabel 3.5

Interpretasi Daya Pembeda Nilai DP Interpretasi

0,00 < DP 0,20 Jelek 0,20 < DP 0,40 Cukup

0,40 < DP 0,70 Baik 0,70 < DP 1 ,00 SangatBaik

Berikut adalah nilai daya pembeda dari tiap butir soal tes yang diujicobakan pada siswa kelas VIII-4 SMPN 9 Bandung sebanyak 31 siswa menggunakan software Anates.Berdasarkan Tabel 3.6, daya pembeda untuk soal nomor 1, 2, 3, 4 dan 5 tergolong cukup artinya soal

(25)

Tabel 3.6

Hasil Analisis Daya Pembeda Tiap Butir Soal

d. Indeks Kesukaran

Menurut Suherman (1990:212) derajat kesukaran suatu butir soal dinyatakan dengan bilangan yang disebut indeks kesukaran. Bilangan tersebut adalah bilangan real pada interval 0,00 sampai 1,00 yang menyatakan tingkatan mudah atau sukarnya suatu soal. Untuk menentukan indek kesukaran soal tipe uraian digunakan rumus:

�� = �

��

Keterangan:

��= indek kesukaran

� = Rata-rata

��= Skor Maksimal Ideal

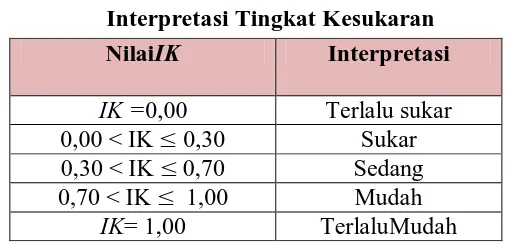
Adapun klasifikasi indeks kesukaran disajikan dalam tabel berikut:

Tabel 3.7

Interpretasi Tingkat Kesukaran

Berdasarkan data dari hasil ujicoba tes kemampuan berpikir kritis matematis yang dilakukan kepada siswa kelas VIII-4 SMPN 9 Bandung sebanyak 31 siswa, maka diperoleh nilai derajat kesukaran dari tiap

No Soal Daya Pembeda Kriteria

1 0,25 Cukup

2 0,31 Cukup

3 0,37 Cukup

4 0,25 Cukup

5 0,37 Cukup

NilaiIK Interpretasi

IK =0,00 Terlalu sukar 0,00 < IK 0,30 Sukar 0,30 < IK 0,70 Sedang 0,70 < IK 1,00 Mudah

(26)

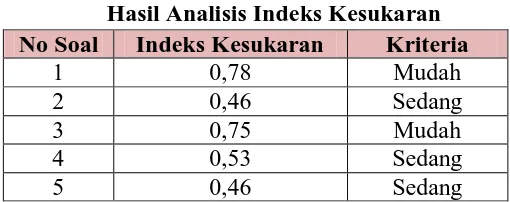
butir soal dengan menggunakan Software Anates pada Tabel 3.8. Berdasarkan Tabel 3.8, teryata untuk soal 1 dan 3 indeks kesukarannya mudah. Untuk soal no 2, 4, dan 5 indeks kesukarannya sedang. Untuk soal sedang hal ini berarti soal tersebut dapat dijawab benar oleh hanya sebagian siswa sedangkan untuk soal mudah hal ini berarti sebagian besar siswa dapat menjawab soal tersebut.

Tabel 3.8

Hasil Analisis Indeks Kesukaran

Data hasil analisis butir soal dengan menggunakan program komputer ANATES secara lengkap dapat dilihat pada lampiran.

2. Instrumen Non-Tes

a. Angket sikap siswa

Suherman (2003:56) mengemukakan bahwa angket adalah sebuah daftar pertanyaan atau pernyataan yang harus dijawab oleh orang yang akan dievaluasi (responden). Angket berfungsi sebagai alat pengumpul data, yang berupa keadaaan atau data diri, pengalaman, pengetahuan, sikap, pendapat mengenai suatu hal. Dalam penelitian ini, yang bertindak sebagai responden adalah siswa kelas eksperimen. Angket ini diberikan kepada siswa untuk mengetahui sikap siswa terhadap model pembelajaran yang digunakan di dalam kelas yaitu model pembelajaran berbasis masalah. Angket yang digunakan dalam penelitian ini, menggunakan skala Likert dengan derajat penilaian siswa terhadap suatu pernyataan terbagi kedalam 5 (lima) kategori yang tersusun secara

bertingkat, mulai dari Sangat Setuju (SS), Setuju (S), Netral(N), Tidak Setuju (TS) dan Sangat Tidak Setuju (STS). Angket ini diberikan kepada siswa pada pertemuan terakhir setelah posttestt.

No Soal Indeks Kesukaran Kriteria

1 0,78 Mudah

2 0,46 Sedang

3 0,75 Mudah

4 0,53 Sedang

(27)

b. Lembar observasi

Lembar observasi merupakan lembar aktivitas guru dan aktivitas siswa selama proses pembelajaran berlangsung. Lembar observasi ini bertujuan untuk mengetahui efektivitas penggunaan modelpembelajaran berbasis masalah di dalam kelas. Selain itu, lembar observasi ini juga digunakan sebagai bahan evaluasi bagi guru dengan melihat apakah pembelajaran yang berlangsung telah sesuai dengan indikator dan

langkah-langkah pelaksanaan model pembelajaran yang digunakan, sehingga akan ada perbaikan pada pembelajaran selanjutnya. Lembar observasi ini diisi oleh observer selama proses pembelajaran berlangsung.

c. Jurnal harian siswa

Jurnal harian siswadigunakan untuk mengetahui respon siswa terhadap pembelajaran matematika yang menggunakan model pembelajaran berbasis masalah. Selain itu, jurnal juga digunakan sebagai informasi untuk melakukan perbaikan pada pembelajaran berikutnya. Jurnal harian diberikan pada tiap akhir pembelajaran.

E. Prosedur Pelaksanaan Penelitian

Terdapat tiga tahap dalam posedur pelaksanaan penelitian ini yaitu tahap persiapan, tahappelaksanaan, dan tahap analisispenelitian.

1. Tahap Perencanaan

Tahap-tahap yang dilakukan dalam melakukan persiapan sebagai

berikut.

1) Mengidentifikasi masalah.

2) Menetapkanpokokbahasan yang akandigunakandalampenelitian. 3) Membuat instrumen penelitian.

(28)

6) Membuat rencana pelaksanaan pembelajaran dan bahan ajar penelitian.

7) Uji kelayakan RPPdaninstrumenpenelitianolehdosenpembimbing.

2. Tahap Pelaksanaan

Pada pelaksanaan penelitian dilakukan tahapan-tahapan sebagai berikut :

1) Melaksanakan pretest pada kelas kontrol dan kelas eksperimen. 2) Melaksanakan pembelajaran dengan penerapan pembelajaran

berbasis masalah pada kelas eksperimen dan pembelajaran dengan

metode konvesional. Kegiatan observasi dilakukan pada tahap pembelajaran ini. Tiap akhir pembelajaran siswa harus menulis dan mengumpulkan jurnal harian.

3) Pelaksanaan posttest pada kelas kontrol dan kelas eksperimen. 4) Penyebaran angket pada seluruh siswa.

3. Tahap Analisis

Pada tahap analisis dilakukan sebagai berikut : 1) Mengumpulkan data hasil penelitian.

2) Mengolah dan menganalisis hasil data kuantitatif (hasil test).

3) Mengolah dan menganalisis hasil data kualitatif (hasil angket dan observasi).

F. Teknik Analisis Data

Data yang diperoleh dari hasil penelitian adalah data kuantitatif dan kualitatif. Analisis data kuantitatif dalam penelitian ini meliputi analisis data pretest, posttest, dan indeksgain sedangkan data kualitatif diperoleh dari hasil pengisian angket, jurnal harian siswa, dan lembar observasi. Berikut ini analisis data kuantitatif dan data kualitatif.

(29)

Pengolahan data kuantitatif menggunakan uji statistik terhadap skor pretest, skor posttest, dan indek gain. Proses analisis data kuantitatif tersebut adalah:

a. Analisis kemampuan berpikir kritis matematis awal (pretest)

Untuk mengetahui kemampuan berpikir kritis matematis awal siswa pada kelas eksperimen dan kelas kontrol, analisis dilakukan pada data pretest. Pada pengolahan data penulis menggunakan bantuan software Statistical Product and Service Solution (SPSS) versi 16.0for Windows. Adapun langkah-langkah uji statistiknya adalah sebagai berikut.

1) Analisis Data Deskriptif

Sebelum dilakukan pengujian terhadap data hasil pretest terlebih dahulu dilakukan perhitungan terhadap deskripsi data yang meliputi rata-rata, simpangan baku, nilai maksimum, dan nilai minimum. Hal ini dilakukan untuk memperoleh gambaran mengenai data yang akan diuji. Adapun langkah-langkahnya sebagai berikut:

a) Uji Normalitas

Uji normalitas dilakukan untuk mengetahui apakah skor skor pretest sampel berasal dari populasi yang berdistribusi normal atau tidak. Pengujian normalitas dilakukan dengan menggunakan uji statistik Saphiro-Wilk dengan taraf signifikansi 0,05.Jika skor pretest berdistribusi normal, uji statististik selanjutnya yang dilakukan adalah uji homogenitas varians.Tetapi, jika minimal terdapat satu kelas penelitian yang berdistribusi tidak normal maka uji homogenitas tidak perlu dilakukan melainkan dilakukan uji statistika non-parametrik, yaitu

uji Mann-Whitney U. Perumusan hipotesis pengujian normalitas adalah sebagai berikut.

H0: skor pretest berasal dari populasi yang berdistribusi normal H1: skor pretest berasal dari populasi yangberdistribusi tidak normal

(30)

 Jika nilai Sig < 0,05 maka H0 ditolak

 Jika nilai Sig 0,05 maka H0 diterima

b) Uji Homogenitas Varians

Uji homogenitas varians dilakukan untuk mengetahui apakah variansinya homogen atau tidak homogen antara kelas eksperimen dengan kelas kontrol. Apabila skor berdistribusi normal maka dilanjutkan dengan uji homogenitas varians dengan menggunakan uji Levene’s test dengan taraf signifikansi 0,05. Perumusan hipotesisnya sebagai berikut.

H0: Tidak terdapat perbedaan variansi skor pretestantara siswa yang

mengikuti pembelajaran dengan model pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran konvensional.

H1: Terdapat perbedaan variansi skor pretestantara siswa yang mengikuti pembelajaran dengan model pembelajaran berbasis masalah dengan

siswa yang mengikuti pembelajaran konvensional.

Dengan menggunakan taraf signifikansi 5%, maka kriteria pengujiannya adalah sebagai berikut:

c) Uji Kesamaan Dua Rata-Rata

Uji kesamaan dua rata-rata dilakukan untuk mengetahui apakah ada perbedaan rata-rata skorpretest secara signifikan antara kedua kelas penelitian. Jika kedua kelas berasal dari populasi yang berdistribusi normal dan varians homogen, maka untuk pengujian hipotesis dilakukan uji t. Jika kedua kelas berasal dari populasi yang berdistribusi normal dan tidak homogen maka, pengujian hipotesis dilakukan uji t’. Perumusan hipotesis pengujiannya adalah sebagai berikut.

H0: Tidak terdapat perbedaan kemampuan berpikir kritis matematis awal siswa yang mengikuti pembelajaran dengan model pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran

(31)

H1:Terdapat perbedaan kemampuan komunikasi matematis awal siswa yang mengikuti pembelajaran dengan model pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran konvensional. Dengan menggunakan tarafsignifikansi 5%, maka kriteria pengambilan keputusannya adalah sebagai berikut:

b. Analisis Kemampuan Berpikir Kritis Matematis Akhir (Posttest).

Untuk mengetahui kemampuan berpikir kritis matematis akhir siswa di kelas eksperimen dan kelas kontrol, analisis dilakukan pada data posttest. Pada pengolahan data penulis menggunakan bantuan software Statistical Product and Service Solution (SPSS) versi 16.0 for Windows. Adapun langkah-langkah uji statistiknya adalah sebagai berikut.

Sebelum dilakukan pengujian terhadap skor hasil posttest terlebih dahulu dilakukan perhitungan terhadap deskripsi data yang meliputi rata-rata, simpangan baku, nilai maksimum, dan nilai minimum. Hal ini dilakukan untuk memperoleh gambaran mengenai data yang akan diuji. Adapun langkah-langkahnya sebagai berikut:

Uji normalitas dilakukan untuk mengetahui apakah skor posttest sampel berasal dari populasi yang berdistribusi normal atau tidak. Pengujian normalitas dilakukan dengan menggunakan uji statistik Saphiro-Wilk dengan taraf signifikansi 0,05.

Jika skor posttest berdistribusi normal, uji statististik selanjutnya yang dilakukan adalah uji homogenitas varians. Tetapi, jika minimal terdapat satu kelas penelitian yang berdistribusi tidak normal maka uji homogenitas varians tidak perlu dilakukan melainkan dilakukan uji statistik

(32)

H0: skor posttest berasal dari populasi yang berdistribusi normal H1: skor posttest berasal dari populasi yang berdistribusi tidak normal Kriteria pengujiannya sebagai berikut.

b) Uji Homogenitas Varians

Uji homogenitas dilakukan untuk mengetahui apakah variansinya homogen atau tidak homogen antara kelas eksperimen dengan kelas kontrol. Apabila skor berdistribusi normal maka dilanjutkan dengan uji

homogenitas varians dengan menggunakan uji Levene’s test dengan taraf signifikansi 0,05. Perumusan hipotesis pengujiannya adalah sebagai berikut.

H0: Tidak terdapat perbedaan variansi skor postestantara siswa yang

mengikuti pembelajaran dengan model pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran konvensional.

H1:Terdapat perbedaan variansi skor postestantara siswa yang mengikuti pembelajaran dengan model pembelajaran berbasis masalah dengan siswa yang mengikuti pembelajaran konvensional.

Dengan menggunakan taraf signifikansi 5%, maka kriteria pengujiannya adalah sebagai berikut:

c) Uji Perbedaan Dua Rata-Rata

Uji perbedaan dua rata dilakukan untuk mengetahui apakah rata-rata skor posttest kedua kelas sama atau tidak. Jika kedua kelas berasal dari populasi yang berdistribusi normal dan varians homogen maka, untuk pengujian hipotesis dilakukan uji t atau Independent Sample T-Test. Sedangkan jika kedua kelas berasal dari populasi yang berdistribusi normal dan varians tidak homogen, maka pengujian hipotesis dilakukan uji

(33)

H0: Kemampuan berpikir kritis matematis siswa yang mengikuti pembelajaran dengan model pembelajaran berbasis masalah tidak lebih baik dengan siswa yang mengikuti pembelajaran konvensional. H1:Kemampuan berpikir kritis matematis siswa yang mengikuti

pembelajaran dengan model pembelajaran berbasis masalahlebih baik daripada siswa yang mengikuti pembelajaran konvensional. Dengan menggunakan taraf signifikansi 5%, maka kriteria pengambilan keputusannya adalah sebagai berikut:

c. AnalisisPeningkatan Kemampuan Berpikir Kritis Matematis Siswa

Jika hasil pretest menunjukkan bahwa tidak terdapat perbedaan

kemampuan berpikir kritis matematis siswa yang signifikan antara kelas eksperimen dan kelas kontrol, maka untuk mengetahui peningkatan kemampuan berpikir kritis matematis siswa dapat menggunakan data hasil posttest, gain, atauindeksgain (gain ternormalisasi). Akan tetapi jika pada hasil pretest menunjukkan bahwa terdapat perbedaan kemampuan berpikir kritis matematis awal siswa antara kelas eksperimen dan kelas kontrol yang signifikan, maka peningkatan kemampuan berpikir kritis matematis siswa dapat diketahui melalui indeks gain. Analisis ini dilakukan untuk mengetahui apakah peningkatan kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran dengan model pembelajaranberbasis masalah lebih baik daripada siswa yang memperoleh pembelajaran

konvensional. Adapun indeks gain dihitung dengan rumus sebagai berikut:

Indeks gain = � – � �

� − � �

(34)

Selanjutnya, dalam mengolah data penulis menggunakan bantuan software Statistical Product and Service Solution (SPSS) versi 16.0for Windows.

Sebelum melakukan pengujian terhadap data indeks gain terlebih dahulu dilakukan perhitungan terhadap deskripsi data yang meliputi rata-rata, simpangan baku, nilai maksimum, dan nilai minimum.Hal ini dilakukan untuk memperoleh gambaran mengenai data yang akan diuji. Adapun langkah-langkahnya sebagai berikut:

Uji normalitas dilakukan untuk mengetahui apakah skor indeks gain sampel berasal dari populasi yang berdistribusi normal atau tidak. Pengujian normalitas dilakukan dengan menggunakan uji statistik Saphiro-Wilk dengan taraf signifikansi 0,05.

Jika data indeks gainberdistribusi normal, uji statististik selanjutnya yang dilakukan adalah uji homogenitas varians. Tetapi, jika terdapat minimal satu kelas penelitian yangberdistribusi tidak normal, maka uji homogenitas varians tidak perlu dilakukan melainkan dilakukan uji statistika non-parametrik, yaitu uji Mann-WhitneyU. Perumusan hipotesisnya sebagai berikut.

H0: skorindeks gain berasal dari populasi yang berdistribusi normal H1: skorindeks gain berasal dari populasi yang tidak berdistribusi

normal

Kriteria pengujiannya sebagai berikut.  Jika nilai Sig < 0,05 maka H0 ditolak

b)Uji Homogenitas Varians

(35)

homogen. Apabila data berdistribusi normal, maka dilanjutkan dengan uji homogenitas varians dengan menggunakan uji Levene’s test dengan taraf signifikansi 0,05. Perumusan hipotesisnya sebagai berikut.

H0: Tidak terdapat perbedaan varians peningkatan berpikir kritis matematis siswa antara yang mengikuti pembelajaran dengan model pembelajaran berbasis masalahdengan siswa yang mengikuti pembelajaran konvensional.

H1: Terdapat perbedaan peningkatan kemampuan berpikir kritis matematis siswa yang mengikuti pembelajaran dengan model

pembelajaran berbasis masalahlebih baik daripada siswa yang mengikuti pembelajaran konvensional.

Dengan menggunakan taraf signifikansi� = 5%, maka kriteria pengujiannya adalah sebagai berikut:

c) Uji Perbedaan Dua Rata-Rata

Uji perbedaan dua rata-rata dilakukan untuk mengetahui apakah

rata-rata skorindeks gainkelas eksperimen lebih baik daripada kelas kontrol atau tidak. Jika kedua kelas berasal dari populasi yang berdistribusi normal dan varians homogen, maka untuk pengujian hipotesis dilakukan uji t atau Independent Sample T-Test. Sedangkan jika kedua kelas berasal dari populasi yang berdistribusi normal dan varians tidak homogen maka, pengujian hipotesis dilakukan uji t’. Perumusan hipotesisnya sebagai berikut.

H0: Peningkatan kemampuan berpikir kritis matematis siswa yang mengikuti pembelajaran dengan model pembelajaran berbasis masalah tidak lebih baik dengan siswa yang mengikuti pembelajaran konvensional.

(36)

masalahlebih baik daripada siswa yang mengikuti pembelajaran konvensional.

Dengan menggunakan taraf signifikansi� = 5%, maka kriteria pengambilan keputusannya adalah sebagai berikut:

 Jika 1

2nilai Sig < 0,05 maka H0 ditolak

 Jika 1

2nilai Sig 0,05 maka H0 diterima

d. Analisis Kualitas Peningkatan Kemampuan Berpikir Kritis Matematis

Kualitas peningkatan kemampuan berpikir kritis matematis siswa dihitung dengan menggunakan indeks gain. Kemudian secara deskriptif dilakukan analisis dengan menggunakan kriteria klasifikasi indeks gain. Adapun kriteria klasifikasi indeks gain tersebut terdapat dalam tabel berikut(Hake, 1999).

Tabel 3.9

Kriteria Klasifikasi Indeks Gain

Indeksgain Kriteria

<�>> 0,70 Tinggi 0,30 << �> 0,70 Sedang

<�> 0,30 Rendah

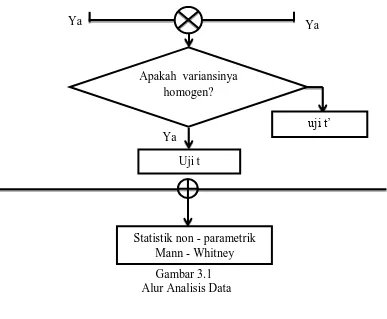
Adapun alur analisis data, selebihnya dapat dilihat pada gambar berikut.

Data pretest Data posttest

Apakah data berdistribusi

Apakah data berdistribusi Tidak

(37)

Gambar 3.1 Alur Analisis Data

Keterangan :

= Dan

= Atau

2. Analisis Data Kualitatif

a. Data Angket

Tujuan adanya angket adalah untuk mengetahui sikap siswa terhadap pembelajaran yang berlangsung. Setelah semua data angket terkumpul, langkah selanjutnya adalah melakukan analisis dengan

Apakah variansinya homogen?

Uji t

uji t’

Ya _Ya

Statistik non - parametrik Mann - Whitney

Ya

(38)

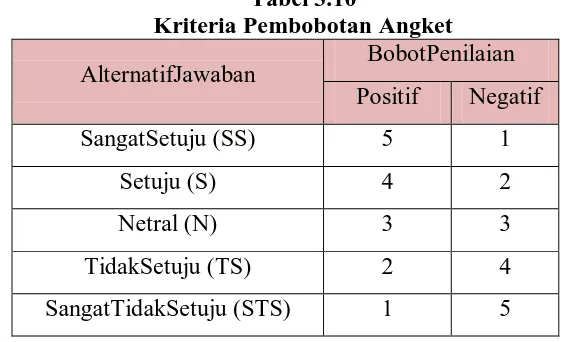
cara memberi bobot pada setiap pernyataan siswa (Suherman, 2003: 190). Pembobotan yang diberikan adalah sebagai berikut.

Tabel 3.10

Kriteria Pembobotan Angket

AlternatifJawaban BobotPenilaian Positif Negatif

SangatSetuju (SS) 5 1

Setuju (S) 4 2

Netral (N) 3 3

TidakSetuju (TS) 2 4

SangatTidakSetuju (STS) 1 5

Pada penelitian ini, pilihan jawaban Netral (N) tidak digunakan karena siswa yang ragu-ragu mengisi pilihan jawaban memiliki

kecenderungan yang besar untuk memilih jawaban Netral (N). Kriteria penilaian sikap dari angket tersebut adalah jika skor pernyataan kelas lebih dari 3 maka siswa menunjukkan sikap positif, jika skor pernyataan kurang dari 3 maka siswa menunjukkan sikap negatif (Suherman, 2003 : 191).

b. Pengolahan Data Observasi

Penilaian data hasil observasi dilakukan dengan menyimpulkan hasil pengamatan observer selama pembelajaran berlangsung dan disajikan dalam bentuk tabel. Kemudian dianalisis mengenai keberhasilan model pembelajaran yang diterapkan.

c. Analisis Jurnal Harian Siswa

(39)

(40)

74

BAB V

KESIMPULAN DAN SARAN

A. Kesimpulan

Berdasarkan hasil analisis data dan pembahasan pada keseluruhan tahapan penelitian, diperoleh beberapa kesimpulan yang berkaitan dengan penerapan pembelajaran berbasis masalah terhadap peningkatan kemampuan berpikir kritis matematis siswa kelas VII di SMPN 15 Bandung. Adapun kesimpulan yang diambil dari penelitian ini adalah sebagai berikut:

1. Peningkatan kemampuan berpikir kritis matematis siswa yang mendapatkan pembelajaran dengan pembelajaran berbasis masalah lebih besar daripada siswa yang mendapatkan pembelajaran dengan pembelajaran konvesional.

2. Siswa menunjukkan sikap yang positif terhadap pembelajaran berbasis masalah danterhadap pelajaran matematika.

B. Saran

Berdasarkan hasil penelitian dan kesimpulan mengenai pembelajaran berbasis masalah, maka dapat direkomendasikan beberapa hal sebagai berikut:

1. Pada tahap kegiatan dibutuhkan waktu yang cukup panjang. Oleh karena itu, dibutuhkan kecakapan guru dalam mengelola kelas agar waktu yang terpakai cukup efektif sehingga pembelajaran dapat selesai sesuai dengan tujuan yang telah direncanakan.

2. Ketika proses pembelajaran berlangsung guru harus lebih tegas dalam

(41)

DAFTAR PUSTAKA

Amir, M. T. (2009). Inovasi Pendidikan Melalui Problem Based Learning. Jakarta: Kencana Prenada Media Group.

Charles, R. (1987). The National Of Teachers Of Mathematics, Inc. America: Reston

Depdiknas. (2006). Kurikulum 2006 Model Matematika SMP/MTs. Jakarta: Departemen Pendidikan Nasional.

Fachrurazi. (2011). Penerapan Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Berpikir Kritis dan Komunikasi Matematis Siswa Sekolah Dasar. Disertasi FPMIPA UPI Bandung: Tidak diterbitkan.

Fauzi, M. A. (2011). Peningkatan Kemampuan Koneksi Matematis dan Kemandirian Belajar Siswa dengan Pendekatan Pembelajaran Metakognitif di Sekolah Menengah Pertama. Disertasi FPMIPA UPI Bandung. Tidak diterbitkan.

Fisher, A. (2009). Bepikir Kritis. Jakarta: Erlangga.

Hake.R.(1999).Analizing Change/Gain Scores.[Online].Tersedia: http://www.physics.indiana.edu/~sdi/AnalyzingChange-Gain.pdf [7 Januari 2014].

Malik, A. (2011). Meningkatkan Kemampuan Berpikir Logis Dan Sikap

Positif Siswa Terhadap Matematika Melalui Realistic Mathematics Education (RME) Pada Materi Aritmatika Sosial Siswa Kelas V11 MTs Surya Buana Malang. [Online]. Tersedia:

http://library.um.ac.id/ptk/index.php?mod=detail&id=47085.

Mayadiana, D. (2005). Pembelajaran dengan Pendekatan Diskursif untuk Meningkatkan Kemampuan Berpikir Kritis Matematika Mahasiswa Calon Guru Sekolah Dasar. Tesis PPS UPU Bandung. Tidak diterbitkan

Noer, S. H. (2009). Peningkatan Kemampuan Berpikir Kritis Matematis Siswa SMP Melalui Pembelajaran Berbasis Masalah. Makalah Seminar Nasional Matematika dan Pendidikan Matematika Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

(42)

Nurafiah, F. (2013). Perbandingan Peningkatan Kemampuan Berpikir Kritis Siswa SMP Antara Memperoleh Pembelajaran MEANS-ENDS ANALYSIS (MEA) dan Problem Based Learning (PBL). Skripsi UPI. Bandung: tidak diterbitkan.

Palacios, Andres., dkk. (2014). Attitudes Towars Mathematics: Construction and Validation of a Measurement Instrument. [Onilne]: tersedia:http://www.ehu.es/ojs/index.php/psicodidactica/article/downl oad/8961/9945. [23 Mei 2014].

Prabawanto, S. (2013). Peningkatan Kemampuan Pemecahan Masalah, Komunikasi dan Self-Efficacy Matematis Mahasiswa Melalui Pembelajaran dengan Pendekatan Metacognitive Scaffolding. Disertasi PPS UPI: Tidak diterbitkan.

Prastowo, A. (2011). Panduan Kreatif Membuat Bahan Ajar Inovatif. Jogjakarta: DIVA Press.

Razali, N. (2011). Power Comparisons Of Shapiro-Wilk, Kolmogorov-Smirnov, Liliefors and Anderson-Dailing Tests. [Online]. Tersedia: http://instatmy.org.my/downloadss/e-jurnal%202/3.pdf. [10April 2014].

Rohayati, A. (2005). Pendekatan Kontekstual dalam Pembelajaran Matematika untuk Meningkatkan Berpikir. Skripsi FPMIPA UPI Bandung: Tidak diterbitkan.

Rohaeti, E. E. (2008). Pembelajaran dengan Pendekatan Eksplorasi Untuk Mengembangkan Kemampuan Berpikir Kritis Dan Kreatif Matematik Siswa Sekolah Menengah Pertama. Disertasi Sekolah Pasca Sarjana UPI. Bandung : Tidak diterbitkan.

Ruseffendi, E.T. (1988). Pengantar kepada membantu guru mengembangkan

kompetensinya dalam pengajaran matematilia untuk meningkatkan CBSA. Bandung: Tarsito.

Russefendi, dkk. (2014). Seminar Nasional Pendidikan Matematika Program Pasca Sarjana STKIP Siliwangi Bandung Tahun 2014.

[Online]. Tersedia:

http://publikasi.stkipsiliwangi.ac.id/keyword/seminar-nasional- pendidikan-matematika-program-pasca-sarjana-stkip-siliwangi-bandung-tahun-2014/. [6 Jun 2014].

(43)

Ruseffendi, E. T. (2005). Dasar-dasar Matematika Modern dan Komputer untuk Guru Edisi 5. Bandung: Tarsito.

Rusgianto. (2006). Hubungan Antara Sikap Terhadap Matematika, Kecerdasan Emosional Dalam Interaksi Sosial Di Kelas Dengan Hasil Belajar Matematika Siswa Smp Negeri 5 Yogyakarta Tahun 2006Dipresentasikan dalam Seminar Nasional Matematika dan Pendidikan Matematika 2006 dengan tema “Trend Penelitian dan Pembelajaran Matematika di Era ICT “yang diselenggarakan pada tanggal24 Nopember 2006.

Sihotang, K. (2012). Critical Thinking. Jakarta: PT. Pustaka Sinar Harapan.

Silalahi, Y. S. (2013). Peningkatan Kemampuan Berpikir Kritis Matematis Siswa SMP Dengan Menggunakan Model Pembelajaran Generatif. Skripsi FPMIPA UPI Bandung: Tidak diterbitkan.

Sodikin.(2009). Penyesuaian Dengan Modus Pembelajaran untuk Siswa

SMK Kelas X [Online]. Tersedia:

http://eprints.binadarma.ac.id/443/1/JURNAL%20PENYESUAIAN% 20DENGAN%20MODUS%20PEMBELAJARAN%20UNTUK%20S ISWA%20SMK%20KELAS%20X.pdf. [ 22 Jan 2014]

Sugiyono. (2002). Buku Statistika untuk Peneltian. Bandung: CVAlfabeta

Sukiman. (2008). Teori Pembelajaran Dalam Pandangan Konstruktivisme dan Pendidikan Islam. [Online]. Tersedia: http://digilib.uinsuka.ac.id/8586/1/SUKIMAN%20TEOR1%20PEMB ELAJARAN%20DALAM%20PANDANGAN%20KONSTRUKTIVI SME%20DAN%20PENDIDIKAN%20ISLAM.pdf. [26 Mei 2014]

Suherman, E., dkk. (2001). Strategi Pembelajaran Matematika Kontemporer. Bandung: JICA

Suherman, E. (2003). Eveluasi Pembelajaran Matematika. Bandung: JICA.

Suherman, Erman. (1990). Evaluasi Pendidikan Matematika. Bandung: Wijayakusumah.

(44)

pada tanggal 3 Desember 2011 di Jurusan Pendidikan Matematika FMIPA UNY.

Suryadi, D. (2011). Pendidikan Matematika. [Online]. Tersedia:

http://didi-suryadi.staf.upi.edu/files/2011/06/PENDIDIKAN-MATEMATIKA.pdf.[29 Mei 2014]

Tim MKPBM. (2001). Strategi Pembelajaran Matematika Kontemporer. Bandung: JICA – Universitas Pendidikan Indonesia.

Tim Sosialisasi KTSP Dikti. Pengembangan Bahan Ajar. [Online]. Tersedia: http://www.dikti.go.id/files/atur/KTSP/11.ppt [10 April 2013]

Widarti, A. (2007). Efektifitas Penggunaan Model Pembelajaran Kooperatif Tipe Thunk Pair Share Terhadap Hasil Belajar Pokok Bahasan Segi Empat Pada Siswa Kelas VII Semester 2. [Online]. Tersedia:http://digilib.unnes.ac.id/gsdl/collect/skripsi/archives/HASH 019d.dir/doc.pdf [12 April 2014].

Wijaya, Adi. (2014). Bukti Empirik Keberhasilan Model Pembelajaran Berbasis Masalah (Problem Based Learning) dalam Proses dan Hasil Pembelajaran Matematika SMP. [Online]. Tersedia: