i
ANALISIS TITIK EKUILIBRIUM DAN SOLUSI MODEL
INTERAKSI MUTUALISME DUA SPESIES MENGGUNAKAN
METODE ITERASI VARIASIONAL
TESIS
Diajukan untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Magister Pendidikan Program Studi Magister Pendidikan Matematika
Oleh :
Benedictus Dwi Yuliyanto
NIM: 15 1442 005
HALAMAN JUDUL
PROGRAM STUDI MAGISTER PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
iv
HALAMAN MOTTO
Ibarat makan,
belajar bukan lagi suatu keinginan, melainkan kebutuhan.
Rasa lapar akan pengetahuan, datang disetiap hari.
(B.Dwi Yuliyanto)
Jika kau punya mimpi, tetap fokus dan nikmatilah.
Lalu bangun dan wujudkanlah!
(B.Dwi Yuliyanto)
Hanya mereka yang berani gagal dapat meraih keberhasilan.
(Robert F. Kennedy)
vi
ABSTRAK
Benedictus Dwi Yuliyanto, 2017. Analisis Titik Ekuilibrium dan Solusi Model
Interaksi Mutualisme Dua Spesies Menggunakan Metode Iterasi Variasional.
Tesis. Program Studi Magister Pendidikan Matematika, Jurusan Pendidikan
Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu
Pendidikan, Universitas Sanata Dharma, Yogyakarta.
Tesis ini mengkaji tentang analisis titik ekuilibrium dan solusi model interaksi dua spesies. Pada bidang biologi, seringkali dilakukan penelitian atau percobaan mengenai laju pertumbuhan populasi suatu spesies. Penelitian-penelitian tersebut dilakukan untuk mengetahui berbagai macam perkembangan makhluk hidup di lingkungannya. Pemodelan matematika sangat berperan dalam membantu penelitian tersebut. Salah satu model matematika yang pernah diteliti adalah model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik.
Pada penelitian ini, peneliti akan memodifikasi model matematika tersebut dengan tujuan menambah variasi dari model dasar yang sudah ada. Modifikasi model yang akan diteliti adalah model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik yaitu: pertama, terdapat unsur pemanenan pada salah satu jenis spesies, dan yang kedua, terdapat unsur pemanenan pada kedua jenis spesies.
Setelah melakukan modifikasi pada model, peneliti melakukan analisis kestabilan dari titik ekuilibrium yang didapat. Selanjutnya akan dicari solusi dari perumuman model interaksi dua spesies menggunakan metode iterasi variasional.
vii
ABSTRACT
Benedictus Dwi Yuliyanto, 2017. Analysis of Equilibrium Points and Solutions
of Models of Two Species Mutualism Interaction Using Variational Iteration
Method. Thesis. Study Program of Master of Mathematics Education,
Department of Mathematics and Science Education, Faculty of Teacher
Training and Education, Sanata Dharma University, Yogyakarta.
This tesis discusses about analysis of equilibrium points and solutions of models of two species interaction. In biology, research or experiment about population growth rate is done frequently. The research has been succeesful for knowing many kinds of organism in their environment. Mathematical modelling is important for helping that research. One of the mathematical models that has been studied before is the mutualism interaction model of two species in logistic growth. In this research, the researcher will modify the mathematical model to add the variations of the basic model before. The modifications studied in this thesis are: first, there is a harvesting parameter on one of species, and second, on both of them. After doing the modifications on the model, the researcher analyses the stability of equilibrium points. Furthermore, the modified model is solved using the variational iteration method.
ix
DAFTAR PUBLIKASI HASIL PENELITIAN TESIS
Sebagian hasil dari tesis ini telah dipresentasikan dalam konferensi internasioanl dan/atau dipublikasikan dalam jurnal internasional sebagai berikut: [1]. B.D. Yuliyanto dan S. Mungkasi, “Variational iteration method for solving
x
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Esa, karena hanya dengan berkat dan karunia-Nya, serta campur tangan-Nya, penulis dapat menyelesaikan tesis yang berjudul “Analisis Titik Ekuilibrium dan Solusi Model Interaksi Mutualisme Dua Spesies Menggunakan Metode Iterasi Variasional” dengan baik dan tepat waktu.
Pada kesempatan ini penulis juga ingin mengucapkan rasa terima kasih kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dosen pembimbing yang sudah meluangkan waktu dan dengan sabar membimbing penulis, sehingga tesis ini dapat diselesaikan dengan baik.
2. Bapak Dr. Marcellinus Andy Rudhito, S.Pd., selaku Ketua Program Studi Magister Pendidikan Matematika.
3. Bapak Dr. rer. nat. Herry Pribawanto Suryawan yang telah membimbing pada awal penulisan tesis ini.
4. Segenap dosen JPMIPA yang telah membantu dan memberikan dukungan selama penulis menempuh kuliah, sehingga akhirnya penulis dapat menyelesaikan studi dengan tepat waktu.
xi
6. Kedua orang tua yaitu Bapak Mario Subiyanto dan Ibu Christina Sarasni, yang selalu memberikan dukungan serta doa yang melimpah kepada penulis sehingga tesis ini dapat diselesaikan tepat waktu.
7. Segenap keluarga, terutama Simbah Yohanes Sadji Ciptotanyono dan Mas Albertus Magnus Bayu Pratomo yang selalu memberi semangat, motivasi, serta inspirasi kepada penulis sehingga penulis mampu menyelesaikan studi dengan baik.
8. Elisabeth Evi Alviah, yang selalu memberikan semangat, dukungan, serta motivasi yang sangat berguna bagi penulis selama menjalankan studi. 9. Semua teman seperjuangan dari Program Studi Magister Pendidikan
Matematika angkatan 2015-2016 yang memberikan dukungan kepada penulis selama studi.
10.Semua pihak yang tidak dapat disebutkan satu per satu, yang telah membantu sehingga penulis dapat menyelesaikan tesis ini.
Akhirnya penulis berharap semoga tesis ini dapat berguna bagi para pembaca.
Penulis,
xii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... viii
DAFTAR PUBLIKASI HASIL PENELITIAN TESIS ... ix
KATA PENGANTAR ... x
BAB II LANDASAN TEORI ... 10
A. Pemodelan Matematika ... 10
B. Persamaan Diferensial ... 12
C. Sistem Persamaan Diferensial Nonlinear ... 15
D. Model Pertumbuhan Logistik ... 33
E. Model Interaksi Simbiosis Mutualisme Dua Spesies yang Bertumbuh secara Logistik ... 40
F. Metode Iterasi Variasional ... 50
G. Kerangka Berpikir ... 51
BAB III HASIL DAN PEMBAHASAN ANALISIS KESTABILAN MODEL ... 52
xiii
B. Model Interaksi Simbiosis Mutualisme Dua Spesies yang Bertumbuh secara
Logistik dengan Unsur Pemanenan pada Kedua Jenis Spesies ... 61
BAB IV HASIL DAN PEMBAHASAN SOLUSI MODEL DENGAN METODE ITERASI VARIASIONAL ... 71
BAB V ASPEK PENDIDIKAN ... 83
A. Pembelajaran di SMA ... 84
B. Pembelajaran di S1 ... 85
C. Refleksi Penelitian di Bidang Matematika ... 86
BAB VI PENUTUP ... 90
A. Kesimpulan ... 90
B. Saran ... 91
1
BAB I
PENDAHULUAN
BAB I PENDAHULUANA. Latar Belakang
Pada bidang biologi, salah satu masalah yang sering dihadapi adalah masalah mengenai pertumbuhan populasi. Seringkali dilakukan penelitian atau percobaan mengenai laju pertumbuhan populasi suatu spesies untuk mengetahui berbagai macam perkembangan makhluk hidup di lingkungannya.
Pertumbuhan populasi suatu spesies ditandai dengan adanya perubahan populasi setiap satuan waktu yang dipengaruhi oleh jumlah kematian, kelahiran, serta perpindahan (migrasi). Jumlah populasi suatu spesies dapat diamati secara langsung dalam jangka waktu tertentu. Selain itu, dapat juga dilakukan perhitungan untuk mengetahui laju pertumbuhan dari suatu spesies tersebut dengan data yang sudah ada. Salah satu cabang ilmu matematika yang dapat membantu menyelesaikan permasalahan tersebut adalah pemodelan matematika.
B. Tinjauan Pustaka
Berbagai penelitian mengenai dinamika populasi suatu spesies dan penggunaan metode iterasi variasional untuk menyelesaikan persamaan diferensial sudah banyak dilakukan. Diagram 1.1 memberikan gambaran letak dari penelitian yang dilakukan dengan penelitian-penelitian yang sudah ada.
Diagram 1.1 Bagan dari letak penelitian yang dilakukan
Stability analysis of
Variational iteration method for solving the population dynamics model of two species
(Yuliyanto dan Mungkasi, 2017) Analisis titik ekuilibrium model interaksi
Beberapa penelitian sejenis yang membahas tentang dinamika populasi suatu spesies dan metode iterasi variasional antara lain:
Pertama, penelitian B. Ravindra Reddy (2012) dengan judul “Stability analysis of two mutually interacting species with unlimited resources for both the
species”. Makalah ini membahas mengenai analisis dari model dua spesies yang saling berinteraksi dengan sumber daya atau daya dukung untuk kedua spesies yang tak terbatas. Karakteristik dari model merupakan dua sistem persamaan diferensial biasa nonlinear order satu. Sebelum mendiskripsikan model, dibuat asumsi sebagai berikut: � merupakan banyaknya individu dalam populasi dari spesies pertama, � merupakan banyaknya individu dalam populasi dari spesies kedua, dan berturut-turut adalah laju pertumbuhan alami dari spesies pertama dan kedua, merupakan laju peningkatan pertumbuhan dari spesies pertama akibat interaksi dengan spesies kedua, dan merupakan laju peningkatan pertumbuhan dari spesies kedua akibat interaksi dengan spesies pertama. Catatan lebih lanjut bahwa variabel � , � dan parameter , , , bernilai tak negatif. Jika laju kematian lebih besar dari laju kelahiran, maka digunakan notasi yang sama dengan tanda negatif pada tingkat pertumbuhan alami untuk membedakannya. Persamaan dasar untuk laju pertumbuhan spesies pertama � adalah sebagai berikut:
�
= � + � � . (1.1)
Persamaan dasar untuk laju pertumbuhan spesies kedua � adalah sebagai berikut:
�
Syarat ekuilibrium � = dan � = , sehingga diperoleh
� + � = dan � + � = . (1.3)
Solusi �̅ , �̅ dari (1.3) merupakan ekuilibrium dari sistem (1.1)-(1.2). Sistem tersebut memiliki satu keadaan setimbang yaitu �̅ = , �̅ = , dalam keadaan ini, kedua spesies bertumbuh tanpa batas.
Kedua, penelitian Batiha, Noorani, dan Hashim (2007) dengan judul
“Variational iteration method for solving multispecies Lotka -Volterra equations”.
Makalah tersebut membahas mengenai penggunaan metode iterasi variasional untuk menyelesaikan atau mencari solusi dari model pertumbuhan populasi suatu spesies yang bertumbuh secara logistik, atau model pertumbuhan dengan menggunakan persamaan Lotka-Volterra. Pada makalah tersebut dibahas juga mengenai beberapa metode yang digunakan untuk menyelesaikan masalah yang sama. Hasil dari penggunaan metode iterasi variasional untuk mencari pendekatan solusi model, dibandingkan dengan metode dekomposisi Adomian dan Runge-Kutta order empat.
Dari tinjauan pustaka mengenai dinamika populasi suatu spesies tersebut, didapat bahwa pemodelan dari dinamika populasi merupakan suatu hal yang penting dalam proses mengontrol laju dari pertumbuhan populasi suatu spesies. Pertumbuhan populasi suatu spesies dapat diprediksi dengan menggunakan model yang diteliti.
spesies yang bertumbuh secara logistik, yaitu dengan adanya pemanenan pada salah satu jenis spesies dan adanya pemanenan pada kedua jenis spesies. Selain itu, penelitian ini juga membahas mengenai solusi dari hasil perumuman model yang diselesaikan menggunakan metode iterasi variasional, serta diberikan beberapa kasus khusus dari model yang terbentuk.
C. Perumusan Masalah
Berdasarkan latar belakang di atas, dapat dirumuskan beberapa masalah yang akan dibahas dalam penelitian ini, yaitu:
1. Bagaimana modifikasi serta analisis kestabilan titik ekuilibrium pada model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan adanya unsur pemanenan pada salah satu jenis spesies dan adanya unsur pemanenan pada kedua jenis spesies?
2. Bagaimana solusi model yang diperoleh dengan menggunakan metode iterasi variasional?
D. Batasan Masalah
Pada penelitian ini, dibatasi masalah-masalah sebagai berikut:
1. Model pertumbuhan populasi yang dibahas adalah model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan adanya unsur pemanenan.
interaksi dengan spesies lain, sehingga laju pertumbuhan populasi hanya dipengaruhi oleh interaksi kedua spesies tersebut.
3. Model yang dibahas adalah model kontinu, yaitu menggunakan sistem persamaan diferensial biasa nonlinear order satu.
4. Analisis kestabilan dari titik ekuilibrium menggunakan nilai eigen pada matriks Jacobi hasil dari pelinearan model.
5. Metode yang akan dibahas untuk menyelesaikan model adalah metode iterasi variasional.
E. Metode Penelitian
modifikasi kemudian hasil perumuman model diselesaikan atau dicari solusinya menggunakan metode iterasi variasional. Langkah terakhir adalah menyimpulkan hasil modifikasi model yang diperoleh beserta hasil analisis kestabilan titik ekuilibriumnya dan solusi dari perumuman model menggunakan metode iterasi variasional.
Diagram 1.2 merupakan bagan metode penelitian dari penelitian ini:
Diagram 1.2 Bagan metode penelitian
F. Tujuan Penelitian
Tujuan dari penelitian ini adalah:
1. Menghasilkan modifikasi model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan adanya unsur pemanenan pada salah
Memodifikasi model dasar mengenai pertumbuhan populasi dua spesies
Mencari solusi dari perumuman model menggunakan metode iterasi variasional
Menyimpulkan hasil modifikasi model beserta analisisnya dan solusi yang diperoleh menggunakan metode iterasi
variasional
Masalah di dunia nyata yang terkait dengan bidang biologi yaitu pertumbuhan populasi dua spesies
Memperoleh model dasar mengenai pertumbuhan populasi dua spesies
satu jenis spesies dan adanya unsur pemanenan pada kedua jenis spesies, serta mengetahui hasil analisis kestabilan dari titik ekuilibrium yang diperoleh. 2. Memperoleh solusi dari perumuman model dengan menggunakan metode
iterasi variasional.
G. Manfaat Penelitian
Manfaat dari penelitian ini adalah untuk menambah pengetahuan mengenai pemodelan matematika beserta penerapannya dalam kehidupan nyata dan menambah referensi bahan ajar bagi guru/dosen dalam menjelaskan materi mengenai sistem persamaan diferensial biasa nonlinear order satu. Selain itu, penelitian ini juga dapat untuk menambah wawasan mengenai penggunaan metode iterasi variasional untuk mencari pendekatan solusi sistem persamaan diferensial biasa nonlinear order satu.
H. SistematikaPenulisan
Sistematika penulisan akan dibagi menjadi enam bagian, yaitu: BAB I: PENDAHULUAN
Pada bab ini dijelaskan mengenai latar belakang, tinjauan pustaka, perumusan masalah, batasan masalah, metode penelitian, tujuan penelitian, manfaat penelitian, dan sistematika penulisan.
BAB II: LANDASAN TEORI
ekuilibrium), model pertumbuhan logistik, model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik, serta metode Iterasi Variasional. BAB III: HASIL DAN PEMBAHASAN ANALISIS KESTABILAN MODEL
Pada bab ini akan dipaparkan hasil serta pembahasan mengenai analisis dari model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada salah satu jenis spesies dan pemanenan pada kedua jenis spesies, mulai dari menentukan titik ekuilibrium hingga menganalisis kestabilan dari masing-masing titik ekuilibrium yang diperoleh.
BAB IV: HASIL DAN PEMBAHASAN SOLUSI MODEL
Pada bab ini akan dipaparkan mengenai proses memperoleh solusi dari model yang sudah diperumum beserta hasilnya dengan menggunakan metode Iterasi Variasional.
BAB V: ASPEK PENDIDIKAN
Pada bab ini dibahas mengenai keterkaitan penelitian yang dilakukan dengan proses pembelajaran di sekolah ataupun di kampus. Ada tiga hal yang dibahas pada bab ini, pertama mengenai keterkaitan hasil atau proses penelitian dengan pembelajaran di SMA, kedua keterkaitan hasil atau proses penelitian dengan pembelajaran di S1, dan yang ketiga adalah refleksi penelitian di bidang matematika.
BAB VI: PENUTUP
10
BAB II
LANDASAN TEORI
BAB II LANDASAN TEORIA. Pemodelan Matematika
Pemodelan Matematika merupakan suatu proses merepresentasikan dan menjelaskan permasalahan pada dunia nyata ke dalam persamaan matematika. Dengan kata lain, pemodelan matematika adalah proses membangun suatu model dengan menggunakan teori matematika untuk menggambarkan dinamika suatu sistem. Oleh karena itu, pemodelan matematika hampir selalu terkait dengan bidang-bidang ilmu yang lain.
Sebagai suatu proses, pemodelan matematika mencakup beberapa tahap yang saling berhubungan. Tahapan-tahapan tersebut dapat digambarkan pada bagan berikut:
Diagram 2.1 Bagan proses pemodelan matematika
Berikut penjelasan dari bagan proses pemodelan matematika seperti tampak pada Diagram 2.1.
a. Merumuskan permasalahan dari dunia nyata ke dalam bentuk matematika
Pada langkah ini dibutukan pemahaman dari permasalahan yang akan dimodelkan, karena akan dibentuk hubungan antar variabel yang dihasilkan dari permasalahan tersebut. Pada langkah ini, juga disertakan beberapa asumsi untuk membatasi model dari masalah yang akan diteliti. Adanya perbedaan asumsi-asumsi yang diterapkan oleh setiap peneliti menyebabkan perbedaan model meskipun penelitian dilakukan pada masalah yang sama. Setelah asumsi-asumsi ditentukan, dilakukan formulasi model yang akan dianalisis.
b. Menganalisis model matematika
Analisis dari model matematika dilakukan untuk memperoleh solusi dari model matemaika yang diteliti. Solusi dari model matematika yang diperoleh dapat berupa persamaan matematika atau uraian mengenai masalah matematika secara teoristis.
d. Menguji solusi dari model matematika ke dalam dunia nyata
Menguji solusi yang telah diperoleh dilakukan untuk melihat kesesuaian solusi dari model dengan data di dunia nyata. Kesesuaian solusi model dipengaruhi oleh asumsi-asumsi yang digunakan. Apabila solusi dari model kurang realistis, maka akan dilakukan kembali proses pembentukan model dari langkah pertama sehingga nantinya diperoleh model matematika yang lebih baik.
Dari uraian di atas, dapat disimpulkan bahwa proses membangun model matematika bersifat dinamis untuk menghasilkan model yang lebih baik.
B. Persamaan Diferensial
Persamaan diferensial adalah persamaan yang memuat turunan satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas. Berdasarkan banyaknya variabel bebas yang terdapat dalam persamaan, persamaan diferensial diklasifikasikan menjadi persamaan diferensial biasa dan persamaan diferensial parsial.
Persamaan diferensial biasa adalah suatu persamaan diferensial yang melibatkan turunan dari satu atau lebih variabel terikat terhadap satu variabel bebas, sebagai contoh: jika merupakan fungsi satu variabel dengan sebagai variabel bebas dan sebagai variabel terikat, maka suatu persamaan diferensial biasa dapat dinyatakan dalam bentuk:
dan jika = maka persamaan diferensial (2.1) disebut persamaan diferensial homogen, sedangkan jika ≠ maka persamaan diferensial (2.1) disebut persamaan diferensial nonhomogen. Persamaan diferensial parsial adalah suatu persamaan diferensial yang melibatkan turunan dari satu atau lebih variabel terikat terhadap dua atau lebih variabel bebas.
Pada persamaan diferensial, order didefinisikan sebagai tingkat turunan tertinggi yang muncul dalam persamaan diferensial. Berikut diberikan beberapa contoh persamaan diferensial beserta jenisnya berdasarkan banyak variabel dan ordernya:
Contoh 2.1
a. − = merupakan persamaan diferensial biasa order satu. b. ′′+ ′− = merupakan persamaan diferensial biasa order dua.
c. ��
� + ��
� = merupakan persamaan diferensial parsial order satu. d. � �
� + � � � −
� �
� � = merupakan persamaan diferensial parsial order dua. Pada persamaan diferensial order satu, terdapat bentuk persamaan diferensial variabel terpisah. Bentuk umum persamaan diferensial variabel terpisah adalah sebagai berikut:
+ = , (2.2)
menyelesaikan persamaan diferensial variabel terpisah adalah metode pemisahan variabel. Persamaan (2.2) selanjutnya diintegralkan masing-masing sukunya untuk memperoleh penyelesaiannya, sehingga didapat persamaan berikut:
∫ + ∫ = ,
dengan ∈ ℝ. Contoh 2.2
Tentukan solusi persamaan diferensial berikut:
− + = . (2.3)
Jawab:
Persamaan diferensial tersebut merupakan persamaan diferensial variabel terpisah. Bentuk (2.3) dapat diubah menjadi
−
+ =
dengan cara membagi masing-masing sukunya dengan ≠ . Selanjutnya masing-masing suku diintegralkan
∫ − + ∫ =
kemudian dengan manipulasi aljabar, bentuk fungsi diubah menjadi
∫ ( − − ) + ∫ =
sehingga diperoleh
− − ln + + ln + =
dengan = − −
= �+
= ,
dengan = �.
C. Sistem Persamaan Diferensial Nonlinear
Sistem persamaan diferensial tidak hanya berperan penting dalam bidang matematika, namun berperan penting juga dalam bidang lain seperti ekonomi, fisika, biologi, dan lain sebagainya. Sistem persamaan diferensial disebut sebagai sistem persamaan diferensial nonlinear apabila memenuhi paling sedikit satu dari kriteria berikut:
a. Memuat variabel tak bebas dan turunan-turunannya berpangkat selain satu. b. Terdapat perkalian dari variabel tak bebas dan/ atau turunan-turunannya. Diberikan sistem persamaan diferensial berikut:
̇ = , , … , � ,
̇ = , , … , � ,
̇� = � , , … , � ,
(2.4)
dengan �: ⊆ ℝ� → ℝ�, ̇� = ̇�, � = , , … , � dan , , … , � ∈ . Diberikan pula kondisi awal � = � , � = , , … , �.
Sistem (2.4) dapat ditulis menjadi
̇ = , (2.5)
Sistem (2.5) disebut sistem persamaan diferensial autonomous karena variabel waktu tidak muncul secara eksplisit. Selanjutnya, jika , , … , � masing-masing linear dalam , , … , �, maka sistem (2.4) disebut sistem persamaan diferensial linear. Sistem (2.4) juga dapat ditulis dalam bentuk:
̇ = + + + � �
̇ = + + + � �
̇� = � + � + + �� �.
(2.6)
Sistem (2.6) dinyatakan dalam bentuk
̇ = , (2.7)
Jadi, sistem (2.7) disebut sistem persamaan diferensial linear dari sistem (2.4). Namun, jika sistem (2.4) tidak dapat dinyatakan dalam bentuk sistem (2.7) maka sistem (2.4) disebut sistem persamaan diferensial nonlinear.
Pada sistem persamaan diferensial juga dibahas mengenai beberapa hal berikut: a. Titik Ekuilibrium
Titik ekuilibrium merupakan solusi dari sistem (2.5) yang tidak mengalami perubahan terhadap waktu.
Definisi 2.1 (Perko, 2001)
Titik ̂ ∈ ℝ� disebut titik ekuilibrium dari (2.5) jika ̂ = . Berikut diberikan contoh mengenai Definisi 2.1
Contoh 2.3
= ( −− )
Jawab:
Titik ekuilibrium diperoleh jika ̂ = , sehingga sistem tersebut menjadi
− =
atau dapat ditulis menjadi
− = .
Berdasarkan persamaan tersebut diperoleh ̂ = dan ̂ = . Jika ̂ = dan menurut persamaan
− = ,
maka diperoleh = sehingga didapat titik ekuilibrium , �. Jika ̂ = dan menurut persamaan
− = ,
maka diperoleh = ± sehingga didapat titik ekuilibrium , � atau − , �.
b. Pelinearan
Taylor untuk sistem = , , … , � � di sekitar titik ekuilibrium ̂ = ̂ , ̂ , … , ̂� � dengan ̂ = sebagai berikut
̇ = = �� ̂ − ̂ +�� ̂ − ̂ +
+�� ̂
� � − ̂� + Ο ‖ − ̂‖ ,
̇ = =�� ̂ − ̂ +�� ̂ − ̂ +
+�� ̂
� �− ̂� + Ο ‖ − ̂‖ ,
̇� = � = ��� ̂ − ̂ +��� ̂ − ̂ +
+��� ̂
� �− ̂� + Ο ‖ − ̂‖ .
Apabila suku-suku nonlinearnya diabaikan maka diperoleh
̇ = = �� ̂ − ̂ +�� ̂ − ̂ +
+� ̂
� � � − ̂� ,
̇ = =�� ̂ − ̂ +�� ̂ − ̂ +
+�� ̂
̇� = � = ��� ̂ − ̂ +��� ̂ − ̂ +
Jika bentuk (2.8) dinyatakan dalam bentuk matriks, maka diperoleh
̇ = ( ̂ ,
dengan ( ̂ merupakan matriks Jacobi dan fungsi di titik ekuilibrium ̂. Berikut definisi dari matriks Jacobi:
Definisi 2.2 (Perko, 2001)
Diberikan fungsi = , , … , � dengan � ∈ , � = , , … , �, ⊆ ℝ� dan himpunan terbuka.
Matriks
Selanjutnya diberikan definisi mengenai pelinearan pada sistem persamaan nonlinear.
Definisi 2.3 (Perko, 2001)
Diberikan matriks Jacobi ( pada (2.8). Sistem linear ̇ = ( ̂
disebut pelinearan dari sistem ̇ = disekitar titik ̂. c. Analisis Kestabilan Titik Ekuilibrium
identitas, dan merupakan nilai eigen dari matriks Jacobi. Nilai eigen yang diperoleh dapat digunakan untuk memeriksa kestabilan dari titik ekuilibrium. Kriteria kestabilan dari titik ekuilibrium berdasarkan nilai eigen menurut Boyce dan DiPrima (2012 : 504) adalah seperti pada Tabel 2.1.
Tabel 2.1 Kriteria kestabilan dari titik ekuilibrium
Nilai Eigen Jenis Titik Kritis Kestabilan
> > Simpul Tak stabil
< < Simpul Stabil asimtotik
< < Titik sadel Tak stabil
= > Simpul sejati atau simpul tak sejati Tak stabil
= < Simpul sejati atau simpul tak sejati Stabil asimtotik
, = ± � Titik spiral
> Tak stabil
< Stabil asimtotik
= � , = −� Pusat Stabil
Berdasarkan Tabel 2.1, dapat disimpulkan bahwa titik ekuilibrium akan mencapai keadaan stabil asimtotik apabila nilai , = ± � dan < , dengan merupakan bagian dari bilangan realnya dan merupakan bagian dari bilangan kompleksnya.
Berikut beberapa contoh sistem persamaan diferensial beserta penyelesaiannya sebagai ilustrasi gambar mengenai kriteria kestabilan dari titik ekuilibrium yang digambar menggunakan software Matlab.
Contoh 2.5
= + ,
= + .}
Syarat titik ekuilibrium: = = ,
+ = ,
+ = .}
Diperoleh titik ekuilibrium , .
Misalkan = .
Analisis kestabilan dari titik ekuilibrium
− =
− =
−
− =
− − − =
− + =
− − =
= ∨ = .
Gambar 2.1 Diagram fase Contoh 2.5 (titik simpul yang bersifat tak stabil)
Contoh 2.6
Diberikan sistem persamaan diferensial = ,
= − − .}
Syarat titik ekuilibrium: = = ,
= ,
− − = .}
Diperoleh titik ekuilibrium , .
Misalkan = − − .
Analisis kestabilan dari titik ekuilibrium
− =
− − − =
−
− − − + =
+ + =
+ + =
= − ∨ = − .
Karena < < , titik ekuilibrium , merupakan titik simpul yang bersifat stabil asimtotik. Gambar 2.2 adalah diagram fase dari sistem persamaan diferensial Contoh 2.6 untuk beberapa nilai awal yang berbeda.
Gambar 2.2 Diagram fase Contoh 2.6 (titik simpul yang bersifat stabil asimtotik)
Contoh 2.7
Diberikan sistem persamaan diferensial
= + ,
= − .}
Syarat titik ekuilibrium: = = ,
+ = ,
Diperoleh titik ekuilibrium , .
Misalkan = − .
Analisis kestabilan dari titik ekuilibrium
− =
− − =
−
− − =
− − − − =
+ − =
+ − =
= − ∨ = .
Karena < < , titik ekuilibrium , merupakan titik sadel yang bersifat tak stabil. Gambar 2.3 memuat diagram fase dari sistem persamaan diferensial Contoh 2.7 untuk beberapa nilai awal yang berbeda.
Contoh 2.8
Diberikan sistem persamaan diferensial
= ,
= .}
Syarat titik ekuilibrium: = = ,
= , = .}
Diperoleh titik ekuilibrium , .
Misalkan = .
Analisis kestabilan dari titik ekuilibrium
− =
− =
−
− =
− − =
= = .
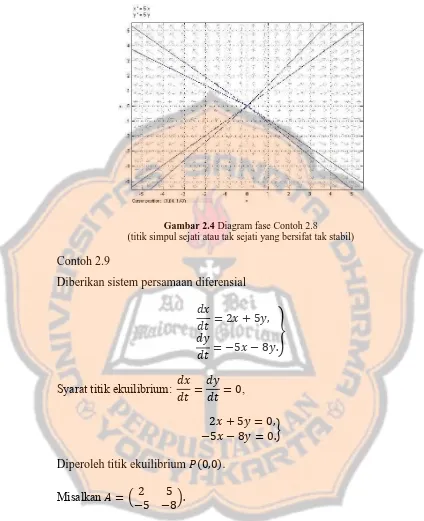
Gambar 2.4 Diagram fase Contoh 2.8
(titik simpul sejati atau tak sejati yang bersifat tak stabil)
Contoh 2.9
Diberikan sistem persamaan diferensial
= + ,
= − − .}
Syarat titik ekuilibrium: = = ,
+ = ,
− − = .}
Diperoleh titik ekuilibrium , .
Misalkan = − − .
Analisis kestabilan dari titik ekuilibrium
− =
−
− − − =
− − − + =
+ + =
+ =
= = − .
Karena = < , titik ekuilibrium , merupakan titik simpul sejati atau titik simpul tak sejati yang bersifat stabil asimtotik. Gambar 2.5 menunjukkan diagram fase dari sistem persamaan diferensial Contoh 2.9 untuk beberapa nilai awal yang berbeda.
Gambar 2.5 Diagram fase Contoh 2.9
(titik simpul sejati atau tak sejati yang bersifat stabil asimtotik)
Contoh 2.10
Diberikan sistem persamaan diferensial
= + ,
Syarat titik ekuilibrium: = = ,
+ = ,
− − = .}
Diperoleh titik ekuilibrium , .
Misalkan = − − .
Analisis kestabilan dari titik ekuilibrium − = .
− − − =
−
− − − =
− − − + =
− + =
, = ± √ −
, = ± �.
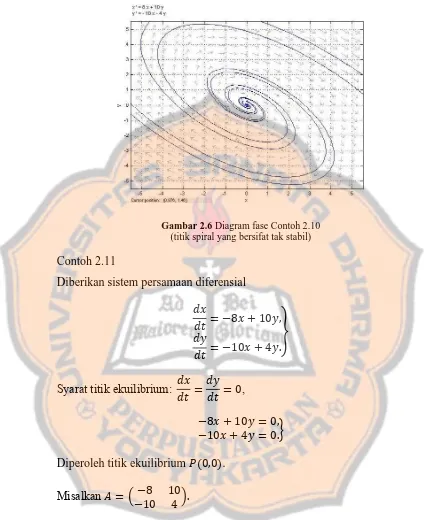
Gambar 2.6 Diagram fase Contoh 2.10 (titik spiral yang bersifat tak stabil)
Contoh 2.11
Diberikan sistem persamaan diferensial
= − + ,
= − + .}
Syarat titik ekuilibrium: = = ,
− + = ,
− + = .}
Diperoleh titik ekuilibrium , .
Misalkan = −− .
Analisis kestabilan dari titik ekuilibrium
− =
−
− −
− − =
− − − + =
+ + =
, = − ± √ −
, = − ± �.
Karena , = ± � dan < , titik ekuilibrium , merupakan titik spiral yang bersifat stabil asimtotik. Gambar 2.7 adalah diagram fase dari sistem persamaan diferensial Contoh 2.11 untuk beberapa nilai awal yang berbeda.
Gambar 2.7 Diagram fase Contoh 2.11 (titik spiral yang bersifat stabil asimtotik)
Contoh 2.12
Diberikan sistem persamaan diferensial
= ,
Syarat titik ekuilibrium: = = ,
= ,
− = .}
Diperoleh titik ekuilibrium , .
Misakan = − .
Analisis kestabilan dari titik ekuilibrium
− =
− − =
−
− − =
+ =
= −
, = �√
= � ∨ = − �.
Gambar 2.8 Diagram fase Contoh 2.12 (titik pusat yang bersifat stabil)
D. Model Pertumbuhan Logistik
Model pertumbuhan populasi untuk satu spesies dikemukakan pertama kali oleh Malthus. Model diberikan oleh masalah nilai awal sebagai berikut:
{ � = � ,
� = � ,
dengan � banyaknya individu di dalam populasi pada waktu , dengan adalah variabel waktu, dan konstanta laju pertumbuhan. Model tersebut dapat diselesaikan menggunakan metode pemisahan variabel sebagai berikut:
�
= �
�
� =
∫ �� = ∫
� = +�
� = �
dengan = dan diperoleh penyelesaian umum
� = .
Substitusi nilai awal � = �
� =
� = ,
untuk memperoleh penyelesaian khusus dari model
� = � .
Penyelesaian tersebut menandakan pertumbuhan populasi bertumbuh secara eksponensial dan bergantung pada nilai awal � , konstanta laju pertumbuhan , dan waktu . Karena penyelesaian dari model Malthus berupa persamaan eksponensial, maka model Malthus ini juga disebut model eksponensial. Model eksponensial ini tidak realistis, sebab untuk nilai > , dan jika diambil menuju tak hingga, maka diperoleh � menuju tak hingga, yakni lim
→∞� = ∞. Tidak mungkin suatu populasi bertumbuh tanpa batas.
Titik ekuilibrium dari model pertumbuhan populasi satu spesies yang dikemukakan oleh Malthus adalah sebagai berikut:
Syarat titik ekuilibrium � = , sehingga diperoleh
� =
� = .
bersifat tak stabil. Sebagai ilustrasi, untuk nilai awal � > populasi akan bergerak menjauhi nol, hal ini berarti titik ekuilibrium � = merupakan solusi yang bersifat tak stabil. Gambar 2.9 menunjukkan grafik penyelesaian yang digambar menggunakan software Matlab dari model Malthus atau model eksponensial untuk beberapa nilai awal yang berbeda.
Gambar 2.9 Grafik penyelesaian model Malthus dengan = ,
Model Verhulst merupakan salah satu modifikasi dari model Malthus. Adanya daya dukung yang berupa konstanta ditambahkan pada model bermaksud untuk membuat model lebih realistik. Daya dukung yang dimaksud meliputi keterbatasan ruang / kapasitas tempat tinggal, keterbatasan makanan, dan sebagainya. Model Verhulst atau model logistik diberikan oleh persamaan:
{ �
= � −� ,
� = � ,
ln � − ln| − � | = +
ln | − � | =� +
�
− � = �
� = � − ��
� + �� = �
+ � � = �
� = �
+ �
dengan = �, diperoleh penyelesaian umum
� = + .
Substitusi nilai awal � = � sehingga diperoleh penyelesaian khusus dari model sebagai berikut
� =
+
� = +
� + � =
− � = �
= �− � .
� =
Penyelesaian tersebut lebih realistis dibandingkan dengan penyelesaian model Malthus, sebab jika diambil nilai menuju tak hingga maka diperoleh:
lim→∞ + �
Titik ekuilibrium dari model pertumbuhan populasi satu spesies yang dikemukakan oleh Verhulst adalah sebagai berikut: � = , sehingga diperoleh
� ( −� ) =
� = ∨ −� =
� = ∨ � = .
Jadi, terdapat dua titik ekuilibrium yaitu � = atau � = . Jika � =
� −�� , maka ′ � = − �
titik ekuilibrium � = adalah ′ = − , karena > maka ′ < , sehingga titik ekuilibrium � = bersifat stabil asimtotik. Dengan kata lain, untuk setiap nilai awal � > populasi akan bergerak menjauhi nol, jadi titik ekuilibrium � = merupakan solusi yang bersifat tak stabil. Berbeda dengan � = , untuk setiap � > berlaku:
lim→∞
� − − +
= ,
sehingga � = adalah solusi yang stabil asimtotik.
Berikut grafik penyelesaian dari model Verhulst atau model logistik yang digambar menggunakan software Matlab untuk beberapa nilai awal yang berbeda.
Gambar 2.10 Grafik penyelesaian model Verhulst dengan = , dan =
Gambar 2.10 menunjukkan bahwa dalam jangka waktu yang panjang atau menuju tak hingga, jumlah populasi konvergen menuju ke koefisien daya dukung atau =
E. Model Interaksi Simbiosis Mutualisme Dua Spesies yang Bertumbuh
secara Logistik
Simbiosis mutualisme adalah interaksi yang erat dan khusus antara dua makhluk hidup yang berbeda jenis namun saling menguntungkan bagi kedua pihak. Beberapa contoh makhluk hidup yang berinteraksi secara simbiosis mutualisme adalah interaksi antara kerbau dan burung jalak, zebra dan burung oxpecker, buaya dan burung plover, anemon laut dan ikan badut, bunga dan kupu-kupu, bunga dan lebah, dan lain sebagainya.
Interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara eksponensial dapat dimodelkan sebagai berikut:
{ = + ,
= + ,
dengan dan adalah jumlah populasi pada waktu . Parameter dan berturut-turut merupakan laju pertumbuhan intrinsik dari populasi dan , konstanta
dan b menunjukkan koefisien dari interaksi antara dua populasi yang dapat meningkatkan jumlah masing-masing populasi dan .
Analisis kestabilan titik ekuilibrium model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara eksponensial adalah sebagai berikut: Dicari titik ekuilibrium dengan syarat titik ekuilibrium = = , sehingga diperoleh:
+ = ,
Terdapat dua titik ekuilibrium, yakni , dan − , − . Setelah itu dilakukan pelinearan sehingga diperoleh matriks Jacobi
� =
Analisis kestabilan titik ekuilibrium , dengan matriks Jacobi
Diketahui < , < sehingga > > (dua bilangan real berbeda lebih dari nol). Jadi titik ekuilibrium , merupakan titik simpul yang bersifat tak stabil.
Analisis kestabilan titik ekuilibrium
− , − ,
dengan matriks Jacobi
= −
− ),
diperoleh nilai eigen
− =
(
−
− ) −
) =
− −
− − ) =
− =
, = ± √
= √ ∨ = −√ .
Gambar 2.11 adalah grafik model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara eksponensial yang digambar menggunakan software Matlab untuk beberapa nilai awal yang berbeda.
Gambar 2.11 Grafik model interaksi simbiosis mutualisme populasi dua spesies yang
bertumbuh secara eksponensial = , , = , , = . dan = .
Model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik adalah sebagai berikut:
= ( − ) + ,
= − + .
Analisis kestabilan titik ekuilibrium interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik adalah sebagai berikut:
Dicari titik ekuilibrium dengan syarat titik ekuilibrium = = , sehingga
terdapat empat titik ekuilibrium, yakni , ,
Setelah memperoleh keempat titik ekuilibrium, dilakukan pelinearan sehingga diperoleh matriks Jacobi
Dengan mensubstitusikan nilai-nilai � pada � diperoleh
= ,
= (− + ),
a. Analisis kestabilan titik ekuilibrium , dengan matriks Jacobi
= , lebih dari nol). Jadi titik ekuilibrium , merupakan titik simpul yang bersifat tak stabil.
b. Analisis kestabilan titik ekuilibrium ( , dengan matriks Jacobi
= ( + − ),
− =
(( + − ) − ) =
+ −
− − =
( + − − − =
+ − = ∨ − − =
= + ∨ = − .
Diketahui < , < , > , dan > sehingga < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium ( , merupakan titik sadel yang bersifat tak stabil.
c. Analisis kestabilan titik ekuilibrium , dengan matriks Jacobi
= (− + ),
diperoleh nilai eigen
− =
(− + ) − =
(− − + − ) =
− − + − =
− − = ∨ + − =
Diketahui < , < , > , dan > sehingga < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium , merupakan titik sadel yang bersifat tak stabil.
d. Analisis kestabilan titik ekuilibrium +
Sehingga diperoleh nilai eigen sebagai berikut
(
untuk memperoleh nilai kalikan kedua ruas dengan , sehingga diperoleh
− − − − − ( =
diperoleh < < (dua bilangan real berbeda kurang dari nol). Jadi titik ekuilibrium ( � + � �
Jadi titik ekuilibrium ( � + � �
diperoleh > > (dua bilangan real berbeda lebih dari nol). Jadi titik ekuilibrium ( � + � �
diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium ( � + � �
− � � ,
� + � �
− � � ) merupakan titik sadel yang bersifat tak stabil.
Gambar 2.12 merupakan grafik model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik yang digambar menggunakan software Matlab dengan nilai parameter = , ; = , ; = , ; =
, ;
Gambar 2.12 Grafik model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik
Gambar 2.12 menunjukkan bahwa untuk beberapa nilai awal yang berbeda, grafik menuju ke suatu titik yaitu titik , , , , dimana titik tersebut merupakan titik ekuilibrium yang bersifat stabil asimtotik.
F. Metode Iterasi Variasional
Metode iterasi variasional terdiri dari tiga konsep dasar, yaitu: fungsi koreksi, variasi terbatas, dan pengali Lagrange. Sebagai gambaran dari konsep dasar metode iterasi variasional, diberikan persamaan diferensial non linear berikut
+ � = , (2.9)
dengan adalah operator linear, � adalah operator non linear, dan adalah fungsi kontinu. Metode iterasi variasional dapat dibentuk dan dianalisis dengan menggunakan sebuah fungsi koreksi sebagai berikut
�+ = � + ∫ � [ � � + � ̃� � − � ] �,
dengan adalah pengali Lagrange, indeks � adalah solusi hampiran ke-�, ̃� adalah variasi terbatas dengan ̃� = , dan adalah turunan variasional (Wazwaz: 2009, 47).
G. Kerangka Berpikir
52
BAB III
HASIL DAN PEMBAHASAN
ANALISIS KESTABILAN MODEL
BAB III HASIL DAN PEMBAHASAN ANALISIS KESTABILAN MODEL
Simbiosis adalah pola interaksi yang erat dan khusus antara dua makhluk hidup yang berlainan jenis. Salah satu jenis simbiosis adalah simbiosis mutualisme, dan makhluk hidup yang bersimbiosis disebut dengan simbion. Mutualisme adalah hubungan sesama makhluk hidup yang saling menguntungkan kedua pihak. Jadi simbiosis mutualisme adalah interaksi yang erat dan khusus antara dua makhluk hidup yang berbeda jenis dan saling menguntungkan bagi kedua pihak.
dan ikan badut menangkal ikan kupu-kupu yang suka memakan anemon, ikan badut juga akan memakan parasit yang terdapat pada tentakel anemon yang berupa invertebrata kecil, serta di sisi lain kotoran dari ikan badut memberi nutrisi bagi anemon. Bunga matahari dan lebah, dalam hubungan bunga matahari dan lebah, bunga diuntungkan karena dibantu proses penyerbukannya oleh lebah, sedangkan lebah diuntungkan karena memperoleh makanan dari bunga berupa sari bunga.
Pada suatu ekosistem tertutup, terdapat dua spesies yang saling berinteraksi secara mutualisme (saling menguntungkan). Di dalam ekosistem tertutup tersebut diasumsikan tidak ada gangguan atau faktor lain yang mempengaruhi pertumbuhan dua populasi selain interaksi antara kedua spesies. Laju pertumbuhan dari masing-masing spesies pada saat merupakan turunan dari jumlah populasi spesies terhadap waktu (turunan dari atau terhadap ) yaitu dan , dengan dan merupakan jumlah masing-masing populasi dari kedua spesies pada saat , dan merupakan variabel dari waktu. Terdapat parameter-parameter yang mempengaruhi pertumbuhan populasi kedua spesies. Parameter yang menunjukkan laju pertumbuhan intrinsik dari masing-masing spesies dimisalkan dengan dan , dengan merupakan laju pertumbuhan intrinsik dari spesies dan merupakan laju pertumbuhan intrinsik dari spesies . Karena kedua spesies bertumbuh secara logistik, maka terdapat kapasitas ambang atau daya dukung dari masing-masing spesies. Daya dukung untuk spesies adalah dan daya dukung untuk spesies adalah . Jadi, pemodelan pertumbuhan dari masing-masing spesies yang bertumbuh secara logistik adalah = −
model tersebut, belum terdapat interaksi antara kedua spesies. Jika kedua spesies berinteraksi secara mutualisme maka mengakibatkan bertambahnya populasi dari masing-masing spesies. Misalkan merupakan laju pertumbuhan spesies akibat interaksi dengan spesies dan merupakan laju pertumbuhan spesies akibat interaksi dengan spesies , model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dapat dituliskan sebagai berikut:
= ( − ) + ,
= − + .
Bab ini membahas mengenai modifikasi model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik yaitu dengan adanya unsur pemanenan pada salah satu jenis spesies dan adanya unsur pemanenan pada kedua jenis spesies serta analisis kestabilan titik ekuilibrium pada model hasil modifikasi.
A. Model Interaksi Simbiosis Mutualisme Dua Spesies yang Bertumbuh
secara Logistik dengan Unsur Pemanenan pada Salah Satu Jenis Spesies
Jika dilakukan pemanenan pada salah satu dari spesies, misal pemanenan dilakukan pada spesies , dengan merupakan laju pemanenan spesies , maka model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada salah satu jenis spesies dapat dituliskan sebagai berikut:
= − + . (3.2)
Analisis kestabilan titik ekuilibrium pada model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada salah satu jenis spesies adalah sebagai berikut:
Dicari titik ekuilibrium dengan syarat titik ekuilibrium = = , sehingga
Terdapat empat titik ekuilibrium, yakni , ,
Dilakukan pelinearan sehingga diperoleh matriks Jacobi
� =
Dengan mensubstitusikan nilai-nilai � pada � diperoleh:
= ( − + − ),
a. Analisis kestabilan titik ekuilibrium , dengan matriks Jacobi
= − ,
Jika > , maka diperoleh > > (dua bilangan real berbeda lebih dari nol). Jadi titik ekuilibrium , merupakan titik simpul yang bersifat tak stabil.
Jika < , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium , merupakan titik sadel yang bersifat tak stabil.
b. Analisis kestabilan titik ekuilibrium ( , dengan matriks Jacobi
= ( − + − ),
diperoleh nilai eigen
− =
(( − + − ) − ) =
− + −
− − =
( − + − − − =
− + − = ∨ − − =
= − + ∨ = −
Diketahui < , < , > , > dan > , dapat disimpulkan dua analisis kestabilan yaitu:
Jika + < , maka diperoleh < < (dua bilangan real berbeda kurang dari nol). Jadi titik ekuilibrium ( , merupakan titik simpul yang bersifat stabil asimtotik.
Jika > , maka dapat diperoleh dua nilai yang berbeda. Jika > − , maka dapat disimpulkan > > (dua bilangan real berbeda lebih dari nol). Jadi titik ekuilibrium − � , merupakan titik simpul yang bersifat tak stabil. Sedangkan jika < − , maka dapat disimpulkan < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium − � , merupakan titik sadel yang bersifat tak stabil.
Jika < , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium − � , merupakan titik sadel yang bersifat tak stabil.
= ( − + − ,
= + − − ,
= − − − ,
diperoleh nilai eigen
− =
( ) − =
( − − ) =
− − − =
− + − = .
Digunakan rumus untuk memperoleh nilai dan dengan nilai = ,
= − , dan = − sebagai berikut
, = ± √ − . .. −
, = ± √ − −
Diketahui < , < ; , , , > ; dan > , sehingga dapat disimpulkan beberapa analisis kestabilan sesuai dengan nilai eigen yang diperoleh.
Kriteria kestabilan dari ( − +
− ,
dapat dilihat pada Tabel 2.1 disesuaikan dengan nilai dan .
Gambar 3.1 merupakan grafik model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada salah satu jenis spesies yang digambar menggunakan software Matlab dengan nilai =
, ; = , ; = , ; = , ;
� = , ; � = , ; dan =
, untuk beberapa nilai awal yang berbeda.
Gambar 3.1 Grafik interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada salah satu jenis spesies
Gambar 3.1 menunjukkan bahwa untuk beberapa nilai awal yang berbeda, grafik menuju ke suatu titik dimana titik tersebut merupakan salah satu titik ekuilibrium yang bersifat stabil asimtotik.
B. Model Interaksi Simbiosis Mutualisme Dua Spesies yang Bertumbuh
secara Logistik dengan Unsur Pemanenan pada Kedua Jenis Spesies
maka model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada kedua jenis dapat dituliskan sebagai berikut:
= ( − ) + − , (3.3)
= − + − . (3.4)
Analisis kestabilan titik ekuilibrium pada model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada kedua jenis spesies adalah sebagai berikut:
Dicari titik ekuilibrium dengan syarat titik ekuilibrium = = , sehingga diperoleh:
( − ) + − = ,
− + − = ,
}
atau − + − = ,
( − + − = . }
Terdapat empat titik ekuilibrium, yakni , ,
, − ,
−
, , dan
− + −
− ,
− + −
− .
�=
Dengan mensubstitusikan nilai-nilai � pada � diperoleh:
= − − ,
a. Analisis kestabilan titik ekuilibrium , dengan matriks Jacobi
− − − − = berbeda lebih dari nol). Jadi titik ekuilibrium , merupakan titik simpul yang bersifat tak stabil.
Jika > dan < , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium , merupakan titik sadel yang bersifat tak stabil.
Jika < dan > , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium , merupakan titik sadel yang bersifat tak stabil.
Jika < dan < , maka diperoleh < < (dua bilangan real berbeda kurang dari nol). Jadi titik ekuilibrium , merupakan titik simpul yang bersifat stabil asimtotik.
b. Analisis kestabilan titik ekuilibrium
diperoleh nilai eigen berbeda dan berbeda tanda). Jadi titik ekuilibrium , − � merupakan titik sadel yang bersifat tak stabil.
Jika > dan < , maka dapat diperoleh dua nilai yang berbeda. Jika − > − , maka dapat disimpulkan > > (dua
bilangan real berbeda lebih dari nol). Jadi titik ekuilibrium , − � merupakan titik simpul yang bersifat tak stabil. Sedangkan jika − <
berbeda dan berbeda tanda). Jadi titik ekuilibrium , − � merupakan titik sadel yang bersifat tak stabil.
Jika < dan > , maka dapat diperoleh dua nilai yang berbeda. Jika − > − , maka dapat disimpulkan < < (dua
bilangan real berbeda kurang dari nol). Jadi titik ekuilibrium , − � merupakan titik simpul yang bersifat stabil asimtotik. Sedangkan jika
− < − , maka dapat disimpulkan < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium
, − � merupakan titik sadel yang bersifat tak stabil.
Jika < dan < , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium , − � merupakan titik sadel yang bersifat tak stabil.
c. Analisis kestabilan titik ekuilibrium −
, ,
dengan matriks Jacobi
= −
−
− + −
),
diperoleh nilai eigen
(
− −
− + −
) −
) =
− − −
− + − −
) =
− − − + − − =
− − = ∨ − + − − =
= − ∨ = − + −
Diketahui < , < ; , > ; dan , > , dapat disimpulkan beberapa analisis kestabilan yaitu:
Jika > dan > , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium − � , merupakan titik sadel yang bersifat tak stabil.
Jika > dan < , maka dapat diperoleh dua nilai yang berbeda. Jika − > − , maka dapat disimpulkan < < (dua bilangan real berbeda kurang dari nol). Jadi titik ekuilibrium − � , merupakan titik simpul yang bersifat stabil asimtotik. Sedangkan jika
Jika < dan > , maka dapat diperoleh dua nilai yang berbeda. Jika − > − , maka dapat disimpulkan > > (dua bilangan real berbeda lebih dari nol). Jadi titik ekuilibrium − � , merupakan titik simpul yang bersifat tak stabil. Sedangkan jika − <
− , maka dapat disimpulkan < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium − � , merupakan titik sadel yang bersifat tak stabil.
Jika < dan < , maka diperoleh < < (dua bilangan real berbeda dan berbeda tanda). Jadi titik ekuilibrium − � , merupakan titik sadel yang bersifat tak stabil.
d. Analisis kestabilan titik ekuilibrium
= − + −− ,
= − + −
− ,
= − + −
− ,
diperoleh nilai eigen
− =
( ) − =
( − − ) =
− − − =
− + − = .
Digunakan rumus untuk memperoleh nilai dan dengan nilai = ,
= − , dan = − sebagai berikut
, = ± √ − . .. −
, = ± √ − −
Diketahui < , < ; , , , > ; dan , > , sehingga dapat disimpulkan beberapa analisis kestabilan sesuai dengan nilai eigen yang diperoleh.
Kriteria kestabilan dari
− + −
− ,
− + −
dapat dilihat pada Tabel 2.1 dengan menyesuaikan nilai dan .
Gambar 3.2 merupakan grafik model interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada kedua jenis spesies yang digambar menggunakan software Matlab dengan nilai = , ; =
, ; = , ; = , ;
� = , ; � = , ; = , ; dan =
, untuk beberapa nilai awal yang berbeda.
Gambar 3.2 Grafik interaksi simbiosis mutualisme dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada kedua jenis spesies
71
BAB IV
HASIL DAN PEMBAHASAN SOLUSI MODEL
DENGAN METODE ITERASI VARIASIONAL
BAB IV HASIL DAN PEMBAHASAN SOLUSI MODEL DENGAN METODE ITERASI VARIASIONAL Pada bab sebelumnya, telah dibahas mengenai analisis dari model pertumbuhan populasi dua spesies yang sudah dimodifikasi. Selanjutnya akan dibahas pendekatan dari solusi model tersebut menggunakan metode iterasi variasional. Sebelum menggunakan metode iterasi variasional untuk menyelesaikan model, akan dibentuk perumuman dari model hasil modifikasi.
Model pertama dari hasil modifikasi adalah model interaksi simbiosis mutualisme populasi dua spesies yang bertumbuh secara logistik dengan unsur pemanenan pada salah satu jenis spesies dan dimodelkan pada sistem persamaan (3.1)-(3.2).
= ( − ) + − , (3.1)
= − + . (3.2)
Dengan menggunakan sifat distributif perkalian dan sifat asosiatif, sistem persamaan (3.1)-(3.2) dapat ditulis menjadi
{
pemanenan pada kedua jenis spesies dan dimodelkan pada sistem persamaan (3.3)-(3.4).
= ( − ) + − , (3.3)
= − + − . (3.4)
Dengan menggunakan sifat distributif perkalian dan sifat asosiatif, sistem persamaan (3.3)-(3.4) dapat ditulis menjadi
{
= − + − ,
= − + − ,
⇔
{
= − − + ,
= − − + .
Perumuman model dilakukan dengan memisalkan koefisien , , pada persamaan pertama secara berturut-turut dengan , , dan koefisien , , pada persamaan kedua secara berturut-turut dengan , , . Sehingga diperoleh persamaan umum model
= + + , (4.1)
= + + , (4.2)
dengan,
∶ menyatakan jumlah populasi spesies pertama, ∶ menyatakan jumlah populasi spesies kedua,
∶ laju penurunan pertumbuhan spesies akibat bertambahnya spesies dalam populasi,
∶ laju penurunan pertumbuhan spesies akibat bertambahnya spesies dalam populasi,
∶ laju pertumbuhan spesies akibat interaksi dengan spesies , dan ∶ laju pertumbuhan spesies akibat interaksi dengan spesies .
Sistem (4.1) dan (4.2) akan diselesaikan menggunakan metode iterasi variasional. Langkah pertama dari metode iterasi variasional adalah membentuk fungsi koreksi dari sistem persamaan diferensial. Fungsi koreksi dari sistem (4.1)-(4.2) adalah
�+ = �
+ ∫ [ � − � − ̃�
− ̃� ̃� ] ,
(4.3)
�+ = �
+ ∫ [ � − � − ̃�
− ̃� ̃� ] ,
(4.4)
�+ = �
+ ∫ [ � − � − − ]
= � + ∫ [ � − � ] ,
(4.5)
�+ = �
+ ∫ [ � − � − − ]
= � + ∫ [ � − � ] .
(4.6)
Menggunakan integral parsial, persamaan (4.5) menjadi �+ = �
+ � − ∫ ′ �
− ∫ �
= ( + �
− ∫ [ ′
� + � ] ,
= ( + � − ∫ [( ′ + � ] .
Menggunakan integral parsial, persamaan (4.6) menjadi �+ = �
+ � − ∫ ′ �
− ∫ �
= ( + � − ∫ [ ′ � + � ]
= ( + � − ∫ [( ′ + � ] .
(4.8)
Pengali Lagrange dan dapat diperoleh dengan menyelesaikan sistem berikut:
+ = , ′ + | = = , (4.9)
+ = , ′ + | = = . (4.10)
Sehingga, diperoleh pengali Lagrange = − − − dan = − − − . Solusi untuk sistem (4.1)-(4.2) dalam bentuk linearisasi (misalkan =
= = = ) adalah sebagai berikut: Penyelesaian persamaan (4.1)
= =
Penyelesaian persamaan (4.2)
= =
= + + = + +
= =
ln = + ln = +
= +� = +�
= � = �
dengan memisalkan � = dan � = diperoleh:
= , (4.11)
= . (4.12)
Iterasi variasional untuk sistem 4.1-4.2 dengan = − − − dan = − − − adalah:
�+ = �
+ ∫ − − − [ � −
� − �
− � � ] ,
(4.13)
�+ = �
+ ∫ − − − [ � −
� − �
− � � ] .
(4.14)
Dari pembahasan sebelumnya, nilai dan dapat diperoleh dari nilai awal. Sebagai contoh, diasumsikan bahwa = dan = . Sehingga diperoleh
= dan = , oleh sebab itu, = dan = .
Pada bab ini dibahas solusi model menggunakan metode iterasi variasional untuk contoh model pertumbuhan populasi dua spesies yang berinteraksi secara simbiosis mutualisme, simbiosis parasitisme, dan kompetisi.
4.1. Model Mutualisme
Pada subbab ini diberikan solusi dari sistem (4.1)-(4.2) untuk model pertumbuhan populasi dua spesies yang berinteraksi secara simbiosis mutualisme menggunakan metode iterasi variasional. Diasumsikan bahwa = , ; = , ; =
− , ; = − , ; = , ; dan = , , sehingga solusi iterasi
variasional sampai pada dan dengan menggunakan software Maple adalah sebagai berikut:
= . . − . . + . . 8 , (4.15)
= . . 8 + . . 8 − . . 6 , (4.16)
= . . − . .
+ . . 8 − . . 8
+ . . 8 + . . 6
− . . + . . 6
− . . + . . ,
= . . 8 + . . 8
− . . 6 + . .
− . . − . . 8
− . . 8 − . . 6
+ . .
+ . . 6 .
(4.18)
(a) (b)
Gambar 4.1 Grafik solusi untuk model Mutualisme: (a). , (b). with .
Representasi dari solusi model pertumbuhan populasi dua spesies yang berinteraksi secara simbiosis mutualisme diplot pada Gambar 4.1 untuk dan . Pada Gambar 4.1 dapat diamati bahwa karena simbiosis mutualisme, populasi dari kedua spesies meningkat terhadap waktu.
4.2. Model Parasitisme
− , ; = − , ; = , ; dan = − , . Representasi dari deret solusi iterasi variasional yang diselesaikan menggunakan software Maple adalah sebagai berikut:
= . . − . . + . . 8 , (4.19)
= . . 8 − . . 8 − . . 6 , (4.20)
= . . − . . + . . 8
− . . 6 − . . 8
+ . . 8 + . . 6 − . .
− . . + . . ,
(4.21)
= . . 8 − . . 8
− . . 6 + . .
− . . + . . 6
+ . . 8 − . . 8
+ . . 6 + . . .
(4.22)
(a) (b)
Representasi dari solusi model pertumbuhan populasi dua spesies yang berinteraksi secara simbiosis parasitisme diplot pada Gambar 4.2. untuk dan . Pada Gambar 4.2 dapat diamati bahwa karena simbiosis parasitisme, salah satu populasi menurun terhadap waktu, hal ini kemudian diikuti oleh populasi lain. 4.3. Model Kompetisi
Pada subbab ini diberikan solusi dari sistem (4.1)-(4.2) untuk model pertumbuhan populasi dua spesies yang saling berkompetisi menggunakan metode iterasi variasional. Diasumsikan bahwa = , ; = , ; = − , ; =
− , ; = − , ; dan = − , . Representasi dari deret solusi iterasi
variasional yang diselesaikan menggunakan software Maple adalah sebagai berikut:
= . . − . . − . . 8 , (4.23)
= . . 8 − . . 8 − . . 6 , (4.24)
= . . − . . − . . 8
− . . − . . 6
+ . . 8 − . . 8
+ . . − . .
+ . . 6 ,
(4.25)
= . . 8 − . . 8 − . . 6
+ . . − . .
− . . − . . 6
+ . . 8 − . . 8 + . . 6 .
(a) (b)
Gambar 4.3 Grafik solusi untuk model Kompetisi: (a). , (b). with .
Representasi dari solusi model pertumbuhan populasi dua spesies yang saling berkompetisi diplot pada Gambar 4.3 untuk dan . Untuk waktu yang kecil, kedua populasi meningkat terhadap waktu.
Perhitungan numerik untuk ketiga kasus (mutualisme, parasitisme, dan kompetisi) diberikan pada Tabel 4.1.
Table 4.1 Hasil numerik dari metode iterasi variasional berdasarkan contoh yang diberikan.
Model Mutualisme Model Parasitisme Model Kompetisi
0.0 4.00000 10.00000 4.00000 10.00000 4.00000 10.00000
0.1 4.04279 10.07385 4.04279 10.06657 4.03307 10.06657
0.2 4.08606 10.14822 4.08605 10.13347 4.06636 10.13349
0.3 4.12979 10.22309 4.12978 10.20071 4.09988 10.20075
0.4 4.17401 10.29848 4.17398 10.26829 4.13362 10.26836
0.5 4.21871 10.37440 4.21867 10.33621 4.16758 10.33632
0.6 4.26391 10.45083 4.26384 10.40446 4.20177 10.40463
0.7 4.30960 10.52779 4.30950 10.47304 4.23618 10.47328
0.8 4.35579 10.60528 4.35566 10.54197 4.27083 10.54228
0.9 4.40249 10.68330 4.40232 10.61123 4.30569 10.61163
1.0 4.44970 10.76185 4.44949 10.68083 4.34079 10.68133