Modul 8
Graph
1.
Tujuan
1.
Memahami konsep Graph
2.
Mampu menerapkan konsep Graph untuk menyelesaikan masalah-masalah
yang ada.
2.
Dasar Teori
Dalam berbagai masalah yang berkaitan dengan objek-objek diskret dan relasi
biner, representasi secara grafik seringkali merupakan penyajian yang
memudahkan. Salah satu contohnya adalah graph, yaitu representasi grafik yang
melibatkan sekumpulan objek yang dilambangkan dengan simpul atau verteks
(vertex), dan relasi-relasi biner antar objek-objek diskret tersebut yang
dilambangkan dengan rusuk atau sisi (edge).
Beberapa contoh masalah yang dapat disajikan dalam bentuk graph:
1.
Peta jalan raya yang menghubungkan kota-kota.
2.
Flowchart (diagram alir) suatu program.
3.
Topologi fisik suatu LAN (Local Area Network).
Beberapa Istilah penting dalam Graph:
1.
Graph Berarah (
Directed Graph
) dan Graph Tidak Berarah (
Undirected Graph
)
Graph tidak berarah adalah suatu pasangan berurut (V,E), dengan V adalah suatu
himpunan simpul dan E adalah himpunan rusuk yang merupakan himpunan bagian
dari V x V. Pada graph tidak berarah keterhubungan antar simpul tidak memiliki
arah (rusuknya tidak memiliki arah).
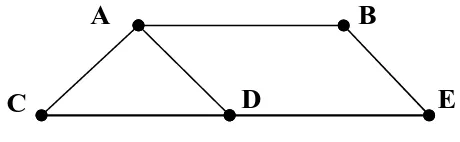
Graph G = (V,E) pada contoh diatas dapat dinyatakan dengan:
E
D
B
C
V= {A,B,C,D,E}
E = {{(A,B) , (A,C) , (A.D) , (B,E) , (C,D) , (D,E)} }
G = ( V,E )
Graph berarah adalah graph yang rusuk-rusuknya memiliki arah, contohnya:
Pada graph diatas rusuk (C,D) berinsidensi dari C ke D. Untuk rusuk (C,D), simpul
C dinamakan Simpul Awal (
initial vertex
) dan simpul D dinamakan Simpul
Terminal (
terminal vertex
).
Pada Graph tidak berarah rusuk (C,D) sama dengan rusuk (D,C), tetapi pada Graph
berarah rusuk (C,D) berbeda dengan rusuk (D,C).
2.
Graph Berbobot (
Weighted Graph
)
Graph berbobot adalah graph yang simpul atau rusuknya memiliki tambahan
informasi lain atau bobot, pembobot ini biasanya berupa bilangan, lambang, atau
bersaran lain yang kita berikan. Misalnya pada graph yang menggambarkan
jaringan jalan raya antar kota-kota, mungkin perlu ditambahkan angka pada simpul
untuk mengidentifikasi kota-kota, dan bilangan pada rusuk untuk menunjukkan
jarak antar kota.
Representasi graph dapat digunakan untuk mempermudah penyelesaian beberapa
masalah dalam riset operasi (operation research). Dapat disebutkan beberapa contoh
masalah riset operasi sebagai berikut:
Michigan
New York
4
7
5
2
Texas
Seattle
Los Angeles
5
3
2
1
4
2
E
D
B
C
1.
Shortest Path (Shortest Route) Problem
Yaitu masalah untuk menentukan jalur atau rute terpendek dari suatu simpul
asal ke simpul tujuan dalam suatu jaringan (network). Pengertian jaringan disini
sama dengan pengertian Graph. Terdapat beberapa algoritma untuk
memecahkan model masalah seperti ini, dan algoritma yang cukup terkenal
adalah
Algoritma Djikstra
.
2.
Spanning Tree Problem
Masalah untuk menentukan pohon perentang minimum dari suatu jaringan
(
network
). Algoritma yang cukup terkenal dan sering dipakai untuk
menyelesaikan masalah ini adalah Algoritma
Minimum Spanning Tree
(MST).
3.
Maximal Flow Problem
Masalah aliran maksimum, yaitu masalah untuk menentukan aliran maksimal
dari suatu simpul awal (
source
) ke suatu simpul tujuan (
destination
) pada suatu
jaringan tertentu, dimana setiap rusuk pada jaringan tersebut memiliki kapasitas
maksimal untuk melewatkan suatu komoditas. Untuk memecahkan model
masalah seperti ini dapat digunakan algoritma
Maximal Flow Minimum Cut
,
algoritma Pelabelan Termodifikasi, dll.
Graph Traversal
Masalah yang paling fundamental pada graph ialah mengunjungi atau menelusuri
(
traverse
) setiap Vertex didalam Graph secara sistematis. Kebanyakan dari algoritma
dasar yang kita perlukan untuk operasi pada Graph merupakan aplikasi dari penelusuran
Graph (
Graph Traverse
), antara lain meliputi:
1.
Menampilkan atau mevalidasi isi dari Edge dari suatu Vertex.
2.
Meng-
copy
suatu Graph atau mengubah Graph ke dalam representasi yang
berbeda.
3.
Menghitung cacah dari node dan atau vertex.
4.
Mengidentifikasi komponen yang saling berhubugan pada Graph.
5.
Menemukan jalur antara dua vertex, atau
cycles
jika ada.
Terdapat dua metode terkenal untuk Graph Traversal yaitu:
1.
Depth First Search
Metode ini menggunakan Stack sebagai struktur data dari penyimpanannya,
dikunjungi dari suatu vertex dengan terlebih dahulu mengunjungi semua
successor yang belum pernah dikunjungi dari prodecessor vertex tersebut.
2.
Bread First Search
Metode ini menggunakan Queue sebagai struktur data dari penyimpanannya.
Bread First Search
a kan mengunjungi semua successor yang belum pernah
dikunjungi dari suatu vertex terlebih dahulu sebelum mengunjungi semua
successor yang belum pernah dikunjungi dari successor vertex tersebut.
1. Depth First Search
2. Bread First Search
A – B – D – C
A – B – C – D
Graph sendiri dapat direpresentasikan ke dalam bentuk matriks (
Edge Matrix
atau
Adjacency Matrix
) atau dengan menggunakan konsep multi list.
Contoh sebuah Graph:
( 4 )
( 2 )
( 3 )
( 1 )
A
C
D
B
( 2 )
( 3 )
( 4 )
( 1 )
A
C
D
B
4
4
6
3
5
3
2
B
A
D
F
E
C
Representasi Graph dalam bentuk matriks:
A
B
C
D
E
F
A
0
1
1
0
1
0
B
0
0
1
0
0
0
C
0
0
0
1
0
1
D
0
0
0
0
0
1
E
0
0
0
0
0
1
F
0
0
0
0
0
0
Representasi Graph diatas dalam bentuk Multi List, digambarkan sebagai berikut:
Vertex A
A
D
B
F
C
E
2
5
4
3
3
6
4
7
Edge dari vertex A ke
Struktur data pembentukan Graph dengan menggunakan konsep Multi List.
typedef struct tVertex *adrVertex;
typedef struct tEdge *adrEdge;
typedef struct tVertex
{
char VertexLabel;
adrVertex NextVertex;
adrEdge FirstEdge;
} Vertex;
typedef struct tEdge
{
int Weight;
adrEdge NextEdge;
adrVertex AdjacentVertex;
} Edge;
typedef adrVertex Graph;
3.
DEMO
File
Graph.h
/*Nama : No.Mhs : Kelas : */
#include<iostream.h> #include<stdlib.h>
typedef char infotype;
typedef struct tVertex *adrVertex; typedef struct tEdge *adrEdge;
typedef struct tVertex {
infotype VertexLabel; adrVertex NextVertex; adrEdge FirstEdge; }Vertex;
typedef struct tEdge {
int Weight;
adrEdge NextEdge;
adrVertex AdjacentVertex; }Edge;
void CreateEmpty(Graph &G);
/* IS : G sembarang
FS : G terdefinisi dan kosong */
bool IsEmpty(Graph G);
/* I : G terdefinisi mungkin kosong
O : mereturnkan nilai True jika G kosong, False jika tidak kosong*/
adrVertex CreateVertex(infotype vlabel);
/* I : vlabel terdefinisi
O : node vertex baru terbentuk dengan VertexLabel = vlabel */
adrEdge CreateEdge(int weight);
/* I : weight terdefinisi
O : node edge baru dengan Weight = weight terbentuk */
bool IsVertexFound(Graph G, infotype vlabel);
/* I : G terdefinisi mungkin kosong, label terdefinisi sebagai label vertex yang dicari.
O : mereturnkan True jika vertex yang dicari ada pada Graph G, False jika tidak */
adrVertex FindVertex(Graph G, infotype vlabel);
/* I : G terdefinisi mungkin kosong, label terdefinisi sebagai label vertex yang dicari.
O : mereturnkan alamat jika vertex yang dicari ada pada Graph G, jika tidak ditemukan maka return NULL*/
bool IsEdgeFound(Graph G, infotype source, infotype destination);
/* I : G terdefinisi tidak kosong, source dan destination terdefinisi sebagai label vertex asal dan tujuan edge yang dicari.
O : mereturnkan True jika edge dengan vertex asal source dan vertex tujuan destination ditemukan, False jika tidak */
adrEdge FindEdge(Graph G, infotype source, infotype destination);
/* I : G terdefinisi tidak kosong, source dan destination terdefinisi sebagai label vertex asal dan tujuan edge yang dicari.
O : mereturnkan alamat jika edge dengan vertex asal source dan vertex tujuan destination ditemukan, False jika tidak */
void InsertVertexFirst(Graph &G, adrVertex V);
/* I : G terdefinisi mungkin kosong, V alamat vertex yang akan disisipkan.
O : V menjadi vertex pertama dalam G */
void InsEdgeLast(Graph &G, infotype source, infotype destination, int weight);
/* I : G terdefinisi tidak kosong, source dan destination terdefinisi sebagai label vertex asal dan tujuan edge yang akan disisipkan. O : edge dengan vertex tujuan destination dan info weight menjadi
edge terakhir dari vertex asal source pada Graph G */
void PrintAllVertex(Graph G);
/* I : G terdefinisi mungkin kosong.
O : Menampilkan semua vertex pada Graph G */
void PrintEdge(adrVertex source);
void PrintAllEdge(Graph G);
/* I : G terdefinisi mungkin kosong.
O : Menampilkan seluruh edge pada Graph G */
file
Graph.cpp
/*void CreateEmpty(Graph &G)
{
G=NULL; }
bool IsEmpty(Graph G)
{
return G==NULL; }
adrVertex CreateVertex(infotype vlabel)
{
adrVertex V=new Vertex; if(!IsEmpty(V))
adrEdge CreateEdge(int weight)
{
adrEdge E=new Edge; if(E!=NULL)
bool IsVertexFound(Graph G, infotype vlabel)
{
return FindVertex(G,vlabel)!=NULL; }
adrVertex FindVertex(Graph G, infotype vlabel)
{
if(IsEmpty(G)) return NULL;
else if(G->VertexLabel==vlabel) return G;
else
bool IsEdgeFound(Graph G, infotype source, infotype destination)
{
return FindEdge(G,source,destination)!=NULL; }
adrEdge FindEdge(Graph G, infotype source, infotype destination)
{
adrVertex V=FindVertex(G,source); adrEdge temp,hasil=NULL;
if(!IsEmpty(V))
return hasil; }
void InsertVertexFirst(Graph &G, adrVertex V)
{
V->NextVertex=G; G=V;
}
void InsEdgeLast(Graph &G, infotype source, infotype destination, int weight)
{
adrVertex V1=FindVertex(G,source); adrVertex V2=FindVertex(G,destination); adrEdge E,temp;
E=CreateEdge(weight);
void PrintAllVertex(Graph G)
{
if(!IsEmpty(G)) {
cout<<G->VertexLabel<<ends<<" "; PrintAllVertex(G->NextVertex); }
void PrintEdge(adrVertex source)
{
adrEdge temp=source->FirstEdge; while(temp!=NULL)
{
cout<<source->VertexLabel<<" -> "<<temp->AdjacentVertex-> VertexLabel<<" = "<<temp->Weight<<endl;
temp=temp->NextEdge; }
}
void PrintAllEdge(Graph G)
{
file
MGraf.cpp
#include"graph.h"void main() {
Graph G;
int pilih,bobot;
char asal,tujuan,label;
CreateEmpty(G); do
{
system("CLS");
cout<<" MENU"<<endl<<endl;
cout<<"1. Insert New Vertex First"<<endl; cout<<"2. Insert New Edge"<<endl;
cout<<"3. Print All Vertex"<<endl; cout<<"4. Print All Edge"<<endl; cout<<"0. EXIT."<<endl<<endl; cout<<"Masukkan Pilihan : "; cin>>pilih;
switch(pilih) {
case 1 :
cout<<"Masukkan label dari vertex : "; cin>>label; if(IsVertexFound(G,label))
cout<<"Vertex dengan label "<<label<<" sudah ada pada Graph!"<<endl;
else {
InsertVertexFirst(G,CreateVertex(label)); cout<<"Insert Vertex sukses..."<<endl; }
system("PAUSE"); break;
case 2 :
if(!IsVertexFound(G,asal))
cout<<"vertex asal tidak ditemukan pada graph!"<<endl;
else {
cout<<"Masukkan label vertex tujuan : "; cin>>tujuan;
if(!IsVertexFound(G,tujuan))
cout<<"vertex tujuan tidak ditemukan pada graph!"<<endl;
else {
if(IsEdgeFound(G,asal,tujuan))
cout<<"Edge dari "<<asal<<" ke " <<tujuan<<" sudah ada pada
Graph!"<<endl; else
{
cout<<"Masukkan jarak antar vertex : "; cin>>bobot;
InsEdgeLast(G,asal,tujuan,bobot); cout<<"Insert Edge sukses."<<endl; }
} }
system("PAUSE"); break;
case 3 :
cout<<"Daftar vertex yang ada pada Graph"<<endl; if(IsEmpty(G))
cout<<"Graph kosong.."<<endl; else
PrintAllVertex(G);cout<<endl; system("PAUSE");
break; case 4 :
cout<<"Daftar edge yang ada pada Graph"<<endl; if(IsEmpty(G))
cout<<"Graph kosong.."<<endl; else
PrintAllEdge(G); system("PAUSE");
break; }
}