MODUL 2 BILANGAN KOMPLEKS

(1)

MODUL 2

BILANGAN KOMPLEKS

Satuan Acara Perkuliahan Modul 2 (Bilangan Kompleks) sebagai berikut. Petemuan ke- Pokok/Sub PokokBahasan TujuanPembelajaran 4 Bilangan Kompleks Pengantar Bilangan Kompleks

Lambang Bilangan dan Bidang Kompleks Formula Euler

Sekawan Kompleks

Aljabar Kompleks

Mahasiswa diharapkan mampu:  memahami bilangan kompleks

 menggambarkan kurva pada bidang kompleks,

 menuliskan bilangan kompleks dalam bentuk polar/formula Euler,

 mengetahui bahwa setiap bilangan kompleks memiliki sekawan

 menentukan hasil penjumlahan, pengurangan, dan perkalian bilangan kompleks

 menentukan hasil kali dan hasil bagi bilangan kompleks dalam bentuk polar

 memecahkan persamaan kompleks

5 Bilangan Kompleks Pangkat dan Akar Bilangan Kompleks

Fungsi eksponen dan Trgonometri

Aplikasi dalam Rangkaian Listrik AC

Mahasiswa diharapkan mampu:

 menentukan hasil pemangkatan bilangan kompleks

 menentukan akar-akar dari bilangan kompleks

 mengetahui bentuk eksponen dari sinus dan cosinus

 menentukan nilai sinus dan cosinus dari bilangan kompleks

 menggunakan bentuk sinus dan cosinus untuk menghitung integral trigonometri

 mengunakan konsep bilangan kompleks untuk menganalisis rangkaian listrik AC RLC seri

(2)

2.1 Pengantar

Tinjau kembali persamaan kuadrat dalam aljabar, yakni 0 2

c bz

az .

Nilaiz yang memenuhipersamaan di atasdapatdicarimenggunakanrumusabc:

a ac b b z 2 4 2 . Permasalahan muncul ketika diskriminan, 2 4 0

ac b

D (negatif), karena bilangan negatif tidak memiliki akar. Untuk mengatasi hal tersebut, diperkenalkan bilangan imajiner, yakni

1

j

dengan pemahaman bahwa j2 1. Selanjutnya

j

2

4 , 2 j 2 , j3 j

adalah bilangan-bilangan imajiner. Akan tetapi, 1

2

j , 2 2 j 2 j 2 2, 4 1

j

merupakan bilangan-bilangan real.

Dengan diperkenalkannya bilangan imajiner ini, persamaan kuadrat yang diskriminannya negatif dapat memiliki akar yang merupakan kombinasi dari bilangan real dan bilangan imajiner. Sebagaicontoh, akar-akardaripersamaankuadrat 0 3 2 2 z z adalah

2

1

2

8

2

12

4

2 j

z

yang terdiri dari bilangan real, yakni 1, dan bilangan imajiner, yakni j2 2. Semua bilangan yang mencakup bilangan real, imajiner, dan kombinasi keduanya disebut bilangan kompleks.

LATIHAN 2.1

Tentukan nilai x dari persamaan berikut.

1. x 16

2. x 2 8

3. x2 4 0

Untuk n = bilangan bulat positif, tentukan nilai dari

4. j4n

(3)

2.2 BilanganKompleks

2.2.1 LambangBilanganKompleks

Bilangankompleks, secaraumum, memilikimemilikiduabagianbilangan, yaitubagianrealdanbagianimajiner.Bilangankompleksdilambangkanolehz danditulissebagaiberikut.

jy x z

dengan x = Re z = bagianrealdari z, dan

y = Imz = bagianimajinerdari z.

Sebagaicontoh, z = 2 + j5 (atauz = 2 + 5j) memiliki Re z = 2

Imz = 5

Perhatikan bahwa bagian imajiner dari bilangan kompleks adalah bilangan real, bukan imajiner. Pada contoh di atas, bagian imajiner dari z adalah 5 (bukanj5 atau 5j).

Bagianrealdanbagianimajinerbolehsaja nol. Sebagaicontoh, z = 0+ 2j = 2jatauz = 2 + 0j = 2. Jikax = 0, makaz = jydandisebutimajinermurni.

2.2.2 Bidang Kompleks. Bentuk Polar Bilangan Kompleks

Bilangankompleksselalumerupakanpasanganduabilanganreal, yaituxdany. Olehkarenaitu,bilangankompleksdapatdigambarkandalambidangkompleks, yaknibidanginiyang samadenganbidangkartesius,

hanyasajasumbuvertikalnyamerupakanbagianimajinerdansumbuhorisontalnyamerupakanbagianrea l, sepertidiperlihatkanpadaGambar 2.1. Berdasarkan hal tersebut, bilangan kompleks dapat ditulis sebagai z=(x,y) yang maknanya sama dengan z = x + jy.

Gambar 2.1 Bidang kompleks.

Jarak antara titik (x, y) dan titik asal (0,0) disebut modulus atau nilai mutlak dari z, ditulis 2

2 |

|z x y . Sudut dari z disebut fase atau argumen dari z dan memenuhi

x

y

arctan

.

Dari Gambar 2.1,x dan y masing-masing memenuhi cos | | z x dan y | z|sin sehinggadiperoleh ) sin (cos | | sin | | cos | |z j z z j jy x z x y |z| (x, y)

(4)

Ungkapan ) sin (cos | |z j z

disebut bentuk polar dari bilangan kompleks.

2.2.3 Formula Euler

Untuk bilangan real (dinyatakan dalam radian), bentuk deret Maclaurin dari sin dan cos (lihat Bab 1) sebagai berikut.

... ! 7 ! 5 ! 3 sin 7 5 3 ... ! 6 ! 4 ! 2 1 cos 6 4 2

Selanjutnya dari representasi deretex, yakni

... ! 4 ! 3 ! 2 1 4 3 2 x x x x ex , jikaxdigantiolehj , diperoleh ... ! 4 ! 3 ! 2 1 4 3 2 j j ej ... ! 5 ! 3 ... ! 4 ! 2 1 5 3 4 2 j sin cos j

Dengan demikian, bentuk polar bilangan kompleks, z |z|(cos jsin ), dapat ditulis sebagai j

e z z | | atau sering disingkat dalam bentuk

| | z

z .

2.2.4 SekawanKompleks

Sekawan kompleks dari z ditulis z atau z*. Sekawan kompleks diperoleh dengan mengubah tanda pada bagian imajiner dari z = x + jy, yakni menjadi

jy x

z .

Dalambentuk polar ditulis,

(5)

CONTOH 1 Tulis z 1 i dalam bentuk polar. Tentukan pula Sekawan kompleks dari z. Penyelesaian

Dari z 1 i diperoleh x = –1 dan y = –1 maka modulus dari z 2 ) 1 ( ) 1 ( | |z x2 y2 2 2 danfasenya n x y 2 4 5 1 1 tan tan 1 1

dengan n bilangan bulat. Sudut bilangan kompleks harus berada pada kuadran yang sama dengan keberadaan titik bilangan. Pada kasus ini, titik (x, y) = ( –1, –1 ) berada di kuadran III dan sudut yang memenuhi adalah

4 5

atau 4 3

. Dengan demikian, bentuk polar dariz 1 i(dapat ditulis dalam 4 cara) sebagai berikut.

4 5 sin 4 5 cos 2 j z 4 5 2ej z o o j z 2 cos225 sin225 o z 2 225 .

Selanjutnya, Sekawan kompleks dari z 1 i adalah z 1 i atau dalam bentuk polar,

4 5 sin 4 5 cos 2 j z 4 5 2e j z o o j z 2 cos225 sin225 o z 2 225

LATIHAN 2.2

Nyatakan bilangan kompleks pada Soal 1 – 5 berikut ke dalam bentuk z |z|ej atau

| | z

z . Tentukan pula Sekawan kompleksnya. 1. z 1 j 2. z 2 j 3. z 1 j 3 4. z 4j 5.

z

1

NyatakanSoal 6 – 10 berikut ke dalam bentuk z = x + jy. 6. 4 sin 4 cos 2 j z 7. 6 sin 6 cos 3 j z 8. _z ₃_ej2 9. z e j2 10. z 2 150o

(6)

2.3 AljabarKompleks

2.3.1 Penjumlahan,Pengurangan, danPerkalian

Penjumlahan, pengurangan, dan perkalian bilangan kompleks mengikuti aturan aljabar biasa.

CONTOH 1 Jika z1 2 5j dan z2 5 j, tentukan z1 z2, z1 z2, dan z1z2. Penyelesaian j j j j j z z1 2 (2 5 ) (5 ) (2 5) (5 ) 7 4 j j j j j z z1 2 (2 5 ) (5 ) (2 5) (5 ) 3 6 j j j j j j j j j z z1 2 (2 5 ) (5 ) 2 5 2 ( ) 5 5 5 ( ) 10 2 25 5 15 23

CONTOH 2 Jikaz = 2 + j, tentukanz2. Penyelesaian j j j j j z2 (2 )2 4 2 2 4 2 1 3 2

CONTOH 3 Jika z 3 4j, tentukan zz . Bandingkan hasilnya dengan |z|. Apa simpulan yang dapat diperoleh?

Penyelesaian

Sekawan kompleks dari z 3 4j adalahz 3 4j maka

5 25 16 9 16 9 ) 4 3 ( ) 4 3 ( 2 j j j z z . Selanjutnya, 5 25 16 9 4 3 | | 2 2 z . Simpulannya adalah |z | zz .

2.3.2 HasilBagi; PenyederhanaankedalamBentukz = x + jy

Hasilbagibilangankompleksdapatdisederhanakankedalambentukz = x + jydengancaramengalikanpembilangdanpenyebutdenganSekawankomplekspenyebut. CONTOH 4 Sederhanakanbentukberikut: i i z 3 4 2 . Penyelesaian

Kalikan pembilang dan penyebut dengan Sekawan kompleks penyebut maka

j j j j j j j j j j z 5 2 5 1 25 10 5 9 16 3 10 8 9 16 3 10 8 3 4 3 4 3 4 2 2 2

(7)

2.3.3 Perkalian dan Pembagian dalam Bentuk Polar

Jika _| _| 1 1 1 j e z z dan _| _| 2 2 2 j e z z maka ) ( 2 1 2 1 2 1 2 1 2 1 _| _| _| _|| _| | |z ej z ej z z ej z z dan ) ( 2 1 2 1 2 1 1 2 2 1 | | | | | | | | j j j e z z e z e z z z . CONTOH 5 Diketahui ₂ 2 1 i e z dan ₄ 4 2 j e z . Tentukan z₁z₂ dan z₁/ z₂. Penyelesaian

Akan lebih mudah jika sudutnya dinyatakan dalam derajat. Dalam hal ini 45o

4 dan o 90 2 maka 4 3 8 8 8 4 2 90 45 (90 45) 135 2 1 j j j j j e e e e e z z o o o o o 4 2 1 2 1 2 1 4 2 (9 0 4 5) 4 5 4 5 9 0 2 1 j j j j j e e e e e z z o o o o o

atau bisa juga ditulis sebagai berikut.

o o o z z1 2 (2 90 )(4 45 ) 8 135 dan o o o z z 45 2 1 45 4 90 2 2 1 .

2.3.4 PersamaanKompleks

Dua bilangan kompleks dikatakan sama jika dan hanya jika bagian real dan bagian imajiner dari kedua bilangan tersebut sama.

CONTOH 6 Tentukan x dan y yang memenuhi persamaan (x jy)2 2j

. Penyelesaian xy j y x jy x ) 2 ( 2 2 2

maka persamaan di atas dapat ditulis menjadi

j xy j y

x2 2 2 2 . Dari persamaan ini diperoleh

(1) 2 2 0

y

x

y

x

atau

y

x

(2) j2xy 2j xy 1 Masukkan hasil (1) ke (2), diperoleh

1 2

(8)

Akan tetapi, xdanyadalahbilanganreal (bukanimajiner) sehinggapersamaan 2 1

x

tidakmemenuhisyarat.Dengan demikian, diperoleh 1 2 x x 1 dan x 1 dan 1 x y dany x 1

Jadi, solusi persamaan (x jy)2 2j adalah x y 1ataux y 1

LATIHAN 2.3

Untuk Soal 1 – 5, diberikan z1 3 4j dan j

z2 8 6 . Tentukan operasi bilangan kompleks berikut. Nyatakan hasilnya dalam bentuk polar z = |z|ej.

1. z₁ z₂ 2. z₁ z₂ 3. z1z2 4. 2 1 z z 5. z1z1

Sederhanakan bentuk pada Soal 6–8 ke dalam bentuk z = x + jy.

6. j 1 1 7. j j 2 2 2 5 8. j j 2 3

Tentukan x dan y yang memenuhi persamaan kompleks pada Soal 9 – 10 berikut.

9. j2x 3 y j

10. (x jy)2 j2x

2.4 PangkatdanAkarBilanganKompleks

Dengan menggunakan aturan untuk perkalian dan pembagian bilangan kompleks dalam bentuk polar, diperoleh n j n z e z e z zn j n n jn n sin cos | | | | | | dan n j n z e z e z z n j n n j n n sin cos | | | | | | 1/ 1/ / 1/ / 1

(9)

CONTOH 1 Tentukan (1 j)4. Penyelesaian Ambil z 1 j maka | | 12 ( 1)2 2 z dan

2 n

4

1

1 tan

1 dengan n =

bilangan bulat (titik zdi kuadran IV bidang kompleks). Ambil

4

maka 4

2

1 j

e

j

z

. Dengan demikian,

4 )

0

1 (

4 sin

cos

4

2 )

1 (

4 4 4

_z

_e

4

_e

_j

j

j j . CONTOH 2 Tentukan (1 j)1/3. Penyelesaian Ambil z 1 j maka | | 12 12 2 z dan

2 k

4

1

1 arctan

(k = 0, 1, 2, …) sehingga k j e j z 2 4 2 1 . Dengan demikian, 3 2 12 4 6 3 / 1 2 3 / 1 3 / 1 2 2 ) 1 ( k j k j e e z j . Untuk k = 0, 12 6 3 / 1 2 ) 1 ( j ej . Untuk k = 1, 4 3 6 3 / 1 2 ) 1 ( j ej . Untuk k = 2, 12 17 6 3 / 1 2 ) 1 ( j ej .

Untuk k = 3, 4, 5, … merupakan pengulangan kembali dari k = 0, 1, 2. Dengan demikian, akar pangkat 3 dari (1 + j) ada 3, yaitu

12 6 3 / 1 2 ) 1 ( j ej , 4 3 6 2ej , 12 17 6 2ej . Catatan: z1/n

(10)

CONTOH 3 Tentukan nilai-nilai dari 4 ₆₄

. Penyelesaian

Nilai dari 4

64 ada 4 (karena n = 4). Ambil z 64 64 j0maka| | ( 64)2 64

z

dan 2k

64 0 tan 1

(k = 0, 1, 2, …). Ambil 4 nilai , yaitu , 3 , 5 , 7 . Dengan demikian, diperoleh

4 4 ₂ ₂ 2 2 64 64 1/4 1/4 4 j j j e e e z , 4 3 2 2 ej , 4 5 2 2 ej , 4 7 2 2 ej .

LATIHAN 2.4

Tentukan akar-akar berikut. 1. 3₁ 2. 4₁₆ 3. 3 ₈ 4. 5

_j

5. 3

₂

_j

2.5 FungsiEksponendanTrigonometri

Telahdiperolehbahwa sin cos j ej dan sin cos j e j

Jikakeduapersamaan di atasdiselisihkandandijumlahkan, masing-masinghasilnyasebagaiberikut. sin 2 ) sin (cos ) sin (cos j j j e ej j cos 2 ) sin (cos ) sin (cos j j e ej j Dari keduapersamaanterakhirdiperoleh j e ej j 2 sin dan 2 cos j j e e

Jika digantioleh z, diperoleh

j e e z jz jz 2 sin dan 2 cos jz jz e e z

(11)

Penyelesaian j e j j j j e e j e e j e j j j j 1752 , 1 2 1 2 2 sin 1 1 1

CONTOH 2 Gunakanbentukeksponendaricosinusuntukmenghitung cos23xdx

. Penyelesaian

Dalam bentuk eksponen:

2 3 cos 3 3x j x j e e x maka 4 2 2 3 cos 6 6 2 3 3 2 x j x j x j x j e e e e x sehingga

x

e

j

e

j

dx

e

dx

x

j x j x j x j x

2

6

1

6

1

4

1

2

4

1

3 cos

2 6 6 6 6

2

6

1

6

1

2

6

1

6

1

4

1

j6 j6 j j6

e

j

e

j

e

j

e

j

2

6

1

6

1

2

6

1

6

1

4

1 j

j

Catatan: 1 0 1 6 sin 6 cos 6 j ej 1 0 1 6 sin 6 cos 6 j e j

LATIHAN 2.5

Nyatakan berikut ini ke dalam bentuk

jy x

z .

1. ej( /4)ln3

2.

cos

j

3. Buktikan bahwa sin2z cos2z 1.

Nyatakan sinus dan kosinus dalam bentuk eksponen untuk menghitung integral berikut. 4. cos2xsin2xdx

5. sin24xdx

(12)

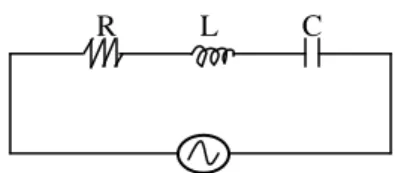
Tinjau rangkaian listrik ac RLC seri pada Gambar 2.2berikut.

Gambar 2.2Rangkaian AC RLC Seri

Jika arus yang mengalir dalam rangkaian adalah i, tegangan pada tiap komponen sebagai berikut.

Ri v_R , dt di L vL , idt C vC 1 . Tegangan totalnya memenuhi

C L R v v v

v .

Sejauh ini, arus bolak-balik dinyatakan oleh i I0sin t. Jika persamaan arus seperti ini

digunakan untuk menghitung tegangan total, akan cukup rumit dan memerlukan waktu lama. Dalam analisis kompleks, arus bolak-balik dapat dinyatakan oleh

t j

e I i 0 .

Dengan persamaan arus ini, tegangan pada komponen L dan C masing-masing

Li j e LI j dt di L vL 0 jt i C j e I C j dt e I C idt C v j t jt C 1 1 1 1 0 0 .

Dengan demikian, diperoleh

i C L j R v v v v R L C 1 .

Perbandingan antara v dan i disebut impedansi kompleks, diberi simbol Z, yakni

C L j R i v Z 1

Besar impedansi sama dengan modulus kompleksnya, yakni 2 2 1 | | L L R Z . R L C

(13)

LATIHAN 2.6

Jika dua komponen yang impedansinya masing-masing Z1 dan Z2 dirangkai seri, impedansi totalnya adalahZ_S Z₁ Z₂ dan jika dirangkai paralel,

2 1 1 1 1 Z Z ZP . Tentukan ZS dan ZPpada Soal 1 – 2 jika diketahui

1. Z1 2 3j dan Z2 1 5j 2. Z2 20 3 30o dan

o

Z2 20 120

3. Tegangan dan arus ac pada sebuah komponen masing-masing adalah

o

v 220 2 45 dan i 5 90o. Berapakah impedansi komponen?

Soal 4 – 5 mengacu pada rangkaian ac RLC seri seperti Gambar 2.2.

4. Cari dalam kaitannya dengan R, L, dan C jika sudut fasenya 45o.

5. Pada keadaan resonansi, Z adalah real. Tentukan pada keadaan ini.