TRANSFER MOMENTUM
TINJAUAN MIKROSKOPIK
GERAKAN FLUIDA
Hingga sejauh ini kita sudah mempelajari tentang momentum, gaya-gaya pada fluida statik, dan ihwal fluida bergerak dalam hal neraca massa dan neraca energi. Pada bagian ini kita akan mempelajari lebih dalam tentang profil kecepatan aliran fluida, gaya dorong yang menyebabkan fluida bergerak dan gaya yang menghambat gerakan itu, dan mempelajari bagaimana laju alir fluida dipengaruhi oleh sifat-sifat fluida dan rangkaian pipanya.
Analisis situasi terhadap fluida bergerak kita mulai dari konsepsi gerak dan deformasi fluida sebagaimana telah kita bangun pada bagian awal perkuliahan ini. Sekarang mari kita perhatikan kembali gambar berikut.
Dan kita telah sampai ke persamaan
=
=
F
Bentuk awal Bentuk akhir
x
z
y
Sekarang situasinya kita ganti dengan aliran fluida dalam pipa, seperti berikut.
Pipa berjari-jari R. Fluida bergerak di dalam pipa ke arah X positif. Fluida memiliki densitas sebesar
ρ
dan memiliki viskositas sebesarµ
. Volume atur (ControlVolume) untuk fluida memiliki panjang sebesar L dan mengisi penuh pipa pada arah r.
Karena fluida bergerak ke arah X positif (ke kanan), itu sama saja dengan mengatakan bahwa pipa bergerak ke kiri. Kalau pipa bergerak ke kiri maka akan ada transfer momentum dari dinding pipa menuju ke pusat pipa melalui fluida; dan sebaliknya jika kita meninjau fluida bergerak ke kanan maka akan ada transfer momentum dari dalam fluida menuju dinding pipa.
Dengan menggunakan asumsi bahwa antara fluida dengan permukaan pipa tidak terjadi slip (fluida tidak tergelincir) dan fluida bergerak ke arah X positif maka akan ada transfer momentum ke arah r. Berapakah laju transfer momentum ke arah r ini? Sekarang fluida pada sistem gambar di atas kita tinjau dalam lingkup yang lebih kecil dengan mengambil elemen fluida itu setebal dr ke arah r seperti berikut ini. Di sini diasumsikan fluidanya bersifat tak-mampu mampat (incompressible).
L
r
x
R
p
2p
1Fluida: ρ , μ
X = 0 X = LPada elemen volume fluida ini berlaku hukum kekekalan momentum, yang pada keadaan stedi dapat ditulis sbb.
−
+ = 0
Ada momentum (gaya viskous) masuk ke elemen volume melalui permukaan
dalam pada posisi r, yaitu:
[2
.
]
Ada momentum (gaya inersia) masuk pada penampang 1, (pada x = 0), sebesar
.
=
.
/
. Ingat:= ∀.
Jadinya:.
= ∀
=
.
Garis pusat pipa
X
r + ∆r
r
∆r
L
ELEMEN VOLUME FLUIDA
1
2
S = 2πr∆r
Garis pusat pipaX
r + ∆r
r
∆r
L
ELEMEN VOLUME FLUIDA
1
2
Dan karena
=
dan
= 2
∆ ,
maka:.
= (2
∆ .
)(
)
Jadi, momentum (gaya inersia) pada titik 1 (x=0) adalah:
(2
∆ .
)(
)
Kita tuliskan:
[
2
∆
.
]
Ada gaya (tekanan) terhadap permukaan fluida pada penampang 1 (pada x=0),
sebesar:
(2
∆ )
Ada gaya (tekanan) terhadap permukaan fluida pada penampang 2 (pada x=L),
sebesar:
−(2
∆ )
Ada momentum (gaya viskous) keluar dari elemen volume melalui permukaan
luar pada posisi r+∆r, yaitu:
[2
.
]
∆
Ada momentum (gaya inersia) keluar pada penampang 2, (pada x = L), sebesar
[
2
∆
.
]
Pada sistem ini juga ada bekerja gaya gravitasi, namun karena posisi
aliran adalah datar, maka gaya gravitasi ini tidak memberi konstribusi
terhadap gerak aliran.
Sekarang akan kita jumlahkan semua gaya yang telah diuraikan itu; kita peroleh:
[2
.
] + [2
∆
.
]
+ (2
∆ )
− (2
∆ )
− [2
.
]
∆− [2
∆
.
]
= 0
Dan kita susun kembali:
[2
.
] − [2
.
]
∆+
[
∆
.
]
−
[
∆
.
]
+ (2
∆ )(
−
) = 0
Karena fluida diasumsikan bersifat incompressible dan luas penampang pada z = 0 sama dengan luas penampang pada z = L, maka vz sama pada dua penampang itu;
dan dengan demikian suku ke tiga dan suku ke empat pada persamaan di atas akan saling meniadakan. Persamaan terakhir tersebut menjadi:
[2
.
] − [2
.
]
∆= −(2
∆ )(
−
)
atau:
[2
.
]
∆− [2
.
] = (2
∆ )(
−
)
Kalau persamaan ini kita bagi dengan
2
∆
dan kita ambil limit untuk∆
mendekati nol; kita peroleh:lim
∆ →
[
]
∆− [
]
∆
=
(
−
)
Suku sebelah kiri tak lain adalah turunan pertama (first derivative) dari terhadap
;
dan(
−
) = ∆
. Dari itu kita peroleh:(
) =
∆
Atau:
(
) =
∆
Untuk memperoleh distribusi fluks momentum, persamaan ini kita ingtegralkan:
(
) =
∆
Kita peroleh:
=
∆
1
2
+
atau=
∆
2
+
C1 adalah konstanta integrasi. Berapakah nilai C1 ini? Ingatlah bahwa fluksi momentum bukanlah tak berhingga pada posisi r = 0. Artinya, pada r = 0, ada nilainya dan berhingga. Konsekuensi logisnya haruslah C1 = 0. Lalu kita peroleh fluksi momentum pada fluida yang bergerak dalam pipa itu, yaitu:
=
∆
(*)
ini menyatakan fluksi momentum ke arah radial (jari-jari), r, yang disebabkan oleh bergeraknya fluida ke arah tangensial, x.Selanjutnya kita akan melihat profil kecepatan gerak fluida pada arah x terhadap posisi r.
= −
(**)
yang diperoleh dari Hukum Newton tentang viskositas. Kenapa di sini ada tanda minus? Karena berkurang jika bertambah, atau dengan kata lain,/
bernilai negatif, sedangkan tak pernah negatif; dan begitu juga dengan.
Dari persamaan (*) dan (**) kita peroleh:= −
∆
2
dan diperoleh dengan mengintegralkan persamaan tersebut.
∫
= −
∆∫
= −
∆
4
+
C2 adalah konstanta integrasi. Berapakah nilai C2 ini? Kita mempunyai informasi bahwa fluida yang bersentuhan dengan permukaan pipa (artinya fluida yang berada pada posisi r = R) kecepatannya ke arah tangensial (arah x ) adalah nol. Secara matematis kita tulis:
[ ]
= −
∆
4
+
= 0
Jelaslah bahwa:
=
∆
4
=
∆
4
−
∆
4
=
∆
4
1 −
Jika kita plot hubungan antara Vx dengan r akan kita peroleh kurva persamaan kuadrat. Dimanakah letak titik maksimumnya? Pertama haruslah:
= −
∆
2
= 0
yang mengharuskan pula r = 0. Pada r = 0, apakah kecepatannya maksimum atau minimum? Kita harus menguji turunan ke dua (second derivative):
= −
∆
2
< 0
Karena turunan ke dua bernilai negatif (lebih kecil dari nol), kita ambil kesimpulan bahwa, kecepatan gerak fluida ke arah x pada posisi r = 0 merupakan kecepatan maksimum; yaitu sebesar:
,
=
∆
4
Terlihat bahwa kecepatan gerak fluida bergantung pada
faktor dari luar berupa ∆p, dimensi pipa berupa R dan L,
dan faktor pada sifat fluida itu sendiri berupa µ.
Persamaan Kurva ini diplot untuk nilai ∆ dipasang sebesar 25 satuan dan nilai R (jari-jari pipa) = 10 satuan. Ilustrasi alirannya kira-kira seperti pd gbr brkt.
= ∆ −
R = 10
Dinding pipa Dinding pipa
Lapisan –lapisan fluida pipa
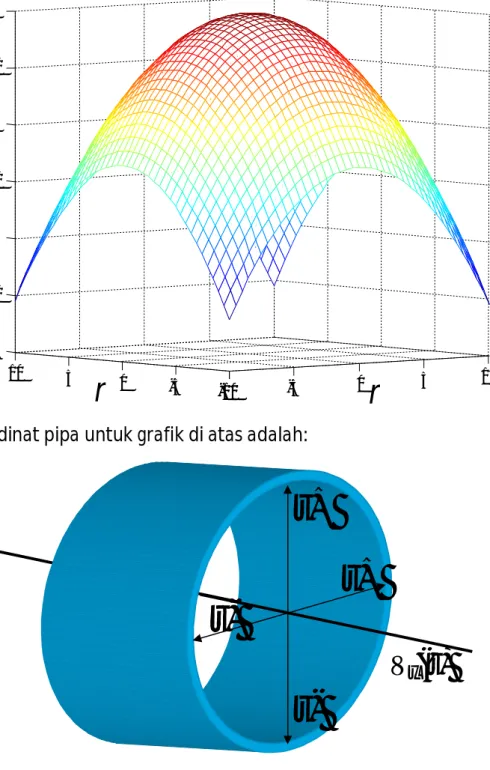
Gambar di bawah ini adalah hasil kerja MATLAB. Sumbu datar menunjukkan arah jari-jari pipa dan sumbu tegak menunjukkan kecepatan ke arah x. Kecepatan maksimum berada pada posisi (0,0) di tengah-tengah bidang sumbu datar.
Sketsa koordinat pipa untuk grafik di atas adalah:
-10 -5 0 5 10 -10 -5 0 5 10 -5 0 5 10 15 20 25
r
r
V
x(r)
r-
r+
r+
r-
V
x(r)
Hingga pada tahap ini anda sudah memperoleh:
Distribusi fluksi momentum
=
∆
2
Distribusi kecepatan=
∆
4
1 −
Kecepatan maksimum ,
=
∆
4
untuk fluida newton yang incompressible di dalam pipa datar.
Nah, terlihat bahwa kecepatan aliran fluida ke arah x bergantung pada posisi r; artinya kecepatan fluida itu bervariasi terhadap r. Kalau begitu, berapakah kecepatan rata-ratanya? Kecepatan rata-rata adalah jumlah kecepatan di semua posisi r dan dibagi dengan luas penampang aliran.
Jumlah semua kecepatan itu adalah pada posisi r dari r = 0 hingga ke r = R untuk satu lingkaran penuh dari sudut θ = 0 derajat hingga θ = 360 derajat atau dari θ = 0 hingga θ = 2π; yaitu:
Jumlah semua kecepatan =
Ingat bahwa adalah fungsi . Solusi dari integral ini adalah:
Jumlah semua kecepatan =
∆
8
Adapun luas penampang aliran (luas penampang pipa) adalah:
yang apabila diselesaikan diperoleh:
Luas penampang aliran =
Dengan demikian, kecepatan rata-rata, <Vx>, aliran fluida dalam pipa adalah:
< v > =
∆
8
=
∆
8
Sudah kita ketahui pula bahwa:
,
=
∆
4
Artinya, kecepatan rata-rata adalah setengah dari kecepatan maksimum.
Bagaimana dengan laju alir volumetris? Laju alir volumteris adalah luas penampang alira (luas penampag pipa) dikalikan dengan kecepatan rata-rata, yaitu:
= <
>.
2=
∆
4
8
Persamaan terakhir ini dikenal sebagai Persamaan
Hagen-Poiseuille
. Dari konsepsi laju, jelas dikatakan bahwa:=
Pada aliran fluida ini, gaya dorongnya adalah beda tekanan,
∆ .
Dan dengan demikian hambatannya adalah8
/
.
---