KARAKTERISTIK KOPRODUK GRUP HINGGA

KARAKTERISTIK KOPRODUK GRUP HINGGA

Edi Kurniadi, Stanley P. Dewanto, Alit Kartiwa

Jurusan Matematika FMIPA Universitas Padjadjaran Jalan Raya Bandung Sumedang Km 21 Jatinangor 45363

E-mail: edikrnd@gmail.com; stanleypd@bdg.centrin.net.id; alit_kartiwa@yahoo.com

ABSTRAK

KARAKTERISTIK KOPRODUK GRUP HINGGA

.

Dalam makalah ini diteliti bagaimana mengonstruksi koproduk dari dua buah grup. Lebih jauh fokus dalam makalah ini adalah karakteristik yang dimiliki oleh koproduk dan kaitannya dengan direct produk. Karakteristik yang sangat menarik dalam penelitian ini adalah produk bebas dari grup-grup hingga yang tidak mengawetkan keterhinggaan.

Kata kunci: universal properties of products, trivial dan nontrivial grup, tensor produk

ABSTRACT

THE PROPERTIES COPRODUCT OF A FINITE GROUP. In this paper, we did the research how to construct the coproduct of groups. The focus of this paper ts characteristics and its relation of the direct product. The interested characteristic indeed in this research that the coproduct of finite groups does not preserve fineteness.

Key words : the universal properties of products, trivial and nontrivial grups, tensor products

1. PENDAHULUAN

Fokus utama dalam makalah ini adalah meneliti karakteristik koproduk dari grup hingga yang tidak mengawetkan keterhinggaan. Hal ini berbeda dengan karakteristik yang dimiliki oleh produk langsung. Hal pertama yang dilakukan dalam adalah mengonstruksi suatu koproduk melalui diagram komutatif dari suatu produk langsung dan produk amalgamated sebagaimana telah dikembangkan oleh [8] dan [5]. Selanjutnya akan didefinisikan grup bebas yang mempunyai generator berbentuk pasang terurut dan grup bagian yang dibangun oleh generator tertentu. Dalam hal ini, koproduk akan didapatkan dari produk langsung sebagai dualnya.

Dalam [1] telah diperoleh grup bagian Frattini sebagai perluasan dari koproduk yang menunjukkan bahwa koproduk selalu mempunyai grup maksimal. Selain itu, dalam [3] telah didapat grup bagian near Frattini dari

perluasan koproduk. Dalam makalah berikutnya [2] juga telah membuktikan grup bagian upper Frattini dari perluasan koproduk. Deskripsi di atas telah menunjukkan bahwa koproduk sangat penting dalam grup bagian Frattini dan sejauh ini karakteristik koproduk dari grup-grup hingga yang tidak mengawetkan keterhinggaan belum ada yang membahas secara detail. Aplikasi koproduk bisa digunakan untuk mempelajari struktur yang berkaitan dengan dualisasi seperti aljabar dan koaljabar yang telah dibahas oleh [7]. Aplikasi lainnya telah diterapkan oleh M.K. Azarian seputar grup bagian Frattini [4]

Termotivasi oleh kajian-kajian di atas, dalam makalah ini diteliti tentang karakteristik koproduk dari grup hingga yang tidak mengawetkan keterhinggaan.

2. TEORI

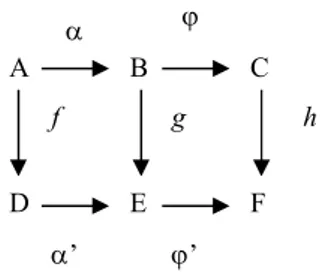
Definisi 1. [8] Suatu diagram dikatakan komutatif jika didapatkan komposisi homomorfisma yang sama ketika mengikuti arah panah sepanjang jalur yang berbeda dari satu grup ke grup yang lain dalam diagram.

Sebagai contoh perhatikan gambar berikut

Gambar 1. Diagram komutatif grup

Dari diagram 1 di atas, akan diperoleh kesamaan homomorfisma , , dan . Oleh karenanya, diagram 1 di atas komutatif.

Diagram Komutatif ini digunakan untuk mengonstruksi koproduk yang lebih detail dijelaskan dalam pembahasan.

2.1 Produk Langsung

Untuk sembarang family modul , diindeks oleh himpunan indeks sembarang. Produk dapat dipandang sebagai :

1 Himpunan semua fungsi

sedemikian sehingga untuk semua , dengan operasi modul didefinisikan titik demi

titik yaitu dan

untuk semua . 2 Semu strings atau himpunan

Sedangkan jumlah langsung

didefinisikan sebagai modul bagian dari yang memuat semua elemen berbentuk yang mempunyai sejumlah hingga komponen tak nol.

2.2 Karakteristik Produk dan Jumlah Langsung

i. Misalkan dan

yang didefinisikan oleh . Untuk sembarang modul dan homomorfisma

Dengan maka terdapat secara tunggal

homomorfisma sedemikian

sehingga untuk semua

ii. Untuk sembarang modul dan

pemetaan terdapat

secara tunggal pemetaan

sedemikian sehingga untuk semua

Diagram dalam (i) dan (ii) bersifat komutatif.

2.3 Tinjauan terhadap Hasil Kali Tensor

Pendefinisian koproduk identik dengan pendefinisian hasil kali tensor sebagaimana telah dibahas dalam [7]. Dalam makalah ini penulis melakukan suatu tinjauan ulang terhadap hasil kali tensor dari dua buah modul atas gelanggang.

Definisi 2. [8] Misalkan AR dan RB

berturut-turut menyatakan R-modul kanan dan kiri. Jika U menyatakan grup Abelian aditif, maka

φ

:

A

x

B



U

dikatakan pemetaan

balance jika dipenuhi :

1.

φ

(a1 + a2, b) =

φ

(a1, b) +

φ

(a2, b) 2.

φ

(a, b1 + b2) =

φ

(a, b1) +

φ

(a, b2) 3.

φ

(ar, b) =

φ

(a, rb),

untuk semua a, a1, a2  A , b, b1, b2  B dan

r  R.

Kondisi (1) dan (2) mengatakan bahwa

φ

suatu pemetaan bilinier.. Dapat ditunjukkan bahwa jika  : U  U` suatu homomorfisma grup maka pemetaan komposisi  : A x B 

U` suatu pemetaan balance.

Jika AR dan RB sebarang R-modul,

definisikan S =S(A, B) menjadi grup komutatif bebas atas A x B. Grup komutatif bebas artinya jumlah langsung dari pembangun suatu grup siklik tak hingga dan A x B memuat semua pembangun dari S. Dalam hal ini S = <(ai, bi)>

dengan i  I ). Dengan kata lain, setiap unsur di

S dapat ditulis secara tunggal sebagai suatu

jumlah hingga  za,b(a, b) dengan z bilangan

bulat.

Misalkan H subgrup dari S yang dibangun oleh unsur-unsur dengan bentuk sebagai berikut. 1. (a1+a2, b) - (a1, b) - (a2, b)

2. (a, b1+b2) - (a, b1) - (a, b2)

3. (ar, b) - (a, rb), untuk semua a, a1, a2  A , b, b1, b2  B dan r  R.

Sekarang didefinisikan AB menjadi suatu

A B C

D E F

 

f g h

grup komutatif aditif S/H.

Untuk (a, b)  S, didefinisikan ab = (a, b) +

H = 1(a, b) + H  AB. Restriksi pada S  S/H

oleh A x B menghasilkan  :AxB  AB. Berdasarkan pendefinisian H di atas dapat dilihat bahwa  suatu pemetaan balance.

Dari konstruksi di atas dapat diperoleh definisi hasilkali tensor sebagai berikut :

Definisi 3. [6] Untuk modul AR dan RB atas

suatu ring R, suatu hasilkali tensor dari A dan B adalah pasangan (T,

φ

) dengan T adalah grup

komutatif dan

φ

: A x B  T suatu pemetaan

balance. Untuk sebarang pemetaan balance f : A x B  C ke sebarang grup komutatif C, terdapat homomorfisma grup komutatif yang tunggal f` : T  C sedemikian sehingga f =

f`.

Diagramnya dapat dilihat sebagai berikut :

A x B  T

f  C

Gambar 2. Diagram Hasil Kali Tensor

Proposisi 1 [6] Misalkan AR dan RB adalah R-modul. Maka (ARB, ) suatu hasilkali tensor

dari A dan B atas R. Lebih jauh, jika (X, `)

sebarang hasilkali tensor lain, maka terdapat isomorfisma grup komutatif  : AB  X

sedemikian sehingga ` = .

Bukti :

Sebelumnya telah dibuktikan bahwa ARB

suatu grup komutatif dan  : AxB  AB

suatu pemetaan balance. Sekarang, misalkan :

AxB  U sembarang pemetaan balance. Karena S modul bebas atas AxB, pengaitan (a, b)



(a,b) menentukan suatu homomorfisma `: S  U. Karena  pemetaan balance maka ` memetakan setiap generator dari H ke nol atau `(H) = 0. Jadi, H  ker(`). Dari teorema

isomorfisma grup terdapat  : S/H  U sedemikian sehingga [(a,b) + H ]= `[(a, b)]= (a, b). Tetapi dari pendefinisian awal S/H =

AB dan (a, b) + H =ab. Oleh karenanya,  :

S/H = AB  U suatu homomorfisma dengan

(ab) = (a, b) .

Berikut akan ditunjukkan bahwa  unik. Misalkan f : AB  U suatu homomorfisma grup komutatif lain sehingga  = f. Ambil  unsur di AB dan tuliskan  =  ab, yaitu jumlah hingga. Sekarang perhatikan, f()= f(a, b) =  (a, b) = (). Hal ini menunjukkan bahwa  = f.

Karena (X, `) suatu hasilkali tensor maka ` :

AxB  X suatu pemetaan balance dan terdapat

 : AB  X dengan ` = . Demikian juga karena (AB, ) suatu hasilkali tensor maka  : AxB  AB suatu pemetaan balance dan terdapat : X AB dengan  = `.

Jadi diperoleh ` = ` dan juga  = . Hal ini menunjukkan bahwa  dan  suatu pemetaan identitas. Jadi,  : AB  X mendefinisikan suatu isomorfisma.

3. HASIL DAN PEMBAHASAN

3.1 Konstruksi Koproduk

Diberikan dua buah grup dan .

Koproduk adalah grup dengan

homomorfisma dan

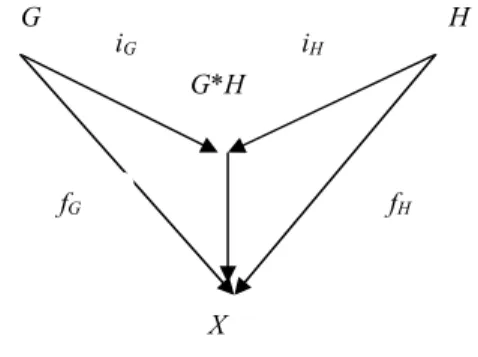
sedemikian sehingga jika diberikan sembarang grup dengan homomorfisma dan homomorfisma maka ada secara tunggal homomorfisma .

Secara diagram dapat ditunjukkan sebagai berikut :

Gambar 3. Diagram Konstruksi Koproduk Di sini dapat ditunjukkan bahwa untuk sembarang grup , dapat ditentukan secara tunggal hingga isomorfisma. Selanjutnya akan diberikan suatu contoh grup yang memenuhi

G*H

X

G H

fG fH

sifat ini.

Misalkan suatu monomorfisma yaitu homomorfisma yang satu-satu. Ganti dengan sehingga menjadi identitas di . Selanjutnya menjadi homomorfisma trivial yaitu mengaitkan semua unsur ke identitas di

. Dapat ditunjukkan bahwa Ker Ker . Tetapi komposisi ini haruslah homomorfisma identitas di yang mempunyai trivial kernel dan haruslah . Dengan kata lain peta dari dan terletak di .

Selanjutnya, diperiksa relasi antara unsur yang terletak di dengan unsur yang terletak di .

Gantikan dengan dan misalkan mengaitkan semua unsur dengan pangkat dari generator yaitu didefinisikan suatu homomorfisma dari ke . Sementara mengaitkan semua unsur di ke suatu pangkat dari generator . Jika ada relasi antara unsur dan di , maka tidak dapat terpenuhi

universal property. Oleh karenanya,

isomorf dengan , hanya sebagai pengganti pergantian pangkat dan dari unsur-unsur di dan . Di sini diperoleh bahwa unsur-unsur di

berbentuk .

Hasil dari koproduk sangat berperan dalam aljabar topologi seperti dalam tulisan [8].

3.2 Koproduk Grup Hingga Tidak Mengawetkan Keterhinggaan

Misalkan penyajian untuk grup dengan himpunan semua generator untuk dan himpunan semua relasinya. Hal yang sama dilakukan untuk grup yaitu

penyajiannya .

Sesuai dengan konstruksi di atas diperoleh bahwa

Yaitu grup hasil koproduk

dibangun oleh generator bersama-sama dengan generator , dengan relasi dari bersama-sama dengan relasi dari .

Sebagai contoh pandang grup siklik dengan order 4 yang disajikan dalam bentuk

dan grup siklik dengan

order 5 dengan penyajian .

Sesuai dengan konstruksi di koproduk diperoleh .

Perhatikan bahwa

penyajian dari grup dihedral tak hingga. Teorema 1.[5] Misalkan dan grup hingga maka selalu tak hingga.

Bukti : Konstruksi koproduk dengan himpunan semua generator untuk dan himpunan semua relasinya. Hal yang sama dilakukan untuk grup yaitu penyajiannya . Telah dijelaskan pada konstruksi koproduk bahwa unsur-unsur nontrivial dari grup dan tidak komutatif satu sama lain maka

tak hingga.

4. KESIMPULAN

Telah diberikan bagaimana mengonstruksi koproduk dari dua buah grup. Karakteristik dari koproduk dua buah grup hingga yang tidak mengawetkan keterhinggan juga telah dibuktikan dalam Teorema 1 berikut contohnya. Untuk penelitian lanjutan dapat dikaji generalisasi koproduk dua buah grup dengan produk amalgamated berikut penerapan koproduk dalam masalah sinyal dan sistem.

5. UCAPAN TERIMAKASIH

Kami mengucapkan terima kasih kepada Jurusan Matematika FMIPA UNPAD yang telah mendanai penelitian swadana ini tahun anggaran 2012.

6. DAFTAR PUSTAKA

1. ALLENBY and TANG, On the frattini subgroups of generalized free products, Bull. Amer. Math. Soc., 80 (1974), 119-121 2. ALLENBY, On the upper near Frattini

subgroup of the generalized free product, Houston J. Math., 31(2005), no 4, 999-1005 3. AZARIAN, Near Frattini subgroups of

certain generalized free products of groups, International Journal of Pure and Applied Mathematics, Vol 28, No.3, 2006, pp.

337-385. Mathematical Reviews,

MR2230953(2008b:20032), February 2008, p.1056. Zbl 1122.20011

4. AZARIAN, Conjectures and questions regarding Near Frattini Subgroups of generalized free products of groups,

International Journal of Algebra., (2011), no. 1, 1 -15.

5. BRIAN OSSEMAN, osserman, Free Products and amal gamated products, 1990

6. DAUNS, J. Modules and Rings, Cambridge University Press, 1994.

7. KURNIADI dan IRAWATI, Aljabar atas

suatu lapangan dan dualisasinya, Institut

Teknologi Bandung, 2007.

8. LASZLO FUCHS. Infinite Abelian Groups. 252-274, 1970.

9. MASSEY, Algebraic Topology : An introduction, Springer Verlag, New York,