Design and Analysis of Algorithms CNH2G3- Week 4
Kompleksitas waktu algoritma rekursif part 1
Dr. Putu Harry Gunawan (PHN)
Quiz I
1. Tentukan operasi dasar, cop dan C(n) untung masing-masing algoritma berikut. Serta tambahkan analisis untuk Tmax(n), Tmin(n) dan Tavg(n):
(a) l <-- 1 for j=0 to l++ for l=1 to 3 a=sqrt(5/4) end end (b) j=1; while j<n for k=1 to j if(A[k] == A[j]) return k; endIf endFor endWhile (c) L=2n; do k=L+3; L=L/2; while(L<0); 1
2. Berikan definisi masing-masing Big oh, Big Omega dan Big Theta beserta ilus-trasinya!
Big-Oh Big-Omega Big-Theta
∃ · · · T(n)∈ O(g(n)) ⇐⇒ ∃ · · · T(n)∈Ω(g(n)) ⇐⇒ ∃ · · · T(n)∈Θ(g(n)) ⇐⇒
ilustrasi ilustrasi ilustrasi
3. Buktikan pernyataan berikut ini: (a) T(n) = 12(n−2)(n−3)∈Θ(n2) (b) T(n) =Pn−3 i=2 5i∈Θ(n2) (c) T(n) =n2+ 10nlog(n2)∈ O(n2) Jawab
Review
1. Buatlah algoritma rekursif untuk menghitung faktorial! Contoh
10! = 10×9× · · · ×2×1 (0.1) 2. Buatlah algoritma rekursif untuk menentukan nilai baris fibonanci ke-n
Contoh: Baris fibonanci ke 6
1,1,2,3,5,8 (0.2)
1
Pendahuluan
Pada bab ini, akan dibahas mengenai menghitung waktu asismtotik untuk algoritma rekur-sif. Kita mulai dengan definisi-definisi algoritma rekursif:
1.1 Dikatkan bentuk rekursif:
1. suatu subrutin atau fungsi/ prosedur yang memanggil dirinya sendiri. 2. bentuk dimana pemanggilan subrutin terdapat di dalam body subrutin 3. dengan rekursi, program akan lebih mudah dilihat.
1.2 Tujuan dibuat rekursif:
1. menyederhanakan penulisan program 2. menggantikan bentuk iterasi
1.3 Syarat bentuk rekursif:
1. ada kondisi terminal
2. adasubroutine call yang melibatkan parameter yang nilainya menuju kondisi termi-nal
Sehingga untuk menghitung kompleksitas bentuk rekursif, maka digunakan teknik per-hitungan kompleksitas dengan relasi rekurens.
2
Relasi Rekurens Faktorial
Perhatikan algoritma berikut:Function Factorial(input n: integer) -> integer
Algoritma if n=0 then return 1 else return (n * Factorial(n-1)) endif Kompleksitas waktu:
• untuk kasus basis, tidak ada operasi perkalian →0
• untuk kasus rekurens, kompleksitas waktu diukur dari jumlah perkalian (1) ditambah kompleksitas wasktu untuk faktorial (n-1).
Sehingga relasi rekursinya dapat dibentuk menjadi:
T(n) =
(
0, n= 0,
Jadi menghitung waktunya adalah T(n) = 1 +T(n−1) = 1 + 1 +T(n−2) = 2 +T(n−2) = 2 + 1 +T(n−3) = 3 +T(n−3) =· · · =n+T(0) =n+ 0 JadiT(n) =n→ O(n).
Secara umum, untuk menganalisis waktu efisiensi dari algoritma rekursif: 1. Putuskan dalam parameter, yang mengindikasikan ukuran inputan. 2. Identifikasi operasi dasar algoritma
3. Cek apakah jumlah operasi dasar akan berbeda jika ukuran masukan berbeda?, kalau iya maka dapat dihitung, waktu terbaik, terburuk, dan rata-rata secara terpisah. 4. Buat relasi rekursi dengan kondisi awal yang sesuai, untuk jumlah operasi dasar
yang dijalankan.
5. Selesaikan relasi rekursi, atau paling tidak tentukan orde kenaikannya.
3
Relasi Rekurens Hanoi Tower
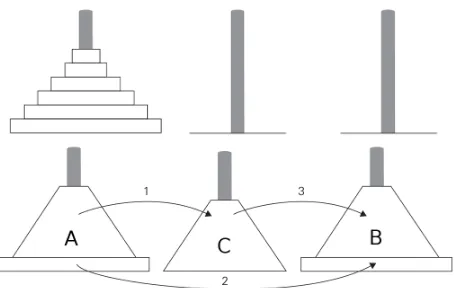
Selanjutnya adalah contoh masalah yang dikenal sebagai the Tower of Hanoi puzzle. Dalam permainan ini, pemain diberikan tiga buah batu yang memiliki ukuran berbeda. Batu-batu tersebut selanjutnya disusun berdasarakan ukuran, yakni ukuran terbesar berada paling bawah.
Tujuan dari permainan ini adalah, memindahkan tumpukan batu di tiang A ke B tanpa mengubah posisi batu besar paling bawah. Disediakan tiang C sebagai perantara.
Procedure Hanoi (input n, A, B, C:integer)
Algoritma
If n=1 then
Write (Pindahkan piringan dari,A,ke,B) Else
Hanoi(n-1,A,C,B)
Writeln(Pindahkan piringan dari,A,ke,B) Hanoi(n-1,C,B,A)
Endif
Operasi dasar dari algoritma Hanoi adalah ’Writeln()’, sehingga dengan jelas bahwa pergerakanT(n) bergantung pada nyang relasi rekursinya berupa:
Figure 1: Solusi rekursif untuk masalah Menara Hanoi.
Dengan kondisi awalT(1) = 1, maka relasi rekursinya ditulis ulang dalam bentuk:
T(n) =
(
1, n= 1
2T(n−1) + 1, n >1 (3.2)
Maka kompleksitas waktunya dapat dihitung sebagai berikut:
T(n) = 2T(n−1) + 1 = 2(2T(n−2) + 1) + 1 = 22T(n−2) + 2 + 1 = 22(2T(n−3) + 1) + 2 + 1 = 23T(n−3) + 22+ 2 + 1 =· · · = 2n−2(2T(n−(n−1)) + 1) + 2n−3+· · ·+ 22+ 2 + 1 = 2n−2·2T(1) + 2n−2+ 2n−3+· · ·+ 22+ 2 + 1 = 2n−1+ 2n−2+ 2n−3+· · ·+ 22+ 2 + 1 = 2n−1 SehinggaT(n) = 2n−1→ O(2n).
4
Relasi Rekursi Min Max
Perhatikan algoritma mencari data maksimum dan minimum dari suatu tabel berikut
procedure MinMaks2(input A : TabelInt, i, j : integer, output min, maks : integer) { Mencari nilai maksimum dan minimum di dalam tabel A
yang berukuran n elemen secara Divide and Conquer.
Masukan: tabel A yang sudah terdefinisi elemen- elemennya Keluaran: nilai maksimum dan nilai minimum tabel
}
min1, min2, maks1, maks2 : integer
if i=j then {Jika satu elemen} min <-- A[i]
maks <-- A[i] else
if (i = j-1) then {Jika dua elemen} if A[i] < A[j] then
maks <-- A[j] min <-- A[i] else maks <-- A[i] min <-- A[j] endif else
k=(i+j) div 2 { bagidua tabel pada posisi k } MinMaks2(A, i, k, min1, maks1)
MinMaks2(A, k+1, j, min2, maks2) if min1 < min2 then
min <-- min1 else min <-- min2 endif if maks1<maks2 then maks <-- maks2 else maks <-- maks2 endif endif endif
Dari algoritma tersebut dapat dibuat relasi rekursi sebagai berikut:
T(n) = 0, n= 1 1, n= 2 2T(n/2) + 2, n >2 (4.1)
Misaln= 2k, sehingga T(n) = 2T(n/2) + 2 = 2(2T(n/4) + 2) + 2 = 4T(n/4) + 4 + 2 = 4(2T(n/8) + 2) + 4 + 2 = 8T(n/8) + 8 + 4 + 2 = 23T(2k/23) + 8 + 4 + 2 = 23T(2k−3) + 23+ 22+ 21, n= 2k =· · · = 2k−1T(2) + 2k−1+· · ·+ 22+ 21 = 2k−1+ k−1 X i=1 2i = 2k−1+ 2k−2
Selanjutnya bawa ke bentukn atauk=2 logn,
T(n) = 2k−1+ 2k−2 = 22logn−1+ 22logn−2 = n 2 +n−2 = 3n 2 −2∈ O(n)
5
Tambahan
Untuk mengetahui kompleksitas bentuk rekursif, maka T(n) harus diubah dalam bentuk yang bukan rekursif.
Bagaimana mengubah bentuk rekursif ke non rekursif ? Ada dua macam cara untuk menyelesaikan masalah ini, yaitu cara coba-coba dan dengan persamaan karakteristik :
1. Cara coba-coba (deret).
2. Metode dengan persamaan karakteristik
5.1 Cara coba-coba
Cara ini dilakukan dengan menentukan pola deret yang terbentuk (cara deret). Con-toh untuk cara ini telah ditunjukkan dalam mencari kompleksitas waktu untuk beberapa bentuk rekursif sebelumnya. Cara ini agak sulit dan perlu pengalaman.
Example 5.1 Tentukan waktu rekursi berikut:
T(n) =
(
a, n= 1,2
Solusi dari contoh diatas dengan cara coba coba adalah sebagi berikut: T(1) =T(2) =a T(3) =T(2) +T(1) +b=a+a+b= 2a+b T(4) =T(3) +T(2) +b= (2a+b) +a+b= 3a+ 2b T(5) =T(4) +T(3) +b= (3a+ 2b) + (2a+b) +b= 5a+ 4b T(6) =T(5) +T(4) +b= (5a+ 4b) + (3a+ 2b) +b= 8a+ 7b · · ·
Sangat sulit untuk bisa diformulasikan. Sehingga harus mencari cara lain utntuk menghi-tung waktu algoritma. Salah satu caranya adalah dengan menggunakanmetode karak-teristik. Metode ini akan dijelaskan pada peretemuan selanutnya.
References
1. Anany, L. (2003). Introduction to the design and analysis of algorithms. Villanova University.
2. http://www.annedawson.net/BigOh.htm
6
Exercise
1. Selesaikan relasi rekurensi berikut: (a) T(n) = ( 0, n= 1 T(n−1) + 5, n≥2 (6.1) (b) T(n) = ( 4, n= 1 3T(n−1), n≥2 (6.2) (c) T(n) = ( 0, n= 0 T(n−1) +n, n >0 (6.3) (d) T(n) = ( 1, n= 1 T(n/2) +n, n >1 (6.4) (e) T(n) = ( 1, n= 1 T(n/3) + 1, n >1 (6.5)
2. Diberikan algoritma untuk menghitung jumlah pangkat 3 dari deret, S(n) = n3 + (n−1)3+· · ·+ 23+ 13.
ALGORITHM S(n)
//Input: A positive integer n
//Output: The sum of the first n cubes if n = 1 return 1
else return S(n - 1) + n * n * n
(a) Tentukan relasi rekursi dari algoritma di atas dan selesaikan. (b) Bandingkan dengan algoritma yang tidak ditulis dengan rekursif.