BAB 2 TINJAUAN PUSTAKA

Bab ini membahas penyelesaian masalah yang akan disimulasi, dan algoritma program yang akan digunakan.

Bab IV Hasil dan Pembahasan

Bab ini memberikan hasil uji coba simulasi dengan membandingkan pola lintasan yang didasarkan pada sudut variasi sudut lintang. Titik yang diambil yaitu pada kutub bumi (90o), khatulistiwa (0o), dan sembarang tempat antara kutub bumi dan khatulistiwa; Medan (3o) dan Jakarta (6o).

Bab V Kesimpulan dan saran

Bab ini memberikan kesimpulan dari hasil perancangan program yang telah dilakukan dan juga memberikan saran-saran untuk penelitian selanjutnya.

BAB 2

TINJAUAN PUSTAKA

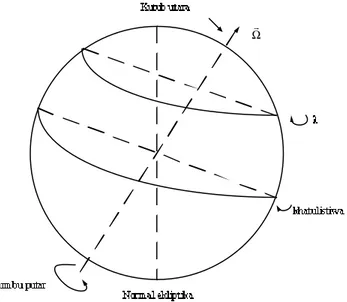
2.1. Rotasi Bumi

Rotasi adalah perputaran benda pada suatu

sumbu

yang tetap, misalnya

perputaran

gasing

dan perputaran

planet

Bumi

pada

sumbunya

. Pada rotasi bumi,

gerak rotasi ini terjadi pada garis/poros/sumbu utara-selatan (garis tegak dan sedikit

miring ke kanan). Adapun kecepatan rotasi bumi dapat dihitung sesuai dengan

persamaan 2.1.

v = 2?rBumi cos ?/24

(2.1)

Dengan ? ?adalah besarnya derajat lintang suatu tempat di permukaan bumi. Faktor cos ? muncul pada persamaan 2.1 karena tiap titik di permukaan bumi berputar terhadap sumbu

putar bumi, bukan terhadap titik pusat bumi. Seperti yang telah diketahui bahwa rBumi pada khatulistiwa sama dengan 6375 km, sehingga kecepatan bumi berdasarkan persamaan 2.1 yaitu sebesar 1669 cos ? km/jam. Jika diambil posisi pada garis khatulistiwa, atau pada ? = 0 maka akan diperoleh kecepatan bumi sebesar 463 meter per detik yang ternyata sudah melampaui besar kecepatan suara di udara. Pengaruh dari rotasi bumi ini secara garis besar, yaitu:

a. Pergantian Siang dan malam b. Perbedaan waktu

c. Perbedaan percepatan gravitasi bumi d. Pembelokan arah angin

e. Pembelokan arus laut

f. Peredaran semu harian benda-benda langit

Salah satu cara untuk menganalisa rotasi bumi beserta pengaruhnya adalah dengan menggunakan pendulum Foucault (akan dijelaskan lebih lanjut pada subbab 2.3). (Pikatan, 2009)

Ωr

Gambar 2.1. Rotasi Bumi

Gaya Coriolis adalah suatu proses alam yang dinamakan sesuai dengan penemunya yaitu Gaspard Gustave Coriolis (1844) dari Prancis. Ia menemukan bahwa rotasi bumi selalu menyebabkan simpangan terhadap setiap gerakan yang terjadi pada permukaan bumi. Besar kecilnya penyimpangan tergantung dari lintang geografi, dimana gerakan itu terjadi.

Pada belahan bumi utara setiap gerak di belokkan ke kanan dan pada belahan bumi selatan di belokkan ke kiri dari arah kecepatan. Pembelokkan atau perubahan arah ini hanya dapat di terangkan dengan menganggap atau menambahkan adanya gaya tidak

nyata yang bekerja pada suatu benda. Gaya khayal atau gaya fiktif ini dinamakan gaya coriolis. Gaya semacam ini yang bekerja pada satu satuan massa atau percepatan yang ditimbulkan disebut percepatan coriolis.

Besarnya percepatan coriolis secara matematis dapat dinyatakan sebagai berikut.

φ

sin

2

Ω

=

v

a

c (2.2)

v adalah kecepatan benda yang bergerak, ? kecepatan sudut rotasi bumi yang besarnya sama dengan

7

,

27

x

10

−5

rad

/

s

, ? besarnya derajat lintang. Dari persamaan tersebut di atas dapat dilihat bahwa untuk kecepatan yang sama pengaruh coriolis terbesar terdapat di kutub. Pengaruh ini makin berkurang dengan berkurangnya lintang tempat dan sama dengan nol di khatulistiwa.

Sering pula persamaan di atas ditulis:

vf

a

_c

=

dengan

f

=

2

Ω

sin

φ

(2.3)

f dinamakan parameter coriolis.

Arah percepatan coriolis ialah tegak lurus pada kecepatan, ke kanan di belahan bumi utara dan ke kiri di belahan bumi selatan. (Susilo Prawirowardoyo,1996).

Pendulum Foucault adalah suatu alat yang berguna untuk menunjukkan arah rotasi bumi. Alat ini ditemukan oleh Jean Bernard Léon Foucault. Alat eksperimen ini terdiri atas bandul panjang yang bebas bergerak kesana kemari pada latar vertikal. Diagram dari pendulum Foucault diberikan pada gambar 2.2.

Gambar 2.2 pendulum Foucault

Pertunjukan pertama bandul Foucault kepada khalayak terjadi pada bulan Februari 1851 di Ruang Meridian yang ada di Observatorium Paris. Beberapa minggu kemudian, Léon Foucault membuat bandul terkenalnya ketika ia menggantung potongan logam seberat 28 kg dengan kabel sepanjang 67 meter dari kubah Panthéon di Paris. Hal itu untuk membuktikan bahwa bumi berputar pada porosnya. Pesawat osilasi dari pendulum Foucault berputar sepanjang hari sebagai akibat dari rotasi bumi. Pesawat osilasi menyelesaikan seluruh lingkaran dalam interval T, yang tergantung pada lintang geografis.

ini selanjutnya digunakan untuk menganalisis rotasi bumi pada porosnya, dengan bandul yang cukup berat yang digantungkan pada tali panjang, agar dapat bertahan berayun-ayun cukup lama. Oleh rotasi bumi, tentunya bandul akan berosilasi karena seolah-olah tertinggal oleh rotasi bumi. Untuk menyelidiki gerakan bandul yang memperlihatkan adannya rotasi itu, dapat tinjau bandul yang dipasang di tempatnya misalnya ?.(peter,2000)

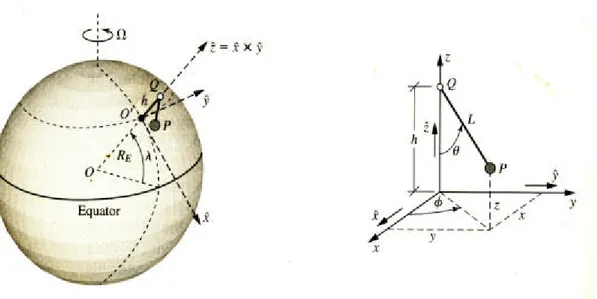
Gambar 2.3 Pendulum yang menunjukkan rotasi bumi.

pendulum yang terdiri dari partikel P dengan massa dan kawat (diperkirakan tak bermassa ) panjang, dan yang menyangga pada titik Q dekat lintang permukaan bumi seperti yang ditunjukkan pada gambar 2.3 untuk mempermudah, jarak vertikal h antara titik O ',yang mana pada permukaan bum, penyangga pada Q adalah diambil menjadi h=L.

Skala dari gambar 2.3 terlalu dibesarkan dengan diasumsikan panjang L dari pendulum terlalu kecil dari radius

R

_E di bumi, dengan bumi yang homogen sebagai massa

M

_E. Hal ini juga diasumsikan bahwa gaya pada P adalah tegangan tali QP, besarnya N dan gaya

gravitasi bumi. Besarnya gaya gravitasi yang

bekerja pada P ini diperkirakan sebagai

GM

_E

m

/

R

2E

=

mg

_,

dimana g = 9,81 m/s2 adalah percepatan gravitasi di permukaan bumi. Dan juga karena L sangat kecil dibandingkan dengan

R

_E, gaya gravitasi yang bekerja pada P dinyatakan dalam arah −zˆdimana zˆadalah sebuah vektor satuan yang diarahkan ke atas sepanjang gatis vertikal OO’. Koordinar rectangular x, y, dan z ditunjukkan pada gambar 2.3 digunakan untuk menganalisis efek ? sebagai gaya pendulum yang bergerak relatif terhadap bumi.

Istilah partikel yang diam di bumi dinyatakan dalam vektor satuan

(

x

ˆ

,

y

ˆ

,

z

ˆ

=

x

ˆ

×

y

ˆ

)

yang ditunjukkan pada 2.3 dengan resultan gaya Fr dengan persamaan:

(

)

_











+

+

−

−

−

=

−

−

≈

L

z

L

z

y

y

x

x

N

z

mg

QP

QP

N

z

mg

F

r

ˆ

ˆ

ˆ

ˆ

ˆ

(2.4)

Dimana x, y dan z adalah koordinat rectangular dengan P adalah titik axis pada permukaan bumi dan titik tengah di O’. perhatikan bahwa, panjang pendulum L adalah konstan, variabel x, y dan z din yatakan dengan persamaan:

(

)

2 2 2 2 L L z y x + + − =

Dengan ? menjadi lokasi lintang titik O’ di bumi, dengan kecepatan angular

ω

v

dari

{

x

ˆ

,

y

ˆ

,

z

ˆ

}

yang ditunjukkan pada gambar 2.3

(

λ

λ

)

ω

r

≈

Ω

z

ˆ

sin

−

x

ˆ

cos

_(2.5)

dimana ? = 2p rad/hari ≈7,27.10-5 rad/s. Pada persamaan 2.5 rotasi garis dari matahari ke pusat O di bumi. Dengan kecepatan angular 2p rad/tahun. Diabaikan karena lebih kecil ? di sekitar titik pusat bumi. Dengan posisi vektor bumi dari O’ ke P dinyatakan sebagai

z

z

y

y

x

x

P

O

'

=

ˆ

+

ˆ

+

ˆ

dan di pusat O di bumi sekarang pada kerangka inersia. Posisi vektor sebenarnya dari P adalah:

z z y y x x z R rr_p = _Eˆ+ ˆ+ ˆ+ ˆ

Oleh karena itu, kecepatan υr_p dan percepatan ar_p di P adalah: p p p

x

x

y

y

z

z

r

dt

r

d

_r

_r

&

&

&

r

r

₌

₌

₊

₊

₊

_ω

_×

υ

ˆ

ˆ

ˆ

=

(

x

&

−

Ω

y

sin

λ

)

x

ˆ

+

[

y

&

+

Ω

x

sin

λ

+

Ω

(

R

_E

+

z

)

cos

λ

] (

y

ˆ

+

z

&

−

Ω

y

cos

λ

)

z

ˆ

(2.6) { } p z y x p p p dt d dt d a υ υ ωr υv r r r _{+ ×}     = = ˆ , ˆ , ˆ

(

)(

)

[

]

(

)

(

)

(

)

[

z

y

x

R

z

]

z

y

y

z

x

y

x

z

R

y

x

E E

ˆ

cos

cos

sin

cos

2

ˆ

cos

2

sin

2

ˆ

cos

sin

sin

2

2 2 2 2 2

λ

λ

λ

λ

λ

λ

λ

λ

λ

+

Ω

−

Ω

−

Ω

−

+

Ω

−

Ω

+

Ω

+

+

+

Ω

−

Ω

−

=

&

&

&

&

&

&

&

&

&

&

(2.7)

Dengan Fr dan ar_p sebenarnya ditunjukkan pada persamaan 2.4 dan 2.7 di bawah ini adalah persamaan skalar yang diperoleh langsung dari

F

v

=

m

a

r

_p

(

)(

)

[

]

N L x z R x y x

m_&&−2Ω_&sin λ−Ω)2 sin2λ−Ω2 _E + sinλ cosλ =−

(2.8)

(

)

N L y y z x y m + Ω + Ω −Ω2 =− cos 2 sin 2 & λ & λ & & (2.9)

(

)

(

)

[

]

N L L z mg z R x y z m E − − − = + Ω − Ω − Ω − λ 2 λ λ 2 2λ cos cos sin cos 2 & & & (2.10)

Persamaan 2.8 sampai 2.10 di subsitusikan ke persamaan 2.5 yang mempengaruhi gaya dari pendulu m relatif terhadap perputaran bumi. Efek dari ? sangat kecil pada gerakan pendulum dan sekarang dibahas secara rinci. dimana ? = 2p rad/hari ≈7,27.10-5 rad/s sangat kecil, perkiraan sekarang dibuat untuk mengurangi kompleksitas pada persamaan 2.8 sampai 2.10 tapi masih mempertahankan efek ? tentunya. Karena ayunan cukup kecil, gerakan pendulum boleh dikatakan berada pada bidang datar, maksudnya komponen gerakan ke atas dan ke bawahnya boleh diabaikan yang berarti

z

&

dan

z

&

&

adalah 0.

Maka persamaan pendulum Foucault adalah ditunjukkan pada persamaan 2.11 dan 2.12.

0 sin 2Ω + = − x L g y x& & & λ (2.11) 0 sin 2Ω + = + y L g x y& & & λ (2.12)

Persamaan 2.11 dan 2.12 diatas menghubungkan gerakan-gerakan sepanjang sumbu x dan sepanjang sumbu y yang berarti menentukan bentuk lintasan pendulum.(Marcelo da Silva,2004)

2.4. Metode Runge-Kutta

Salah satu metode numerik yang digunakan dalam penyelesaian persamaan differesial adalah metode Runge-Kutta. Metode ini mencapai ketelitian suatu pendekatan deret Taylor tanpa memerlukan kalkulasi turunan yang lebih tinggi. Banyak perubahan terjadi, tetapi semuanya dapat ditampung dalam bentuk umum dari persamaan 2.13

yi+1 = yi + f(xi, yi, h) h (2.13)

dimana f (xi, yi, h) disebut suatu fungsi yang dapat diinterpretasikan sebagai sebuah slope

rata-rata sepanjang interval. Fungsi tersebut dapat ditulis dalam bentuk umum dalam persamaan 2.14.

f = a1 k1 + a2 k2 + … + an kn (2.14)

dimana setiap a adalah konstanta dan setiap k besarnya adalah persamaan-persamaan 2.15.

k1 = f(xi , yi )

k2 = f(xi + p1h, yi + q11 k1h)

k3 = f(xi + p2h, yi + q21 k1h + q22k2h) (2.15)

M

kn = f(xi + pn-1h, yi + qn-1,1 k1h + qn-1,2 k2h + ...+ qn-1,n -1 kn-1h)

Semua harga k berhubungan secara rekurensi. Artinya k1 muncul dalam persamaan untuk k 2, yang muncul lagi dalam persamaan untuk k3, dan seterusnya. Rekurensi ini membuat metode RK efisien untuk kalkulasi oleh komputer (Raymond et al, 1991).

Berbagai jenis metode Runge-Kuttadapat direncanakan dengan melaksanakan jumlah suku-suku yang berbeda pada fungsi tersebut seperti dinyatakan oleh n. untuk n = 1 atau RK orde pertama ternyata adalah metode Euler, yaitu persamaan 2.16.

y1 = y0+ h f(x0,y0) (2.16)

Dalam deret Taylor didapatkan persamaan 2.17.

...

)

,

(

'

2

)

,

_{0 0} 2 0 0 0 0 0

=

+

=

+

+

f

x

y

+

!

h

y

h f(x

y

h)

y(x

y

(2.17)

Untuk metode RK orde kedua diberikan oleh persamaan-persamaan 2.18.

x

h

k

y

k

y

h

x

hf

k

hf(x , y)

k

∆

=

=

∆













₊

₊

=

=

dengan

,

2

1

,

2

1

2 1 2 1 (2.18)

Metode RK orde tiga diberikan oleh persamaan-persamaan 2.19.

)

4

(

6

1

)

2

,

(

2

1

,

2

1

3 2 1 1 2 3 1 2 1

k

k

k

y

k

k

y

h

x

hf

k

k

y

h

x

hf

k

hf(x , y)

k

+

+

=

∆

−

+

+

=













₊

₊

=

=

(2.19)

Metode RK orde empat diberikan oleh persamaan-persamaan 2.20.

y

x

y

h

x

y

k

k

k

k

y

k

y

h

x

hf

k

k

y

h

x

hf

k

k

y

h

x

hf

k

hf(x , y)

k

∆

+

=

+

+

+

+

=

∆

+

+

=













₊

₊

=













₊

₊

=

=

)

(

)

(

)

2

2

(

6

1

)

,

(

2

1

,

2

1

2

1

,

2

1

4 3 2 1 3 4 2 3 1 2 1 (2.20)

Sedangkan untuk menyelesaikan persamaan differensial orde dua digunakan metode RK orde empat dengan terlebih dahulu membuat permisalan. Ditinjau persamaan differensial orde dua seperti pada persamaan 2.21.

)

,

,

(

2 2

dx

dy

y

x

f

dx

y

d

=

(2.21)

Dengan y(x0) = y0, dan y’(x0)= y0’ . Persamaan 2.19. dibuat permisalan sehingga diperoleh persamaan-persamaan 2.22. ) , , ( ) , , (x y y f x y z f y z dx dz z y dx dy = ′ = ′′ = ′ = = ′ = (2.22)

Persamaan-persamaan 2.16. merupakan persamaan-persamaan simultan yang dapat juga dituliskan sebagai f1(x,y,z)=z dan f2(x,y,z)=f(x,y,z). Berdasarkan persamaan-persamaan

2.16 tersebut, persamaan differensial orde tersebut diselesaikan dengan mengikuti aturan metode RK orde empat pada persamaan 2.14 (Kandasamy et al,1997).

Contoh Runge kutta:

0

' "

+

_xy

+

_y

=

y

dengan

_y

( )

0

=

1

;

_y

'

( )

0

=

1

;

_y

( )

0

,

1

=

_y

1

' ' "

_xy

_y

_z

y

=

−

−

=

z

y

'

=

(

x y z

)

f z dx dy , , 1 = =

(

x

y

z

)

f

y

xz

dx

y

d

,

,

2 2 2

=

−

−

=

Dengan memberikan nilai awal y₀ =1,z₀ =y'0 =0 maka:

(

₀

,

₀

,

₀

)

0

,

1

₁

(

0

,

1

,

0

)

0

,

1

( )

0

0

1 1

=

hf

x

y

z

=

f

=

=

k

(

₀

,

₀

,

₀

)

0

,

1

₂

(

0

,

1

,

0

)

0

,

1

(

( )( ) ( )

0

0

1

)

0

,

1

( )

1

0

,

1

2 1

=

hf

x

y

z

=

f

=

−

−

=

−

=

−

l

      _{+ + +} = 1 0 0 1 0 1 2 2 1 , 2 1 , 2 1 l z k y h x hf k

( )

( )

( )

(

)

      _{+ + + −} = 0,1 2 1 0 , 0 2 1 1 , 1 , 0 2 1 0 1 , 0 f1 =0,1f1

(

0,05,1,0,005

)

005 , 0 2 =− k













₊

₊

₊

=

2 0 0 1 0 1 2

2

1

,

2

1

,

2

1

l

z

k

y

h

x

hf

l

(

0.05,1, 0.005

)

1 , 0 2 − = f 09975 , 0 2 = − l       _{+ + +} = 1 0 0 2 0 2 3 2 1 , 2 1 , 2 1 l z k y h x hf k

(

0.05,0.9975, 0.0499

)

1 , 0 1 − = f = -0.00499













₊

₊

₊

=

2 0 0 2 0 2 3

2

1

,

2

1

,

2

1

l

z

k

y

h

x

hf

l

(

0.05,0.9975, 0.0499

)

1 , 0 2 − = f = -0.09950

(

0 0 3 0 3

)

1 4

hf

x

h

,

y

k

,

z

l

k

=

+

+

+

= -0.00995

(

0 0 3 0 3

)

2 4

hf

x

h

,

y

k

,

z

l

l

=

+

+

+

(

0.1,0.99511, 0.0995

)

1 , 0 2 − = f = -0.0985

(

0

.

1

,

0

.

99511

,

0

.

0995

)

1

,

0

₁

−

=

f

y

y

y

=

+

∆

∴

1 0 =

[

0 2

(

0.005

) (

2 0.00499

)

0.00995

]

2 1 1+ + − + − − = 0.9950 2.5 Mathematica 6

Mathematica adalah pemograman komputer yang dapat di kerjakan dengan matematika. Mathematica sering digunakan untuk instruksi, pekerjaan rumah, riset, dan penulisan. Mathematica cocok digunakan untuk numerik dan kemampuan dalam proses pemrograman sangat baik. Mathematica dapat juga dipakai sebagai pemodelan, perhitungan intensif, proyek disertasi, dan lain sebagainya.

Elemen dasar :

A. Membuka paket Mathematica 6

a. Cari ikon Mathematica 6, kemudian klik dengan cepat dua kali, jendela kerja Mathematica 6 muncul.

b.

Perintah (Command) dari Mathematica 6 di tuliskan dengan memakai

symbol

Matematika.

c.

Setelah selesai menggunakan Mathematica 6, ketik quit dan [enter], atau

klik file/EXIT

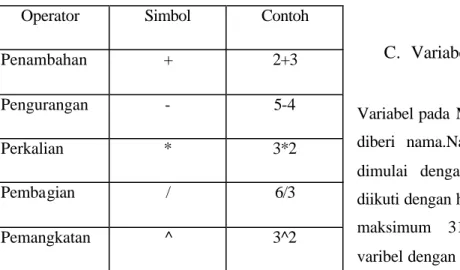
Tabel 2.1 Operator Mathematica

C.

Variabel

Variabel pada Mathematica 6 harus diberi nama.Nama variabel harus dimulai dengan huruf, dan bisa diikuti dengan huruf lain atau angka maksimum 31 karakter. Nama varibel dengan huruf besar (kapital) dianggap berbeda dengan nama variabel yang ditulis dengan huruf kecil.

D.

konstanta/tetapan

Beberapa tetapan yang berlaku pada Mathematica adalah sebagai berikut:

pi nilai p = 3,14452…

eps nilai epsilon, bilangan natural e = 2.71828

inf nilai tak berhingga ~

E.

Tanda baca

% Digunakan untuk mengawali komentar (command)

Operator Simbol Contoh

Penambahan + 2+3

Pengurangan - 5-4

Perkalian * 3*2

Pembagian / 6/3

, digunakan untuk memisahkan dua pernyataaan dalam sebaris

; digunakan untuk memisahkan dua pernyataan tanpa echo

… digunakan untuk melanjutkan statemen ke baris berikutnya.

F. Kontrol Program

Mathematica 6 menyediakan beberapa instruksi yang memugkinkan pengguna membuat program atau fungsi, antara lain instruksi pemilihan (seleksi) dan instruksi perulangan (loop)

Instruksi seleksi:

a. Pemilihan bersyarat:

if (syarat-1)

instruksi-1

else if

instruksi-2

else

instruksi-3

end.

Pemilihan diatas digunakan untuk memilih satu diantara beberapa instruksi sesuai

dengan syarat yang dipenuhi. Bila syarat 1 dipenuhi maka laksanakan instruksi 1 , bila

syarat 2 dipenuhi, maka laksanakan instruksi 2 bila tidak ada syarat yang dipenuhi

maka laksanakan instruksi-3.

b. Pemilihan kasus

switch variabel

case 1 {nilai-1} instruksi-1

case 2 {nilai-2} instruksi-2

case 3 {nilai-3} instruksi-3

…

Otherwise instruksi n

End.

Instruksi seleksi ini akan memilih satu instruksi berdasarkan nilai yang diberikan pada

variabel. Bila nilainya adalah nilai -1 maka instruksi 1 dilaksanakan. Bila nilainya

adalah 2 maka instruksi 2 yang dilaksanakan. Bila nilainya adalah 2 maka instruksi 2

yang dilaksanakan.

Instruksi perulangan

a. Perulangan dengan

for

for var = n1:n2:n3

instruksi- instruksi

end

contoh:

For[i=0,i<4,i++,Print[i]]

0

1

2

3

………

For[i=1;t=x,i^2<10,i++,t=t^2+i;Print[t]]

1+x

2

2+(1+x^2)

2

3+(2+(1+x^2)^2)

2

Perulangan yang dibatasi oleh nilai var, mulai dari n1 hingga n3 dengan

perubahan nilai sebesar n2 pada setiap putaran. Apakah n2=1 maka n2 tidak perlu

ditulis, sehingga bentuknya menjadi:

for var = n1: n3

instruksi- instruksi

end

b. Perulangan denganWhile

while (syarat)

insruksi- instruksi

end

Perulangan yang ditentukan oleh suatu syarat. Selama syarat terpenuhi maka

perulangan akan berlangsung. (Wolfram,1991).

BAB 3

ANALISIS MASALAH DAN PERANCANGAN PROGRAM

3.1. Analisis Masalah

3.1.1. Persamaan Gerak Pendulum Foucault

Pada subbab ini akan dijelaskan persamaan pendulum Foucault yang akan diselesaikan yaitu persamaan 3.1 dan 3.2. 0 sin 2Ω + = − x L g y x& & & _λ (3.1) 0 sin 2Ω + = + y L g x y& & & λ (3.2)

Dimana:

x,y = koordinat titik pendulum bob dilihat dari permukaan bumi ? = kecepatan sudut bumi (rad/s)