1
Tinjauan Pustaka
2.1
Penelitian Sebelumnya
Pada penelitian yang berjudul “Prediksi Produksi Padi Menggunakan Weighted Rainfall Index Dengan Pendekatan Fast And Robust Bootstrap For Least Trimmed Square (Studi Kasus Di Kabupaten Gunungkidul)” tenaga kerja digunakan sebagai variabel untuk memprediksi produksi padi (Munir, 2010). Berdasarkan penelitian tersebut, dapat disimpulkan bahwa tenaga kerja dapat digunakan sebagai salah satu variabel untuk memprediksi produksi padi di Kabupaten Sukoharjo. Berbeda dengan penelitian sebelumnya, pada peneltian ini metode yang digunakan untuk membentuk model prediksi produksi panen komoditas padi adalah metode regresi linier berganda.
Penelitian yang pernah dilakukan oleh Suhermin Ari
Pujiati berjudul “Analisis Regresi Linier Berganda Untuk Mengetahui Hubungan Antara Beberapa Aktifitas Promosi
dengan Penjualan Produk” disebutkan metode regresi linear
digunakan dalam bidang pertanian. Metode regresi linier berganda tidak hanya digunakan untuk mempelajari pola hubungan antar variabel, namun juga digunakan sebagai metode untuk memprediksi produksi panen komoditas padi di Kabupaten Sukoharjo.
Dalam penelitian yang berjudul “Pengaruh Luas
Lahan, Tenaga Kerja, Penggunaan Benih dan Pupuk Terhadap Produksi Padi di Jawa Tengah Tahun1994 - 2008”, disebutkan luas lahan sangat berpengaruh terhadap produksi padi. Apabila luas lahan padi semakin luas maka produksi beras akan semakin meningkat. Sebaliknya apabila luas lahan padi semakin sempit maka produksi beras akan semakin sedikit (Zulmi, 2011). Pada penelitian sebelumnya regresi linier berganda digunakan untuk mengetahui seberapa besar pengaruh luas lahan, tenaga kerja, penggunaan benih dan pupuk terhadap produksi padi. Berbeda dengan penelitian sebelumnya, pada penelitian ini metode regresi linier berganda digunakan untuk memprediksi produksi panen komoditas padi. Pada penelitian ini data yang digunakan untuk memprediksi produksi panen komoditas padi adalah luas lahan, irigas dan tenaga kerja Kabupaten Sukoharjo tahun 2007 hingga 2011.
2.2
Kabupaten Sukoharjo
Surakarta di sebelah utara, Kabupaten Karanganyar di sebelah timur, Kabupaten Gunung Kidul di sebelah selatan dan Kabupaten Klaten di sebelah barat. Bengawan Solo membelah kabupaten ini menjadi dua bagian, bagian utara pada umumnya merupakan dataran rendah dan bergelombang, sedangkan bagian selatan dataran tinggi dan pegunungan. Secara administratif, Sukoharjo terbagi menjadi 12 kecamatan, yaitu Sukoharjo, Grogol, Baki, Gatak, Kartosuro, Mojolaban, Polokarto, Bendosari, Nguter, Tawangsari, Bulu dan Weru, 150 desa dan 17 kelurahan (Wikipedia, 2011).
2.3
Produksi Padi
Padi merupakan salah satu tanaman budidaya terpenting dalam peradapan. Diduga padi berasal dari India atau Indocina dan masuk ke Indoneisa sekitar 1500 SM (Wikipedia, 2012). Padi merupakan sumber karbohidrat utama bagi mayoritas penduduk dunia. Padi dapat tumbuh pada ketinggian 0-1500 mdpl dengan temperatur 19-270C, memerlukan penyinaran matahari penuh tanpa naungan. Padi tumbuh pada tanah lumpur yang subur dengan ketebalan 18 cm sampai 22 cm dan ph tanah antara 4 sampai 7 (Sandiwantoro,2009).
Produksi pada dasarnya merupakan hasil kali luas panen dengan produktivitas per Ha lahan, sehingga seberapa besar produksi suatu wilayah, tergantung seberapa luas panen pada tahun yang bersangkutan atau berapa tingkat produktivitasnya (Triyanto, 2006). Tidak hanya luas lahan, banyak hal dapat mempengaruhi produksi padi, antara lain irigasi dan tenaga kerja. Tingkat pengairan yang sesuai dan tenaga kerja yang tepat dapat mempengaruhi produksi padi.
berswasembada beras. Berjalannya waktu kondisi produksi beras di Indonesia tidak selalu stabil, mengalami kenaikan dan penurunan. Pada tahun 1997, produksi padi Indonesia merosot sebesar 3.4%, sedangkan pada tahun 1998 produksi padi Indonesia kembali merosot sebesar 4,6% (Triyanto, 2006). Hal ini menyebabkan produksi beras Indonesia jauh tertinggal dari permintaan, sementara tingkat konsumsi beras di Indonesia cukup tinggi, yaitu sekitar 97% hingga 100% (Achmad, 2001). Sejak tahun 1992 Indonesia terpaksa melakukan import beras untuk memenuhi kebutuhan beras di Indoneisa yang sangat tinggi.
2.4
Pengaruh Luas Lahan Terhadap Produksi
2.5
Pengaruh Irigasi Terhadap Produksi
Berdasarkan Peraturan Pemerintah Nomer 77 tahun 2001 tentang perairan menyatakan bahwa irigasi merupakan usaha pengadaan dan pengaturan air secara buatan, baik air tanah maupun air permukaan untuk menunjang pertanian (Hendra, 2006). Irigasi yang dibangun di lahan pertanian berfungsi sebagai penjamin kelangsungan proses fisiologi dan biologi tanaman untuk evapotranspirasi, proses asimilasi, pelarut unsur hara, media pengangkut unsur-unsur di dalam tubuh tanaman dan pengaturan tegangan sel atau tugor (Dumairy, 1992). Tingkat produksi padi sangat dipengaruhi oleh kondisi irigasi, dimana suatu usaha tani yang terjamin irigasinya memberikan hasil produksi yang lebih tinggi daripada usaha tani yang tidak terjamin irigasinnya (Kalo, 1983).
berakibat pada rendahnya produktivitas tanaman. Penerapan irigasi yang tidak efisien bisa terjadi melalui cara pemberian air yang tidak tepat baik jumlah dan waktunya ataupun oleh kehilangan air yang berlebihan melalui rembesan (seepage).
2.6
Pengaruh Tenaga kerja Terhadap Produksi
Tenaga kerja merupakan salah satu faktor produksi dalam bidang pertanian, terutama untuk produksi padi di Jawa tengah. Tenaga kerja di sektor pertanian seringkali menjadi kendala, seiring dengan menurunnya minat tenaga kerja muda untuk terjun di sektor pertanian maka sering dijumpai kelangkaan tenaga kerja pada saat pengolahan lahan atau pada saat panen raya.
Seorang produsen yang rasionil tentunya akan mengombinasikan faktor-faktor produksi sedemikian rupa untuk mencapai usaha tani yang efisien. Tenaga kerja merupakan salah satu faktor yang terpenting dalam proses produksi. Tenaga kerja mempunyai pengaruh yang nyata terhadap produksi padi (Zulmi, 2010).
2.7
Prediksi (
Forecasting
)
Sistem prediksi yang baik adalah sistem prediksi yang menghasilkan prediksi yang akurat dengan biaya yang terjangkau dan dapat menyederhanakan permasalahan yang rumit (Algifari, 1997). Metode perediksi dapat diklasifikasikan menjadi dua (Gujarati, 1991), yaitu :
1. Metode Kualitatif
Metode ini digunakan dimana tidak ada model matematika, hal ini dikarenakan data yang ada tidak cukup representatif untuk memprediksikan masa yang akan datang (long term forecasting).
2. Metode Kuantitatif
Metode yang penggunaannya didasari ketersediaan data mentah disertai serangkaian kaidah matematis untuk meramalkan hasil di masa depan. Metode kuantitatif dibagi menjadi tiga macam, yaitu model regresi, model ekonometrik dan model time series analysis.
2.8
Regresi Linier Berganda
atau lebih peubah bebas (independen atau prediktor) (Thomasyunigunarto, 2000). Persamaan regresi juga menggambarkan hubungan antara variabel-variabel yang ada di dalamnya (Supranto, 2001). Nilai variabel terikat dinyatakan dengan konotasi Y dan nilai variabel bebas dinyatakan dengan konotasi X. Regresi dikatakan linier, apabila hubungan antara variabel bebas dan variabel terikatnya adalah linier. Regresi dikatakan non linier, apabila hubungan antara variabel bebas dan variabel terikatnya tidak linier (Usman dan Purnomo, 2000).
dalam rentang data dari variabel-variabel bebas yang digunakan untuk membentuk model regresi tersebut (Kutner dkk, 2004).
Regresi linier berganda dapat dirumuskan sebagai berikut (Galton, 1911):
(1)
Dimana :
Dalam suatu model regresi terdapat koefisiensi yang merupakan nilai duga parameter di dalam model regresi untuk kondisi yang sebenarnya (true condition). Koefisiensi untuk model regresi merupakan suatu nilai rata-rata yang berpeluang terjadi pada variabel terikat (Y) bila suatu variabel bebas (X) diberikan. Kuat tidaknya hubungan antara variabel bebas dengan variabel terikat dapat diukur menggunakan koefisiensi korelasi, sedangkan besarnya pengaruh variabel bebas terhadap variabel terikat dapat diukur menggunakan koefisiensi regresi. Koefisiensi regresi dibagi menjadi dua, yaitu:
1. Intersep (Intercept)
Secara matematis, intersep didefinisikan sebagai suatu titik perpotongan antara suatu garis dengan
Y : Variabel terikat
A : Konstanta atau intersep
b1, b2 : Koefisien regresi
sumbu Y pada diagram atau sumbu kartesius saat nilai X sama dengan 0. Sedangkan definisi secara statistika adalah nilai rata-rata pada variabel Y apabila nilai pada variabel X bernilai 0. Jika X tidak memberikan kontribusi, maka secara rata-rata variabel Y akan bernilai sebesar intersep. Intersep hanyalah suatu konstanta yang memungkinkan munculnya koefisien lain di dalam model regresi. Apabila data pengamatan pada variabel X tidak mencakup nilai 0 atau mendekati 0, maka intersep tidak memiliki makna yang berarti, sehingga tidak perlu diinterpretasikan (Kurniawan, 2008).
2. Slope
Secara matematis, slope merupakan ukuran kemiringan dari suatu garis. Slope adalah koefisien regresi untuk variabel X. Dalam konsep statistika,
slope merupakan suatu nilai yang menunjukkan seberapa besar kontribusi yang diberikan suatu variabel X terhadap variabel Y. Nilai slope dapat diartikan pula sebagai rata-rata pertambahan atau pengurangan yang terjadi pada variabel Y untuk setiap peningkatan satu satuan variabel X (Kurniawan, 2008).
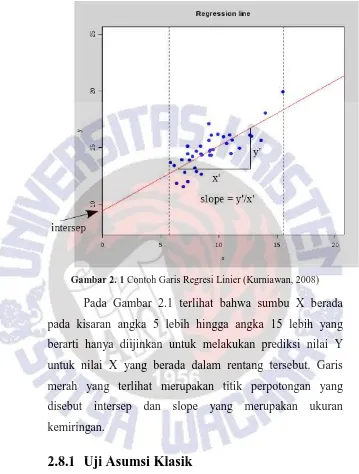
Gambar 2. 1 Contoh Garis Regresi Linier (Kurniawan, 2008)
Pada Gambar 2.1 terlihat bahwa sumbu X berada pada kisaran angka 5 lebih hingga angka 15 lebih yang berarti hanya diijinkan untuk melakukan prediksi nilai Y untuk nilai X yang berada dalam rentang tersebut. Garis merah yang terlihat merupakan titik perpotongan yang disebut intersep dan slope yang merupakan ukuran kemiringan.
2.8.1
Uji Asumsi Klasik
diminimalisir dan merupakan yang terbaik dengan syarat memenuhi beberapa asumsi yang disebut asumsi klasik regresi linier. Untuk mengetahui apakah koefisien regresi yang kita dapat benar atau dapat diterima diperlukan pengujian terhadap kemungkinan adanya pelanggaran asumsi klasik tersebut. Secara manual, sebelum melakukan uji asumsi klasik diharuskan untuk mendapatkan data residual. Namun hal ini tidak berlaku saat menggunakan software
statistik, karena sebelum melakukan uji asumsi klasik,
software statistik terlebih dahulu menghitung data residualnya (Kurniawan, 2008)
Uji asumsi klasik terdiri dari uji normalitas, uji multikolinearitas, uji heteroskedastisitas dan uji autokorelasi yang akan dijelaskan di bawah ini.
1. Uji Normalitas
Uji normalitas adalah uji untuk melihat apakah nilai residual terdistribusi secara normal atau tidak. Model regresi yang baik adalah model regresi yang memiliki nilai residual yang terdistribusi secara normal. Uji normalitas tidak dilakukkan pada masing-masing variabel, tetapi pada nilai residualnya (Statistik, 2009).
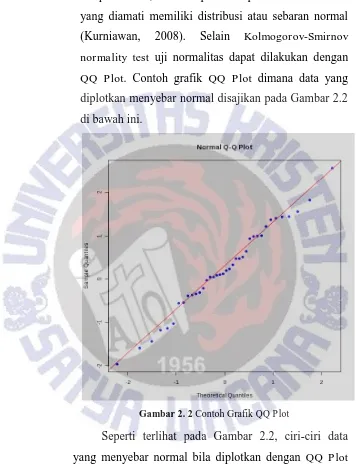
dihipotesiskan, maka dapat disimpulkan bahwa data yang diamati memiliki distribusi atau sebaran normal (Kurniawan, 2008). Selain Kolmogorov-Smirnov normality test uji normalitas dapat dilakukan dengan
QQ Plot. Contoh grafik QQ Plot dimana data yang diplotkan menyebar normal disajikan pada Gambar 2.2 di bawah ini.
Gambar 2. 2 Contoh Grafik QQ Plot
Seperti terlihat pada Gambar 2.2, ciri-ciri data yang menyebar normal bila diplotkan dengan QQ Plot
2. Uji Multikolinearitas
Uji multikolinearitas adalah uji untuk melihat ada atau tidaknya korelasi yang tinggi antara variabel-variabel bebas dalam suatu model regresi linear berganda. Jika ada korelasi yang tinggi di antara variabel-variabel bebasnya, maka hubungan antara variabel bebas terhadap variabel terikatnya menjadi terganggu (Statistik, 2009).
Uji statistik yang sering digunakan untuk menguji gangguan multikolinearitas adalah Variance Inflation Factor (VIF), korelasi pearson antara variabel-variabel bebas atau dengan melihat eigenvalues dan Condition Index (CI). Pada uji statistik Variance Inflation Factor
(VIF), apabila nilai VIF lebih besar dari sepuluh mengindikasi adanya multikolinearitas yang serius (Zulmi, 2012).
3. Uji Heteroskedastisitas
Uji heteroskedastisitas adalah uji untuk melihat apakah terdapat ketidaksamaan varians dari residual satu ke pengamatan yang lain. Model regresi yang memenuhi persyaratan adalah terdapat kesamaan varians dari residual satu pengamatan ke pengamatan yang lain tetap atau disebut homoskedastisitas.
tertentu pada grafik, seperti mengumpul di tengah, menyempit kemudian melebar atau sebaliknya melebar kemudian menyempit. Uji statistik yang dapat digunakan adalah uji Breusch Pagan Test, uji Glejser, uji Park atau uji White (Statistik, 2009).
4. Uji Autokorelasi
Uji autokorelasi adalah uji untuk melihat apakah terjadi korelasi antara suatu periode t dengan periode sebelumnya (t -1). Analisis regresi merupakan cara untuk melihat pengaruh antara variabel bebas terhadap variabel terikat, sehingga tidak diperbolehkan adanya korelasi antara observasi dengan data observasi sebelumnya. Uji autokorelasi hanya dilakukan pada data time series (runtut waktu) dan tidak perlu dilakukan pada data cross section seperti pada kuesioner di mana pengukuran semua variabel dilakukan secara serempak pada saat yang bersamaan.
Uji statistik yang sering digunakan dalam uji autokorelasi adalah uji Durbin Watson, Run Test dan jika observasi di atas 100 data sebaiknya menggunakan uji Lagrange Multiplier (Kurniawan, 2008).
2.8.2
Uji Simultan Model Regresi
Uji simultan pada konep regresi linier adalah pengujian yang bertujuan untuk mengetahui apakah model regresi yang diperoleh benar-benar dapat diterima. Uji simultan menunjukan apakah semua variabel bebas yang dimasukkan ke dalam model regresi mempunyai pengaruh secara bersama-sama terhadap variabel terikat. Secara statistik formulasi uji simultan disajikan pada persamaan 2 (Gujarati, 2003) di bawah ini :
(2)
Dimana :
F : Uji simultan
R2 : Koefisiensi determinasi
K : Banyaknya variabel yang diamati
N : Jumlah pengamatan
Bila F hitung > F tabel pada tingkat derajat kepercayaan 5% dan tingkat kepercayaan tertentu atau nilai probabilitas signifikansi lebih kecil dari 0,05 maka H0 ditolak yang berarti variabel bebas secara bersama-sama mempengaruhi variabel terikat.
Jika Fhitung Ftabel ( db1 , db2 ) maka H0 diterima,
sedangkan
Jika Fhitung Ftabel ( db1 , db2 ) maka H0 ditolak
db1 dan db2 adalah parameter-parameter Ftabel yang
mempunyai persamaan seperti di bawah ini :
(3)
(4)
Dimana :
db1 dan db2 : Derajat bebas
P : Banyaknya parameter model regresi linier
N : Banyaknya pengamatan
Apabila H0 ditolak, maka model regresi yang diperoleh
dapat digunakan.
2.8.3
Uji Parsial
Uji parsial digunakan untuk menguji apakah variabel bebas benar-benar memberikan kontribusi terhadap variabel terikat. Uji parsial dapat diuji menggunakan statistik t, yaitu
Jika thitung ttabel (n – p), maka H0 diterima Jika thitung ttabel (n – p), maka H0 ditolak
Dimana :
(n – p) : Parameter ttabel
N : Banyaknya pengamatan
Apabila H0 ditolak, maka variabel bebas tersebut
memiliki kontribusi yang siknifikan terhadap variabel terikat.
2.8.4
Koefisien Determasi
Koefisien determinasi adalah besarnya keragaman (informasi) di dalam variabel Y yang dapat diberikan oleh model regresi yang didapatkan. Nilai R2 berkisar antara 0
sampai dengan. 1. Apabila nilai R2 dikalikan 100%, maka hal
ini menunjukkan persentase keragaman (informasi) di dalam variabel Y yang dapat diberikan oleh model regresi yang didapatkan. Semakin besar nilai R2 , semakin baik model