Systems of interval min-plus linear equations and its application on shortest path problem with interval travel times.

(1)

(2)

Conference Proceedings

!

INTERNATIONAL CONFERENCE ON RESEARCH,

IMPLEMENTATION AND EDUCATION

OF MATHEMATICS AND SCIENCES (ICRIEMS) 2014

Yogyakarta, 18 – 20 May 2014

!

ISBN 978-979-99314-8-1

!

Global Trends and Issues

on Mathematics and Science

and The Education

!

(3)

!

ICRIEMS 2014 : Global Trends and Issues on Mathematics and Science

and The Education

!

Mathematics & Mathematics Education

!

Physics & Physics Education

!

Chemistry & Chemistry Education

!

Biology & Biology Education

!

Science Education

!

Editorial Board:

Hari Sutrisno

Wipsar Sunu Brams Dwandaru

Kus Prihantoso Krisnawan

Denny Darmawan

Erfan Priyambodo

Evy Yulianti

Sabar Nurohman

Board of Reviewer

Prof. Dr. Saberi bin Othman (Universiti Pendidikan Sultan Idris, Malaysia)

Prof. Samsuuk Ekasit (Mahidol University, Thailand)

Prof. Dean Zollman (Kansas State University, U.S.)

Prof. Tran Vui (Hue University, Vietnam)

Prof. Dr. Amy Cutter-Mackenzie (Southern Cross University, Australia)

Dr. Alexandra Lynman (Universitas Hindu Indonesia)

Prof. Dr. Rusgianto Heri Santoso (Yogyakarta State University)

Prof. Dr. Marsigit (Yogyakarta State University)

Prof. Dr. Mundilarto (Yogyakarta State University)

Prof. Dr. Zuhdan Kun Prasetyo (Yogyakarta State University)

Prof. Dr. K.H. Sugijarto (Yogyakarta State University)

Prof. Dr. A.K. Prodjosantoso (Yogyakarta State University)

Prof. Dr. Djukri (Yogyakarta State University)

(4)

Proceeding of International Conference On Research, Implementation And Education Of Mathematics And Sciences 2014, Yogyakarta State University, 18-20 May 2014

!

! "#!

Table of Content

01

02

03

04

05

06

Front Cover

Editorial Board and Reviewers

Preface

Forewords From The Head of Committee

Forewords From The Dean of Faculty

Table of Content

Plenary Session

Using Dynamic Visual Representations To Discover Possible

Solutions In Solving Real-Life Open-Ended Problems

Prof. Tran Vui

Parallel Session

MATHEMATICS

Probability Density Function of M/G/1 Queues under (0,k)

Control Policies: A Special Case

Isnandar Slamet, Ritu Gupta, Narasimaha R. Achuthan

!

!-Valued Measure And Some Of Its Properties

Firdaus Ubaidillah , Soeparna Darmawijaya , Ch. Rini Indrati

Applied Discriminant Analysis in Market Research

Hery Tri Sutanto

Characteristic Of Group Of Matrix 3x3 Modulo P, P A Prime

Number

Ibnu Hadi, Yudi Mahatma

The Properties Of Group Of

3_!3

Matrices Over Integers

Modulo Prime Number

Ibnu Hadi, Yudi Mahatma

Random Effect Model And Generalized Estimating Equations

For Binary Panel Response

page

i

ii

iii

iv

vi

ix

I-1

M-1

M-9

M-17

M-25

M-31

(5)

!

! "!

07

08

09

10

11

12

13

14

15

16

17

Jaka Nugraha

The Properties of Ordered Bilinear Form Semigroup

in Term of Fuzzy Quasi-Ideals

Karyati, Dhoriva Urwatul Wutsqa

Symmetry Of Limit Cycles On A Liénard-Type Dynamical

System

Kus Prihantoso Krisnawan

Systems Of Interval Min-Plus Linear Equations And Its

Application On Shortest Path Problem With Interval Travel

Times

M. Andy Rudhito and D. Arif Budi Prasetyo

Some Properties Of Primitive

!

Henstock Of Integrable

Function In Locally Compact Metric Space Of Vector Valued

Function

Manuharawati

Learning Gauss-Jordan Elimination Using Ms Excel

Meifry Manuhutu

Linear Matrix Inequality Based Proportional Integral

Derivative Control For High Order Plant

M. Khairudin

Bayesian With Full Conditional Posterior Distribution

Approach For Solution Of Complex Models

Pudji Ismartini

Optimal Control Analyze And Equilibrium Existence Of Seir

Epidemic Model With Bilinear Incidence And Time Delay In

State And Control Variables

Rubono Setiawan

Selection Of The Best Univariate Normality Test On The

Category Of Moments Using Monte Carlo Simulation

Sugiyanto and Etik Zukhronah

Additive Main Effect and Multiplicative Interaction on Fixed

Model of Two Factors Design

Suwardi Annas and Selfi Dian Purtanti

Gram

-

Schmidt

Super

Orthogonalization

Process For

Super

Linear

Algebra

M-45

M-55

M-61

M-69

M-77

M-83

M-93

M-101

M-111

M-119

(6)

M-61

M -

SYSTEM S OF I NTERVAL M I N-PLUS LI NEAR EQUATI ONS

AND I TS APPLI CATI ON ON SHORTEST PATH PROBLEM

WI TH I NTERVAL TRAVEL TI M ES

M . Andy Rudhito and D. Arif Budi Prasetyo

Department of Mathematics and Natural Science Education Universitas Sanata Dharma, Paingan Maguwoharjo Yogyakarta

Abstract

The travel times in a network are seldom precisely known, and then could be represented into the interval of real number, that is called interval travel times. This paper discusses the solution of the iterative systems of interval min-plus linear equations its application on shortest path problem with interval travel times. The finding shows that the iterative systems of interval min-plus linear equations, with coefficient matrix is semi-definite, has a maximum interval solution. Moreover, if coefficient matrix is definite, then the interval solution is unique. The networks with interval travel time can be represented as a matrix over interval min-plus algebra. The networks dynamics can be represented as an iterative system of interval min-plus linear equations. From the solution of the system, can be deter-mined interval earliest starting times for each point can be traversed. Furthermore, we can determine the interval fastest time to traverse the network. Finally, we can determine the shortest path interval with interval travel times by determining the shortest path with crisp travel times.

Key words: Min-Plus Algebra, Linear System, Shortest Path, Interval.

I NTRODUCTI ON

Let RH := R{H} with Rthe set of all real numbers and H : = f. In RH defined two operations : a,b RH, ab := min(a, b) andab : = ab. We can show that (RH, , ) is a commutative idempotent semiring with neutral element H = f and unity element e = 0. Moreover, (RH, , ) is a semifield, that is (RH, , ) is a commutative semiring, where for every aR there exist a such that a (a) = 0. Thus, (RH, , ) is amin-plus algebra, and is written as Rmin. One can define x0:= 0, xk:= x xk1, H0: = 0 and Hk: = H, for k = 1, 2, ... ..The operations and in Rmin can be extend to the matrices operations inRmu_minn, with

n mu

min

R : = {A = (Aij)~AijRmin, for i = 1, 2, ..., m andj = 1, 2, ..., n}, the set of all matrices over

max-plus algebra. Specifically, for A,B Rnu_minn we define (AB)ij = AijBijand (AB)ij =

kj ik n

k

B A

1

.We also define matrix E Rnu_minn, (E )ij : =

¯ ®

z j i ,

j i ,

if if 0

H and

H

Rmuminn , (H)ij := H for

every i and j . For anymatrices ARnu_minn, one can define A0 = En and k

(7)

Rudhito and Prasetyo/ System of Interval Min-Plus« ISBN 978-979-99314-8-1

M‐62

1, 2, ... . For any weighted, directed graph G = (V,A) we can define a matrix A Rnu_minn , Aij =

¯ ®

. ) , ( if

, ( if ) , (

A ,

A ) ,

i j

i j i j w

H , called the weight-matrix of graphG.

A matrix A nun

min

R is said to be semi-definite if all of circuit inG(A) have nonnegative weight, and it is said definite if all of circuit inG(A) have positive weight. We can show that if

any matrices A is semi-definite, then ptn, Ap %_mEA ... An1. So, we can defineA* : =

E A ... AnAn1... .Define Rn_min_:₌_{x_{= [}_x_1,_x_{2, ... ,}_x_n]T_|_x_iR_min_,_i_{= 1, 2, ... ,}

n}.Notice that we can be seen Rn_min as R_minnu1. The elements of Rn_maxis called vector over R_min_.In general, min-plus algebra is analogous to max-plus algebra. Further details about max-plus algebra, matrix and graph can be found in Baccelli et.al (2001) and Rudhito (2003).

The existence and uniqueness of the solution of the iterative system of min-plus linear equation and its application to determine the shortest path in the with crisp (real) travel times had been discussed in Rudhito (2013). The followings are some result in brief. LetA Rnu_minnand b

1 min

u n

R _.IfA is semi-definite, thenx*_=A*b_{is a solution of system}x _=Ax b_._{Moreover, if}_A_is definite, then the system has a unique solution.A one-way path networkSwith crisp activity times, is a directed, strongly connected, acyclic, crisp weighted graph S = (V, A), with V = {1, 2,, ... , n} suct that if (i, j) A, then i<j. In this network, point represent crosspathway, arc expresses a pathway, while the weight of the arc representtravel time, so that the weights in the network is always positive.Let

x

_ieis earliest starting timesfor point i can be traversedand xe_{= [}

e

x₁,x₂e, ... , x_ne]T. For the network with crisptravel times, with nnodes and Athe weight matrix of graph of the networks, then

xe_{= (}_E_A_..._An1₎be₌_A*be

with be_{= [0,}H_{, ... ,}H_]T_{. Furthermore,} e n

x is the fastest times to traverse the network.Letx_il

is be

latest times leftpoint i and xl _{= [}_xl

1,

l

x₂ .... , xl_n]. For the network above, vector xl₌_{( (}_AT₎* bl₎

withbl_{= [}H_,H_{, ... ,} e n

x ]T.Define, a pathway (i, j) A_{in the one-way path network}_S_{is called}

shortestpathwayif xie= l i

x dan

x

ej= l

j

x

.Define, A pathpPin the one-way path networkS is calledshortest pathif all pathways belonging to p are shortest pathway. From this definition, we can show that apathpPis a shortest path if and only ifp has minimum weight, that is equal tox_ne

. Also, a pathway is a shortest pathway if and only if it belonging to a shortest path.

DI SCUSSI ON

We discusses the solution of the iterative systems of interval min-plus linear equations its application on shortest path problem with interval travel times. The discussion begins by reviewing some basic concepts of interval min-plus algebra and matrices over interval min-plus algebra. Definition and concepts in the min-plus algebra analogous to the concepts in the max-plus algebra which can be seen in Rudhito (2011).

(8)

M-63

x= [ x , x ] = {x Rmin_x %mx %m x }.

The interval x in Rmin is called min-plus interval, which is in short is called interval.Define I(R)H := {x= [ x , x ] _x , xR , H%m x %_m x } { H }, where H := [H, H].

In the I(R)H , define operation and as

x y= [xy , xy ] and x y= [ xy , xy ] , x, yI(R)H.

Since (RH, , ) is an idempotent semiring and it has no zero divisors, with neutral element H,

we can show that I(R)H is closed with respect to the operation and . Moreover, (I(R)H,,

) is a comutative idempotent semiring with neutral elementH =[H, H] and unity element 0 = [0, 0]. This comutative idempotent semiring (I(R)H,,) is called interval min-plus algebra which

is written as I(R)min.

Define I(R)m_minun := {A= (Aij)~AijI(R)min, for i = 1, 2, ..., m and j = 1, 2, ..., n }. The

element of I(R)m_minun are called matrices over interval min-plus algebra. Furthermore, this matrices are called interval matrices. The operations and in I(R)min can be extended to the

matrices operations of in I(R)mun

max . Specifically, for A, B I(R) n nu

min and DI(R)min we define

(D A)ij = D Aij , (AB)ij = AijBij and (AB)ij = ik kj n

k

B A

1

.

MatricesA, BI(R)m_minunare equalifAij = Bij , that is if A = ij Bij and A = ij Bij for everyiandj.

We can show that (I(R)n_minun,,) is a idempotent semiring with neutral element is matrix H,

with (H)ij:= H for every i and j, and unity element is matrix E, with (E)ij : = ¯ ®

z j i

j i

if , İ

if , 0

. We can

also show that I(R)m_minunis a semi-module over I(R)min.

For any matrix AI(R)_minmun, define the matrices A = (A ) _ij R_minmun and A= (A ) _ij Rm_minun,

which is called lower bound matrices and upper bound matrices ofA, respectively. Definematrices interval of A, that is

[ A ,A] = { ARm_minun¨A %mA %m A} and I(R n

mu

min ) *

= { [ A ,A] _AI(R)n_minun}.

Specifically, for [ A ,A], [ B ,B] I(R_minmun)* and DI(R)min we define

D[ A ,A] = [DA , D A], [ A ,A] [ B ,B]= [ AB ,AB] and [ A ,A] [ B ,B]= [ AB ,AB].

The matrices interval [ A ,A] and [ B ,B]I(R_minmun)*are equalif A = B and A = B. We can

show that (I(Rn_minun)*,, ) is an idempotent semiring with neutral element matrix interval [H,

H] and the unity element is matrix interval [E, E]. We can also show that I(Rn_minun)* is a semimodule over I(R)min.

The semiring (I (R)n_minun, , ) is isomorfic with semiring (I(Rn_minun)*,, ). We can

define a mapping f, where f (A) = [ A ,A], A I (R)_minnun. Also, the semimodule I (R)n_minun is

(9)

M‐64

determine matrices interval [ A ,A]I₍Rnun

min ) *

. Conversely, for every [ A ,A] I₍Rnun

min ) *

,then

A ,ARnun

min , such that [ Aij ,Aij ] I(R)min, i and j. The matrix interval [ A ,A] is called

matrix interval associated with the intervalmatrix A and which is written A |[ A ,A]. So we

have DA |[DA ,DA], AB |[ AB ,AB] and AB | [ AB ,AB].

We define for any interval matricesAI₍R₎nun

min , where A | [ A ,A], is said to be

semi-definite (semi-definite) if every matrices A [ A ,A] is semi-definite (definite). We can show that

interval matrices AI₍R₎nun

max , where A | [ A ,A] is semi-definite (definite) if and only ifA R

n nu

maxsemi-definite (definite).

Define I₍R₎n

min:= { x = [x1, x2, ... , xn ]T | xiI(R)min, i = 1, 2, ... , n }. The set I(R)

n

min can be seen

as set I₍R₎ 1 min

u n

. The Elements of I₍R₎n

min is called interval vector over I(R)min. The interval vector

x _{associated with}_{vector interval}_[x_,x_{], that is}x |_[x_,x_].

Definition1_. _Let_AI₍R₎nun

minandbI(R)

n

min.A interval vectorx

*

I₍R₎n

minis calledinterval

solution_{of iterative system of interval min-plus linear equations}x_=A x b_ifx*_{satisfy the} system.

Theorem 1. _Let_A I₍R₎nun

max andbI(R)min1

u n

. IfA is semi-definite, then intervalvectorx* |_[

b

*

A , _A*b_],_{is an interval solution of system}x_=Ax b_._{Moreover, if}_A_{is definite, then}

interval solution is unique.

Proof._{Proof is analogous to the case of max-plus algebra as seen in the Rudhito (2011)}

Next will be discussed theearliest starting times intervalfor point i can be traversed.The discussion is analogous to the case of (crisp) travel time (Rudhito, 2013), using the interval min-plus algebra approach.

LetESi=

x

ei is earliest starting times intervalfor point i can be traversed, with e i

x

= [

x

e_i ,

x

_ie].

Aij= ¯ ® f f A , A ) , ( if ]) [ İ ) , ( if point to point from time travel interval i j i j i j .

We assume that

x

e_i = 0 = [0, 0] and with interval min-plus algebra notation we have

e i

x

=

°¯ ° ® !

d d 1 if ) x (A 1 if 0 1 i i e j ij n j

. (1)

Let Ais the interval weight matrix of the interval-valued weighted graph of the networks, xe_{= [}

e

1

x

,

x

e₂, ... ,

x

e_n]T dan be_{= [0,}H_{, ... ,}H_]T_{, then equation (1) can be written in an iterative system of}

interval max-plus linear equations

xe_{= A}xebe ₍₂₎

(10)

M-65

xe = A*be| [

A

*

b

e,

A

*

b

e]

= [(EA...

A

n1)

b

e, (E

A

«

A

n1)

b

e]

is a unique solution of the system(2), that is the vector of earliest starting times intervalfor point i can be traversed.

Notice that

x

e_nis the fastest times interval to traverse the network. We summarize the description above in the Theorem 2.

Teorema 2.Given a one-way path networknetwork with interval travel times, with n node and Ais the weight matrix of the interval-valued weighted graph of networks. The interval vector of earliest starting times intervalfor point i can be traversed is given by

xe| [(EA...

A

n1)

b

e, (E

A

«

A

n1)

b

e]

with be= [0, H, ... , H]T. Furthermore,

x

e_nis thefastest timesinterval to traverse the network.

Bukti: (see description above) . Ŷ

Example 1 Consider the project network in Figure 1.

We have A= » » » » » » » » » ¼ º « « « « « « « « « ¬ ª İ 8] [6, 8] [5, 9] [7, İ İ İ İ İ 7] [4, 3] [2, İ İ İ İ İ İ 0] [0, 3] [2, İ İ İ İ İ İ 5] [3, 3] [2, İ İ İ İ İ İ İ 4] [2, İ İ İ İ İ İ 3] [1, İ İ İ İ İ İ İ .

Using MATLAB computer program, we have

x4 x5 x3 x6 x7 1x

[1, 3] _{[7, 9]}

[2, 3]

[3, 5] [6, 8] [4, 7] [5, 8] [2, 4] x2 [2, 3] [2, 3]

[image:10.595.102.486.378.508.2]

(11)

Rudhito and Prasetyo/ System of Interval Min-Plus« ISBN 978-979-99314-8-1 M‐66 * A = » » » » » » » » » ¼ º « « « « « « « « « ¬ ª 0 6 5 5 7 7 8 0 4 2 5 4 5 0 0 2 2 3 0 3 2 3 0 2 0 1 0 H H H H H H H H H H H H H H H H H H H H H H

, A = *

» » » » » » » » » ¼ º « « « « « « « « « ¬ ª 0 8 8 8 11 11 14 0 7 3 8 6 9 0 0 3 3 6 0 5 3 6 0 4 0 3 0 H H H H H H H H H H H H H H H H H H H H H H , e

x

_{= [0, 1, 2, 3, 3, 5, 8]} T

dan

x

e_{= [0, 3, 4, 6, 6, 9, 14]} T

.

So the vector of earliest starting times intervalfor point i can be traversed is

xe_{= [ [0, 0], [1, 3], [2, 4], [3, 6], [3, 6], [5, 9], [8, 14]]}T_{and the fastest times interval to}

traverse the network

x

e_n = [16, 25].

Next given shortest path interval definition and theorem that gives way determination. Definitions and results is a modification of the definition of critical path-interval and theorem to determine the critical path method-interval, as discussed in Chanas and Zielinski (2001) and Rudhito (2011).We also give some examples for illustration.

Definition 2._{A pathp}_{P is called an}_{interval-shortest path}_in_S_{if there exist aset of travel timesA}_ij

[A_ij, A_ij], (i, j) A,such thatp is shortest path, after replacing the interval travel timesAijwith

the travel timeAij .

Definisi 3._{A pathway}₍_k_,_l₎A_{is called an}interval-shortest pathway in Sif there exist aset of

travel timesAij [Aij, Aij], (i, j) A,such that(k, l) is shortest pathway, after replacing the

interval travel timesAijwith the travel timeAij .

The following theorem is given which relates the shortest path and interval-shortest pathway.

Teorema 3._{If path p}_{P is an shortest path, then all pathways in the p are}

interval-shortest pathway.

Proof : _{Let path}_p_P_{is an interval shortest path, then according to Definition 2, there exist a set}

of timesAij [

A

ij,

A

ij], (i, j) A,such that p is shortest path, after replacing the interval travel

times Aijwith the travel timeAij . Next, according to the definition of shortest path above, all

pathways inp are shortest pathways for a set of travel times Aij [

A

ij,

A

ij], (i, j) A.Thus

according to Definiton 3, all pathways in p are interval-shorstest pathways. Ŷ

The following theorem is givena necessary and sufficient condition a path is an interval-shortestpath.

Teorema 4._{A pathp}_{P is an}_{interval-shortest path}_in_S_{if and only if p is a shortest path, with}

interval travel times Aij [

A

ij,

A

ij], (i, j) A,have been replace with travel times Aijwhich is

(12)

M-67

Aij =

°¯ ° ® p j i A p j i A ij ij ) , ( jika ) , ( jika

. (3)

Bukti : : Letp is an interval-shortest path, then according to Definition 2, there exist a set of travel times Aij, Aij [

A

ij,

A

ij], (i, j) A,such thatp is shortest pathway, after replacing the

interval travel timesAij with travel timesAij , (i, j) A. If the travel times for all pathwayis located

at p isreduced from Aij to

A

ijand for all pathway is not located p is increased fromAijto

A

ij, then p

is a path with minimum weight in Sfor new travel time formation. Thus pathp is a shortest path. : Since pathp a shortest path with a set of travel times Aij [

A

ij,

A

ij],which is determined by

the formula(9), then according to Definition 2, pathp is an interval-shortest path. Ŷ

Example 2.We consider the network in Example 1. We will determine all interval-shortest path in this network. For path1o3o5o7, by applying formula (9), we have weight

» » » » » » » » » ¼ º « « « « « « « « « ¬ ª İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ İ 8 4 9 8 3 0 2 5 3 2 3 .

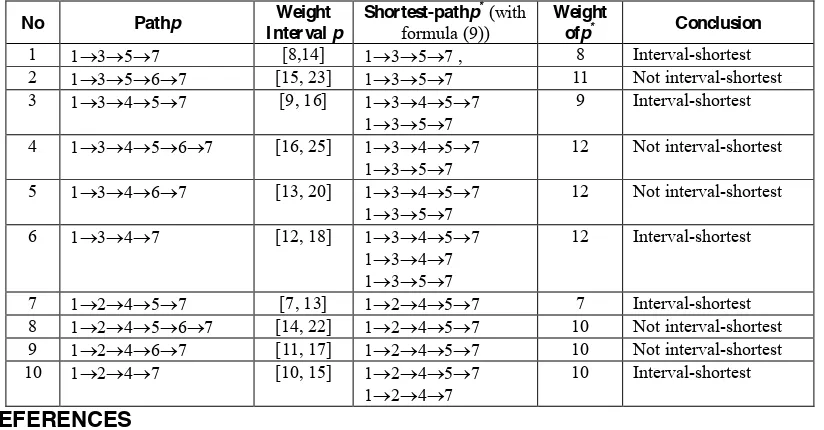
[image:12.595.94.506.512.727.2]

Using MATLAB computer program, we have a shortest path 1o3o5o7 with minimum weight of path is 8. Thus 1o3o5o7 is an interval-shortest path. The results of the calculations for all possible path in the network are given in Table 1 below.

Tabel 1Calculation results of all path

No Pathp Weight I nterval p

Shortest-pathp* (with formula (9))

Weight

ofp* Conclusion

1 1o3o5o7 [8,14] 1o3o5o7 , 8 Interval-shortest 2 1o3o5o6o7 [15, 23] 1o3o5o7 11 Not interval-shortest 3 1o3o4o5o7 [9, 16] 1o3o4o5o7

1o3o5o7

9 Interval-shortest

4 1o3o4o5o6o7 [16, 25] 1o3o4o5o7 1o3o5o7

12 Not interval-shortest

5 1o3o4o6o7 [13, 20] 1o3o4o5o7 1o3o5o7

12 Not interval-shortest

6 1o3o4o7 [12, 18] 1o3o4o5o7 1o3o4o7 1o3o5o7

12 Interval-shortest

7 1o2o4o5o7 [7, 13] 1o2o4o5o7 7 Interval-shortest 8 1o2o4o5o6o7 [14, 22] 1o2o4o5o7 10 Not interval-shortest 9 1o2o4o6o7 [11, 17] 1o2o4o5o7 10 Not interval-shortest 10 1o2o4o7 [10, 15] 1o2o4o5o7

1o2o4o7

10 Interval-shortest

(13)

M‐68

1. F. Bacelli, et al., Synchronization and Linearity, John Wiley & Sons, New York, 2001. 2. S. Chanas, S., P. Zielinski, P, Critical path analysis in the network with fuzzy activity times.

Fuzzy Sets and Systems. ₁₂₂. 195±204., 2001.

3. M. A. Rudhito, Sistem Linear Max-Plus Waktu-Invariant, Tesis: Program Pascasarjana Universitas Gadjah Mada, Yogyakarta, 2003.

4. M. A. Rudhito, Aljabar Max-Plus Bilangan Kabur dan Penerapannya pada Masalah

Penjadwalan dan Jaringan Antrian Kabur. Disertasi: Program Pascasarjana Universitas

Gadjah Mada. Yogyakarta., 2011.

5. M. A. Rudhito, Sistem Persamaan Linear Min-Plus dan Penerapannya pada Masalah Lintasan Terpendek. Prosiding Seminar Nasional Matematika dan Pendidikan Matematika.

Jurusan Pendidikan Matematika FMIPA UNY, Yogyakarta, 9 November 2013. pp: MA-29 ±