PERBANDINGAN KEMAMPUAN KOMUNIKASI MATEMATIS DAN KEMANDIRIAN BELAJAR ANTARA SISWA YANG BELAJAR DENGAN PROBLEM BASED LEARNING DAN DISCOVERY LEARNING.

(1)

PERBANDINGAN KEMAMPUAN KOMUNIKASI MATEMATIS DAN KEMANDIRIAN BELAJAR

ANTARA SISWA YANG BELAJAR DENGAN PROBLEM BASED LEARNING DAN DISCOVERY LEARNING

(Studi Kuasi Eksperimen pada Siswa kelas VII di salah satu SMP Kota Bandung) TESIS

Diajukan untuk Memenuhi Sebagian dari Syarat untuk Memperoleh Gelar Magister Pendidikan Program Studi Pendidikan Matematika

Disusun Oleh: Aulia Sthephani

1207156

PROGRAM STUDI PENDIDIKAN MATEMATIKA SEKOLAH PASCASARJANA

(2)

PERBANDINGAN KEMAMPUAN KOMUNIKASI MATEMATIS DAN KEMANDIRIAN BELAJAR

ANTARA SISWA YANG BELAJAR DENGAN PROBLEM BASED LEARNING DAN DISCOVERY LEARNING

(Studi Kuasi Eksperimen pada Siswa kelas VII di salah satu SMP Kota Bandung)

Oleh Aulia Sthephani

S.Pd Universitas Islam Riau, 2011

Sebuah Tesis yang diajukan untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan (M.Pd.) pada Program Studi Pendidikan Matematika

Januari 2015

Hak Cipta dilindungi undang-undang.

Tesis ini tidak boleh diperbanyak seluruhya atau sebagian,

(3)

(4)

Ema Sulistiowati, 2015

Penggunaan media himpunan garis untuk meningkatkan kemampuan siswa tunagrahita ringan dalam memahami konsep pembagian bilangan bulat sampai 20

Universitas Pendidikan Indonesia | repository.upi.edu | perpustakaan.upi.edu

ABSTRAK

Aulia Sthephani (2015). “Perbandingan Kemampuan Komunikasi Matematis dan Kemandirian Belajar antara Siswa yang Belajar dengan Problem Based Learning dan Discovery Learning”

Tujuan penelitian ini adalah untuk mengetahui: (1) perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning, (2) perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning jika ditinjau dari kemampuan awal matematis, dan (3) perbedaan kemandirian belajar siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning. Penelitian ini merupakan penelitian kuasi eksperimen yang terdiri dari kelas eksperimen yang memperoleh Discovery Learning dan Problem Based Learning. Populasi penelitian ini siswa SMP dikota Bandung Jawa Barat dengan sampel penelitian siswa kelas VII. Analisis data dilakukan secara kuantitatif yang digunakan untuk menghitung rataan gain ternormalisasi antara kedua kelas sampel dengan menggunakan Uji-t dan analasis kualitatif untuk menelaah sikap siswa setelah memperoleh pembelajaran dengan memperoleh Discovery Learning dan Problem Based Learning. Hasil penelitian menunjukkan tidak terdapat perbedaan peningkatan kemampuan komunikasi secara signifikan untuk kedua kelas eksperimen, dan tidak terdapat perbedaan peningkatan kemampuan komunikasi secara signifikan jika ditinjau dari kemampuan awal matematis. Analisis data angket memperlihatkan bahwa kemandirian belajar siswa yang memperoleh Discovery Learning tidak berbeda secara signifikan dengan siswa yang memperoleh Problem Based Learning.

(5)

ABSTRACT

Aulia Sthephani (2015). “Comparison of Communication Mathematics Ability and Self-Regulated between Student Learning by Problem Based Learning and Discovery Learning. The purpose of this study was to determine: (1) differences in students’ communication mathematics ability increase the gain of Problem Based Learning with students who obtain Discovery Learning, (2) differences in students' communication mathematics ability increase the gain of Problem Based Learning with students who obtain Discovery Learning if review of early mathematical ability, and (3) differences in student learning gained self-regulation Problem Based Learning with students who obtain Discovery learning. This study was a quasi-experimental research which consists of classroom experiments to obtain Discovery Learning and Problem Based Learning. This study population junior high school students in the city of Bandung in West Java with a sample of students of class VII. Analysis of quantitative data were used to calculate the average gain is normalized between the two classes of samples by using t-test and qualitative analysis to examine the attitudes of students after learning gained by acquiring Discovery Learning and Problem Based Learning. The results showed no differences significantly increase communication ability for both experimental class and no differences in terms of improvement if early mathematical ability. Analysis of questionnaire data show that student learning gained self-regulation Discovery Learning did not differ significantly with students who obtain Problem Based Learning.

(6)

Aulia Sthephani, 2015

Perbandingan kemampuan komunikasi matematis dan kemandirian belajar antara siswa yang belajar dengan problem based learning dan discovery learning

DAFTAR ISI

Halaman

LEMBAR PENGESAHAN ... ii

LEMBAR PERNYATAAN ... iii

ABSTRAK ... iv

KATA PENGANTAR ... v

UCAPAN TERMAKASIH ... vi

DAFTAR ISI ... vii

DAFTAR TABEL ... ix

DAFTAR LAMPIRAN ... x

BAB I PENDAHULUAN A. Latar Belakang Masalah ... 1

B. Rumusan Masalah ... 7

C. Tujuan Penelitian ... 8

D. Manfaat Penelitian ... 8

E. Definisi Operasional... 9

BAB II KAJIAN PUSTAKA A. Kemampuan Komunikasi Matematis ... 11

B. Kemampuan Kemandirian Belajar Siswa ... 17

C. Pembelajaran Matematika ... 19

D. Discovery Learning ... 22

E. Problem Based Learning ... 26

F. Kerangka Berpikir ... 29

G. Hipotesis Penelitian ... 31

(7)

A. Desain Penelitian ... 33

B. Populasi dan Sampel... 33

C. Variabel Penelitian ... 34

D. Instrumen Penelitian ... 35

1. Tes Kemampuan Komunikasi Matematis ... 35

2. Skala Kemandirian Belajar Siswa ... 38

E. Teknik Analisis Instrumen ... 39

1. Analisis Validitas Instrumen ... 39

a. Validitas Logis ... 40

b. Validitas Empiris ... 40

2. Analisis Reliabilitas Instrumen ... 42

3. Analisis Tingkat Kesukaran ... 43

4. Analisis Daya Pembeda... 44

F. Skala Kemandirian Belajar Siswa ... 46

G. Prosedur Penelitian... 46

H. Teknik Pengumpulan Data ... 47

I. Teknik Analisis Data ... 48

1. Data Hasil Tes Kemampuan Komunikasi Matematis . 48 2. Data Skala Kemandirian Belajar Siswa ... 50

BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. Hasil Penelitian ... 51

1. Kemampuan Komunikasi Matematis ... 51

2. Kemandirian Belajar Siswa ... 61

B. Pembahasan ... 63

(8)

A. Kesimpulan ... 69

B. Saran ... 69

DAFTAR PUSTAKA ... 71

DAFTAR TABEL Halaman Tabel 2.1 Pembelajaran dengan Model DL... 25

Tabel 2.2 Pembelajaran dengan model PBL ... 28

Tabel 3.1 Kisi-Kisi Tes Kemampuan Komunikasi Matematis ... 36

Tabel 3.2 Pedoman Penskoran Tes Kemampuan Komunikasi ... 38

Tabel 3.3 Kisi-kisi Angket Kemandirian Belajar Siswa ... 38

Tabel 3.4 Klasifikasi Koefisisen korelasi Validitas ... 41

Tabel 3.5 Validitas Soal Tes Komunikasi Matematis ... 41

Tabel 3. 6 Klasifikasi koefisien Reliabilitas ... 42

Tabel 3.7 Reliabilitas Soal Tes Kemampuan Komunikasi Matematis ... 43

Tabel 3.8 Klasifikasi Tingkat Kesukaran Tes ... 43

Tabel 3.9 Tingkat Kesukaran Soal Tes Komunikasi Matematis ... 44

Tabel 3.10 Klasifikasi Daya Pembeda Tes ... 45

Tabel 3.11 Daya Pembeda Soal Tes Komunikasi Matematis ... 45

Tabel 3.12 Klasifikasi Gain Ternormalisasi ... 48

Tabel 4.1 Statistik Deskriptif Skor Kemampuan Komunikasi Matematis .... 51

Tabel 4.2 Deskriptif Kemampuan komunikasi Berdasarkan KAM ... 52

Tabel 4.3 Hasil Uji Normalitas Pretes ... 54

Tabel 4.4 Hasil Uji Maan-Whitney ... 55

Tabel 4.5 Hasil Uji Normalitas N-Gain Kemampuan komunikasi ... 56

(9)

Tabel 4.7 Hasil Uji Kesamaan Rataan N-Gain Kemampuan Komunikasi

Matematis Siswa ... 57

Tabel 4.8 Hasil Uji Normalitas N-Gain Kemampuan Komunikasi Matematis Berdasarkan KAM ... 58

Tabel 4.9 Hail Uji Homogen N-Gain Berdasarkan KAM ... 59

Tabel 4.10 Hasil Uji Kesamaan Rataan N-Gain Berdasarkan KAM ... 60

Tabel 4.11 Uji Anova Satu Jalur Kelas DL dan PBL ... 61

Tabel 4.12 Uji Scheffe Kelas DL dan PBL ... 61

Tabel 4.13 Hasil Uji Mann-Whitney Kemandirian Belajar ... 62

DAFTAR LAMPIRAN Halaman LAMPIRAN A: BAHAN AJAR A.1 Silabus ... 76

A2 RPP Discovery Learning (DL) ... 81

A3 RPP Problem Based Learning (PBL) ... 121

A4 Lembar Kerja Siswa (LKS) Dengan Pembelajaran DL ... 161

A5 Lembar Kerja Siswa (LKS) Dengan Pembelajaran PBL ... 189

LAMPIRAN B: INTRUMEN PENELITIAN B.1 Kisi-kisi Tes Kemampuan Komunikasi Matematis ... 212

B.2 Soal Uji Coba Kemampuan Komunikasi Matematis ... 217

B.3 Soal Tes Kemampuan Komunikasi Matematis ... 218

B.4 Skala Sikap Kemandirian Belajar Siswa ... 219

LAMPIRAN C: HASIL UJI COBA C.1 Hasil Uji Coba Tes Kemampuan Komunikasi ... 223

(10)

LAMPIRAN D: ANALISIS DATA PRETES, POSTES, N-GAIN DAN

SKALA SIKAP KEMANDIRIAN BELAJAR SISWA

D.1 Data Pretes, Postes, N-Gain KAM Kelas DL ... 235 D.2 Data Pretes, Postes, N-Gain KAM Kelas PBL ... 239

(11)

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Pendidikan merupakan kebutuhan manusia sepanjang hayat. Pendidikan sangat penting artinya, sebab tanpa pendidikan manusia akan sulit berkembang dan bahkan akan terbelakang. Pendidikan merupakan suatu upaya untuk meningkatkan kualitas sumber daya manusia baik fisik, mental maupun spritual. Majunya suatu negara dapat dilihat dari tingkat ilmu pengetahuan yang dimiliki oleh warga negara tersebut. Salah satu ilmu pengetahuan yang erat kaitannya dengan kemajuan bangsa dan peningkatan sumber daya manusia adalah matematika.

Matematika merupakan ilmu universal yang mendasari perkembangan teknologi modern, mempunyai peran penting dalam berbagai disiplin dan memajukan daya pikir manusia. Oleh karena itu, matematika perlu diberikan kepada semua peserta didik mulai dari sekolah dasar untuk membekali peserta didik dengan kemampuan berpikir logis, analitis, sistematis, kritis, dan kreatif, serta kemampuan bekerja sama (Depdiknas, 2006).

Depdiknas (2006) menyatakan bahwa setelah pembelajaran siswa harus memiliki seperangkat kompetensi matematika yang harus ditunjukkan pada hasil belajarnya dalam mata pelajaran matematika. Kecakapan atau kemahiran matematika yang diharapkan dapat dicapai siswa dalam belajar matematika yaitu: (1) pemahaman konsep; (2) penalaran; (3) komunikasi; (4) pemecahan masalah; dan (5) memiliki sikap menghargai kegunaan matematika dalam kehidupan.

(12)

2

problem solving); (4) koneksi matematika (mathematical connection); dan (5) Pembentukan sikap positif terhadap matematika (positive attitudes toward mathematics).

Berdasarkan hal di atas, terlihat bahwa kemampuan komunikasi merupakan salah satu kompetensi penting yang harus dikembangkan. Hal ini dikarenakan melalui komunikasi matematis, siswa dapat mengorganisasikan berpikir matematisnya baik secara lisan maupun secara tulisan yang terjadi dalam proses pembelajaran. Peressini dan Bassett (1996) mengemukakan bahwa tanpa komunikasi dalam matematika kita akan memiliki sedikit keterangan, data, dan fakta tentang pemahaman siswa dalam melakukan proses dan aplikasi matematis. Pentingnya kemampuan komunikasi dalam pembelajaran matematika diungkapkan oleh Dahlan (2011) bahwa kemampuan komunikasi memegang peranan penting dalam pembelajaran matematika sebagaimana aktivitas sosial di masyarakat. Komunikasi matematis sebagai aktivitas yang dapat membantu siswa dalam mengekspresikan ide-ide matematika dengan bahasa sendiri dan dapat dipahami oleh orang lain.

Selanjutnya Greenes dan Schulman (Tandiling, 2011) menyatakan bahwa komunikasi matematik merupakan: (1) kekuatan sentral bagi siswa dalam merumuskan konsep dan strategi matematik; (2) modal keberhasilan bagi siswa terhadap pendekatan dan penyelesaian dalam eksplorasi dan investigasi matematik; (3) wadah bagi siswa dalam berkomunikasi dengan temannya untuk memperoleh informasi, membagi pikiran dan penemuan, curah pendapat, menilai dan mempertajam ide untuk meyakinkan yang lain.

(13)

3

himpunan yang telah mereka pelajari dalam menyelesaikan soal yang peneliti berikan. Dari 35 siswa yang berpartisipasi, masih banyak siswa kurang bisa mengemukakan permasalahan dalam model matematika. Hanya 13 siswa yang menjawab mengarah benar. Di antara siswa yang menjawab salah, terdapat enam siswa tidak menjawab. Soal yang peneliti ujikan kepada siswa tersebut sebagai berikut:

Dari seluruh siswa di kelas VII A diketahui bahwa 22 siswa gemar basket, 21 siswa gemar volley dan 7 siswa kedua-duanya. Nyatakan persoalan tersebut dalam model matematika dan tentukan banyaknya seluruh siswa.

Berdasarkan studi pendahuluan yang dilakukan Izzati (2012) terhadap siswa kelas VII pada salah satu siswa SMP berstandar nasional di kota Bandung, menunjukan bahwa siswa belum mampu mengemukakan penyelesaiannya ke dalam model matematika yang benar. Berikut soal matematika tentang luas segitiga yang diberikan kepada siswa:

Sebuah taman berbentuk segitiga sama kaki dengan sisi yang sama 10 m, panjang sisi lainnya 12 m dan tingginya 8 m. jika taman tersebut akan ditanami rumput dengan biaya Rp 60.00,00/m2, berapakah keseluruhan biaya yang diperlukan?

Temuan Izzati (2012) dari 39 siswa yang berpartisipasi menjawab soal di atas, belum ada yang menunjukan bahwa mereka memiliki kemampuan komunikasi matematis yang baik/efektif. Misalnya menyatakan ide matematika ke dalam model model matematika. Dari 39 siswa hanya 19 siswa yang menjawab

(14)

4

Pembelajaran matematika tidak hanya dimaksudkan untuk mengembangkan aspek kognitif, melainkan juga aspek afektif, seperti kemandirian belajar siswa. Kemandirian belajar merupakan faktor penting dalam pembelajaran matematika, karena faktor ini merupakan hal yang juga turut menentukan keberhasilan belajar. Zimerman dan Martinez-Pons (1986), Pintrich dan Groot (1990) dan Reyero dan Touron (dalam Montalvo dan Torres, 2004) menunjukan bahwa kemandirian belajar berkorelasi kuat dengan kesuksesan seorang siswa. Sumarmo (2013) menyatakan bahwa “ individu yang belajar matematika dituntut memiliki disposisi matematis yang tinggi, selanjutnya akan

menghasilkan kemampuan berpikir matematis yang diharapkan.” Karakteristik

disposisi matematis mengarah kepada kemandirian belajar. Tuntutan kemadirian belajar tersebut akan semakin kuat dengan pemanfaatan teknologi informasi dalam pembelajaran matematika. Menurut Hargis (Sumarmo, 2013) bahwa : siswa yang memiliki kemandirian yang tinggi : (1) cenderung belajar lebih baik dalam pengawasannya sendiri dari pada dalam pengawasan program, (2) mampu memantau, mengevaluasi, dan mengatur belajarnya secara efektif, (3) menghemat waktu dalm menyelesaikan tugasnya, dan (4) mengatur belajar dan waktu secara efisien.

(15)

5

pembelajaran. Untuk kemampuan komunikasi matematis dan kemandirian belajar siswa masih membutuhkan perhatian yang khusus. Padahal sikap tersebut merupakan factor yang mendukung untuk mengembangkan kecakapan matematik siswa.

Salah satu cara untuk mengembangkan kemampuan komunikasi matematis dan kemandirian belajar siswa adalah dengan memilih dan menggunakan strategi, pendekatan, metode, dan teknik yang melibatkan siswa aktif dalam belajar, baik secara mental, fisik, maupun sosial. Seperti dikatakan Wahyudin (2008), salah satu aspek penting dari perencanaan bertumpu pada kemampuan guru untuk mengantisipasi kebutuhan dalam proses pembelajaran dan materi-materi atau model-model yang dapat membantu para siswa untuk mencapai tujuan pembelajaran. Case (dalam Samuelsson, 2010) berpendapat bahwa variasi pembelajaran penting karena pembelajaran yang berbeda akan menarik perhatian berbagai kompetensi dalam matematika sehingga siswa dapat berpartisipasi secara aktif dalam belajar. Pembelajaran yang membuat siswa aktif akan membantu siswa dalam melatih keterampilan social siswa seperti bertanya, berpendapat, dan mendorong siswa pasif untuk aktif dalam proses pembelajaran. Pernyataan di atas sejalan dengan Suherman (2003) menyebutkan bahwa kondisi pembelajaran dengan kelompok kecil menonjolkan interaksi dalam kelompok, sehingga terjadi komunikasi antarsiswa terutama dalam menyelesaikan suatu masalah. Oleh karena itu diperlukan suatu model pembelajaran yang dapat meningkatkan minat dan motivasi belajar, sehingga pada akhirnya akan berdampak positif pada prestasi belajar siswa dan tujuan pembelajaran yang akan dicapai.

(16)

6

Pembelajaran melalui Discovery learning dan Problem Basen Learning merupakan pembelajaran yang melatih siswa untuk aktif dalam proses pembelajaran. Ruseffendi (1991) mengemukakan bahwa metode Discovery adalah metode mengajar yang diatur sedemikian rupa sehingga anak memperoleh pengetahuan yang sebelumnya belum diketahuinya itu tidak melalui pemberitahuan, dimana sebagian atau seluruh pengetahuan ditemukan sendiri dengan bantuan guru. Pada metode discovery struktur pembelajarannya adalah induktif, yaitu menekankan siswa untuk menemukan pola-pola, aturan, prinsip, dan struktur matematik melalui eksplorasi terhadap contoh-contoh. Menurut Suryosubroto (2002) pembelajaran Discovery salah satu pembelajaran yang banyak digunakan di sekolah-sekolah karena merupakan suatu cara untuk mengembangkan cara belajar siswa aktif dan dengan menemukan dan menyelidiki sendiri konsep yang dipelajari, maka hasil yang diperoleh akan tahan lama dalam ingatan. Menurut Markaban (2006) bahwa penggunaan model penemuan terbimbing dalam belajar matematika dapat meningkatkan kemampuan kognitif

siswa, kemampuan komunikasi siswa dan kemampuan penalaran siswa. Oleh

karena itu Discovery merupakan salah satu pembelajaran yang dapat

meningkatkan kemampuan kognitif siswa antara lain komunikasi matematis.

(17)

7

siswa yang memperoleh pembelajaran berbasis masalah secara signifikan lebih baik dari pada siswa yang memperoleh pembelajaran kovensional.

Pembelajaran Problem Based Learning dan Discovery Learning merupakan model pembelajaran yang disarankan untuk digunakan di kelas dalam implementasi kurikulum 2013. Model Problem Based Learning merupakan sebuah pembelajaran yang diawali dengan menyajikan suatu masalah kontekstual sehingga merangsang siswa untuk belajar lebih lanjut. Model Discovery Learning merupakan sebuah pembelajaran yang mendorong siswa untuk mengidentifikasi apa yang ingin diketahui dilanjutkan dengan mencari imformasi kemudian mengorganisasi apa yang mereka ketahui sehingga mendapatkan konsep pembelajaran yang baru. Dengan keunggulan masing-masing model pembelajaran ini, diharapkan dapat menjembatani siswa dalam memiliki kompetensi dasar dalam kurikulum 2013. Untuk itu penulis menduga bahwa Model Problem Based Learning (PBL) dan Discovery Learning (DL) dapat meningkatkan kemampuan komunikasi dan kemandirian belajar siswa.

(18)

8

Discovery Learning dan Problem Based Learning cocok diterapkan untuk semua level kemampuan.

Berdasarkan hal-hal tersebut di atas, Problem Based Learning dan Discovery Learning memiliki keunggulan yang masing-masing dianggap dapat meningkatkan kemampuan komunikasi matematis dan kemandirian belajar siswa. Oleh karena itu pada penelitian ini akan dikaji “perbandingan kemampuan komunikasi matematis dan kemandirian belajar antara siswa yang belajar dengan Problem Based Learning dan Discovery Learning”.

B. Rumusan Masalah

Berdasarkan uraian pada latar belakang di atas, maka rumusan masalah yang akan dikaji dalam penelitian ini adalah sebagai berikut:

1. Apakah terdapat perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning?

2. Apakah terdapat perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning jika dilihat dari kemampuan awal matematis?

3. Apakah terdapat perbedaan kemandirian belajar siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning?

C. Tujuan Penelitian

Adapun tujuan penelitian ini adalah untuk menelaah :

(19)

9

2. Perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning jika dilihat dari kemampuan awal matematis.

3. Perbedaan kemandirian belajar siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning.

D. Manfaat Penelitian

Penelitian ini bermanfaat: 1. Manfaat Proses

a. Pembelajaran Problem Based Learning dan Discovery Learning dapat menciptakan suasana pembelajaran yang menyenangkan dan membuat siswa berpartisipasi secara aktif dalam pembelajaran.

b. Melatih siswa dalam bekerja sama, mengeluarkan ide-idenya dan memecahkan masalah.

2. Manfaat Hasil

a. Dapat memberikan sumbangan untuk mengembangkan teori pembelajaran yang berkaitan dengan kemampuan komunikasi matematis dan kemandirian belajar siswa dalam pembelajaran matematika melalui model Problem Based Learing dan Discovery Learning. Serta menjadi sumbangan pemikiran baru bagi perkembangan dunia pendidikan agar kualitas pendidikan menjadi lebih baik.

b. Dapat memberikan informasi tentang sejauh mana peningkatan kemampuan komunikasi matematis dan kemamdirian belajar siswa dengan pembelajaran Problem Based Learning dan Discovery Larning. Hasil dari penelitian ini dapat digunakan sebagai tambahan referensi dalam memilih model pembelajaran yang efektif untuk meningkatkan kemampuan komunikasi matematis dan kemandirian belajar siswa.

(20)

10

Untuk menghindari terjadinya perbedaan pendapat mengenai hal-hal yang dimaksud dalam penelitian ini, maka peneliti memberikan definisi opersional sebagai berikut:

1. Kemampuan komunikasi matematis adalah kemampuan: (1) menyatakan suatu situasi atau ide-ide matematis dalam bentuk gambar, diagaram atau grafik; (2) menganalisis dan mengevaluasi terhadap suatu informasi yang diberikan; (3) menjelaskan konsep, ide atau persoalan dengan bahasa sendiri; (4) menyatakan situasi atau ide-ide matematis ke dalam model matematika

2. Kemandirian belajar siswa adalah sikap siswa terhadap dirinya dalam belajar yang meliputi : inisiatif belajar; mendiagnosa kebutuhan belajar; menetapkan tujuan belajar; memonitor, mengatur, dan mengontrol belajar; memandang kesulitan sebagai tantangan; memanfaatkan dan mencari sumber yang relevan; memilih dan menerapkan strategi belajar yang tepat; konsep diri.

3.

Model Problem Based Learning atau pembelajaran berbasis masalah adalah

pembelajaran yang dimulai dengan menyiapkan masalah-masalah yang relevan dengan konsep yang akan dipelajari. Pembelajaran PBL terdiri dari beberapa tahapan yaitu: 1) orientasi siswa kepada masalah; 2) mengorganisasikan siswa untuk belajar; 3) membimbing penyelidikan individu dan kelompok; 4) mengembangkan dan menyajikan hasil karya; 5) menganalisa dan mengevaluasi proses pemecahan masalah.

4.

Model Discovery Learning adalah pembelajaran yang membimbing siswa dalam menemukan suatu konsep matemtika. Model pembelajaran Discovery Learning terdiri dari beberapa langkah yaitu: 1) stimulasi/pemberian rangsangan; 2) pernyataan/identifikasi masalah; 3) pengumpulan data; 4) pengolahan data; 5) pembuktian; 6) menarik kesimpulan/generalisasi.

(21)

11

(22)

33

BAB III

METODE PENELITIAN

A. Desain Penelitian

Jenis penelitian ini adalah quasi-experimental dengan desain penelitiannya non-equilvalent control group design. Quasi-experiment yang dimaksud dalam penelitian terdapat dua kelas, yaitu kelas eksperimen DL dan kelas eksperimen

PBL yang pengelompokannya tidak secara acak, tetapi peneliti menerima keadaan

subjek apa adanya (Ruseffendi, 2005). Kelas eksperimen DL merupakan siswa

yang diberikan pembelajaran dengan Discovery Learning sedangkan kelas

eksperimen PBL merupakan siswa yang diberikan pembelajaran dengan Problem

Based Learning. Penelitian dilakukan pada siswa dari dua kelas yang memiliki

kemampuan setara dengan model pembelajaran yang berbeda. Dua kelas tersebut

diberikan tes awal (pretest) untuk kedua kelompok sebelum perlakuan diberikan,

kemudian setelah perlakuan diberikan kepada masing-masing kelompok, maka

diberikan tes akhir (posttest). Soal yang diberikan untuk pretes dan postes

merupakan soal yang serupa. Berikut merupakan gambaran desain penelitian.

O X1 O O X2 O Keterangan:

O : pretest dan posttest

X1 : Model Discovery Learning

X2 : Model Problem Based Learning

(Ruseffendi, 2005)

B. Populasi dan Sampel

(23)

34

sekolah. Dipilih dua kelas yang akan dijadikan sebagai kelas eksperimen DL dan eksperimen PBL.

C. Variabel Penelitian

Menurut Sugiyono (2008), jika dilihat berdasarkan hubungan antar satu variabel dengan variabel yang lain, maka jenis-jenis variabel dapat dibedakan menjadi dua jenis variabel yaitu variabel bebas (independent variabel) dan variabel terikat (dependent variabel). Dalam penelitian ini, variabel yang ada terdiri atas variabel bebas (X) dan variabel terikat (Y).

1. Variabel Bebas (X)

Sugiyono (2008) berpendapat bahwa variabel bebas merupakan variabel yang akan mempengaruhi dan dapat dikatakan sebagai variabel sebab. Berdasarkan pengertian tersebut, maka yang menjadi variabel bebas dalam penelitian ini adalah: (1) model pembelajaran Problem Based Learning; (2) model pembelajaran Discovery learning. Definisi model pembelajaran Discovery learning dan Problem Based Learning yaitu:

Model Discovery Learning adalah pembelajaran yang membimbing siswa dalam menemukan suatu konsep matemtika. Model pembelajaran Discovery Learning terdiri dari beberapa langkah yaitu: 1) stimulasi/pemberian rangsangan; 2) pernyataan/identifikasi masalah; 3) pengumpulan data; 4) pengolahan data; 5) pembuktian; 6) menarik kesimpulan/generalisasi.

(24)

35

Dalam pembahasan selanjutnya, model pembelajaran Problem Based Learning disingkat dengan PBL, sedangkan model pembelajaran Discovery learning disingkat dengan DL. PBL diberikan di kelas VIID dan DL diberikan di kelas VIIC.

2. Variabel Terikat (Y)

Sugiyono (2010) berpendapat bahwa variabel terikat merupakan variabel yang dipengaruhi oleh variabel bebas atau yang menjadi akibat dari variabel bebas. Berdasarkan pengertian tersebut, maka yang menjadi variabel terikat dalam penelitian ini adalah: (1) komunikasi matematis siswa; (2) kemandirian belajar siswa. Definisi operasional kemampuan komunikasi maatematis dan kemandirian belajar siswa yaitu:

Kemampuan komunikasi matematis adalah kemampuan: (1) menyatakan suatu situasi atau ide-ide matematis dalam bentuk gambar, diagaram atau grafik; (2) menganalisis dan mengevaluasi terhadap suatu informasi yang diberikan; (3) menjelaskan konsep, ide atau persoalan dengan bahasa sendiri; (4) menyatakan situasi atau ide-ide matematis ke dalam model matematika.

Kemandirian belajar siswa adalah sikap siswa terhadap dirinya dalam belajar yang meliputi : inisiatif belajar; mendiagnosa kebutuhan belajar; menetapkan tujuan belajar; memonitor, mengatur, dan mengontrol belajar; memandang kesulitan sebagai tantangan; memanfaatkan dan mencari sumber yang relevan; memilih dan menerapkan strategi belajar yang tepat; konsep diri.

D. Instrumen Penelitian

(25)

36

1. Tes Kemampuan Komunikasi Matematis

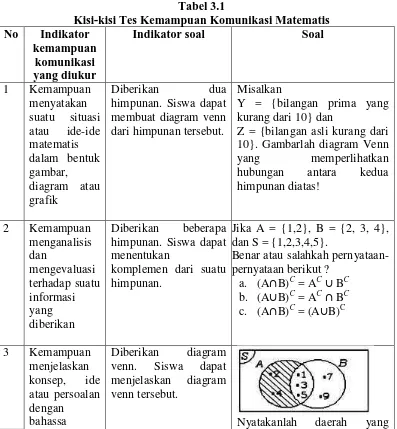
Tes kemampuan komunikasi matematis disusun dalam bentuk uraian. Tes ini digunakan untuk mengukur kemampuan komunikasi matematis siswa. Tes kemampuan komunikasi matematis disusun dalam bentuk uraian. Adapun kisi-kisi dari tes kemampuan komunikasi matematis sebagai berikut:

Tabel 3.1

Kisi-kisi Tes Kemampuan Komunikasi Matematis No Indikator

himpunan. Siswa dapat membuat diagram venn hubungan antara kedua himpunan diatas! himpunan. Siswa dapat menentukan

komplemen dari suatu himpunan.

(26)

37

No Indikator kemampuan

komunikasi yang diukur

Indikator soal Soal

sendiri diarsir pada gambar diatas

dalam himpunan A dan

Diberikan soal cerita tentang irisan dua himpunan. Siswa dapat menyajikan data yang ada pada soal dalam volly dan 7 siswa gemar kedua-duanya.

a. Nyatakan persoalan tersebut dalam model matematika! b. Tentukan banyaknya seluruh

siswa!

Diberikan soal cerita tentang irisan dua himpunan. Siswa dapat menyajikan data yang ada pada soal dalam bentuk simbol/bahasa matematika dan siswa dapat menentukan komplemen dari gabungan kedua himpunan tersebut.

Berdasarkan survey pada sebuah kelas, terdapat 15 orang anak gemar membaca novel, 20 orang anak gemar membaca komik, dan 7 orang anak gemar membaca keduanya. Jika jumlah siswa dalam kelas itu ada 30 orang,

(27)

38

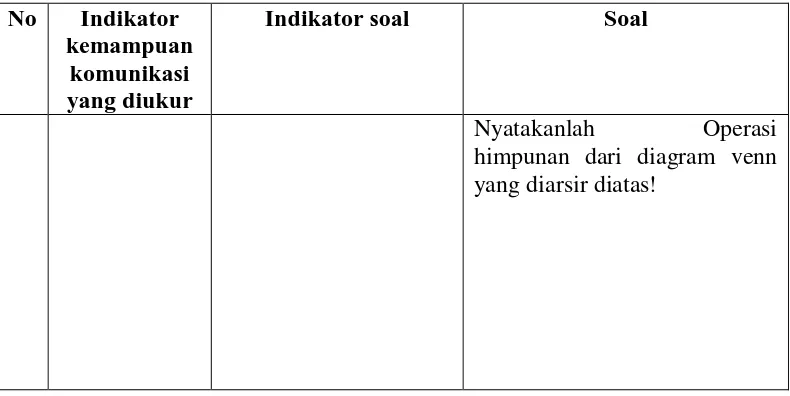
No Indikator kemampuan

komunikasi yang diukur

Indikator soal Soal

Nyatakanlah Operasi himpunan dari diagram venn yang diarsir diatas!

Pedoman penskoran tes kemampuan komunikasi matematis, menggunakan pedoman yang diusulkan Cai, Lane dan Jakabcin (1996).

Tabel 3.2

Pedoman Penskoran Tes Kemampuan Komunikasi Matematis

Skor Kriteria

4 Penjelasan secara matematis masuk akal dan benar dan tersusun secara logis

3 Penjelasan secara matematis masuk akal dan benar, meskipun tidak tersusun secara logis dan ada sedikit kesalahan

2 Penjelasan secara matematis masuk akal, namun hanya sebagian yang lengkap dan benar

(28)

39

Skor Kriteria

0 Tidak ada jawaban/salah menginterpretasikan 2. Skala Kemandirian Belajar Siswa

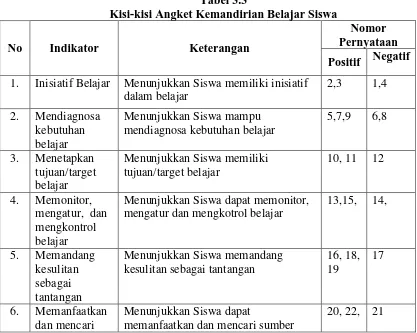
Angket kemandirian belajar diberikana kepada siswa di kelas eksperimen DL dan eksperimen PBL terdiri dari 33 butir pernyataan diantaranya: 20 pernyataan positif dan 13 pernyataan negative. Skala kemandirian belajar ini telah disesuaikan dengan indikator kemandirian belajar yang diadopsi dan dimodifikasi dari skala kemandirian belajar siswa Sumaarmo (2013)

Angket kemandirian belajar siswa yang dibuat berpedoman pada bentuk skala sikap Likert. Ada lima kategori pada skala likert, yaitu Sangat Setuju (SS), Setuju (S), Tidak Setuju (TS), Sangat Tidak Setuju (STS). Adapun kisi-kisi dari angket kemandirian belajar siswa yaitu:

Tabel 3.3

Kisi-kisi Angket Kemandirian Belajar Siswa

No Indikator Keterangan

Nomor Pernyataan

Positif Negatif

(29)

40

No Indikator Keterangan

Nomor

mengevaluasi proses dan hasil belajar

28, 26,27

9 Konsep diri Menunjukkan Siswa memiliki kosep diri

29,30, 33

31, 32

E. Teknik Analisis Instrumen

Bahan tes diambil dari materi pelajaran Matemtika yang berkaitan dengan soal tes kemampuan komunikasi matematis. Sebelum soal instrumen digunakan dalam penelitian, soal tersebut diujicobakan terlebih dahulu pada siswa yang telah memperoleh materi yang berkenaan dengan yang akan diteliti. Ujicoba dilakukan untuk mendapatkan alat ukur yang sesuai. Data yang diperoleh dari hasil ujicoba tes kemampuan komunikasi matematis ini dianalisis untuk mengetahui reliabilitas, validitas, daya pembeda dan tingkat kesukaran tes. Data diolah dengan menggunakan bantuan Anates V.4 for Windows.

1. Analisis Validitas Instrumen

Suatu alat evaluasi disebut valid (absah atau sahih) apabila alat tersebut mampu mengevaluasi apa yang seharusnya dievaluasi (Suherman, 2003). Oleh karena itu, keabsahannya tergantung pada sejauh mana ketepatan alat evaluasi itu dalam melaksanakan fungsinya. Dengan demikian suatu alat evaluasi disebut valid jika ia dapat mengevaluasi dengan tepat sesuatu yang dievaluasi itu (Suherman, 2003). Dalam penelitian ini, untuk memperoleh suatu instrumen yang dapat mengukur kemampuan komunikasi matematis siswa dengan baik dilakukan dengan menggunakan validitas logis dan validitas empirik.

(30)

41

Validitas logis atau validitas teoritik untuk sebuah instrumen evaluasi menunjuk pada kondisi bagi sebuah instrumen yang memenuhi persyaratan valid berdasarkan teori dan ketentuan yang ada. Pertimbangan terhadap soal tes kemampuan komunikasi matematis berkenaan dengan validitas muka dan validitas isi. Validitas muka dilakukan dengan melihat dari sisi muka atau tampilan dari instrumen itu sendiri (Suherman, 2003). Validitas muka dalam penelitian ini dilakukan dengan melihat apakah kalimat atau kata-kata dari instrumen tes yang digunakan sudah tepat dan layak digunakan sehingga tidak menimbulkan tafsiran lain termasuk juga kejelasan gambar dan soal. Sedangkan validitas isi berkenaan dengan keshahihan instrumen tes dengan materi yang akan ditanyakan, baik tiap butir soal maupun menurut soalnya secara keseluruhan. Jadi validitas isi instrumen tes dalam penelitian ini dilakukan dengan membandingkan antara isi instrumen dengan materi pelajaran yang diajarkan, serta dengan melihat kesesuain dengan indikator kemampuan yang diamati.

Validitas muka dan isi dalam penelitian ini dilakukan dengan meminta pertimbangan ahli (judgment) yang berkompeten dengan kemampuan dan materi yang dipelajari, dalam hal ini yang bertindak sebagai ahli. Setelah instrumen tes dianalisis validitas logisnya, instrumen tes kemudian dilakukan uji coba.

b) Validitas Empiris

Validitas empiris adalah validitas yang ditinjau dengan kriteria tertentu. Kriteria ini digunakan untuk menentukan tinggi rendahnya koefisien validitas alat evaluasi yang dibuat melalui perhitungan korelasi product moment dengan menggunakan angka kasar (Arikunto, 2010) yaitu:

r xy ∑ ∑ ∑

√ ∑ ∑ ∑ ∑

Keterangan :

(31)

42

Y = Jumlah skor total suatu butir tes N = Jumlah subyek

Dengan mengambil taraf signifikan 0,05 dan taraf kebebasan (dk) = n – 2 , sehingga didapat kemungkinan interpretasi:

(i) Jika thit≤ ttabel , maka soal tidak valid (ii) Jika thit > ttabel , maka soal valid

Dengan ketentuan klasifikasi koefisien korelasi validitas sebagai berikut: Tabel 3.4

Klasifikasi Koefisien Korelasi Validitas

Koefisien Validitas Interpretasi Sumber : Guilford (Suherman, 2003)

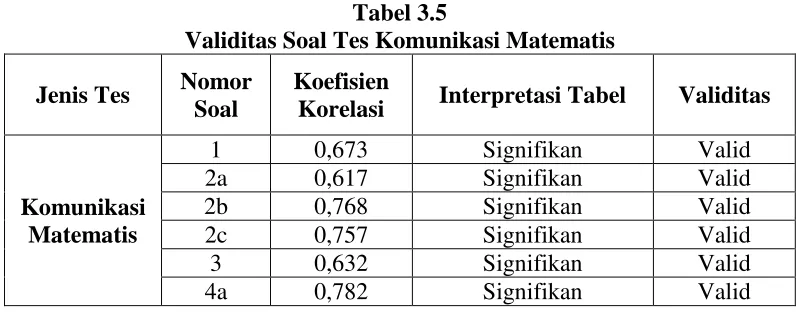
Pengujian Validitas tes dalam penelitian ini dilakukan dengan menggunakan bantuan software Anates V.4 for Windows untuk soal uraian. Berdasarkan hasil perhitungan pada lampiran, validitas dari soal uji coba instrumen tes komunikasi matematis adalah sebagai berikut:

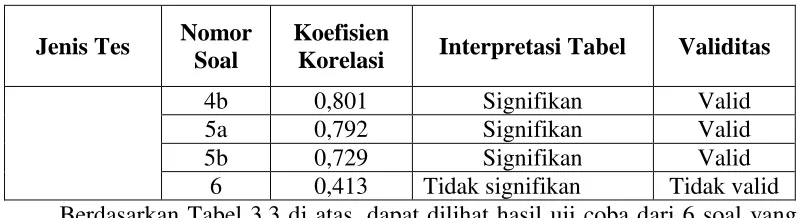
Tabel 3.5

Validitas Soal Tes Komunikasi Matematis

Jenis Tes Nomor Soal

Koefisien

Korelasi Interpretasi Tabel Validitas

(32)

43

Koefisien

Korelasi Interpretasi Tabel Validitas

4b 0,801 Signifikan Valid

5a 0,792 Signifikan Valid

5b 0,729 Signifikan Valid

6 0,413 Tidak signifikan Tidak valid Berdasarkan Tabel 3.3 di atas, dapat dilihat hasil uji coba dari 6 soal yang mengukur kemampuan komunikasi matematis, terdapat 5 soal yang valid dan 1 soal yang tidak valid.

2. Analisis Reabilitas Instrumen

Reliabilitas berhubungan dengan masalah kepercayaan. Suatu tes dapat dikatakan mempunyai taraf kepercayaan yang tinggi jika tes tersebut dapat memberikan hasil yang tetap. Jadi pengertian reliabilitas tes, berhubungan dengan masalah ketetapan hasil tes (Arikunto, 2010). Suatu alat evaluasi disebut reliabel jika hasil evaluasi tersebut relatif tetap jika digunakan untuk subjek yang sama. Rumus yang digunakan untuk menghitung reliabilitas tes ini adalah rumus Cronbach’s Alpha (Arikunto, 2010).

[_]∑

Keterangan:

r11 = Reliabilitas instrumen

∑σi2 = Jumlah varians skor suatu butir tes σt2 = Varians total

n = Banyaknya butir tes

Dengan ketentuan klasifikasi koefisien reliabilitas sebagai berikut: Tabel 3.6

(33)

44

r11 ≤ 0,20 Sangat rendah

Sumber : Guilford (Suherman, 2003)

Pengujian reliabilitas tes dilakukan dengan bantuan software Anates V.4 for Windows untuk soal uraian. Berdasarkan hasil perhitungan pada lampiran,

reliabilitas dari soal uji coba kemampuan komunikasi matematis adalah sebagai berikut:

Tabel 3.7

Reliabilitas Soal Tes Kemampuan Komunikasi Matematis Jenis Tes Koefisien Reliabilitas Tingkat Reliabilitas

Komunikasi Matematis 0,92 Sangat Tinggi

Berdasarkan Tabel 3.5 di atas, dapat dilihat bahwa reliabilitas untuk soal yang mengukur kemampuan komunikasi matematis siswa termasuk ke dalam kategori sangat tinggi.

3. Analisis Tingkat Kesukaran

Tingkat kesukaran adalah bilangan yang menunjukkan sukar dan mudahnya suatu soal tes (Arikunto, 2010). Tingkat kesukaran untuk soal uraian dapat dihitung dengan rumus sebagai berikut:

̅

(Suherman , 2003) Keterangan:

IK = Indeks Kesukaran

̅ = rata-rata skor kelompok atas dan kelompok bawah b = bobot, nilai maksimal soal

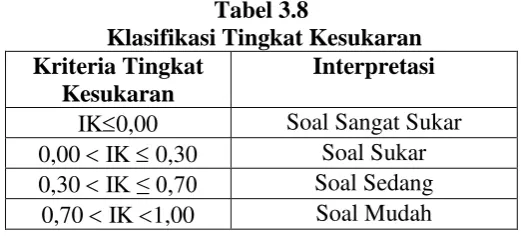
Ketentuan klasifikasi tingkat kesukaran soal sebagai berikut: Tabel 3.8

Klasifikasi Tingkat Kesukaran Kriteria Tingkat

Kesukaran

Interpretasi

IK0,00 Soal Sangat Sukar 0,00  IK  0,30 Soal Sukar 0,30  IK ≤ 0,70 Soal Sedang

(34)

45

IK = 1,00 Soal Sangat Mudah Sumber: (Suherman, 2003)

Perhitungan tingkat kesukaran dilakukan dengan bantuan software Anates V.4 for Windows untuk soal uraian. Berdasarkan hasil perhitungan yang tertera

pada lampiran, tingkat kesukaran dari soal uji coba kemampuan komunikasi matematis adalah sebagai berikut:

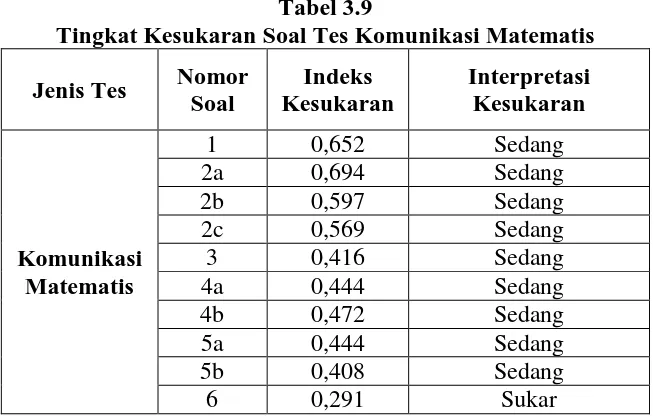
Tabel 3.9

Tingkat Kesukaran Soal Tes Komunikasi Matematis

Jenis Tes Nomor tabel tersebut, dapat dilihat bahwa soal tes nomor 6 yang mengukur kemampuan komunikasi matematis tergolong ke dalam kategori sukar, ini tidak berarti bahwa soal yang diberikan memang benar-benar sukar, tetapi lebih dikarenakan jarangnya siswa mendapatkan soal-soal dengan karakteristik komunikasi matematis. Sedangkan untuk soal lainnya tergolong pada kategori sedang.

4. Analisis Daya Pembeda

Daya pembeda sebuah butir soal tes adalah kemampuan butir soal itu untuk membedakan antara siswa yang berkemampuan tinggi dengan siswa yang berkemampuan rendah (Suherman, 2003). Daya pembeda butir soal dapat diketahui dengan melihat besar kecilnya angka indeks diskriminasi item. Rumus yang digunakan untuk menentukan daya pembeda adalah :

(35)

46

Keterangan:

DP = Daya pembeda

̅A = skor rata-rata kelas atas ̅B = skor rata-rata kelas bawah b = bobot

Ketentuan klasifikasi interpretasi daya pembeda soal sebagai berikut: Tabel 3.10

Klasifikasi Daya Pembeda Tes Kriteria Daya

Perhitungan daya pembeda instrumen dilakukan dengan bantuan software Anates V.4 for Windows untuk soal uraian. Berdasarkan hasil perhitungan dengan menggunakan software Anates V.4 for Windows seperti yang tertera pada lampiran, daya pembeda dari soal uji coba kemampuan komunikasi matematis adalah sebagai berikut:

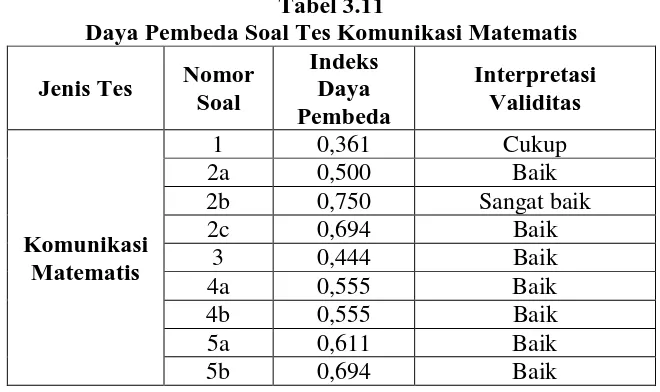
Tabel 3.11

Daya Pembeda Soal Tes Komunikasi Matematis

(36)

47

Indeks Daya Pembeda

Interpretasi Validitas

6 0,472 Baik

Dari Tabel 3.9 terlihat daya pembeda untuk soal kemampuan komunikasi matematis memiliki daya pembeda dari kategori cukup, baik dan sangat baik.

F. Skala Kemandirian Belajar Siswa

Perhitungan skor angket kemandirian belajar siswa menggunakan Microsoft office excel 2013 dan berbantuan IBM SPSS 21. Sebelum instrumen digunakan dilakukan uji validitas menggunakan uji Spearmann dan reliabilitasnya menggunakan Cronbach’s Alpha, berdasarkan hasil analisis angket semua pernyataan memiliki skor sig 0,05. Artinya pernyataan valid. Hasil signifikan dari data angket dapat dilihat di lampiran.

G. Prosedur Penelitian

Prosedur pada penelitian ini terdiri dari tiga tahapan yaitu tahap pendahuluan, tahap pelaksanaan, tahap pengumpulan data. Uraian dari ketiga tahap tersebut adalah sebagai berikut:

a. Tahap Persiapan

Tahap persiapan penelitian meliputi tahap-tahap penyusunan proposal, dan seminar proposal, menetapkan jadwal kegiatan dan materi pelajaran matematika, penyusunan instrumen penelitian (silabus, RPP, lembar kerja siswa, skala kemadirian belajar siswa, soal tes kemampuan komunikasi matematis), pengujian instrumen dan perbaikan instrumen.

b. Tahap pelaksanaan

(37)

48

pembelajaran Discovery Learning, sedangkan kelas VIID belajar melalui model pembelajaran Problem Based Learning.

c. Tahap pengumpulan data

Tahap penulisan laporan meliputi tahap pengolahan data, analisis data, dan penyusun laporan secara lengkap. Berikut ini adalah tahapan – tahapan yang dilakukan dalam penelitian :

Identifikasi Masalah Penyusunan Bahan Ajar

Uji Coba Instrumen Penyusunan Instrumen

Analisis validitas, Reliabilitas,Tingkat Kesukaran dan Daya Pembeda Pelaksanaan Penelitian

Tes Awal (Pretest)

Pembelajaran matematika dengan model Problem based Learning

Pembelajaran matematika dengan model Discovery Learning

Tes Akhir (Post test) Perlakuan Pembelajaran

(38)

49

H. Teknik Pengumpulan Data

Data yang berkaitan dengan kemampuan awal matematis siswa diambil melalui nilai UTS siswa. Untuk data kemampuan komunikasi matematis dikumpulkan melalui pretes dan postes. Pretes diberikan pada kedua kelas sampel sebelum diberi perlakuan, dan postes juga diberikan pada kedua kelas sampel setelah diberikan perlakuan. Selanjutnya, data yang berkaitan dengan kemandrian belajar siswa dikumpulkan melalui angket.

I. Teknik Analisis Data

Data yang diperoleh dari penelitian ini adalah data kuantitatif. Untuk itu pengolahan terhadap data yang telah dikumpulkan, dilakukan secara kuntitatif. Data-data kuantitatif diperoleh dalam bentuk hasil uji instrumen, data pretes, postes, N-Gain serta skala kemandirian siswa. Data hasil uji instrumen diolah dengan software Anates V.4 for Windows untuk memperoleh validitas, reliabilitas, daya pembeda serta derajat kesukaran soal. Sedangkan data hasil pretes, postes, N-Gain dan skala sikap kemandirian belajar siswa diolah dengan bantuan program Microsoft Excel dan software SPSS Versi 21 for Windows.

1. Data Hasil Tes Kemampuan Komunikasi Matematis

Hasil tes kemampuan komunikasi matematis digunakan untuk menelaah perbedaan peningkatan kemampuan komunikasi matematis siswa yang belajar melalui model pembelajaran PBL dan DL. Data yang diperoleh dari hasil tes kemampuan komunikasi matematis diolah melalui tahapan sebagai berikut:

Kesimpulan

(39)

50

1) Memberikan skor jawaban siswa sesuai dengan kunci jawaban dan pedoman penskoran yang digunakan.

2) Menentukan skor peningkatan kemampuan komunikasi matematis dengan rumus gain ternormalisasi (Meltzer, 2002) yaitu:

Gain ternormalisasi ini untuk melihat mutu peningkatan kompetensi yang terjadi sebelum dan sesudah pembelajaran.

Hasil perhitungan gain kemudian diinterpretasikan dengan menggunakan klasifikasi sebagai berikut:

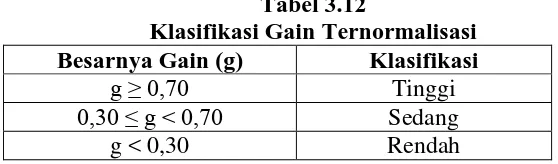
Tabel 3.12

Klasifikasi Gain Ternormalisasi Besarnya Gain (g) Klasifikasi

g ≥ 0,70 Tinggi

0,30 ≤ g < 0,70 Sedang

g < 0,30 Rendah

3) Menyajikan statistik deskriptif skor pretes, skor postes, dan skor N-Gain yang meliputi skor terendah (Xmin), skor tertinggi (Xmaks), rata-rata , dan simpangan baku (S).

4) Melakukan uji normalitas pada data pretes dan N-Gain kemampuan komunikasi matematis. Uji normalitas digunakan untuk mengetahui normal atau tidaknya distribusi data yang menjadi syarat untuk menentukan jenis statistik yang digunakan dalam analisis selanjutnya. Hipotesis yang diuji adalah:

H0 : data pretes berdistribusi normal H1 : data pretes berdistribusi tidak normal

Uji normalitas ini menggunakan statistik uji yaitu Kolmogorov- Smirnov atau Shapiro-Wilk.

(40)

51

5) Menguji homogenitas varians data skor pretes dan N-Gain kemampuan komunikasi matematis. Pengujian homogenitas antara dua kelompok data dilakukan untuk mengetahui apakah varians kedua kelompok homogen atau tidak homogen.

Adapun hipotesis yang akan diuji adalah: H0 : data pretes kedua kelompok homogen H1 : data pretes kedua kelompok tidak homogen

Uji statistiknya menggunakan Uji Levene. Kriteria pengujian H0 diterima apabila nilai signifikansi > taraf signifikansi (α = 0,05).

6) Setelah data memenuhi syarat normal dan homogen, selanjutnya dilakukan uji kesamaan rataan skor pretes menggunakan uji-t yaitu Independent Sample T-Test. Apabila data berdistribusi normal tetapi tidak homogen maka digunakan uji-t'. Apabila data berdistribusi tidak normal maka digunakan kajian statistik non parametric yaitu menggunakan uji Mann-Whitney U.

7) Melakukan uji perbedaan peningkatan kemampuan komunikasi matematis siswa yang belajara melalui model pembelajaran PBL dan DL berdasarkan kategori kemampuan awal matematis siswa (tinggi, sedang, rendah). Uji statistik yang digunakan adalah analysis of variance (ANOVA) dua jalur dilanjutkan uji Tukeyuntuk melihat letak perbedaanya. Selain itu uji ANOVA dua jalur ini juga untuk melihat interaksi antara model pembelajaran dan KAM terhadap kemampuan komunikasi matematis siswa.

2. Data Skala Kemandirian Belajar Siswa

(41)

52

(42)

69

Penggunaan media himpunan garis untuk meningkatkan kemampuan siswa tunagrahita ringan dalam memahami konsep pembagian bilangan bulat sampai 20

BAB V

KESIMPULAN DAN SARAN

A. Kesimpulan

Berdasarkan hasil penelitian ini disimpulkan bahwa:

1. Tidak terdapat perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning

2. Tidak terdapat perbedaan peningkatan kemampuan komunikasi matematis siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning jika ditinjau dari kemampuan awal matematis

3. Tidak terdapat perbedaan kemandirian belajar siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning

B. Saran

Dalam penelitian ini, ada beberapa saran yang akan peneliti kemukakan, diantaranya sebagai berikut.

1. Teoritis:

a. Dari hasil penelitian diketahui bahwa tidak terdapat perbedaan peningkatan yang signifikan antara siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning. Ini berarti bahwa kedua model tersebut dapat digunakan sebagai alternatif pembelajaran untuk meningkatkan kemampuan komunikasi.

(43)

70

c. Dari hasil penelitian juga diketahui tidak terdapat perbedaan yang signifikan kemandirian belajar siswa yang memperoleh Problem Based Learning dengan siswa yang memperoleh Discovery Learning. Ini berarti kedua model tersebut dapat digunakan sebagai alternatif pembelajaran untuk meningkatkan kemandirian belajar siswa.

2. Praktis:

a. Perlu diperhatikan kondisi pembagian kelompok siswa, sehingga nantinya setiap siswa dapat berpartisipasi aktif dalam proses belajar mengajar.

b. Pengaturan waktu sebaik mungkin agar proses pembelajaran sesuai dengan yang diharapkan. Karena pembelajaran dengan discovery learning dan problem based learning sesungguhnya membutuhkan waktu yang cukup banyak sehingga perlu manajemen waktu yang baik.

(44)

DAFTAR PUSTAKA

Aguspinal. (2011). Peningkatan Kemampuan Berpikir Kreatif dan Komunikasi Matematis Siswa SMA Melalui Pendekatan opend-Ended dengan Strategi Group-to-Group. Tesis UPI Bandung: tidak dditerbitkan

Arikunto, S. (2010). Dasar-Dasar Evaluasi Pendidikan. Jakarta: Bumi Aksara

Asikin, M. (2012). Menumbuhkan Kemampuan Komunikasi Matematika melalui Pembelajaran Matematika Realistik. Prosiding Konferensi Nasional Matematika XI

Cai, J., Lane, S., dan Jakabcin, M.S. (1996). Assesing Student Mathematical Communication. Official Journal of The Science an Mathematics 238-246 Dahlan, A. J. (2011). Analisis Kurikulum Matematika. Jakarta: Universitas Terbuka. Depdiknas. (2006). Standar Kompetensi dan Kompetensi Dasar. Jakarta: Direktorat

Jenderal Manajemen Pendidikan Dasar dan Menengah.

. (2013). Materi Pelatihan implementasi Kurikulum 2013. Badan Pengembangan Kemendikbud.

Ginting, A. (2010). ESENSI PRAKTIS: Belajar dan Pembelajaran. Bandung: Humaniora.

Hanafiah, N. (2010). Konsep Strategi Pembelajaran. Bandung: Refika Aditama. Herdian. (2010). Pengaruh Metode Discovery Terhadap Kemampuan Analogi Dan

Generalisasi Matematis Siswa SMP. Tesis PPs UPI. Bandung: Tidak diterbitkan

Herman, T. (2006). Pembelajaran Berbasis Masalah untuk Kerangka berpikir Matematis Tingkat Tinggi Siswa SMP. Disertasi SPs UPI Bandung: tidak diterbitkan.

. (2007). Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Penalaran Matematis Siswa SMP. Jurnal FMIPA-UPI. Cakrawala Pendidikan. Februari, 41-62.

Hudoyo, H. (1985). Teori Belajar dalam Proses Belajar-Mengajar Matematika. Jakarta: Depdikbud.

(45)

72

Jihad, A. (2008). Pengembangan kurikulum Matematika tinjauan teoritis dan historis. Bandung: Multi Pressindo.

Kimberley, H.C dan Oshkosh, N. 2008. Mathematical Communication conceptual Understanding, and Students’Attitudes Toward Mathematic. Departement of Mathematica University of Nebraska_Lincoln.

Izzati, N. (2012). Peningkatan Kemampuan Komunikasi Matematis dan Kemandirian Belajar Siswa SMP melalui Pendekatan Pendidikan Matematika Realistik. Disertasi SPs UPI : tidak diterbitkan.

Liperkiene, J. (2009). A Wide Concept of Mathematical Communication. ICTMT9b XXX.

Lindquist, M. M. dan Elliott, P. C. (1996). Communication-an Imperative for Change: A Conversation with Mary Linquist. Dalam P.C Elliot and M.J Kenney (Eds). Yearbook. Communication in Mathematics, K-12 and Beyond, 1-10. Reston: NCTM, Inc.

Markaban. (2006). Model pembelajaran matematika dengan penemuan terbimbing. Jogjakarta: Depertemen Pendidikan Nasional

Montalvo, f. T. dan torres, M. C. G. (2004). “ Self_Regulated Learning: Current And Future Direction”. Electronic Journal of research Psychology. 2, (1). 1-34. Mulyasa, E. (2007). Kurikulum Berbasis Kompetensi, Konsep, Karakteristik, dan

Implementasi. Bandung: Remaja Rosdakarya.

National Council of Teachers of Mathematics. (2000). Priciples and Standards for School Mathematics. Reston, VA: NCTM

Peressini, D dan Bassett, J. (1996). Mathematical Communication in Students’ Responses to a Performance-Assessment Task. Dalam P.C Elliot and M.J Kenney (Eds). Yearbook. Communication in Mathematics, K-12 and Beyond, 146-158. Reston: NCTM, Inc.

(46)

73

Pintrich, P. R. (2004). A Conceptual Framework for Assessing Motivation and Self-Regulated Learning in College Student. Educational Psychology Review. 16, (4), 305-407.

Rochaminah, S. (2008). Pengaruh Pembelajaran Penemuan terhadap Kemampuan Berpikir Kritis dan Matematis Mahasiswa Calon Guru. Disertasi UPI Bandung: Tidak diterbitkan

Rohaeti, E. E. (2003). Pembelajaran dengan Metode IMPROVE untuk meningkatkan Pemahaman dan Kemampuan Komunikasi Matematik Siswa SLTP. Tesis SPs UPI: tidak diterbitkan.

Ruseffendi, E.T. (1991). Pengantar Kepada Membantu Guru Mengembangkan Kompetensinya dan Pengajaran Matematika untuk Meningkatkan CBSA. Bandung: Tarsito.

.(2005). Dasar-dasar penelitian Pendidikan dan Bidang Non-Eksakta Lainnya. Bandung: Tarsito.

Samuelsson, J. (2010). The Impact of Theching Approaches on Students’ Mathematical Proficiency in Sweden. Intenational Electronic Journal of Mathematics Education. 5, (2), 61-78.

Setiawan, A. (2008). Pembelajaran Berbasis Masalah untuk Meningkatkan Kemampuan Komunikasi dan Pemecahan Masalah Matematik Siswa SMP. Tesis UPI Bandung: tidak diterbitkan

Shadiq, F. (2004). Penalaran, Pemecahan Masalah dan Komunikasi Matematika. Diklat Instruktur/ Pengembangan Matematika SMP Jenjang Dasar. PPPG Matematika: Yogyakarta.

Silver, C. E. H. (2004). Problem-Based Learning: What and Students Learn?. Educational Psychology Review. 16, (3), 235-266.

Slavin, R. E. (2009). Cooperative Learning: Teori, Riset dan Praktik. Bandung: Nusa Media

(47)

74

Sugiyono. (2008). Statistika Untuk Penelitian. Bandung: Alfabeta.

. (2009). Statistik Nonparametrik Untuk Penelitian. Bandung: Alfabeta. Suherman, E dkk. (2001). Common TexBook Strategi Pembelajaran Matematika

Kontemporer. Bandung: Jurusan Pendidikan Matematika UPI Bandung.

. (2003). Evaluasi Pembelajaran Matematika. Bandung: UPI

Sumarmo, U. (2013). Berpikir dan Disposisi Matematik serta Pembelajarannya. Bandung: UPI Press.

Suyadi. (2013). Strategi Pembelajaran Pendidikan Karakter. Bandung: Remaja Rosdakarya.

Suyitno, A. (2006). Dasar-dasar dan Proses Pembelajaran Matematika I. Semarang: Jurusan Matematika FMIPA Universitas Negeri Semarang. Tersedia pada: http://www.indoskripsi.com. Diakses: 12 November 2014.

Syaban, M. (2009). Menumbuhkembangkan Daya dan Disposisi Matematis Siswa Sekolah Menengah Atas Melalui Pembelajaran Investigasi. Vol III No.2 Juli 2009

Tandililing, E. (2011). Peningkatan Pemahaman dan Komunikasi Matematis serta Kemandirian Belajar Siswa Sekolah Menengah Atas melalui Strategi PQ4R dan Bacaan Refutation Text. Disertasi SPs UPI: tidak diterbitkan.

Trianto. (2007). Model-Model Pembelajaran Inovatif Berorientasi Konstruktivistik. Jakarta: Prestasi Pustaka

Wahyudin. (2008). Pembelajaran dan Model-model Pembelajaran. Bandung: UPI Press.

Wahyuni, A. E. (2010). Peningkatan Kemampuan Komunikasi dan koneksi Matematis Siswa SMP Melalui Pembelajaran Berbasis Masalah. Tesis UPI Bandung: tidak diterbitkan.

(48)

75

Wardani, S. (2008). Pembelajaran Inquiry Model Silver Untuk Mengembangkan Kreativitas dan Kemampuan Pemecahan Masalah Matematik siswa SMA. Disertasi SPS UPI Bandung: Tidak Dipublikasikan

Wena, M. (2011). Strategi Pembelajaran Inovatif Kontemporer. Jakarta: Bumi Aksara

Yamin, M. (2004). Strategi Pembelajaran Berbasis Kompetensi. Jakarta: Gaung Persada Press.

Yuniarti. Y. (2007). Meningkatkan Kemampuan Penalaran dan Komunikasi Matematis Siswa Sekolah Menengah Pertama Melalui Pembelajaran dengan Pendekatan Inkuiri. Tesis SPs UPI: tidak diterbitkan.