xvi DAFTAR ISI
halaman
HALAMAN JUDUL i
HALAMAN PERSEMBAHAN ii
LEMBAR PERSETUJUAN PEMBIMBING iii
RIWAYAT HIDUP iv
PERNYATAAN ix
KATA PENGANTAR x
ABSTRAK xiv
ABSTRACT xv
DAFTAR ISI xvi
DAFTAR TABEL xx
DAFTAR DIAGRAM xxii
DAFTAR LAMPIRAN xxiii
BAB I PENDAHULUAN 1
A. Latar Belakang Masalah 1
B. Rumusan Masalah 17
C. Tujuan Penelitian 19
D. Manfaat Penelitian 20
E. Peristilahan 21
F. Hipotesis Penelitian 23
BAB II KAJIAN PUSTAKA 25
A. Kemampuan Pemecahan Masalah Matematis 25
B. Kemampuan Komunikasi Matematis 34
C. Keyakinan terhadap Pembelajaran Matematika 40
D. Perkuliahan Berbasis Masalah 45
1. Pengertian 45
2. Landasan Teoritis 46
3. Pembelajaran Konvensional versus PBL 48
4. Implementasi PBL 50
E. Perkuliahan Kolaboratif 54
1. Pengertian 54
xvii
3. Kooperatif versus kolaboratif 59
F. Strategi Perkuliahan Kolaboratif Berbasis Masalah 61
BAB III METODE PENELITIAN 64
A. Disain Penelitian 64
B. Subyek Penelitian 66
C. Mata Kuliah Matematika Diskret 67
D. Pengembangan Instrumen 68
1. Tes Kemampuan Pemecahan Masalah Matematis dan Kemampuan Komunikasi Matematis
69
2. Skala Keyakinan (Belief) terhadap Pembelajaran Matematika
76
3. Panduan Wawancara 78
4. Lembar Observasi 78
E. Alat dan Bahan Ajar 79
F. Prosedur Pelaksanaan Penelitian 81
G. Teknik Analisis Data 83
BAB IV HASIL PENELITIAN DAN PEMBAHASAN 85
A. Hasil Penelitian 85
1. Pengaruh Strategi Perkuliahan dan Jenis Program 85
a. Deskripsi Data 85
b. Pengujian Hipotesis 88
2. Perbandingan Kemampuan Pemecahan Masalah Matematis
100
a. Mahasiswa Kelas Kontrol dan Kelas Eksperimen 100 b. Mahasiswa Program Reguler dan Program Non
Reguler
102
3. Perbandingan Peningkatan Kemampuan Komunikasi Matematis
104
a. Mahasiswa Kelas Kontrol dan Kelas Eksperimen 104 b. Mahasiswa Program Reguler dan Program Non
Reguler
106
4. Perbandingan Peningkatan Keyakinan terhadap Pembelajaran Matematika
xviii a. Mahasiswa Kelas Kontrol dan Kelas Eksperimen 107 b. Mahasiswa Program Reguler dan Program Non
Reguler
1. Pengaruh Strategi Perkuliahan dan Jenis Program 129 2. Kemampuan Pemecahan Masalah Matematis
Mahasiswa: Kolaboratif versus Konvensional
133
3. Kemampuan Pemecahan Masalah Matematis Mahasiswa: Program Reguler versus Program Non Reguler Program Reguler versus Program Non Reguler
143
Pembelajaran Matematika: Program Reguler versus Program Non Reguler
150
8. Interaksi antar Faktor terhadap Kemampuan Pemecahan Masalah Matematis
150
9. Interaksi antar Faktor terhadap Peningkatan Kemampuan Komunikasi Matematis
151
10. Interaksi antar Faktor terhadap Peningkatan Keyakinan terhadap Pembelajaran Matematika
152
11. Keunggulan dan kelemahan Strategi Kolaboratif Berbasis Masalah
153
C. Keterbatasan 155
BAB V KESIMPULAN, IMPLIKASI, DAN REKOMENDASI 157
xix
B. Implikasi 160
C. Rekomendasi 161
DAFTAR PUSTAKA 165
xx DAFTAR TABEL
halaman
Tabel 3.1 Rancangan Penelitian 65
Tabel 3.2 Subyek Penelitian 67
Tabel 3.3 Kriteria Tingkat Validitas 72
Tabel 3.4 Kriteria Tingkat Reliabilitas 73
Tabel 3.5 Kriteria Tingkat Kesukaran 74
Tabel 3.6 Kriteria Daya Pembeda 75
Tabel 3.7 Ringkasan Analisis Butir Soal Uji Coba 76 Tabel 4.1 Statistik Data Kemampuan Pemecahan Masalah
Matematis, Peningkatan Kemampuan Komunikasi Matematis, dan Peningkatan Keyakinan terhadap Pembelajaran Matematika
85
Tabel 4.2 Uji Levene untuk Kesamaan Ragam Galat 90
Tabel 4.3 Hasil Uji MANOVA 94
Tabel 4.4 Hasil Pengujian Pengaruh Faktor terhadap Masing-Masing Respon
96
Tabel 4.5 Statistik Data Kemampuan Pemecahan Masalah Matematis (KPM) Mahasiswa Kelas Kontrol (K) dan Kelas Eksperimen (E)
100
Tabel 4.6 Rata-rata Skor Kemampuan Pemecahan Masalah
Matematis Per Nomor Soal untuk Kelas Kontrol (K) dan Kelas Eksperimen (E)
101
Tabel 4.7 Statistik Data Kemampuan Pemecahan Masalah
Matematis (KPM) Mahasiswa Program Reguler (R) dan Non Reguler (NR)
102
Tabel 4.8 Rata-rata Skor Kemampuan Pemecahan Masalah Per Nomor Soal Mahasiswa Kelas Reguler (R) dan Non Reguler (NR)
103
Tabel 4.9 Statistik Kemampuan Komunikasi Matematis
Mahasiswa Kelas Kontrol (K) dan Kelas Eksperimen (E)
104
xxi (PKM) Mahasiswa Program Reguler (R) dan Non Reguler
(NR)
Tabel 4.11 Rata-rata Skor Peningkatan Keyakinan terhadap
Pembelajaran Matematika Mahasiswa Kelas Kontrol (K) dan Kelas Eksperimen (E) Per Butir Pernyataan
108
Tabel 4.12 Persentase Respon Keyakinan terhadap Pembelajaran Matematika Mahasiswa Kelas Kontrol
111
Tabel 4.13 Persentase Respon Keyakinan terhadap Pembelajaran Matematika Mahasiswa Kelas Eksperimen
112
Tabel 4.14 Statistik Peningkatan Keyakinan terhadap Pembelajaran Matematika untuk Mahasiswa Kelas Kontrol (K) dan Kelas Eksperimen (E)
114
Tabel 4.15 Statistik Peningkatan Keyakinan terhadap Pembelajaran Matematika (PKY) untuk Mahasiswa Program Reguler (R) dan Non regular (NR)
116
Tabel 4.16 Skor Hasil Pengamatan Observer di Kelas Kontrol (K) dan Kelas Eksperimen (E)
119
Tabel 4.17 Ringkasan Hasil Wawancara 120
xxii DAFTAR DIAGRAM
halaman
Diagram 4.1a Histogram Data Kemampuan Pemecahan Masalah Matematis
87 Diagram 4.1b Histogram Data Peningkatan Kemampuan
Komunikasi Matematis
87 Diagram 4.1c Histogram Data Peningkatan Keyakinan terhadap
Pembelajaran Matematika
87 Diagram 4.2a Plot Kuantil
λ
2Data Kelompok Reguler-Kontrol 91 Diagram 4.2b Plot Kuantil
λ
2Data Kelompok Reguler-Eksperimen 91 Diagram 4.2c Plot Kuantil
λ
2Data Kelompok Non Reguler-Kontrol
92 Diagram 4.2d Plot Kuantil
λ
2Data Kelompok Non Reguler-Eksperimen
xxiii DAFTAR LAMPIRAN
halaman
Lampiran 1 Statistik Hasil Ujian Nasional Tahun 2007 Mata Pelajaran Matematika
171
Lampiran 2a Kisi-Kisi Soal Tes Kemampuan Pemecahan Masalah Matematis dan Kemampuan Komunikasi Matematis
172
Lampiran 2b Kisi-Kisi Skala Keyakinan terhadap Pembelajaran Matematika
173
Lampiran 3 Lembar Pertimbangan Validator 174
Lampiran 4a Draf Soal 176
Lampiran 4b Soal Ujian Matematika Diskret 178 Lampiran 5a Kunci Jawaban dan Pedoman Penyekoran Tes
Kemampuan Komunikasi Matematis (Tertulis)
180
Lampiran 5b Kunci Jawaban dan Pedoman Penyekoran Tes Kemampuan Pemecahan Masalah Matematis
187
Lampiran 6 Data Uji Coba Instrumen Tes 196
Lampiran 7 Instrumen Belief 197
Lampiran 8 Skor Skala Belief 200
Lampiran 9 Panduan Wawancara dan Lembar Pertanyaan 201
Lampiran 10 Lembar Pengamatan Observer 203
Lampiran 11 Bahan Ajar Konvensional 205
Lampiran 12 Bahan Ajar Berbasis Masalah 256
Lampiran 13a Rencana Perkuliahan Kelas Kontrol 314 Lampiran 13b Rencana Perkuliahan Kelas Eksperimen 317
Lampiran 14 Data Penelitian 321
BAB I PENDAHULUAN A. Latar Belakang Masalah
Salah satu masalah dalam pendidikan matematika di Indonesia yang tidak mudah mengatasinya adalah prestasi belajar matematika sebagian siswa yang belum memuaskan beberapa pihak, seperti orang tua siswa dan guru. Dengan memperhatikan data nilai ujian nasional Matematika tahun ajaran 2008/2009 dari http://puspendik.info/un09/laphasil/index.html sebagaimana terdapat pada Lampiran 1, dapat diketahui bahwa persentase siswa yang mendapat nilai matematika kurang dari 6 relatif besar, baik untuk SMA/MA, SMP/MTs, maupun SMK. Baik untuk SMA dan MA IPA, SMA dan MA IPS, SMA dan MA Bahasa, SMA dan MA Agama, SMP dan MTs, maupun SMK, persentase siswa yang mendapat nilai matematika kurang dari 6 semuanya lebih dari 10%. Bahkan, untuk SMA dan MA Bahasa persentase tersebut mencapai 28,01%. Meskipun di setiap jenjang sekolah selalu ada siswa yang mendapat nilai matematika 10, namun adanya siswa yang mendapat nilai 0, bahkan di SMP ada sebanyak 543 siswa (0,02%), cukup memprihatinkan juga.
Dalam skala internasional, meskipun pada akhir-akhir ini sudah mulai terdengar prestasi gemilang putra-putri Indonesia pada forum-forum olimpiade matematika di tingkat internasional, namun hasil penelitian The Trends in Mathematics and Science Study (TIMSS) pada tahun 2007 yang menunjukkan bahwa kemampuan siswa Indonesia kelas 8 dalam matematika ada pada urutan ke-34 dari 49 negara peserta (TIMSS & PIRLS International Study Center, 2007), merupakan informasi yang sangat bermanfaat untuk mengevaluasi diri. Ada masalah apa dengan pendidikan matematika di Indonesia?
Banyak faktor yang diduga sebagai penyebab hasil belajar siswa dalam matematika yang belum memuaskan. Salah satu di antara faktor tersebut adalah masih banyak siswa yang menganggap matematika sebagai pelajaran yang sangat sulit. Akibatnya, sebagian besar siswa tidak cukup antusias dan percaya diri dalam belajar matematika.
Bagaimanapun, para guru matematika di sekolah memegang peranan penting dalam memberikan gambaran yang wajar tentang pelajaran matematika kepada siswa. Kunci dari gambaran siswa yang dibangun melalui interaksinya dengan para guru ini terletak pada apa yang telah guru-guru berikan kepada siswa selama ini, dan bagaimana para guru mengomunikasikannya. Pengalaman belajar matematika seperti apa yang sudah didapatkan para siswa dalam kelasnya, dan bagaimana selama ini para guru matematika mengomunikasikan konsep, struktur, teorema, atau rumus matematis kepada para siswa, akan berpengaruh kepada anggapan mereka terhadap pelajaran matematika.
Selain gambaran pelajaran matematika yang sangat sulit, menurut Suryanto (2002) banyak siswa yang menganggap matematika sebagai pelajaran yang kurang tampak kegunaannya, kecuali untuk berhitung. Gambaran bahwa matematika kurang tampak kegunaannya, boleh jadi sebagai akibat kurangnya siswa mendapat pengalaman untuk belajar memecahkan masalah, khususnya masalah-masalah matematika yang berkaitan dengan dunia nyata. Oleh karena itu, pendekatan kontekstual (Contextual Teaching and Learning, disingkat CTL), akhir-akhir ini direkomendasikan para ahli pendidikan untuk diimplementasikan para guru di sekolah.
Pendekatan kontekstual adalah suatu pendekatan pembelajaran yang menekankan penggunaan masalah kontekstual. Pendekatan kontekstual ini merupakan konsep belajar yang membantu guru mengaitkan materi yang diajarkan dengan situasi dunia nyata siswa dan mendorong siswa membuat hubungan antara pengetahuan yang dimilikinya dengan penerapannya dalam kehidupan mereka sebagai anggota keluarga dan masyarakat (Depdiknas, 2002). Dengan konsep yang demikian, hasil pembelajaran diharapkan lebih bermakna bagi siswa.
sebagai fasilitator dan mediator yang membantu agar proses belajar siswa dalam rangka mengonstruksi pengetahuannya dapat berjalan dengan baik.
Karena pendekatan kontekstual menekankan penggunaan masalah kontekstual, maka kemampuan para guru matematika dalam pemecahan masalah (problem solving) matematika kontekstual haruslah di atas kemampuan siswa yang diajarnya. Untuk itu, seorang guru matematika selain dituntut untuk menguasai materi matematika dan cara mengomunikasikannya, juga dituntut untuk kreatif mencari atau membuat masalah yang kontekstual dan menguasai berbagai strategi untuk menyelesaikannya. Dengan demikian, mempunyai kemampuan komunikasi matematis dan kemampuan pemecahan masalah matematis sangatlah penting bagi seorang guru matematika.
Dengan alasan bahwa para guru matematikalah yang berperan dalam membangun gambaran siswa tentang pelajaran matematika, maka program pendidikan untuk calon guru matematika haruslah menaruh perhatian yang sangat serius terhadap pembekalan ketrampilan memecahkan masalah matematis, ketrampilan berkomunikasi secara matematis, dan pembentukan sikap positif terhadap matematika dan pembelajarannya, bagi para mahasiswanya. Pertanyaan yang kemudian muncul adalah: (1) Apakah setiap mahasiswa calon guru matematika di Indonesia sudah cukup mendapatkan pembekalan tersebut; dan (2) Apakah kemampuan pemecahan masalah matematis , kemampuan komunikasi matematis, dan keyakinan mahasiswa calon guru matematika selama ini sudah cukup memadai untuk menjadikan mereka nantinya guru matematika sesuai kebutuhan dan harapan siswa?
kurikulum yang ada dalam praktek-praktek perkuliahan di kelas-kelas, besar kemungkinan juga lebih beragam lagi. Dengan demikian menjadi tidak mudah untuk mengetahui kemampuan apa saja yang telah dibekalkan kepada mahasiswa calon guru matematika.
Secara teori, para mahasiswa calon guru matematika, khususnya calon guru matematika sekolah menengah, minimal sudah mendapatkan pengetahuan tentang pemecahan masalah matematis dan komunikasi matematis, misalnya dalam mata kuliah kependidikan matematika, seperti mata kuliah Strategi Belajar-Mengajar Matematika, atau mata kuliah Dasar-dasar Proses Pembelajaran Matematika. Namun, seringkali pada mata kuliah yang demikian ini mahasiswa lebih banyak mendapatkan teorinya saja, tanpa mempraktekkannya. Hal demikian inilah yang diduga menjadikan kemampuan pemecahan masalah matematis dan kemampuan komunikasi matematis para mahasiswa calon guru matematika selama ini dipandang masih lemah, masih belum cukup memadai untuk menjadikannya guru matematika yang efektif.
Indikasi lemahnya kemampuan pemecahan masalah matematis mahasiswa terlihat terutama pada pekerjaan ujian para mahasiswa, yaitu apabila mereka mendapatkan soal ujian yang agak berbeda dengan soal-soal yang ada di buku teks atau berbeda dengan soal ujian tahun-tahun sebelumnya, maka sebagian besar mahasiswa kesulitan untuk menyelesaikannya dengan segera. Indikasi lemahnya kemampuan komunikasi matematis mahasiswa, terutama tampak pada saat mahasiswa mengerjakan soal-soal pembuktian, atau ketika ujian lisan pada saat ujian skripsi. Pada umumnya mahasiswa kesulitan menjelaskan ide atau gagasannya, atau kesulitan memberikan alasan atau penjelasan untuk setiap langkah penyelesaian masalah yang dipilihnya.
Pendekatan pembelajaran atau perkuliahan berbasis masalah (Problem-based Learning, disingkat PBL), secara teori diduga kuat cukup menjanjikan kemungkinan untuk dapat meningkatkan kemampuan pemecahan masalah matematis dan kemampuan komunikasi matematis para mahasiswa calon guru matematika, karena mempunyai karakteristik: (1) Pembelajaran dipandu oleh masalah yang menantang; (2) Para mahasiswa bekerja dalam kelompok kecil; dan (3) Dosen mengambil peran sebagai “fasilitator” dalam perkuliahan. PBL menampilkan perkuliahan sebagai kegiatan pemecahan masalah bagi mahasiswa. Dalam rangka menyelesaikan masalah tersebut para mahasiswa akan belajar dalam kelompok kecil, saling mengajukan ide kreatif mereka, berdiskusi, dan berfikir secara kritis (Roh, 2003). Juga, mahasiswa-mahasiswa yang mengikuti perkuliahan dengan pendekatan PBL mempunyai kesempatan yang lebih besar untuk belajar proses matematika yang berkaitan dengan komunikasi, representasi, pemodelan, dan penalaran. Dibandingkan pendekatan pembelajaran tradisional, PBL membantu para mahasiswa dalam mengonstruksi pengetahuan dan ketrampilan penalaran (Tan, 2004).
kompetensi-kompetensi yang diperlukan untuk menjadi sukses, yaitu kemampuan untuk: (1) berfikir secara kritis dalam menganalisis serta menyelesaikan masalah dunia nyata yang kompleks; (2) menemukan, mengevaluasi, dan menggunakan sumber belajar yang sesuai; (3) bekerja secara kooperatif dalam tim atau kelompok kecil; (4) menunjukkan ketrampilan komunikasi lisan dan tulisan yang efektif; dan (5) menggunakan materi pengetahuan dan ketrampilan intelektual untuk menjadi pembelajar sepanjang hayat.
Melalui PBL para mahasiswa akan belajar berbagai ketrampilan, tidak hanya ketrampilan memecahkan masalah matematis, tetapi juga ketrampilan yang diperlukan untuk dapat mempunyai kemandirian dalam belajar, kebebasan menyaring informasi, belajar secara kolaboratif, dan berfikir reflektif, sebagaimana Tan (2004) menyebutkan bahwa, tujuan dari PBL mencakup “content learning, acquisition of process skills and problem-solving skills, and lifewide learning”. Istilah “lifewide learning” menunjukkan ketrampilan seperti self-directed learning, independent information mining, collaborative learning, dan reflective thinking.
kemampuan representasi multipel matematis mahasiswa lebih tinggi dibandingkan dengan mahasiswa yang diperlakukan dengan pembelajaran konvensional”. Dari dua hasil penelitian ini dapat disimpulkan bahwa PBL mempunyai keunggulan dibandingkan pendekatan pembelajaran yang konvensional, setidaknya dalam hal meningkatkan prestasi belajar dan kemampuan representasi multipel mahasiswa.
Meskipun PBL diyakini mempunyai sejumlah keunggulan jika dibandingkan dengan pembelajaran konvensional, namun berdasarkan studi pendahuluan yang peneliti lakukan terhadap para dosen di Jurusan Pendidikan Matematika FMIPA UNY yang telah mempraktekkan PBL, dijumpai juga beberapa kendala dalam pelaksanaan PBL. Kendala pertama, karena PBL mendasarkan kepada masalah yang menantang, yang dapat memandu para mahasiswa belajar konsep tertentu melalui masalah tersebut, maka pemilihan masalahnya tidaklah selalu mudah bagi masing-masing dosen. Kendala ke-dua, pada umumnya waktu yang digunakan untuk mempelajari materi tertentu relatif lebih lama. Dewanto (2007) bahkan mengatakan dengan PBL dibutuhkan waktu dua atau tiga kali lebih banyak dalam menyelesaikan materi tertentu, dibandingkan dengan pembelajaran yang konvensional. Kendala ke-tiga, kemampuan awal, tingkat dan kecepatan berfikir, dan aspek-aspek lain pada diri mahasiswa pada kelas yang heterogen, seringkali juga menjadi masalah tersendiri. Bagaimanapun, para dosen tidak dapat mengabaikan keheterogenan mahasiswa ini jika berharap dapat menjamin hak setiap mahasiswa untuk memperoleh pembelajaran yang bermakna.
kolaboratif adalah pembelajaran yang dilaksanakan dalam kelompok, namun tujuannya bukan untuk mencapai kesatuan yang didapat melalui kegiatan kelompok, namun, para siswa dalam kelompok didorong untuk menemukan beragam pendapat atau pemikiran yang dikeluarkan oleh tiap individu dalam kelompok. Pembelajaran tidak terjadi dalam kesatuan, namun pembelajaran merupakan hasil dari keragaman atau perbedaan.
Pada dasarnya pembelajaran kolaboratif merujuk pada suatu metode pembelajaran dengan siswa/mahasiswa dari tingkat performa yang berbeda (heterogen) bekerja bersama dalam suatu kelompok kecil. Setiap siswa/mahasiswa ikut bertanggung jawab terhadap pembelajaran siswa/mahasiswa yang lain, sehingga kesuksesan seorang siswa/mahasiswa diharapkan dapat membantu siswa atau mahasiswa lain untuk menjadi sukses. Gokhale (1995) menyebutkan bahwa “collaborative learning fosters development of critical thinking through discussion, clarification of ideas, and evaluation of other’s ideas”. Selain menjembatani keheterogenan, model perkuliahan kolaboratif juga memungkinkan mahasiswa untuk lebih serius belajar “sesuatu” dari kelompoknya, termasuk bagaimana menyelesaikan masalah yang diberikan oleh dosen.
guru matematika (mahasiswa Program Studi Pendidikan Matematika), namun fokus penelitiannya adalah pada peningkatan daya matematik mahasiswa secara keseluruhan. Penelitian Dewanto (2007) menggunakan subyek mahasiswa Program Studi Matematika, dan fokus penelitiannya adalah peningkatan kemampuan representasi multipel mahasiswa.
Dalam mengimplementasikan PBL, pembelajaran yang dilaksanakan pada penelitian Dewanto menggunakan model Floating Facilitator (Dewanto, 2007), yang diterapkan untuk kelas ukuran sedang (30-40 mahasiswa) dengan satu fasilitator, yaitu pengajar sendiri. Secara ringkas, dalam tiap pertemuan, tahapan PBL dalam penelitian Dewanto berlangsung dalam sesi-sesi sebagai berikut: (1) Memperkenalkan rencana pembelajaran pada setiap awal pertemuan; (2) Mahasiswa dalam kelompok selama 10-15 menit mendiskusikan masalah yang disajikan; (3) Di depan kelas, selama 10 menit setiap kelompok melaporkan apa isu yang paling penting dan apa yang mereka telah pelajari selama seminggu; (4) Pada saat diskusi dalam kelompok sekitar 30 menit, fasilitator memiliki kesempatan untuk memulai suatu diskusi dengan rasionalitas dari masing-masing kelompok; (5) Sisa waktu (dari total 150 menit) digunakan fasilitator untuk menyimpulkan apa yang dipelajari oleh mahasiswa, dan mahasiswa diminta membuat laporan lengkap untuk diserahkan dalam waktu satu minggu.
Dalam kedua penelitian tersebut, aspek kolaborasi yang dimaksudkan untuk menjembatani keheterogenan mahasiswa belum cukup mendapat penekanan, sehingga masih dimungkinkan adanya mahasiswa atau kelompok mahasiswa yang belum memperoleh pemahaman seperti yang diharapkan. Oleh karena itu, penelitian tentang peningkatan kemampuan pemecahan masalah matematis dan kemampuan komunikasi matematis mahasiswa calon guru matematika sekolah menengah melalui perkuliahan berbasis masalah (PBL) dengan model kolaboratif ini sangat penting untuk dilakukan. Gabungan antara pendekatan perkuliahan berbasis masalah dan model perkuliahan kolaboratif inilah yang selanjutnya disebut dengan strategi perkuliahan kolaboratif berbasis masalah.
Secara teoritis, penggabungan model perkuliahan kolaboratif dengan pendekatan perkuliahan berbasis masalah diduga kuat akan mampu meningkatkan kemampuan pemecahan masalah matematis dan kemampuan komunikasi matematis mahasiswa calon guru matematika. Namun, mengingat pada kenyataannya di kebanyakan LPTK negeri terdapat dua kelompok mahasiswa calon guru matematika jika ditinjau dari jalur mereka masuk menjadi mahasiswa, yaitu mereka yang menempuh pendidikan program reguler dan program non reguler, maka apakah peningkatan tersebut secara rata-rata relatif sama untuk kedua kelompok tersebut masih perlu dikaji secara empiris.
mahasiswa program non reguler adalah mereka yang tidak lolos seleksi PBU/SNMPTN. Bahkan, tidak hanya dari segi kemampuan akademik, tetapi dari segi motivasipun besar kemungkinan berbeda pula. Perbedaan dari segi kemampuan akademik dan motivasi kedua kelompok mahasiswa calon guru matematika ini ternyata berdampak pada suasana pembelajaran di kelas masing-masing.
Selain secara teoritis strategi perkuliahan kolaboratif berbasis masalah diduga besar kemungkinan akan mampu meningkatkan kemampuan pemecahan masalah matematis dan kemampuan komunikasi matematis mahasiswa, ada hal penting lain yang diharapkan dapat terjadi sebagai hasil tambahan dari implementasi strategi perkuliahan ini. Hal penting tersebut adalah meningkatnya keyakinan mahasiswa calon guru matematika terhadap pembelajaran matematika. Peningkatan keyakinan ini sangat penting jika dikaitkan dengan peran mereka nantinya dalam membangun keyakinan siswa terhadap matematika. Tanpa memiliki keyakinan yang positif terhadap materi yang akan diajarkan dan cara mengajarkannya, besar kemungkinan para calon guru matematika ini justru akan semakin menguatkan gambaran tentang matematika sebagai pelajaran yang sangat sulit bagi sebagian siswa. Bagaimanapun, keyakinan seseorang guru matematika terhadap matematika dan proses belajar mengajarnya akan berpengaruh terhadap apa yang akan dilakukannya dalam mengajar, sebagaimana Beswick (2006) menyatakan bahwa: “...that what teachers believe influences their teaching”. Juga Ernest (1989) menyatakan bahwa: “...the practice of teaching mathematics depends on a number of key elements, most notably the teacher’s mental contents or schemas, particularly the system of beliefs concerning mathematics and its teaching and learning”.
maka upaya untuk membangun belief yang positif terhadap pembelajaran matematika untuk mahasiswa calon guru matematika tentulah sangat penting untuk dilakukan.
Salah satu upaya yang dimaksudkan untuk meningkatkan belief mahasiswa calon guru matematika terhadap pembelajaran tersebut adalah melalui pemberian pengalaman belajar yang beragam dan sesuai paham konstruktivisme, yaitu melalui perkuliahan dengan strategi kolaboratif berbasis masalah. Peningkatan belief mahasiswa melalui strategi perkuliahan ini sangat mungkin terjadi karena mahasiswa akan memperoleh pengalaman tentang bagaimana belajar dan mengajarkan matematika secara konstruktif.
siswa-siswa akan belajar matematika dengan rasa senang, antusias, dan percaya diri, sehingga dapat mengoptimalkan potensi yang dimilikinya
Mengetahui apakah strategi perkuliahan kolaboratif berbasis masalah dapat meningkatkan secara signifikan kemampuan pemecahan masalah matematis, kemampuan komunikasi matematis, dan keyakinan mahasiswa terhadap pembelajaran matematika, jika dibandingkan pembelajaran konvensional, penting bagi para dosen dan pengelola Program Studi Pendidikan Matematika, sebagai bahan pertimbangan dalam melakukan upaya-upaya peningkatan kualitas pendidikan matematika di Indonesia pada khususnya. Tanpa adanya penelitian yang demikian, besar kemungkinan para guru atau dosen tidak mempunyai cukup data yang akurat untuk dijadikan rujukan dalam menerima atau menolak mempraktekkan strategi perkuliahan kolaboratif berbasis masalah, meskipun secara teori strategi tersebut mempunyai banyak keunggulan.
Mengetahui apakah peningkatan kemampuan pemecahan masalah matematis dan kemampuan komunikasi matematis itu sama ataukah tidak untuk mahasiswa program reguler dan non reguler sangat penting untuk dapat memberi bantuan yang tepat kepada setiap mahasiswa. Mengetahui apakah sebuah strategi perkuliahan kolaboratif berbasis masalah mampu meningkatkan keyakinan mahasiswa calon guru matematika terhadap pembelajaran matematika, penting untuk dijadikan bahan re-orentasi perkuliahan untuk mahasiswa calon guru, sedemikian hingga keyakinan yang semakin positif dapat ditumbuhkan selama mereka mengikuti pendidikan calon guru.
pembelajaran matematika ditumbuhkan kepada mahasiswa calon guru matematika, maka penelitian tentang cara-cara meningkatkan kemampuan pemecahan masalah matematis, kemampuan komunikasi matematis, dan keyakinan terhadap pembelajaran matematika mahasiswa calon guru matematika ini menjadi penting untuk dilakukan. Inilah urgensi penelitian tentang “Analisis Implementasi Strategi Perkuliahan Kolaboratif Berbasis Masalah dalam Mengembangkan Kemampuan Pemecahan Masalah Matematis, Kemampuan Komunikasi Matematis, dan Keyakinan terhadap Pembelajaran Matematika” ini dilakukan.
B. Rumusan Masalah
Berdasarkan latar belakang masalah sebagaimana diuraikan di atas, maka dalam penelitian ini masalah utamanya adalah: “Apakah strategi perkuliahan kolaboratif berbasis masalah untuk mahasiswa calon guru matematika lebih unggul dari strategi perkuliahan konvensional, dalam hal mengembangkan kemampuan pemecahan masalah matematis, kemampuan komunikasi matematis, dan keyakinan mahasiswa terhadap pembelajaran matematika?”
Secara lebih rinci, apa saja yang menjadi masalah dalam penelitian ini dirumuskan sebagai berikut:
1. Apakah terdapat pengaruh strategi perkuliahan, jenis program, dan gabungan strategi perkuliahan dan jenis program, terhadap kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan mahasiswa terhadap pembelajaran matematika?
3. Apakah kemampuan pemecahan masalah matematis mahasiswa program reguler lebih tinggi dibandingkan kemampuan mahasiswa program non reguler?
4. Apakah peningkatan kemampuan komunikasi matematis mahasiswa yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah lebih tinggi dibandingkan peningkatan kemampuan mereka yang mendapatkan perkuliahan secara konvensional?
5. Apakah peningkatan kemampuan komunikasi matematis mahasiswa program reguler lebih tinggi dibandingkan peningkatan kemampuan mahasiswa program non reguler?
6. Apakah peningkatan keyakinan terhadap pembelajaran matematika untuk mahasiswa yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah lebih tinggi dibandingkan peningkatan keyakinan mereka yang mendapatkan perkuliahan secara konvensional?
7. Apakah peningkatan keyakinan terhadap pembelajaran matematika untuk mahasiswa program reguler lebih tinggi dibandingkan peningkatan keyakinan mahasiswa program non reguler?
8. Apakah terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap kemampuan pemecahan masalah matematis mahasiswa calon guru matematika?
10.Apakah terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap peningkatan keyakinan mahasiswa calon guru matematika?
11.Keunggulan dan kelemahan apa yang ditemukan dalam implementasi strategi perkuliahan kolaboratif berbasis masalah dibandingkan dengan perkuliahan secara konvensional?
C. Tujuan Penelitian
Tujuan utama penelitian ini adalah untuk mengkaji atau menganalisis implementasi strategi perkuliahan kolaboratif berbasis masalah dalam mengembangkan kemampuan pemecahan masalah matematis, kemampuan komunikasi matematis, dan keyakinan terhadap pembelajaran matematika dari mahasiswa calon guru matematika.
Secara lebih rinci, penelitian ini bertujuan untuk:
1. Mengkaji apakah terdapat pengaruh strategi perkuliahan, jenis program, dan gabungan antara strategi perkuliahan dan jenis program, terhadap kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan terhadap pembelajaran matematika dari mahasiswa calon guru matematika.
2. Membandingkan kemampuan pemecahan masalah matematis dari mahasiswa yang mendapatkan perkuliahan dengan strategi kolaboratif berbasis masalah dan mereka yang mendapatkan perkuliahan secara konvensional.
3. Membandingkan kemampuan pemecahan masalah matematis mahasiswa program reguler dan mahasiswa program non reguler.
kolaboratif berbasis masalah dan mereka yang mendapatkan perkuliahan secara konvensional.
5. Membandingkan peningkatan kemampuan komunikasi matematis mahasiswa program reguler dan mahasiswa program non reguler.
6. Membandingkan peningkatan keyakinan terhadap pembelajaran matematika dari mahasiswa yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah dan mereka yang mendapatkan perkuliahan secara konvensional.
7. Membandingkan peningkatan keyakinan terhadap pembelajaran matematika dari mahasiswa program reguler dan mahasiswa program non reguler.
8. Mengkaji apakah terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap kemampuan pemecahan masalah matematis mahasiswa calon guru matematika.
9. Mengkaji apakah terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap peningkatan kemampuan komunikasi matematis mahasiswa calon guru matematika.
10.Mengkaji apakah terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap peningkatan keyakinan mahasiswa calon guru matematika terhadap pembelajaran matematika.
11.Mengidentifikasi dan mengkaji keunggulan dan kelemahan apa yang ditemukan dalam implementasi strategi perkuliahan kolaboratif berbasis masalah dibandingkan dengan perkuliahan secara konvensional.
D. Manfaat Penelitian
1. Mahasiswa calon guru matematika, sebagai pengetahuan yang berguna baginya dalam rangka meningkatkan kompetensinya untuk bekal menjadi guru matematika yang profesional di waktu yang akan datang.
2. Staf dosen dan pengelola Program Studi Pendidikan Matematika, sebagai bahan rujukan dalam melakukan upaya-upaya peningkatan kualitas mahasiswa calon guru matematika yang menjadi tanggungjawabnya. Lebih khusus, hasil penelitian ini juga diharapkan bermanfaat bagi staf dosen dan pengelola Program Studi Pendidikan Matematika, sebagai rujukan untuk mengembangkan strategi perkuliahan yang dimaksudkan untuk meningkatkan kemampuan pemecahan masalah, kemampuan komunikasi matematis, dan keyakinan mahasiswa terhadap pembelajaran matematika.
3. Dunia pendidikan matematika di perguruan tinggi, sebagai sumbangan terhadap pengetahuan tentang strategi perkuliahan bagi mahasiswa calon guru matematika.
E. Peristilahan
Dalam penelitian ini yang dimaksud dengan:
1. Kemampuan pemecahan masalah matematis adalah kemampuan seseorang dalam:
a. memahami masalah matematika,
b. memilih strategi untuk menyelesaikan masalah tersebut, c. menyelesaikan masalahnya, dan
d. memeriksa kembali penyelesaian yang didapatkannya.
b. menulis alasan atau penjelasan dari setiap argumen matematis yang digunakannya untuk menyelesaikan masalah matematika,
c. menggunakan istilah, tabel, diagram, notasi atau rumus matematis dengan tepat,
d. memeriksa atau mengevaluasi pikiran matematis orang lain.
3. Perkuliahan konvensional adalah perkuliahan yang dilaksanakan secara klasikal, dan kegiatannya didominasi kegiatan ceramah dari dosen, pemberian contoh-contoh, tanya jawab, dan latihan mengerjakan soal-soal.
4. Strategi perkuliahan kolaboratif berbasis masalah adalah suatu strategi perkuliahan dengan karakteristik:
a. Pembelajaran dipandu oleh masalah yang menantang,
b. Sebelum para mahasiswa belajar dalam kelompok, mereka diberi kesempatan untuk mengidentifikasi masalah yang diberikan oleh dosen dan merancang strategi penyelesaiannya beberapa saat secara mandiri, kemudian dipersilahkan belajar dalam kelompok (2 orang, atau 4 sampai 6 orang) untuk mengklarifikasi pemahaman mereka, mengkritisi ide/gagasan teman dalam kelompoknya, membuat konjektur, memilih strategi penyelesaian, dan menyelesaikan masalah yang diberikan, dengan cara saling bertanya dan beradu argumen,
c. Setelah belajar dalam kelompok, mahasiswa menyelesaikan masalah yang diberikan dosen secara individual,
e. Beberapa mahasiswa yang diberi kesempatan mempresentasikan penyelesaian masalahnya di depan kelas tidak dalam peran mewakili kelompok.
5. Belief (keyakinan) terhadap pembelajaran matematika adalah konstruk psikologis yang menekankan taraf penerimaan seseorang terhadap proposisi tentang karakteristik matematika dan karakteristik proses pembelajaran matematika yang baik. Proses pembelajaran matematika yang dimaksud meliputi aspek metode, pendekatan, model, media, dan teknik evaluasi.
F. Hipotesis Penelitian
Hipotesis utama dalam penelitian ini adalah: “Kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan terhadap pembelajaran matematika, dari mahasiswa calon guru matematika yang mendapatkan perkuliahan menggunakan strategi kolaboratif berbasis masalah lebih tinggi dibandingkan mereka yang mendapatkan perkuliahan secara konvensional”.
Secara lebih rinci, apa saja yang menjadi masalah dalam penelitian ini dirumuskan sebagai berikut:
1. Terdapat pengaruh strategi perkuliahan, jenis program, dan gabungan antara strategi perkuliahan dan jenis program, terhadap kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan mahasiswa terhadap pembelajaran matematika.
3. Kemampuan pemecahan masalah matematis mahasiswa program reguler lebih tinggi dibandingkan kemampuan mahasiswa program non reguler.
4. Peningkatan kemampuan komunikasi matematis mahasiswa yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah lebih tinggi dibandingkan peningkatan kemampuan mereka yang mendapatkan perkuliahan secara konvensional.
5. Peningkatan kemampuan komunikasi matematis mahasiswa program reguler lebih tinggi dibandingkan peningkatan kemampuan mahasiswa program non reguler.
6. Peningkatan keyakinan terhadap pembelajaran matematika untuk mahasiswa yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah lebih tinggi dibandingkan peningkatan keyakinan mereka yang mendapatkan perkuliahan secara konvensional.
7. Peningkatan keyakinan terhadap pembelajaran matematika untuk mahasiswa program reguler lebih tinggi dibandingkan peningkatan keyakinan mahasiswa program non reguler.
8. Terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap kemampuan pemecahan masalah matematis mahasiswa calon guru matematika.
9. Terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap peningkatan kemampuan komunikasi matematis mahasiswa calon guru matematika.
BAB III
METODE PENELITIAN A. Disain Penelitian
Jenis penelitian ini adalah eksperimen, dengan satu faktor perlakuan yang dikenakan pada subyek penelitian, yaitu pemberian perkuliahan dengan strategi tertentu (konvensional, atau kolaboratif berbasis masalah) dan satu faktor lingkungan yaitu jenis program yang ditempuh mahasiswa (reguler atau non reguler). Dalam hal menyangkut pemilihan jenis strategi perkuliahan yang dibandingkan, yaitu konvensional dan kolaboratif berbasis masalah, ditetapkan oleh peneliti dengan pertimbangan tertentu, walaupun banyak strategi pembelajaran yang lain. Dengan demikian faktor perlakuannya bersifat tetap (fixed). Namun, kelompok mana yang mendapatkan perlakuan tertentu dipilih secara acak.
Ada tiga variabel terikat atau respon yang diamati pada subyek penelitian, yaitu: (1) kemampuan pemecahan masalah matematis; (2) kemampuan komunikasi matematis; dan (3) keyakinan terhadap pembelajaran matematika. Ada tiga hipotesis utama dalam penelitian ini yang akan diuji, yaitu: (1) terdapat tidaknya pengaruh faktor strategi perkuliahan terhadap kemampuan pemecahan masalah, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan terhadap pembelajaran matematika; (2) terdapat tidaknya pengaruh faktor jenis program terhadap kemampuan pemecahan masalah, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan terhadap pembelajaran matematika; dan (3) terdapat tidaknya pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap kemampuan pemecahan masalah, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan terhadap pembelajaran matematika.
Karena terdapat satu faktor perlakuan yang terdiri dari dua taraf (konvensional dan kolaboratif berbasis masalah), dan ada satu faktor lingkungan yang terdiri dari dua taraf ( program reguler dan non reguler ) maka rancangan penelitiannya adalah faktorial 2 × 2 dengan 3 variabel terikat, dengan kategori Multivariate Two-Way Fixed Model with interaction (Johnson, R.A, and Wichern, D.W., 1998).
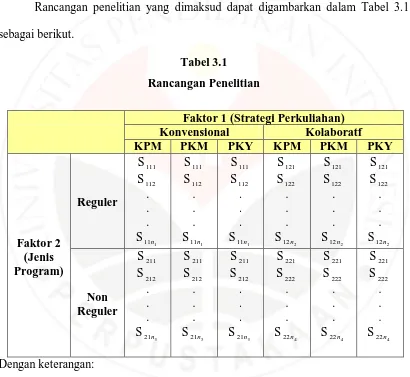
Rancangan penelitian yang dimaksud dapat digambarkan dalam Tabel 3.1 sebagai berikut.
KPM : Kemampuan Pemecahan Masalah Matematis PKM : Peningkatan Kemampuan Komunikasi Matematis
PKY : Peningkatan Keyakinan terhadap Pembelajaran Matematika S111 s.d. S
1
11n : Kelompok mahasiswa program reguler yang
S121 s.d. S 2
12n : Kelompok mahasiswa program reguler yang
mendapatkan perkuliahan dengan strategi Kolaboratif- Berbasis Masalah
S211 s.d. S21n3: Kelompok mahasiswa program non reguler yang
mendapatkan perkuliahan secara konvensional S221s.d. S
4
22n : Kelompok mahasiswa program non reguler yang
mendapatkan perkuliahan dengan strategi Kolaboratif- Berbasis Masalah
B. Subyek Penelitian
Subyek penelitian ini adalah mahasiswa semester 5 pada Program Studi Pendidikan Matematika, FMIPA UNY, yang sedang menempuh perkuliahan Matematika Diskret pada semester September – Desember 2009, sejumlah 83 mahasiswa yang berasal dari 1 kelas mahasiswa program reguler dan 1 kelas mahasiswa program non reguler.
Mahasiswa calon guru matematika program reguler di Program Studi Pendidikan Matematika, FMIPA UNY, adalah mereka yang diterima melalui jalur Penelusuran Bibit Unggul (PBU) dan Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN), sedangkan mahasiswa program non reguler adalah mereka yang diterima melalui jalur selain PBU dan SNMPTN. Mahasiswa program reguler dapat dianggap mempunyai kemampuan akademik yang lebih tinggi dibandingkan mahasiswa program non reguler karena pada kenyataan sebagian besar mahasiswa program non reguler adalah mereka yang tidak lolos seleksi PBU/SNMPTN.
kolaboratif berbasis masalah dan 1 kelompok yang lain mendapat perkuliahan dengan strategi konvensional. Kelas kontrol adalah kelas yang mendapatkan perkuliahan menggunakan strategi konvensional, sedangkan kelas eksperimen adalah kelas yang mendapatkan perkuliahan menggunakan strategi kolaboratif berbasis masalah.
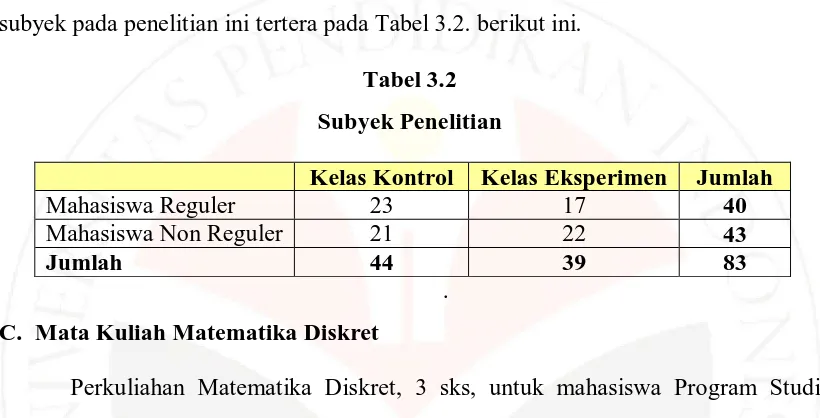
Banyak mahasiswa pada kelas kontrol dan kelas eksperimen yang menjadi subyek pada penelitian ini tertera pada Tabel 3.2. berikut ini.
Tabel 3.2 Subyek Penelitian
Kelas Kontrol Kelas Eksperimen Jumlah
Mahasiswa Reguler 23 17 40
Mahasiswa Non Reguler 21 22 43
Jumlah 44 39 83
. C. Mata Kuliah Matematika Diskret
Mata kuliah Matematika Diskret di Program Studi Pendidikan Matematika FMIPA UNY pada khususnya, dan di program studi matematika atau pendidikan matematika perguruan tinggi lain pada umumnya, sebagian besar berisi bahasan konsep-konsep, prinsip-prinsip, prosedur atau algoritma tentang dasar-dasar kaedah pencacahan, permutasi, kombinasi, relasi rekurensi, fungsi pembangkit, dan pengantar teori graf, serta penerapannya dalam berbagai bidang. Standar kompetensi lulusan mata kuliah Matematika Diskret adalah lulusan mampu: (1) Memahami konsep-konsep dasar, prinsip, prosedur/algoritma tentang dasar-dasar kaedah pencacahan, permutasi, kombinasi, relasi rekurensi, fungsi pembangkit, dan pengantar teori graf; (2) Menggunakan konsep-konsep dasar, prinsip, prosedur atau algoritma dalam matematika diskret untuk menganalisis dan memecahkan masalah-masalah yang terkait; dan (3) Memiliki sikap menghargai Matematika (khususnya Matematika Diskret) dan kegunaannya dalam kehidupan sehari-hari dan dalam bidang-bidang lain.
D. Pengembangan Instrumen
ketentuan pembuatan instrumen yang baik. Selain melalui pemberian tes dan skala pada subyek penelitian, digunakan juga wawancara dan observasi untuk memperkuat atau melengkapi data yang diperoleh dari tes dan skala.
Untuk mengukur peningkatan kemampuan komunikasi matematis mahasiswa setelah mengikuti perkuliahan selama satu semester, kepada subyek penelitian diberikan dua kali tes komunikasi matematis yang sama, yaitu di awal dan di akhir semester. Demikian juga untuk mengukur peningkatan keyakinan mahasiswa terhadap pembelajaran matematika, skala psikologi yang sama diberikan kepada subyek penelitian sebanyak dua kali. Skor peningkatan diperoleh dari skor tes ke-2 dikurangi skor tes-1.
Berdasarkan rumusan masalah, tujuan penelitian, dan pengkajian teori tentang kemampuan pemecahan masalah, kemampuan komunikasi matematis, dan keyakinan terhadap pembelajaran matematika, sebagaimana sudah disebutkan pada bagian Kajian Pustaka, dan dengan memperhatikan makna istilah (definisi operasional) untuk ketiga variabel tersebut, maka disusunlah kisi-kisi untuk dasar mengembangkan soal tes maupun skala yang diperlukan. Kisi-kisi yang dimaksud terdapat dalam Lampiran 2a dan 2b.
Berikut ini penjelasan rinci untuk pengembangan masing-masing instrumen dan pedoman penyekorannya.
1. Tes Kemampuan Pemecahan Masalah Matematis dan Kemampuan Komunikasi Matematis
kepentingan untuk dapat mengukur kemampuan pemecahan masalah dan kemampuan komunikasi matematis, yang tidak mungkin diukur dengan tes bentuk obyektif.
Sebelum soal tes uraian diujicobakan, soal telah divalidasi terlebih dahulu, baik validitas isi maupun validitas mukanya. Validasi dilakukan oleh 2 dosen Matematika Diskret, 1 dosen Kombinatorika, dan 1 dosen Pemodelan Matematika. Dari keempat validator ini, 3 diantaranya adalah dosen di FMIPA UNY, dan 1 dosen di UIN Sunan Kalijaga Yogyakarta. Dari keempat validator ini 3 orang diantaranya berpendidikan S2, dan 1 orang berpendidikan S3. Selain divalidasi oleh keempat validator tersebut, instrumen juga telah diperiksa dan mendapat masukan konstruktif dari para promotor.
Keempat validator memberikan penilaian yang sama, yaitu bahwa semua butir soal dianggap valid, baik untuk validitas isi maupun validitas muka. Meskipun keempat validator menganggap semua butir soal valid, namun mereka juga memberi beberapa masukan untuk perbaikan instrumen tersebut. Contoh masukan dari validator terdapat dalam Lampiran 3. Setelah instrumen direvisi berdasarkan masukan para validator dan para promotor, selanjutnya instrumen diujicobakan. Instrumen sebelum dan sesudah direvisi terdapat dalam Lampiran 4a dan 4b.
Berkaitan dengan validitas butir (item) soal, Suharsimi (2001) menyatakan bahwa sebuah item dikatakan valid apabila mempunyai dukungan yang besar terhadap skor total. Dengan kata lain dapat dikemukakan bahwa sebuah item memiliki validitas yang tinggi jika skor pada item mempunyai kesejajaran dengan skor total. Kesejajaran ini dapat diartikan sebagai korelasi, sehingga untuk mengetahui validitas butir soal dapat digunakan rumus korelasi produk momen dari Pearson sebagai berikut:
r = koefesien korelasi antara variabel X (skor butir) dengan Y (skor total) N = jumlah responden, X = skor butir, Y = skor total,
Untuk menguji signifikansi setiap koefisien korelasi yang diperoleh dilakukan pengujian hipotesis sebagai berikut:
i). H0: ρ = 0, yaitu tidak ada hubungan yang signifikan antara skor butir soal dengan skor total
= , dengan n = ukuran sampel dan r = koefisien korelasi
sampel (didapatkan dari data uji coba)
iv). Kriteria keputusannya adalah H0 ditolak jika nilai t > tα/2,n−2
Tabel 3.3
Menurut Ruseffendi (2005) reliabilitas instrumen atau alat evaluasi adalah ketetapan alat evaluasi dalam mengukur atau ketetapan responden dalam menjawab alat evaluasi itu. Suatu alat evaluasi dikatakan baik bila, antara lain, reliabilitasnya tinggi. Surapranata (2005) juga menyatakan bahwa reliabilitas dihubungkan dengan pengertian ketetapan suatu tes dalam pengukurannya. Reliabilitas dapat dinyatakan sebagai tingkat keajegan atau kemantapan hasil pengukuran terhadap hal yang sama. Karena tes yang diujicobakan dalam penelitian ini berbentuk soal uraian, sehingga jawaban mahasiswa bisa bervariasi, maka untuk menentukan reliabilitas butir tesnya digunakan rumus koefisien reliabilitas Cronbach-Alpha (Ruseffendi,
2005), yaitu: 2
DB adalah variansi skor seluruh soal menurut skor perorangan,
2
i
DB adalah variansi skor soal ke-i,
∑
2i
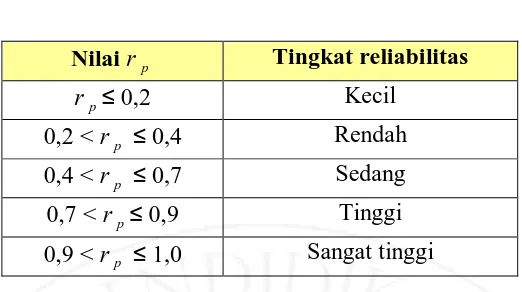
Tabel 3.4
Kriteria Tingkat Reliabilitas
Nilai rp Tingkat reliabilitas
rp≤ 0,2 Kecil
0,2 < rp ≤ 0,4 Rendah 0,4 < rp ≤ 0,7 Sedang 0,7 < rp≤ 0,9 Tinggi 0,9 < rp ≤ 1,0 Sangat tinggi
Terkait dengan tingkat kesukaran, menurut Suharsimi (2001), soal yang baik adalah soal yang tidak terlalu mudah atau tidak terlalu sukar. Soal yang terlalu mudah tidak merangsang siswa untuk mempertinggi usaha memecahkannya. Sebaliknya, soal yang terlalu sukar akan menyebabkan siswa menjadi putus asa dan tidak mempunyai semangat untuk mencoba lagi karena di luar jangkauannya. Bilangan yang menunjukkan sukar atau mudahnya suatu soal disebut tingkat atau indeks kesukaran (difficulty index), diberi simbol P dari kata “proporsi”.
Masih menurut Suharsimi (2001), tingkat atau indeks kesukaran dihitung
dengan rumus: P = JS
B
, di mana P = indeks kesukaran, B = banyaknya siswa yang
menjawab soal itu dengan benar, JS = jumlah seluruh siswa peserta tes. Memodifikasi rumus tersebut untuk soal bentuk uraian, maka tingkat atau indeks kesukaran soal dapat dihitung dari proporsi (perbandingan) total skor yang dicapai seluruh siswa untuk nomor soal tersebut dibandingkan total skor maksimum yang mungkin. Dengan demikian nilai P dapat dihitung dari rumus: P =
JS B
, di mana P =
Klasifikasi yang digunakan untuk menentukan sukar tidaknya suatu soal, mengikuti Suharsimi (2001), dengan sedikit modifikasi dari peneliti, adalah sebagaimana terdapat dalam Tabel 3.5 berikut.
Tabel 3.5
Kriteria Tingkat Kesukaran
Nilai P Kategori
P ≤ 0,30 Sukar
0,30 < P ≤ 0,70 Sedang
P > 0,70 Mudah
Analisis atas daya pembeda soal diperlukan untuk mengetahui dapat tidaknya suatu soal membedakan kelompok dalam aspek yang diukur sesuai dengan perbedaan yang ada dalam kelompok itu. Indeks yang digunakan dalam membedakan antara peserta tes yang berkemampuan tinggi dengan peserta tes yang berkemampuan rendah adalah indeks daya pembeda (item discrimination). Indeks daya pembeda soal-soal ditetapkan dari selisih proporsi yang menjawab benar dari masing-masing kelompok (Surapranata, 2005).
Menurut Suharsimi (2001) soal yang baik adalah soal yang dapat dijawab benar oleh siswa-siswa yang pandai saja. Bagi suatu soal yang dapat dijawab benar oleh siswa pandai maupun siswatidak pandai, maka soal tersebut tidak baik karena tidak mempunyai daya pembeda. Demikan pula jika semua siswa, baik pandai maupuntidak pandai, tidak dapat menjawab soal tersebut dengan benar, maka soal tersebut juga tidak baik karena tidak mempunyai daya pembeda.
dari skor tertinggi ke skor terendah; (2) Misalkan 27% peserta tes urutan teratas disebut sebagai kelompok atas, dan 27% peserta tes urutan terbawah disebut sebagai kelompok bawah; (3) untuk setiap nomor soal, hitung total skor seluruh peserta kelompok atas (= BA) dan total skor seluruh peserta kelompok bawah (BB);
kemudian (4) untuk setiap nomor soal, hitung PA = A
Menurut Suherman (2003) kriteria yang digunakan untuk mengklasifikasikan daya pembeda dari butir soal terdapat dalam Tabel 3.6 berikut.
Tabel 3.6
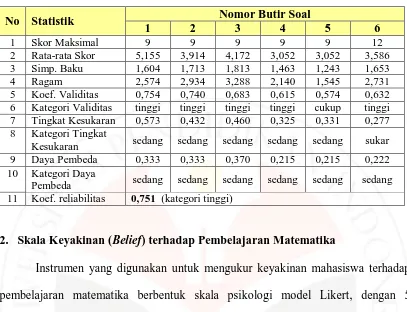
Tabel 3.7
Ringkasan Analisis Butir Soal Uji Coba
No Statistik Nomor Butir Soal
1 2 3 4 5 6
1 Skor Maksimal 9 9 9 9 9 12
2 Rata-rata Skor 5,155 3,914 4,172 3,052 3,052 3,586 3 Simp. Baku 1,604 1,713 1,813 1,463 1,243 1,653 4 Ragam 2,574 2,934 3,288 2,140 1,545 2,731 5 Koef. Validitas 0,754 0,740 0,683 0,615 0,574 0,632 6 Kategori Validitas tinggi tinggi tinggi tinggi cukup tinggi 7 Tingkat Kesukaran 0,573 0,432 0,460 0,325 0,331 0,277 8 Kategori Tingkat
Kesukaran sedang sedang sedang sedang sedang sukar 9 Daya Pembeda 0,333 0,333 0,370 0,215 0,215 0,222 10 Kategori Daya
Pembeda sedang sedang sedang sedang sedang sedang 11 Koef. reliabilitas 0,751 (kategori tinggi)
2. Skala Keyakinan (Belief) terhadap Pembelajaran Matematika
Instrumen yang digunakan untuk mengukur keyakinan mahasiswa terhadap pembelajaran matematika berbentuk skala psikologi model Likert, dengan 5 alternatif jawaban, yaitu sangat tidak setuju (STS), tidak setuju (TS), ragu-ragu atau tidak tahu (RR), setuju (S), dan sangat setuju (SS). Instrumen terdiri dari 28 butir pernyataan, yang mencakup 7 aspek, yaitu keyakinan terhadap matematika, metode mengajar matematika, pendekatan pembelajaran matematika, model pembelajaran matematika, penggunaan media pembelajaran matematika, teknik evaluasi pembelajaran matematika, dan belajar matematika. Instrumen terdiri dari 16 butir pernyataan negatif dan 12 butir pernyataan positif.
Oktober 2009, dikenakan pada mahasiswa dari kelas yang sama dengan ujicoba pertama, namun jumlah mahasiswa hanya 42 orang.
Hasil analisis terhadap data ujicoba pertama menunjukkan adanya satu butir pernyataan yang validitasnya tergolong sangat rendah, yaitu butir nomor 13 dengan koefisien validitas sebesar 0,19, dan tujuh butir dengan validitas tergolong rendah, yaitu mempunyai koefisien validitas antara 3,00 dan 4.00, yaitu butir nomor 6, 9, 16, 17, 20, 25, dan 28. Setelah dilakukan pencermatan ulang dan dikonsultasikan kepada promotor, butir-butir pernyataan pada nomor-nomor tersebut kemudian direvisi dalam hal struktur kalimatnya, dan instrumen diujicobakan kembali.
Hasil analisis terhadap data uji coba kedua menunjukkan bahwa butir pernyataan nomor 13 yaitu “Tidak ada suatu metode pembelajaran matematika tertentu yang cocok untuk semua topik” tergolong butir yang mempunyai validitas rendah, dengan koefisien validitas sebesar 0,29. Karena hanya 1 butir pernyataan yang tergolong mempunyai validitas rendah, sedang ke 26 butir yang lain tergolomg mempunyai validitas cukup, serta 1 butir mempunyai validitas tinggi, yaitu butir nomor 10 dengan pernyataan “Matematika akan selamanya menjadi pelajaran yang ditakuti kebanyakan siswa”, maka instrumen yang digunakan pada uji coba kedua ini digunakan dalam penelitian ini untuk mengukur keyakinan mahasiswa terhadap pembelajaran matematika. Instrumen yang dimaksud terdapat pada Lampiran 7.
dari setiap butir pernyataan dapat berbeda-beda. Hasil penyekoran selengkapnya terdapat dalam Lampiran 8.
3. Panduan Wawancara
Karena salah satu tujuan penelitian ini adalah mengidentifikasi keunggulan dan kelemahan apa yang ditemukan dalam implementasi strategi perkuliahan kolaboratif berbasis masalah dibandingkan dengan pembelajaran secara konvensional, maka sejumlah wawancara terhadap mahasiswa subyek penelitian perlu dilakukan untuk mendapatkan data yang diperlukan. Wawancara juga dimaksudkan untuk menggali lebih jauh tentang belief mahasiswa terhadap pembelajaran matematika.
Untuk keperluan wawancara ini telah dipilih secara acak 6 mahasiswa kelas kontrol dan 6 mahasiswa kelas eksperimen. Kepada para mahasiswa yang terpilih ini telah ditanyakan beberapa hal, seputar pelaksanaan perkuliahan. Pertanyaan difokuskan pada 3 hal, yaitu pendapat mereka tentang: (1) metode diskusi versus ceramah; (2) proses versus produk; dan (3) belajar sendiri versus belajar kelompok. Meskipun wawancara hanya dilakukan terhadap 12 mahasiswa, namun semua mahasiswa di akhir perkuliahan juga diminta menjawab secara tertulis pertanyaan-pertanyaan sebagaimana terdapat pada Lampiran 9.
4. Lembar Observasi
yang bersangkutan melaporkan hasil observasinya dalam bentuk isian lembar pengamatan sebagaimana terdapat dalam Lampiran 10.
Selain diobservasi seorang dosen, perkuliahan di kedua kelas juga direkam oleh seorang kameraman berpengalaman menggunakan kamera video. Tujuan perekaman pelaksanaan perkuliahan ini terutama untuk mendapatkan tambahan data yang diperlukan untuk membandingkan aktivitas mahasiswa di kelas kontrol dan kelas eksperimen. Baik untuk kelas kontrol maupun kelas eksperimen, perekaman dilakukan masing-masing sebanyak 5 kali.
E. Alat dan Bahan Ajar
Penelitian ini tidak menggunakan peralatan pembelajaran yang khusus. Buku teks yang digunakan adalah buku Discrete Mathematics and Its Applications, karangan Rosen, H. K., terbitan McGraw-Hill tahun 1999. Bahan ajar tambahan, berupa handout, diberikan baik pada kelas kontrol (perkuliahan konvensional) maupun kelas eksperimen (menggunakan strategi perkuliahan kolaboratif berbasis masalah). Handout disusun oleh peneliti, dimintakan masukan kepada teman dosen matematika diskret dan pembimbing, serta telah diujicobakan untuk mengetahui keterbacaannya.
Berangkat dari standar kompetensi dan kompetensi dasar yang sama untuk perkuliahan pada kelas kontrol maupun kelas eksperimen, maka perbedaan utama dalam bahan ajar yang konvensional dan yang berbasis masalah adalah pada struktur bahan ajar tersebut, dan pada perlakuan (treatment) terhadap penyajiannya, sedangkan cakupan maupun kedalaman, serta soal-soal latihan yang diberikan, relatif sama atau setara untuk keduanya.
perkuliahan; dan (2) kolaborasi yang kuat antar mahasiswa untuk “melampaui batas dan melompat”, maka bahan ajar yang dimaksud disusun dengan struktur yang khusus. Bahan ajar diawali dengan pemberian masalah yang menantang yang harus diselesaikan mahasiswa, kemudian didiskusikan dengan sesama teman mahasiswa (cukup diskusi dengan teman sebelahnya ataukah diskusi dalam kelompok tergantung pada tingkat kesukaran dan kandungan konsep/prinsip dari masalah tersebut) untuk mengklarifikasi pemahaman, dugaan, atau strategi untuk menyelesaikan masalah tersebut, kemudian ada sedikit arahan untuk menemukan dan membuat formalisasi pengertian, konsep, atau formulasi prinsip yang dimaksud, dan diakhiri dengan pemberian soal-soal latihan.
Karena secara teoritis kolaborasi antar mahasiswa akan muncul jika masalah yang diberikan cukup menantang mereka, maka masalah-masalah yang terdapat dalam bahan ajar yang berbasis masalah pada umumnya dipilih masalah-masalah yang tidak terlalu mudah (kecuali untuk pengertian, konsep, atau prinsip awal yang memang sangat sederhana), bahkan beberapa diantaranya dipilih yang tidak rutin, mempunyai struktur kategori cukup atau open-ended. Demikian juga pilihan untuk kata tanya yang digunakan, kebanyakan digunakan “mengapa demikian”, “apakah persamaan atau perbedaannya”, “bagaimana jika”, dan sebagainya, terutama dimaksudkan untuk lebih menantang mahasiswa agar berfikir lebih kritis dalam menyelesaikan masalah yang dimaksud.
konvensional maupun untuk yang berbasis masalah terdapat dalam Lampiran 11 (konvensional) dan Lampiran 12 (berbasis masalah).
F. Prosedur Pelaksanaan Penelitian
Penelitian ini dilaksanakan dengan prosedur sebagai berikut. 1. Tahap Persiapan
a. Menyusun rencana perkuliahan (Lampiran 13), instrumen penelitian dan bahan ajar, termasuk uji coba dan revisinya,
b. Membentuk kelas kontrol dan kelas eksperimen,
c. Melakukan pengontrolan terhadap faktor atau variabel yang diduga besar kemungkinan akan berpengaruh terhadap respon yang diamati. Faktor-faktor tersebut adalah dosen, waktu dan lama perkuliahan serta fasilitas. Oleh karena itu, kedua kelas mendapatkan dosen yang sama (peneliti), waktu perkuliahan yang relatif sama, lama perkuliahan yang sama, dan fasilitas yang relatif sama.
2. Tahap Pelaksanaan
a. Pemberian perlakuan kepada kedua kelas dilaksanakan selama satu semester penuh (enam belas minggu).
b. Perkuliahan diawali dengan penjelasan rencana perkuliahan, penyepakatan kontrak perkuliahan, dan pemberian tes untuk mengukur kemampuan komunikasi matematis mahasiswa. Tes diberikan pada tanggal 3 September 2009.
d. Kegiatan perkuliahan pada kelas kontrol pada dasarnya dilaksanakan secara konvensional. Sebagian besar perkuliahan didominasi oleh kegiatan ceramah dari dosen, pemberian contoh-contoh, dan latihan mengerjakan soal-soal. e. Kegiatan perkuliahan pada kelas eksperimen menggunakan strategi
perkuliahan kolaboratif berbasis masalah. Sebagian besar perkuliahan diawali dengan pemberian masalah. Masalah tersebut telah dipilih sedemikian hingga dapat memandu mahasiswa belajar konsep, pengertian, atau rumus tertentu. Setelah pemberian masalah, kegiatan dilanjutkan dengan pemberian kesempatan kepada mahasiswa untuk memahami permasalahan yang diberikan secara individual, dilanjutkan dengan pemberian kesempatan untuk berdiskusi dalam kelompok (kecil (2 – 3) orang, atau sedang(4 -6) orang) untuk mengolaborasikan pemikiran masing-masing, dan kemudian pemberian kesempatan kepada mahasiswa untuk merumuskan penyelesaian masalah yang diberikan secara individual. Sering, beberapa mahasiswa diminta untuk mempresentasikan penyelesaian dari masalah yang diberikan ke depan kelas, namun bukan sebagai wakil kelompok.
f. Selama perkuliahan, mahasiswa mendapat 2 kali instrumen non tes berupa skala psikologi untuk mengukur keyakinan mahasiswa terhadap pembelajaran matematika, yaitu pada tanggal 23 Oktober 2009 dan pada tanggal 23 Desember 2009.
h. Selama dan setelah proses perkuliahan, beberapa mahasiswa diwawancarai dengan tujuan untuk mendapatkan tambahan data yang diperlukan sesuai tujuan penelitian yang telah dirumuskan.
3. Tahap Analisis dan Pelaporan
a. Setelah data terkumpul, dilakukan analisis data, pembahasan, dan penarikan kesimpulan.
b. Sebelum disusun menjadi sebuah desertasi, draft laporan penelitian ini telah dikonsultasikan terlebih dahulu kepada para promotor/pembimbing untuk mendapat koreksi dan masukan.
G. Teknik Analisis Data
Untuk setiap subyek penelitian, telah dihitung skor kemampuan pemecahan masalah matematis, peningkatan skor kemampuan komunikasi matematis, dan peningkatan skor keyakinan terhadap pembelajaran matematika. Untuk menguji hipotesis digunakan program SPSS versi 17, khususnya untuk General Linear Model, pada bagian Multivariate.
Ada tiga macam pengujian hipotesis yang dilakukan secara serentak dengan menggunakan MANOVA 2 jalur, yaitu yang menyangkut pengaruh faktor pertama (strategi perkuliahan), faktor kedua (jenis program), dan interaksi kedua faktor tersebut, terhadap ketiga respon yang diamati, yaitu: (1) kemampuan pemecahan masalah; (2) kemampuan komunikasi matematis; dan (3) keyakinan terhadap pembelajaran matematika. Pengujian dilakukan pada taraf signifikansi 5%. Profile Plots untuk skor ketiga variabel terikat ditampilkan untuk melihat secara visual pola interaksi antar faktor yang terlibat dalam penelitian ini.
BAB V
KESIMPULAN, IMPLIKASI, DAN REKOMENDASI
A. Kesimpulan
Berdasarkan hasil pengujian hipotesis dan pembahasan di BAB IV, dengan menggunakan taraf signifikansi
α
= 0,05 dapat disimpulkan bahwa kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan terhadap pembelajaran matematika, dari mahasiswa calon guru matematika yang mendapatkan perkuliahan menggunakan strategi kolaboratif berbasis masalah dapat dianggap lebih tinggi dibandingkan mereka yang mendapatkan perkuliahan secara konvensional. Ini berarti bahwa strategi perkuliahan kolaboratif berbasis masalah untuk mahasiswa calon guru matematika lebih unggul dari strategi perkuliahan konvensional, dalam hal mengembangkan kemampuan pemecahan masalah matematis, kemampuan komunikasi matematis, dan keyakinan mahasiswa terhadap pembelajaran matematika.Secara lebih rinci, data penelitian ini juga mendukung kesimpulan bahwa: 1. a. Terdapat pengaruh strategi perkuliahan terhadap kemampuan pemecahan
masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan mahasiswa calon guru matematika terhadap pembelajaran matematika.
b. Terdapat pengaruh jenis program terhadap kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan mahasiswa calon guru matematika terhadap pembelajaran matematika.
c. Tidak terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program, terhadap kemampuan pemecahan masalah matematis, peningkatan kemampuan komunikasi matematis, dan peningkatan keyakinan mahasiswa calon guru matematika terhadap pembelajaran matematika.
2. Kemampuan pemecahan masalah matematis mahasiswa calon guru matematika yang mendapatkan perkuliahan dengan strategi kolaboratif berbasis masalah dapat dianggap lebih tinggi dibandingkan kemampuan mereka yang mendapatkan perkuliahan secara konvensional.
3. Kemampuan pemecahan masalah matematis mahasiswa calon guru matematika program reguler dapat dianggap lebih tinggi dibandingkan kemampuan mahasiswa program non reguler.
4. Peningkatan kemampuan komunikasi matematis mahasiswa calon guru matematika yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah dapat dianggap lebih tinggi dibandingkan peningkatan kemampuan mereka yang mendapatkan perkuliahan secara konvensional.
5. Peningkatan kemampuan komunikasi matematis mahasiswa calon guru matematika program reguler dapat dianggap lebih tinggi dibandingkan peningkatan kemampuan mahasiswa program non reguler.
6. Peningkatan keyakinan terhadap pembelajaran matematika untuk mahasiswa calon guru matematika yang mendapatkan perkuliahan dengan strategi perkuliahan kolaboratif berbasis masalah dapat dianggap lebih tinggi dibandingkan peningkatan keyakinan mereka yang mendapatkan perkuliahan secara konvensional.
7. Peningkatan keyakinan terhadap pembelajaran matematika untuk mahasiswa calon guru matematika program reguler dapat dianggap tidak lebih tinggi dibandingkan peningkatan keyakinan mahasiswa program non reguler.
8. Tidak terdapat pengaruh gabungan (interaksi) antara strategi perkuliahan dan jenis program terhadap kemampuan pemecahan masalah matematis mahasiswa calon guru matematika. Ini berarti bahwa kemampuan pemecahan masalah matematis mahasiswa kelas kolaboratif dapat dianggap lebih tinggi dibandingkan kemampuan mahasiswa kelas konvensional, baik untuk kelompok mahasiswa program reguler maupun non reguler, dengan selisih rata-rata kemampuan mahasiswa kelas kolaboratif dan kelas konvensional dapat dianggap hampir sama besarnya antara yang diperoleh mahasiswa program reguler dan non reguler.