1
PERBANDINGAN LUAS ANTARA SEGITIGA EXCENTRAL DENGAN SEGITIGA ASAL
Yulia Rahmi1*, Hasriati2, M. Natsir2
1
Mahasiswa Program S1 Matematika
2
Dosen JurusanMatematika
Fakultas Matematika dan Ilmu Pengetahuan Alam Univeritas Riau Kampus Bina Widya 28293 Indonesia
*[email protected] ABSTRACT
This paper discusses how to determine the length of excentral triangle sides through the relation of the excentral triangle sides and original triangle sides. Ratio between the excentral triangle area and original triangle area can be obtained by Heron formula. In addition, the paper also discusses how to obtain the comparison between the radius of incircle and radius of circumcirlcle of excentral triangle and original triangle.
Keywords: collinier, comparation of area, comparation of incircle radius,
comparationof circumcircle radius, excentral triangle.
ABSTRAK
Artikel ini membahas bagaimana menentukan panjang sisi segitiga excentral menggunakan hubungan antara sisi segitiga excentral dengan sisi segitiga asal dan perbandingan luas segitiga excentral dengan segitiga asal menggunakan formula Heron. Pembahasan ini dilanjutkan dengan menentukan perbandingan jari-jari lingkaran dalam segitiga excentral dengan segitiga asal dan perbandingan jari-jari lingkaran luar segitiga
excentral dengan segitiga asal.
Kata kunci : kolinieritas, perbandingan luas segitiga, perbandingan jari-jari
lingkaran dalam, perbandingan jari-jari lingkaran luar, segitiga excentral.
1. PENDAHULUAN
Suatu bidang datar yang memiliki tiga titik sudut dan tiga sisi, , , dan , disebut segitiga ( ). Suatu memiliki titik konkurensi yaitu incenter,
circumcenter, dan excenter yang masing-masing merupakan titik pusat dari lingkaran
dalam, lingkaran luar [1, h.503], dan lingkaran singgung luar suatu segitiga [2, h.24]. Pada terdapat tiga buah excenter sehingga terdapat tiga buah lingkaran singgung. Misalkan titik pusat masing-masing lingkaran singgung adalah , , dan , sehingga dengan menghubungkan ketiga titik pusat lingkaran tersebut dapat dibentuk
2
I
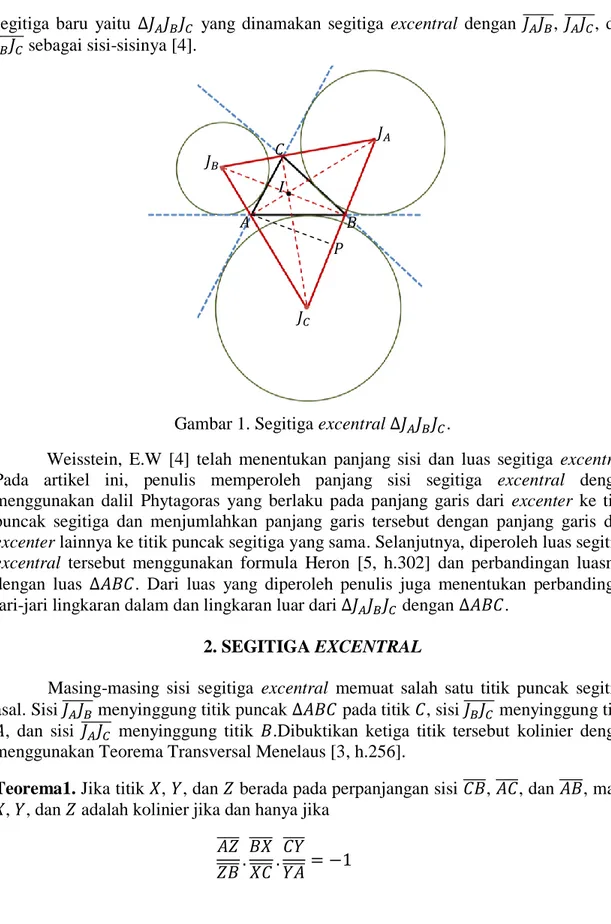
segitiga baru yaitu yang dinamakan segitiga excentral dengan , , dan sebagai sisi-sisinya [4].
Gambar 1. Segitiga excentral .
Weisstein, E.W [4] telah menentukan panjang sisi dan luas segitiga excentral. Pada artikel ini, penulis memperoleh panjang sisi segitiga excentral dengan menggunakan dalil Phytagoras yang berlaku pada panjang garis dari excenter ke titik puncak segitiga dan menjumlahkan panjang garis tersebut dengan panjang garis dari
excenter lainnya ke titik puncak segitiga yang sama. Selanjutnya, diperoleh luas segitiga excentral tersebut menggunakan formula Heron [5, h.302] dan perbandingan luasnya
dengan luas . Dari luas yang diperoleh penulis juga menentukan perbandingan jari-jari lingkaran dalam dan lingkaran luar dari dengan .
2. SEGITIGA EXCENTRAL
Masing-masing sisi segitiga excentral memuat salah satu titik puncak segitiga asal. Sisi menyinggung titik puncak pada titik , sisi menyinggung titik , dan sisi menyinggung titik .Dibuktikan ketiga titik tersebut kolinier dengan menggunakan Teorema Transversal Menelaus [3, h.256].
Teorema1. Jika titik , , dan berada pada perpanjangan sisi , , dan , maka , , dan adalah kolinier jika dan hanya jika
3
Gambar 2. Titik , , dan adalah kolinier.
Bukti : Perhatikan , tarik garis dari titik ke , misalkan pada titik , sedemikian hingga . Perhatikan dan
karena maka
dan
Dari kesebangunan Sd-Sd-Sd [1, h.336] maka , sehingga diperoleh perbandingan sisi
Seperti memperoleh persamaan , ditunjukkan sehingga diperoleh
Dari persamaan dan diperoleh
Jika segmen garis searah jarum jam akan bernilai positif dan jika berlawanan arah akan bernilai negatif maka , , dan , sehingga persamaan menjadi
Untuk membuktikan sebaliknya, misalkan hasil kali perbandingan ketiga garis bernilai maka ditunjukkan bahwa titik , , dan kolinier. Misalkan garis , dan
berpotongan dititik , sehingga titik , , dan kolinier dengan dengan menggabungkan persamaan Teorema Transversal Menelaus dengan persamaan diperoleh
Diperoleh , maka titik dan titik merupakan titik yang sama. Jadi titik , , dan adalah kolinier. ∎
Pada bagian ini, Teorema Transversal Menelaus digunakan untuk membuktikan bahwa titik , , dan kolinier, begitu juga dengan titik , , dan serta titik , , dan . Pada Gambar 1, perhatikan . Tarik garis sejajar dari titik ke , misalkan pada titik , sedemikian hingga . Selanjutnya, perhatikan dan ,
4 karena maka dan
Dari kesebangunan Sd-Sd-Sd, maka , sehingga diperoleh perbandingan sisi
Seperti memperoleh persamaan , ditunjukkan sehingga diperoleh
Dari persamaan dan diperoleh
Sehingga dapat disimpulkan bahwa titik , , dan adalah kolinier. Dengan cara yang sama maka titik , , dan serta titik , , dan adalah kolinier.
Kemudian, ditentukan panjang sisi-sisi , , , dan , menggunakan hubungan sisi segitiga excentral dengan segitiga asal.
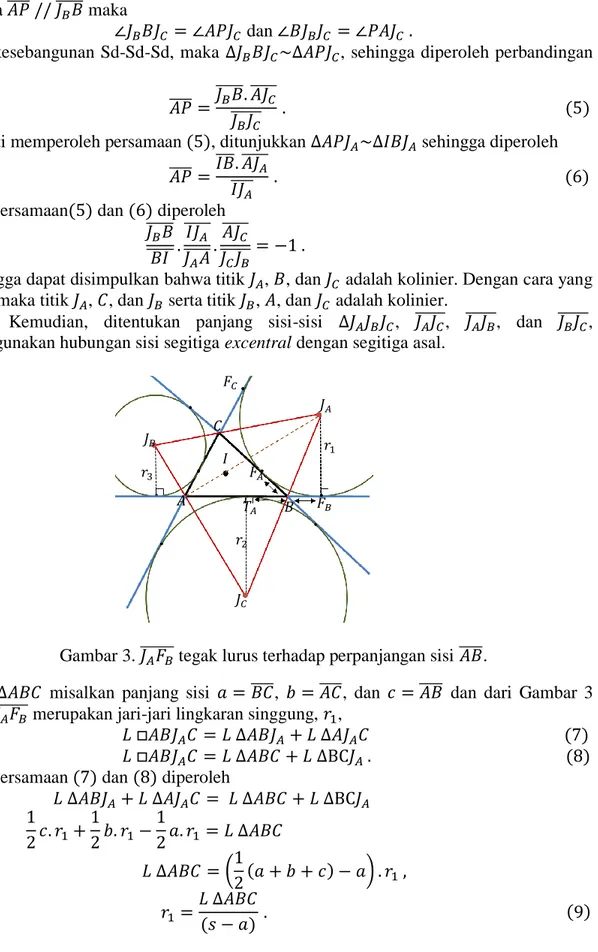
Gambar 3. tegak lurus terhadap perpanjangan sisi .
Pada misalkan panjang sisi , , dan dan dari Gambar 3 garis merupakan jari-jari lingkaran singgung, ,
Dari persamaan dan diperoleh
5
Kedua garis singgung lingkaran yang ditarik dari sebuah titik diluar lingkaran mempunyai panjang yang sama [1, h. 454], sehingga
dengan dan Dengan menjumlahkan persamaan dan diperoleh
Sehingga
Untuk mengetahui panjang dan , misalkan
maka
Dengan menggunakan persamaan diperoleh
karena nilai menyatakan nilai dan maka
dan
Dari persamaan dan , dapat ditentukan panjang menggunakan dalil Phytagoras, sehingga
Berdasarkan formula Heron, maka nilai luas pada berlaku
Dengan mensubstitusikan persamaan ke diperoleh
Dengan cara yang sama memperoleh persamaan , untuk panjang diperoleh
Dengan menjumlahkan persamaan dan maka
6 Dengan menggunakan cara yang sama memperoleh persamaan diperoleh
dan
3. PERBANDINGAN LUAS ANTARA SEGITIGA EXCENTRAL DENGAN SEGITIGA ASAL
Pada bagian 2 telah diperoleh panjang sisi-sisi segitiga excentral. Akan digunakan formula Heron untuk menentukan luas . Misalkan merupakan setengah keliling maka
Untuk memudahkan dalam menentukan luas , misalkan
dan Substitusikan persamaan , , dan ke maka diperoleh
Selanjutnya akan ditentukan luas dengan menggunakan formula Heron, sehingga diperoleh
Dengan mensubstitusikan persamanaan , , dan ke maka diperoleh
7
Substitusikan persamaan , , dan ke maka diperoleh
Dari persamaan , perbandingan luas antara segitiga excentral dengan segitiga asal dapat dinyatakan
4. PERBANDINGAN JARI-JARI LINGKARAN DALAM SEGITIGA
EXCENTRAL DENGAN SEGITIGA ASAL
Lingkaran yang berada didalam sebarang segitiga dan menyinggung ketiga sisi segitiga dinamakan lingkaran dalam segitiga. Titik pusatnya adalah incenter suatu segitiga. Pada bagian ini, akan ditentukan jari-jari lingkaran dalam segitiga asal dan segitiga excentral, dan kemudian akan ditentukan perbandingannya.
Gambar 4. Titik merupakan titik pusat lingkaran dalam .
Jarak titik terhadap ketiga sisi adalah sama yaitu , dan adalah jari-jari, . Selanjutnya teorema berikut memberikan persamaan umum jari-jari lingkaran dalam suatu segitiga.
Teorema 2. Diberikan sebarang dengan panjang sisi , , dan . Jari-jari lingkaran dalam dinotasikan dengan , dinyatakan dengan
8
Bukti : Pada Gambar 4, luas dapat dihitung dengan menjumlahkan luas dari , , dan .
karena , substitusikan ke persamaan maka diperoleh
∎ Pada dengan panjang sisi , , dan dan jari-jari lingkaran dalam dinotasikan dengan maka dengan menggunakan cara yang sama dalam menentukan jari-jari lingkaran dalam , diperoleh
Gambar 5. merupakan jari-jari lingkaran dalam .
Akan ditentukan hubungan antara jari-jari lingkaran dalam dengan . Substitusikan persamaan ke maka diperoleh
karena , maka
Dari persamaan , perbandingan jari-jari lingkaran dalam antara segitiga excentral dengan segitiga asal dapat dinyatakan
9
5. PERBANDINGAN JARI-JARI LINGKARAN LUAR SEGITIGA
EXCENTRAL DENGAN SEGITIGA ASAL
Suatu lingkaran yang melalui ketiga titik sudut suatu segitiga dinamakan sebagai lingkaran luar segitiga. Titik pusatnya adalah circumcenter suatu segitiga.
Gambar 6. Lingkaran luar dengan circumcenter .
Teorema berikut memberikan persamaan umum jari-jari lingkaran luar suatu segitiga, Teorema 3. Diberikan sebarang dengan panjang sisi , , dan . Jari-jari lingkaran luar yang dinotasikan dengan dan dinyatakan dengan
Bukti : Pada Gambar 6, misalkan tegak lurus terhadap dan merupakan garis yang melalui titik pusat , sehingga . Jika titik dan dihubungkan, maka karena menghadap busur setengah lingkaran sehingga
karena dan menghadap busur maka
. Dari kesebangunan Sd-Sd, diperoleh
dan diperoleh perbandingan sisi
karena maka maka
∎ Dengan menggunakan cara yang sama dalam menentukan jari-jari lingkaran luar , maka pada dengan panjang sisi-sisinya , , dan , jari-jari lingkaran luarnya adalah
10
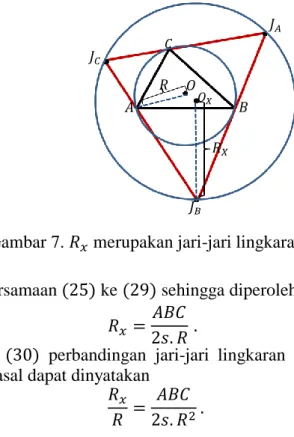
Gambar 7. merupakan jari-jari lingkaran luar . Substitusikan persamaan ke sehingga diperoleh
Dari persamaan perbandingan jari-jari lingkaran luar antara segitiga excentral dengan segitiga asal dapat dinyatakan
6. KESIMPULAN
Semakin besar nilai sisi-sisi segitiga asal maka nilai sisi-sisi segitiga excentral akan semakin lebih besar. Sehingga luas segitiga excentral lebih besar dibanding segitiga asal. Sama halnya dengan lingkaran dalam dan lingkaran luar segitiga excentral dan segitiga asal, dengan menentukan jari-jari lingkaran segitiga tersebut diperoleh bahwa segitiga excentral akan memiliki jari-jari yang lebih besar dibanding jari-jari lingkaran dalam dan lingkaran luar segitiga asal.
DAFTAR PUSTAKA
[1] Down Jr., F.L.1964. Geometry. Addison-Wesley Publishing Company, INC., Reading.
[2] Godfray, C & Siddons, A.W. 1908. Modern Geometry. Cambridge University Press, London.
[3] Mashadi. 2012. Geometri. Pusbangdik. Universitas Riau. Pekanbaru.
[4] Weisstein, E.W. 2013. Excentral Triangle. Math World. http://mathworld. wolfram.com/ExcentralTriangle.html, 18 November 2013. pk.08.05.
[5] Yiu, P. 2003. Recreational Mathematics.1119 hal.http://math.fau.edu/yiu/ RecreationalMathematics.2003.pdf, 20 Desember 2013. pk. 10.50.