BAB 2
TINJAUAN PUSTAKA
2.1 Definisi Citra
Citra adalah suatu representasi (gambaran), kemiripan, atau imitasi dari suatu objek.
Citra sebagai keluaran suatu sistem perekaman data dapat bersifat optik berupa foto,
bersifat sinyal-sinyal video seperti gambar pada monitor televisi, atau bersifat digital
yang dapat langsung disimpan pada media penyimpanan (Sutoyo, et al. 2009).
Menurut arti secara harfiah citra (image) adalah gambar pada bidang dua dimensi. Ditinjau dari sudut pandang matematis, citra merupakan fungsi menerus
(continue) dari intensitas cahaya pada bidang dua dimensi. Sumber cahaya menerangi objek, objek memantulkan kembali sebagian dari berkasi cahaya. Pantulan cahaya ini
ditangkap oleh alat-alat optik, seperti mata pada manusia, kamera, pemindai
(scanner), dan lain-lain sehingga bayangan objek dalam bentuk citra dapat terekam. Citra sebagai output dari suatu sistem perekaman data dapat bersifat:
1. Optik, berupa foto,
2. Analog berupa sinyal video, seperti gambar pada monitor televisi,
3. Digital yang dapat langsung disimpan pada suatu pita magnetic.
Citra dapat dikelompokkan menjadi dua bagian yaitu citra diam (still image) dan citra bergerak (moving image). Citra diam adalah citra tunggal yang tidak bergerak. Sedangkan citra bergerak adalah rangkaian citra diam yang ditampilkan secara
beruntun (sekuensial) sehingga memberi kesan pada mata sebagai gambar yang
bergerak. Setiap citra didalam rangkaian itu disebut frame. Gambar-gambar yang tampak pada film layar lebar atau televisi pada hakikatnya terdiri dari ratusan sampai
2.2 Citra Digital
Citra digital adalah citra yang dapat diolah oleh komput er. Citra digital disebut juga
citra diskrit di mana citra tersebut dihasilkan melalui proses digitalisasi terhadap citra kontinu. Citra tersebut dikatakan sebagai citra digital karena bentuk representasinya
yang berupa bilangan (numbers). Oleh komputer akan dikenal dalam urutan ‘0’ dan
‘1’.
Ada beberapa format citra digital, antara lain: BMP, PNG, JPG, GIF dan
sebagainya. Masing-masing format mempunyai perbedaan satu dengan yang lain
terutama pada header file. Namun ada beberapa yang mempunyai kesamaan, yaitu penggunaan palette untuk penentuan warna piksel. Sebagai studi kasus dalam tugas akhir ini akan digunakan format citra *.gif yang dikeluarkan oleh Microsoft.
2.3 GIF
Graphics Interchange Format atau yang sering disingkat GIF adalah sebuah format
berkas citra yang diperkenalkan pada tahun 1987 oleh CompuServe untuk menggantikan
format RLE yang hanya mampu menampilkan gambar dengan warna hitam dan putih
saja. GIF adalah salah satu format berkas citra yang paling sering ditemui di dunia digital.
Hal ini terjadi karena format ini berukuran relatif kecil. Sebagai contoh untuk citra yang
sama, berkas dengan format GIF dapat berukuran lebih kecil jika dibandingkan dengan
format JPG. Hal ini disebabkan karena file GIF hanya menggunakan 256 palet warna.
Sehingga tentunya ukuran file akan lebih kecil. Namun 256 palet warna tersebut tidak
mutlak hanya 256 warna tertentu. Warna tersebut dapat dipilih dari 24-bit palet warna
RGB atau dapat disimpulkan bahwa berkas dengan format GIF akan membuang palet
warna yang tidak diperlukan dan mengambil hanya 256 palet warna yang diperlukan.
(Putra,D. 2010)
Format gambar GIF memiliki dua versi, yaitu GIF87a dan GIF89a. GIF87a adalah
versi pertama dari format GIF yang berupa gambar statis. CompuServe kemudian
memperkenalkan versi lanjutan, yaitu GIF89a. GIF89a dapat menampilkan gambar
dinamis (animasi) dan latar belakang transparan.
Format GIF juga memiliki kekurangan. Format ini jarang sekali digunakan untuk
citra fotografi karena hanya dapat menampung 256 buah warna sementara citra fotografi
biasanya menggunakan lebih dari 256 warna. Jika citra fotografi direpresentasikan dalam
2.4 Kompresi Citra
Kompresi citra merupakan proses untuk mereduksi atau mengurangi ukuran suatu data
untuk menghasilkan representasi digital yang padat atau mampat namun tetap mewakili kuantitas informasi yang terkandung pada data tersebut (Putra, 2010).
Pemampatan citra atau kompresi bertujuan untuk meminimalkan kebutuhan
memori dalam merepresentasikan citra digital dengan mengurangi duplikasi data di
dalam citra sehingga memori yang dibutuhkan menjadi lebih sedikit daripada
representasi citra semula.
2.4.1 Teknik Kompresi Citra
Ada dua teknik yang dapat dilakukan dalam melakukan kompresi citra yaitu:
1. Lossless Compression
Lossless Compression merupakan kompresi citra di mana hasil dekompresi dari citra terkompresi sama dengan citra aslinya, tidak ada informasi yang hilang. Akan tetapi
rasio kompresi dengan metode ini umumnya sangat rendah. Banyak aplikasi yang
memerlukan kompresi tanpa cacat atau berkehilangan seperti aplikasi radiografi, hasil
diagnosis medis, satelit, dll (Sutoyo, et al. 2009).
2. Lossy Compression
Lossy Compression adalah kompressi citra di mana hasil dekompresi dari citra yang terkompresi tidak sama dengan citra aslinya karena ada informasi yanghilang, tetapi
masih dapat ditolerir oleh persepsi mata. Mata tidak dapat membedakan perubahan
kecil pada gambar. Metode ini menghasilkan ratio kompresi yang lebih tinggi dari metode lossless. Contoh dari algoritma lossless adalah Color Reduction, Chroma Subsampling, dan Transform Coding (Sutoyo, et al. 2009).
2.4.2 Kriteria Kompresi Citra
Dalam kompresi citra biasanya kriteria yang digunakan untuk mengukur pemampatan
citra adalah:
1. Waktu kompresi dan waktu dekompresi
Proses kompresi merupakan proses mengkodekan citra (encode) sehingga diperoleh
disimpan dalam file dengan format tertentu. Sedangkan proses dekompresi adalah
proses untuk menguraikan citra yang dimampatkan untuk dikembalikan lagi
(decoding) menjadi citra yang tidak mampat (mengembalikan ke bentuk semula). Algoritma pemampatan yang baik adalah algoritma yang membutuhkan waktu untuk
kompresi dan dekompresi paling sedikit (paling cepat). Gambar 2.1 merupakan
gambar mengenai proses kompresi dan dekompresi citra (Sutoyo, et al. 2009).
Gambar 2.1 Alur Kompresi Citra
2. Kebutuhan memori
Suatu metode kompresi yang mampu mengompresi file citra menjadi file yang
berukuran paling minimal adalah metode kompresi yang baik. Dimana memori yang
dibutuhkan untuk menyimpan hasil kompresi berkurang secara berarti. Akan tetapi
biasanya semakin besar persentase pemampatan, semakin kecil memori yang
diperlukan sehingga kualitas citra makin berkurang. Sebaliknya semakin kecil
persentase yang dimampatkan, semakin bagus kualitas hasil pemampatan tersebut
(Sutoyo, et al. 2009).
3. Kualitas pemampatan
Metode kompresi yang baik adalah metode yang dapat mengembalikan citra hasil
kompresi menjadi citra semula tanpa kehilangan informasi apapun. Walaupun ada
informasi yang hilang akibat pemampatan, sebaiknya hal tersebut ditekan seminimal
mungkin. Semakin berkualitas hasil pemampatan, semakin besar memori yang
dibutuhkan, sebaliknya semakin jelek kualitas pemampatan, semakin kecil kebutuhan
memori yang harus disediakan (Sutoyo, et al. 2009).
2.4.3 Pengukuran kinerja kompresi citra
Pada suatu teknik yang digunakan dalam proses kompresi data terdapat beberapa
faktor atau variabel yang biasa digunakan untuk mengukur kualitas dari suatu teknik
1. Ratio of Compression (Rc)
Ratio of Compression (Rc) adalah perbandingan antara ukuran data sebelum
dikompresi dengan ukuran data setelah dikompresi.
Rc
=
���������������������������
��������������������������� R
Misalkan didapat sebuah nilai Ratio of Compression sebesar 2.75. Itu berarti besar data sebelum kompresi adalah 2.75 kali lipat dari besar data setelah dikompresi.
2. Compression Ratio (CR Compression Ratio (C
)
R) adalah persentasi besar data yang telah dikompresi yang didapat dari hasil perbandingan antara ukuran data setelah dikompresi dengan ukuran
data sebelum dikompresi.(Salomon & Motta, 2010)
C
R=
���������������������������
���������������������������R
x 100 %
Misalkan didapat sebuah nilai Compression Ratio sebesar 35%. Itu berarti setelah dikompresi ukuran data adalah 35% dari data sebelum dikompresi.
3. Space Savings (SS)
Space saving (penghematan ruang) didefinisikan sebagai pengurangan dalam ukuran
relatif terhadap ukuran uncompressed.
SS = 1 – CR
4. Waktu Kompresi dan Dekompresi
Waktu kompresi dan dekompresi adalah waktu yang dibutuhkan oleh sebuah sistem
untuk melakukan proses kompresi dan dekompresi dari mulaipembacaan data hingga
2.5 Kompleksitas Algoritma
Algoritma merupakan salah satu cabang ilmu komputer yang membahas prosedur
penyelesaian suatu permasalahan. Dalam beberapa konteks, algoritma merupakan spesifikasi urutan langkah untuk melakukan pekerjaan tertentu. Algoritma adalah
prosedur komputasi yang terdefenisi dengan baik yang menggunakan beberapa nilai
sebagai masukan dan menghasilkan beberapa nilai sebagai masukan dan
menghasilkan beberapa nilai yang disebut keluaran. (Munir R, 2007).
Adanya algoritma yang baik maka komputer bisa menyelesaikan perhitungan
dengan cepat dan benar. Sebaliknya jika algoritma kurang baik maka penyelesaian
lambat dan bahkan tidak didapat solusi yang diharapkan. Baik buruknya sebuah
algoritma dapat dibuktikan dari kompleksitas waktu yang digunakan.
Dua hal penting untuk mengukur efektivitas suatu algoritma yaitu
kompleksitas ruang (keadaan) dan kompleksitas waktu. Kompleksitas ruang berkaitan
dengan sistem memori yang dibutuhkan dalam eksekusi program. Kompleksitas waktu
dari algoritma berisi ekspresi bilangan dan jumlah langkah yang dibutuhkan sebagai
fungsi dari ukuran permasalahan. Analisa asimtotik menghasilkan notasi Ο (Big O) dan dua notasi untuk komputer sain yaitu ϴ
Kinerja algoritma dibuktikan dengan menjumlahkan bilangan bulat dari
masing-masing operasi ketika algoritma di jalankan. Kinerja sebuah algoritma
dievaluasi sebagai fungsi ukuran masukan n dan konstanta modulo pengali yang digunakan. Pada penelitian ini kompleksitas yang digunakan adalah Big(Ο).
(Big Theta) dan Ω (Big Omega) .
2.5.1 Big-O (O)
2.5.2 Big Omega(Ω)
Ω(g(n)) merupakan himpunan semua fungsi dengan tingkat pertumbuhan lebih besar atau sama dengan g(n) (hingga beberapa konstanta, sampai n ke tak terhingga).
Sebuah fungsi t(n) dikatakan bagian dari Ω(g(n)), dilambangkan dengan t(n) Є Ω(g(n)), jika t(n) batas bawahnya adalah beberapa konstanta positif dari g(n) untuk semua n besar. Terdapat konstanta c positif dan beberapa bilangan bulat non-negatif n0 seperti t(n) ≥ cg(n), (untuk setiap n ≥ n0). (Levitin A, 2011)
2.5.3 Big Theta (θ)
θ (g(n)) adalah himpunan semua fungsi yang memiliki tingkat pertumbuhan yang sama dengan g(n) (hingga beberapa konstanta, sampai n ke tak terhingga). Sebuah fungsi t(n) dikatakan bagian dari θ (g(n)), dilambangkan dengan t(n) Є θ (g(n)), jika t(n) batas atas dan bawahnya adalah beberapa konstanta positif g(n) untuk semua n yang besar, yaitu jika ada beberapa konstanta positif c1 dan c2 serta beberapa bilangan
bulat non-negatif n0 seperti c2g(n) ≤ t(n) ≤ c1g(n) untuk semua n ≥ n0. (Levitin A,
2011)
2.6 Algoritma Elias Delta Code
Elias Delta Code merupakan satu dari tiga Elias Code yang dipelopori oleh Peter Elias. Jika pada Elias Gamma Code, Peter Elias menambahkan panjang pada unary (α) makanya pada Elias Delta Code ditambahkan pada binary (β). Elias Delta Code
juga digunakan untuk melakukan pengkodean pada bilangan bulat positip, namun sedikit lebih kompleks daripada Elias Gamma Code. Adapun aturan untuk mengkodekan sebuah bilangan dengan menggunakan Elias Delta Code adalah sebagai berikut :
1. Tuliskan n dalam bilangan biner (binary). Bit yang paling kiri (paling signifikan) akan menjadi 1.
3. Kurangi 1 dari perhitungan langkah ke-2 dan tambahkan jumlah nol ke kode.
Ketika langkah-langkah ini diterapkan pada integer ke-17, hasilnya adalah : 17 =
100012 (lima bit). Hapus angka 1 yang paling kiri dan tambahkan 5 = 1012 sehingga
hasilnya 101|0001. Tiga bit sudah ditambahkan, kemudian tambahkan 2 nol untuk mendapatkan kode delta 00|101|0001.
Selain dengan langkah-langkah pengkodean di atas, pengkodean Elias Delta juga
dapat dilakukan dengan menggunakan kode Elias Gamma. Berikut adalah
langkah-langkahnya:
1. Tentukan bilangan bulat N yang terbesar sehingga 2N≥ n < 2N+1 dan tuliskan n =
2N
2. Lakukan pengkodean N + 1 dengan Elias Gamma Code.
+ L. Perhatikan bahwa L merupakan bilangan bulat N yang paling besar.
3. Tambahkan nilai biner dari L, sebagai integer dari N-bit pada hasil dari langkah kedua.
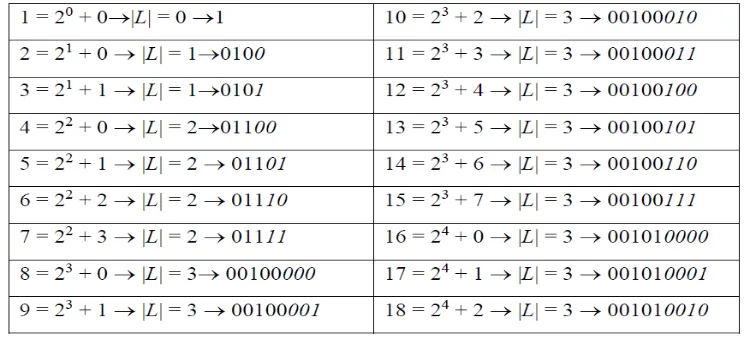
Ketika langkah-langkah ini diterapkan pada n = 17, hasilnya adalah : 17 = 2N + L = 24
+ 1. Kode gamma dari N + 1 = 5 adalah 00101, dan tambahkan L = 0001 sehingga
hasilnya adalah 00101|0001.
Tabel Elias Delta Codes yang menunjukkan 18 kode Elias Delta Codes dapat dilihat
pada tabel 2.1 di bawah ini.
Untuk melakukan decode dengan Elias Delta Code, berikut adalah
langkah-langkahnya:
1. Baca bit dari kode sampai proses decode dengan Elias Gamma Code dapat dilakukan. Proses ini dapat dilakukan dengan beberapa langkah berikut ini:
a. Hitung jumlah nol terdepan dari kode tersebut lalu gantikan perhitungan
tersebut dengan C.
b. Periksa bit bagian kiri 2C + 1 (C nol, diikuti dengan 1, lalu diikuti dengan bit C selebihnya). Ini merupakan decode Elias Gamma CodeM + 1.
2. Baca bit M berikutnya. Sebut ini sebagai L. 3. Bilangan bulat yang di decode adalah 2M + L.
Pada kasus dimana n = 17, kode deltanya adalah 001010001. Lewati dua nol, sehingga
C = 2. Nilai bit paling kiri dari 2C + 1 = 5 adalah 00101 = 5, jadi M + 1 = 5.
Pembacaan akan dilakukan berikutnya pada M = 4 bit 0001, dan diakhirnya dengan
nilai decode 2M + L = 24 + 1 = 17.
2.7 Algoritma Levenstein
Kode yang sedikit diketahui untuk bilangan bulat non-negatif ini digagas pada tahun
1968 oleh Vladimir Levenshtein. Baik encoding dan decoding adalah proses multi langkah (Salomon, 2007).
Levenstein Code untuk nol adalah 0 tunggal. Untuk kode angka positif n, berikut
adalah langkah encode-nya:
1. Set angka pertama dari C dengan 1. Letakkan kode-sejauh-ini pada string kosong. 2. Ambil nilai biner dari n tanpa angka 1 di awal dan tambahkan pada kode
sejauh-ini.
3. Nyatakan M sebagai jumlah bit yang ditambahkan pada tahap 2.
4. Jika M ≠ 0, tambahkan C dengan 1 dan lakukan langkah 2 kembali, tetapi dengan nilai M, bukan n.
5. Jika M = 0, tambahkan 1 diikuti dengan 0 pada C ke kode-sejauh-ini dan berhenti. Untuk contoh kasus, kita anggap n = 18. Nilai biner dari 18 adalah 10010, kita
ambil 0010 dan tambahkan dibelakang 1. Tambahkan 1 pada kode, kemudian
nilai 00,tambahkan di belakang penambahan tadi. Ulangi langkah tersebut sampai
kita dapati nilai M = 0, kemudian tambahkan 10. Sehingga 18 pada kode
Levenstein adalah 11110|0|00|0010. Berikut Levenstein Code yang menunjukkan 18 kode Levenstein Code dapat dilihat pada tabel 2.2 di bawah ini.
Tabel 2.2 Tabel Kode Levenstein (Salomon, 2007)
Decoding dilakukan sebagai berikut:
1. Set C dengan jumlah berturut-turut angka1 sebelum angka 0 yang pertama. 2. Jika C = 0, nilai di-decode adalah nol, berhenti.
3. Set N = 1, dan ulangi langkah 4 (C-1) kali.
4. Baca N bit, tambahkan 1, dan tetapkan hasil bitstring ke N (dengan demikian menghapus nilai sebelumnya dari N).
String ditugaskan untuk N dalam iterasi terakhir adalah nilai decode-nya. Sebagai contoh kita ambil kode Levenstein 11110|0|00|0010. Decoder pertama menghitung jumlah 1 sebelum 0 dan menemukan bahwa ada 4 iterasi. Kemudian baca
0 dan tambahkan awalan 1 menjadi 10. Decode 10 dan menemukan bahwa jumlah bit dalam representasi biner dari panjang codeword sama dengan 2. Kemudian baca 00 dan tambahkan awalan 1 menjadi 100. Artinya bahwa panjang representasi biner sama
2.8 Penelitian Terkait
Berikut ini beberapa penelitian yang terkait dengan algoritma Elias Delta Code dan
Levenstein :
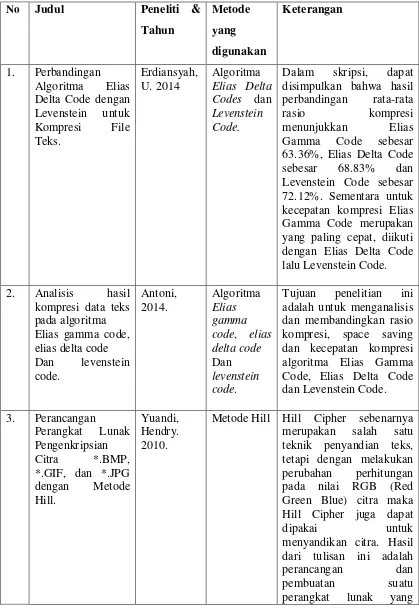
Tabel 2.3 Tabel Penelitian Terkait
No Judul Peneliti &
Tahun 63.36%, Elias Delta Code sebesar 68.83% dan Levenstein Code sebesar 72.12%. Sementara untuk kecepatan kompresi Elias Gamma Code merupakan yang paling cepat, diikuti dengan Elias Delta Code lalu Levenstein Code. Code, Elias Delta Code dan Levenstein Code.
Metode Hill Hill Cipher sebenarnya merupakan salah satu teknik penyandian teks, tetapi dengan melakukan perubahan perhitungan pada nilai RGB (Red Green Blue) citra maka Hill Cipher juga dapat
dipakai untuk menyandikan citra. Hasil
dari tulisan ini adalah
perancangan dan
dapat melakukan penyandian citra dengan
Hill Cipher.
4. Analisis
Perbandingan File Berformat PNG, GIF dan TIFF Pada Kompresi Citra Digital
menggunakan Metode Fraktal.
Rialni, Nova. 2015.
Metode Fraktal