Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR TABEL ix
DAFTAR GAMBAR x
DAFTAR LAMPIRAN xi
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Rumusan Masalah 5
1.3 Tujuan Penelitian 5
1.4 Manfaat Penelitian 6
BAB 2 TINJAUAN PUSTAKA 7
2.1 Penalaran dalam Pembelajaran Matematika 7
2.2 Pembuktian Deduktif formal dalam Matematika 8
2.3 Tahapan Berpikir Geometri Menurut Van Hiele 13
2.4 Penalaran Deduktif dalam Geometri 16
2.5 Jenis-Jenis Permasalahan yang Sesuai untuk Permasalahan
da-lam Pembuktian Secara Deduktif 19
2.7 Tujuan Pembelajaran Matematika Secara Deduksi 23
BAB 3 METODOLOGI PENELITIAN 25
3.1 Tahapan Penelitian 25
3.2 Metode Penelitian 28
3.3 Desain Penelitian 28
3.4 Lokasi Penelitian 28
3.5 Populasi dan Sample Penelitian 29
3.6 Model Analisis 29
3.7 Kemampuan Penalaran Matematika 29
3.8 Indikator Pemecahan Masalah 33
3.9 Proses Pembuktian Pemecahan Masalah Geometri 34
3.10 Konten Pengetahuan Geometri dalam Pemecahan Masalah 36
3.11 Keterampilan Pemecahan Masalah Umum 39
3.12 Implikasi Pengajaran Geometri Melalui Pembuktian Deduktif Formal Melalui Aspek Penilaian Test Kemampuan Penalaran
Matematika (KPM) 42
3.13 Gambaran Umum Hasil Tes Siswa 45
3.13.1 Uji hipotesis 48
BAB 4 KESIMPULAN DAN SARAN 55
4.1 Kesimpulan 55
4.2 Saran 57
Nomor Judul Halaman
3.1 Variabel-variabel pada penelitian 46
3.2 Nilai koefisient persamaan liner berganda 46
3.3 Nilai kontribusi tiap variable 48
3.4 Uji F 48
DAFTAR GAMBAR
Nomor Judul Halaman
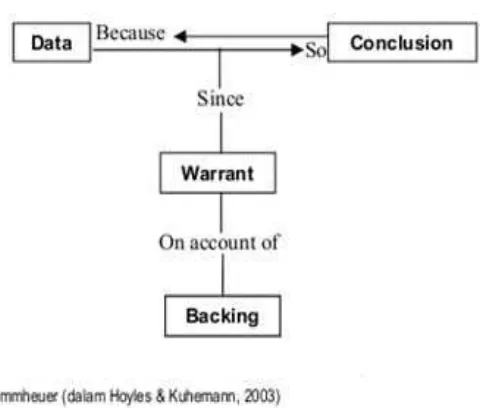
2.1 Skematik untuk mengalalisis argumentasi 11
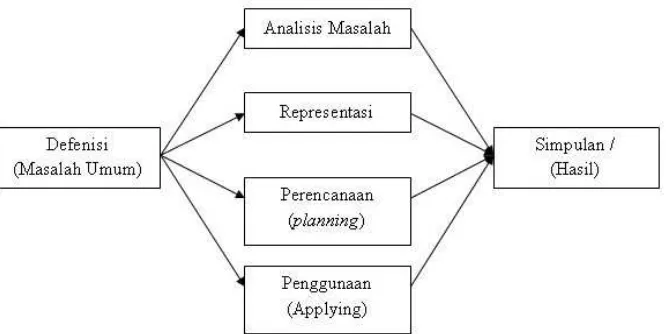
2.2 Skema penalaran deduktif 12
2.3 Dua garis sejajar dipotong garis lain 16
2.4 Dua garis sejajar dan dipotong dua garis lain 17
2.5 Diagram penalaran deduktif tentang jumlah besar sudut dalam segitiga
1800
18
3.1 Skema tahap I 25
3.2 Skema tahap II 27
4.1 Diagram penalaran deduktif tentang jumlah besar sudut dalam segitiga 180o
56
4.2 Segi 4 64
4.3 Segitiga siku-siku 64
4.4 Segitiga siku-siku 65
4.5 Setengah lingkaran 66
4.6 Segitiga sama siku 67
4.7 Jajarangenjang 68
Nomor Judul Halaman
1. Data penelitian nilai siswa 61
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Pandangan para pakar pendidikan matematika terhadap perlunya pembuk-tian matematika diperkenalkan di tingkat sekolah mengalami perkembangan yang sangat menarik. Pada tahun 1970 dan 1980 ada suatu diskusi yang intensif di kalangan guru matematika di Amerika Serikat untuk membahas apakah pem-buktian matematika perlu dimasukkan sebagai bagian dari kurikulum sekolah menengah atas. Para guru matematika itu berpendapat bahwa pembuktian ma-tematika di sekolah sebenarnya telah dikembangkan dalam suatu pokok bahasan yang menekankan aspek-aspek formal, tetapi kurang memperhatikan pada pema-haman matematika (Hanna, 1983). Pandangan ini terus berkembang hingga Na-tional Council of Teachers of Mathematics, NCTM (1989) mengeluarkan suatu pernyataan bahwa (1) pembuktian secara deduktif tidak perlu lagi diajarkan di sekolah karena teknik heuristik lebih berguna bagi siswa dalam mengembangkan keterampilan penalaran dan jastifikasi dibandingkan pembuktian secara deduk-tif, dan (2) pembelajaran pembuktian di sekolah hanya diberikan kepada siswa yang bermaksud akan melanjutkan pendidikannya ke perguruan tinggi. Pandan-gan terakhir mengenai perlunya pembuktian matematika diperkenalkan di sekolah direkomendasikan oleh NCTM (2000) bahwa pembuktian merupakan bagian dari kurikulum matematika di semua tingkatan. Bagian ” Reasoning dan Proof” dalam dokumen NCTM ini dinyatakan bahwa siswa seharusnya dapat:
1. Mengenal penalaran dan pembuktian sebagai aspek-aspek fundamental ma-tematika;
2. Membuat konjektur dan memeriksa kebenaran dari konjektur itu;
3. Mengembangkan dan mengevaluasi argumen dan pembuktian matematika;
Berdasarkan uraian diatas maka pembuktian deduktif formal merupakan salah satu pendekatan pembelajaran yang memungkinkan dapat menumbuh kem-bangkan kemampuan membuktikan dalam pembelajaran geometri. Hal yang sama juga disebutkan
”Formal deductive proof has its own instructional requirements. These require-ments are not addressed in instructional practices born in the research related to algorithmic mathematical problem solving processes. Instead of prescriptive pro-cedures, heuristicstrategies may be required on emergence. Appropriate knowledge elements related tocontent knowledge, skills in problem solving process including representational advancesand planning strategies, metacognitive functions are ma-jor requirements for learningproof-type geometry problem solving”.( Maduna B. E. : 2003)
Rekomendasi dari NCTM (2000) itu mengindikasikan bahwa pembuktian matematika merupakan salah satu aspek yang harus diperhatikan dalam pembela-jaran matematika di sekolah. Sedikit atau banyaknya pengalaman siswa di dalam menyusun suatu pembuktian di sekolah menengah atas akan berdampak pada kemampuan membuktikan ketika mengikuti kuliah di perguruan tinggi tingkat
men-3
capai kesimpulan), bahkan evaluasi (mengevaluasi aturan-aturan penarikan ke-simpulan dari fakta-fakta yang diberikan atau yang diperoleh dan strategi pem-buktian secara kritis), dan aspek komunikasi matematik (mengekspresikan ide serta proses pembuktian secara lisan maupun tulisan).
Kesulitan siswa menengah atas dalam pembuktian itu tentu saja akan ber-pengaruh pada pembelajaran matematika topik yang lebih berat yang sarat de-ngan pembuktian, seperti topik geometri, dan yang lainnya. Geometri adalah mata pelajaran khusus yang membantu perkembangan keahlian deduktif yang di buktikan secara formal di tingkat pendidikan umum. Pemecahan dari permasala-han pada pembuktian deduktif formal ini dianggap sebagai bukti dari pencapaian tingginya tingkat kompetensi matematika. Untuk alasan ini, pembuktian deduktif formal tampaknya menjadi alat ukur/indikator yang wajar siswa menengah per-tama bagaimana kemampuan penalalarannya tidak hanya geometri tetapi materi lain dari kurikulum matematika SMP .
Saat ini, dapat di perhatikan hanya sedikit sekali penelitian yang di bu-at khusus untuk pengembangan permasalahan pembuktian deduktif formal pada siswa menengah pertama. Pada level SMP, siswa mulai mempelajari secara khusus
Berdasarkan uraian diatas peneliti ingin mengupaya untuk mengembang-kan suatu model pembelajaran yang dapat mengatasi kesulitan-kesulitan siswa menengah pertama dan dapat menjembatani peningkatan tahap berpikir siswa menengah pertama. Sehingga dapat meningkatkan kompetensi kemampuan siswa menegah atas atas dapat berkembang secara optimal dan dapat meningkatkan minat siswa untuk membiasakan diri menggunakan pembuktian deduktif formal dalam memecahkan masalah geometri sehingga pembuktian deduktif formal dapat strategi yang efektif dalam pembelajaran untuk membantu para siswa memecah-kan masalah dalam geometri.
Pembuktian deduktif formal merupakan salah satu pendekatan pembela-jaran yang memungkinkan dapat menumbuh kembangkan kemampuan membuk-tikan dalam pembelajaran geometri. Pendekatan ini merupakan suatu pendekatan pembelajaran yang dimulai dengan menyajikan masalah kepada siswa menengah pertama, kemudian siswa dituntut untuk dapat mengelaborasi setiap informasi atau fakta yang diberikan. Melalui pendekatan ini, masalah yang diberikan harus dapat mengantarkan siswa menengah pertama untuk memahami objek-objek ma-tematika dan kaitan antara objek mama-tematika yang satu dengan objek yang lain-nya.
Guru mendorong siswa menengah pertama untuk melakukan transactive rea-soning seperti mengkritik, menjelaskan, mengklarifikasi, menjastifikasi dan menge-laborasi suatu gagasan yang diajukan, baik yang diinisiasi oleh siswa maupun gu-ru. Untuk dapat terlibat didalam diskusi transaktif, kemampuan awal matema-tika siswa memegang peranan yang sangat penting, sehingga suatu gagasan yang muncul dapat berkembang secara bertahap sehingga membangun suatu konsep matematika yang komprehensif.
5
1.2 Rumusan Masalah
Berdasarkan uraian pada latar belakang masalah, rumusan masalah dalam penelitian ini adalah sebagai berikut:
Pembuktian pemecahan masalah jenis geometri (PJG), Konten Pengetahuan Geometri (KPG), dan Pemecahan Masalah Umum (PMU) terhadap Kemampuan Penalaran Matematika (KPM)
1. Bagaimanakah kemampuan pembuktian pemecahan masalah jenis geometri (PJG) pada siswa menengah pertama;
2. Bagaimanakah Konten Pengetahuan Geometri (KPG) siswa menengah per-tama dalam pelajaran geometri;
3. Bagaimanakah kemampuan Pemecahan Masalah Umum (PMU) siswa me-nengah pertama dalam pembelajaran geometri;
4. Bagaimanakan Kemampuan Penalaran Matematika (KPM) siswa menengah pertama dalam pembelajaran geometri.
5. Bagaimanakah implikasi pengajaran geometri melalui pembuktian deduktif formal melalui aspek penilaian test untuk kemampuan pembuktian pemeca-han masalah jenis geometri (PJG), Konten Pengetahuan Geometri (KPG), dan Pemecahan Masalah Umum (PMU), serta Kemampuan Penalaran Ma-tematika (KPM)
1.3 Tujuan Penelitian
1. Untuk mengetahui kemampuan pembuktian pemecahan masalah jenis geo-metri (PJG) pada siswa menengah pertama;
2. Untuk mengetahui Konten Pengetahuan Geometri (KPG) siswa menengah pertama dalam pelajaran geometri;
4. Untuk mengetahui Kemampuan Penalaran Matematika (KPM) siswa me-nengah pertama dalam pembelajaran geometri;
5. Untuk mengetahui implikasi pengajaran geometri melalui pembuktian de-duktif formal melalui aspek penilaian test untuk kemampuan pembuktian pemecahan masalah jenis geometri (PJG), Konten Pengetahuan Geometri (KPG), dan Pemecahan Masalah Umum (PMU), serta Kemampuan Pe-nalaran Matematika (KPM).
1.4 Manfaat Penelitian
Manfaat yang dapat diambil dari penelitian ini adalah:
Manfaat Praktis:
Hasil penelitian dapat mengatasi kesulitan yang dialami siswa dalam menye-lesaikan masalah geometri melalui pembuktian deduktif formal, khususnya siswa
SMP N 1 Medan.
Manfaat Teoritis :
BAB 2
TINJAUAN PUSTAKA
2.1 Penalaran dalam Pembelajaran Matematika
Selama mempelajari Matematika di kelas, aplikasi penalaran sering dite-mukan meskipun tidak secara formal disebut sebagai belajar bernalar. Beberapa contohnya adalah:
1. Jika besar dua sudut pada suatu segitiga adalah 60o dan 100o maka sudut yang ketiga adalah 180o
−(100o + 60o
) = 20o
. Hal ini didasarkan pada teori matematika yang menyatakan bahwa jumlah besar sudut-sudut suatu segitiga adalah 180o
.
2. Jika (x−1)(x+ 10) = 0 maka x= 1 atau x=−10.
Sejalan dengan contoh-contoh yang telah dikemuka kan di atas, dimana telah terjadi proses penarikan kesimpulan dari beberapa fakta yang telah diketahui siswa, maka istilah penalaran (jalan pikiran atau reasoning ) dijelaskan Keraf (1982: 5) sebagai: ”Proses berpikir yang berusaha menghubung-hubungkan fakta-fakta atau evidensi-evidensi yang diketahui menuju kepada suatu kesimpulan”. Sebagai contoh, Dari pengetahuan tentang besar dua sudut suatu segitiga yaitu 60o
dan 100o
maka dapat disimpulkan ataupun dibuat pernyataan lain bahwa besar sudut yang ketiga pada segitiga itu adalah 20o
. Pada intinya, penalaran merupakan suatu kegiatan, suatu proses atau suatu ak tivitas berpikir untuk menarik kesimpulan atau membuat suatu pernyataan baru yang benar berdasar pada beberapa pernyataan yang kebenarannya telah dibuktikan atau diasumsikan sebelumnya.
materi matematika dipahami melalui penalaran dan penalaran dipahami dan di-latihkan melalui belajar materi matematika.”
Bayangkan sekarang jika para siswa tidak belajar matematika, apa yang akan terjadi dengan keterampilan berpikir siswa? Pola berpikir yang dikem-bangkan matematika seperti dijelaskan di atas memang membutuhkan dan meli-batkan pemikiran kritis, sistematis, logis, dan kreatif. Sekali lagi, bayangkan jika para siswa tidak belajar matematika. Akan cepatkah siswa menarik kesimpulan dari beberapa fakta atau data yang siswa dapatkan ataupun yang di ketahui? Kemampuan bernalar tidak hanya dibutuhkan para siswa ketika siswa belajar matematika maupun mata pelajaran lainnya, namun sangat dibutuhkan setiap manusia di saat memecahkan masalah ataupun di saat menentukan keputusan, sebagaimana dikemukakan mantan Presiden AS Thom as Jefferson dan dikutip Copi (1978: vii) berikut ini: ” In a republican nation, whose citizens are to be led by reason and persuasion and not by force, the art of reasoning becomes of first importance”. Pernyataan itu menunjukkan pentingnya penalaran dan argumen-tasi dipelajari dan di kembangkan di suatu negara sehingga setiap warga negara akan dapat dipimpin dengan daya nalar (otak) dan bukannya dengan kekuatan (otot) saja.
Pendapat mantan Presiden AS Thomas Jefferson di atas sudah seharusnya makin meningkatkan tekad para guru matematika untuk makin meningkatkan kemampuan bernalar para siswanya. Sekali lagi, kemampuan dan keterampilan bernalar ini akan dibutuhkan para siswa dan seluruh warga bangsa ini ketika mem-pelajari matematika, ilmu lain, maupun ketika terjun langsung ke masyarakat. Dikenal dua macam penalaran, yaitu induksi atau penalaran induktif dan deduk-si atau penalaran deduktif. Namun padathededuk-sis ini hanya penlaran deduktif saja yang akan dibahas.
2.2 Pembuktian Deduktif formal dalam Matematika
9
meningkatkan pemahaman siswa terhadap bukti suatu pernyataan. Bukti generik diberikan dalam level contoh yang menjelaskan konsep secara umum dengan me-mandang contoh khusus. Hal ini tentu saja berbeda dengan pembuktian secara umum yang mensyaratkan abstraksi dengan level yang lebih tinggi.
Kemudian, Leron (dalam Tall, 1991) mengajukan bukti terstruktur dengan sifat menggabungkan metode penyajian formal dan informal ke dalam suatu pem-buktian. Tujuan utama dari bukti terstruktur ini bukan untuk meyakinkan, tetapi untuk membantu pembaca dalam meningkatkan pemahamannya terhadap gagasan di belakang bukti itu, dan bagaimanakah hubungannya dengan hasil-hasil matematika lainnya.
Menurut Suriasumantri (2001: 49), ” Penalaran deduktif adalah cara berpikir di mana dari pernyataan yang bersifat umum ditarik suatu kesimpulan yang bersi-fat khusus.”
Contoh :
Semua manusia akan mati.
Si Polan adalah manusia.
Jadi Si Polan akan mati.
Salah satu karakteristik matematika adalah bersifat deduktif. Dalam pem-belajaran matematika, pola pikir deduktif itu penting dan merupakan salah satu tujuan yang bersifat formal, yang memberi tekanan pada penataan nalar. Pola pikir deduktif itu sangat penting, namun dalam pembelajaran matematika. Menu-rut Soedjadi (2000: 46), ”Bila kondisi kelas memungkinkan, kebenaran teorema dapat dibuktikan secara deduktif. Namun jika pembuktian dipandang berat, pola pikir deduktif dapat diperkenalkan melalui penggunaan definisi ataupun teore-ma”. Pendekatan deduktif merupakan pendekatan yang berproses dari umum ke khusus, dari teorema ke contoh-contoh. Teorema diberikan kepada siswa dan
Berdasarkan pemikiran, Reiss dan Renkl (2002) mengajukan konsep contoh jawab huristik yang menyediakan overviu dari suatu jenis contoh yang tidak hanya memberikan bukti dari contoh itu, tetapi juga membantu siswa menunjukkan aspek-aspek pembuktian secara umum. Langkah-langkah huristik dalam contoh yang dibuktikan itu adalah sebagai berikut: (1) mengeksplorasi situasi masalah, (2) membuat konjektur, (3) mengumpulkan informasi untuk memeriksa konjektur, (4) membuktikan konjektur, (5) memeriksa kembali.
Pendekatan penalaran secara umum dapat dilakukan dengan cara mengeks-plorasi secara intuitif terhadap pernyataan yang harus dibuktikan dengan perta-nyaan-pertanyaan sebagai berikut: What happens if ? Why does it happen? How do different cases occur ? What is true here ? (Uhlig, 2003). Dengan pertanyaan yang bersifat eksploratif ini, diyakini bahwa pengetahuan tentang Theorems yang dihadapinya akan bertambah. Demikian pula pemahamannya secara konseptual. Pendekatan ini mengembangkan suatu pembuktian dengan melakukan pertanyaan yang di singkat dengan WWHWT.
Strategi pembuktian yang telah dikembangkan di atas, belum ada yang membahas secara eksplisit bagaimana memunculkan gagasan utama dari
struk-tur pembuktian, baik untuk memahami pembuktian yang ada maupun untuk mengkonstruksi suatu pembuktian.
11
Gambar 2.1 Skematik untuk mengalalisis argumentasi
Hubungannya dengan pembuktian matematika, pernyataan-pernyataan di dalam pembuktian matematika dipandang sebagai salah satu bentuk argumen-tasi. Di dalam argumentasi pembuktian matematika, sebagai data adalah premis-premis, sedangkan yang menjadi warrant adalah definisi atau teorema. Diagram skematik ini dapat digunakan sebagai model untuk membantu membaca pem-buktian suatu pernyataan matematika, dan dengan sedikit modifikasi dapat di-gunakan untuk mengkonstruksi pembuktian matematika.
Diagram skematik Krummheuer dapat juga digunakan untuk mengembang-kan suatu model strategi pembuktian matematika secara informal. Konklusi di dalam skematik itu, baik sebagai target-conclussion maupun claim perantara yang dilakukan di atas menggunakan penarikan kesimpulan secara deduktif. Argumen-tasi dengan cara seperti ini dinamakan argumenArgumen-tasi deduktif .
dikonver-sikan ke dalam suatu bentuk lain misalnya menjadi bentuk simbolis, diagram atau persamaan untuk mempercepat memproses. Diagram permasalahan berguna un-tuk mempermudah pemecahan masalah.
Gambar 2.2 Skema penalaran deduktif
Perencanaan yang mencakup strategi untuk menemukan proses informasi untuk menemukan proses informasi untuk mengubah permasalahan informasi menjadi tujuan sebenarnya. Dalam penyelesaian masalah pembuktian geomet-ri, membuat dugaan atau inferensi logis untuk teorema yang berlaku, bekerja mundur, dan menggambar garis bantu yang sering digunakan sebagai strategi dalam bidang geometri. Perencanaan yang mencakup keputusan antara langkah-langkah adalah tergantung subjektif dan orang. (Koedinger et al.,1993).
pemeca-13
han masalah kemampuan sehingga harus menyertakan kemampuan menganalisis masalah, representasi (keterwakilan), perencanaan dan penggunaan pengetahuan mendapatkan data.
2.3 Tahapan Berpikir Geometri Menurut Van Hiele
Salah satu pelajaran matematika di sekolah yang dipelajari oleh siswa adalah pelajaran geometri. Geometri adalah cabang matematika yang sudah dikenal siswa sejak kecil karena geometri banyak dijumpai dalam kehidupan sehari-hari. Dalam Pembelajaran geometri terdapat beberapa teori belajar yang relevan, di antaranya dikemukakan oleh Van Hiele.
Dalam teori yang kemukakan, berpendapat bahwa dalam mempelajari geo-metri para siswa mengalami perkembangan kemampuan berpikir melalui
tahap-tahap tertentu. Van Hiele (Suherman, 2001: 52) menyatakan bahwa terdapat 5 tahap dalam berpikir gometri, yaitu: tahap pengenalan, tahap analisis, tahap pengurutan, tahap deduksi, dan tahap akurasi. Tahapan tersebut diuraikan se-bagai berikut:
a. Tahap pengenalan (visualisasi)
Pada tahap ini, siswa memandang suatu bangun geometri sebagai suatu ke-seluruhan. Pada tahap ini siswa belum memperhatikan komponen-komponen dari masing-masing bangun. Dengan demikian, meskipun pada tahap ini siswa sudah mengenal nama sesuatu bangun, siswa belum mengamati sifat-sifat dari bangun itu. Sebagai contoh, pada tahap ini siswa tahu suatu bangun bernama persegi panjang, tetapi siswa belum menyadari sifat-sifat bangun persegi panjang tersebut.
b. Tahap analisis
bangun merupakan persegipanjang karena bangun itu mempunyai empat sisi, sisi-sisi yang berhadapan sejajar, dan semua sudutnya siku-siku.
c. Tahap pengurutan (deduksi informal)
Pada tahap ini, siswa sudah bisa memahami hubungan antar ciri yang satu dengan ciri yang lain pada sesuatu bangun. Sebagai contoh, pada tahap ini siswa sudah bisa mengatakan bahwa jika pada suatu segiempat sisi-sisi yang berhadapan sejajar, maka sisi-sisi yang berhadapan itu sama panjang. Di samping itu pada tingkat ini siswa sudah memahami perlunya definisi untuk tiap-tiap bangun. Pada tahap ini, siswa juga sudah bisa memahami hubungan antara bangun yang satu dengan bangun yang lain. Misalnya pada tahap ini siswa sudah bisa memahami bahwa setiap persegi adalah juga persegipanjang, karena persegi juga memiliki ciri-ciri persegipanjang.
d. Tahap deduksi
Pada tahap ini siswa sudah memahami peranan pengertian-pengertian pang-kal, definisi-definisi, aksioma-aksioma, dan teorema-teorema dalam geomet-ri. Pada tahap ini siswa sudah mulai mampu menyusun bukti-bukti secara formal. Ini berarti bahwa pada tahap ini siswa sudah memahami proses berpikir yang bersifat deduktif-aksiomatis dan mampu menggunakan proses
berpikir tersebut.
e. Tahap akurasi Pada tahap ini, siswa mampu melakukan penalaran secara formal tentang sistem-sistem matematika (termasuk sistem-sistem geomet-ri), tanpa membutuhkan model-model yang konkret sebagai acuan. Pada tahap ini, siswa memahami bahwa dimungkinkan adanya lebih dari satu geometri. Menurut teori Van Hiele adalah sebagai berikut:
(a) Belajar merupakan suatu proses yang diskontinu, yaitu ada lompatan dalam kurva belajar yang menyatakan adanya tahap pemikiran diskret dan berbeda secara kualitatif.;
15
tergantung pada pembelajaran dari pada umur atau kematangan bio-logis;
(c) Konsep-konsep yang secara implisit dipahami pada suatu tahap menja-di eksplisit menja-dipahami pada tahap berikutnya. Setiap tahap mempunyai bahasa dan simbol bahasa sendiri yang menghubungkan simbol-simbol itu.
Pada tahap ini, siswa mampu melakukan penalaran secara formal tentang sistem-sistem matematika (termasuk sistem-sistem geometri), tanpa membutuh-kan model-model yang konkret sebagai acuan. Pada tahap ini, siswa memahami bahwa dimungkinkan adanya lebih dari satu geometri. Teori Van Hiele adalah sebagai berikut:
1. Belajar merupakan suatu proses yang diskontinu, yaitu ada lompatan da-lam kurva belajar yang menyatakan adanya tahap pemikiran diskret dan berbeda secara kualitatif;
2. Tahap-tahap tersebut berurutan dan hierarkhi. Agar siswa dapat berpe-ran dengan baik pada suatu tahap berikutnya dalam hirarkhi Van Hiele, maka dia harusmenguasai sebagian besar dari tahap yang lebih rendah. Ke-majuan darisatu tahap ke tahap berikutnya lebih banyak tergantung pada pembelajaran dari pada umur atau kematangan biologis;
3. Konsep-konsep yang secara implisit dipahami pada suatu tahap menjadi eksplisit dipahami pada tahap berikutnya;
2.4 Penalaran Deduktif dalam Geometri
perhatikan masalah atau pertanyaan berikut, yaitu:
Tunjukkan bahwa jumlah besar sudut-sudut suatu segitiga adalah 1800
Untuk membuktikan bahwa 1800
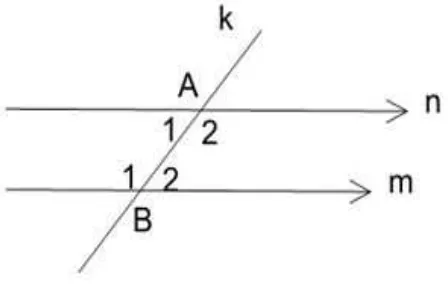
merupakan jumlah besar sudut-sudut su-atu segitiga adalah dengan menggunakan penalaran deduktif yang proses pembuk-tiannya akan melibatkan teori atau rumus matematika lainnya yang sebelumnya sudah dibuktikan kebenarannya secara deduktif juga, yaitu: ”Jika dua garis seja-jar dipotong garis lain, maka sudut-sudut dalam berseberangannya adalah sama,” seperti ditunjukkan gambar 2.3.
Gambar 2.3 Dua garis sejajar dipotong garis lain
Pada gambar 2.3,∠A1 = ∠B2 dan∠A2 =∠B1 karena garismdann
meru-pakan dua garis sejajar dan dipotong garis ketiga, sehingga sudut-sudut dalam berseberangannya akan sama besar, yaitu ∠A1 = ∠B2 dan ∠A2 = ∠B1.
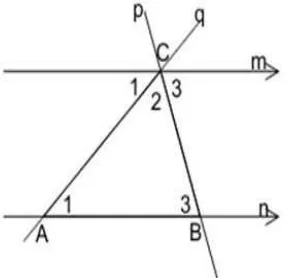
Per-hatikan △ABC di bawah ini, dimana melalui titik C telah dibuat garis m yang
17
Gambar 2.4 Dua garis sejajar dan dipotong dua garis lain
Dengan demikian, berdasar gambar 2.4
∠A1 = ∠C1
∠B3 = ∠C3
∠C2 =∠C2
∠A1 +∠B3 +∠C2 =∠C1 +∠C3 +∠C2
Karena ∠C1 +∠C3 +∠C2 = 1800
maka:
∠A1 +∠B3 +∠C2 =∠A+∠B+∠C = 1800
Contoh di atas menunjukkan bahwa pada penalaran deduktif, suatu ru-mus, teorema, atau dalil tentang jumlah besar sudut-sudut suatu segitiga adalah 1800
telah dibuktikan dengan menggunakan atau melibatkan teori maupun rumus matematika sebelumnya yang sudah dibuktikan kebenarannya secara deduktif ju-ga. Sedangkan teori maupun rumus matematika yang digunakan sebagai dasar pembuk tian itu tadi telah dibuktikan berdasar teori maupun rumus matema-tika sebelumnya lagi. Begitu seterusnya. Disamping itu, pem buktian tentang jumlah besar sudut-sudut suatu segitiga adalah 1800
telah melibatkan atau me nggunakan definisi yang sudah ditetapkan sebelumnya, seperti pengertian sudut lurus besarnya 1800
. Proses di atas dapat digambarkan dengan diagram berikut.
Gambar 2.5 Diagram penalaran deduktif tentang jumlah besar sudut dalam se-gitiga 1800
Aksioma atau sifat pangkal adalah semacam dalil yang kebenarannya tidak per-lu dibuktikan namun sangat menentukan, karena sifat pangkal inilah yang akan menjadi dasar untuk membuktikan dalil atau teorema matematika selanjutnya. Depdiknas (2002: 6) menyatakan bahwa: ”Unsur utama pekerjaaan matematika adalah penalaran deduktif yang bekerja atas dasar asumsi, yaitu kebenaran suatu konsep atau pe rnyataan diperoleh sebagai akibat logis dari kebenaran sebelum nya”.
Disamping itu, pengertian-pengertian matematika secara berantai didefi-nisikan dari pengertian sebelumnya. Sebagaimana aksioma yang tidak perlu dibuktikan kebenarannya karena akan menjadi dasar pembuktian dalil atau sifat berikutnya, maka pengertian pangkal tidak didefinisikan karena pengertian pang-kal akan menjadi dasar pendefinisian pengertian-pengertian atau konsep-konsep matematika berikutnya. Suatu bangunan matematika akan runtuh jika terda-pat sifat, dalil, atau teorema yang diturunkan dari aksioma serta pengertian pangkalnya ada yang saling bertentangan (kontradiksi).
diang-19
gap benar. Karenanya, Jacobs (1982: 32) menyatakan: ”Deductive reasoning is a method of drawing conclusions from facts that we accept as true by using log-ic ”. Artinya, penalaran deduktif adalah suatu cara penarikan kesimpulan dari pernyataan atau fakta-fakta yang dianggap benar dengan menggunakan logika.
Sekali lagi, bangunan pengetahuan matematika didasarkan pada deduksi semata-mata,kepada aksioma-aksioma yang dianggap benar tadi. Suatu hal yang banyak sudah jelas benar pun harus ditunjukkan atau dibukt ikan kebenarannya dengan langkah-la ngkah yang benar secara deduktif. Karena itulah, bangunan matematika dikenal sebagai mata pelajaran yang dikembangkan secara deduktif-aksiomatis, atau sistem aksiomatik.
2.5 Jenis-Jenis Permasalahan yang Sesuai untuk Permasalahan dalam Pembuktian Secara Deduktif
Jenis masalah adalah kriteria utama dalam merancang pembelajaran (Jo-nassen, 2000:63). Dalam menentukan jenis permasalahan, sedangkan pada pem-buktian jenis permasalah geometri, jawabannya (tujuannya) diberikan, tetapi prosedurnya tidak diketahui. Dengan demikian solusi terhadap masalah pem-buktian deduktif ini adalah untuk mencapai tujuan dari informasi yang diberikan. Penyelesaian tentang masalah jenis pembuktian geometri didasarkan pada tujuan-nya. Hal ini menunjukkan bahwa pembuktian deduktif ini adalah non-algoritma. Perencanaan ini sangat penting dalam permasalahan nonalgoritma, sebab logika pengambilan keputusan terjadi selama proses pemecahan masalah.
Praktek yang luas dalam penyelesaian permasalahan non-algoritma adalah
permasalahan yang mengarah ke pengenalan dari pada ke prorosedurnya. Meski-pun pembuktian deduktif adalah non-algoritmia, namun permasalahannya sangat terstruktur. Fasilitas ini mendukung rancangan pembelajaran. Sehingga pembe-lajaran menjadi lebih berarti.
2.6 Syarat untuk Menyelesaikan Permasalahan Matematika
lang-sung tahu caranya. Jika seorang anak dihadapkan pada suatu permasalah ma-tematika dan anak tersebut langsung tahu cara menyelesaikannya dengan benar, maka masalah yang diberikan tidak dapat digolongkan pada kategori soal pemeca-han masalah. Pada awal abad ke sembilan belas, pemecapemeca-han masalah dipandang sebagai kumpulan keterampilan bersifat mekanis, sistematik, dan seringkali abs-trak sebagaimana keterampilan yang digunakan pada penyelesaian soal sistem persamaan. Penyelesaian masalah seperti ini seringkali hanya berlandaskan pada solusi logis yang bersifat tunggal.
Hudoyo (2002:427) yang menyatakan ”Secara alami manusia selalu mengha-dapi masalah karena itu pembelajaran matematika didasarkan masalah”. Masalah sering ditemukan dalam kehidupan sehari-hari. Masalah yang dihadapi seseorang berbeda dengan masalah yang dihadapi orang lain. Suatu pertanyaan atau soal dapat merupakan masalah bagi seseorang tetapi mungkin tidak merupakan ma-salah bagi orang lain.
Beberapa pandangan tentang masalah dalam pembelajaran matematika te-lah dikemukakan oleh para ahli. mengemukakan bahwa suatu situasi adate-lah suatu masalah bagi seseorang jika orang tersebut sadar akan adanya situasi itu,
me-ngakui bahwa situasi itu memerlukan tindakan, menginginkan atau memerlukan tindakan dan tidak dengan segera dapat memecahkan situasi tersebut. Polya (1981:117) mengemukakan bahwa suatu masalah berarti mencari dengan sadar beberapa tindakan yang tepat untuk mencapai suatu tujuan yang jelas, tetapi tujuan tidak dapat segera dicapai.
Selanjutnya Polya mengemukakan bahwa didalam belajar matematika ter-dapat dua macam masalah yaitu masalah untuk menemukan dan masalah untuk membuktikan. Ruseffendi (1988:336) menyatakan bahwa: Suatu persoalan itu merupakan masalah bagi seseorang. Pertama bila persoalan itu tidak dikenalnya, maksudnya ialah siswa belum memiliki prosedur atau algoritma tertentu untuk menyelesaikannya.
ma-21
salah baginya, bila siswa ada niat menyelesaikannya. Hudoyo (1988:175) berpen-dapat bahwa: Suatu pertanyaan merupakan suatu masalah apabila pertanyaan tersebut menantang untuk dijawab yang jawabannya tidak dapat dilakukan secara rutin saja. Lebih lanjut pertanyaan yang menantang ini menjadi masalah bagi seseorang bila orang itu menerima tantangan itu.
Dengan demikian suatu pertanyaan menjadi masalah bagi siswa, apabila siswa diberi motivasi untuk menjawab masalah itu. Pandangan-pandangan ten-tang pengertian masalah dalam pembelajaran matematika banyak kesamaannya namun pada prinsipnya sama. Suatu soal atau pertanyaan dikatakan masalah bagi seseorang apabila soal itu tidak dikenalnya atau belum memiliki prosedur atau algoritma tertentu untuk menyelesaikannya.
Konten pengetahuan yang berhubungan dengan pembuktian jenis masalah geometri ini terdiri dari konsep geometrik, relasi/hubungan, penalaran deduktif aksioma yang logis, dan ketentuan dalam bukti resmi matematika secara formal. Berdasarkan pada pembuktian analisis terhadap para siswa, Reisset al.,(2001:97) menunjukkan bahwa pengetahuan konten geometris saja tidak cukup untuk meng-hasilkan bukti matematika. Reisset al.,(2001:97) membantah bahwa pengetahuan
dan keahlian pemahaman secara metodologi juga mempengaruhi keberhasilan pe-mecahan bukti-jenis masalah geometri.
Menurut Reiss et al., (2001:97), metodologi pengetahuan merupakan per-paduan dari tiga aspek: membuktikan rencana/program, membuktikan struktur dan rangkaian logika. Di antaranya, membuktikan skema merujuk pada argumen deduktif, membuktikan struktur yang merujuk kepada keabsahan dalil matema-tika deduktif, dan rantai logika mengacu pada transparansi yang logis dari kema-juan secara bertahap. Ketiga aspek yang merupakan logika pemikiran deduktif maupun kesepakatan bersama secara formal bukti matematika.
dipengaruhi oleh mengenal permasalahan, strategi dan kemampuan pemahaman-nya. Gambaran permasalahan, perencanaan, dan penggunaan data pengetahuan yang didukung oleh kemampuan menangani dengan diagram geometris.
Pembuktian masalah geometri menggunakan langkah-langkah pemrosesan-nya tentang memecahkan masalah secara umum misalpemrosesan-nya seperti soal, perwaki-lan analisis perencanaan,dan pemakaian pengetahuan mendapatkan data. Hal ini membutuhkan pengoperasian matematika dan penalaran matematika. Ope-rasi seperti antara penjumlahan, pengurangan, kesamaan, dan ketidaksamaan sangat diperlukan dalam proses pemecahan masalah pembuktian jenis geomet-ri. Dalam kelas siswa sebelumnya, para siswa menemukan pemecahan masalah geometri memiliki kemampuan penalaran matematika, seperti penalaran induktif siswa dan kemampuan berfikir deduktif secara non formal.
Kompleksitas pembuktian proses pemecahan masalah geometri
Pembuktian Non-algoritma dari permasalah geometri mendorong para siswa untuk menerapkan pengetahuan tersebut dapat mengarahkan pembuktian:
Geometry proof problem solving is hard. Of the 27 definitions, postulates and theorems that are introduced prior to such a problem in a traditional curriculum, 7 can be applied at the beginning of this problem. Some of these rules can be applied in more than one way yielding 45 possible inferences that can be made from this problem’s givens. The number of options continues to increase at further layers at minimum it takes 6 such layers of inferences to reach the problem goal (Koedinger and Anderson, 1993:16-17)
meru-23
pakan aturan tetapi heuristika yang dapat mengurangi kesimpulan yang tidak perlu. Kesesuaian strategi pada umumnya seperti heuristika dan perencanaan yang di sorot dalam pemecahan masalah geometri (Schoenfeld,1985:125; Chin-nappan & Lawson, 1996:3).
2.7 Tujuan Pembelajaran Matematika Secara Deduksi
Menurut Russeffendi (Dahlan, 2004) pembelajaran matematika secara de-duksi dilatarbelakangi oleh anggapan bahwa matematika merupakan ilmu yang terstruktur dan terorganisasikan, sehingga pengetahuan matematika dimulai dari unsur-unsur yang tidak didefinisikan; seperti titik, garis, dan lain-lain. Titik itu dianggap ada, tetapi tidak dapat dinyatakan dalam suatu kalimat dengan tepat, sebab titik itu adalah unsur yang tidak didefinisikan. Paling hanya mampu mem-berikan penjelasan misalnya: ”titik itu adalah sesuatu yang tidak mempunyai ukuran panjang dan luas, isi, atau berat, yang belum jelas. Meskipun sepakat bahwa titik itu ada. Dari unsur yang tidak didefinisikan, maka munculah unsur-unsur yang didefinisikan, seperti lengkungan, sudut, dan lain-lain.
Menurut Ruseffendi (Dahlan, 2004) dari unsur yang tidak didefinisikan dan didefinisikan dapat dibuat asumsi-asumsi dasar atau aksioma atau postulat, yakni pernyataan dasar dalam matematika yang tidak dibuktikan kebenarannya kare-na kebekare-narannya tidak disangsikan lagi. Setelah itu disusunlah teori-teori atau dalil-dalil yang benar yang berlaku umum. Dalil ini disusun dengan pembuktian kebenarannya.
berfikir dapat bekerja dengan dasar simbol yang tidak memerlukan referensi dunia nyatanya.