Metode Bagi Dua (Biseksi)

Metode Bagi Dua (Biseksi)

terdapat akar persamaan bila f(a) dan f(b) berlawanan tanda atau dituliskan:

. < 0

Setelah diketahui dibagian mana terdapat akar, maka batas bawah dan batas atas diperbaharui

sesuai dengan range dari bagian yang mempunyai akar

Langkah – langkah dalam menjalankan metode interval tengah

1. Pilih a sebagai batas bawah x sebagai batas atas untuk taksiran akar sehingga terjadi

perubahan tanda fungsi dalam selang interval tersebut. Atau periksa apakah benar bahwa . < 0

2. Taksiran nilai akar baru, x diperoleh

=

3. Lakukan evaluasi berikut untuk menentukan dalam selang interval mana akar berada

• Jika . < 0, maka = , =

• Jika . > 0, maka = , =

=

= 00 ,

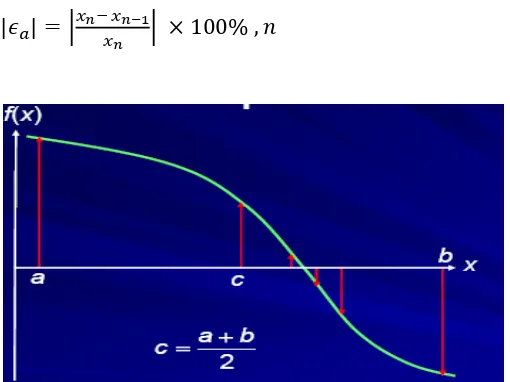
Gambar 1. 1 grafik fungsi metode bagi dua

Misalkan kita telah menentukan selang , ! sehingga < 0.Pada setiap kali lelaran,

selang , ! kita bagi dua di = " , sehingga terdapat dua buah upaselang yang berukuran sama

,yaitu selang , "! dan ", ! Selang yang diambil untuk lelaran berikutnya adalah selang yang

memuat akar,bergantung pada apakah " < 0 atau " < 0

, !

Bagi dua di = "

[ a,c ] [ c,b ]

" < 0 #

ya tidak

Selang yang baru di bagi dua lagi dengan cara yang sama. Begitu seterusnya sampai ukuran

perbandingan dua buah bilangan riil, sehingga perbandingan " = 0 dibenarkan.

Namun kalau kita kembali ke konsep awal bahwa dua buah bilangan riil tidak dapat

dibandingkan kesamaannya karena representasinya didalam mesin tidak tepat ,maka kita

tidak dapat menggunakan bilangan yang sangat kecil (misalnya epsiln mesin) sebagai

pengganti nilai 0. Dengan demikian, menguji kesamaan " dapat kita hampiri dengan

" < epsilon_mesin.

Misalkan pada lelaran ke-r kita mendapatkan selang ₍ , ₍ !.

− = − _{, = − 22} ,

:− : = − , = − 2₂ , :

…

(− ( = ( − ( , = − 2₂ , (

Pada lelaran ke – r, posisi "₍ (akar hampiran) dan / (akar sejati) adalah seperti diagram berikut:

Berdasarkan diagram diatas jelaslah bahwa

/ − "( ≤ (−₂ (

Selanjutnya,

/ − "( ≤ (−₂ ( = 2 ₂− = ₂₍−

Jadi, selisih antara akar sejati dengan akar hampiran tidak pernah lebih dari setengah epsilon.

Dengan mengingat criteria berhenti adalah ₍− ₍ < %, maka dari (i) terlihat bahwa / − "₍ <

2 ,

Sehingga

( s "₍

−

Yang dalam hal ini R adalah jumlah lelaran (jumlah pembagian selang) yang dibutuhkan untuk

menjamin bahwa c adalah hampiran akar yang memiliki galat kurang dari %.

Contoh : 1

8 1.414063 1.421875 1.41796875 -0.01064

9 1.414063 1.417969 1.416015875 -0.0051

10 1.414063 1.416016 1.415039438 -0.00234

Akar dari 2 adalah 1,4150

Contoh : 2

4 1,125 1,1875 1,25 -0,201171875 0,237060546875 0,703125

5 1,125 1,15625 1,1875 -0,201171875 0,014556884765625 0,237060546875

6 1,125 1,140625 1,15625 -0,201171875 -0,0941429138183594 0,0145568847656

7 1,140625 1,1484375 1,15625 -0,09414291381835 -0,0400032997131348 0,01455688476562

8 1,1484375 1,15324375 1,15625 -0,04000329971313 -0,0127759575843811 0,01455688476562

9 1,16324375 1,154296875 1,15625 -0,01277559575843 0,000877253711223 0,0145568847656

Jadi akar 2 adalah 1,154297

Contoh : 3

Carilah salah satu akar dari persamaan berikut :

G = :_{+ − 3 − 3}

Disyaratkan bahwa batas kesalahan relatif % < 0,01 %

Hasil hitungan ditabelkan dalam tabel berikut :

Iterasi _{H ) (} ( _H) f(xu) f(xr) ( H). f(xr) % (%)

1 1 2 1,5 -4 3 -1,875 7,5

2 1,5 2 1,75 -1,875 3 0,171875 -0,3222656 14,285714

3 1,5 1,75 1,625 -1,875 0,171875 -0,9433594 1,7687988 -7, 6923077

4 1,625 1,75 1,6875 -0,9433594 0,171875 -0,4094238 0,3862338 3,7037037

5 1,6875 1,75 1,71875 -0,4094238 0,171875 -0,1247864 0,0510905 1,8181818

6 1,71875 1,75 1,734375 -0,1247864 0,171875 0,02202299 -0,002749 0.9009009

7 1,71875 1,734375 1,7265625 -0,1247864 0,0220299 -0,0517554 0,0064584 -0,4524887

8 1,7265625 1,734375 1,7304688 -0,0517554 0,0220299 -0,0149572 0,0007741 0,2257336

9 1,7304688 1,734375 1,7324219 -0,0149572 0,0220299 0,0035127 -5,254E-05 0,11227396

11 1,7314453 1,7324219 1,7319336 -0,0057282 0,0035217 -0,0011092 6,354E-06 0,0281928

12 1,7319336 1,7324219 1,7321777 -0,0011092 0,0035217 0,0012013 -1,333E-06 0,0140944

13 1,7319336 1,7321777 1,7320557 -0,0011092 0,0011092 4,596E-05 -5,098E-08 -0,0070477

Dari hasil hitungan tampak bahwa akar persamaan adalah 1,7320557 bandingkan dengan

akar eksaknya yang bernilai D3 = 1,73205080756…..

Contoh 4

Kesalahan relative semu = IJKLMLNOP JML5QROS TU

Iterasi 8

d = _ = 1,3046875 (1,3046875) = −0,0838361

d = _ = 1,3125 (1,3125) = −0,0515137

d = i i= ,:9`ed_Y ,: Y= 1,30859375

f(1,30859375 ) = -0,0677348

f( _d). f( _d) = (−0,0838361).( −0,0677348)

= 0,0056786 > 0

Z77[7 = ,:9`ed_Y ,:9dYg:_Y_{,:9dYg:_Y} = 0,0029851

Jadi f( _d). f( _d) > 0

Iterasi 9

g = d = 1,30859375 (1,30859375) = −0,0677348

g= d = 1,3125 (1,3125) = −0,0515137

g = j j = ,:9dYg:_Y ,: Y= 1,31054688

f(1,31054688 ) = -0,0596392

f( _g). f( _g) = (−0,0677348 ).( −0,0596392)

= 0,0040396 > 0

Z77[7 = ,:9`ed_Y ,:9dYg:_Y_{,:9dYg:_Y} = 0,0014903

Jadi f( _g). f( _g) > 0

Iterasi 10

9 = g = 1,31054688 (1,31054688) = −0,0596392

9 = g = 1,3125 (1,3125) = −0,0515137

f(1,31152344 ) = -0,0555802

f( ₉). f( ₉) = (−0,0596392).( −0,0555802)

= 0,0033148 > 0

Z77[7 = ,: 9Y`edd ,: Y :``<sub>,: Y :``</sub> = 0,0007446

Jadi f( ₉). f( ₉) > 0

Iterasi 11

= 9 = 1,31152344 (1,31152344) = −0,0555802

= 9 = 1,3125 (1,3125) = −0,0515137

= = ,: Y :`` ,: Y = 1,31201172

F(1,31201172 ) = -0,0535479

f( ). f( ) = (−0,0555802 ).( −0,0535479)

= 0,00297762 > 0

Z77[7 = ,: Y :`` ,: 9 __{,: 9 _} = 0,0003722

Jadi f( ). f( ) > 0

Iterasi 12

= = 1,31201172 (1,31201172) = −0,0535479

= = 1,3125 (1,3125) = −0,0515137

= X X₌ ,: 9 _ ,: Y _{= 1,31225586}

f(1,31225586) = -0, 052531

f( ). f( ) = (−0,0535479 ).( −0, 052531)

= 0,0028129 > 0

Z77[7 = ,: 9 __{,: YYde},: YYde = 0,000186

Z77[7 = ,: `:dg_ ,: `eg`g<sub>,: `eg`g</sub> = 0,0000232

Jadi f( _{`</sub>). f( <sub>`}) > 0

Iterasi 16

Karena ( _Y). ( _Y) > 0

e = Y = 1,31246949 (1,31246949 ) = −0,0513137

Y = Y = 1,3125 (1,3125) = −0,0515137

Y = c c= ,: `eg`g ,: Y= 1,31248475

(1,31248475) = −0,0494923

( e) ( e) = (−0,0513137)(−0,0494923) = 0,0025558

Z77[7 = ,: `eg`g ,: `d`_Y_{,: `d`_Y} = 0,0000117

Hasil hitungan ditabelkan dalam tabel berikut:

6 1,28125 1,3125 1,296875 -0,177948 -0,0515137 -0,1156807 0,0343427

7 1,296875 1,3125 1,3046875 -0,1156807 -0,0515137 -0,0838361 0,0096982

8 1,3046875 1,3125 1,30859375 -0,0838361 -0,0515137 -0,0677348 0,0056786

9 1,30859375 1,3125 1,31054688 -0,0677348 -0,0515137 -0,0596392 0,0040396

10 1,31054688 1,3125 1,31152344 -0,0596392 -0,0515137 -0,0555802 0,0033148

11 1,31152344 1,3125 1,31201172 -0,0555802 -0,0515137 -0,0555802 0,0029762

12 1,31201172 1,3125 1,31225586 -0,0535479 -0,0515137 -0,052531 0,0028129

13 1,31225586 1,3125 1,31237793 -0,052531 -0,0515137 -0,0519003 -0,0027264

14 1,31237793 1,3125 1,31243897 -0,0519003 -0,0515137 -0,0515849 0,0026773

15 1,31243897 1,3125 1,31246949 -0,0515849 -0,0515137 -0,0516408 0,00266389

16 1,31246949 1,3125 1,31248475 -0,0516408 -0,0515137 -0,0494923 0,002558

Iterasi dihentikan Sampai pada kesalahan relative terkecil.

( _g). ( g) > 0

Z77[7 = ,:eg `9e: ,:ed e`9__{,:ed e`9_} = 0,00071377

• Iterasi 10

9 = g= 1,36816407 ( 9) = −0,0135842

9 = g= 1,36914063 ( 9) = 0,0070156

9 = ,:ed e`9_ ,:eg `9e:= 1,36865235

( 9) = (1,36865235):+ 2(1,36865235) + 10(1,36865235) − 20 = 2,56377226 + 3,74641852 + 13,6865235 − 20

= −0,0032857

Z77[7 = ,:ed e`9_ ,:edeY :Y_{,:edeY :Y} = 0,0003568

• Iterasi 11

= 9= 1,36865235 ( ) = −0,0032857

= 9 = 1,36914063 ( 9) = 0,0070156

= ,:edeY :Y ,:eg `9e:= 1,36889649

( ) = (1,36889649):_{+ 2(1,36889649) + 10(1,36889649) − 20}

= 2,56514447 + 3,7477552 + 13,6889649 − 20 = 0,0018646

( ). ( ) = (−0,0032857). (0,0018646) = −0,00000613

( ). ( ) < 0

Hasil hitungan ditabelkan dalam tabel berikut:

I m_n o_n p_n q(m_n) q(o_n) q(p_n) q(m_n). q(p_n)

1 1 1,5 1,25 -7 2,075 -2,421875 16,953125

2 1,25 1,5 1,375 -2,421875 2,895 0,1308594 -0,31692511

3 1,25 1,375 1,3125 -2,421875 0,1308594 -1,1687012 2,8304822

4 1,3125 1,375 1,34375 -1,1687012 0,1308594 -0,5248108 0,613347

5 1,34375 1,375 1,359375 -0,5248108 0,1308594 -0,1984596 0,1041537

6 1,359375 1,375 1,3671875 -0,1984596 0,1308594 -0,0341275 0,00677293

7 1,3671875 1,375 1,37109375 -0,0341275 0,1308594 0,0482501 -0,0016467

8 1,3671875 1,37109375 1,36914063 -0,0341275 0,0482501 0,0070156 -0,0002394

9 1,3671875 1,36914063 1,36816407 -0,0341275 0,0070156 0,0135842 0,00046359

10 1,36816407 1,36914063 1,36865235 -0,013584 0,0070156 -0,0032857 0,0000446

11 1,36865235 1,36914063 1,36889649 -0,0032857 0,0070156 0,0018646 -0,00000613

Jadi akar dari persamaan ( ) = :+ 2 + 10 − 20 = 0 dengan selang 1; 1,5! adalah

SECTION PERTANYAAN

1. Nama : Abdul Nazir

Nim : 2010 121 240

Pertanyaan :

Pada contoh 1 diketahui (2) = −2 , bagaimana cara mendapatkan nilai −2 tersebut ?

Jawaban :

2. Nama : Putri Nurjannah Utami

Nim : 2010 121 264

Pertanyaan :

Kapan iterasinya berhenti jika pada soal di ketahui nilai epsilon ?

Jawaban :

Penghitungan iterasi berhenti jika nilai ( ) < %

3. Nama : Veny Ramadhanty

Nim : 2010 121 270

Pertanyaan :

Kapankah iterasi berhenti jika nilai epsilon tidak diketahui ?

Jawaban :

Iterasi itu dihentikan pada standar error (kesalahan relative semu) yang paling terkecil.

Dimana rumus standar error ( kesalahan relative semu )

DAFTAR PUSTAKA

A,Salusu. 2008. Metode Numerik. Yogyakarta: Graha Ilmu

Munir,rinaldi. 2008. Metode Numerik. Bandung: Informatika