Perbandingan Metode Empirical Bayes (EB) dan Empirical Best Linear Unbiased Prediction (EBLUP) pada Pendugaan Area Kecil (Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor)

(1)

Linear Unbiased Prediction (EBLUP) pada Pendugaan Area Kecil (Studi Kasus Pendugaan Pengeluaran per Kapita di Kota Bogor). Dibimbing oleh BUDI SUSETYO dan KUSMAN SADIK.

Pendugaan area kecil (small area estimation) merupakan suatu metode untuk menduga parameter pada area kecil dengan memanfaatkan informasi dari luar area, dari dalam area itu sendiri, dan dari luar survei. Untuk meningkatkan keakuratan dalam pendugaan area kecil digunakan pendugaan secara tidak langsung (indirect estimation). Metode yang dapat digunakan dalam pendugaan area kecil adalah penduga berbasis rancangan dan penduga berbasis model. Yang termasuk dalam metode berbasis model diantaranya adalah Empirical Bayes (EB), Empirical Best Linear Unbiased Prediction (EBLUP), dan Hierarchical Bayes (HB). Tingkat keakuratan dari pendugaan parameter pendugaan langsung dan pendugaan tidak langsung dapat diketahui dari nilai Relative Root Mean Squared Error (RRMSE) yang diperoleh.

Metode EB dan EBLUP digunakan untuk melakukan pendugaan tidak langsung terhadap pengeluaran per kapita di kota Bogor. Pendugaan tidak langsung menggunakan metode EB dan EBLUP menghasilkan nilai RRMSE yang lebih kecil dibandingkan dengan pendugaan langsung, yang menunjukkan bahwa kedua metode tersebut dapat memperbaiki hasil pendugaan langsung. Dalam menduga pengeluaran per kapita, metode EB menghasilkan nilai RRMSE yang lebih kecil dibandingkan metode EBLUP.

(2)

(Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor)

AGUSTINA DWI WARDANI

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(3)

Linear Unbiased Prediction (EBLUP) pada Pendugaan Area Kecil (Studi Kasus Pendugaan Pengeluaran per Kapita di Kota Bogor). Dibimbing oleh BUDI SUSETYO dan KUSMAN SADIK.

Pendugaan area kecil (small area estimation) merupakan suatu metode untuk menduga parameter pada area kecil dengan memanfaatkan informasi dari luar area, dari dalam area itu sendiri, dan dari luar survei. Untuk meningkatkan keakuratan dalam pendugaan area kecil digunakan pendugaan secara tidak langsung (indirect estimation). Metode yang dapat digunakan dalam pendugaan area kecil adalah penduga berbasis rancangan dan penduga berbasis model. Yang termasuk dalam metode berbasis model diantaranya adalah Empirical Bayes (EB), Empirical Best Linear Unbiased Prediction (EBLUP), dan Hierarchical Bayes (HB). Tingkat keakuratan dari pendugaan parameter pendugaan langsung dan pendugaan tidak langsung dapat diketahui dari nilai Relative Root Mean Squared Error (RRMSE) yang diperoleh.

Metode EB dan EBLUP digunakan untuk melakukan pendugaan tidak langsung terhadap pengeluaran per kapita di kota Bogor. Pendugaan tidak langsung menggunakan metode EB dan EBLUP menghasilkan nilai RRMSE yang lebih kecil dibandingkan dengan pendugaan langsung, yang menunjukkan bahwa kedua metode tersebut dapat memperbaiki hasil pendugaan langsung. Dalam menduga pengeluaran per kapita, metode EB menghasilkan nilai RRMSE yang lebih kecil dibandingkan metode EBLUP.

(4)

Oleh:

AGUSTINA DWI WARDANI

G14104007

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

(5)

Nama

: Agustina Dwi Wardani

NRP :

G14104007

Menyetujui:

Pembimbing I

Pembimbing II

Dr. Ir. Budi Susetyo, MS

Kusman Sadik, S.Si, M.Si

NIP. 131624193

NIP.132158751

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. drh. Hasim, DEA

NIP. 131578806

(6)

dan Maturina Beti Riani. Penulis adalah putri kedua dari dua bersaudara.

Penulis menyelesaikan pendidikan dasar di SD Negeri II Kaliwinasuh pada tahun 1998, kemudian menyelesaikan pendidikan menengahnya di SLTP Negeri I Purworejo Klampok dan SMA Negeri I Banjarnegara berturut-turut pada tahun 2001 dan 2004. Penulis diterima sebagai mahasiswa Departemen Statistika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor pada tahun 2004 melalui jalur Undangan Seleksi Masuk IPB (USMI).

(7)

rahmat, dan karuniaNya sehingga penulis dapat menyelesaikan penyusunan karya ilmiah dengan judul “Perbandingan Metode Empirical Bayes (EB) dan Empirical Best Linear Unbiased Prediction (EBLUP) pada Pendugaan Area Kecil (Studi Kasus Pendugaan Pengeluaran Per Kapita di Kota Bogor)”.

Karya ilmiah ini disusun sebagai salah satu kewajiban akademik yang harus dipenuhi dan merupakan salah syarat kelulusan mahasiswa untuk mendapatkan gelar Sarjana Sains (S.Si) pada Departemen Statistika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Penulis mengucapkan terima kasih yang sebesar-besarnya kepada Bapak Dr. Ir. Budi Susetyo, MS dan Bapak Kusman Sadik, S.Si, M.Si selaku pembimbing yang selalu memberikan saran, kritik, dan masukan kepada penulis dalam penyusunan karya ilmiah ini. Terima kasih juga penulis sampaikan kepada semua pihak yang telah turut serta membantu dalam penyusunan karya ilmiah ini, antara lain:

1. Bapak Dr. Ir. Hari Wijayanto, MS. beserta seluruh dosen yang telah memberikan bekal ilmu, wawasan dan pengetahuan selama penulis menuntut ilmu di Departemen Statistika, Bapak Dr. Ir. M. Nur Aidi selaku dosen penguji, serta kepada seluruh staf administrasi dan karyawan Departemen Statistika atas bantuannya selama ini.

2. Ibu dan Bapak serta kakak tersayang Eka Wardani Rahmawati atas cinta, kasih sayang, doa, dukungan dan semangat yang diberikan.

3. Geng SAE’ers: Ratih, Ika, Irene, Rere, dan Noko sebagai tempat bertukar pikiran dan diskusi. 4. Mala, Sevrien, Yusri, Neng, Rani pd, Meta, Amey, dan Cheri atas persahabatan, semangat dan

dukungannya.

5. DIAYISHI atas persahabatan,dukungan, dan semangat yang kalian berikan kepadaku. 6. Lia, Fisca, Rizqa, dan Coy teman seperjuanganku.

7. Ufi, Vinny, Toki, Nikhen, Lele, Rangga, Wiwik, Zul, Inal, Wita, Dhika, Doddy, Efril, Kus, dan semua teman-teman STK’41 yang tidak dapat disebutkan satu-persatu atas dukungan dan kebersamannya selama empat tahun ini.

8. Adik-adik kelas STK’42, STK’43, dan STK’44.

9. Bapak Supriyanto dan Ibu Yani atas kasih sayang yang diberikan serta keluarga besar Pondok Ginastri atas semangat, dukungan, dan kebersamaannya.

Semoga bantuan yang telah diberikan kepada penulis mendapat balasan dari Allah SWT. Penulis menyadari bahwa tulisan ini jauh dari sempurna. Oleh karena itu, sangat diharapkan kritik, saran, dan masukannya agar tulisan ini bisa lebih baik lagi di masa yang akan datang serta dapat memberikan manfaat.

Bogor, September 2008

(8)

DAFTAR TABEL... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

PENDAHULUAN... 1

Latar Belakang ... 1

Tujuan ... 1

TINJAUAN PUSTAKA... 1

Pengeluaran per kapita ... 1

Pendugaan Area Kecil ... 1

Penduga Langsung ... 2

Penduga Sintetik... 2

Model Area Kecil ... 2

Metode Empirical Bayes (EB)... 3

Pendekatan Jackknife... 4

Metode Empirical Best Linier Unbiased Predictions (EBLUP) ... 4

BAHAN DAN METODE ... 5

Bahan ... 5

Metode ... 5

HASIL DAN PEMBAHASAN ... 6

Pendugaan Langsung Pengeluaran per kapita... 6

Eksplorasi Data ... 6

Pendugaan Parameter dengan Penduga EB ... 6

Pendugaan Parameter dengan Penduga EBLUP ... 7

Perbandingan Hasil Pendugaan Metode EB dan EBLUP... 8

KESIMPULAN ... 9

(9)

Halaman 1. Nilai Statistik Pengeluaran per kapita (x Rp.100.000,00) ... 6 2. Nilai Dugaan Parameter Beta... 7 3. Perbandingan nilai statistik RRMSE antara penduga langsung dan pendugaan EB

pendekatan jackknife... 7 4. Perbandingan nilai statistik RRMSE antara penduga langsung dan pendugaan EBLUP.. 8

DAFTAR GAMBAR

Halaman 1. Diagram Kotak Garis Pengeluaran per kapita Hasil Pendugaan Langsung ... 6 2. Perbandingan nilai RRMSE antara pendugaan langsung dan pendugaan EB pendekatan

jackknife... 7 3. Perbandingan nilai RRMSE antara pendugaan langsung dan pendugaan EBLUP ... 7 4. Perbandingan nilai RRMSE antara penduga EB pendekatan jackknife dan penduga EBLUP ... 8 5. Selisih RRMSE metode EB pendekatan Jackknife dan metode EBLUP ... 8

DAFTAR LAMPIRAN

Halaman 1. Hasil Pendugaan Pengeluaran per kapita (x Rp.100.000,00) Pendugaan Langsung ... 11 2. Diagram pencar dan nilai korelasi peubah-peubah pendukung (xi)... 12

3. Keluaran SAS bagi Pendugaan Parameter ... 14 4. Hasil Pendugaan Pengeluaran per kapita (x Rp.100.000,00) dengan pendugaan langsung,

(10)

PENDAHULUAN

Latar Belakang

Pendugaan terhadap parameter membutuhkan ketelitian dan keakuratan yang tinggi. Ketelitian suatu penduga dapat diukur dengan nilai ragam yang dihasilkan oleh penduga, sedangkan keakuratan penduga dapat diukur dengan nilai Relative Root Mean Squared Error (RRMSE). Ketelitian dan keakuratan tersebut dapat dicapai salah satunya adalah dengan mengambil ukuran contoh yang mencukupi untuk melakukan pendugaan. Pada suatu survei berskala besar atau nasional, seringkali ukuran contoh yang diambil terlalu sedikit, terutama survei yang dilakukan pada area kecil. Suatu area disebut kecil apabila area tersebut merupakan bagian dari wilayah populasi baik berdasarkan geografi, ekonomi, sosial budaya, ataupun yang lainnya (Rao 2003). Menurut Ramsini et al. (2001), pendugaan langsung pada suatu area kecil merupakan penduga tak bias tetapi memiliki ragam yang besar karena diperoleh dari ukuran contoh yang kecil.

Pendugaan pada area kecil (small area estimation, SAE) merupakan salah satu upaya untuk meningkatkan keakuratan, yaitu dengan menggunakan pendugaan secara tidak langsung (indirect estimation). Pendugaan parameter dalam area kecil dapat didekati dengan dua jenis metode, yaitu metode berbasis model (model based estimator) dan metode berbasis rancangan (design based estimator). Pendugaan dengan metode berbasis model artinya menduga parameter suatu area yang didasarkan informasi yang berhubungan dengan parameter, dimana informasi tersebut berasal dari area yang sama, dari area lain dari survei yang sama dan dari area diluar survei yang dilakukan. Sedangkan pendugaan dengan metode berbasis rancangan dilakukan berdasarkan data contoh dari area tempat survei dilakukan. Salah satu metode yang termasuk dalam metode ini adalah pendugaan langsung (direct estimator).

Beberapa metode yang tergolong dalam metode berbasis model adalah metode Empirical Bayes (EB), Empirical Best Linear Unbiased Predictions (EBLUP), dan Hierarchical Bayes (HB). Penelitian ini akan membahas lebih lanjut mengenai metode EB dan EBLUP.

Metode EB merupakan metode pendugaan parameter pada area kecil yang didasarkan pada model Bayes. Pada metode EB digunakan pendekatan jackknife yang dipakai

untuk mengoreksi bias akibat adanya pendugaan pada parameternya.

Metode EBLUP dilahirkan dari metode pendugaan BLUP. Pada metode BLUP diasumsikan komponen ragam diketahui. Namun dalam kenyataannya, komponen ragam sulit untuk diketahui sehingga diperlukan pendugaan terhadap komponen ragam melalui data contoh. Metode EBLUP mensubstitusi komponen ragam yang tidak diketahui ini ke dalam penduga BLUP (Saei & Chambers 2003).

Penerapan pendugaan parameter baik melalui pendugaan langsung, EB dan EBLUP dalam penelitian ini akan menggunakan data SUSENAS dengan memanfaatkan peubah pendukung (auxiliary variable) yang bersumberkan dari data PODES.

Tujuan

Tujuan dari penelitian ini adalah membandingkan hasil penggunaan metode langsung, EB dan EBLUP dalam menduga pengeluaran per kapita desa/kelurahan di kota Bogor.

TINJAUAN PUSTAKA

Pengeluaran per kapita

Menurut Badan Pusat Statistik (BPS), pengeluaran per kapita menunjukkan besarnya pengeluaran setiap anggota rumah tangga dalam kurun waktu satu bulan. Rumah tangga dalam definisi ini adalah sekelompok orang yang mendiami sebagian atau seluruh bangunan fisik dan biasanya tinggal bersama serta makan dari satu dapur (BPS 2003). Dalam satu rumah tangga bisa terdiri dari satu, dua, atau lebih kepala keluarga.

Pengeluaran per kapita biasa dirumuskan sebagai berikut:

p y

q

=

dimana:

y = pengeluaran per kapita

p = pengeluaran rumah tangga sebulan q = jumlah anggota rumah tangga

Pendugaan Area Kecil

(11)

dalam area itu sendiri, dan dari luar survei (Longford 2005).

Pendugaan pada area kecil merupakan salah satu upaya untuk meningkatkan keakuratan, yaitu dengan menggunakan pendugaan secara tidak langsung. Pendugaan tidak langsung dapat dilakukan dengan memanfaatkan peubah-peubah tambahan dalam menduga parameter. Peubah-peubah pendukung tersebut dapat berupa informasi tambahan yang didapatkan dari area lain yang serupa, survei terdahulu yang dilakukan di daerah yang sama, atau peubah yang lain yang berhubungan dengan peubah yang ingin diduga. Pendugaan tidak langsung pada area kecil memiliki beberapa keuntungan, yaitu memilki dugaan yang optimal, memperoleh model valid yang berasal dari data contoh, dan dapat menjelaskan berbagai macam model berdasar pada respon alami suatu peubah dan kekomplekan struktur data (Rao 2003).

Proses pendugaan pada suatu area atau subpopulasi dapat dibagi menjadi dua macam, yaitu:

1. Penduga Berbasis Rancangan

Rao (2003) menyebutkan bahwa pendugaan pada metode berbasis rancangan merupakan pendugaan pada suatu area berdasarkan data contoh dari area tersebut. Pada proses pendugaan tersebut dapat digunakan informasi tambahan (auxiliary information) untuk menduga parameter yang menjadi perhatian. Pendekatan yang digunakan pada proses pendugaan ini adalah pendekatan berbasis rancangan. Pada pendugaan ini diasumsikan tidak terjadi galat pengukuran.

2. Penduga Berbasis Model

Pendugaan pada metode berbasis model merupakan pendugaan pada suatu area dengan cara menghubungkan informasi pada area tersebut dengan area lain melalui model yang tepat. Hal ini berarti bahwa dugaan tersebut mencakup data dari area lain (Kurnia & Notodiputro 2006). Penduga tidak langsung berdasarkan model area kecil (small area model) dikatakan sebagai penduga berbasis model (Rao 2003). Ramsini et al. (2001) menyatakan bahwa penduga tidak langsung yang diperoleh dengan memanfaatkan informasi peubah lain yang berhubungan dengan parameter yang diamati sering disebut sebagai penduga berbasis model. Metode pendugaan yang termasuk dalam penduga berbasis model adalah metode EB, EBLUP, dan HB.

Penduga Langsung

Penduga langsung merupakan penduga berbasis rancangan dan hanya dapat digunakan jika semua area dalam suatu populasi digunakan sebagai contoh (Rao 2003). Penduga langsung menggunakan nilai dari peubah yang menjadi perhatian hanya pada periode waktu dan unit contoh pada area yang menjadi perhatian (Ramsini et al. 2001). Data contoh dari suatu survei dapat digunakan untuk mendapatkan pendugaan langsung yang dapat dipercaya bagi suatu area besar. Ramsini et al. (2001) menyebutkan bahwa nilai hasil pendugaan langsung pada suatu area kecil merupakan penduga tak bias meskipun memiliki ragam yang besar dikarenakan dugaannya diperoleh dari ukuran contoh yang kecil.

Penduga Sintetik

Gonzalez (1973) dalam Rao (2003) menyebutkan bahwa suatu penduga disebut sebagai penduga sintetik apabila suatu penduga langsung yang diperoleh dari suatu survei contoh untuk area besar, digunakan untuk mendapatkan pendugaan tak langsung bagi area kecil dengan mengasumsikan bahwa area kecil tersebut memiliki karakteristik yang sama dengan area besar.

Penduga sintetik dalam pendugaan area kecil dapat digunakan dalam menduga nilai respon pada area lain yang tidak disurvei dengan mengasumsikan area tersebut memiliki karakteristik yang sama dengan area yang telah diduga.

Model Area Kecil

Dalam pendugaan area kecil terdapat dua jenis model dasar yang digunakan, yaitu basic area level model dan basic unit level model (Rao 2003).

1. Basic area level model

Merupakan model yang didasarkan pada ketersediaan data pendukung yang hanya ada untuk level area tertentu, misalkan xi=(x1i,……,xpi)T dengan parameter yang akan

diduga adalah θi yang diasumsikan

mempunyai hubungan dengan xi. Data

pendukung tersebut digunakan untuk membangun model θi = xiTβ + bivi, dengan

i=1,…..,m dan vi ~ N(0, σ2v), sebagai

pengaruh acak yang diasumsikan menyebar normal. Kesimpulan mengenai θi, dapat

diketahui dengan mengasumsikan bahwa model penduga langsung yi telah tersedia,

yaitu: yi = θi + ei, dengan i = 1,…...,m dan

sampling error ei ~ N(0, σ2ei), dengan σ2ei

(12)

Kemudian kedua model tersebut digabung sehingga didapatkan model gabungan: yi =

xiTβ + bivi + ei, dengan i=1,…..,m dan bi

diketahui bernilai positif konstan. Model tersebut merupakan bentuk khusus dari model linier campuran (general linear mixed model). 2. Basic unit level model

Merupakan suatu model dimana data-data pendukung yang tersedia bersesuaian secara individu dengan data respon, misal xij=(xij1,…..,xijp)T sehingga didapatkan suatu

model regresi tersarang yij = xijTβ + vi + eij,

dengan i = 1,…..,m; j = 1,…..,Ni, vi ~ N(0,

σ2

v) dan ei ~ N(0, σ2ei).

Saei dan Chambers (2003) mengemukakan dua ide utama dalam mengembangkan model untuk SAE yaitu (1) asumsi bahwa keragaman di dalam subpopulasi peubah respon dapat diterangkan seluruhnya oleh hubungan keragaman yang bersesuaian pada informasi tambahan, disebut model pengaruh tetap (fixed effect), (2) asumsi keragaman spesifik subpopulasi tidak dapat diterangkan oleh informasi tambahan dan merupakan pengaruh acak subpopulasi (random effect). Gabungan dari kedua asumsi tersebut membentuk model pengaruh campuran (mixed model). Namun, kelemahan terjadi jika model yang dibuat tidak merepresentasikan kondisi sebenarnya (Breidt 2001).

Metode Empirical Bayes (EB)

Metode Empirical Bayes (EB) merupakan metode pendugaan parameter pada area kecil yang didasarkan pada metode Bayes.

Dalam metode Bayes, sebaran posterior yang digunakan untuk parameter yang diamati dinotasikan dengan f(θi|yi,β,σ2v) dengan

asumsi β dan σ2v diketahui. Sedangkan pada

metode EB, inferensia yang diperoleh didasarkan pada dugaan sebaran posterior dari θi dengan memasukkan nilai dugaan β dan σ2v

yaitu f(θi|yi,βˆ,σˆv2).

Model Fay dan Herriot (1979) untuk model basic area level adalah:

yi = xiTβ + vi + ei

dengan vi ~ N(0, σ2v) dan ei ~ N(0, σ2ei),

dimana vi dan ei saling bebas. β dan σ2v tidak

diketahui sedangkan σ2ei diasumsikan

diketahui (Kurnia & Notodiputro 2006). Misal σ2v dan σ2ei disimbolkan dengan A

dan Di, selanjutnya merupakan penduga

Bayes untuk θi, dengan mengikuti model

Bayes:

(a) yi | θi ~ N(θi, Di)

(b) θi ~ N(xiTβ, A) adalah sebaran prior untuk

θi dan i = 1, . . . ,m.

Model Bayes tersebut dapat dijelaskan oleh:

f(yi | θi) = 1 _exp 1 ₍ ₎2

2

2 i i i i

y D D θ π ⎛ ⎞ − − ⎜ ⎟ ⎝ ⎠ dan

π(θi) = 1 _exp 1 ₍ ₎2

2 2

T i xi

A

A θ β

π

⎛₋ ₋ ⎞

⎜ ⎟

⎝ ⎠dan

f(yi,θi|β,A) = 2

1

1 1

exp ( )

2 2

m

i i

i i i

y D D θ π = ⎛ ⎞ − − ⎜ ⎟ ⎝ ⎠

∏

1 _exp 1 ₍ ₎2

2 2

T i xi

A

A θ β

π

⎛₋ ₋ ⎞

⎜ ⎟

⎝ ⎠

untuk yi = (y1, y2,….., ym)T dan θi = (θ1, θ2,…..,

θm)T.

Fungsi eksponensial tanpa faktor (-1/2) dari f(yi, θi| β, A) dapat dilihat sebagai berikut:

= 1 ₍ ₎2 1₍ 2

D A

T i i i i i

y −θ + θ −x β)

=

(

₂ ₂

)

(

₂

( )

2

)

1 1

2 2

D A

T T i i i i i i i i i

y − yθ θ+ + θ − θ βx + x β

= 1 1 2 ₂ _a*

D A D A

T i i

i i

y x β

θ ⎛ ⎞θ _i

⎛ ⎞ + − + + ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ = 2 * 1 1 2

D A D A

1 1 1 1

a

D A D A

D A

1 1

x

D A D A

T i i i i i i T i i i i i i T i i i i y x y x y x β θ θ β β ⎧ ⎛ ⎛ ⎞ ⎛ ⎞⎞⎫ − + + ⎪ ⎜_⎜ ⎜ ⎟ ⎜ ⎟⎟_⎟⎪ ⎝ ⎠ ⎝ ⎠ ⎪ ⎝ ⎠⎪ ⎪ _⎧ _⎫ ⎪ ⎡ ⎤ ⎛ ₊ ⎞⎪ ⎛ ₊ ⎞ ⎛ ₊ ⎞ ⎪ ⎪ ⎪ ⎨ ⎢ ⎥ ⎬ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠⎪_{+ ⎨}⎪⎣ ⎦ ⎪ ⎪ ⎬ ⎪ _⎡_⎛ _{⎞ ⎛} _⎞_⎤ ⎪ ⎪ ⎪ ⎪ _⎢_⎜ ₊ _{⎟ ⎜} ₊ _⎟_⎥ ⎪ ⎪ ⎪ ⎪ _⎩ _⎣_⎝ _{⎠ ⎝} _⎠_⎦_⎭ ⎪ ⎩ ⎭ + = 2 *

1 1 1 1

a

D A D A

D A T i i i i i i i

y x β

θ ⎧ ⎛ ⎞ ⎛ ⎞⎫ ⎪ ⎪ ⎛ ⎞ + ⎨ −⎜ + ⎟ ⎜ + ⎟⎬ + ⎪ ⎝ ⎠ ⎝ ⎠⎪ ⎝ ⎠ ⎩ ⎭ ⎜ ⎟ i

dengan a*adalah konstanta dan bebas dari θ

i.

(θi|yi,β,A) ~N

1

A D 1 1

,

A+D D A

T i i i

i i

y x β −

⎡_⎛ ₊ _{⎞ ⎛} _⎞ ⎤

⎢_⎜ _{⎟ ⎜} + _⎟ ⎥

⎢⎝ ⎠ ⎝ ⎠ ⎥

⎣ ⎦

(θi|yi,β,A) ~ N

(

)

i

AD A

,

A+D A+D

T T i

i i i

i

x β y x β

⎛ ⎞

⎜ + − ⎟

⎝ ⎠

Berdasarkan formula tersebut maka akan diperoleh suatu penduga:

B

ˆ

i

θ = E(θi | yi, β, A) = xiTβ + (1- Bi) (yi - xiTβ),

dengan Bi = Di/(A + Di)

MSE ( _ˆB i

θ ) = Var(θi| yi, β, A) = ADi/(A + Di)

Metode pendugaan yang dapat digunakan dalam menduga parameter A adalah metode momen, minimum variance quadratic unbiased estimation (MIVQUE), maximum likelihood (ML), dan restricted/residual maximum likelihood (REML). Sedangkan parameter β dapat diduga dengan metode momen dan weighted least square (WLS).

B i

(13)

Jika A dan β diduga, maka akan diperoleh suatu penduga empirical Bayes:

EB

ˆ T ˆ _{(1 B )(}ˆ T ₎

i xi i yi xi ˆ

θ = β+ − − β

dengan _Bˆ _D _(A+Dˆ

i = i+ i)

ˆ

i

Berdasarkan metode Bayes maka diperoleh:

EB

ˆ ˆ ˆ ˆ

MSE(θ_i )=Var(θ_i|y_i, , A)=AD / (A+D )β _i

Adanya pendugaan pada nilai A dan β mengakibatkan penduga bersifat bias. Hal tersebut dapat dikoreksi dengan menggunakan pendekatan jackknife (Jiang, Lahiri, dan Wan (2002) dalam Rao 2003) maupun dengan pendekatan bootstrap (Butar dan Lahiri (2003) dalam Rao 2003). Metode EB juga dapat diaplikasikan dalam pemodelan data biner.

Pendekatan Jackknife

Pendekatan jackknife diperkenalkan oleh Tukey (1958) dan kemudian berkembang menjadi suatu metode yang dapat digunakan untuk mengoreksi bias suatu penduga. Pendekatan jackknife merupakan salah satu metode yang sering digunakan dalam survei karena konsepnya yang sederhana. Prosedur yang dilakukan dalam pendekatan Jackknife adalah dengan menghapus pengamatan ke-i dimana i=1,2,….,m.

Tahapan-tahapan untuk menghitung nilai MSE (_ˆEB

i

θ ) adalah sebagai berikut: (a)hitung nilai M1i dengan rumus:

( )

2

(

2

)

( )

1i 1i 1i ( ) 1i

1

m-1

M g s g s g s

m

v v u

u − = ⎛ ⎞ _⎡ _⎤ = −_⎜ _⎟ _⎣ − ⎝ ⎠

∑

2 v ⎦

Nilai

(

2

)

1i ( )

g sv−u diperoleh dengan menghapus

pengamatan ke-u pada himpunan data

( )

2 1i

g sv dan u = 1, 2, . . . ,m.

(b)hitung nilai M2i dengan rumus:

( ) ( )

2

EB EB

2i ( )

1

m-1 _ˆ _ˆ

M m

m

i u i u θ − θ = ⎛ ⎞ _⎡ _⎤ =_⎜ _⎟ _⎣ − _⎦ ⎝ ⎠

∑

dimana ( ) diperoleh dengan menghapus

pengamatan ke-u pada himpunan data

EB ( ) ˆ i u θ ₋ EB ˆ i θ . (c)hitung nilai MSE dengan rumus sebagai

berikut:

( )

EB

1i 2i

ˆ

MSE θ_i =M +M

Metode Empirical Best Linier Unbiased Predictions (EBLUP)

Best Linier Unbiased Prediction (BLUP) merupakan suatu pendugaan parameter yang meminimumkan MSE diantara kelas-kelas pendugaan parameter linier tak bias lainnya (Kurnia & Notodiputro 2006). BLUP dihasilkan dengan asumsi bahwa komponen

ragam telah diketahui. Namun dalam prakteknya, komponen ragam tidak diketahui. Oleh karena itu, diperlukan pendugaan terhadap komponen ragam tersebut melalui data contoh. Metode EBLUP mensubtitusi komponen ragam yang tidak diketahui ini dengan penduganya (Saei & Chambers 2003). Model dasar dalam pengembangan pendugaan area kecil didasarkan pada bentuk model linier campuransebagai berikut:

y = Xβ + Zv + e

dengan X adalah matriks berukuran nxp dan

Z matriks berukuran nxq, sedangkan β merupakan pengaruh tetap dan v merupakan pengaruh acak dimana e ~ N(0, D) serta v ~ N(0, A). A dan D merupakan komponen ragam yang tidak diketahui dan bisa diduga dari data dimana A = σ2v dan D = σ2e (Rao

2003).

Nilai harapan y jika v diketahui adalah E(y|v) = Xβ+Zv, dengan ragam D. Dari persamaan model linier campuran diatas dapat diketahui bahwa distribusi marginal bagi y adalah menyebar normal dengan nilai tengah Xβ dan ragam V = D + ZAZT sehingga log-kemungkinan bagi (β, θ) untuk θ = (σ2v, σ2e)

adalah:

Log L(β,θ) = -1/2 log |V| - 1/2 (y – Xβ)TV-1 (y - Xβ)

jika θ fixed (tetap) maka penduga bagi β merupakan penyelesaian dari:

(XTV-1X)β = XTV-1y

yang tidak lain adalah penyelesaian melalui generalized atau weighted least square (WLS).

Log-kemungkinan untuk seluruh parameter (β,θ,v) adalah sebagai berikut:

L(β,θ,v)=p(y|v)p(v).

Berdasarkan persamaan tersebut diatas dan v ~ N(0, A), maka:

Log L(β,θ v) = -1/2 log |D| - 1/2 (y - xβ - Zv)T D-1(y – Xβ - Zv) – 1/2 log |A| - 1/2 vT A-1v

untuk (β,θ) diketahui maka didapatkan turunan persamaan log L(β,θ,v) terhadap v adalah sebagai berikut:

(

)

1 1

logL

Z DT y-X -Z A

d

v v

dv β

− −

= −

dan penduga bagi v merupakan penyelesaian dari:

(ZTD-1Z+A-1)v=ZTD-1(y–Xβ).

(14)

pengaruh acak area. Penduga tersebut kemudian dikenal sebagai BLUP.

(

)

BLUP 2

ˆ ˆ _|

i i yi v

θ =θ σ

= A

(

)

A+D T T i i i i x

x β+⎛_⎜ ⎞_⎟ y − β

⎝ ⎠

X V X) X− −

Ghosh dan Rao (1994) dalam Kurnia dan Notodiputro (2005) mengemukakan bahwa MSE(

θ

ˆ_iBLUP) =g1i(A) + g2i(A), dengan g1i(A)

= Var(θi|yi, β, A) = ADi /(A + Di) dan g2i(A) =

(Di)2/(A + Di)[X (T_i T 1 1 _i].

Jika A diduga menggunakan metode ML, REML, ataupun momen sehingga dengan mensubtitusi β oleh

β

ˆdan A oleh Aterhadap

penduga BLUP ( ), maka akan diperoleh suatu penduga baru, yaitu:

ˆ BLUP ˆ i

θ

(

)

EBLUP

ˆ ˆ _{| A}

i i yi

θ =θ ˆ

= Aˆ

(

)

ˆ A+D T T i i i i x x β+⎛⎜_⎜ ⎞⎟_⎟ y − β

⎝ ⎠

i

Didefinisikan MSE dari adalah sebagai berikut:

EBLUP ˆ

i

θ

EBLUP EBLUP 2

ˆ ˆ

MSE(θi )=E(θi −θ)

= _Var(ˆEBLUP_{) [Bias(}ˆEBLUP_)]2

i i

θ + θ

ˆ

i

ˆ (A)+g (A)+2g (A)

persamaan tersebut dapat diuraikan menjadi:

EBLUP BLUP EBLUP BLUP 2

ˆ ˆ ˆ

MSE(θ_i )=MSE(θ_i ) E(+ θ_i −θ )

Prasad dan Rao (1990) dalam Rao (2003) menggunakan ekspansi deret Taylor untuk menduga MSE (θˆEBLUP) sehingga diperoleh:

MSE(

θ

ˆ_iEBLUP)=g1i ˆ 2i ˆ 3i

dengan 2 2

3i 2 3

1 i

ˆ 2D

ˆ ˆ ˆ

g (A) (A+D )

ˆ ˆ m (A+D )

m i

i i=

=

∑

BAHAN DAN METODE

Bahan

Sumber data yang digunakan dalam penelitian ini adalah data SUSENAS 2005 dengan informasi data berbasis rumah tangga serta PODES 2006 sebagai sumber data peubah pendukung.

Peubah respon yang menjadi perhatian dalam penelitian ini adalah pengeluaran per kapita pada desa/kelurahan di kota Bogor. Peubah pendukung xi yang dianalisis adalah

sebanyak 10 peubah, diantaranya: x1 = Persentase keluarga pertanian.

x2 = Persentase jumlah pra KS dan KS1.

x3 = Persentase jumlah penerima "kartu

sehat/kartu program kesehatan masyarakat miskin" =1th.

x4 = Persentase jumlah surat miskin

dikeluarkan dalam setahun terakhir. x5 = Persentase jumlah keluarga yang

berlangganan telepon kabel. x6 = Jumlah toko/warung kelontong.

x7 = Jumlah bank umum (kantor

pusat/cabang/capem). x8 = Jumlah koperasi.

x9 = Jumlah penduduk.

x10 = Jumlah keluarga.

Peubah respon diperoleh dari data SUSENAS sedangkan peubah pendukung berasal dari data PODES.

Metode

Tahapan-tahapan yang dilakukan pada penelitian ini adalah:

1. Penyiapan data dilakukan dengan memilih gugus data kota Bogor dari kumpulan data SUSENAS 2005 dan PODES 2006. 2. Menghitung pendugaan langsung terhadap

pengeluaran per kapita desa/kelurahan kota Bogor menggunakan proc means pada SAS berdasarkan data SUSENAS 2005.

3. Memilih peubah pendukung yang

mempengaruhi pengeluaran per kapita pada beberapa desa di kota Bogor.

4. Penerapan metode EB.

(i) Melakukan pendugaan A dengan metode REML pada proc mixed pada SAS dan βdengan metode WLS. (ii) Menduga pengeluaran per kapita

desa/kelurahan kota Bogor.

(iii)Menghitung MSE (θ_ˆEB_{) dengan}

konsep jackknife.

(iv)Menghitung nilai RRMSE (θ_ˆEB

) . 5. Penerapan metode EBLUP.

(i) Melakukan pendugaan A dengan metode REML pada proc mixed pada SAS dan βdengan metode WLS. (ii) Menduga pengeluaran per kapita

desa/kelurahan kota Bogor. (iii)Menghitung MSE(θ_ˆEBLUP).

(iv)Menghitung nilai RRMSE(θ_ˆEBLUP). 6. Membandingkan hasil pendugaan metode

EB dan EBLUP berdasarkan nilai Relative Root Mean Squared Error (RRMSE). Formula bagi RRMSE adalah sebagai berikut:

ˆ MSE( ) ˆ

RRMSE( )= x100%

ˆ

θ θ

θ

(15)

HASIL DAN PEMBAHASAN

Pendugaan Langsung Pengeluaran per Kapita

Pengeluaran per kapita dicari dengan membagi jumlah pengeluaran makanan dan bukan makanan rumah tangga dibagi dengan jumlah anggota rumah tangga dengan umur diatas 5 tahun. Hasil dari pendugaan langsung tersebut berupa pengeluaran per kapita pada masing-masing desa/kelurahan yang tersurvei di kota Bogor.

Penghitungan pengeluaran per kapita dilakukan terhadap 37 desa/kelurahan pada kota Bogor dengan banyaknya contoh pada masing-masing desa/kelurahan adalah 16 rumah tangga kecuali pada desa Kedung Halang sebanyak 15 rumah tangga dan desa Kedung Badak sebanyak 32 rumah tangga. Dari hasil pendugaan langsung seperti yang tertera pada Lampiran 1, dapat diketahui bahwa desa Pabaton memiliki pengeluaran per kapita paling tinggi.

Eksplorasi Data

Pengeluaran per kapita desa/kelurahan kota Bogor seperti yang tertera pada Lampiran 1, menunjukkan bahwa pengeluraran per kapita desa-desa tersebut cukup beragam. Hal tersebut ditunjukkan dengan nilai koefisien keragaman yang cukup besar yaitu 60.98%.

Tabel 1 Nilai Statistik Pengeluaran per kapita (x Rp.100.000,00).

Statistik Pengeluaran per kapita

Rataan 3.947

SE Rataan 0.396

Koef.keragaman 60.98 Minimum 1.781 Median 3.627 Maksimum 16.049

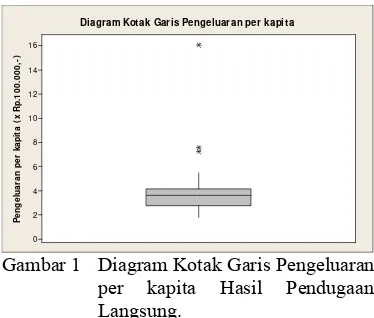
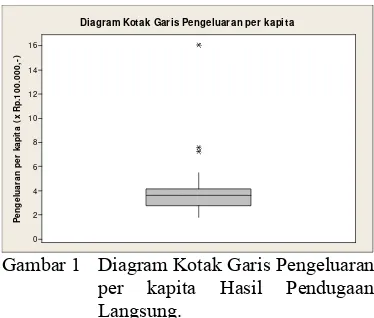
Gambar 1 memperlihatkan terdapat tiga titik nilai pengeluaran per kapita yang berada di luar kotak. Tiga titik tersebut adalah desa Pabaton, desa Kebon Kelapa, dan desa Sindangbarang. Desa-desa tersebut memiliki pengeluaran per kapita yang lebih besar dibandingkan dengan desa/kelurahan yang lain.

Ragam sampling error (Di) dugaan

pengeluaran per kapita didapatkan dengan membagi ragam dengan banyaknya contoh (si2/ni). Nilai ragam Di dapat diduga secara

langsung dari data. Hasil ragam sampling error (Di) dugaan pengeluaran per kapita

dapat dilihat pada Lampiran 1.

P e n g e lu a ra n p e r k a p it a ( x R p .1 0 0 .0 0 0 ,-) 16 14 12 10 8 6 4 2 0

Diagram Kotak Garis Pengeluaran per kapita

Gambar 1 Diagram Kotak Garis Pengeluaran per kapita Hasil Pendugaan Langsung.

Pemilihan peubah-peubah pendukung yang diasumsikan mempengaruhi pengeluaran per kapita dilakukan dengan melakukan eksplorasi terhadap data menggunakan diagram pencar dan nilai korelasi Pearson yang tersaji pada Lampiran 2. Peubah-peubah pendukung yang dipilih adalah sebanyak 10 peubah. Diagram pencar dan nilai korelasi Pearson bagi data peubah-peubah pendukung menunjukkan bahwa terdapat hubungan antara peubah pendukung dengan pengeluaran per kapita.

Hasil dari nilai korelasi Pearson menunjukkan bahwa terdapat 4 peubah yang memiliki korelasi yang cukup kuat dengan pengeluaran per kapita. Peubah-peubah tersebut adalah persentase jumlah keluarga yang berlangganan telepon kabel, jumlah toko/warung kelontong, jumlah bank umum (kantor pusat/cabang/capem), dan jumlah koperasi. Dari nilai korelasi yang didapat bisa diketahui bahwa pengeluaran per kapita berhubungan positif dengan keempat peubah tersebut.

Berdasarkan hasil yang ditunjukkan oleh diagram pencar dan nilai korelasi Pearson maka peubah-peubah tersebut dapat digunakan untuk menggambarkan pengeluaran per kapita pada beberapa desa/kelurahan di kota Bogor.

Pendugaan Parameter dengan Metode EB

Pendugaan parameter dilakukan terhadap 4 peubah penjelas hasil dari eksplorasi data dan didapatkan 2 peubah penjelas yang berpengaruh nyata terhadap pengeluaran per kapita, yaitu persentase jumlah keluarga yang berlangganan telepon kabel dan jumlah toko/warung kelontong seperti yang tertera pada Lampiran 3.

(16)

REML. Sedangkan dugaan parameter β didapatkan dengan menggunakan metode WLS. Nilai A yang didapatkan adalah 4.5071. Sedangkan nilai parameter β yang didapatkan adalah sebagai berikut:

Tabel 2 Nilai Dugaan Parameter Beta.

xi Beta duga

x0 2.2275879

x5 0.0317819

x6 0.0047288

Nilai MSE yang diperoleh dari metode EB memiliki bias dikarenakan pendugaan pada parameternya sehingga dilakukan koreksi dengan menggunakan pendekatan jackknife. Hasil penghitungan metode EB dengan pendekatan jackknife dapat dilihat pada Lampiran 4.

Gambar 2 Perbandingan nilai RRMSE antara pendugaan langsung dan pendugaan EB pendekatan jackknife.

Gambar 2 memperlihatkan bahwa metode EB pendekatan jackknife menghasilkan nilai RRMSE yang lebih kecil dibandingkan dengan hasil pendugaan langsung. Namun terdapat satu nilai RRMSE metode EB pendekatan jackknife yang lebih besar dibandingkan hasil pendugaan langsung yaitu desa Pabaton. Secara umum pendugaan pengeluaran per kapita pada area kecil dengan menggunakan metode EB pendekatan jackknife menghasilkan dugaan dengan tingkat akurasi dan presisi yang lebih baik dibandingkan dengan hasil pendugaan langsung. Hal tersebut dapat diketahui dari nilai RRMSE penduga langsung dan penduga EB pendekatan jackknife seperti yang tertera pada Lampiran 4. Oleh karena itu, dapat dikatakan bahwa hasil pendugaan metode EB pendekatan jackknife dapat memperbaiki hasil pendugaan langsung. Berikut disajikan tabel nilai statistik RRMSE antara penduga

langsung dengan metode EB pendekatan jackknife.

Tabel 3 Perbandingan nilai statistik RRMSE antara penduga langsung dan pendugaan EB pendekatan jackknife.

Statistik

RRMSE Dugaan

Langsung RRMSE EB_Jackknife Rataan 11.442 10.978 SE Rataan 0.784 0.704 Minimum 3.908 3.9 Kuartil 1 8.271 8.184 Median 10.707 10.326 Kuartil 3 13.506 12.847 Maksimum 24.753 23.616

Pendugaan Parameter dengan Metode EBLUP

Metode EBLUP menggunakan metode pendugaan parameter yang sama dengan metode EB pendekatan jackknife dalam menduga parameter keragaman antar desa (A) dan parameter β sehingga hasil dugaan parameter yang didapatkan adalah sama.

I ndex P e n g e lu a ra n p e r k a p it a ( x R p .1 0 0 .0 0 0 ,-) 36 32 28 24 20 16 12 8 4 25 20 15 10 5

Var iab le RRMSE Dir ect RRMSE EB_Jack k n ife Plot of RRMSE Direct, RRMSE EB_ Jackknife

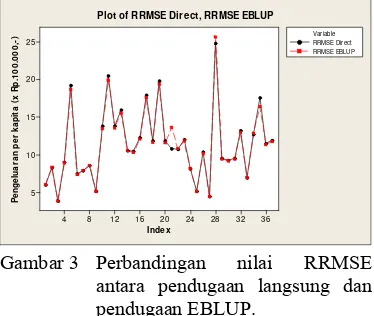
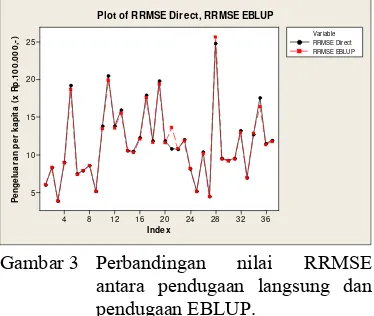
Pendugaan pengeluaran per kapita pada metode EBLUP menghasilkan nilai yang sama dengan nilai pendugaan yang dihasilkan metode EB pendekatan jackknife. Hal ini dikarenakan hasil dugaan metode EB pendekatan jackknife identik dengan dugaan yang dihasilkan oleh metode EBLUP (Lampiran 4). I ndex P e n g e lu a ra n p e r k a p it a ( x R p .1 0 0 .0 0 0 ,-) 36 32 28 24 20 16 12 8 4 25 20 15 10 5 Var iable RRMSE Dir ect RRMSE EBLUP Plot of RRMSE Direct, RRMSE EBLUP

Gambar 3 Perbandingan nilai RRMSE antara pendugaan langsung dan pendugaan EBLUP.

(17)

menggunakan metode EBLUP menghasilkan dugaan dengan tingkat akurasi dan presisi yang lebih baik dibandingkan dengan hasil pendugaan langsung. Hasil dugaan pengeluaran per kapita dan nilai RRMSE metode EBLUP tersaji pada Lampiran 4. Berikut disajikan tabel nilai statistik RRMSE antara penduga langsung dengan metode EBLUP.

Tabel 4 Perbandingan nilai statistik RRMSE antara penduga langsung dan pendugaan EBLUP.

Statistik

RRMSE Dugaan

Langsung RRMSE EBLUP Rataan 11.442 11.373 SE Rataan 0.784 0.774 Minimum 3.908 3.904 Kuartil 1 8.271 8.217 Median 10.707 10.798 Kuartil 3 13.506 13.502 Maksimum 24.753 25.616

Perbandingan Hasil Pendugaan Metode EB dan EBLUP

Keakuratan pendugaan tidak langsung, menggunakan metode EB pendekatan jackknife dan metode EBLUP dapat dilihat dari nilai RRMSE yang dihasilkan. Nilai RRMSE yang kecil menunjukkan bahwa suatu penduga memiliki akurasi yang baik. Perbandingan nilai RRMSE metode EB pendekatan jackknife dengan metode EBLUP dapat dilihat pada Lampiran 4.

Gambar 4 Perbandingan nilai RRMSE antara penduga EB jackknife dan penduga EBLUP.

Gambar 4 memperlihatkan bahwa titik-titik RRMSE metode EBLUP menunjukkan nilai yang lebih tinggi dibandingkan dengan metode EB pendekatan jackknife. Akan tetapi, perbedaan nilai RRMSE di antara kedua metode tersebut tidak terlalu jauh.

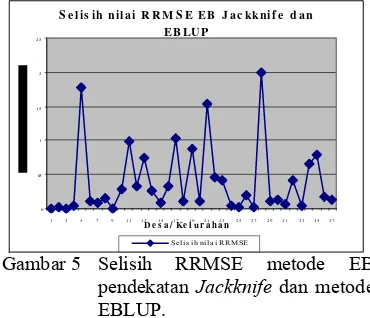
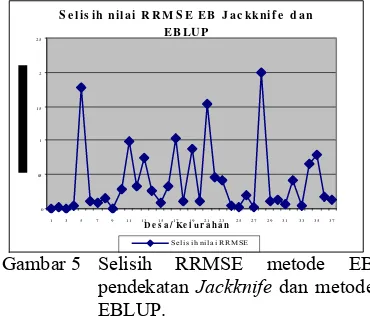
Gambar 5 memperlihatkan perbedaan nilai RRMSE dari metode EB pendekatan jackknife dengan metode EBLUP. Desa Batu tulis, desa Pabaton, dan desa Sindang barang memiliki selisih RRMSE antara metode EB pendekatan jackknife dengan metode EBLUP yang cukup besar yaitu 1.783787, 1.52885, dan 2.002435. Selisih nilai RRMSE yang bertanda positif menunjukkan bahwa metode EB pendekatan jackknife memiliki nilai RRMSE yang lebih kecil dibandingkan dengan metode EBLUP. Berdasarkan hal tersebut maka dapat diketahui bahwa metode EB pendekatan jackknife menghasilkan nilai dugaan yang lebih akurat dalam menduga pengeluaran per kapita dibandingkan dengan metode EBLUP.

S e l i s i h ni l a i R R M S E EB J a c kkni f e d a n EB LU P

0 0.5 1 1 .5 2 2 .5

1 3 5 7 9 1 1 1 3 1 5 1 7 1 9 2 1 2 3 2 5 2 7 2 9 3 1 3 3 3 5 3 7

D e s a / Ke l u r a h a n

Se l i s i h n i l a i R R M SE

Gambar 5 Selisih RRMSE metode EB pendekatan Jackknife dan metode EBLUP.

Meskipun selisih RRMSE antara kedua metode tersebut relatif kecil tetapi hal tersebut cukup memperlihatkan bahwa

metode EB pendekatan jackknife

menghasilkan nilai dugaan yang lebih akurat dibandingkan metode EBLUP.

I ndex P e n g e lu a ra n p e r k a p it a ( x R p .1 0 0 .0 0 0 ,-) 36 32 28 24 20 16 12 8 4 25 20 15 10 5 Variable RRMSE EB_Jack k n ife RRMSE EBLUP Plot of RRMSE EB_ Jackknife, RRMSE EBLUP

Beberapa desa/kelurahan kota Bogor tidak tersurvei pada SUSENAS 2005. Dalam hal ini konsep penduga sintetik dapat digunakan untuk menduga pengeluaran per kapita desa/kelurahan yang tidak disurvei tersebut, dengan asumsi perilaku antar desa adalah sama. Hal ini ditunjukkan dengan nilaiβˆ yang sama. Pengeluaran per kapita dapat dihitung dengan menggunakan nilai harapan dari model area kecil. Formula yang digunakan adalah sebagai berikut:

ˆ

ˆ T

i i

y =x β

Sedangkan formula pendugaan MSE bagi pengeluaran per kapita desa/kelurahan yang tidak disurvei adalah sebagai berikut:

MSE(

y

ˆ

_i) = Var(

x

_iT

β

ˆ

)=

2 2 0 pi p

x

=

(18)

Hasil pendugaan pengeluaran per kapita bagi desa/kelurahan yang tidak disurvei pada SUSENAS 2005 terdapat pada Lampiran 5.

KESIMPULAN

Pendugaan area kecil pada pengeluaran per kapita menggunakan metode EB pendekatan jackknife dan metode EBLUP memiliki hasil yang lebih akurat dibandingkan dengan pendugaan langsung. Pendugaan dengan kedua metode tersebut dapat memperbaiki nilai RRMSE pendugaan langsung walaupun datanya memiliki ragam sampling error yang tidak homogen dan keragaman desa yang besar.

Selisih RRMSE yang kecil antara pendugaan langsung dengan metode EB pendekatan jackknife dan EBLUP dipengaruhi oleh pemilihan peubah-peubah pendukung. Korelasi yang kuat antara peubah respon dengan peubah-peubah pendukung dapat menghasilkan pendugaan tidak langsung yang lebih akurat.

Metode pendugaan EB pendekatan jackknife menghasilkan nilai RRMSE yang lebih kecil dibandingkan dengan metode EBLUP dalam menduga pengeluaran per kapita desa/kelurahan di kota Bogor.

SARAN

Kajian lebih lanjut diperlukan dalam meyelesaikan masalah pendugaan pada area kecil dengan memakai berbagai metode pendugaan area kecil. Pemilihan peubah pendukung pada pendugaan tidak langsung sebaiknya berkaitan erat dengan peubah respon dan dapat menggambarkan peubah respon dengan baik.

DAFTAR PUSTAKA

[BPS]. Badan Pusat Statistika. 2003. http://www.bps.go.id/publikasi/2003. [24 April 2008]

Breidt, F. J. 2001. Small Area Estimation for Natural Resource Survey. http://www.stat.colostate.edu/~nsu/starma

p/pps/breidt.msts.pdf. [24 April 2008]

Fay, R. E. & Herriot, R. A. 1979. Estimates of Income for Small Places: An Application of James-Stein Procedures to Census Data. Journal of the American

Statistical Association, Vol. 74, p:269-277.

Kurnia, A & Notodiputro, K. A. 2005. Pendekatan General Linear Mixed Model pada Small Area Estimation. Forum Statistika dan Komputasi, Oktober 2005, Vol. 10 No.2, p:12-16.

Kurnia, A & Notodiputro, K. A. 2006. Penerapan Metode Jackknife dalam Pendugaan Area Kecil. Forum Statistika dan Komputasi, April 2006, Vol. 11 No.1, p:12-16.

Longford, N. T. 2005. Missing Data and Small Area Estimation: Modern Analytical Equipment for the Survey Statistician. New York: Springer Science + Business Media, Inc.

Ramsini, B et.al. 2001. Uninsured Estimates by County: A Review of Options and Issues.

http://www.odh.ohio.gov/Data/OFHSurv/ ofhsrfq7.pdf. [24 April 2008]

Rao, J. N. K. 2003. Small Area Estimation. New Jersey: John Willey & Sons, Inc.

(19)

(20)

Lampiran 1 Hasil Pendugaan Langsung Pengeluaran per kapita (x Rp.100.000,00).

Kode Nama Desa N Y Di RRMSE

3271010002 PAMOYANAN 16 1.836318924 0.012399590 6.063949130

3271010004 GENTENG 16 2.078412326 0.030043913 8.339625312

3271010008 HARJASARI 16 2.266177098 0.007841601 3.907585933

3271010011 CIPAKU 16 2.367348569 0.045770481 9.037130033

3271010013 BATUTULIS 16 4.535360296 0.759085609 19.21027515

3271010015 EMPANG 16 4.064044625 0.091906254 7.459574662

3271010016 CIKARET 16 3.575890490 0.080249717 7.922049354

3271020002 SINDANGRASA 16 4.207016543 0.131953871 8.634493116

3271020004 KATULAMPA 16 1.781063864 0.008569654 5.197591587

3271020005 BARANANGSIANG 16 3.067304501 0.179205574 13.80126406

3271020006 SUKASARI 16 3.061545748 0.394405391 20.51307029

3271030001 BANTARJATI 16 3.067304501 0.179205574 13.80126406

3271030002 TEGALGUNDIL 16 3.698020573 0.349383193 15.98386054

3271030003 TANAHBARU 16 4.484000124 0.225759967 10.59638797

3271030004 CIMAHPAR 16 2.541006135 0.070439659 10.44486689

3271030006 CIBULUH 16 3.987393103 0.238184455 12.23961208

3271030007 KEDUNGHALANG 15 5.487278227 0.968046728 17.93044960

3271030008 CIPARIGI 16 2.486632316 0.086505714 11.82798663

3271040003 BABAKANPASAR 16 3.653514872 0.524980050 19.83172631

3271040004 TEGALLEGA 16 3.069650481 0.132158640 11.84292155

3271040007 PABATON 16 16.04853340 3.029173909 10.84493001

3271040010 KEBONKELAPA 16 7.242935268 0.601457702 10.70749651

3271050001 PASIRMULYA 16 4.011220220 0.233425078 12.04473502

3271050003 PASIRJAYA 16 2.705775092 0.049254071 8.202181415

3271050004 GUNUNGBATU 16 3.924132378 0.041171932 5.170790864

3271050006 MENTENG 16 3.643572917 0.143144795 10.38389565

3271050008 CILENDEK BARAT 16 3.930712798 0.031339146 4.503729155 3271050009 SINDANGBARANG 16 7.537768011 3.481180034 24.75258012

3271050012 SITUGEDE 16 3.357647073 0.102258783 9.523909602

3271050014 SEMPLAK 16 4.332930868 0.160339706 9.241421571

3271060001 KEDUNGWARINGIN 16 2.761356824 0.069161704 9.523801036

3271060002 KEDUNGJAYA 16 3.627281126 0.229602256 13.21012294

3271060003 KEBONPEDES 16 3.018711071 0.044441699 6.983510358

3271060005 KEDUNGBADAK 32 5.378548288 0.464636028 12.67334825

3271060008 CIBADAK 16 3.772850712 0.442116940 17.62377569

3271060009 KAYUMANIS 16 2.999030403 0.118243169 11.46587392

(21)

Lampiran 2 Diagram pencar dan nilai korelasi peubah-peubah pendukung (xi).

Y

30 15

0 15 10 5

40 20

0 10 25 400 8 16

100 50

0 0 200 400 0 5 10 0 5 10

15 10 5

24000 16000 8000 15 10 5

6000 4000 2000

x1 x2 x3 x4

x5 x6 x7 x8

x9 x10

Scatterplot of Y vs x1, x2, x3, x4, x5, x6, x7, x8, x9, x10

Korelasi Nilai Korelasi P-Value

Pearson correlation of Y and x1 -0.204 0.227

Pearson correlation of Y and x5 0.449 0.005

x1 = Persentase keluarga pertanian.

x2 = Persentase Jumlah Pra KS dan KS1

x3 = Persentase Jml penerima "kartu sehat/kartu program kes.Masy.miskin" =1th

x4 = Persentase Jumlah surat miskin dikeluarkan dalam setahun terakhir

x5 = Persentase Jumlah keluarga yang berlangganan telpon kabel

x6 = Jumlah Toko/Warung kelontong

x7 = Jumlah Bank Umum (Kantor Pusat/Cabang/Capem)

x8 = Jumlah Koperasi

x9 = Jumlah Penduduk

(22)

Lampiran 2 (lanjutan).

Correlations: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10

x1 x2 x3 x4 x5 x6 x7 x8 x9

x2 0.210 0.212

x3 0.191 0.056

0.258 0.742

x4 0.041 0.182 0.105

0.811 0.282 0.535

x5 -0.471 -0.181 -0.298 0.120 0.003 0.283 0.073 0.479

x6 -0.226 -0.008 -0.001 0.058 0.418 0.179 0.963 0.994 0.735 0.010

x7 -0.230 -0.067 -0.047 -0.155 0.329 0.597

0.170 0.692 0.781 0.360 0.047 0.000

x8 -0.222 -0.093 -0.113 -0.311 0.316 0.289 0.595

0.186 0.585 0.505 0.061 0.056 0.083 0.000

x9 -0.274 -0.046 -0.372 -0.188 0.260 0.038 -0.190 0.149

0.100 0.789 0.024 0.265 0.120 0.825 0.261 0.377

x10 -0.296 -0.047 -0.367 -0.185 0.247 0.073 -0.165 0.147 0.991 0.075 0.783 0.026 0.273 0.141 0.670 0.328 0.385 0.000

Cell Contents: Pearson correlation

(23)

Lampiran 3 Keluaran SAS bagi Pendugaan Parameter.

The SAS System The Mixed Procedure

Model Information

Data Set WORK.DUGAAN Dependent Variable Y

Covariance Structure Variance Components Estimation Method REML

Residual Variance Method Profile Fixed Effects SE Method Model-Based Degrees of Freedom Method Containment

Dimensions

Covariance Parameters 2 Columns in X 5 Columns in Z 1 Subjects 1 Max Obs Per Subject 19 Observations Used 18 Observations Not Used 1 Total Observations 19

Iteration History

Iteration Evaluations -2 Res Log Like Criterion

0 1 80.96467652

1 1 80.96467652 0.00000000

Convergence criteria met.

Covariance Parameter Estimates

Cov Parm Estimate

A 0 Residual 4.5071

Fit Statistics

(24)

The SAS System The Mixed Procedure

Solution for Fixed Effects

Standard

Effect Estimate Error DF t Value Pr > |t|

Intercept 3.1632 0.9733 12 3.25 0.0070 X5 0.01862 0.02636 12 0.71 0.0480 X6 0.001977 0.004360 12 0.45 0.0953 X7 0.08066 0.4619 12 0.17 0.8643 X8 -0.06571 0.1894 12 -0.35 0.7347

Type 3 Tests of Fixed Effects

Num Den

Effect DF DF F Value Pr > F

(25)

Lampiran 4 Hasil Pendugaan Pengeluaran per kapita (x Rp.100.000,00) dengan pendugaan langsung, pendugaan metode EB, dan pendugaan metode EBLUP serta nilai RRMSE.

Pendugaan Langsung EB pendekatan jackknife EBLUP No Nama Desa Y MSE RRMSE Yˆ MSE RRMSE Yˆ MSE RRMSE

1 PAMOYANAN 1.8363189 0.0123996 6.0639491 1.83966649 0.0123424 6.038941 1.8396665 0.0123701 6.0457015 2 GENTENG 2.0784123 0.0300439 8.3396253 2.08049189 0.0296375 8.274742 2.0804919 0.0298706 8.3072236 3 HARJASARI 2.2661771 0.0078416 3.9075859 2.26638573 0.0078136 3.900241 2.2663857 0.0078297 3.9042709 4 CIPAKU 2.3673486 0.0457705 9.03713 2.37286194 0.0448592 8.92593 2.3728619 0.0453763 8.9772248 5 BATUTULIS 4.5353603 0.7590856 19.210275 4.42421338 0.5591986 16.90235 4.4242134 0.6834567 18.686132 6 EMPANG 4.0640446 0.0919063 7.4595747 4.05813981 0.0881721 7.317092 4.0581398 0.0905773 7.416221 7 CIKARET 3.5758905 0.0802497 7.9220494 3.56760869 0.0774551 7.800953 3.5676087 0.0790846 7.8825848 8 SINDANGRASA 4.2070165 0.1319539 8.6344931 4.18829948 0.1246105 8.428291 4.1882995 0.1290966 8.578663 9 KATULAMPA 1.7810639 0.0085697 5.1975916 1.78360241 0.0085434 5.182243 1.7836024 0.0085556 5.1859333 10 BARANANGSIANG 3.0673045 0.1792056 13.801264 3.09600017 0.1666769 13.18672 3.0960002 0.173952 13.471432 11 SUKASARI 3.0615457 0.3944054 20.51307 3.05017877 0.3318935 18.88748 3.0501788 0.3674967 19.874738 12 BANTARJATI 3.0673045 0.1792056 13.801264 3.08437608 0.1658344 13.20292 3.0843761 0.1742285 13.532945 13 TEGALGUNDIL 3.6980206 0.3493832 15.983861 3.75880233 0.3080072 14.76492 3.7588023 0.339809 15.508434 14 TANAHBARU 4.4840001 0.22576 10.596388 4.43187365 0.2067198 10.25897 4.4318737 0.2175843 10.525105 15 CIMAHPAR 2.5410061 0.0704397 10.444867 2.55019258 0.0683238 10.24974 2.5501926 0.069577 10.343318 16 CIBULUH 3.9873931 0.2381845 12.239612 3.9508744 0.215465 11.74885 3.9508744 0.2280582 12.087308 17 KEDUNGHALANG 5.4872782 0.9680467 17.93045 5.17939945 0.7330865 16.53097 5.1793994 0.8270465 17.558425 18 CIPARIGI 2.4866323 0.0865057 11.827987 2.50167043 0.0834645 11.54838 2.5016704 0.0851448 11.664038 19 BABAKANPASAR 3.6535149 0.52498 19.831726 3.82984198 0.5037212 18.53166 3.829842 0.5520145 19.399672 20 TEGALLEGA 3.0696505 0.1321586 11.842922 3.10771515 0.1268528 11.46064 3.1077152 0.1294844 11.578906 21 PABATON 16.048533 3.0291739 10.84493 12.1366632 2.1686199 12.13368 12.136663 2.7479482 13.658562

22 KEBONKELAPA 7.2429353 0.6014577 10.707497 6.82405764 0.4966153 10.32684 6.8240576 0.5429624 10.797972

23 PASIRMULYA 4.0112202 0.2334251 12.044735 4.02512095 0.211137 11.41572 4.025121 0.2267894 11.8313 24 PASIRJAYA 2.7057751 0.0492541 8.2021814 2.71956645 0.0484377 8.092672 2.7195665 0.0488467 8.1267735 25 GUNUNGBATU 3.9241324 0.0411719 5.1707909 3.92623531 0.0404273 5.121073 3.9262353 0.0408943 5.1505648 26 MENTENG 3.6435729 0.1431448 10.383896 3.67471991 0.1363871 10.04992 3.6747199 0.1417336 10.245004 27 CILENDEK BARAT 3.9307128 0.0313391 4.5037292 3.92890897 0.0308961 4.473832 3.928909 0.0311743 4.4939307 28 SINDANGBARANG 7.537768 3.48118 24.75258 5.78541194 1.8663619 23.61368 5.7854119 2.196317 25.616113

29 SITUGEDE 3.3576471 0.1022588 9.5239096 3.33842354 0.0981786 9.385709 3.3384235 0.1002862 9.485911 30 SEMPLAK 4.3329309 0.1603397 9.2414216 4.29264171 0.1509043 9.049533 4.2926417 0.1556691 9.1912911 31 KEDUNGWARINGIN 2.7613568 0.0691617 9.523801 2.77687641 0.0673706 9.347136 2.7768764 0.0683417 9.4142661 32 KEDUNGJAYA 3.6272811 0.2296023 13.210123 3.65455829 0.2089371 12.50757 3.6545583 0.2231437 12.925801 33 KEBONPEDES 3.0187111 0.0444417 6.9835104 3.02688182 0.0436581 6.902987 3.0268818 0.0441449 6.9413642 34 KEDUNGBADAK 5.3785483 0.464636 12.673348 5.50501888 0.4535698 12.23385 5.5050189 0.5035909 12.890808

(26)

Lampiran 5 Dugaan Pengeluaran per kapita untuk Desa tidak Tersurvei.

Kode Nama Desa

Y

ˆ

MSE RRMSE

3271010001 MULYAHARJA 2.95898847 0.1075603 11.083649

3271010003 RANGGAMEKAR 2.99270771 0.1204063 11.594723

3271010005 KERTAMAYA 3.27133811 0.1449422 11.637830

3271010006 RANCAMAYA 2.52286045 0.0926119 12.062578

3271010007 BOJONGKERTA 2.64882127 0.0975757 11.792835

3271010009 MUARASARI 3.18126407 0.1273781 11.218833

3271010010 PAKUAN 4.88997270 0.4761560 14.111338

3271010012 LAWANGGINTUNG 2.93601150 0.1150944 11.554986

3271010014 BONDONGAN 3.81882843 0.2232565 12.372911

3271020001 SINDANGSARI 3.78168135 0.2046072 11.961223

3271020003 TAJUR 3.81060007 0.1812871 11.173523

3271030005 CILUAR 2.92067338 0.1135850 11.539248

3271040001 PALEDANG 5.43257357 0.4796370 12.748255

3271040002 GUDANG 5.10057256 0.3582669 11.735036

3271040005 BABAKAN 3.86880354 0.2196220 12.113266

3271040006 SEMPUR 4.37086146 0.2511491 11.465652

3271040008 CIBOGOR 4.39469379 0.2480861 11.333722

3271040009 PANARAGAN 4.42157970 0.2842207 12.057309

3271040011 CIWARINGIN 3.78755564 0.1869992 11.417232

3271050002 PASIRKUDA 3.38828744 0.1460608 11.279416

3271050005 LOJI 3.85201488 0.1774658 10.936275

3271050007 CILENDEK TIMUR 3.67478795 0.2032774 12.269088

3271050010 MARGAJAYA 5.20268050 0.4326308 12.642459

3271050011 BALUNGBANG JAYA 2.56403126 0.0924882 11.860957

3271050013 BUBULAK 3.63474875 0.1825234 11.753979

3271050015 CURUGMEKAR 4.02472916 0.2628551 12.738596

3271050016 CURUG 5.00599543 0.4593362 13.538636

3271060004 TANAHSAREAL 4.89819473 0.3239412 11.619757

3271060006 SUKARESMI 3.09841037 0.1144569 10.918977

3271060007 SUKADAMAI 2.22758790 0.0882565 13.336399

(27)

PENDAHULUAN

Latar Belakang

Tujuan

TINJAUAN PUSTAKA

Pengeluaran per kapita

p y

q

=

dimana:

Pendugaan Area Kecil

(28)

AGUSTINA DWI WARDANI

(29)

PENDAHULUAN

Latar Belakang

Tujuan

TINJAUAN PUSTAKA

Pengeluaran per kapita

p y

q

=

dimana:

Pendugaan Area Kecil

(30)

dalam area itu sendiri, dan dari luar survei (Longford 2005).

Pendugaan pada area kecil merupakan salah satu upaya untuk meningkatkan keakuratan, yaitu dengan menggunakan pendugaan secara tidak langsung. Pendugaan tidak langsung dapat dilakukan dengan memanfaatkan peubah-peubah tambahan dalam menduga parameter. Peubah-peubah pendukung tersebut dapat berupa informasi tambahan yang didapatkan dari area lain yang serupa, survei terdahulu yang dilakukan di daerah yang sama, atau peubah yang lain yang berhubungan dengan peubah yang ingin diduga. Pendugaan tidak langsung pada area kecil memiliki beberapa keuntungan, yaitu memilki dugaan yang optimal, memperoleh model valid yang berasal dari data contoh, dan dapat menjelaskan berbagai macam model berdasar pada respon alami suatu peubah dan kekomplekan struktur data (Rao 2003).

Proses pendugaan pada suatu area atau subpopulasi dapat dibagi menjadi dua macam, yaitu:

1. Penduga Berbasis Rancangan

Rao (2003) menyebutkan bahwa pendugaan pada metode berbasis rancangan merupakan pendugaan pada suatu area berdasarkan data contoh dari area tersebut. Pada proses pendugaan tersebut dapat digunakan informasi tambahan (auxiliary information) untuk menduga parameter yang menjadi perhatian. Pendekatan yang digunakan pada proses pendugaan ini adalah pendekatan berbasis rancangan. Pada pendugaan ini diasumsikan tidak terjadi galat pengukuran.

2. Penduga Berbasis Model

Pendugaan pada metode berbasis model merupakan pendugaan pada suatu area dengan cara menghubungkan informasi pada area tersebut dengan area lain melalui model yang tepat. Hal ini berarti bahwa dugaan tersebut mencakup data dari area lain (Kurnia & Notodiputro 2006). Penduga tidak langsung berdasarkan model area kecil (small area model) dikatakan sebagai penduga berbasis model (Rao 2003). Ramsini et al. (2001) menyatakan bahwa penduga tidak langsung yang diperoleh dengan memanfaatkan informasi peubah lain yang berhubungan dengan parameter yang diamati sering disebut sebagai penduga berbasis model. Metode pendugaan yang termasuk dalam penduga berbasis model adalah metode EB, EBLUP, dan HB.

Penduga Langsung

Penduga langsung merupakan penduga berbasis rancangan dan hanya dapat digunakan jika semua area dalam suatu populasi digunakan sebagai contoh (Rao 2003). Penduga langsung menggunakan nilai dari peubah yang menjadi perhatian hanya pada periode waktu dan unit contoh pada area yang menjadi perhatian (Ramsini et al. 2001). Data contoh dari suatu survei dapat digunakan untuk mendapatkan pendugaan langsung yang dapat dipercaya bagi suatu area besar. Ramsini et al. (2001) menyebutkan bahwa nilai hasil pendugaan langsung pada suatu area kecil merupakan penduga tak bias meskipun memiliki ragam yang besar dikarenakan dugaannya diperoleh dari ukuran contoh yang kecil.

Penduga Sintetik

Gonzalez (1973) dalam Rao (2003) menyebutkan bahwa suatu penduga disebut sebagai penduga sintetik apabila suatu penduga langsung yang diperoleh dari suatu survei contoh untuk area besar, digunakan untuk mendapatkan pendugaan tak langsung bagi area kecil dengan mengasumsikan bahwa area kecil tersebut memiliki karakteristik yang sama dengan area besar.

Penduga sintetik dalam pendugaan area kecil dapat digunakan dalam menduga nilai respon pada area lain yang t