PEMODELAN PENYEBARAN INFEKSI HIV PADA KOMUNITAS
INJECTING DRUG USERS
(IDU)
SKRIPSI
HAMKA SUTRA
100803063
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PEMODELAN PENYEBARAN INFEKSI HIV PADA KOMUNITAS
INJECTING DRUG USERS
(IDU)
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai
gelar Sarjana Sains
HAMKA SUTRA
100803063
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Pemodelan Penyebaran Infeksi HIV pada Komunitas Injecting Drug Users (IDU)
Kategori : Skripsi
Nama : Hamka Sutra
Nomor Induk Mahasiswa : 100803063
Program Studi : Sarjana (S1) Matematika Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, April 2014
Komisi Pembimbing
Pembimbing 2, Pembimbing 1,
Dr. Esther S. M. Nababan, M.sc. Prof. Dr. Tulus, M.Si. Ph.D. NIP. 19610318 198711 2 001 NIP. 19620901 198803 1 002
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
PEMODELAN PENYEBARAN INFEKSI HIV PADA KOMUNITAS
INJECTING DRUG USERS (IDU)
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri. Kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, April 2014
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Allah SWT Tuhan Yang Maha Pemurah dan
Maha Penyayang, atas semua kasih sayang dan limpahan karunia-Nya sehingga
penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Pemodelan
Penyebaran Infeksi HIV Pada Komunitas Injecting Drug Users (IDU).
Terimakasih penulis sampaikan kepada Prof. Dr. Tulus, M.Si. Ph.D. selaku
pembimbing 1 dan Dr. Esther S. M. Nababan, M.Sc. selaku pembimbing 2 yang telah
meluangkan waktunya selama penyusunan skripsi ini. Terimakasih kepada Prof. Dr.
Tulus, M.Si. Ph.D. dan Dr. Mardiningsih, M.Si. selaku Ketua Departemen dan
Sekretaris Departemen Matematika FMIPA-USU Medan, Dekan dan Pembantu Dekan
FMIPA USU, seluruh Staf dan Dosen Matematika FMIPA USU, pegawai FMIPA
USU dan rekan-rekan kuliah angkatan 2010 Matematika FMIPA USU. Akhirnya tidak
terlupakan ucapan terimakasih kepada Ayahanda Khairuman (Alm) dan Ibunda
Yulianis (Almh) serta saudara-saudari penulis Mazwanni, Elma Diana, Mizral, Ismar
Rosidi, Safrillah dan Litriyanni yang selama ini memberikan bantuan baik secara
materi maupun moral dan dorongan semangat yang diperlukan. Semoga Allah SWT
PEMODELAN PENYEBARAN INFEKSI HIV PADA KOMUNITAS
INJECTING DRUG USERS (IDU)
ABSTRAK
HIV (Human Immunodeficiency Virus) merupakan virus yang dapat menyebabkan AIDS (Acquired Immune Deficiency Sindrome) dan belum dapat disembuhkan. Penularan infeksi HIV pada komunitas pecandu narkoba suntik (Injecting Drug Users
/ IDU) sangat rentan terjadi melalui mekanisme pertukaran jarum suntik. Pemodelan penyebaran infeksi menggunakan asumsi bahwa pecandu yang sudah mengidap AIDS ikut berbagi jarum suntik dalam kmonuitas IDU. Kekuatan infeksi sangat dipengaruhi oleh mekanisme pertukaran jarum suntik dan untuk menganalisa perilaku penyebaran infeksi pada komunitas IDU terlebih dahulu menentukan basic reprodution ratio ( ) dan dua titik kesetimbangan dari model yaitu titik kesetimabngan bebas infeksi dan titik kesetimbangan epidemik. Kemudian ditentukan titik kestabilan dari titik kesetimbangan bebas infeksi tersebut dengan menggunakan teorema kestabilan Lyapunov. Kesimpulan dari penelitian menunjukkan bahwa jika > 1 maka infeksi HIV mewabah pada komunitas IDU dan sebaliknya jika ≤ 1 maka infeksi HIV tidak mewabah pada komunitas IDU.
MODELS FOR TRANSMISSION OF HIV INFECTION IN INJECTING DRUG USERS (IDU) COMMUNITY
ABSTRACT
HIV (Human Immunodeficiency Virus) is a virus that can cause AIDS (Acquired Immune Deficiency Syndrome) and can not be cured. Transmission of HIV infection in injecting drug addicts community (Injecting Drug Users / IDU) are vulnerable happen through needle exchange mechanism. Modeling the spread of infection using the assumption that addicts who already have AIDS participated in a community syringe sharing IDU. Infection is strongly influenced by the strength of needle exchange mechanism and to analyze the behavior of the spread of infection in the IDU community first determine the basic reprodution ratio ( ) and two equilibrium points of the model are free infection equilibrium and the equilibrium point of the epidemic. Then, determined point stability of the free infection equilibrium point by using Lyapunov stability theorem. Conclusions of the study indicate that if > 1 then the epidemic of HIV infection in the IDU community and otherwise if ≤ 1 then no epidemic of HIV infection in the IDU community.
DAFTAR ISI
Halaman
Persetujuan i
Pernyataan ii
Penghargaan iii
Abstrak iv
Abstract v
Daftar Isi vi
Daftar Tabel viii
Daftar Gambar ix
Daftar Lampiran x
Bab 1. Pendahuluan
1.1. Latar Belakang 1
1.2. Perumusan Masalah 3
1.3. Batasan Masalah 3
1.4. Tujuan Penelitian 3
1.5. Kontribusi Penelitian 4
1.6. Metodologi Penelitian 4
Bab 2. Tinjauan Pustaka
2.1. Sistem Persamaan Diferensial 6 2.1.1. Sistem Persamaan Diferensial Linier 7 2.1.2. Sistem Persamaan Diferensial Nonlinier 7 2.2. Kesetimbangan dan Kestabilan 7
2.3. Peluang 12
2.3.1. Peluang Bersyarat 12
2.4. Distribusi Poisson 13
2.4.1. Proses Poisson 15
2.5. Basic Reproduction Ratio 16
Bab 3. Pemodelan Penyebaran Infeksi HIV pada komunitas Injecting Drug Users
(IDU).
3.1. Pembentukan Model 19
3.2. Kekuatan Infeksi 23
3.3. Analisis Kualitatif Model 29
3.4. Basic Reproduction Ratio 34
Bab 4. Simulasi Pemodelan Penyebaran Infeksi HIV pada komunitas Injecting Drug Users (IDU).
4.1. Simulasi 1 : Dinamika 44
4.2. Simulasi 2 : Potret Fase pada saat 1 49 4.3. Simulasi 3 : Potret Fase pada saat > 1 51
Bab 5. Kesimpulan dan Saran
5.1. Kesimpulan 55
5.2. Saran 56
DAFTAR TABEL
Nomor Judul Halaman
Tabel
3.1. Variabel dan parameter model 21
DAFTAR GAMBAR
Nomor Judul Halaman
Gambar
DAFTAR LAMPIRAN
Nomor Judul Halaman
Lampiran
PEMODELAN PENYEBARAN INFEKSI HIV PADA KOMUNITAS
INJECTING DRUG USERS (IDU)
ABSTRAK
HIV (Human Immunodeficiency Virus) merupakan virus yang dapat menyebabkan AIDS (Acquired Immune Deficiency Sindrome) dan belum dapat disembuhkan. Penularan infeksi HIV pada komunitas pecandu narkoba suntik (Injecting Drug Users
/ IDU) sangat rentan terjadi melalui mekanisme pertukaran jarum suntik. Pemodelan penyebaran infeksi menggunakan asumsi bahwa pecandu yang sudah mengidap AIDS ikut berbagi jarum suntik dalam kmonuitas IDU. Kekuatan infeksi sangat dipengaruhi oleh mekanisme pertukaran jarum suntik dan untuk menganalisa perilaku penyebaran infeksi pada komunitas IDU terlebih dahulu menentukan basic reprodution ratio ( ) dan dua titik kesetimbangan dari model yaitu titik kesetimabngan bebas infeksi dan titik kesetimbangan epidemik. Kemudian ditentukan titik kestabilan dari titik kesetimbangan bebas infeksi tersebut dengan menggunakan teorema kestabilan Lyapunov. Kesimpulan dari penelitian menunjukkan bahwa jika > 1 maka infeksi HIV mewabah pada komunitas IDU dan sebaliknya jika ≤ 1 maka infeksi HIV tidak mewabah pada komunitas IDU.
MODELS FOR TRANSMISSION OF HIV INFECTION IN INJECTING DRUG USERS (IDU) COMMUNITY
ABSTRACT
HIV (Human Immunodeficiency Virus) is a virus that can cause AIDS (Acquired Immune Deficiency Syndrome) and can not be cured. Transmission of HIV infection in injecting drug addicts community (Injecting Drug Users / IDU) are vulnerable happen through needle exchange mechanism. Modeling the spread of infection using the assumption that addicts who already have AIDS participated in a community syringe sharing IDU. Infection is strongly influenced by the strength of needle exchange mechanism and to analyze the behavior of the spread of infection in the IDU community first determine the basic reprodution ratio ( ) and two equilibrium points of the model are free infection equilibrium and the equilibrium point of the epidemic. Then, determined point stability of the free infection equilibrium point by using Lyapunov stability theorem. Conclusions of the study indicate that if > 1 then the epidemic of HIV infection in the IDU community and otherwise if ≤ 1 then no epidemic of HIV infection in the IDU community.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
HIV (Human Immunodeficiency Virus) merupakan virus yang dapat menyebabkan AIDS (Acquired Immune Deficiency Sindrome) yang menyerang sel darah putih yang bernama CD4 (sel T) sehingga dapat merusak sistem kekebalan tubuh manusia yang
pada akhirnya tidak dapat bertahan dari gangguan penyakit walaupun yang ringan
sekalipun. Kasus infeksi HIV dan AIDS merupakan kasus penyakit yang sudah lama
terjadi, namun hingga saat ini belum ditemukan obat untuk menyembuhkan penyakit
ini.
Pertumbuhan HIV dalam tubuh manusia sangatlah cepat di awal terserang
infeksi HIV. Setiap tahapan pertumbuhan virus HIV dapat menimbulkan gejala yang
berbeda-beda. Gejala yang ditimbulkan memiliki ciri yang sama dengan gejala infeksi
virus lainnya, sehingga membuat orang tidak menyadari bahwa dirinya sudah
terinfeksi. Infeksi HIV menular ke manusia lain melalui kontak langsung dengan
penderita, seperti melalui hubungan seks, tindik, donor darah dan pemakaian jarum
suntik secara bergantian. Oleh karena itu, HIV dapat menyebar secara cepat di
komunitas pecandu Narkoba (Narkotika dan Obat Terlarang) suntik dan pelaku seks
bebas.
Menurut Nasronudin (2007), penyakit infeksi HIV masih merupakan masalah
kesehatan global, termasuk di Indonesia. Masalah yang berkembang sehubungan
dengan penyakit infeksi HIV adalah angka kejadian dan kematian yang masih tinggi.
Meskipun telah dicapai berbagai kemajuan di bidang kedokteran dan farmasi, serta
telah berbagai upaya pencegahan primer maupun sekunder, tetapi angka kesakitan dan
kematiannya tetap tinggi.
Menurut WHO, hingga Desember 2000, dilaporkan 58 juta jiwa penduduk
jiwa meninggal akibat AIDS setiap hari. Transmisi HIV masih tetap saja berlangsung
hingga kini, 16.000 jiwa terinfeksi HIV baru setiap harinya.
Tingkat penularan HIV di Indonesia juga semakin meningkat, pada tahun 2010
sekitar 400.000 orang menjadi ODHA (Orang Dengan HIV-AIDS) dan 100.000 orang
meninggal akibat AIDS. Diproyeksikan bahwa pada tahun 2015 jumlah ODHA akan
mencapai 1.000.000 dengan kematian 350.000 orang. Kesakitan dan kematian tersebut
harus dicegah dan ditekan dengan mengubah perjalanan epidemologi HIV/AIDS di
Indonesia demikian disampaikan Nafisah Mboi pada 1 Desember 2006 pada saat
memperingati hari AIDS sedunia (Nasronudin.2007. hal 15).
Penelitian tentang Model Matematika Penyebaran Infeksi HIV pada komunitas
IDU telah diteliti sebelumnya (Mardhiyah, I., 2012.). Model yang diperoleh adalah
= = Ʌ – S– ,
=
= – – .Dimana,
= menyatakan laju perubahan populasi pecandu susceptibles terhadap waktu t
= menyatakan laju perubahan populasi pecandu infectious terhadap waktu t
Ʌ = Laju pertambahan populasi IDU dari manusia biasa menjadi pecandu narkoba suntik (IDU)
= Laju kematian alami IDU per kapita
S = Ukuran populasi pecandu Susceptibles
= Ukuran populasi pecandu Infectious
= Laju perubahan dari terinfeksi menjadi HIV menjadi penyakit AIDS per
kapita
= Kekuatan penyebaran infeksi (force of infection) dalam komunitas IDU
dengan asumsi bahwa pecandu yang menyadari sudah mengidap AIDS tidak ikut
berbagi jarum suntik pada komunitas IDU. Komunitas pecandu narkoba suntik (IDU)
merupakan kelompok beresiko tinggi untuk terkena infeksi HIV. Pola hidup pecandu
diantaranya saling berbagi jarum suntik (DIE / Drug Injecting Equipment). Maka peneliti mencoba untuk meneliti “Pemodelan Penyebaran Infeksi HIV pada Komunitas Injecting Drug Users (IDU)”. Dengan asumsi bahwa pecandu yang
menyadari sudah mengidap AIDS ikut berbagi jarum suntik pada komunitas IDU.
1.2 Perumusan Masalah
Permasalah yang dibahas pada penelitian ini adalah bagaimana penyebaran infeksi
HIV dengan kekuatan infeksi yang dipengaruhi mekanisme pertukaran jarum suntik
pada komunitas IDU.
1.3 Batasan Masalah
Penelitian tentang Analisis Pemodelan Penyebaran Infeksi HIV pada Komunitas
Injecting Drug Users ini dibatasi oleh :
1. Pecandu yang menyadari sudah mengidap AIDS ikut berbagi jarum suntik pada
komunitas IDU
2. Infeksi HIV hanya menular melalui kontak langsung dengan penderita
3. Populasi pecandu tertutup (tidak ada proses migrasi), yaitu tidak ada pecandu
yang masuk maupun keluar dari komunitas IDU
4. Infeksi HIV tidak dapat disembuhkan, sehingga dalam model tidak diperhatikan
laju perubahan populasi pecandu yang sembuh (recovered) 5. Tidak ada masa inkubasi apabila terjadi proses penularan
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah memodelkan penyebaran infeksi HIV dengan
kekuatan infeksi yang dipengaruhi mekanisme pertukaran jarum suntik pada
komunitas IDU.
Penelitian ini diharapkan dapat digunakan untuk menganalisis dinamika penyebaran
infeksi HIV pada komunitas pengguna narkoba suntik dan dapat menjadi refrensi di
dunia kesehatan sehingga dapat mengurangi dampak penularan HIV khususnya pada
komunitas IDU.
1.6 Metodologi Penelitian
Langkah-langkah yang akan dilakukandalam penelitian ini antara lain
1. Menelaah dan mengidentifikasi berbagai refrensi yang berhubungan dengan
topik penelitian
2. Menentukan hubungan antara penularan infeksi HIV dengan pengguna
narkoba suntik
3. Membuat pemodelan penyebaran infeksi HIV pada komunitas IDU
4. Menentukan titik kesetimbangan dan kestabilan Model
5. Membuat simulasi Model dengan menggunakan MATLAB
BAB 2
TINJAUAN PUSTAKA
Pada bab ini dibahas mengenai tinjauan pustaka yang digunakan dalam penelitian ini,
khususnya yang diperlukan dalam Bab 3. Teori yang dibahas adalah teori yang
mendukung pembentukan dan analisis sistem dinamik pemodelan penyebaran infeksi
HIV pada komunitas Injecting Drug Users (IDU). Dalam bab ini dibahas mengenai sistem persamaan diferensial, kesetimbangan dan kesetabilan sistem, basic
reproduction ratio, teori peluang dan distribusi Poisson.
Pecandu yang terinfeksi HIV yang belum menyadari bahwa sudah terinfeksi
HIV ikut berbagi jarum suntik kepada kelompoknya, sehingga penyebaran HIV di
komunitas pecandu narkoba suntik meningkat. Sekitar 56 persen laki-laki dan 36
persen perempuan pecandu narkoba suntik di Indonesia berbagi jarum suntik ketika
menyuntik dan hanya 1,4 persen di antaranya merebus jarumnya sebelum digunakan
kembali (Hugo, G., 2001).
Model penyebaran infeksi HIV pada komunitas IDU digunakan untuk
mengetahui laju penyebaran suatu wabah penyakit dalam suatu populasi tertutup dan
bersifat endemik. Oleh karena infeksi HIV sangat berbahaya hingga tidak ada yang
sembuh dari infeksi HIV, maka model memperhatikan tiga kelompok individu yaitu
kelompok individu yang sehat namun rentan dan dapat terinfeksi HIV (Susceptibles) atau disimbolkan dengan S, kelompok individu yang telah terinfeksi (Infectious) atau disimbolkan dengan I dan kelompok individu yang sudah menderita penyakit AIDS akibat infeksi HIV yang terlalu lama disimbolkan dengan A (AIDS).
Pembentukan pemodelan penyebaran infeksi HIV pada komunitas IDU sangat
berkaitan erat dengan sistem persamaan diferensial. Selanjutnya, perlu dibahas
mengenai kesetimbangan dan kestabilan sistem. Dalam komunitas IDU, biasanya
memungkinkan mereka membentuk grup dalam komunitas IDU. Pembentukan grup
dalam komunitas IDU berperan penting dalam kekuatan penyebaran infeksi HIV
dikalangan komunitas IDU. Terdapat banyak kemungkinan dalam pembentukan grup
dan mekanisme pertukaran jarum suntik dalam grup. Oleh karena itu, dalam
pembahasan penelitian ini diperlukan pembahasan mengenai teori peluang yang
menyangkut pembentukan grup dan mekanisme pertukaran jarum suntik (DIE) dalam
komunitas IDU. Pembentukan grup dalam kmunitas IDU merupakan kejadian diskrit
dengan banyak percobaan yang diasumsikan menuju tak hingga. Dengan demikian,
distribusi Poisson dibahas untuk menjelaskan terjadinya pembentukan grup dan
ukuran grup dalam komunitas IDU.
2.1 Sistem Persamaan Diferensial
Berikut ini diberikan sistem persamaan diferensial
= G(t,x), (2.1)
dengan x , t , = , G: D → merupakan fungsi kontinu di D.
Sistem persamaan diferensial (2.1) dikatakan sistem persamaan autonomous jika variabel t dinyatakan secara implisit, sedangkan jika variabel t dinyatakan secara eksplisit maka sistem persamaan (2.1) dikatakan sistem persamaan non- autonomous. Sistem persamaan autonomous dapat ditulis dalam bentuk
= G(x) (2.2)
Apabila sistem (1.2) dapat ditulis dalam bentuk
1 = + + + , 2 = + + + ,
, (2.3)
n= + + . . . + ,
dengan adalah bilangan riil maka sistem (2.2) merupakan sistem persamaan
di (2.3), maka sistem (2.2) merupakan sistem persamaan diferensial autonomous
nonlinier.
Sistem persamaan diferensial dapat menunjukkan suatu dinamika (perubahan)
dari suatu keadaan yang bergerak atau mengalami perubahan. Oleh karena itu, Sistem
persamaan diferensial dapat direpresentasikan sebagai sistem dinamik dari suatu
keadaan yang diperhatikan.
2.1.1 Sistem Persamaan Diferensial Linier
Sistem persamaan diferensial linier dapat dilihat dari bentuk persamaannya. Misalkan
x = , A = (2.4)
Maka sistem persamaan diferensial autonomous linier dalam persamaan (2.3) dapat ditulis sebagai
= Ax. (2.5)
2.1.2 Sistem Persamaan Diferensial Nonlinier
Misalkan sistem persamaan diferensial nonlinier orde satu dalam bentuk
= F(t,x), (2.6)
dengan x , t , = , F : D → merupakan fungsi yang nonlinier yang kontinu dan terdiferensialkan di D. Dalam penelitian ini variabel t dinyatakan secara implisit, sehingga sistem persamaan (2.6) dikatakan sistem persamaan
diferensial autonomous nonlinier dan ditulis
2.2 Kesetimbangan dan Kesetabilan
Sistem persamaan diferensial memiliki perilaku yang berbeda-beda di setiap titik,
namun terdapat titik kesetimbangan ketika sistem dalam keadaan setimbang (konstan).
Melalui titik kesetimbangan, sistem dapat lebih muda diamati perilaku kestabilannya.
Definisi 2.1. (Titik Kesetimbangan)
Suatu titik x* disebut titik kesetimbangan dari sistem persamaan = F(x), x
jika memenuhi persamaan F(x*) = 0.
Definisi 2.2. (Titik Kesetimbangan Hiperbolik)
Titik x* disebut titik kesetimbangan hiperbolik dari persamaan (2.7) jika
memenuhi persamaan F(x*) = 0 dan matriks
=
Tidak mempunyai nilai eigen yang bagian riiilnya bernilai nol.
Hal yang sangat terkait dengan titik kesetimbangan adalah kestabilan dari titik
tersebut. Kestabilan adalah bentuk perilaku sistem yang dilihat dari titik
kesetimbangan sistem. Berikut ini definisi mengenai kestabilan titik kesetimbangan
sistem.
Definisi 2.3. (Kestabilan Titik Kesetimbangan)
Misalkan x* adalah titik kesetimbangan dari = F(x) dan x0 adalah titik awal.
2. x* dikatakan stabil asimtotik, jika x* dan terdapat r > 0, sedemikian sehingga
→ 0 saat t→ untuk semua x0 yang memenuhi <
r.
3. x* dikatakan tidak stabil, jika terdapat suatu η > 0 sedemikian sehingga untuk sebarang > 0 terdapat sebuah x0 dengan < dan > 0
sedemikian sehingga > η.
Berdasarkan definisi (2.3), dapat disimpulkan bahwa sistem = F(x) dikatakan
stabil pada titik kesetimbangan x* jika kondisi awal (x0) berada di sekitar x* sejauh
dengan adalah bilangan positif terkecil maka sifat solusi sistem ( ) berada di
sekitar titik kesetimbangan. Jika kondisi awal berada sangat dekat dengan x* dan
solusi cenderung mendekati titik kesetimbangan x*, maka sistem dikatakan stabil
asimtotik. Selain itu, jika sifat solusi sistem menjauh dari titik kesetimabangan x*
akibat perubahan kecil pada kondisi awal, maka sistem dikatakan tidak stabil.
Untuk menganalisa kestabilan titik kesetimbangan disekitar titik tersebut,
sistem persamaan nonlinier (2.7) harus dilinierkan terlebih dahulu. Hal ini dilakukan
untuk menaksir perilaku kelinieran sistem (2.7) di sekitar titik kesetimbangan.
Linierisasi Sistem
Misalkan x* adalah titik kesetimbangan dari sistem persamaan (2.7) yaitu F(x) yang
memiliki ekspansi deret Taylor di titik x* yang secara matemati dapat ditulis
F(x) = F( )
+
+
O(2.8)
Oleh karena x* merupakan titik kesetimbangan, maka F(x*) = 0. Dalam
melinierkan persamaan (2.7), suku pada (2.8) yang mempunyai orde lebih besar dari
satu dapat diabaikan. Dengan demikian, persamaan (2.8) dapat ditulis
F(x) =
. (2.9)
Berdasarkan persamaan (2.7) dan (2.9) diperoleh
Misalkan
y = dan =
dengan
=
Persamaan (2.10) dapat ditulis
ẏ = y, (2.11)
dengan matriks adalah matrik Jacobian dari persamaan (2.7) di titik x*. Selanjutnya bagiaan ruas kanan persamaan (2.11) disebut bagian linier dari fungsi nonlinier F(x) di
titik x*. Dengan demikian, kestabilan titik kesetimbangan dapat dilihat melalui bagian liniernya.
Kestabilan titik kesetimbangan dari persamaan (2.7) dapat dianalisa dengan
menggunakan nilai-nilai eigen dari matriks yang merupakan solusi atau akar-akar
karakteristik dari persamaan karakteristik det ( I – ) = 0. Persamaan karakteristik tersebut dapat ditulis
+ + ... + + = 0
dengan , , ..., , adalah konstanta dan akar-akar karakteristiknya adalah
nilai eigen , , ..., . Nilai eigen tersebut dapat digunakan untuk menentukan
kestabilan titik kesetimbangan lokal dari sistem persamaan (2.7) sesuai dengan
teorema berikut ini.
Teorema 2.1.
Jika matriks pada sistem (2.7) adalah matriks koefisien dengan nilai eigen , ,
..., , maka titik kesetimbangan x* dari sistem (2.7), dikatakan : 1. Stabil, jika Re( ) 0, untuk i = 1, 2, ..., n
3. Tidak stabil, jika Re( ) 0, untuk i = 1, 2, ..., n
dengan Re( ) adalah bagian riil dari x.
Teorema 2.1 dapat digunakan untuk menentukan kestabilan lokal suatu titik
kesetimbangan. Titik kesetimbangan yang stabil atau stabil asimtotik hanya pada suatu
daerah tertentu dalam lingkungan solusi sistem dikatakan stabil lokal atau stabil
asimtotik lokal. Titik kesetimbangan dikatakan stabila global atau stabil asimtotik
global jika titik kesetimbangan tersebut stabil atau stabil asimtotik pada setiap
lingkungan solusi sistem. Berikut ini definisi solusi pada sistem
Definisi 2.4. (Solusi Periodik)
Misalkan x = Φ(t) merupakan solusi untuk persamaan = F(t,x), x D dan
misalkan terdapat bilangan positif terkecil T sedemikian sehingga Φ(t + T) = Φ(t)
untuk setiap t , maka Φ(t) disebut solusi periodik dari persamaan = F(t,x) dengan periodenya T.
Jika a* stabil asimtotik global maka solusi di sekitar a* cenderung menuju ke
a*. Namun jika terdapat solusi periodik pada sistem maka solusi yang berada di luar solusi periodik tidak cenderung menuju a* karena dibatasi oleh solusi periodik dalam
sistem. Hal tersebut memberikan kesimpulan bahwa a* bersifat stabil asimtotik namun
tidak secara global.
Definisi 2.5. (Kestabilan Lyapunov)
Misalkan x* adalah titik kesetimbangan dari sisetm = F(x) dan y adalah sebarang
solusi.
1. x*(t) dikatakan stabil Lyapunov jika untuk setiap > 0 terdapat = ( ) > 0 sedemikian sehingga untuk solusi lain y(t) dengan < maka memenuhi pertidaksamaan < untuk setiap t > , . 2. x*(t) dikatakan stabil asimtotik, jika x* stabil Lyapunov dan terdapat
Teorema 2.2.
Misalkan z* adalah titik kesetimbangan untuk sistem (2.7) dan L : → merupakan fungsi definit positif terdiferensialkan pada lingkungan z* dalam himpunan ,
sedemikian sehingga
a. jika L(z*) = 0 dan (z) > 0 dengan z z*
b. (z) 0 pada ,
maka z* dikatakan stabil, selanjutnya
c. Jika memenuhi (z) < 0 pada ;
maka z* dikatakan stabil asimtotik, dengan
= ,
jika = maka pada kasus c, z* dikatakan stabil asimtotik global.
2.3 Peluang
Misalkan Ω merupakan suatu himpunan yang terdiri dari semua hasil yang mungkin
terjadi pada suatu percobaan acak. Ω disebut sebagai ruang contoh (sampel). Selanjutnya untuk setiap himpunan bagian dari Ω didefinisikan suatu fungsi peluang himpunan P dan P( ) menyatakan besar peluang bahwa merupakan hasil dari suatu percobaan acak. Jika 1, 2, 3, ... adalah himpunan-himpunan bagian dari Ω maka
dapat didefinisikan fungsi himpunan peluang, yaitu
Definisi 2.6.
Jika P( ) didefinisikan sebagai himpunan bagian dari himpunan Ω dan jika memenuhi
a. P( ) ≥ 0,
b. P(Ω) = 1,
c. P( 1 2 3 ) = P( 1) + P( 2) + P( 3) + , dengan himpunan i, i = 1, 2, 3, ..., sedemikian sehingga tidak ada dua himpunan, i dan j yang
memiliki satu anggota yang sama yakni ( i ∩ j = Ø atau i dan j merupakan dua kejadian saling lepas i ≠ j), maka P dikatakan fungsi himpunan peluang dari hasil percobaan acak (Dudewicz, J.E., Mishra, N.S.
Kejadian 0 dan E dikatakan saling lepas jika 0 E =Ø, yakni jika 0 dan E
tidak dapat terjadi bersamaan. Misalkan E0,E2,E3, ... merupakan kejadian saling lepas
dengan Ei Ej = Ø untuk i ≠ j . jika 0, Ei dan E saling lepas maka berlaku aturan
penjumlahan :
1. P( 0 E) = P( 0) + P(E)
2. P( ) =
2.3.1 Peluang Bersyarat
Untuk sebarang kejadian dan E, peluang bersyarat diberikan E ditulis P( E), didefinisikan dengan :
P( E) = ; P(E) > 0. (2.12)
Berdasarkan persamaan (2.12) diperoleh
P( E) = P( E) P(E). (2.13)
Misalkan E0,E2,E3, ... merupakan kejadian saling lepas dengan Ei Ej = Ø untuk i ≠ j maka menurut hukum peluang total dan persamaan (2.13) maka
P(E) = . (2.14)
Selanjutnya kejadian A dan E dikatakan saing bebas jika P( E) = P( ) atau
P(E ) = P(E), sehingga berlaku P( E) = P( ) x P(E).
2.4 Distribusi Poisson
Distibusi Poisson merupakan salah satu distribusi peluang diskrit yang didasari oleh
terjadinya percobaan Poisson. Percobaan Poisson adalah suatu percobaan yang
menghasilkan nilai-nilai yang diskrit dari suatu variabel acak yang terjadi dalam suatu
selang waktu atau suatu daerah tertentu. Berikut ini ciri-ciri percobaan Poisson
1. banyaknya hasil percobaan yang terjadi dalam suatu selang waktu atau daerah
tertentu tidak bergantung pada banyaknya percobaan yang terjadi pada selang
waktu atau daerah tertentu yang berbeda,
2. peluang terjadinya suatu percobaan dalam suatu selang waktu yang singkat
atau daerah tertentu yang kecil sebanding dengan panjang selang waktu atau
besarnya daerah tertentu tersebut, dan tidak bergantung pada percobaan yang
3. peluang terambilnya lebih dari 1 hasil percobaan dalam suatu selang waktu
yang singkat atau daerah tertentu yang kecil dapat diabaikan. (Walpole, R.E.,
1995)
Misalkan :
N adalah banyaknya percobaan dari suatu populasi kejadian diskrit, v adalah nilai harapan banyaknya percobaan sukses, k adalah banyaknya percobaan sukses pada percobaan N dan p adalah peluang terjadinya percobaan sukses dalam suatu percobaan kejadian diskrit.
Peluang terjadinya percobaan sukses sebanyak k kali dalam N percobaan berdasarkan pendekatan distribusi Binomial adalah
Pp(k | N) = .
Selanjutnya, nilai harapan banyaknya percobaan sukses adalah
v = N p, sehingga diperoleh
Pv/N(k | N) = .
Untuk ukuran sampel N yang sangat besar, peluang terjadinya percobaan sukses sebanyak k kali dalam N percobaan menjadi :
Pv (k) =
=
=
= 1.
.
.1Pv (k) =
Misalkan X adalah variabel acak banyaknya percobaan sukses dalam suatu kejadian diskrit. Dengan demikian, terbentuklah distribusi Poisson dengan parameter
P(X = k) = , untuk k = 0, 1, 2, 3, ... (2.15)
Oleh karena itu, rata-rata atau nilai harapan dan variansi dari variabel acak X adalah
E[G = k] = = v, (2.16)
= var[X = k] = v. (2.17)
Distribusi Poisson merupakan salah satu distribusi untuk variabel acak yang
diskrit. Distribusi Poisson dugunakan untuk peluang dari percobaan sukses yang
ditentukan dan percobaan tersebut terjadi dalam suatu interval waktu atau daerah
tertentu. Percobaan sukses yang diperhatikan dalam distribusi Poisson adalah kejadian
yang terjadi dalam percobaan yang besar dan dilakukan berulang kali sehingga N →
. Selanjutnya dalam penelitian ini, kejadian pembuatan grup komunitas IDU
merupakan percobaan diskrit yang mengikuti distribusi Poisson.
2.4.1 Proses Poisson
Proses kejadian pembentukan grup dalam komunitas IDU, nilainya berubah-ubah
secara tidak pasti dan terkait dengan waktu. Oleh karena setiap variabel yang nilainya
berubah-ubah secara tidak pasti terkait dengan waktu dikatakan mengikuti proses
stokastik, maka pembahasan proses stokastik diperlukan pada bab ini. Misalkan Et adalah variabel acak dari suatu proses pada wakti t T = {0, 1, 2, 3, ...}.
Definisi 2.7.
Proses stokastik adalah koleksi dari variabel acak Et , dengan t adalah parameter bergerak pada himpunan indeks T (Taylor, H.M., S. Karlin, 1998)
Dengan demikian, proses kejadian pembuatan grup pada komunitas IDU yang
merupakan percobaan Poisson yang mengikuti proses stokastik dapat dikatan sebagai
Definisi 2.8. (Proses Poisson)
Suatu intensitas atau tingkat proses Poisson > 0 adalah sebuah nilai bilangan bulat
proses stokastik {E(t); t≥ 0} dengan
1. untuk sebarang titik waktu t0 = 0 < t1 < t2 < ... < tn , dengan proses increments E(t1) –E(t0), E(t2) –E(t1), ..., E(tn) –E(tn-1) (2.18)
meruapakan variabel acak bebas,
2. untuk s ≥ 0 dan t > 0, variabel acak E(s + t) – E(s) berdistribusi Poisson sehingga
P(E(s + t) –E(s) = k) = , untuk k = 0, 1, 2, ...,
3. E(0) = 0, (Taylor, H.M., S. Karlin, 1998).
Berdasarkan definisi proses Poisson di atas dapat dibuktikan bahwa
E[E(t)] = t, (2.19)
var[E(t)] = t (2.20)
2.5 Basic Reproduction Ratio ( )
Dalam pemodelan epidemik penyakit, terdapat ukuran penyebaran penyakit pada
populasi yang diperhatikan. Ukuran (rasio) diperhatikan untuk menganlisa model
penyebaran epidemik penyakit dan selanjutnya disebut Basic Reproduction Ratio. Pada subbab ini, dijelaskan mengenai pengertian dasar dan metode penentuan Basic Reproduction Ratio yang dinotasikan dengan .
Definisi 2.9.
Basic Reproduction Ratio adalah rata-rata banyaknya kasus kedua (individu infectious
baru) yang disebabkan satu individu yang terinfeksi (infectious) selama masa terinfeksinya dalam keseluruhan populasi susceptibles dan pengidap AIDS.
Dalam metode ini, Basic Reproduction Ratio ( ) didefinisikan sebagai radius spektral dari operator generasi selanjutnya.
Definisi 2.10.
Misalkan Φ adalah matriks nxn dan , , ..., adalah nilai eigen dari matriks Φ , maka radius spektral dari matriks Φ didefinisikan sebagai
(Φ) = .
Metode Operator Generasi Selanjutnya
Metode operator generasi selanjutnya merupakan metode yang dilakukan dengan cara
mengeompokkan populasi kedalam 3 kelompok individu yaitu kelompok individu
yang tidak terinfeksi, kelompok individu terifeksi tetapi tidak menularkan, dan
kelompok individu terinfeksi dan menularkan. Misalkan
1. Komponen X menyatakan kelas-kelas individu yang tidak terinfeksi penyakit
yang sedang diobservasi
2. Komponen Y menyatakan kelas-kelas individu yang terinfeksi penyakit yang
sedang diobservasi, tetapi tidak menularkan penykit tersebut
3. Komponen Z menyatakan kelas-kelas individu yang terinfeksi penyakit yang
sedang diobservasi dan dapat menularkan penykit tersebut.
Dengan demikian, model epidemik suatu penyakit dapat dituliskan dalam bentuk
= f (X, Y, Z),
= (X, Y, Z), (2.21)
= h (X, Y, Z),
dengan X , Y , dan Z ; r, s, n ≥ 0 ; dan h (X, 0, 0) = 0.
Dalam metode operator generasi selanjutnya dimisalkan
= (X*, 0, 0) adalah titik kesetimbangan bebas-infeksi dari sistem
persamaan (2.21), yang diperoleh dari persamaan f (X*, 0, 0) = 0, (X*, 0, 0) = 0, dan
diperoleh solusi Y = (X*, Z). Oleh karena itu, dapat diperoleh sebuah matriks berukuran nxn ,
Φ = h (X*, (X*, 0), 0).
Misalkan Φ dapat dituliskan dalam bentuk Φ = J – , dengan J ≥ 0, ( ≥ 0) dan ≥
0 adalah matriks diagonal. Dengan demikian didefinisikan sebagai radius spektral dari
matriks J , sehingga berdasarkan Definisi 2.10, diperoleh
BAB 3
PEMODELAN PENYEBARAN INFEKSI HIV PADA KOMUNITAS IDU
Pada bab ini akan dibahas pemodelan penyebaran infeksi HIV pada komunitas
Injecting Drug Users (IDU). Berdasarkan penjelasan pada Bab 2 akan dilakukan analisa dinamik mengenai model penyebaran infeksi HIV pada komunitas IDU.
Sebelum melakukan anlisa dinamik terhadap model penyebaran infeksi HIV pada
komunitas IDU, dibahas mengenai pembentukan model. Pembentukan model didasari
oleh asumsi yang sesuai dengan keadaan komunitas IDU dan sifat infeksi HIV.
Pada alur dinamika penyebaran infeksi HIV dalam komunitas IDU, terdapat
faktor kekuatan infeksi. Faktor kekuatan infeksi memperhatikan asumsi-asumsi
mekanisme pertukaran jarum suntik yang menyebabkan terjadinya penyebaran infeksi
HIV di dalam komunitas IDU. Selanjutnya, perilaku sistem dinamik dibahas dengan
mengamati turunan parsial fungsi kekuatan infeksi dan faktor yang mempengaruhi
laju perubahan populasi pada komunitas IDU.
Untuk mengetahui pola penyebaran infeksi pada komunitas IDU melalui
sistem dinamik, maka dicari basic reproduction ratio dan menentukan titik kesetimbangan dari sistem dinamik. Dengan demikian, melalui titik kesetimbangan
dinamika penyebaran infeksi HIV pada komunitas IDU dapat diamati dengan
menetukan kestabilannya melalui basic reproduction ratio.
3.1. Pembentukan Model
Dalam penyebaran infeksi HIV pada komunitas IDU, komunitas tersebut diasmusikan
terdiri dari tiga kelompok individu pecandu narkoba, yaitu :
S(t) : Susceptibles : ukuran populasi individu yang sehat namun rentan dan dapat terinfeksi HIV pada waktu t, selanjutnya disebut ukuran populasi
susceptibles pada saat t.
(t) : AIDS : ukuran populasi individu yang sudah mengidap penyakit AIDS pada waktu t.
Pada penelitian ini diasumsikan total ukuran populasi “aktif” pecandu dalam komunitas IDU adalah
= S + I + .
Dengan demikian, peluang seorang “sharer” (pembagi jarum suntik) merupakan
seorang pecandu terinfeksi adalah
= = (3.1)
Asumsi Model
Dalam pemodelan penyebaran infeksi HIV pada komunitas IDU terdapat fakta yang
diperhatikan yakni infeksi HIV tidak dapat disembuhkan, sehingga dalam model tidak
diperhatikan laju perubahan populasi pecandu yang sembuh (recovered). Pemodelan penyebaran infeksi HIV pada komunitas pecandu pecandu narkoba suntik (IDU)
sesuai model klasik epidemik SIR menggunakan asumsi :
1. Pecandu yang menyadari sudah mengidap AIDS ikut berbagi jarum suntik pada
komunitas IDU.
2. Infeksi HIV hanya menular melalui kontak langsung dengan penderita.
3. Populasi pecandu tertutup (tidak ada proses migrasi), yaitu tidak ada pecandu
yang masuk maupun keluar dari komunitas IDU.
Tabel 3.1 memuat variabel dan parameter yang digunakan dalam proses pembentukan
[image:35.595.106.525.146.507.2]model.
Tabel 3.1. Variabel dan parameter model
Simbol Definisi Simbol Syarat Satuan
S Ukuran populasi pecandu Susceptibles S > 0 Individu
I Ukuran populasi pecandu Infectious I ≥ 0 Individu Ukuran populasi pecanduyang sudah
mengidap AIDS
≥ 0 Individu
Ukuran total pecandu “aktif” dalam komunitas IDU
> 0 Individu
Laju pertambahan populasi IDU dari
manusia biasa menjadi pecandu narkoba
suntik (IDU)
> 0 Individu /
waktu
Laju kematian alami IDU per kapita > 0 1/waktu
Laju kematian alami pecandu yang
mengidap AIDS per kapita
> 0 1/waktu
Laju perubahan dari terinfeksi menjadi
HIV menjadi penyakit AIDS per kapita
> 0 1/waktu
Kekuatan penyebaran infeksi (force of infection) dalam komunitas IDU
≥ 0 1/waktu
Proses penyebaran infeksi HIV di dalam komunitas IDU diasumsikan mengikuti
[image:35.595.144.491.580.727.2]diagram transmisi berikut
Gambar 3.1. Diagram penyebaran infeksi HIV pada komunitas IDU S
I S
Penurunan model penyebaran infeksi HIV pada komunitas IDU adalah sebagai berikut
1. Laju perubahan populasi susceptibles per satuan waktu dipengaruhi oleh laju pertambahan populasi IDU ( ). Populasi susceptibles sepanjang waktu t akan berkurang akibat laju kematian alami pada pecandu susceptibles ( S) dan pengaruh kekuatan penyebaran infeksi pada pecandu susceptibles
, sehingga dapat ditulis
= – S– .
2. Laju perubahan populasi infectious per satuan waktu dipengaruhi oleh pertambahan populasi infectious sepanjang waktu t akibat kekuatan penyebaran infeksi pecandu susceptibles . Berkurangnya populasi
infectious per satuan waktu dipengaruhi faktor laju kematian alami pada pecandu infectious ( ) dan laju perubahan status pecandu yang terinfeksi HIV menjadi pengidap AIDS pada populasi infectious , sehingga dapat ditulis
= – – .
3. Laju perubahan populasi AIDS per satuan waktu dipengaruhi oleh
pertambahan dan pengurangan populasi AIDS per satuan waktu. Pertambahan
populasi AIDS per satuan waktu merupakan akibat laju perubahan status dari
terinfeksi HIV menjadi pengidap AIDS terhadap populasi infectious ( ). Selain itu, berkurangnya populasi AIDS per satuan waktu dipengaruhi oleh
laju kematian alami pada populasi AIDS ( ) dan laju kematian alami pada
pecandu AIDS sebagai individu pengidap AIDS ( ), sehingga dapat ditulis
= – – .
Dengan demikian, pemodelan penyebaran infeksi HIV pada komunitas IDU
adalah sebagai berikut
= – S– ,
= – – , (3.2)
= – – ,
menyatakan laju perubahan populasi pecandu susceptibles terhadap waktu t,
menyatakan laju perubahan populasi pecandu infectious terhadap waktu t,
menyatakan laju perubahan populasi pecandu yang sudah mengidap AIDS
terhadap waktu t,
Berdasarkan sistem persamaan (2.3), diperoleh persamaan untuk laju
perubahan total populasi pecandu “aktif” terhadap waktu t, yaitu
= – – (3.3)
3.2. Kekuatan Infeksi
Kekuatan infeksi HIV merupakan potesi penyebaran infeksi HIV dari kelompok
pecandi yang terinfeksi HIV (infectious) terhadap kelompok pecandu yang rentan terinfeksi HIV (susceptibles). Dalam penulisan ini, kekuatan infeksi HIV memperhatikan mekanisme pertukaran jarum suntik dikalangan pecandu narkoba
suntik (IDU). Untuk mendefinisikan fungsi kekuatan infeksi diberikan asumsi
mekanisme pertukaran jarum suntik sebagai berikut
1. semua individu (pecandu) masuk ke dalam grup secara acak,
2. ukuran grup dinotasikan dengan G, merupakan variabel acak berdistribusi Poisson dengan parameter v > 0. Jika G = k, maka posisi pecandu dinotasikan dengan i = 1, 2, 3, ..., k,
3. setiap grup memperoleh satu jarum suntik baru (yang tidak terinfeksi) pada
penyuntikan pertama, selanjutnya jarum suntik digunakan secara terurut oleh
setiap anggota grup, setelah itu jarum suntik dibuang,
4. pembuatan grup seorang pecandu terjadi mengikuti proses Poisson dengan
parameter > 0 dengan asumsi tanpa dipengaruhi oleh pembuatan grup
pecandu lain,
5. suatu jarum suntik dikatakan terinfeksi jika jarum suntik tersebut telah
digunakan oleh pecandu yang terinfeksi dan yang sudah mengidap AIDS,
6. peluang seorang pecandu susceptibles ke-i berpotensi “membersihkan” jarum
dinotasikan sebagai = . Hal ini dikarenakan darah terinfeksi yang
tersisa di ujung jarum suntik masuk seluruhnya ke dalam tubuh pecandu yang
tidak terinfeksi tersebut,
7. sebarang pecandu susceptibles yang menggunakan jarum suntik terinfeksi diasumsikan terinfeksi HIV, tetapi pecandu tersebut memungkinkan membuat jarum suntik menjadi “bersih” untuk pecandu urutan selanjutnya,
8. pecandu susceptibles menjadi terinfeksi hanya dikarenakan berbagi jarum suntik dalam grup,
9. peluang seorang pecandu menjadi terinfeksi (dan langsung dapat menularkan)
jika terdapat paparan HIV adalah ,
10.kejadian pecandu ke-i tidak terinfeksi saling bebas dengan kejadian pecandu
ke-i tidak berpotensi “membersihkan” jarum suntik dari sisa darah yang
terinfeksi,
11.kejadian pecandu ke-i terinfeksi saling bebas dengan kejadian pecandu setelahnya (pecandu lain) tidak terinfeksi dan tidak berpotensi
“membersihkan” jarum suntik dari sisa darah terinfeksi,
12.kejadian pecandu ke-i adalah pecandu terinfeksi dan dapat menularkan infeksi HIV kepada pecandu setelahnya saling lepas dengan kejadian pecandu yang
lain.
Berdasarkan asumsi-asumsi di atas, fungsi dari kekuatan infeksi HIV dalam
grup pada komunitas IDU dapat didefinisikan sebagai berikut
= (3.4)
dengan merupakan peluang seorang pecandu terpapar HIV yakni peluang
bahwa seorang pecandu memasukkan jarum suntik yang terinfeksi ke dalam tubuhnya.
Dengan demikian, dapat dikatakan sebagai potensi (penyebaran) seorang
pecandu dalam grup dapat terkena infeksi HIV (dan langsung dapat menularkan)
setelah memasukkan jarum suntik terinfeksi ke dalam tubuh pecandu dengan
Misalkan :
E : kejadian seorang pecandu menggunakan jarum suntik terinfeksi,
R(k) : posisi urutan pecandu dalam berbagi jarum suntik dalam grupnya yang berukuran k
Oleh karena itu, peluang seorang pecandu memasukkan jarum suntik terinfeksi ke
dalam tubuhnya adalah
= P(E) =
= .(3.5)
Dalam hal ini hanya ukursn grup yang lebih besar dan sama dengan dua (k ≥ 2)
yang relevan dalam pembentukan suatu grup yang memungkinkan dalam masalah
penyebaran infeksi. Berdasarkan asumsi kekuatan infeksi (2), ukuran grup
berdistribusi poisson dengan fungsi peluang (p.m.f).
= , untuk k = 2, 3, 4, ... (3.6)
= v + 2 adalah rata-rata ukuran grup.
Dalam grup, setiap pacandu berada pada posisi berbeda dalam urutan
penggunaan jarum suntik. Setiap pecandu memiliki kemungkinan yang sama berada
pada posisi ke-j. Jika ukuran grup adalah k, maka peluang bahwa seorang pecandu berada pada posisi ke-j adalah
= k = 2, 3, 4, ... (3.7)
Misalkan seorang pecandu berada di posisi ke-j dalam grup berukuran k maka peluang seorang pecandu menggunakan jarum suntuk terinfeksi adalah
dengan
adalah kejadian bahwa pecandu ke-i adalah pecandu terinfeksi, dan
= ke-h tidak terinfeksi (sebelum menggunakan jarum suntik) dan tidak “membersihkan” jarum suntik yang terinfeksi.
didefinisikan sebagai kejadian pecandu ke-i adalah pecandu terinfeksi dan dapat menularkan infeksi HIV pada pecandu selanjutnya.
Oleh karena asumsi kekuatan infeksi (6) dan P( ) = = sesuai
persamaan (3.1), peluang dapat ditulis sebagai berikut
P( ) =
= P xP x xP
= P x P xP xP x xP x P
= x x x x x x
= x ,
dengan
: kejadian bahwa pecandu ke-h tidak terinfeksi,
: kejadian bahwa pecandu ke-htidak mampu “membersihkan” jarum suntik dari
sisa darah yang terinfeksi HIV
Berdasarkan teori peluang pada subbab 2 dan asumsi kekuatan infeksi (11) dan
(12), persamaan peluang (3.8) dapat dijabarkan sebagai berikut
= + + +
= + +
= +
+
Oleh karena itu peluang menggunakan jarum suntik terinfeksi pada posisi
pecandu ke-jdalam grup “sahabat” dengan ukuran k adalah
(3.9)
Persamaan (3.9) dapat diselesaikan dalam beberapa kasus penjumlahan dengan
menggunakan deret geometri agar memenuhi persamaan (3.5). untuk mempermudah
penyelesaian persamaan (3.9), misalkan
1. ,
2. .
Berikut ini kasus-kasus penjumlahan berdasarkan persamaan (3.9)
1. Kasus 1,
=
=
=
=
=
2. Kasus 2,
=
=
=
=
=
=
=
=
4. Kasus 4,
=
=
=
=
=
=
Berdasarkan penjabaran beberapa kasus penjumlahan diatas, maka persamaan
(3.5) dapat ditulis sebagai berikut
=
=
=
=
= (3.10)
Oleh karena adalah suatu peluang dan berdasarkan persamaan (3.1),
persamaan (3.10) dibatasi bahwa ≠ 0, dengan
=
=
Selanjutnya, dapat ditulis
=
=
.
(3.11)Terlihat bahwa bergantung pada variabel S, I dan melalui variabel pada persamaan (3.1) yaitu peluang seorang pecandu merupakan pecandu
yang terinfeksi. Berdasarkan (3.10) dan fungsi dapat ditulis sebagai
= (3.12)
dengan
=
3.3. Analisa Kualitatif Model
Pada penelitian ini, diasumsikan bahwa pecandu narkoba suntik (IDU) yang
menyadari sudah mengidap AIDS ikut berbagi suntikan dan bergabung dalam grup.
Oleh karena itu, model yang diperhatikan laju perubahan kelompok pecandu
= = – S– , (3.13)
= = – – , (3.14)
= = – – , (3.15)
Untuk setiap R dengan I≠ 0 dapat dimisalkan
= (3.16)
=
=
Berdasarkan (3.4), persamaan (3.14) dapat ditulis :
= – –
= –
= –
= – .
Misalkan
= – , untuk I ≠ 0, (3.17)
= ,
untuk I≥ 0. (3.18)
Selanjutnya persamaan (3.14) dapat ditulis
= . (3.19)
merupakan faktor yang berpengaruh penting dalam menekan laju
pertambahan populasi pecandu infectious per satuan waktu.
Berdasarkan sistem persamaan (3.13), (3.14) dan (3.15), fungsi sangat
berpengaruh dalam sistem dinamik tersebut. Oleh karena itu turunan parsial terhadap
variabel S, I dan fungsi dan fungsi-fungsi lain yang berhubungan dengan sistem perlu diamati untuk mempermudah analisa sistem
Turunan Parsial
Untuk lebih mudah mengamati turunan parsial fungsi , maka dapat dilihat
dari persamaan = sesuai (3.11), sehingga dapat ditulis sebagai
berikut
=
.
Misalkan
1. D = 2. R = 3. T =
4. W =
=
Oleh karena dan merupakan suatu peluang > 0 dan > 0, maka jelas
bahwa
a. 0 1
b. 0 1
c. 0 1
d. 0 1
dengan demikian dapat disimpulkan
1. D = ≥ 0 2. R ≥ 0
4. W ≥ 0
5.
6. 0 1
7.
8. , maka ≥ 0.
Untuk melihat tanda dari , dan
,
dapat dilihat dari bentuk , dengan1.
=
02. = ≥ 0
3. = > 0
4. = ≥ 0
5. = 2 < 0
6. = ≥ 0
Oleh karena = ≤ 0
,
= ≥ 0 dan= ≤ 0 maka diperoleh kesimpulan bahwa
≤ 0 (3.20)
≤ 0 dan (3.21)
Dengan demikian (3.20), (3.21) dan (3.22) mengakibatkan turunan parsial fungsi
kekuatan infeksi sesuai (3.4) adalah ≤ 0, ≥ 0 dan
≤ 0.
Turunan Parsial
Oleh karena = = , maka untuk melihat
perilaku (bernilai positif atau nagatif) dari turunan parsial
,
dan dapatlebih muda dilihat melalui persamaan
=
Dengan 0 ≤ ≤ 1. Dengan demikian turunan parsial terhadap adalah
=
≤0Oleh karena ≤ 0
,
≥ 0 dan ≤ 0 maka diperoleh kesimpulan ≥ 0,
≤ 0 dan ≥ 0 untuk semua R.
Turunan parsial
Berdasarkan persamaan (3.17) maka turunan parsial terhadap
adalah sebagai berikut
Oleh karena ≥ 0 dan ≥ 0, maka ≥ 0. Turunan parsial
terhadap adalah
=
Berdasarkan kesimpulan sebelumnya bahwa Oelh karena ≥ 0 dan ≥ 0, maka
≤ 0.
Selanjutnya turunan parsil terhadap adalah
=
Berdasarkan kesimpulan sebelumnya bahwa Oelh karena ≥ 0 dan ≥ 0, maka
≥ 0.
Dengan demikian dapat disimpulkan
≥ 0. (3.23)
≤ 0. (3.24)
≥ 0. (3.25)
3.4. Basic Reproduction Ratio
Untuk memahami penyebaran HIV melalui model matematika, dapat dilakukan
dengan melakukan analisa dinamika model matematika (3.13), (3.14) dan (3.15).
Analisa dinamika pada pemodelan penyebaran infeksi HIV pada komuniatas IDU
dimaksudkan untuk mengetahui pada nilai batasan mana yan mampu mempengaruhi
penyebaran infeksi HIV pada komunitas IDU. Nilai batasan yang di maksud dalam
Berdasarkan landasan teori pada subbab 2.5, pada kasus ini X = S, Y = I, Z = A
maka dengan mencari solusi = 0, = 0 dan = 0 sesuai
persamaan (3.13), (3.14) dan (3.15) diperoleh
= =
Berdasrakan metode operator generasi selanjutnya, dalam menentukan Φ
diperlukan informasi sebagai berikut
= .
Dengan demikian Φ, dapat ditulis dalam bentuk
Φ =
=
= .
Oleh karena Φ dapat dituliskan dalam bentuk Φ = dengan
= ≥ 0 dan = > 0, maka sesuai dengan
definisi radius spektral diperoleh
= (J ) =
.
Dengan demikian, basic reproduction ratio untuk sistem persemaan (3.13), (3.14) dan (3.15) adalah
=
.
(3.26)3.5. Kesetimbangan dan Kestabilan Model
Sistem dinamik (3.13), (3.14) dan (3.15) memiliki perilaku sistem yang berbeda-beda
di setiap titiknya. Untuk melihat perilaku sistem dinamik dapat diamati melalui titik
disebut sebagai titik kesetimbangan. Selanjutnya pengamatan sistem akibat perubahan
pada kondisi awal dapat lebih mudah diamati melalui titik kesetimbangannya.
Sistem (3.13), (3.14) dan (3.15) merupakan model epidemik penyakit infeksi,
sedemikian sehingga titik kesetimbangan yang diperhatikan adalah titik
kesetimbangan bebas infeksi dan titik kesetimbangan epidemik. Titik kesetimbangan
bebas infeksi merupakan titik kesetimb angan pada saat tidak terdapat anggota
komunitas IDU yang tidak terinfeksi atau I = 0 dan = 0. Titik kesetimbangan espidemik adalah titik yang menunjukkan jumlah pecandu susceptibles dan jumlah
pecandu infectious pada keadaan setimbang terjadinya epidemik dalam komunitas
IDU dengan I > 0 dan > 0.
3.5.1 Titik Kesetimbangan Bebas Infeksi
Pada kenyataannya keadaan yang diharapkan dalam suatu komunitas IDU adalah
keadaan saat tidak ada pecandu yang terinfeksi dalam komunitas IDU sehingga
penyebaran infeksi HIV tidak mewabah pada komunitas IDU. Selanjutnya pada
subbab ini pencarian titik kesetimbangan bebas infeksi untuk mengamati perilaku
sistem (3.13), (3.14) dan (3.15). Untuk mencari titik kesetimbangan bebas infeksi,
sesuai definisi 2.3,
= – S– = 0, (3.27)
= – = 0, (3.28)
= – = 0. (3.29)
Berdasarkan persamaan (3.19) dan (3.18), persamaan (3.28) dapat ditulis
= = 0 dan memperoleh solusi = 0 atau = 0.
Oleh karena itu, untuk memperoleh titik kesetimbangan bebas infeksi, dipilih solusi
= 0 dan = 0. Dengan mensubstitusikan = 0 dan = 0 kedalam persamaan (3.27)
maka – – = 0. Oleh karena = 0 artinya tidak ada
kekuatan infeksi, maka diperoleh = dengan = 0 dan = 0. Dengan demikian,
= .
Pada saat tidak ada kelompok pecandu yang terinfeksi HIV lagi dalam
komunitas IDU, jumlah pecandu yang tidak terinfeksi namun rentan terhadap infeksi
HIV terdapat sebanyak = . Dengan demikian, keadaan bebas infeksi pada
komunitas IDU tercapai saat tidak ada pecandu infectious, saat tidak ada pecandu pengidap AIDS dan jumlah pecandu susceptibles berbanding lurus dengan tingkat pertambahan pecandu baru yang susceptibles, namun berbanding terbalik dengan tingkat alami kematian pecandu.
3.5.2 Titik Kesetimbangan Epidemik
Selain memperhatikan titik kesetimbangan bebas infeksi, dalam menganalisa sistem
dinamik (3.13), (3.14) dan (3.15) diperlukan analisa sistem dinamik titik
kesetimbangan epidemik. Titik kesetimbangan epidemik diperoleh dengan cara yang
sama dengan mencari titik kesetimbangan bebas infeksi, yaitu dengan mencari solusi
(3.27), (3.28) dan (3.29) dengan I > 0. Berdasarkan persamaan (3.27) diperoleh
= – (3.30)
Sehingga diperoleh = . Oleh karena > 1, diperoleh
= dan solusi <
.
Berdasarkan solusi , dan ≥ 0 maka diperoleh
= dan mengakibatkan
≤ (3.31)
Dengan demikian titik kesetimbangan epidemik untuk sistem dinamik (3.13), (3.14)
dan (3.15) adalah
= , = dan <
.
3.5.3.Kestabilan Titik Kesetimbangan Model
Untuk menganalisa perilaku penyebara infeksi HIV pada komunitas IDU, diperlukan
analisa kestabilan titik-titik kesetimbangan sistem dengan memperhatikan ukuran
(rasio) penyebaran yaitu basic reproduction ratio. Analisa kestabilan pada titik kesetimbangan dilakukan untuk mengamati perilaku sistem di sekitar titik
kesetimbangan tersebut. Jika terjadi perubahan pada kodisi awal sistem, maka sistem
akan stabil di titik kesetimbangannya yang stabil. Selanjutnya, dilihat kestabilan
titik-titik kesetimbangan untuk sistem persamaan (3.13), (3.14) dan (3.15) melalui teorema
berikut ini.
Teorema 3.1.
a. Jika 1, maka titik kesetimbangan bebas infeksi
= .
merupakan satu-satunya solusi titik kesetimbangan untuk sistem (3.13) dan
(3.14). Selanjutnya, titik dikatakan stabil asimtotik global (Globally Asymptotically Stable / GAS) pada daerah R.
b. Jika > 1, maka titik solusi dikatakan tidak stabil dan sistem (3.13), (3.14)
dan (3.15) memiliki titik kesetimbangan lain yaitu = dengan
= ,
= ,
dan <
.
Bukti 3.1.
Sebelum membuktikan teorema 3.1. akan dibuktikan
1 0. (3.32)
Pertama, persamaan dijabarakan berdasarkan persamaan (3.18), yaitu :
= . (3.33)
⇒ Akan dibuktikan 1 maka 0.
= 1,
Berdasarkan persamaan (3.33), maka terbukti jika 1 maka 0.
⇐Akan dibuktikan jika 0 maka 1.
=
= 1
Berdasarkan (3.26), maka terbukti jika 0 maka 1. Dengan
demikian terbukti bahwa 1 0.
(a) Pada kenyataannya, saat 1 daerah R tidak memiliki kurva fungsi
diferensial (isocline), = 0. Hal tersebut berdasarkan persamaan (3.18), = 0 jika
dan hanya jika I = 0 dan = 0. Selanjutnya, akan dibuktikan titik
kesetimbangan bebas infeksi = adalah satu-satunya titik kesetimbangan
Misalkan pada sistem persamaan (3.13), (3.14) dan (3.15) terdapat titik
kesetimbangan lain yaitu dengan asumsi , , 0
dan 0. Oleh karena adalah titik kesetimbangan untuk sistem persamaan
(3.13), (3.14) dan (3.15), maka berdasarkan Definisi 2.3., = , memenuhi
persamaan = 0. Dengan demikian = , yang artinya
= – – = 0,
= = 0 dan
= – = 0.
Berdasarkan (3.25) merupakan fungsi turun untuk dan akibat (3.32)
diperoleh
≤ 0. (3.34)
Dengan asumsi 0 maka < 0, akibatnya solusi =
= 0 hanya dipenuhi oleh = 0,
=
0 dan menyebabkan=
.
Hal ini kontradiksi dengan asumsi , , 0 dan 0 sehingga diperoleh
kesimpulan bahwa = . Dengan demikian, terbukti bahwa merupakan
satu-satunya titik kesetimbangan untuk persamaan (3.13), (3.14) dan (3.15) saat 1.
Selanjutnya, akan dilihat sifat kestabilan titik kesetimbangan bebas infeksi,
pada R. Untuk membuktikan bahwa bersifat stabil asimtotik global maka akan digunakan teorema kestabilan Lyapunov. Didefinisikan sustu fungsi yang definit
positif,
= dengan : R .
Fungsi dikatakan fungsi Lyapunov, sedemikian sehingga
=
= + +
Dalam menentukan kestabilan global sesuai teorema 2.2. fungsi
= akan dilihat perilaku (tanda positif dan tanda negatif) pada
saat R – . Oleh karena saat 1 berlaku (3.34) maka berlaku > 0 dan < 0 pada R– . Dengan demikian
a. = 0 dan > 0 untuk dan
b. < 0 pada R– , yaitu saat , dan .
Bedasarkan teorema 2.2, dikatakan stabil asimtotik global untuk sistem
persamaan (3.13), (3.14) dan (3.15).
(b) Berdasarkan (3.31) , saat > 1 berlaku kontra posisi
> 1 > 0. (3.35)
sehingga pada kasus ini kedua isocline terdefinisi di daerah R. Hal tersebut berkaitan
erat dengan penentuan kestabilan titik-titik kesetimbangan. Dalam menentukan
kestabilan lokal dan dapat dilakukan dengan mencari nilai eigen dari matriks
koefisien sistem persamaan (3.13), (3.14) dan (3.15) sesuai Teorema 2.1. Dalam hal
ini matriks koefisien sistem merupakan matriks Jacobian sistem persamaan (3.13),
(3.14) dan (3.15) yaitu Ψ z ,
Ψ =
Dengan demikian, nilai eigen diperoleh dengan mencari solusi karakteristik
det = = 0,
Sistem persamaan (3.13), (3.14) dan (3.15) merupakan sistem persamaan
diferensial nonlinier. Oleh karena penjelasan pada subbab 2.1, kelinieran sistem
(3.13), (3.14) dan (3.15) di sekitar titik kesetimbangan dan dapat ditaksir dengan
mengamati matriks Jacobian Ψ dan Ψ . Selanjutnya untuk menentukan kestabilan lokal titik kesetimbangan bebas infeksi , akan dicari solusi karakteristik
(3.35). oleh karena = 0, = 0, =
< 0,
dan= > 0 maka diperoleh akar-akar karakteristik persamaan (3.36)
adalah
=
<
0 dan=
> 0, oleh karena terdapat nilai eigen yangpositif, maka berdasarkan Teorema 2.1 titik kesetimbangan bebas infeksi dikatakan
tidak stabil pada saat > 1.
Selanjutnya, keberadaan dapat dilihat pada subbab 3.5.2 dan kestabilan
titik epidemik pada saat > 1 dengan 0 akan ditentukan dengan cara yang
sama dengan menentukan ketidakstabilan * z . Oleh karena kurva diferensial (isocline)
= 0 terdefinisi di daerah R dan 0, maka solusi = 0 hanya dipenuhi oleh
= 0. Berdasarkan persamaan (3.22), (3.23), (3.24), (3.25) diperoleh
= ≥ 0,
= ≤ 0 dan
= ≥ 0.
Hal tersebut mengakibatkan
det = > 0 dan
Oleh karena itu persamaan karakteristik (3.36) pada titik memperoleh akar-akar
karakteristik
=
dengan
a = 1 > 0,
b = trace > 0,
c = det > 0 dan
0 <
< 0.
Dengan demikian < 0 dan < 0. Berdasarkan Teorema 2.1, dikatakan stabil
asimtotik lokal dan juga sekaligus stabil asimtotik global.
BAB 4
SIMULASI PEMODELAN PENYEBRAN INFEKSI HIV PADA KOMUNITAS IDU
Pada bab ini dibahas tiga simulasi. Simulasi pertama membahas dinamika
terhadap populasi pecandu susceptibles, infectious dan pengidap AIDS. Pada simulasi kedua dan ketiga dibahas dinamika penyebaran infeksi HIV pada komunitas IDU
dengan memperhatikan kestabilan titik kesetimbangannnya. Simulasi ini bertujuan
memberikan gambaran mengenai dinamika penyebaran infeksi HIV dalam komunitas
IDU melalui gambar dinamika dan potret fase dengan memperhatikan basic reproduction ratio. Simulasi dan model dibahas dengan menggunakan
software MATLAB dengan source code simulasi dapat dilihat pada lampiran 1 penelitian ini.
4.1. Simulasi 1 : Dinamika
Dinamika sangat penting untuk diketahui karena fungsi
merupakan bagian terpenting dalam sistem dinamik penyebaran infeksi HIV pada
komunitas IDU. Mengamati bertujuan untuk mempermudah memahami
perilaku sistem dinamik (3.13), (3.14) dan (3.15). berikut ini nilai parameter yang
digunakan untuk mengamati dinamika peluang seorang pecandu terinfeksi HIV,
[image:58.595.198.434.616.682.2].
Tabel 4.1. Nilai parameter pada simulasi 1
Parameter Nilai Parameter
V 10
0,8
Berdasarkan tabel 4.1. fungsi peluang (3.11) dapat dinyatakan sebagai
Pertama, digambarkan mengenai dinamika peluang terpapar HIV dalam
komunitas IDU berdasarkan populasi pecandu susceptibles, pecandu infectious dan pengidap AIDS. Berikut ini gambar yang menunjukkan dinamika pada
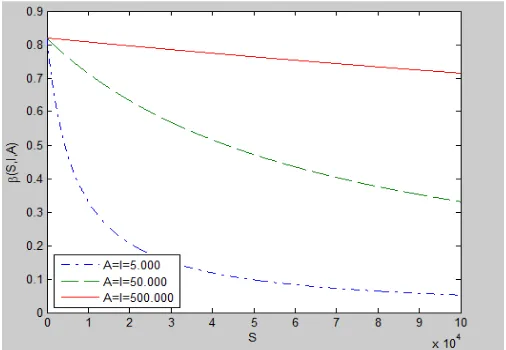
[image:59.595.190.443.197.372.2]populasi susceptibles dengan tiga kasus infectious dan pengidap AIDS yang tetap, yakni 5.000, 50.000 dan 500.000 sebagai berikut
Gambar 4.1. Dinamika pada populasi susceptible
Tabel 4.2 menunjukkan pengamatan nilai pada tiga kasus jumlah
[image:59.595.111.524.473.736.2]susceptible yakni saat susceptibles berjumlah 30.000, 60.000, dan 90.000.
Tabel 4.2. Penurunan terhadap dalam persentase
Jumlah
Suscepibles
Jumlah Infectious dan Pengidap AIDS = 5.000
= 5.000
= 50.000
= 50.000
= 500.000
= 500.0000
= 30.000 = 0,1510 = 0.5688 = 0.7853
Penurunan
(%) 44,97% 23,49% 4,05%
= 60.000 = 0.0831 = 0.4352 = 0.7535
Penurunan
(%) 31,05% 19,03% 3,89%
= 90.000 = 0.0573 = 0.3524 = 0.7242
Selisih Penurunan
(%)
13,92% 4,46% 0,16%
Berdasarkan Tabel 4.2 diperoleh kesimpulan bahwa dengan jumlah pecandu
infectious dan pengidap AIDS yang tetap, semakin banyak jumlah pecandu
susceptibles maka semakin kecil peluang pecandu memasukkan jarum suntik terinfeksi ke dalam tubuhnya. Hal ini sesuai dengan kurva yang ditunjukkan
pada Gambar 4.1. Nilai fungsi berkurang seiring bertambahnya jumlah
susceptibles, dengan selisih penurunan nilai berbeda-beda sesuai dengan pertambahan jumlah infectious dan pengidap AIDS. Semakin kecil jumlah pecandu infectious dan pengidap AIDS, maka semakin tajam penurunan kurva yakni mencapai
selisih penurunan 13,92%.
Dengan demikian, Gambar 4.1. menunjukkan bahwa fungsi
merupakan fungsi turun terhadap populasi pecandu susceptibles, sesuai dengan (3.20). Hal tersebut mengakibatkan fungsi laju perubahan susceptibles terhadap waktu juga merupakan fungsi turun terhadap populasi susceptibles dan fungsi dan merupakan fungsi naik terhadap populasi susceptibles, sesuai dengan persamaan (3.23) dan (3.24).
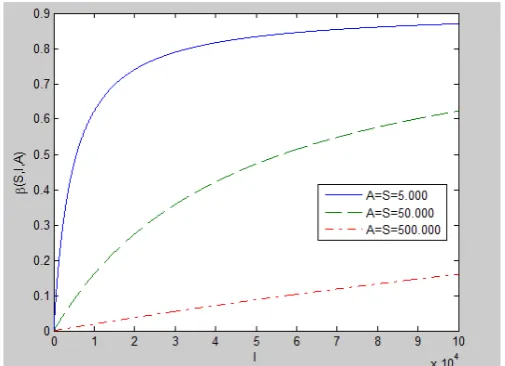
Jika jumlah pecandu infectious besar, maka peluang pecandu terpapar HIV semakin meningkat dengan jumlah pecandu susceptibles dan pengidap AIDS tetap. Hal ini dapat ditunjukkan oleh gambar dinamika peluang terpapar HIV pada populasi
[image:60.595.191.444.539.722.2]pecandu infectious dengan jumlah susceptibles dan AIDS tetap, yakni 5.000, 50.000 dan 500.000 sebagai berikut
Tabel 4.3. Kenaikan terhadap dalam persentase
Jumlah
Infectious
Jumlah Suscepibles dan Pengidap AIDS = 5.000 = 5.000 = 50.000 = 50.000 = 500.000 = 500.000
= 90.000 = 0.8658 = 0.6012 = 0.1469
Kenaikan
(%) 2,44% 17,06% 42,07%
= 60.000 = 0.8452 = 0.5136 = 0.1034
Kenaikan
(%) 7,14% 43,91% 89,03%
= 30.000 = 0.7889 = 0.3569 = 0.0547
Selisih Kenaikan
(%)
4,70% 29,85% 46,96%
Keterangan :
Tabel 4.3. menunjukkan bahwa fungsi merupakan fungsi naik
terhadap populasi pecandu infectious, sesuai dengan Gambar 4.2. Nilai fungsi bertambah seiring bertambahnya jumlah infectious, dengan selisih kenaikan nilai yang berbeda-beda sesuai dengan pertambahan jumlah susceptibles d