SOLUSI NUMERIK MASALAH KONTROL OPTIMUM
PENYEBARAN PENYAKIT INFLUENZA A
SYAHRUL AGUS NASIFA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Solusi Numerik Masalah Kontrol Optimum Penyebaran Penyakit Influenza A adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
SYAHRUL AGUS NASIFA. Solusi Numerik Masalah Kontrol Optimum Penyebaran Penyakit Influenza A. Dibimbing oleh TONI BAKHTIAR dan ALI KUSNANTO.
Influenza A merupakan penyakit pernapasan akut yang disebabkan oleh virus H1N1. Penyebaran utama H1N1 adalah melalui udara dan dapat menular dari manusia ke manusia. Pada karya ilmiah ini, model matematika SIR digunakan untuk membahas penyebaran H1N1, di mana populasi terbagi ke dalam tiga kelas yaitu rentan, terinfeksi, dan sembuh. Analisis dilakukan terhadap dua kasus, yaitu model tanpa dan dengan pemberian kontrol yakni perlakuan vaksinasi. Model penyebaran H1N1 ini diterapkan di Kabupaten dan Kota Bogor dengan total populasi sebanyak 6 juta orang. Pada model tanpa kontrol diperoleh dua titik tetap, kemudian dari nilai batas kestabilan untuk titik tetap bebas penyakit diperoleh bilangan reproduksi dasar . Penyakit akan menghilang untuk dan akan mewabah untuk . Pada model dengan pemberian kontrol diminimumkan banyaknya populasi terinfeksi dan biaya vaksinasi. Solusi numerik sistem persamaan diferensial taklinear yang diperoleh dari penerapan prinsip minimum Pontryagin diselesaikan dengan metode Runge-Kutta orde-4. Hasil simulasi numerik menunjukkan bahwa tanpa pemberian kontrol, bilangan reproduksi dasar menyebabkan jumlah individu terinfeksi H1N1 lebih banyak dibandingkan dengan bilangan reproduksi dasar . Pemberian kontrol menurunkan jumlah individu terinfeksi H1N1 hingga .
Kata kunci: analisis kestabilan, influenza A (H1N1), kontrol optimum, prinsip minimum Pontryagin, Runge-Kutta orde-4
ABSTRACT
SYAHRUL AGUS NASIFA. Numerical Solution of an Optimal Control Problem of Transmission of the Influenza A Disease. Supervised by TONI BAKHTIAR and ALI KUSNANTO.
of numerical simulation show that the model without control administration, basic reproductive number causes more infected individuals than that of
. Meanwhile, the effect of the treatment above decreased the number of H1N1 infected down to .
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
SOLUSI NUMERIK MASALAH KONTROL OPTIMUM
PENYEBARAN PENYAKIT INFLUENZA A
SYAHRUL AGUS NASIFA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi : Solusi Numerik Masalah Kontrol Optimum Penyebaran Penyakit Influenza A
Nama : Syahrul Agus Nasifa
NIM : G54090030
Disetujui oleh
Dr Toni Bakhtiar, MSc Pembimbing I
Drs Ali Kusnanto, MSi Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Mei 2013 ini ialah kontrol optimum, dengan judul Solusi Numerik Masalah Kontrol Optimum Penyebaran Penyakit Influenza A.
Terima kasih penulis ucapkan kepada Bapak Dr. Toni Bakhtiar, M.Sc dan Bapak Drs. Ali Kusnanto, M.Si selaku pembimbing, serta Bapak Ir. Ngakan Komang Kutha Ardana, M.Sc selaku penguji ujian skripsi yang telah banyak memberi saran. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, serta seluruh keluarga, atas segala doa dan kasih sayangnya. Di samping itu, ungkapan terima kasih penulis sampaikan kepada Lola Oktasari, lalu rekan satu bimbingan (Meda, Sonia, Sevira, bang Chastro dan Kak Vivi), teman belajar kompre (Syaepul, Rio, Qowi, Ichsan, Galih, Nisa dan Windi), teman-teman Matematika 46, adik-adik Matematika angkatan 47, 48, dan 49 dan semua pihak yang turut berpartisipasi dalam penelitian ini.
Semoga karya ilmiah ini bermanfaat.
DAFTAR ISI
DAFTAR TABEL DAFTAR GAMBAR DAFTAR LAMPIRAN
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 1
LANDASAN TEORI 2
Sistem Persamaan Diferensial 2
Titik Tetap 2
Pelinearan 2
Nilai Eigen dan Vektor Eigen 3
Kestabilan Titik Tetap 3
Runge-Kutta Orde-4 4
Bilangan Reproduksi Dasar 4
Kontrol Optimum 4
Prinsip Minimum Pontryagin 5
MODEL PENYEBARAN VIRUS H1N1 6
Persamaan Model H1N1 6
Penentuan Titik Tetap Model 8
Analisis Kestabilan Titik Tetap 9
MASALAH KONTROL OPTIMUM 11
SIMULASI NUMERIK 13
Nilai Parameter 13
Hasil Simulasi 14
SIMPULAN 21
DAFTAR PUSTAKA 21
LAMPIRAN 23
DAFTAR TABEL
1 Kondisi kestabilan titik tetap 11
2 Nilai-nilai parameter 14
3 Nilai awal untuk model penyebaran virus H1N1 14
DAFTAR GAMBAR
1 Kompartemen model penyebaran virus H1N1 tanpa kontrol 7 2 Kompartemen model penyebaran virus H1N1 dengan kontrol 8 3 Dinamika populasi terinfeksi tanpa dan dengan kontrol untuk 15 4 Dinamika populasi terinfeksi tanpa dan dengan kontrol untuk 15 5 Dinamika populasi terinfeksi tanpa kontrol untuk dan
16
6 Dinamika populasi rentan tanpa dan dengan kontrol untuk 17 7 Dinamika populasi rentan tanpa dan dengan kontrol untuk 17 8 Dinamika populasi sembuh tanpa dan dengan kontrol untuk 18 9 Dinamika populasi sembuh tanpa dan dengan kontrol untuk 18
10 Kontrol optimum 19
11 Dinamika populasi individu terinfeksi dengan kontrol untuk
, , dan 20
DAFTAR LAMPIRAN
1 Bukti teorema 1 (prinsip minimum Pontryagin) 23
2 Penentuan titik tetap 24
3 Analisis kestabilan titik tetap dan nilai bilangan reproduksi dasar 26
PENDAHULUAN
Latar Belakang
Influenza A (H1N1) merupakan penyakit pernapasan akut pada manusia yang memengaruhi hidung, tenggorokan, dan paru-paru. Penyakit ini disebabkan oleh virus H1N1 yang merupakan subtipe dari virus influenza A. Virus ini pada mulanya diketahui beredar di antara populasi babi dan unggas, kemudian ditemukan dapat menular kepada manusia (Sitepoe 2009).
Pandemi flu merupakan wabah global dari strain baru virus influenza A
H1N1, virus ini sering disebut sebagai “flu babi” di media. Virus ini pertama kali
ditemukan pada April 2009 yang mengandung kombinasi gen dari babi, burung, dan manusia. Penyebaran virus H1N1 yang paling utama adalah melalui udara (El Hia et al. 2012).
Pada Juni 2009, organisasi kesehatan dunia (WHO) menyatakan virus H1N1 sebagai pandemi karena sudah memasuki tahap penularan dari manusia ke manusia dan menyebar keseluruh dunia. Kasus H1N1 di Indonesia sampai pada tanggal 1 Agustus 2009 terdapat 520 kasus positif H1N1 yang terdiri atas 291 laki-laki dan 229 perempuan (Kompas 2009). Pada 22 November 2009, lebih dari 207 negara telah melaporkan kasus yang dikonfirmasi terinfeksi virus H1N1 (WHO 2009).
Sebagian besar pemerintah dari banyak negara merencanakan untuk melakukan vaksinasi secara massal sebagai tindakan pencegahan pandemi virus H1N1. Vaksinasi massal diharapkan dapat mengurangi jumlah individu yang terinfeksi. Teori kontrol optimum digunakan untuk meminimumkan biaya yang dikeluarkan selama vaksinasi, meminimumkan populasi yang terinfeksi, dan menentukan fungsi kontrol ( ) yang optimum.
Pada karya ilmiah ini akan dibahas model penyebaran virus H1N1. Model untuk penyebaran virus H1N1 yang digunakan adalah model Susceptible Infected Recovered (SIR) yang dibahas oleh Hattaf dan Yousfi (2009). Model SIR dengan pemberian kontrol ke dalam sistem dibahas oleh El Hia et al. (2012).
Tujuan Penelitian
Berdasarkan latar belakang di atas, maka tujuan karya ilmiah ini adalah: 1. Merekonstruksi model penyebaran influenza A (H1N1) menggunakan model
SIR dengan dan tanpa kontrol.
2. Menentukan fungsi kontrol yang optimum yang meminimumkan populasi terinfeksi dan membandingkan nilai bilangan reproduksi dasar yang berbeda terhadap dinamika populasi dengan dan tanpa kontrol.
2
LANDASAN TEORI
Pada bagian ini akan dibahas teori-teori yang digunakan untuk menyusun karya ilmiah ini. Teori-teori tersebut meliputi sistem persamaan diferensial, titik tetap, pelinearan, kestabilan titik tetap, nilai eigen dan vektor eigen, metode Runge-Kutta orde-4, bilangan reproduksi dasar, kontrol optimum, dan prinsip minimum Pontryagin.
Misalkan diberikan sistem persamaan diferensial sebagai berikut
̇
maka suatu titik yang memenuhi disebut titik kesetimbangan atau titik tetap dari sistem persamaan diferensial tersebut.
(Tu 1994) Pelinearan
Analisis kestabilan untuk sistem persamaan diferensial taklinear dilakukan dengan menggunakan teknik pelinearan. Sistem persamaan diferensial taklinear didefinisikan sebagai berikut
̇ . (2)
Dengan menggunakan ekspansi Taylor di sekitar titik tetap , maka persamaan (2) dapat ditulis sebagai berikut
̇ . (3) Persamaan (3) merupakan bentuk sistem persamaan diferensial taklinear dengan adalah matriks Jacobi,
3 dan merupakan suku berorde tinggi yang mempunyai sifat . Bentuk sistem persamaan diferensial taklinear setelah dilakukan pelinearan menjadi sebagai berikut
Analisis kestabilan titik tetap dilakukan dengan menggunakan matriks Jacobi yaitu matriks . Titik tetap disubstitusikan ke dalam persamaan matriks Jacobi sehingga diperoleh nilai-nilai eigennya dengan dari persamaan karakteristik
Secara umum kestabilan titik tetap mempunyai tiga perilaku sebagai berikut: 1. Stabil, jika
b. Ada komponen bagian real dari nilai eigen kompleks, lebih besar dari nol ( untuk suatu ).
3. Sadel, jika perkalian dua buah nilai eigen real sembarang adalah negatif ( untuk dan sembarang). Titik tetap sadel ini bersifat takstabil.
4
Runge-Kutta Orde-4
Runge-Kutta adalah salah satu metode yang digunakan untuk menyelesaikan solusi persamaan diferensial secara numerik. Metode ini dikembangkan sekitar tahun 1900 oleh matematikawan Jerman C. Runge dan M.W. Kutta.
Perhatikan masalah nilai awal berikut
Bilangan reproduksi dasar adalah banyaknya individu yang rentan terinfeksi secara langsung oleh individu lain yang telah terinfeksi. Bilangan reproduksi dasar dilambangkan dengan . Bilangan reproduksi dasar dapat diperoleh dengan mencari nilai eigen dari matriks Jacobi yang dihitung pada titik tetap bebas penyakit.
Beberapa kondisi yang akan muncul yaitu:
1. Jika , maka penyakit akan menghilang. 2. Jika , maka penyakit akan menetap.
3. Jika , maka penyakit akan meningkat menjadi wabah.
(Giesecke 1994) Kontrol Optimum
5 state awal pada waktu kepada state akhir pada waktu akhir sedemikian rupa sehingga memberikan nilai maksimum atau nilai minimum bagi fungsional objektif.
Populasi dari tiga kelas epidemiologi yaitu kelas rentan, kelas terinfeksi, dan kelas disembuhkan merupakan peubah state pada karya ilmiah ini. Kemudian ditambahkan strategi vaksinasi ke dalam sistem untuk menurunkan jumlah individu yang terinfeksi.
Sistem dinamik dapat dinyatakan secara matematika oleh sistem persaman diferensial persamaan (8) mempunyai solusi tunggal karena nilai awal diberikan.
Solusi yang diperoleh merupakan respons terhadap peubah kontrol yang dilambangkan dengan . Setiap kontrol dan responsnya state
Fungsi kontrol yang dapat memaksimumkan atau meminimumkan fungsional akan ditentukan dari pemilihan terhadap semua fungsi atau peubah kontrol yang diperoleh. Kontrol yang bersifat demikian disebut kontrol optimum. Permasalahan kontrol optimum dapat dinyatakan sebagai masalah memaksimumkan atau meminimumkan suatu fungsional objektif (9) dengan kendala (8).
(Tu 1993)
Prinsip Minimum Pontryagin
Syarat perlu tercapainya kondisi optimum dalam masalah kontrol optimum adalah terpenuhinya prinsip minimum Pontryagin. Kontrol optimum dipilih untuk membawa sistem dinamik (8) dari keadaan awal ke keadaan akhir
. Masalah kontrol optimum adalah mengoptimumkan (memaksimumkan atau meminimumkan) fungsional objektif (9). Prinsip minimum Pontryagin dapat dilihat pada Teorema 1.
Teorema 1
6
Bukti untuk teorema dapat dilihat pada Lampiran 1.
(Tu 1993)
MODEL PENYEBARAN VIRUS H1N1
Model matematika yang digunakan untuk membahas masalah penyebaran virus H1N1 adalah model Susceptible Infected Recovered (SIR). Pada model SIR populasi dibagi ke dalam tiga kelas epidemiologi yaitu: kelas yang rentan (susceptible) di mana individu dalam populasi tidak terinfeksi tetapi berisiko terinfeksi virus, kelas yang terinfeksi (infected) di mana individu telah terinfeksi dan dapat menularkannya, dan kelas yang disembuhkan (recovered) di mana individu tidak bisa lagi terjangkit penyakit ini karena telah disembuhkan. Pada bagian ini akan dibahas persamaan model H1N1, penentuan titik tetap, dan analisis kestabilan titik tetap.
Persamaan Model H1N1
Model penyebaran virus H1N1 menggunakan tiga asumsi, yaitu:
1. Virus H1N1 akan menular jika ada kontak langsung atau hubungan yang erat antara individu yang sehat dengan individu terinfeksi.
2. Perekrutan individu baru bersifat konstan ( ).
3. Individu yang telah diberi vaksin atau kontrol akan berpindah ke populasi yang disembuhkan.
7
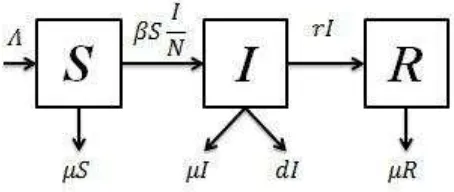
Gambar 1 Kompartemen model penyebaran virus H1N1 tanpa kontrol
Berdasarkan skema hubungan antara tiga kelas pada gambar 1, maka model penyebaran virus H1N1 dibangun dengan mempertimbangkan tiga aspek berikut, yaitu:
1. Perpindahan populasi dari rentan menjadi terinfeksi
Populasi yang rentan akan berpindah menjadi populasi yang terinfeksi bergantung kepada tingkat keefektifan kontak antara populasi rentan dengan populasi terinfeksi dan proporsi individu yang terinfeksi dalam populasi total ( ). Persamaan yang menggambarkan perpindahan populasi yang rentan menjadi terinfeksi diberikan oleh persamaan
dengan dan adalah parameter konstan dan taknegatif. 2. Penyembuhan populasi yang terinfeksi
Populasi yang terinfeksi akan berpindah menjadi populasi yang disembuhkan bergantung kepada tingkat penyembuhan . Persamaan untuk penyembuhan populasi yang terinfeksi diberikan oleh persamaan
dengan adalah parameter konstan dan taknegatif. 3. Kematian alami
Masing-masing populasi akan mati dengan tingkat kematian alami . Individu terinfeksi juga akan mati disebabkan oleh virus H1N1 dengan kematian . Persamaan yang mewakili kematian alami dari masing-masing populasi diberikan oleh persamaan dengan dan merupakan parameter konstan dan taknegatif.
Model penyebaran virus H1N1 dibangun dengan menggabungkan tiga aspek di atas, sehingga diperoleh sistem persamaan diferensial taklinear untuk masalah penyebaran virus H1N1 sebagai berikut
8
kematian alami, merupakan tingkat kematian individu terinfeksi disebabkan oleh virus H1N1, dan merupakan tingkat penyembuhan individu yang terinfeksi. Nilai awal individu rentan, individu terinfeksi, dan individu disembuhkan bernilai positif ( , , ) dan menyatakan total populasi pada waktu .
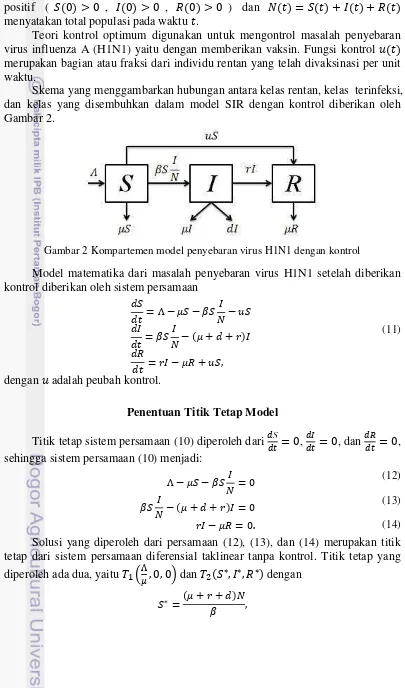
Teori kontrol optimum digunakan untuk mengontrol masalah penyebaran virus influenza A (H1N1) yaitu dengan memberikan vaksin. Fungsi kontrol merupakan bagian atau fraksi dari individu rentan yang telah divaksinasi per unit waktu.
Skema yang menggambarkan hubungan antara kelas rentan, kelas terinfeksi, dan kelas yang disembuhkan dalam model SIR dengan kontrol diberikan oleh Gambar 2.
Gambar 2 Kompartemen model penyebaran virus H1N1 dengan kontrol
Model matematika dari masalah penyebaran virus H1N1 setelah diberikan kontrol diberikan oleh sistem persamaan dengan adalah peubah kontrol.
Penentuan Titik Tetap Model
Titik tetap sistem persamaan (10) diperoleh dari
, tetap dari sistem persamaan diferensial taklinear tanpa kontrol. Titik tetap yang diperoleh ada dua, yaitu dan dengan
9
Agar persamaan (16) dan (17) terpenuhi, maka
(18)
Bukti penentuan titik tetap dapat dilihat pada Lampiran 2. Analisis Kestabilan Titik Tetap
Dengan melakukan pelinearan terhadap persamaan (10), diperoleh matriks Jacobi berikut
Kestabilan titik tetap diperoleh dari nilai eigen yang dihasilkan matriks Jacobi persamaan (10) yang dievaluasi pada titik tetap tersebut. Selanjutnya, kestabilan disekitar titik tetap diperiksa.
Titik tetap disubstitusikan ke dalam persamaan matriks Jacobi persamaan (13), sehingga dihasilkan matriks Jacobi
10
Dari persamaan (21) dan (22) diperoleh bilangan reproduksi dasar sebagai berikut
(23)
Titik tetap bebas penyakit bersifat stabil jika dan bersifat takstabil jika
. Nilai bilangan reproduksi dasar diberikan oleh Teorema 2. Teorema 2
1. Jika maka titik tetap bebas penyakit bersifat stabil asimptotik lokal. 2. Jika maka titik tetap bebas penyakit bersifat takstabil.
Titik tetap disubstitusikan ke dalam persamaan matriks Jacobi persamaan (13), sehingga dihasilkan matriks Jacobi
positif dan kondisi nilai , maka diperoleh dua kasus berikut:
1. dan . 2. dan .
11 Tabel 1 Kondisi kestabilan titik tetap
No Kasus Kondisi
1 - Stabil -
2 dan - Sadel Spiral Stabil
3 dan √ Sadel Sadel
√ Sadel Simpul Stabil
Bukti pelinearan di titik tetap dapat dilihat pada Lampiran 3.
MASALAH KONTROL OPTIMUM
Pada bagian ini akan dibahas kerangka kontrol optimum yang digunakan untuk menyelesaikan sistem persamaan diferensial taklinear dari model penyebaran virus H1N1. Teori kontrol optimum akan digunakan untuk menganalisis perilaku model penyebaran virus H1N1 setelah diberi kontrol (vaksin). Masalah kontrol optimum untuk penyebaran virus H1N1 adalah menentukan fungsi kontrol yang optimum sedemikian sehingga jumlah individu yang terinfeksi minimum pada akhir waktu.
Pada karya ilmiah ini fungsional objektif untuk masalah penyebaran virus H1N1 didefinisikan sebagai berikut
∫ [ ]
dengan merupakan bobot biaya vaksinasi dan mewakili lamanya program vaksinasi. Fungsi kontrol dicari yang optimum sedemikian sehingga
{ } (26)
dengan
{ [ ]} (27)
di mana adalah sekumpulan kontrol yang admissible selama vaksinasi. Masalah kontrol optimum di atas dapat dituliskan sebagai berikut
∫ [ ]
dengan kendala
1. SPD taklinear untuk model penyebaran virus H1N1
̇ (28)
̇ (29)
̇ (30)
2. Batas fungsi kontrol
(31)
12
Peubah state pada fungsi Hamilton ditentukan melalui syarat (1) Teorema prinsip minimum Pontryagin, syarat (1) menghasilkan kembali kendala pada masalah kontrol optimum yang diberikan oleh persamaan berikut:
̇ (32)
̇ (33)
̇ (34)
dengan syarat awal , , dan .
Peubah adjoint , , dan pada fungsi Hamilton nilainya ditentukan melalui syarat (2) Teorema prinsip minimum Pontryagin. Persamaan diferensial untuk peubah adjoint adalah sebagai berikut,
̇ ( ) (35)
̇ ( ) (36)
̇ (37)
dengan syarat di waktu akhir dan solusi dari persamaan diferensial yang diberikan oleh syarat (1) adalah , , , dan .
Durasi untuk program vaksinasi telah ditentukan yaitu pada interval waktu
[ ] dengan dalam hari. Peubah state pada waktu awal diberikan sebagai nilai awal dari sistem, sedangkan peubah state pada waktu akhir bebas dan tidak ada fungsi scrap sehingga dihasilkan syarat transversalitas pada persamaan
( ) ( ) ( ) (38)
Fungsi kontrol pada masalah kontrol optimum ditentukan melalui syarat (3) yang memberikan kondisi sebagai berikut
kemungkinan nilai untuk fungsi kontrol , yaitu:
1. Jika , maka nilai fungsi kontrol .
13 dilakukan untuk mengontrol penyebaran virus H1N1 dengan menggunakan metode Runge-Kutta orde-4 pada perangkat lunak.
Nilai Parameter
Parameter dari model penyebaran virus H1N1 ada enam yaitu tingkat kontak individu terinfeksi dengan individu rentan , tingkat perekrutan individu baru , tingkat kematian alami , tingkat kematian yang disebabkan virus H1N1 , tingkat penyembuhan , dan total populasi .
Tingkat kefektifan kontak dipengaruhi oleh bilangan reproduksi dasar yang ditentukan dari persamaan
. Nilai bilangan reproduksi dasar yang
digunakan untuk simulasi ada dua yaitu dan . Nilai bilangan reproduksi dasar berbanding lurus dengan tingkat kontak. Semakin besar bilangan reproduksi dasar, maka tingkat kontak antara populai terinfeksi dengan populasi rentan juga akan semakin besar. Nilai kontak berturut-turut adalah
dan .
Nilai parameter untuk tingkat perekrutan individu baru bersifat konstan ( ). Tingkat kematian alami individu diasumsikan berbanding terbalik dengan angka harapan hidup saat lahir. Angka harapan hidup saat lahir pada tahun 2012 di Indonesia adalah 71 tahun, sehingga tingkat kematian alami di Indonesia adalah (WHO 2013).
Tingkat kematian yang disebabkan oleh virus H1N1 berbeda untuk masing-masing negara, rata-rata berkisar antara sampai (Vaillant et al. 2009). Pada karya ilmiah ini tingkat kematian disebabkan oleh virus H1N1 adalah
14
Tabel 2 Nilai-nilai parameter
Parameter Definisi Nilai
Tingkat kontak individu terinfeksi dengan individu
rentan
Tingkat perekrutan (lahir dan migrasi)
Tingkat kematian alami
Tingkat kematian yang disebabkan virus H1N1
Tingkat penyembuhan , ,
ket: Nilai untuk . Nilai untuk .
Nilai awal untuk sistem persamaan diferensial taklinear diberikan oleh Tabel 3. Tabel 3 Nilai awal untuk model penyebaran virus H1N1
Nilai awal (orang)
Hasil Simulasi
15
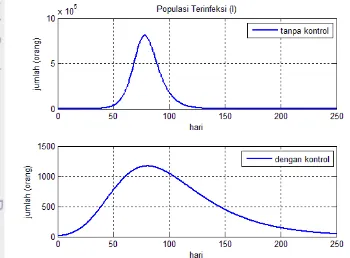
Gambar 3 Dinamika populasi terinfeksi tanpa dan dengan kontrol untuk
Gambar 4 Dinamika populasi terinfeksi tanpa dan dengan kontrol untuk
16
individu terinfeksi setelah pemberian kontrol paling banyak terjadi pada hari
sebanyak orang. Tingkat keefektifan pemberian vaksin untuk mengontrol penyebaran virus H1N1 dihitung dengan membandingkan penurunan jumlah individu terinfeksi setelah pemberian kontrol dengan jumlah individu terinfeksi tanpa kontrol saat penyakit mewabah. Tingkat keefektifan vaksin untuk bilangan reproduksi dasar adalah . Pada Gambar 4, dinamika populasi individu terinfeksi dengan menunjukan peningkatan secara drastis populasi terinfeksi tanpa kontrol dan mencapai titik puncak penyebaran penyakit H1N1 pada hari ke-78 sebanyak orang. Titik puncak penyebaran H1N1 setelah pemberian kontrol terjadi pada hari ke- sebesar orang. Tingkat keefektian pemberian kontrol ke dalam sistem untuk bilangan reproduksi dasar adalah . Penurunan signifikan jumlah individu terinfeksi setelah pemberian kontrol ke dalam sistem menunjukan bahwa fungsi kontrol yang diperoleh berhasil mengontrol penyebaran H1N1.
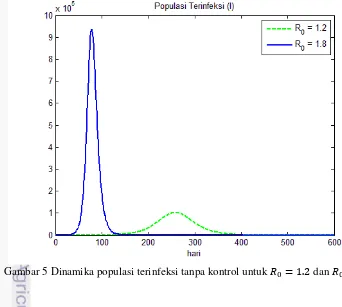
Bilangan reproduksi dasar sangat berpengaruh terhadap dinamika populasi individu terinfeksi. Semakin besar bilangan reproduksi dasar akan menyebabkan semakin besarnya nilai kontak antara individu terinfeksi dengan individu yang rentan, sehingga jumlah individu rentan yang dapat terinfeksi virus H1N1 juga akan semakin banyak. Dinamika populasi individu terinfeksi sebelum pemberian kontrol dengan bilangan reproduksi dasar yang berbeda diberikan pada Gambar 5.
17
Gambar 6 Dinamika populasi rentan tanpa dan dengan kontrol untuk
18
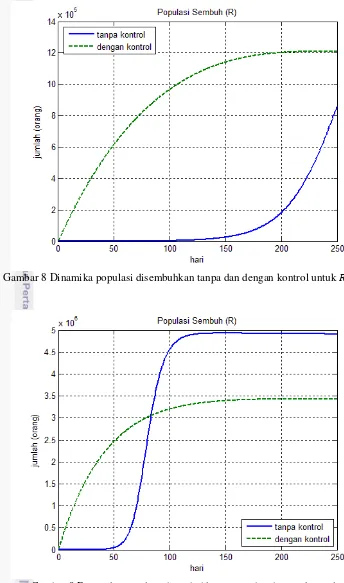
Gambar 8 Dinamika populasi disembuhkan tanpa dan dengan kontrol untuk
19
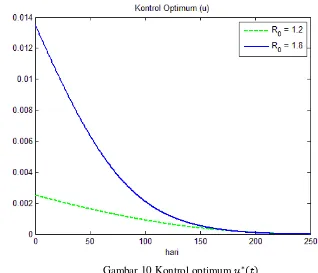
Gambar 10 Kontrol optimum
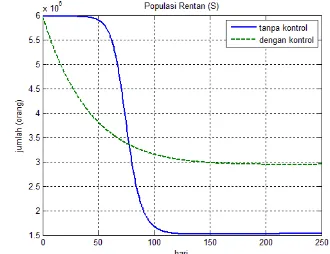
Laju berkurangnya jumlah individu rentan dengan kontrol pada Gambar 6 lebih besar dibandingkan dengan laju berkurangnya jumlah individu rentan tanpa pemberian kontrol untuk . Setelah pemberian kontrol, jumlah individu rentan jauh lebih sedikit dibandingkan dengan tanpa adanya pemberian kontrol. Penurunan populasi rentan setelah kontrol terjadi karena fungsi kontrol mentransfer individu rentan menjadi individu disembuhkan. Populasi rentan untuk
pada Gambar 7 menurun drastis sampai hari ke-77 program vaksinasi. Jumlah individu yang rentan dengan adanya kontrol lebih kecil dibandingkan dengan jumlah individu yang rentan tanpa kontrol sampai hari ke-77 program vaksinasi. Setelah itu, jumlah individu yang rentan dengan kontrol lebih besar dibandingkan dengan jumlah individu yang rentan tanpa kontrol.
Populasi rentan tanpa kontrol untuk berkurang lebih banyak dibandingkan dengan populasi rentan tanpa kontrol untuk . Hal ini disebabkan oleh tingkat kontak yang semakin besar untuk bilangan reproduksi dasar yang besar, sehingga jumlah individu rentan yang ditransfer ke dalam populasi terinfeksi juga semakin banyak.
20
menuju akhir program vaksinasi. Nilai fungsi kontrol yang semakin mengecil mengakibatkan semakin sedikit jumlah individu rentan yang ditransfer ke populasi yang disembuhkan.
Gambar 10 menunjukkan perbandingan nilai fungsi kontrol dengan bilangan reproduksi dasar yang berbeda. Semakin besar bilangan reproduksi dasar yang digunakan akan menghasilkan fungsi kontrol yang lebih besar juga. Hal ini terjadi karena tingkat mewabah suatu penyakit bergantung kepada bilangan reproduksi dasar. Bilangan reproduksi dasar yang lebih besar menyebabkan penyakit akan mewabah lebih cepat dan lebih banyak individu yang tertular penyakit. Namun, kedua fungsi kontrol yang diperoleh berhasil meminimumkan populasi yang terinfeksi virus H1N1 pada akhir program vaksinasi. Kontrol optimum mempunyai nilai maksimum pada awal program vaksinasi yaitu sebesar untuk dan untuk . Nilai fungsi kontrol turun sampai akhir program vaksinasi seiring dengan semakin berkurangnya jumlah individu yang terinfeksi. Pada waktu yang sama populasi yang rentan juga turun disebabkan oleh nilai fungsi kontrol. Nilai fungsional objektif yang dihasilkan berdasarkan nilai fungsi kontrol yang diperoleh adalah
untuk dan untuk .
Simulasi numerik yang kedua adalah membandingkan tingkat penyembuhan yang berbeda terhadap dinamika populasi individu terinfeksi. Tingkat penyembuhan individu terinfeksi bergantung pada lamanya periode pengobatan. Pada simulasi ini menggunakan tiga periode pengobatan yang berbeda yaitu 4, 5, dan 6 hari, sehingga tingkat penyembuhan masing-masing berdasarkan lamanya periode pengobatan secara berturut-turut adalah , , dan
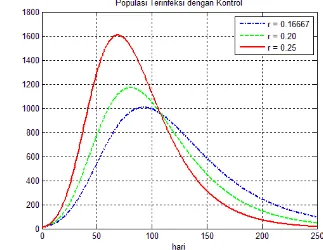
per hari. Dinamika populasi individu terinfeksi dengan tingkat penyembuhan yang berbeda diberikan oleh Gambar 11.
21 Dinamika populasi individu yang terinfeksi dengan menggunakan tingkat penyembuhan mencapai titik puncaknya pada hari ke- , dengan menggunakan tingkat penyembuhan populasi individu terinfeksi mencapai titik puncaknya pada hari ke- , dan dengan menggunakan tingkat penyembuhan
populasi individu terinfeksi mencapai titik puncaknya pada hari ke- . Dinamika populasi individu terinfeksi akan turun secara drastis setelah mencapai titik puncaknya. Gambar 11 menunjukan bahwa tingkat penyembuhan yang lebih besar dapat mengurangi jumlah individu yang terinfeksi dengan lebih banyak di waktu akhir. Program Matlab untuk simulasi numerik dapat dilihat pada Lampiran 4.
SIMPULAN
Model yang digunakan untuk menggambarkan masalah penyebaran virus H1N1 adalah model Susceptible Infected Recovered (SIR). Populasi dalam model SIR dibagi menjadi tiga kelas epidemiologi yaitu kelas yang rentan , kelas yang terinfeksi , dan kelas yang disembuhkan .
Simulasi numerik yang dilakukan ada dua yaitu simulasi numerik untuk membandingkan dinamika masing-masing populasi dengan bilangan reproduksi dasar yang berbeda sebelum dan setelah pemberian kontrol dan simulasi numerik untuk melihat dinamika populasi individu terinfeksi terhadap tingkat penyembuhan yang berbeda. Populasi terinfeksi berkurang secara drastis setelah adanya pemberian kontrol ke dalam sistem. Jumlah individu yang terinfeksi dengan adanya program vaksinasi jauh lebih kecil dibandingkan dengan tanpa adanya program vaksinasi. Semakin besar nilai bilangan reproduksi dasar maka tingkat kontak antara individu terinfeksi dengan individu rentan semakin besar, sehingga individu rentan akan semakin banyak yang terinfeksi virus H1N1 dan penyakit mewabah lebih cepat. Periode pengobatan yang lebih singkat menghasilkan tingkat penyembuhan yang besar dan mengurangi jumlah individu yang terinfeksi virus H1N1 dengan lebih banyak pada waktu akhir.
DAFTAR PUSTAKA
Anton H, Rorres C. 2004. Aljabar Linear Elementer. Ed ke-8. Indriasari R, Harmein I, Penerjemah. Jakarta (ID): Erlangga.
[BPS JABAR] Badan Pusat Statistik Jawa Barat. 2012. Jumlah Penduduk Kabupaten/Kota di Jawa Barat 2004 – 2012. [Internet]. [diacu 2014 Februari]. Tersedia dari: http://jabar.bps.go.id/subyek/jumlah-penduduk-kabupatenkota-di-jawa-barat-2004-2012.
Canale R P, Chapra S C. 2010. Numerical Methods for Engineers 6th Edition. New York(US): McGraw-Hill.
22
Giesecke J. 1994. Modern Infectious Diseases Epidemiology. New York (US): Oxford University Press.
Hattaf K, Yousfi N. 2009. Mathematical Model of the Influenza A(H1N1) Infection. Advanced Studies in Biology. 1(8): 383 – 390.
[Kompas]. 2009. Sebagian Besar Kasus A-H1N1 di Indonesia Bukan Impor. [Internet]. [diacu 2014 Juni]. Tersedia dari: http://lipsus.kompas.com /jalanjalan/read/2009/08/01/20121219/Sebagian.Besar.Kasus.A.H1N1.di.Indo nesia.Bukan.Impor.
Sitepoe M. 2009. Melawan Influenza A(H1N1). Jakarta (ID): Grasindo.
Tu PNV. 1993. Introductory Optimization Dynamics: Optimal Control with Economics and Management Applications. Second Revised and Enlarged Edition. Heidelberg (DE): Springer – Verlag.
Tu PNV. 1994. Dynamical System: An Introduction with Application in Economics and Biology. Second Revised and Enlarged Edition. Heidelberg (DE): Springer – Verlag.
Vaillant L, Ruche G La, Tarantola A, Barboza P. 2009. Epidemiology of Fatal Cases Associated with Pandemic H1N1 Influenza. Eurosurveillance. 14(33): pii = 19309.
[WHO] World Health Organization. 2009. Pandemic (H1N1) 2009. [Internet]. [diacu 2014 Februari]. Tersedia dari: http://www.who.int/csr/don/ 2009_11_27a/en/.
23
LAMPIRAN
Lampiran 1 Bukti Teorema 1 (Prinsip Minimum Pontryagin)
Fungsional objektif yang akan diminimumkan sebagai berikut
∫ [ ] [ ] (40) terhadap kendala
̇ [ ] (41)
diberikan , waktu awal , sedangkan dan keduanya tidak ditentukan. Fungsi “Scrap” dapat didefinisikan sebagai berikut.
∫ (42) sehingga persamaan (36) menjadi
∫ [ ]
∫ [ ̇ ]
(43)
dengan , , , dan secara sederhana dapat dituliskan sebagai dan . Meminimum pada persamaan (43) tidak dipengaruhi oleh pada saat , tetapi ditentukan oleh bentuk integral pada suku kedua dari persamaan (43).
Didefinisikan fungsional objektif yang diperbesar sebagai berikut
∫ ̇ (44)
dengan
̇ ̇ ̇
̇ ̇
(45)
Bentuk disebut sebagai Hamiltonian. Syarat perlu agar fungsional (43) memiliki nilai ekstrim adalah . Berdasarkan kalkulus variasi maka diperoleh sebagai berikut.
∫ [[ ̇] ]
[ ̇ ]
24
Agar persamaan (46) dipenuhi, maka persamaan Euler harus dipenuhi
̇
Variasi dan memberikan sifat saling bebas sehingga koefisiennya bernilai nol, yaitu dan . Persamaan (45) memberikan dan
̇ ̇, sehingga
(50)
̇ (51)
Syarat batas diberikan oleh suku terakhir persamaan (46) yaitu
[ ̇ ] (52) tidak ditentukan, maka syarat batas menjadi
(55)
yang menghasilkan teorema Pontryagin.
(Tu 1994) Lampiran 2 Penentuan Titik Tetap
Penentuan titik tetap
Titik tetap sistem persamaan diferensial taklinear tanpa kontrol (10) diperoleh dari
menjadi persamaan (12), (13), dan (14) berikut:
25
Titik tetap pertama diperoleh dengan mengasumsikan sistem dalam keadaan bebas penyakit ( ), maka dari persamaan (57) dan (60) diperoleh:
Sehingga diperoleh titik tetap bebas penyakit .
Titik tetap kedua diperoleh dengan menyelesaikan persamaan (57), (59), dan (60) secara bersamaan. Dari persamaan (59) diperoleh:
(61)
dengan menyubstitusikan persamaan (61) ke persamaan (57) diperoleh:
(62)
Persamaan (62) disubstitusikan ke persamaan (60), diperoleh persamaan berikut:
26
Karena semua parameter bernilai positif, maka . akan bernilai positif jika , sehingga . akan bernilai positif jika , sehingga .
Lampiran 3 Analisis Kestabilan Titik Tetap dan Nilai Bilangan Reproduksi Dasar Dengan melakukan pelinearan terhadap model H1N1 diperoleh matriks Jacobi sebagai berikut:
Substitusikan titik tetap ke dalam matrik Jacobi dengan cara pendekatan limit
kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik
27 karena semua parameter bernilai positif dan tingkat perekrutan individu baru konstan ( ), maka , , dan nilai eigen ketiga bergantung pada
kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik
28 maka kestabilan bersifat spiral.
Dari syarat batas yang dihasilkan agar titik tetap bernilai positif dan kondisi nilai , maka diperoleh dua kasus berikut:
1. Jika dan , maka titik tetap bersifat stabil dan bersifat sadel.
2. Jika , dan √ , maka maka titik tetap bersifat sadel dan bersifat sadel.
3. Jika , dan √ , maka maka titik tetap bersifat stabil dan bersifat sadel.
Lampiran 4 M-file Matlab metode Runge-Kutta orde-4 1. M-file Matlab untuk solusi model H1N1 tanpa kontrol
29
2. M-file Matlab untuk solusi model H1N1 dengan kontrol
31
3. M-file untuk plot grafik populasi dengan dan tanpa kontrol
clear all
plot(t,S,t,Sc,'--','LineWidth',2); title('Populasi Rentan (S)');
legend('tanpa kontrol','dengan kontrol');
grid; xlabel('hari'); ylabel('jumlah (orang)');
32
figure(2)
subplot(211); plot(t,I,'LineWidth',2); title('Populasi Terinfeksi
(I)'); legend('tanpa kontrol');
grid; xlabel('hari'); ylabel('jumlah (orang)');
subplot(212); plot(t,Ic,'LineWidth',2); legend('dengan kontrol');
grid; xlabel('hari'); ylabel('jumlah (orang)');
hold on
figure(3)
plot(t,R,t,Rc,'--','LineWidth',2); title('Populasi Sembuh (R)');
legend('tanpa kontrol','dengan kontrol',4);
grid; xlabel('hari'); ylabel('jumlah (orang)');
hold on
figure(4)
plot(t,u,'LineWidth',2); title('Kontrol Optimum (u)'); grid;
xlabel('hari');
hold on
figure(5)
plot(t,Ic,'b','LineWidth',2); title('Populasi Terinfeksi (I)');
grid; xlabel('hari');
hold on
figure(6)
plot(t,S,'b',t,I,'r',t,R,'g','LineWidth',2); title('Dinamika
Populasi H1N1'); grid; xlabel('hari');legend('Populasi
Rentan','Populasi Terinfeksi','Populasi Disembuhkan');
hold on
figure(7)
subplot(311); plot(t,lambda1,'LineWidth',2); grid; title('Fungsi
Adjoin (\lambda)'); legend('\lambda_1');
subplot(312); plot(t,lambda2,'LineWidth',2); grid;
legend('\lambda_2');
subplot(313); plot(t,lambda3,'LineWidth',2); grid; xlabel('hari');
legend('\lambda_3');
33
RIWAYAT HIDUP
Penulis dilahirkan di Solok pada tanggal 5 Agustus 1991 sebagai anak pertama dari tiga bersaudara, dengan ayah bernama Nasrul, S.Pd dan ibu bernama Fasmi Halima.
Pada tahun 2009, penulis lulus dari SMA Negeri 1 Kubung dan pada tahun yang sama diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI).
Selama mengikuti perkuliahan di IPB, penulis pernah menjadi pengurus GUMATIKA divisi PSDM pada tahun 2011. Penulis juga aktif dalam futsal Matematika, pengurus IPMM divisi Olahraga, dan ketua OMDA Ikatan Keluarga Mahasiswa Solok (IKMS) periode 2011/2012. Penulis juga aktif dalam beberapa kepanitian di kampus dan di organisasi.