PENDEKATAN
SPACE TIME AUTOREGRESSIVE
(STAR)
DAN
GENERALIZED SPACE TIME AUTOREGRESSIVE
(GSTAR) MELALUI METODE
AUTOREGRESSIVE
(AR) DAN
VECTOR AUTOREGRESSIVE
(VAR)
FERDIAN BANGKIT WIJAYA
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN SUMBER
INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa tesis berjudul Pendekatan Space Time Autoregressive (STAR) dan Generalized Space Time Autoregressive (GSTAR) melalui metode Autoregressive (AR) dan Vector Autoregressive (VAR) adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Oktober 2015
RINGKASAN
FERDIAN BANGKIT WIJAYA. Pendekatan Space Time Autoregressive (STAR) dan Generalized Space Time Autoregressive (GSTAR) melalui metode
Autoregressive (AR) dan Vector Autoregressive (VAR). Dibimbing oleh I MADE SUMERTAJAYA dan ERFIANI.
Pemodelan merupakan proses penyederhanaan suatu kejadian. Salah satu tujuan pembuatan model adalah peramalan. Model yang baik, yaitu model yang mampu menjelaskan keseluruhan data dalam bahasa yang sederhana. Peramalan yang baik, yaitu berasal dari pemodelan yang benar, artinya ketepatan peramalan tergantung pada proses pembuatan model. Proses pembuatan model dapat dilihat dari independensinya terhadap ruang dan waktu. Pengamatan terhadap suatu kejadian seringkali tidak hanya dilihat dari data deret waktu di satu lokasi saja, namun juga dilihat pada beberapa lokasi. Data seperti inilah yang disebut dengan data panel (space time). Pada dasarnya, data panel merupakan gabungan antara data lintas individu/lokasi dan data deret waktu. Contoh dari pemodelan data panel yaitu Space Time Autoregressive (STAR) dan Generalized Space Time Autoregressive (GSTAR). Kendala yang dihadapkan pada identifikasi model STAR dan GSTAR adalah penentuan ordo ruang dan ordo waktu. Penentuan ordo ruang dan waktu biasanya menggunakan kajian latar belakang teori sesuai studi kasus yang digunakan. Penentuan ordo ruang ini akan menentukan jumlah bobot lokasi yang akan digunakan. Pada penelitian ini akan dibatasi dengan bobot matriks Queen Contiguity dengan ordo ruang sebesar 1, yaitu dianggap tetangga lokasi terdekatlah yang mempengaruhi peubah yang diamati. Tujuan dari penelitian ini adalah penentuan ordo waktu dari STAR dan GSTAR yang didekati ordo waktu AR di masing-masing lokasi dan ordo waktu VAR di semua lokasi secara simultan. Selain itu penelitian ini akan membahas evaluasi metode AR, VAR, STAR, dan GSTAR dengan memperhatikan ordo waktu autoregressive
yang sama dan berbeda di setiap lokasi.
Data yang digunakan adalah data hasil simulasi. Metode yang digunakan yaitu dengan membangkitkan data pola autoregressive stasioner ordo satu, AR(1) untuk ordo waktu yang sama serta ordo satu dan dua, AR(1) dan AR(2) untuk ordo waktu yang berbeda dengan parameter tertentu yang stasioner. Lokasi yang dibangkitkan berjumlah 3 dengan masing – masing mempunyai 100 series waktu, 10 persen data digunakan sebagai alat evaluasi antar metode, yaitu dengan mencari nilai Root Mean Square Error (RMSE) peramalan. Metode ini diulang sebanyak 100 kali untuk melihat kekonsistenan RMSE.
Hasil didapatkan bahwa metode STAR paling baik diantara metode AR, VAR, dan GSTAR untuk kasus ordo waktu sama. Hal ini dapat dilihat dari frekuensi RMSE terkecil dari STAR yang paling banyak, yaitu sebanyak 37% di lokasi 1, 32% di lokasi 2, dan 32% di lokasi 3. Sedangkan metode GSTAR paling baik diantara metode AR, VAR, dan GSTAR untuk kasus ordo waktu berbeda, yaitu 22% di lokasi 1, 25% di lokasi 2, dan 31% di lokasi 3.
SUMMARY
FERDIAN BANGKIT WIJAYA. Space Time Autoregressive (STAR) and Generalized Space Time Autoregressive (GSTAR) approaches through Autoregressive (AR) and Vector Autoregressive (VAR) methods. Supervised by I MADE SUMERTAJAYA dan ERFIANI.
Modeling is a process of simplifying an event. One of the purposes of modeling is forecasting. A good model is capable of explaining data entirely in a simple way. A good forecasting is born from a precise modeling, or in other word the accuracy of forecasting depends on modeling process. Modeling process can be seen from its independency against space and time. Observation on an event is often carried out not only based on time series data in a location, but also data in several locations. Such data is known as space-time data. Space-time data or panel data is basically a mixture of cross section data and time series data. Panel data modeling is consist of Space Time Autoregressive (STAR) dan Generalized Space Time Autoregressive (GSTAR). Obstacle faced in the identification of STAR and GSTAR models is determining spatial order and time order. The determination of spatial and time order usually uses the assessment of theoretical background relevant to case study used. The determination of the spatial order will determine the weight of location to be used. The scope of this study will be limited to Queen Contiguity weight matrix with 1 as spatial order, i.e. the neighboring location or the nearest area is considered influencing the observed variable. The aims of the study is the determination of STAR and GSTAR time order will be approached by considering AR order of each location and considering VAR order of all locations simultaneously and then evaluating Autoregressive (AR), Vector Autoregressive (VAR), Space Time Autoregressive (STAR), and Generalized Space Time Autoregressive (GSTAR) modeling methods with same and different time order in each location.
Data used was based on simulation. The methods by generating first order stationary autoregressive pattern data, AR(1) for same time order as well as first and second orders, AR(1) and AR(2) for different time orders with particular stationary parameter. Generated locations were 3, each of which with 100 time series, 10 percent data was used as evaluation tool between methods, i.e. by determining the forecast value of Root Mean Square Error (RMSE). The method was repeated 100 times to determine the consistency of RMSE.
The results show that STAR method is the best among AR, VAR, and GSTAR methods for cases of same time order, indicated by the smallest RMSE frequency is the most, i.e. 37% in location 1, 32% in location 2, and 32% in location 3; while GSTAR method is the best among AR, VAR, and GSTAR method for cases of different time-order, indicated by the smallest RMSE frequency is the most, i.e 22% in location 1, 25% in location 2, and 31% in location 3.
© Hak Cipta Milik IPB, Tahun 2015
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
PENDEKATAN
SPACE TIME AUTOREGRESSIVE
(STAR)
DAN
GENERALIZED SPACE TIME AUTOREGRESSIVE
(GSTAR) MELALUI METODE
AUTOREGRESSIVE
(AR) DAN
VECTOR AUTOREGRESSIVE
(VAR)
FERDIAN BANGKIT WIJAYA
Tesis
sebagai salah satu syarat untuk memperoleh gelar
Magister Sains
pada
Program Studi Statistika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Tesis
: Pendekatan
Space Time Autoregressive ( STAR ) dan Generalized Space Time Autoregressive ( GSTAR ) melalui metode Autoregressive ( AR ) dan Vector Autoregressive (VAR) Nama : Ferdian Bangkit WijayaNIM : G151130061
Disetujui oleh Komisi Pembimbing
Dr.Ir.I Made Sumertajaya, M.Si Dr.Ir.Erfiani, M.Si
Ketua Anggota
Diketahui oleh
Ketua Program Studi Statistika
Dr.Ir.Kusman Sadik, M.Si
Dekan Sekolah Pascasarjana
Dr.Ir.Dahrul Syah, Msc.Agr
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Maret 2015 sampai Mei 2015 ini ialah pemodelan data deret waktu, dengan judul Pendekatan Space Time Autoregressive
(STAR) dan Generalized Space Time Autoregressive (GSTAR) melalui metode
Autoregressive (AR) dan Vector Autoregressive (VAR).
Terimakasih penulis ucapkan kepada Bapak Dr Ir I Made Sumertajaya, M.Si dan Ibu Dr Ir Erfiani, M.Si selaku pembimbing, serta akademisi Statistika yang telah banyak memberi saran. Disamping itu, penghargaan penulis sampaikan kepada Bapak Heri beserta staf Tata Usaha Departemen Statistika Pascasarjana, yang telah membantu selama pelaksanaan penelitian ini. Ungkapan terimakasih juga disampaikan kepada ayah Toirin, ibu Nok Joleha, adik Fenny Rahayu Ferina, keluarga, sahabat keluarga cemara, Wisnu, Agus, sahabat Apollo, Deby Vertisa atas doa dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Oktober 2015
DAFTAR ISI
DAFTAR TABEL x
DAFTAR GAMBAR xi
DAFTAR LAMPIRAN xi
1. PENDAHULUAN Latar Belakang 1
Tujuan Penelitian 2
Manfaat Penelitian 2
2. TINJAUAN PUSTAKA Dekomposisi Cholesky dan Indeks Moran 3 Model Autoregressive (AR) 5 Model Vector Autoregressive (VAR) 4
Model Space Time Autoregressive (STAR) 7 Model GeneralizedSpace Time Autoregressive (GSTAR) 8 Matriks Pembobot QueenContiguity 9 Pendugaan Parameter Model Space Time 9 BIC dan AICC 10
Perbandingan Kinerja Model 11
3. METODE PENELITIAN Data 12
Metode 14
4. HASIL DAN PEMBAHASAN Pembangkitan Data 17
Data Ordo Waktu Autoregressive Sama 17
Data Ordo Waktu Autoregressive Berbeda 18
Model Autoregressive (AR) 19
Kestasioneran dan model tentatif 19
Pendugaan Parameter 21
Analisis Sisaan 22
Peramalan 24
Model Vector Autoregressive (VAR) 28
Kestasioneran dan model tentatif 28
Pendugaan Parameter 29
Analisis Sisaan 31
Model Space Time Autoregressive (STAR) 36
Pendugaan Parameter 36
Analisis Sisaan 38
Peramalan 39
Model GeneralizedSpace Time Autoregressive (GSTAR) 43
Pendugaan Parameter 43
Analisis Sisaan 45
Peramalan 47
Perbandingan Kinerja Model 50
Perbandingan RMSE Peramalan ordo AR sama 51
Perbandingan RMSE Peramalan ordo AR berbeda 53
5. SIMPULAN DAN SARAN Simpulan 57
Saran 57
6. DAFTAR PUSTAKA 58
DAFTAR TABEL
1. Uji ADF AR untuk lokasi 1,2 , dan 3 20
2. Nilai BIC tentatif AR 21
3. Pendugaan parameter AR ordo sama 21
4. Pendugaan parameter AR ordo berbeda 22
5. Kebebasan sisaan AR (p) lokasi 1,2, dan 3 23
6. Peramalan AR (1) di lokasi 1, 2, dan 3 24
7. Peramalan AR (p) di lokasi 1, 2, dan 3 25
8. Nilai asli ordo sama di lokasi 1, 2, dan 3 26
9. Nilai asli ordo berbeda di lokasi 1, 2, dan 3 27
10. Nilai RMSE AR untuk ordo sama dan berbeda 27
11. Kestasioneran model VAR (1) ordo sama 28
12. Kestasioneran model VAR (2) ordo berbeda 28
13. Nilai AICC tentatif VAR ordo sama 29
14. Nilai AICC tentatif VAR ordo berbeda 29
15. Pendugaan parameter VAR (1) ordo sama 30
16. Pendugaan parameter VAR (2) ordo berbeda 31
17. Uji multivariate sisaan VAR 31
18. Uji univariate sisaan VAR 32
19. Peramalan VAR (1) ordo sama 33
20. Peramalan VAR (2) ordo berbeda 34
21. Nilai RMSE VAR untuk ordo sama dan berbeda 35
22. Pendugaan parameter STAR (1;1) ordo sama 37
23. Pendugaan parameter STAR (2;1) ordo berbeda 37
24. Peramalan STAR (1;1) ordo sama 40
25. Peramalan STAR (2;1) ordo berbeda 41
26. Nilai RMSE STAR untuk ordo sama dan berbeda 42
27. Pendugaan parameter GSTAR (1;1) ordo sama 44
28. Pendugaan parameter GSTAR (2;1) ordo berbeda 45
29. Peramalan GSTAR (1;1) ordo sama 47
30. Peramalan GSTAR (2;1) ordo berbeda 49
31. Nilai RMSE GSTAR untuk ordo sama dan berbeda 50
32. RMSE peramalan ordo sama di lokasi 1,2, dan 3 51
33. Uji kesamaan rataan ordo sama 52
34. Uji kesamaan ragam ordo sama 52
35. RMSE peramalan ordo berbeda di lokasi 1,2, dan 3 54
36. Uji kesamaan rataan ordo berbeda 55
DAFTAR GAMBAR
1. Desain posisi lokasi simulasi 12
2. Simulasi lokasi dengan ordo waktu sama 15
3. Simulasi lokasi dengan ordo waktu berbeda 15
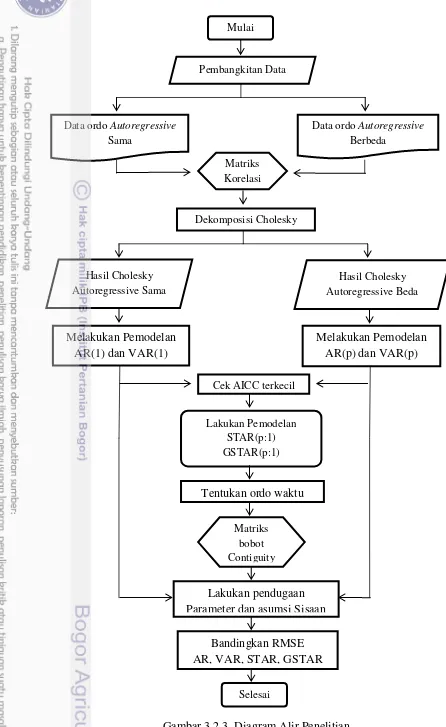
4. Diagram alir penelitian 16
5. Plot ACF dan PACF AR (1) ordo sama lokasi 1 19
6. Plot ACF dan PACF AR (2) ordo berbeda lokasi 1 20
7. Kenormalan sisaan ordo sama dan berbeda di lokasi 1 23
8. Analisis sisaan STAR (1;1) ordo sama di lokasi 1 38
9. Analisis sisaan STAR (2;1) ordo berbeda di lokasi 1 39
10. Analisis sisaan GSTAR (1;1) ordo sama di lokasi 1 46
11. Analisis sisaan GSTAR (2;1) ordo berbeda di lokasi 1 46
12. Boxplot RMSE ordo sama di lokasi 1,2, dan 3 53
13. Boxplot RMSE ordo berbeda di lokasi 1,2, dan 3 56
DAFTAR LAMPIRAN
1. Program SAS 9.3 pembangkitan data ordo waktu sama 612. Program SAS 9.3 pembangkitan data ordo waktu berbeda 62
3. Program Macro SAS 9.3 Perbandingan Kinerja Model 63
4. Output SAS 9.3 uji akar unit ADF ordo waktu sama 72
5. Output SAS 9.3 nilai BIC ordo waktu sama 72
6. Output SAS 9.3 kebebasan sisaan ordo waktu sama 73
7. Output SAS 9.3 kenormalan sisaan ordo waktu sama 74
8. Output SAS 9.3 analisis sisaan STAR (1;1) 75
9. Output SAS 9.3 analisis sisaan GSTAR (1;1) 77
10. Output SAS 9.3 uji akar unit ADF ordo waktu berbeda 78
11. Output SAS 9.3 nilai BIC ordo waktu berbeda 79
12. Output SAS 9.3 kebebasan sisaan ordo waktu berbeda 80
13. Output SAS 9.3 kenormalan sisaan ordo waktu berbeda 81
14. Output SAS 9.3 analisis sisaan STAR (2;1) 82
15. Output SAS 9.3 analisis sisaan GSTAR (2;1) 83
16. Nilai RMSE untuk ordo waktu sama 85
1
PENDAHULUAN
Latar Belakang
Pemodelan merupakan proses penyederhanaan suatu kejadian. Salah satu tujuan pembuatan model adalah peramalan. Model yang baik, yaitu model yang mampu menjelaskan keseluruhan data dalam bahasa yang sederhana. Peramalan yang baik, yaitu berasal dari pemodelan yang benar, artinya ketepatan peramalan tergantung pada proses pembuatan model (Bezivin 2001). Proses pembuatan model dapat dilihat dari independensinya terhadap ruang dan waktu. Pemodelan yang hanya mempertimbangkan pengaruh waktu di satu lokasi dinamakan pemodelan data deret waktu. Secara garis besar, pemodelan data deret waktu dibagi menjadi dua, yaitu pemodelan data deret waktu peubah tunggal (univariate) tanpa/dengan peubah eksogen dan pemodelan data deret waktu peubah ganda (multivariate) tanpa/dengan peubah eksogen. Pemodelan data deret waktu peubah tunggal tanpa peubah eksogen antara lain Pemulusan Rataan Bergerak, Pemulusan Eksponensial, Winter, dan Box-Jenkins (ARIMA), sedangkan Pemodelan data deret waktu peubah tunggal dengan peubah eksogen antara lain Error Correction Model, Distribusi Lag, dan Dekomposisi. Pemodelan data deret waktu peubah ganda tanpa peubah eksogen antara lain Vector Autoregressive (VAR), sedangkan pemodelan data deret waktu peubah ganda dengan peubah eksogen antara lain Fungsi Transfer, Analisis Intervensi, Fourier, dan Vector AutoregressiveX (VARX) (Wei 2006).
Pengamatan terhadap suatu kejadian seringkali tidak hanya dilihat dari data deret waktu di satu lokasi saja, namun juga dilihat pada beberapa lokasi. Data seperti inilah yang disebut dengan data panel (space time). Pada dasarnya, data panel merupakan gabungan antara data lintas individu/lokasi dan data deret waktu (Gujarati 2011). Pemodelan data panel merupakan metode pemodelan yang menggabungkan antara data lintas individu dan data deret waktu, yaitu berupa data yang diamati pada tiap-tiap lokasi pengamatan secara berkala dari waktu ke waktu. Pemodelan data panel pun terbagi menjadi dua, Pemodelan data panel peubah tunggal tanpa/dengan peubah eksogen dan pemodelan data panel peubah ganda tanpa/dengan peubah eksogen. Pemodelan data panel peubah tunggal tanpa peubah eksogen salah satunya adalah Multivariate Dynamic Panel Data, sedangkan pemodelan data panel peubah tunggal dengan peubah eksogen salah satunya analisis regresi data panel (Wei 2006). Pemodelan data panel peubah ganda tanpa peubah eksogen adalah Space Time Autoregressive (STAR) dan
Generalized Space Time Autoregressive (GSTAR), sedangkan Pemodelan data panel peubah ganda dengan peubah eksogen salah satunya adalah analisis regresi peubah ganda data panel (Ruchjana 2002).
Pemodelan Space Time Autoregressive (STAR) diperkenalkan oleh Pfeifer dan Deutch (1980). Dalam jurnal ilmiahnya yang berjudul “A three Stage
Iterative Procedure for Space Time Modeling” , prosedur ini terdiri dari tiga tahap, yaitu identifikasi model space time, estimasi parameter, dan diagnosa pengecekan model. Kelemahan pemodelan ini mensyaratkan nilai-nilai parameter untuk semua wilayah/lokasi sama. Ruchjana (2002) memperkenalkan perluasan model STAR dengan mensyaratkan parameter-parameter model berbeda untuk setiap wilayah/lokasi. Hal ini dapat dilihat dalam tulisannya yang berjudul
“Pemodelan Kurva Produksi Minyak Bumi Menggunakan Model Generalisasi STAR”, kemudian dikaji lebih jauh oleh Suhartono (2008) mengenai optimasi
bobot lokasi/wilayah pada pemodelan GSTAR.
Kendala yang dihadapkan pada identifikasi model STAR dan GSTAR adalah penentuan ordo ruang dan ordo waktu. Penentuan ordo ruang biasanya menggunakan kajian latar belakang teori sesuai studi kasus yang digunakan. Penentuan ordo ruang ini akan menentukan jumlah bobot lokasi/wilayah yang akan digunakan. Pada tulisan ini akan dibatasi dengan bobot matriks Queen Contiguity dengan ordo ruang sebesar 1, yaitu dianggap tetangga lokasi/wilayah terdekatlah yang mempengaruhi peubah yang diamati. Penentuan ordo waktu selama ini berbeda-beda sesuai dengan karakteristik data yang digunakan dalam penelitian. Seringkali didapatkan karakteristik deret waktu yang berbeda di setiap lokasi/wilayah.
Tulisan ini akan membahas evaluasi pemodelan data deret waktu secara
univariate, simultan/multivariate, dan memperhitungkan independensi ruang dan waktu/space time. Evaluasi pendekatan ini dapat dilihat dari kualitas model untuk meramal yang dilihat dari nilai Root Mean Square Error (RMSE). Selain itu, penentuan ordo waktu STAR dan GSTAR akan didekati dengan melihat ordo AR dari masing – masing lokasi dan melihat ordo VAR dari semua lokasi secara simultan.
Tujuan Penelitian
Tujuan dari penelitian ini adalah :
1. Evaluasi pemodelan Autoregressive (AR), Vector Autoregressive (VAR),
Space Time Autoregressive (STAR), dan Generalized Space Time Autoregressive (GSTAR) dengan ordo waktu sama di setiap lokasi/wilayah. 2. Evaluasi pemodelan Autoregressive (AR), Vector Autoregressive (VAR),
Space Time Autoregressive (STAR), dan Generalized Space Time Autoregressive (GSTAR) dengan ordo waktu berbeda di setiap lokasi/wilayah.
Manfaat Penelitian
Penelitian ini diharapkan mampu mengevaluasi beberapa model deret waktu serta dapat menentukan ordo waktu dari model Space Time Autoregressive
2
TINJAUAN PUSTAKA
Dekomposisi Cholesky dan Indeks Moran
Dekomposisi cholesky adalah ketika A merupakan suatu matriks bilangan riil, definit positif, dan simetrik yang kemudian ada suatu matrik segitiga bawah L dengan elemen diagonal positif sedemikian sehingga
A = L��
Penguraian cholesky ini digunakan untuk membentuk data yang saling berkorelasi antar lokasi. Matriks A merupakan matriks korelasi antar lokasi yang ditentukan terlebih dahulu.
Prosedur memperoleh dekomposisi matrik (SAS 9.2) adalah sebagai berikut: 1. Anggap A=[ ]
2. Selesaikan persamaan
A=[ ]=[ ] [ ]
3. Hitung masing-masing elemen matrik L dengan aturan: Untuk k dari 1 sampai n :
lkk = ( ∑
Untuk j dari k+1 sampai n :
= ( ∑
Indeks Moran merupakan statistik uji yang digunakan untuk melakukan pengujian terhadap autokorelasi spasial. Statistik ini adalah ukuran korelasi antara pengamatan yang saling berdekatan dengan membandingkan nilai di suatu lokasi dengan nilai pengamatan di lokasi lainnya. Persamaan untuk menghitung nilai Indeks Moran adalah sebagai berikut :
∑ ∑ ∑ ∑
dengan,
n : banyaknya pengamatan
: nilai pengamatan pada lokasi ke-i dan tetangga ke-j : elemen matriks pembobot spasial baris ke-i kolom ke-j
L ��
(1)
Hipotesis yang digunakan adalah sebagai berikut : : I=0 (tidak ada autokorelasi antar lokasi) : I 0 (ada autokorelasi antar lokasi)
Nilai indeks moran antara -1 dan 1 (-1 menunjukkan autokorelasi negatif sempurna dan 1 menunjukkan autokorelasi positif sempurna). Jika nilai I < 0, artinya terdapat autokorelasi negatif yaitu lokasi yang berdekatan langsung tidak mirip satu sama lainnya, sedangkan jika I > 0 artinya terdapat autokorelasi positif artinya lokasi yang berdekatan langsung mirip satu sama lainnya (Anselin 2006).
Model Autoregressive (AR)
Model autoregressive (AR) merupakan kasus khusus dari pola deret waktu
Autoregressive Moving Average (ARMA). Jika pengamatan pada waktu ke-t dari data deret waktu hanya tergantung pada lag waktu pengamatan ordo pertama, maka disebut dengan AR(1), dengan kata lain pengamatan sekarang hanya dipengaruhi oleh satu waktu pengamatan sebelumnya.
Model AR(1) adalah sebagai berikut :
Atau dalam bentuk operator backshift, yaitu
dengan,
: pengamatan pada waktu ke-t : pengamatan pada waktu ke- t 1
: parameter autoregressive ordo ke-1 : white noise, dimana
Jika pengamatan pada waktu ke-t dari set data deret waktu tergantung pada lag waktu pengamatan ordo ke-p, maka disebut dengan AR(p), dengan kata lain
pengamatan sekarang dipengaruhi oleh “p” waktu pengamatan sebelumnya.
Model AR(p) adalah sebagai berikut :
Atau dalam bentuk operator backshift, yaitu
dengan,
: pengamatan pada waktu ke-t : pengamatan pada waktu ke- t p
: parameter autoregressive ordo ke-p : white noise, dimana
(3)
(4)
(5)
Identifikasi model AR(p) dapat dilihat dari plot Partial Autocorrelation Function (PACF) dan plot Autocorrelation Function (ACF). Model AR(1) memiliki pola PACF cuts off pada lag ke-1 dan pola ACF tails off. Kestasioneran model AR(p) dapat dilihat juga dari pola ACF, jika ACF turun sangat lambat maka data terindikasi tidak stasioner sehingga proses pembedaan (differencing) dibutuhkan untuk memodelkan AR(p). Uji formal untuk melihat kestasioneran data yaitu dengan menggunakan uji akar unit Augmented Dickey Fuller. Model AR(1) dikatakan stasioner jika nilai mutlak dari parameter autoregressive kurang dari satu, . Pemilihan model terbaik menggunakan kriteria Bayesian Information Criterion (BIC), yaitu yang bernilai paling kecil. Pendugaan parameter menggunakan Metode Kuadrat Terkecil (Wei 2006).
Model VectorAutoregressive (VAR)
Model Vector Autoregressive (VAR) merupakan suatu pendekatan peramalan kuantitatif yang biasanya diterapkan pada deret waktu peubah ganda, artinya model ini menjelaskan keterkaitan antar pengamatan pada peubah itu sendiri pada waktu sebelumnya dan juga keterkaitannya dengan pengamatan pada peubah lain pada waktu sebelumnya. Jika nilai pengamatan di satu lokasi/wilayah pada waktu ke-t dipengaruhi oleh nilai pengamatan di satu lag sebelumnya beserta pengamatan di lokasi lain, maka model ini berbentuk VAR(1).
Model VAR(1) adalah sebagai berikut :
Atau dalam bentuk operator backshift, yaitu
dengan,
: vektor pengamatan pada waktu ke-t lokasi ke-n yang berukuran (n x 1) : matriks parameter vectorautoregressive ordo ke-1 yang berukuran (n x n) : vektor white noise, dimana yang berukuran (n x 1)
Sebagai contoh untuk lokasi berjumlah 2, maka model VAR(1) yaitu
dengan,
( , (
,dan (
Jika nilai pengamatan di satu lokasi/wilayah pada waktu ke-t dipengaruhi oleh nilai pengamatan di-“p” lag sebelumnya beserta pengamatan di lokasi lain, maka model ini berbentuk VAR(p).
Model VAR(p) adalah sebagai berikut :
(7)
(8)
Atau dalam bentuk operator backshift, yaitu
(
dengan,
: vektor pengamatan pada waktu ke-t lokasi ke-n yang berukuran (n x 1) : matriks parameter vectorautoregressive ordo ke-p yang berukuran (n x n) : vektor white noise, dimana yang berukuran (n x 1)
Sebagai contoh untuk lokasi berjumlah 2, maka model VAR(p) yaitu
dengan,
( , (
, ( ,
, dan
(
Identifikasi model VAR(1) dapat dilihat dari plot Multivariate Partial Autocorrelation Function (MPACF). Model VAR(1) memiliki pola PACF cuts off
pada lag ke-1. Kestasioneran model VAR(1) dapat dilihat nilai akar ciri dari matriks parameter VAR(1). Pemilihan model VAR terbaik menggunakan kriteria
Akaike Information Corrected Criterion (AICC), yaitu yang bernilai paling kecil (Wei 2006).
Model VAR(p) dikatakan stasioner jika akar ciri matriks parameter (F) kurang dari satu, yaitu
(
)
Contoh kestasioneran untuk model VAR (2), jika matriks F < 1, yaitu
(
)
Jika nilai modulus akar ciri lebih dari satu maka data terindikasi tidak stasioner sehingga proses pembedaan (differencing) dibutuhkan untuk memodelkan VAR(1) maupun VAR(p). Pendugaan parameter menggunakan Metode Kuadrat Terkecil.
Model Space Time Autoregressive (STAR)
Model Space Time Autoregressive (STAR) merupakan salah satu pemodelan ruang dan waktu, artinya model yang didalamnya meggabungkan unsur dependensi waktu dan lokasi/wilayah. Model STAR (1;1) merupakan gabungan model autoregressive ordo ke-1 dan model spasial ordo ke-1
Model STAR (1;1) adalah sebagai berikut :
dengan,
: vektor pengamatan pada waktu ke-t lokasi ke-n yang berukuran (n x 1) : parameter autoregressive ordo waktu ke-1 dan ordo ruang ke-0
: parameter autoregressive ordo waktu ke-1 dan ordo ruang ke-1 : matriks pembobot spasial / ruang yang berukuran (n x n)
Sebagai contoh untuk lokasi berjumlah 2, maka model STAR(1;1) yaitu
dengan,
( , (
, ( ,dan
Model STAR (p; ) merupakan gabungan model autoregressive ordo ke-p dan model spasial ordo ke -
Model STAR (p; ) adalah sebagai berikut :
∑ ∑
dengan,
: vektor pengamatan pada waktu ke-t lokasi ke-n yang berukuran (n x 1) : parameter autoregressive ordo waktu ke-k dan ordo ruang ke-l
: matriks pembobot spasial / ruang yang berukuran (n x n)
Sebagai contoh untuk lokasi berjumlah 2, ordo waktu sebesar 2, dan ordo ruang sebesar 1, maka model STAR(2;1) yaitu
dengan,
( , (
, ( ,dan
Kestasioneran model STAR (1;1) dapat dilihat dari kestasioneran dari masing-masing lokasi. Ruchjana (2002) melakukan pendekatan kestasioneran STAR(1;1) melalui VAR(1), dan dapat disimpulkan model STAR(1;1) stasioner jika . Model STAR (p; ) stasioner jika pada penentuan ordo waktu p juga stasioner. Pendugaan parameter menggunakan Metode Kuadrat Terkecil. Nilai parameter pada model STAR (p; ) disyaratkan sama di setiap lokasi.
(11)
Model GeneralizedSpace Time Autoregressive (GSTAR)
Model Generalized Space Time Autoregressive (GSTAR) merupakan perluasan model STAR dengan asumsi parameter-parameter ruang dan waktu berubah untuk setiap lokasi/wilayah. Model GSTAR (1;1) merupakan gabungan model autoregressive ordo ke-1 dan model spasial ordo ke-1
Model GSTAR (1;1) adalah sebagai berikut :
Dengan,
: vektor pengamatan pada waktu ke-t lokasi ke-n yang berukuran (n x 1) : matriks diagonal parameter autoregressive ordo waktu ke-1 dan ordo ruang ke-0 yang berukuran (n x n)
: matriks diagonal parameter autoregressive ordo waktu ke-1 dan ordo ruang ke-1 yang berukuran (n x n)
: matriks pembobot spasial / ruang yang berukuran (n x n)
Sebagai contoh untuk lokasi berjumlah 2, maka model GSTAR(1;1) yaitu
dengan,
( , (
, ( ,dan
, dan
Model GSTAR (p; ) merupakan gabungan model autoregressive ordo ke-p dan model spasial ordo ke- .
Model GSTAR (p; ) adalah sebagai berikut :
∑ ∑
Dengan,
: vektor pengamatan pada waktu ke-t lokasi ke-n yang berukuran (n x 1) : matriks diagonal parameter autoregressive ordo waktu ke-p dan ordo ruang ke- yang berukuran (n x n)
: matriks pembobot spasial / ruang yang berukuran (n x n)
Sebagai contoh untuk lokasi berjumlah 2, maka model GSTAR(2;1) yaitu
dengan,
( , (
, ( ,dan
,
(13)
( , , , ,
Model GSTAR (p; ) stasioner jika pada penentuan ordo waktu-p juga stasioner. Pendugaan parameter menggunakan Metode Kuadrat Terkecil. Nilai parameter pada model GSTAR (p; ) disyaratkan berbeda di setiap wilayah (Ruchjana 2002).
Matriks Pembobot QueenContiguity
Matriks pembobot spasial pada dasarnya merupakan matriks yang menggambarkan hubungan antar lokasi dan diperoleh berdasarkan informasi jarak atau ketetanggaan. Diagonal dari matriks ini umumnya diisi dengan nilai nol. Karena matriks pembobot menunjukkan hubungan antara keseluruhan observasi, maka dimensi dari matriks ini adalah , dimana n adalah banyaknya observasi atau banyaknya observasi lintas individu. Matriks Queen Contiguity adalah matriks yang menggambarkan hubungan antar lokasi, nilai 1 diberikan jika lokasi-i berdekatan langsung dengan lokaslokasi-i-j, sedangkan nlokasi-ilalokasi-i 0 untuk yang tlokasi-idak berdekatan langsung, matriks ini dinormalisasi sehingga nilai elemen matriks ini, yaitu
, dengan jumlah total per baris adalah 1 (Lee & Wong 2001). Bentuk matriks pembobot ini adalah :
nn n n ij n n w w w w w w w w w w W 2 1 2 22 21 1 12 11
Pendugaan Parameter Model Space Time
Pemodelan STAR dan GSTAR merupakan bentuk khusus dari model umum STARIMA dan GSTARIMA dengan ordo MA = 0. Pendugaan parameter dapat dilakukan dengan meminimumkan jumlah kuadrat sisaan
Dimana, e(t) diturunkan dari persamaan 14 diatas, yaitu
Cara yang sama juga digunakan untuk model STAR. Pendugaan dengan metode kuadrat terkecil ini tidak berlaku jika terdapat komponen moving avarege
(MA) karena nilai S pada persamaan 13 tidak linier sehingga S dapat diminimumkan dengan menggunakan algoritma Gauss-Newton (Zhou & Buongiorno 2006) atau dapat menggunakan algoritma Levenberg-Marquardt. Berikut ini contoh pendugaan parameter GSTAR (1;1) :
Misalkan diberikan model GSTAR seperti pada persamaan 11 dan mempunyai matriks bobot
, maka dugaan paramater nya adalah ̂
Dimana,
̂
(
)
, (
, dan (
(Ruchjana 2002).
Bayesian Information Criterion (BIC) dan Akaike Information Corrected Criterion (AICC)
Setiap kandidat model pada AR(p) , VAR(p), STAR(p;1), dan GSTAR(p;1) dipilih nilai Bayesian Information Criterion (BIC) terkecil untuk model AR(p) dan Akaike Information Corrected Criterion (AICC) terkecil untuk model VAR(p), proses dilakukan secara overfitting sehingga dicari ordo waktu yang memiliki nilai BIC dan AICC terkecil, semakin kecil nilainya maka ketepatan model dalam meramal semakin bagus.
Berikut rumus perhitungan BIC dan AICC :
(| ̃|
(| ̃| ( ⁄
dengan,
̃ : matriks dugaan maksimum likelihood dari Ʃ r : banyaknya parameter yang diduga
T : banyaknya observasi k : banyaknya peubah respon
(Wei 2006).
(19) (18)
Perbandingan Kinerja Model
Kinerja kebaikan model dapat dilihat dari nilai Root Mean Square Error
(RMSE). Model AR, VAR, STAR, dan GSTAR masing-masing mempunyai nilai RMSE peramalan, yaitu seberapa baik model tersebut dapat meramal nilai di waktu yang akan datang. Nilai RMSE yang paling kecil menunjukkan model tersebut paling baik dalam meramal.
Berikut rumus perhitungan RMSE :
√ √ ∑ ̂
dengan,
T : banyaknya observasi
: pengamatan aktual pada waktu ke-t
̂ : pengamatan hasil peramalan pada waktu ke-t
(Montgomery et al 2008).
3
METODE PENELITIAN
Data
Data yang digunakan dalam penelitian ini dibagi menjadi dua bagian analisis berdasarkan ordo waktu. Lokasi ditetapkan sebanyak 3. Data pertama yang digunakan adalah data dari hasil simulasi. Simulasi dirancang sedemikian rupa sehingga memiliki ordo Autoregressive yang sama di setiap lokasi, yaitu ordo waktu bernilai 1 dan ordo ruang bernilai 1. Sedangkan, data kedua yang digunakan adalah yang memiliki ordo Autoregressive berbeda di setiap lokasi, yaitu ordo waktu bernilai p dan ordo ruang bernilai 1. Software untuk analisis yaitu SAS 9.3. Proses simulasi pembangkitan data adalah sebagai berikut :
Data dengan ordo waktu Autoregressive yang sama di 3 lokasi:
1. Membuat desain posisi lokasi, yaitu
2. Bangkitkan satu nilai sebagai nilai awal dimana ~ N (0,1).
3. Tentukan parameter Autoregressive, AR(1) yang stasioner di setiap lokasi, yaitu,
Lokasi 1 : Lokasi 2 : Lokasi 3 :
4. Bangkitkan satu nilai white noise dimana ~ N (0,1).
5. Hitung nilai di setiap lokasi , yaitu berdasarkan persamaan:
6. Ubah nilai menjadi nilai hasil dari langkah 4. 7. Ulangi langkah 3-5 sebanyak 100 kali (T=100).
8. Tentukan matriks simulasi korelasi cholesky agar setiap lokasi saling berkorelasi yaitu,
(
9. Lakukan proses penguraian cholesky sedemikian sehingga nilai di lokasi 1, 2, dan 3 mempunyai korelasi ruang sebesar K.
10.Data siap untuk digunakan dalam pemodelan AR, VAR, STAR, dan GSTAR 11.Program SAS untuk pembangkitan data ordo waktu sama dapat dilihat pada
Lampiran 1.
Data dengan ordo waktu Autoregressive yang berbeda di 3 lokasi:
1. Membuat desain posisi yang sama saperti Gambar 3.1.
2. Bangkitkan satu nilai dan satu nilai sebagai nilai awal dimana ~ N (0,1) dan ~ N (0,1) untuk lokasi 1 dan lokasi 3 yang berpola AR(2).
3. Tentukan parameter Autoregressive :
AR(2) di lokasi 1 dan AR(2) di lokasi 3 dimana parameter harus stasioner di setiap lokasi, yaitu
Lokasi 1 : Lokasi 3 :
4. Bangkitkan satu nilai white noise dimana ~ N (0,1).
5. Hitung nilai di lokasi 1 dan 3 , yaitu berdasarkan persamaan:
6. Ubah nilai menjadi nilai sedangkan menjadi nilai hasil dari langkah 4.
7. Ulangi langkah 3-5 sebanyak 100 kali (T=100).
8. Pembangkitan untuk lokasi 2 serupa dengan pembangkitan “data dengan ordo
autoregressive yang sama (langkah 1-6)”, yaitu AR (1) dengan parameter Lokasi 2 :
9. Tentukan matriks simulasi korelasi cholesky agar setiap lokasi saling berkorelasi yaitu,
(
10. Lakukan proses penguraian cholesky sedemikian sehingga nilai di lokasi 1, 2, dan 3 mempunyai korelasi ruang sebesar K.
Metode
Langkah analisis yang digunakan dalam penelitian ini yaitu :
1. Melakukan proses pembangkitan data seperti yang telah diuraikan pada sub-bab Data.
2. Melakukan pemodelan Autoregressive (AR) dan Vector Autoregressive (VAR) dan kemudian menentukan nilai Root Mean Square Error (RMSE) dan BIC dan AICC untuk melihat kebaikan model untuk data dengan ordo
autoregressive yang sama.
3. Menentukan Matriks Pembobot Spasial Queen Contiguity sesuai dengan desain posisi pada Gambar 3.1, yaitu
(
4. Melakukan pemodelan Space Time Autoregressive (STAR) dan Generalized Space Time Autoregressive (GSTAR) dengan ordo waktu dan ruang yang sama, yaitu (1;1) dan kemudian menentukan nilai Root Mean Square Error
(RMSE) untuk melihat kebaikan model.
5. Ulangi langkah 2-3 dengan data ordo autoregressive yang berbeda
6. Melakukan pemodelan Space Time Autoregressive (STAR) dan Generalized Space Time Autoregressive (GSTAR) dengan ordo waktu dan ruang yang berbeda, yaitu (1;1), (2;1) dan kemudian menentukan nilai Root Mean Square Error (RMSE) untuk melihat kebaikan model.
7. Ulangi langkah 1-6 sebanyak 100 kali kemudian perbandingkan RMSE untuk setiap model :
Ordo Autoregressive sama : AR(1), VAR(1), STAR(1;1), dan GSTAR(1;1). Ordo Autoregressive beda : AR(p), VAR(p), STAR(p;1), dan GSTAR(p;1). 8. Program macro SAS perbandingan kinerja model ini dapat dilihat pada
Ilustrasi simulasi untuk ordo autoregressive yang sama:
Gambar 3.2.1 Simulasi lokasi dengan ordo waktu sama
Gambar 3.2.1 merupakan ilustrasi proses simulasi ordo waktu sama, Lokasi 1, 2, dan 3 terletak sesuai desain posisi. Masing-masing lokasi dibangkitkan deret waktu sebanyak 100 dan berpola Autoregressive yang sama, yaitu AR (1).
Ilustrasi simulasi untuk ordo autoregressive yang berbeda:
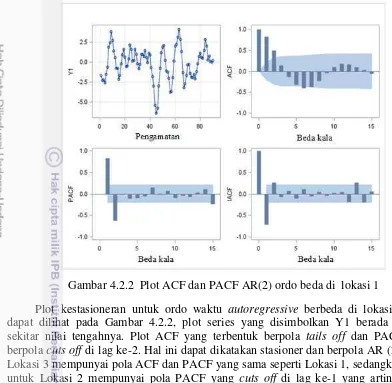
Gambar 3.2.2 Simulasi lokasi dengan ordo waktu berbeda
Gambar 3.2.2 merupakan ilustrasi proses simulasi ordo waktu berbeda, Lokasi 1, 2, dan 3 terletak sesuai desain posisi. Masing-masing lokasi dibangkitkan deret waktu sebanyak 100 dan berpola Autoregressive yang berbeda, yaitu AR (2) untuk lokasi 1, AR (1) untuk lokasi 2, dan AR (2) untuk lokasi 3.
1, 2, 3, ... , 100
AR (1) 1, 2, 3, ... , 100
AR (1) 1, 2, 3, ... , 100
AR (1)
LOKASI 1 LOKASI 3 LOKASI 2
1, 2, 3, ... , 100
AR (1) 1, 2, 3, ... , 100
AR (2) 1, 2, 3, ... , 100
AR (2)
Gambar 3.2.3 Diagram Alir Penelitian Lakukan pendugaan
Parameter dan asumsi Sisaan
Bandingkan RMSE AR, VAR, STAR, GSTAR Melakukan Pemodelan
AR(1) dan VAR(1)
Cek AICC terkecil Pembangkitan Data
Data ordo Autoregressive
Berbeda Mulai
Matriks Korelasi Data ordo Autoregressive
Sama
Dekomposisi Cholesky
Hasil Cholesky Autoregressive Sama
Hasil Cholesky Autoregressive Beda
Melakukan Pemodelan AR(p) dan VAR(p)
Tentukan ordo waktu
Lakukan Pemodelan STAR(p:1) GSTAR(p:1)
Matriks bobot Contiguity
4
HASIL DAN PEMBAHASAN
Pembangkitan Data
Data yang digunakan pada penelitian ini adalah data simulasi, data dibangkitkan mengikuti pola autoregressive stasioner dengan menggunakan software SAS 9.3. Lokasi terlebih dahulu ditetapkan, yaitu berjumlah tiga. Masing -masing lokasi berpola autoregressive dengan ordo waktu yang sudah ditetapkan, yaitu berordo waktu sama dan berordo waktu berbeda. Data diatur sedemikian rupa sehingga mempunyai korelasi antar lokasi, yaitu dengan menerapkan analisis Dekomposisi Cholesky. Pembahasan proses pembangkitan data ini akan diuraikan menjadi 2, yaitu pembangkitan data dengan ordo waktu autoregressive sama sesuai dengan Lampiran 1 dan ordo waktu autoregressive berbeda sesuai dengan Lampiran 2.
Data Ordo Waktu Autoregressive Sama
Proses pembangkitan data dengan ordo waktu Autoregressive sama dimulai dengan menyusun model pola waktu stasioner di 3 lokasi, yaitu
Pola waktu ini ditetapkan berordo autoregressive sama di masing-masing lokasi, yaitu berordo 1. Nilai parameter ditetapkan berbeda di setiap lokasi asalkan tetap memenuhi kestasioneran data deret waktu. Tujuan pembedaan ini untuk keragaman antar lokasi, namun memiliki karakteristik waktu yang sama, yaitu dipengaruhi satu waktu sebelumnya (ordo satu). Nilai parameter di setiap lokasi sebagai berikut :
Lokasi 1 : Lokasi 2 : Lokasi 3 :
Data dibangkitkan sebanyak 100 waktu di masing-masing lokasi. Namun ini tidak dapat menjamin adanya hubungan antar lokasi sehingga untuk pemodelan ruang dan waktu secara simultan tidak dapat dilakukan. Dekomposisi Cholesky digunakan untuk menjadikan hasil bangkitan menjadi saling berkorelasi antar lokasi dengan tidak menghilangkan pola waktu autoregressive di setiap lokasi. Hasil dekomposisi inilah yang akan digunakan kemudian untuk analisis pemodelan ruang dan waktu. Matriks korelasi hasil Dekomposisi Cholesky adalah sebagai berikut :
(
posisi lokasi dapat dilihat pada Gambar 3.1. Hasil dekomposisi memungkinkan adanya perubahan ordo waktu autoregressive. Data yang tidak mengikuti pola Autoregressive ordo satu, tidak digunakan dalam analisis pemodelan ruang dan waktu. Data yang saling berkorelasi ini dapat dibuktikan juga dengan mencari nilai autokorelasi spasial, yaitu Indeks Moran. Indeks Moran ini dicari untuk menunjukkan adanya hubungan spasial. Dari hasil analisis didapatkan nilai Indeks Moran sebesar, I=0.298 yang artinya terdapat autokorelasi positif. Proses pembangkitan data ini diulang sebanyak 100 kali dengan menggunakan fungsi macro SAS dengan tujuan melihat kekonsistenan peramalan pada analisis ruang dan waktu, yaitu Metode AR, VAR, STAR, dan GSTAR yang dilihat dari nilai
Root Mean Square Error (RMSE).
Data Ordo Waktu Autoregressive Berbeda
Proses pembangkitan data dengan ordo waktu Autoregressive berbeda pun dimulai dengan menyusun model pola waktu stasioner di 3 lokasi, yaitu
Pola waktu ini ditetapkan berordo autoregressive yang berbeda di masing-masing lokasi, yaitu berordo 2 di lokasi 1 dan lokasi 3 serta berordo 1 di lokasi 2. Tujuan penetapan ordo waktu yang berbeda ini adalah untuk melihat pengaruhnya dalam proses peramalan ketika dilakukan pemodelan AR dan VAR yang kemudian akan menjadi rujukan dalam penetapan ordo waktu STAR dan GSTAR. Nilai parameter dan ditetapkan berbeda di setiap lokasi asalkan tetap memenuhi kestasioneran data deret waktu. Tujuan pembedaan ini untuk keragaman antar lokasi. Nilai parameter dan di setiap lokasi sebagai berikut :
Lokasi 1 : Lokasi 2 :
Lokasi 3 :
Seperti pembangkitan data dengan ordo Autoregressive sama, data dibangkitkan sebanyak 100 waktu di masing-masing lokasi. Matriks korelasi hasil Dekomposisi Cholesky adalah sebagai berikut :
(
Model Autoregressive (AR)
Pemodelan ini dilakukan secara terpisah di masing-masing lokasi, artinya pendugaan parameter diduga secara terpisah di 3 lokasi dan kemudian dicari ketepatan peramalannya. Pemodelan ini menggunakan contoh data hasil Lampiran 1, yaitu menggunakan data dengan ordo waktu autoregressive sama di 3 lokasi dan data Lampiran 2, yaitu menggunakan data dengan ordo waktu autoregressive
beda di 3 lokasi Hal pertama yang dilakukan adalah membagi 100 data bangkitan menjadi 2 bagian, untuk pemodelan dan ketepatan peramalan. Dari 100 data waktu yang dibangkitkan, 90 data digunakan untuk pemodelan sedangkan 10 data digunakan untuk mencari ketepatan peramalannya, yaitu RMSE.
Kestasioneran dan model tentatif
Kestasioneran pola waktu dapat dilihat dari plot deret waktu yang tertera pada Gambar 4.2.1 untuk Lokasi 1 ordo autoregressive sama dan Gambar 4.2.2. untuk Lokasi 1 ordo autoregressive berbeda.
Gambar 4.2.1 menjelaskan kestasioneran di lokasi 1 untuk ordo waktu
autoregressive sama, dapat dilihat bahwa untuk plot series yang disimbolkan Y1 berada di sekitar nilai tengahnya. Model tentatif Autoregressive dapat dilihat dari plot ACF nya berpola tails off dan plot PACF nya berpola cuts off di lag pertama. Berdasarkan analisis tersebut dapat dikatakan data stasioner dan berpola AR(1). Pola yang sama ditunjukkan untuk lokasi 2 dan 3 yang membentuk pola stasioner pada AR (1). Hasil lebih lengkapnya untuk lokasi 2 dan 3 ordo autoregressive
sama ini dapat dilihat pada Lampiran 4.
Plot kestasioneran untuk ordo waktu autoregressive berbeda di lokasi 1 dapat dilihat pada Gambar 4.2.2, plot series yang disimbolkan Y1 berada di sekitar nilai tengahnya. Plot ACF yang terbentuk berpola tails off dan PACF berpola cuts off di lag ke-2. Hal ini dapat dikatakan stasioner dan berpola AR (2). Lokasi 3 mempunyai pola ACF dan PACF yang sama seperti Lokasi 1, sedangkan untuk Lokasi 2 mempunyai pola PACF yang cuts off di lag ke-1 yang artinya berpola AR (1). Berdasarkan hasil analisis yang didapat bahwa data sesuai dengan desain simulasi awal. Hasil lebih lengkap untuk lokasi 2 dan 3 ordo
autoregressive berbeda ini dapat dilihat pada Lampiran 5.
Selain secara eksploratif, penentuan kestasioneran dapat dilakukan secara uji formal, yaitu dengan menggunakan uji Augmented Dickey-Fuller (ADF) dimana Hipotesis alternatifnya adalah data stasioner. Hasil uji kestasioneran lokasi 1,2, dan 3 untuk ordo autoregressive sama dan berbeda dapat dilihat pada Tabel 4.2.1
Ordo Lokasi Rho Nilai p Tau Nilai p
Sama
1 -39.0816 <.0001 -4.42 <.0001 2 -24.4946 0.0002 -3.47 0.0007 3 -34.0587 <.0001 -4.08 <.0001
Berbeda
1 -63.4547 <.0001 -5.68 <.0001 2 -67.3972 <.0001 -5.69 <.0001 3 -46.7677 <.0001 -4.8 <.0001
Tabel 4.2.1 menjelaskan bahwa data di Lokasi 1, 2, dan 3 untuk ordo
autoregressive sama dan berbeda sudah memenuhi asumsi kestasioneran, hal ini dapat dilihat dari nilai-p, yaitu baik dalam statistik Rho maupun Tau yang nilainya
[image:34.595.78.470.82.465.2]Tabel 4.2.1 Uji ADF AR untuk lokasi 1,2 , dan 3
selalu lebih kecil dari nilai α (0.05), sehingga dapat disimpulkan bahwa data stasioner dalam rataan.
Model tentatif dapat dilihat dari nilai BIC dari setiap ordo waktu, nilai BIC terkecil menunjukkan model Autoregressive terbaik. Nilai BIC tentatif untuk ordo
autoregressive sama dan berbeda dapat dilihat pada Tabel 4.2.2.
Ordo Lokasi Beda Kala Nilai BIC
Sama
1 1 -0.10579
2 1 -0.10162
3 1 -0.11415
Berbeda
1 2 -0.34175
2 1 -0.13124
3 2 0.11318
Tabel 4.2.2 merupakan nilai Bayesian Information Criterion (BIC) terkecil dari berbagai kombinasi beda kala di setiap lokasi. Berdasarkan hasil analisis, untuk ordo autoregressive sama didapatkan nilai BIC terkecil di beda kala 1, artinya di lokasi 1, 2, dan 3 model terbaik adalah model AR (1). Sedangkan untuk ordo autoregressive berbeda didapatkan nilai BIC terkecil di lokasi 1 yaitu AR (2), lokasi 2 yaitu AR (1), dan lokasi 3 yaitu AR (2). Hal ini sesuai dengan proses desain pembangkitan data. Program SAS 9.3 ini menampilkan kombinasi nilai BIC hingga beda kala (lag) ke 5 untuk setiap pola autoregressive dan moving average. Hasil selengkapnya untuk kombinasi nilai BIC ini dapat dilihat pada Lampiran 6 untuk ordo sama dan Lampiran 7 untuk ordo berbeda.
Pendugaan Parameter
Pendugaan parameter model Autoregressive menggunakan metode Ordinary Least Squares (OLS). Dugaan parameter mengikuti model :
, untuk AR (1)
, untuk AR (2)
Hasil dugaan parameter untuk ordo autoregressive sama dapat dilihat pada Tabel 4.2.3 untuk setiap lokasi.
Lokasi Parameter Nilai Dugaan
Galat
Baku Nilai-t
Nilai p Pr > |t| 1 0.64637 0.08147 7.93 <.0001 2 0.71949 0.0739 9.74 <.0001 3 0.65416 0.08058 8.12 <.0001
Tabel 4.2.2 Nilai BIC tentatif AR
Berdasarkan Tabel 4.2.3 dapat dilihat bahwa parameter AR(1) nyata secara statistik. Hal ini dapat dilihat dari nilai-p ( <0.0001 ) kurang dari nilai α (0.05) di semua lokasi. Oleh karena itu, model Autoregressive (1) yang terbentuk adalah :
Lokasi 1 : Lokasi 2 : Lokasi 3 :
Sedangkan hasil dugaan parameter untuk ordo autoregressive berbeda dapat dilihat pada Tabel 4.2.4.
Lokasi Parameter Nilai
Dugaan Galat Baku Nilai-t
[image:36.595.42.480.45.766.2]Nilai p Pr > |t|
1 1.3425 0.08384 16.01 <.0001
-0.618 0.08384 -7.37 <.0001
2 0.3418 0.09971 3.43 0.0009
3 1.05547 0.09898 10.66 <.0001 -0.38326 0.0991 -3.87 0.0002
Tabel 4.2.4 menjelaskan bahwa parameter AR(2) nyata secara statistik di lokasi 1 dan 3 sedangkan AR(1) nyata di lokasi 2. Hal ini dapat dilihat dari nilai
p-value ( <0.0001;0.0009;0.0002) kurang dari nilai α (0.05). Oleh karena itu,
model Autoregressive (2) dan Autoregressive (1) yang terbentuk adalah : Lokasi 1 :
Lokasi 2 :
Lokasi 3 :
Analisis Sisaan
Sisaan yang didapatkan dari model ini dilihat asumsi kebebasan dan kenormalannya. Uji kebebasan sisaan menggunakan uji Box-Pierce Q. Hipotesis alternatif untuk uji kebebasan adalah sisaan tidak saling bebas sedangkan uji kenormalan dapat dilihat dari histogram atau qq-plot, sisaan menyebar normal jika membentuk lonceng pada histogram dan berbentuk garis lurus pada qq-plot.
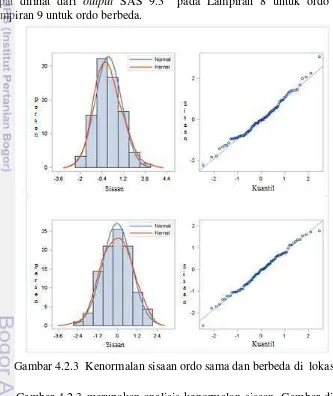
Kebebasan sisaan dapat dilihat pada Tabel 4.2.5 untuk ordo autoregressive sama dan berbeda di setiap lokasi. Kenormalan sisaan dapat dilihat pada Gambar 4.2.3 untuk Lokasi 1 ordo autoregressive sama dan berbeda.
Ordo Beda Kala Lokasi
1 2 3
Sama
6 0.9500 0.6394 0.6683
12 0.7326 0.4287 0.1635
18 0.7721 0.1716 0.2151
24 0.6831 0.4069 0.1794
Berbeda
6 0.5050 0.5987 0.4563
12 0.7891 0.7615 0.4180
18 0.1516 0.8862 0.3044
[image:37.595.103.476.89.816.2]24 0.4133 0.7114 0.3083
Tabel 4.2.5 merupakan nilai-p untuk analisis kebebasan sisaan model AR(p) di setiap lokasi untuk ordo autoregressive sama dan berbeda. Tabel ini menjelaskan bahwa kebebasan sisaan di Lokasi 1,2, dan 3 sudah terpenuhi, hal ini dapat dilihat dari nilai nilai-p di semua lag (0.95 ; 0.7326 ; ... ; 0.3044 ; 0.3083) lebih dari nilai α (0.05). Hasil lebih lengkapnya untuk uji kebebasan sisaan ini dapat dilihat dari output SAS 9.3 pada Lampiran 8 untuk ordo sama dan Lampiran 9 untuk ordo berbeda.
Gambar 4.2.3 merupakan analisis kenormalan sisaan. Gambar diatas untuk ordo autoregressive sama sedangkan yang dibawahnya untuk ordo berbeda.
[image:37.595.126.459.338.734.2]Tabel 4.2.5 Kebebasan sisaan AR (p) lokasi 1,2, dan 3
Berdasarkan gambar bahwa kenormalan sisaan di Lokasi 1 sudah terpenuhi, hal ini dapat dilihat dari bentuk histogram yang menyerupai lonceng simetris, selain itu dilihat dari qq-plot membentuk garis lurus. Pola yang sama diperlihatkan untuk lokasi 2 dan 3 yang dapat dilihat dari output SAS 9.3 pada Lampiran 10 untuk ordo autoregressive sama dan Lampiran 11 untuk ordo berbeda.
Peramalan
Proses peramalan ini dilakukan sebanyak 10 waktu dari model yang sudah didapat. Setelah didapat hasil peramalannya kemudian dihitung nilai ketepatan peramalannya dengan 10 waktu data asli dengan menggunakan nilai Root Mean Square Error (RMSE). Berikut contoh perhitungan peramalan data ke-91 untuk lokasi 1, 2, dan 3 untuk ordo autoregressive sama :
Model AR(1) sebagai berikut : Lokasi 1 : Lokasi 2 : Lokasi 3 :
Kemudian jika diketahui data hasil bangkitan ke-90 di setiap lokasi sebagai berikut :
z1(90) = 1.10354, z2(90) = 0.8278, dan z3(90) = 0.89882
maka peramalan data ke-91 di setiap lokasi adalah sebagai berikut : Lokasi 1 :
Lokasi 2 :
Lokasi 3 :
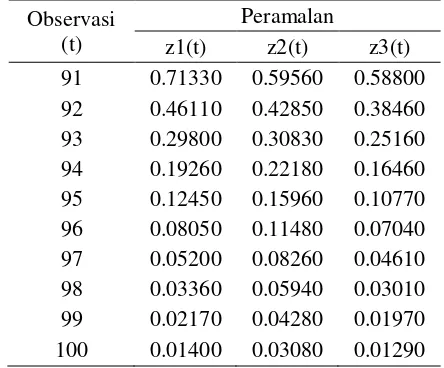
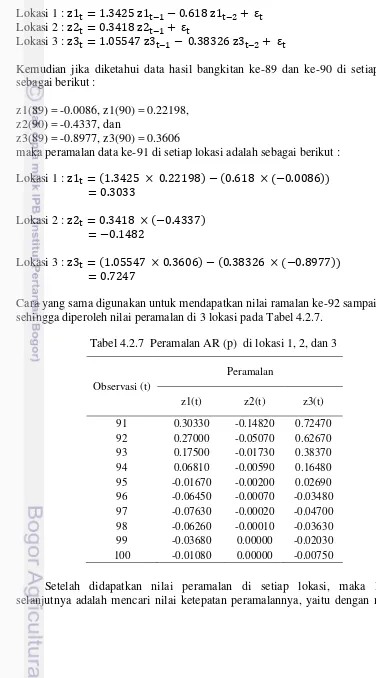
Cara yang sama digunakan untuk mendapatkan nilai ramalan ke-92 sampai ke-100 sehingga diperoleh nilai peramalan di 3 lokasi pada Tabel 4.2.6.
Observasi (t)
Peramalan
[image:38.595.171.393.560.744.2]z1(t) z2(t) z3(t) 91 0.71330 0.59560 0.58800 92 0.46110 0.42850 0.38460 93 0.29800 0.30830 0.25160 94 0.19260 0.22180 0.16460 95 0.12450 0.15960 0.10770 96 0.08050 0.11480 0.07040 97 0.05200 0.08260 0.04610 98 0.03360 0.05940 0.03010 99 0.02170 0.04280 0.01970 100 0.01400 0.03080 0.01290
Sedangkan contoh perhitungan peramalan data ke-91 untuk lokasi 1, 2, dan 3 untuk ordo autoregressive berbeda adalah sebagai berikut :
Jika diketahui :
Model AR(p) sebagai berikut :
Lokasi 1 : Lokasi 2 :
Lokasi 3 :
Kemudian jika diketahui data hasil bangkitan ke-89 dan ke-90 di setiap lokasi sebagai berikut :
z1(89) = -0.0086, z1(90) = 0.22198, z2(90) = -0.4337, dan
z3(89) = -0.8977, z3(90) = 0.3606
maka peramalan data ke-91 di setiap lokasi adalah sebagai berikut : Lokasi 1 :
Lokasi 2 :
Lokasi 3 :
Cara yang sama digunakan untuk mendapatkan nilai ramalan ke-92 sampai ke-100 sehingga diperoleh nilai peramalan di 3 lokasi pada Tabel 4.2.7.
Observasi (t)
Peramalan
z1(t) z2(t) z3(t)
91 0.30330 -0.14820 0.72470 92 0.27000 -0.05070 0.62670 93 0.17500 -0.01730 0.38370 94 0.06810 -0.00590 0.16480 95 -0.01670 -0.00200 0.02690 96 -0.06450 -0.00070 -0.03480 97 -0.07630 -0.00020 -0.04700 98 -0.06260 -0.00010 -0.03630 99 -0.03680 0.00000 -0.02030 100 -0.01080 0.00000 -0.00750
[image:39.595.97.473.148.826.2]Setelah didapatkan nilai peramalan di setiap lokasi, maka langkah selanjutnya adalah mencari nilai ketepatan peramalannya, yaitu dengan mencari
nilai RMSE. Nilai ini pada dasarnya yaitu membandingkan antara nilai peramalan model dengan nilai asli hasil bangkitan.
Jika diketahui nilai data asli hasil bangkitan ke-91 sampai ke-100 untuk data ordo
autoregressive sama adalah sebagai berikut :
Observasi (t) Nilai Asli
z1(t) z2(t) z3(t) 91 1.4118 0.41507 0.68711 92 0.5692 0.36166 0.20667 93 -0.12474 -0.378 -0.57931 94 0.4194 0.64387 0.50875 95 -0.61449 -2.75118 -2.24731 96 0.07767 -4.02016 -2.23841 97 1.28625 -3.38057 -1.06088 98 1.14235 -3.1186 -1.15384 99 -1.0069 -0.83444 -1.70647 100 0.28352 0.89855 0.43823
Maka perhitungan nilai Root Mean Squared Error (RMSE) untuk ordo
autoregressive sama di setiap lokasi adalah sebagai berikut :
Lokasi 1 :
√
Lokasi 2 :
√
Lokasi 3 :
√
Kemudian jika diketahui nilai data asli hasil bangkitan ke-91 sampai ke-100 untuk data ordo autoregressive berbeda adalah sebagai berikut :
Observasi (t)
Nilai Asli
z1(t) z2(t) z3(t) 91 0.21248 1.19999 1.27961 92 -0.08624 0.52783 0.63877 93 -2.4544 -0.76387 -1.81507 94 -1.40745 -1.39568 -1.6807 95 0.16787 1.15772 0.60448 96 1.00749 -0.90331 0.12074 97 2.88539 -0.01945 1.93779 98 2.69251 1.49 2.67683 99 2.39886 1.31187 2.32801 100 3.32847 2.30428 3.61609
Maka perhitungan nilai Root Mean Squared Error (RMSE) untuk ordo berbeda adalah sebagai berikut :
Lokasi 1 :
√
Lokasi 2 :
√
Lokasi 3 :
√
Hasil RMSE ini dapat diringkas pada Tabel 4.2.10. Nilai RMSE tersebut merupakan ketepatan peramalan yang akan digunakan untuk melihat kinerja antar metode ruang dan waktu dalam peramalan.
Ordo Lokasi RMSE
Sama
1 0.71827
2 2.23323
3 1.32344
Berbeda
1 2.09416
2 1.26698
3 1.97108
Model Vector Autoregressive (VAR)
Pemodelan ini dilakukan secara simultan di semua lokasi, artinya pendugaan parameter diduga secara bersama-sama di 3 lokasi dan kemudian dicari ketepatan peramalannya. Hal pertama yang dilakukan adalah membagi 100 data bangkitan menjadi 2 bagian, untuk pemodelan dan ketepatan peramalan. Dari 100 data waktu yang dibangkitkan, 90 data digunakan untuk pemodelan sedangkan 10 data digunakan untuk mencari ketepatan peramalannya, yaitu RMSE.
Kestasioneran dan model tentatif
Kestasioneran model VAR dapat dilihat nilai akar ciri dari matriks parameter VAR. Model VAR dikatakan stasioner jika akar ciri matriks parameter kurang dari satu. Model tentatif VAR dapat dilihat dari nilai AICC terkecil dari kombinasi pola AR dan MA. Hasil akar ciri matriks parameter untuk ordo
autoregressive sama dapat dilihat pada Tabel 4.3.1, sedangkan untuk ordo
autoregressive berbeda dapat dilihat pada Tabel 4.3.2
Akar
[image:42.595.43.475.56.800.2]Ciri Real Imaginary Modulus Radian Degree 1 0.7314 0.0485 0.7330 0.0662 3.7913 2 0.7314 -0.0485 0.7330 -0.0662 -3.7913 3 0.6436 0.0000 0.6436 0.0000 0.0000
Tabel 4.3.1 menjelaskan bahwa model VAR sudah stabil / stasioner. Hal ini dapat dilihat dari 3 nilai modulus akar ciri dari matriks parameter yang semuanya kurang dari 1. Oleh sebab itu tidak perlu proses pembedaan untuk analisis lebih lanjut.
Akar Ciri Real Imaginary Modulus Radian Degree
1 0.78494 0.41622 0.8885 0.4876 27.9354 2 0.78494 -0.41622 0.8885 -0.4876 -27.9354 3 0.62667 0.40007 0.7435 0.5682 32.5545 4 0.62667 -0.40007 0.7435 -0.5682 -32.5545 5 0.05667 0.36181 0.3662 1.4154 81.0976 6 0.05667 -0.36181 0.3662 -1.4154 -81.0976
Akar ciri dari matriks parameter yang terbentuk berjumlah 6 karena mengikuti jumlah parameter VAR (2). Berdasarkan Tabel 4.3.2 dapat dilihat bahwa nilai modulus dari 6 akar ciri matriks parameter bernilai kurang dari 1, oleh karena itu dapat dikatakan model VAR (2) memenuhi asumsi kestasioneran.
Tabel 4.3.1 Kestasioneran model VAR (1) ordo sama
Pemilihan model terbaik pada VAR menggunakan kriteria Akaike Information Corrected Criterion (AICC). Sama halnya dengan BIC pada model AR, Nilai AICC terkecil merupakan model terbaik. Pada sistem SAS ini, akan dihasilkan kombinasi AICC hingga beda kala 5. Berikut hasil nilai AICC terkecil untuk ordo autoregressive sama di semua lokasi pada Tabel 4.3.3
Beda Kala MA 0 MA 1 MA 2 MA 3 AR 0 -1.749434 -2.344852 -2.7021 -2.92701 AR 1 -3.761969 -3.732548 -3.63682 -3.55269 AR 2 -3.640881 -3.744494 -3.53987 -3.4466 AR 3 -3.457788 -3.520692 -3.45553 -3.21344
Tabel 4.3.3 menjelaskan berbagai nilai AICC di lokasi 1, 2, dan 3 secara simultan untuk model VARMA (p;q) secara tentatif. Hasil ini hanya memperlihatkan hingga ordo waktu p dan q sebesar 3. Berdasarkan hasil analisis didapatkan nilai AICC terkecil (-3.761969) yaitu model VARMA (1;0) atau dengan kata lain model VAR (1) merupakan model terbaik.
Beda Kala MA 0 MA 1 MA 2 MA 3
AR 0 -0.280728 -0.858576 -1.433884 -1.88031 AR 1 -2.763326 -3.281666 -3.532297 -3.57785 AR 2 -3.965256 -3.97641 -3.85517 -3.66792 AR 3 -3.776917 -3.832328 -3.692657 -3.46733
Berdasarkan Tabel 4.3.4 diatas dapat dlihat nilai AICC terkecil (-3.97641) yaitu model VARMA (2;1), namun karena penelitian ini dibatasi dengan pola
autoregressive dan nilai AICC terkecil tidak berbeda jauh dengan model VARMA (2;0) atau VAR (2), yaitu -3.965256 maka model terbaik dianggap model VAR(2). Hal ini dimungkinkan dapat terjadi untuk model VAR (p) karena pengaruh ordo waktu yang berbeda dari AR di setiap lokasi, tetapi yang terpenting adalah pola AR di setiap lokasi sesuai dengan data bangkitan awal.
Pendugaan Parameter
Pendugaan parameter model Vector Autoregressive menggunakan metode
Ordinary Least Squares (OLS). Dugaan parameter mengikuti model :
, untuk VAR (1)
Maka model VAR (1) menjadi :
Lokasi 1 : Lokasi 2 : Lokasi 3 :
Tabel 4.3.3 Nilai AICC tentatif VAR ordo sama
, untuk VAR (2)
Maka model VAR (2) menjadi :
[image:44.595.34.504.53.813.2]Lokasi 1: Lokasi 2: Lokasi 3: Hasil dugaan parameter VAR(1) ordo autoregressive sama dapat dilihat pada Tabel 4.3.5 untuk setiap lokasi sedangkan untuk ordo berbeda pada Tabel 4.3.6.
Lokasi Parameter Nilai
Dugaan Galat Baku Nilai t Nilai p Peubah
1
0.62732 0.33998 1.85 0.0685 z1(t-1)
-0.01713 0.22631 -0.08 0.9398 z2(t-1)
0.02665 0.4461 0.06 0.9525 z3(t-1)
2
-0.13439 0.34346 -0.39 0.6966 z1(t-1)
0.67176 0.22863 2.94 0.0042 z2(t-1)
0.11194 0.45067 0.25 0.8044 z3(t-1)
3
-0.12497 0.33659 -0.37 0.7113 z1(t-1) -0.06734 0.22405 -0.3 0.7645 z2(t-1)
0.80723 0.44165 1.83 0.0711 z3(t-1)
Tabel 4.3.5 menjelaskan bahwa parameter VAR(1) yang nyata secara statistik hanya z2(t-1) pada lokasi 2. Hal ini dapat dilihat dari nilai-p ( 0.0042 )
kurang dari nilai α (0.05). Oleh karena itu, model VAR (1) yang terbentuk adalah:
Lokasi 1 : Lokasi 2 : Lokasi 3 :
Tabel 4.3.6 menjelaskan bahwa parameter VAR(2) yang nyata secara statistik hanya z1(t-1) dan z1(t-2) pada lokasi 1, z2(t-1) dan z3(t-1) . Hal ini dapat dilihat dari nilai-p kurang dari nilai α (0.05). Oleh karena itu, model VAR (2) yang terbentuk adalah :
Lokasi 1 :
Lokasi 2 :
Lokasi 3 :
Lokasi Parameter Nilai
Dugaan Galat Baku Nilai t Nilai p Peubah
1
1.5713 0.29159 5.39 0.0001 z1(t-1) -0.03078 0.2257 -0.14 0.8918 z2(t-1) -0.26717 0.39534 -0.68 0.5011 z3(t-1) -0.63261 0.28808 -2.2 0.0309 z1(t-2) 0.01252 0.24379 0.05 0.9592 z2(t-2) 0.02941 0.39991 0.07 0.9416 z3(t-2)
2
0.48086 0.3156 1.52 0.1315 z1(t-1) 0.02465 0.24428 0.1 0.9199 z2(t-1) 0.03276 0.4279 0.08 0.9392 z3(t-1) -0.30243 0.3118 -0.97 0.3349 z1(t-2) -0.17361 0.26387 -0.66 0.5124 z2(t-2) 0.10313 0.43285 0.24 0.8123 z3(t-2)
3
0.29162 0.30551 0.95 0.3426 z1(t-1) -0.81119 0.23647 -3.43 0.0009 z2(t-1) 1.34061 0.41421 3.24 0.0017 z3(t-1) -0.07047 0.30183 -0.23 0.816 z1(t-2) 0.30034 0.25542 1.18 0.2431 z2(t-2) -0.66006 0.419 -1.58 0.119 z3(t-2)
Fokus dari penelitian ini adalah peramalan, oleh sebab itu parameter yang tidak nyata tetap dimasukkan ke dalam model agar memberikan bobot parameter yang sama untuk peramalan.
Analisis Sisaan
Diagnostik sisaan akan dianalisis secara multivariate dan univariate. Uji kebebasan sisaan multivariate menggunakan Uji Portmanteau Q dengan hipotesis alternatif nya adalah sisaan tidak saling bebas. Uji sisaan univariate dilakukan di masing-masing model tiap lokasi. Uji Durbin-Watson untuk menguji kebebasan sisaan, Uji ARCH untuk menguji kehomogenan dengan hipotesis alternatifnya sisaan tidak homogen, dan Uji Jarque-Bera untuk menguji normalitas dengan hipotesis alternatifnya sisaan tidak normal. Uji Portmanteau Q dapat dilihat pada Tabel 4.3.7, Uji Durbin-Watson, ARCH, dan Jarque-Bera pada Tabel 4.3.8
Ordo Beda kala db
Khi-kuadrat Nilai p
Sama 2 9 8.52 0.4823
[image:45.595.51.527.75.802.2]3 18 18.23 0.4407 Berbeda 3 9 10.73 0.2948
[image:45.595.88.523.87.394.2]Tabel 4.3.7 menjelaskan bahwa sisaan model VAR untuk ordo
autoregressive sama dan berbeda sudah memenuhi asumsi kebebasan. Hal ini dapat dilihat dari nilai-p(0.4823;0.4407;0.2948)yang lebih dari α (0.05).
Ordo Lokasi Kebebasan Kenormalan Kehomogenan Khi-kuadrat Nilai p Nilai F Nilai p
Sama
1 1.85199 5.1 0.0781 0.03 0.8584 2 1.90813 1.13 0.5695 0.1 0.7485 3 1.8922 3.57 0.1677 0.04 0.8371
Berbeda
1 2.00233 0.39 0.8219 0.04 0.8393 2 2.03684 5.84 0.0538 0.21 0.6461 3 1.9953 0.76 0.6829 0.66 0.4198
Tabel 4.3.8 menjelaskan bahwa sisaan model VAR untuk