Metode Konjugat Gradien Hibrid Baru: Metode Wyl-Fr Dan Metode Prp-Cd Untuk Menyelesaikan Masalah Optimasi Tak Berkendala.

METODE KONJUGAT GRADIEN HIBRID BARU: METODE

WYL-FR DAN METODE PRP-CD UNTUK MENYELESAIKAN

MASALAH OPTIMASI TAK BERKENDALA

NETTY JULINDA MARLIN GELLA

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa tesis berjudul Metode Konjugat Gradien Hibrid Baru: Metode WYL-FR dan Metode PRP-CD untuk Menyelesaikan Masalah Optimasi Tak Berkendala adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

RINGKASAN

NETTY JULINDA MARLIN GELLA. Metode Konjugat Gradien Hibrid Baru: Metode WYL-FR dan Metode PRP-CD untuk Menyelesaikan Masalah Optimasi Tak Berkendala. Dibimbing oleh BIB PARUHUM SILALAHI dan SUGI GURITMAN.

Optimasi adalah cabang dari matematika yang berhubungan dengan pengambilan keputusan terbaik yaitu memaksimumkan atau meminimumkan suatu fungsi tujuan. Ada beberapa metode untuk menyelesaikan masalah optimasi, salah satunya adalah metode konjugat gradien. Beberapa metode konjugat gradien yang terkenal diantaranya metode HS (Hestenes dan Stiefel 1952), metode FR (Fletcher dan Reeves 1964), metode CD (Fletcher 1987), metode PRP (Polyak 1969), metode LS (Liu dan Storey 1991) dan metode DY (Dai dan Yuan 1999). Metode FR, metode CD atau metode DY memiliki sifat kekonvergenan global tetapi kinerja komputasinya kurang efisien. Di sisi lain, metode PRP, metode HS atau metode LS secara umum tidak memenuhi sifat konvergensi globalnya tetapi metode-metode ini memiliki kinerja komputasi yang lebih baik. Karena itu, Zhang dan Zhou (2007) mengusulkan metode konjugat gradien hibrid yang baru untuk PRP-FR dan HS-DY yang disebut dengan metode NH1 dan NH2. Dengan ide yang sama Zhou, Zhu, Fan dan Qing (2011) juga mengusulkan metode konjugat gradien hibrid yang baru untuk LS-CD yang disebut dengan metode NH3.

Penelitian ini memiliki tiga tujuan utama yaitu: (1) mengusulkan metode-metode konjugat gradien hibrid baru; (2) membuktikan berlakunya sifat-sifat kekonvergenan global pada metode-metode yang diusulkan; dan (3) membandingkan hasil numerik dari metode yang diusulkan dengan metode konjugat gradien hibrid FR-PRP (NH1), HS-DY (NH2) dan LS-CD (NH3) yang ditinjau dari jumlah iterasi dan running time.

Dalam penelitian ini, diusulkan dua metode konjugat gradien hibrid baru yaitu metode hibrid baru WYL-FR (NH6) dan metode hibrid baru PRP-CD (NH7). yang memenuhi kondisi sufficient descent. Kedua metode ini dibuktikan memenuhi sifat kekonvergenan global. Dari hasil numerik kedua metode ini menunjukkan bahwa kedua metode mampu menyelesaikan setiap masalah optimasi tak linear tanpa kendala yang diberikan. Perbandingan hasil numerik kedua metode dengan metode NH1, NH2 dan NH3 menunjukkan bahwa metode NH6 dan NH7 sangat kompetitif dengan metode NH1, NH2 dan NH3 dalam hal jumlah iterasi dan running time-nya. Dengan demikian, metode hibrid baru NH6 dan NH7 cukup kompetitif dan efisien serta menambah koleksi metode hibrid yang sudah tersedia dalam mencari solusi untuk masalah optimasi.

SUMMARY

NETTY JULINDA MARLIN GELLA. New Hybrid Conjugate Gradient Method: WYL-FR Method and PRP-CD Method for Solving Unconstrained Optimization Problems. Supervised by BIB PARUHUM SILALAHI and SUGI GURITMAN.

Optimization is a branch of mathematics which study techniques for finding the best decision, i.e. the maximum or the minimum of a function. There are several methods to solve optimization problems, one of them is the conjugate gradient method. Several well-known conjugate gradient methods are HS method (Hestenes-Stiefel 1952), FR method (Fletcher and Reeves 1964), CD method (Fletcher 1987), PRP method (Polyak 1969), LS method (Liu and Storey 1991) and DY method (Dai and Yuan 1999). The FR method, the CD method or the DY method have nice global convergence property on each algorithm, but their computational performance results are not so well. On the other hand, the PRP method, the HS method and the LS methods have good computational performance but generally these methods do not satify global convergence properties. Therefore, Zhang and Zhou (2007) have proposed a method which was a new hybrid conjugate gradient for PRP-FR and HS-DY called NH1 and NH2 methods. With the same idea, Zhou, Zhu, Fan dan Qing (2011) also proposed a conjugate gradient method for a new hybrid LS-CD called NH3 method.

This research has three main objectives, namely: (1) proposed two new hybrid conjugate gradient methods; (2) proved global convergence properties of the proposed methods; and (3) compared the computational performance of the proposed methods with existing hybrid conjugate gradient methods: the FR-PRP (NH1), HS-DY and LS-CD (NH3) in terms of the number of iteration and the running time.

In this research, we proposed two new hybrid conjugate gradient methods namely, new hybrid method WYL-FR (NH6) and new hybrid method PRP-CD (NH7) which satisfied sufficient descent conditions. Both of these methods have been proved satisfying global convergence. The numerical results showed that both methods are capable to solve any nonlinear optimization unconstrained problems which given. Numerical results of both methods and NH1, NH2 and NH3 showing that NH6 and NH7 very competitive with the method NH1, NH2 and NH3 in iterations number and its running time. Thus, a new hybrid method NH6 and NH7 quite competitive and efficient and increasing the collection of hybrid methods that have been available in the search for a solution to an optimization problem.

© Hak Cipta Milik IPB, Tahun 2015

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

METODE KONJUGAT GRADIEN HIBRID BARU: METODE

WYL-FR DAN METODE PRP-CD UNTUK MENYELESAIKAN

MASALAH OPTIMASI TAK BERKENDALA

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2015

Judul Tesis : Metode Konjugat Gradien Hibrid Baru: Metode WYL-FR dan Metode PRP-CD untuk Menyelesaikan Masalah Optimasi Tak Berkendala.

Nama : Netty Julinda Marlin Gella NIM : G551130231

Disetujui oleh Komisi Pembimbing

Dr Ir Bib Paruhum Silalahi, MKom Ketua

Dr Sugi Guritman Anggota

Diketahui oleh

Ketua Program Studi S2 Matematika Terapan

Dr Jaharuddin, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

PRAKATA

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus karena atas segala kasih, berkat dan anugerah-Nya sehingga karya ilmiah ini telah diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Desember 2014 ini ialah teori optimasi yang berjudul Metode Konjugat Gradien Hibrid Baru: Metode PRP-CD dan Metode WYL-FR untuk Menyelesaikan Masalah Optimasi Tak Berkendala.

Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis juga menyampaikan terima kasih kepada:

1. Bapak Agustinus Wellem Gella dan Almh. Ibu Sultje Tarotjie Gella-Ndoen selaku orang tua penulis serta Alm. Kakak Semi P. C. Gella.

2. Dr Bib Paruhum Silalahi, MKom selaku Ketua Komisi Pembimbing 3. Dr Sugi Guritman selaku Anggota Komisi Pembimbing.

4. Dr Jaharuddin, MS selaku Penguji Luar Komisi Pembimbing dan Ketua Program Studi S2 Matematika Terapan.

5. Seluruh dosen dan staf pegawai tata usaha Departemen Matematika.

6. Direktorat Jendral Pendidikan Tinggi (DIKTI) sebagai sponsor Beasiswa Pendidikan Pascasarjana dalam Negeri (BPP-DN).

7. Seluruh keluarga yang selalu memberi dorongan dan doa untuk keberhasilan studi penulis.

8. Seluruh mahasiswa Departemen Matematika khususnya teman-teman angkatan tahun 2013 di Program Studi S2 Matematika Terapan.

9. Saudari-saudari Wisma Fahmeda (Kak Restu, Kak Mia, Kak Ria, Kak Adriana, Arini, Arista, Risky, Eka, Dini dan Tini), keluarga Persekutuan Oikumene di Bogor, teman-teman UBF Depok, teman-teman GAMANUSRATIM di Bogor dan semua teman serta sahabat yang tidak dapat disebutkan satu persatu yang telah banyak mendukung dan memberi doa untuk keberhasilan studi penulis.

Akhirnya, semoga penulisan tesis ini dapat memperkaya pengalaman belajar dan wawasan kita semua.

DAFTAR ISI

DAFTAR TABEL vi

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

1 PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 1

2 TINJAUAN PUSTAKA 2

Optimasi Matematik 2

Himpunan Konveks 2

Fungsi Konveks 2

Norm Euclidean 3

Vektor Gradien 3

Minimum Global dan Minimum Lokal 3

Himpunan Terbatas 3

Kekontinuan Fungsi Lipschitz 4

Konvergen Global 4

Limit Inferior 4

Iterasi dan Running Time 4

3 METODE 4

4 HASIL DAN PEMBAHASAN 5

Metode Konjugat Gradien 5

Metode Konjugat Gradien Hibrid Baru Zhou dan Zhang 6 Metode Konjugat Gradien Hibrid Baru Zhou, Zhu, Fan dan Qing 7 Metode Konjugat Gradien Hibrid Baru NH6 dan NH7 7 Analisis Kekonvergen Global Metode NH6 dan NH7 9

Hasil Numerik 17

DAFTAR PUSTAKA 22

RIWAYAT HIDUP 26

DAFTAR TABEL

1 Jumlah iterasi dari masing-masing metode konjugat gradien 18 2 Hasil running time dari masing-masing metode konjugat gradien 19

DAFTAR GAMBAR

1 Hasil profil jumlah iterasi masing-masing metode konjugat gradien 20 2 Hasil profil running time masing-masing metode konjugat gradien 21

DAFTAR LAMPIRAN

1 Fungsi-fungsi tak linear yang digunakan dalam pengujian algoritme metode konjugat gradien hibrid untuk mencari hasil iterasi dan running

1

PENDAHULUAN

Latar Belakang

Optimasi merupakan teknik yang berhubungan dengan pengambilan keputusan terbaik (maksimum atau minimum) yang terdiri atas fungsi tujuan dan kendala (atau tanpa kendala). Dalam permasalahan tak linier khususnya permasalahan dimana fungsi tujuannya tak linear dan memiliki banyak variabel, metode numerik adalah suatu cara yang efisien untuk mencari solusi dari permasalahan yang ada. Umumnya penyelesaian optimasi dengan metode numerik bersifat iteratif. Ada beberapa teknik metode numerik untuk menyelesaikan permasalahan optimasi fungsi dengan atau tanpa kendala, salah satunya adalah metode konjugat gradien.

Metode konjugat gradien diusulkan oleh Hestenes dan Stiefel pada tahun 1952 yang dikenal dengan metode HS untuk menyelesaian sistem persamaan linear. Selanjutnya Fletcher dan Reeves (1964) memperluas metode konjugat gradien untuk memecahkan sistem pesamaan tak linear untuk skala besar. Beberapa metode konjugat gradien yang terkenal diantaranya metode HS (Hestenes-Stiefel 1952), metode FR (Fletcher dan Reeves 1964), metode CD (Fletcher 1987), metode PRP (Polyak 1969), metode LS (Liu dan Storey 1991) dan metode DY (Dai dan Yuan 1999). Metode FR, metode CD atau metode DY mempunyai sifat konvergensi yang tercapai pada masing-masing algoritme, tetapi kinerja komputasinya kurang efisien. Di sisi lain, metode PRP, metode HS atau metode LS secara umum sifat konvergensi globalnya belum terpenuhi tetapi metode-metode ini memiliki kinerja komputasi yang lebih baik. Dengan demikian beberapa metode dimodifikasi untuk memperoleh hasil optimasi yang lebih baik. Touati-Ahmed dan Storey (1990) mengusulkan metode hibrid PRP-FR (H1) dan Dai dan Yuan (2001) mengusulkan metode hibrid HS-DY (H2). Kedua metode ini memberikan hasil numerik yang lebih baik dari metode PRP. Berdasarkan ide dari metode H1 dan metode H2, Zhang dan Zhou (2007) mengusulkan metode konjugat gradien hibrid yang baru untuk PRP-FR dan HS-DY yang disebut dengan metode NH1 dan NH2. Dengan ide yang sama Zhou et al. (2011) juga mengusulkan metode konjugat gradien hibrid yang baru untuk LS-CD yang disebut dengan metode NH3.

Berdasarkan ide penelitian-penelitian sebelumnya maka penelitian ini mengusulkan metode konjugat gradien hibrid untuk WYL-FR yang disebut dengan NH6 dan PRP-CD yang disebut NH7

Tujuan Penelitian

Berdasarkan latar belakang dari penelitian ini, diuraikan tujuan penelitian yang akan dicapai yaitu:

1. Mengusulkan dua metode konjugat gradien hibrid baru.

2. Membuktikan berlakunya sifat-sifat kekonvergenan global pada metode-metode yang diusulkan.

2

2

TINJAUAN PUSTAKA

Optimasi Matematik

Definisi 2.1

Optimasi matematik adalah suatu proses formulasi masalah dan penentuan solusi dari suatu masalah optimasi berkendala dengan bentuk umum:



1 2 3



min ( ), f  x x x, , ,xn T n

x x x (2.1)

dengan kendala

 

0, 1, 2, ,

j

g x  j  m

 

0, 1, 2, ,

j

h x  j  r dimana f

   

x ,g_j x ,dan h_j

 

x adalah fungsi dari x.

Komponen-komponen x_i dari x 



x x x₁, ₂, ₃,x_n



T dinamakan variabel keputusan, f

 

x adalah fungsi objektif, g_j

 

x menyatakan fungsi kendala pertidaksamaan, h_j

 

x adalah fungsi-fungsi kendala persamaan. Vektor optimum

x yang menjadi solusi dari masalah dinyatakan dengan x* dan nilai optimumnya adalah f

 

x* . Jika tidak ada kendala maka masalah dinamakan masalah minimasi takberkendala.

(Snyman 2005)

Himpunan Konveks

Definisi 2.2

Sebuah himpunan X adalah konveks jika untuk semua x x1, 2X memenuhi





2 1

1

xx   x X untuk semua 0  1. (2.2) Jika kondisi di atas tidak terpenuhi maka himpuna X tidak konveks. (Snyman 2005)

Fungsi Konveks

Definisi 2.3

Fungsi f didefinisikan pada himpunan X dikatakan konveks jika untuk setiap 1 2

,

x x X dan setiap , 0   1 memenuhi







1 2



 

1





 

2

1 1

f x   x  f x   f x . (2.3) Jika untuk setiap , 0  1 dan 1 2

x x memenuhi







1 2



 

1





 

2

1 1

3

Norm Euclidean

Definisi 2.4

Untuk vektor x_n1, norm Euclidean dari x didefinisikan 

1 2

2 T

1

n i i

x 

 

_{ }  





x x x dimana  n1

x (2.5)



1 2

2 T

1

n i i

x 

 

_{ }  





x x x dimana x n1 (2.6)

(Meyer 2000).

Vektor Gradien

Definisi 2.5

Jika fungsi F memiliki turunan parsial dengan orde rendah (yang biasanya diasumsikan dalam pembentuk algoritme ini), maka pada suatu titik tertentu x, sebuah vektor gradient G

   

x  Gi n didefinisikan dengan komponen

 

 

i i

i F G G

x



 



x x ,



1 i n



(2.7) (Cheney dan Kincaid 2008).

Minimum Global dan Minimum Lokal

Definisi 2.6

1. Titik x* adalah minimum global dari f pada X jika

 

 

f x  f x* (2.8) untuk setiap xX  n .

2. Titik �∗ adalah minimum lokal jika terdapat � > 0 sehingga

 

 

* *

untuk setiap { | }

f x  f x x xx  (2.9)

dengan ‖. ‖ menyatakan norm Euclid. (Snyman 2005)

Himpunan Terbatas

Definisi 2.8

Diberikan X sub himpunan tak kosong dari

a. Himpunan X dikatakan terbatas di atas jika ada sejumlah u sehingga xu untuk semua xX . Setiap u dikatakan batas atas X .

b. Himpunan X dikatakan terbatas di bawah jika ada sejumlah w sehingga wx untuk semua xX . Setiap w dikatakan batas bawah X .

4

Kekontinuan Fungsi Lipschitz

Definisi 2.9

: n m

F D adalah kontinu Holder pada D jika ada konstanta  0

dan p



0,1



sehingga untuk semua x y, D,

 

 

p

F y F x  yx . (2.10)

Jika p1, maka F disebut kontnu Lipschitz pada D dan  adalah konstanta Lipschitz. (Bazaraa et al. 2006)

Konvergen Global

Definisi 2.10

Suatu model algoritme dikatakan konvergen, jika akumulasi titik-titik dari setiap barisan iterasi { }x_n dikonstruksi oleh algoritme dalam P yang merupakan himpunan solusi optimal (Argyros 2008).

Limit Inferior

Definisi 2.11

Limit inferior dari sebuah barisan { }x_n yang dinotasikan sebagai berikut

liminf n

n x (2.11)

adalah definisi dari supremum semua bilangan  dengan mengikuti sifat: Ada bilangan bulat N sedemikian sehingga  x_n untuk semua nN. (Thomson et al. 2007)

Iterasi dan Running Time

Definisi 2.11 (Iterasi)

Iterasi adalah sifat tertentu dari algoritme atau program komputer di mana satu urutan atau lebih dari langkah algoritme yang dilakukan pada loop program (Chapman 2008).

Definisi 2.12 (Running Time)

Running time dari suatu algoritme didefenisikan sebagai ukuran operasi primitive atau tahapan proses yang dieksekusi (Cormen et al. 1990).

3

METODE

5 diusulkan. Terakhir pada tahap ketiga mengimplementasikan metode-metode yang diusulkan ke dalam bahasa pemograman. Kemudian membandingkan hasil numerik dari metode yang diusulkan dengan metode konjugat gradien hibrid FR-PRP (NH1), HS-DY (NH3) dan LS-CD (NH3) dengan melihat iterasi dan running time.

4

HASIL DAN PEMBAHASAN

Metode Konjugat Gradien

Pada pendahuluan telah dijelaskan sebelumnya bahwa metode konjugat gradien adalah metode gradien yang bersifat iteratif untuk menyelesaikan masalah optimasi tak berkendala, baik untuk untuk memecahkan sistem persamaan linear dan masalah optimasi tak linear dengan skala besar. Pada penelitian ini di fokuskan pada menyelesaikan masalah optimasi tak linear tak berkendala.

Diberikan masalah optimasi tak berkendala

min ( ), f x x  n (4.1) dimana f : n adalah fungsi objektif yang terdiferensial kontinu. Diberikan

n R 

0

x yang menjadi dugaan awal solusi atau biasanya disebut titik awal pada masalah (4.1). Metode konjugat gradien tak linear dibentuk dengan sebuah barisan

{ }xk , menggunakan bentuk iteratif

1 , 0,1, 2,...,

k  k k k k 

x x d (4.2) dimana{ }xk adalah titik iterasi sekarang, k 0 adalah ukuran langkah yang ditentukan oleh pencarian garis (line search) baik pencarian garis eksak atau pencarian garis tidak eksak dan d_k adalah garis berarah dari fungsi f pada titik x_k yang didefinisikan oleh

1

jika 0 jika 0

k k

k k k

k k  _     _{  }  g d

g d (4.3) dimana g_k g x( _k) f(x_k)adalah vektor gradien dari f pada x_k dan _k adalah sebuah parameter yang diketehui sebagai koefisien konjugat gradien. Beberapa konjugat gradien yang terkenal yaitu metode FR, metode PRP, metode HS, metode DY, metode CD dan metode LS. Selain itu, ada juga konjugat gradien yang merupakan variasi dari metode PRP yaitu metode WYL (Wei et al. 2006). Koefisien konjugat gradien _� untuk metode konjugat gradien yang telah disebutkan adalah

2 2 1 k FR k k    g g 1 2 1 T PRP k k k

k

 



 g y

g

1

1

T HS k k

k T

k k

 



 g y

d y 2 1 k DY k T k k    g d y 2 1 1 k CD k T k k   

  g

d g

1

1 1

T LS k k

k T

k k

 

 

  g y

d g

1

1 1

2

T k

k k k

k WYL k k               g

g g g

g

g

dimana yk1gk gk1 dan  adalah vektor norm Euclidean. Perbedaan

6

Umumnya, menganalisis kekonvergenan dan implementsi metode konjugat gradien sering menggunakan pencarian garis tidak eksak yaitu kondisi Wolfe atau kondisi kuat Wolfe yang terdiri sufficient decrease dan curvature condition. Pencarian garis kondisi Wolfe untuk menentukan _� adalah sebagai berikut

( ) ( ) ,

( ) ,

T k k k k k k k

T T

k k k k k k

f  f 

 

   

 _{ }



x d x g d

d g x d d g (4.4)

dengan 0 1

2



  dan   1. Pencarian garis kondisi kuat Wolfe untuk menentukan _k adalah

( ) ( ) ,

( ) ,

T k k k k k k k

T T

k k k k k k

f  f 

           

x d x g d

d g x d d g (4.5)

dengan 0 1 2



  dan   1.

Pada penelitian ini digunakan pencarian garis kondisi Wolfe untuk mencari ukuran langkah.

Lemma 4.1 (Kondisi descent)

Misalkan f adalah fungsi monoton dan ukuran langkah  0. Jika x* adalah solusi optimal, maka ada parameter _k*(0,1) sehingga, untuk semua

*

[0, )

k k

   , pencarian arah d_k didefinisikan oleh persamaan (4.3) memenuhi kondisi descent

0 T k k 

g d (4.6)

(Pillo dan Giannessi 1999).

Metode Konjugat Gradien Hibrid Baru Zhou dan Zhang

Zhang dan Zhou (2007) mengusulkan metode konjugat gradien hibrid baru yang disebut metode NH1 dan metode NH2 dengan menggunakan ide dasar dari metode H1 yaitu metode hibrid PRP-FR (Touati-Ahmed dan Storey 1990)

H1

max{0,min{ PRP, FR}}

k k k

    (4.7)

dan metode H2 yaitu metode hibrid HS-DY (Dai dan Yuan 2001)

H2

max{0,min{ HS, DY}}

k k k

    . (4.8)

Metode FR, DY dan CD merupakan metode descent tetapi sifat descent dalam metode-metode ini tergantung pada pencarian garis seperti pencarian garis kuat Wolfe (4.5). Zhang et al. (2006) dan Zhang (2006) melakukan sedikit modifikasi pada metode FR yang disebut metode MFR, yaitu:

1 1

1 2 1

1 1

MFR: = 1

T T

FR k k FR k k FR

k k k k T k k k k k

k k _k

                       

g d g d

d g d g g d

d g g

(4.9) Zhang (2006) juga mengusulkan satu modifikasi metode DY yang disebut metode MDY, yaitu:

1 1

1 2 1

1 1

MDY: = 1

T T

DY k k DY k k DY

k k k k T k k k k k

k k k

                 _ _   

g d g d

d g d g g d

7 Metode MFR dan metode MDY memenuhi g dTk k   gk 2 yang mana tidak tergantung pada pencarian garis yang digunakan.

Metode NH1 dan metode NH2 diperoleh dengan mengantikan FR k

 dalam persamaan (4.9) dan _kDY dalam persamaan (4.10) dengan _kH1 dan _kH2 yaitu:

H1 1 H1

1 2

NH1: = 1

T k k

k k k k k

k         _ _    g d

d g d

g

(4.11)

H2 1 H2

1 2

NH2: = 1

T k k

k k k k k

k         _ _    g d

d g d

g

(4.12) Dua metode hibrid baru di atas memenuhi T 2

k k   k

g d g , yang menunjukkan bahwa metode-metode ini adalah descent dan tidak bergantung pada pencarian garis yang digunakan. Zhang dan Zhou (2007) telah membuktikan kekonvergenan global dari dua metode NH1 dan NH2 dan telah menunjukkan efesiensi metode-metode ini dalam hasil numerik.

Metode Konjugat Gradien Hibrid Baru Zhou, Zhu, Fan dan Qing

Zhou et al. (2011) menggunakan ide yang sama dengan metode konjugat gradien hibrid baru Zhang-Zhou tetapi didasarkan pada metode CD dan mengusulkan

a. Metode hibrid LS-CD yang disebut dengan metode H3 yaitu

H3

max{0,min{ LS, CD}}

k k k

    (4.13) b. Metode CD yang dimodifikasi yang disebut metode MCD, yaitu

1 1

1 2 1

1 1

MCD: = 1

T T

CD k k CD k k CD

k k k k T k k k k k

k k _k

g                        

g d g d

d g d g d

d g g

(4.14) c. Metode hibrid LS-CD baru dan disebut metode NH3 yaitu dengan mengantikan

CD k

 pada (4.14) denganH3,

H3 1 H3

1 2

NH3: = 1

T k k

k k k k k

k         _ _    g d

d g d

g

. (4.15) Metode MCD dan metode NH3 di atas memenuhi sufficient descent, g dT_{k k}   g_k 2. Zhou et al. (2011) telah membuktikan metode H3, metode MCD dan metode NH3 memenuhi kekonvergenan global dan telah menunjukkan hasil numerik dari metode-metode ini cukup efisien dalam meyelesaikan masalah optimasi tanpa kendala.

Metode Konjugat Gradien Hibrid Baru NH6 dan NH7

8

H6

max{0,min{ WYL, FR}}

k k k

    (4.16)

H7

max{0,min{ PRP, CD}}

k k k

    . (4.17) Setelah itu menggantikan _kFRdan _kCD pada metode MFR (4.9) dan metode MCD (4.14) dengan H6

k

 dan H7

k

 dan mengusulkan dua metode hibrid baru WYL-FR dan PRP-CD yang disebut metode NH6 dan metode NH7 yaitu:

H6 1 H6

1 2

NH6: = 1

T k k

k k k k k

k

  



 

  _ _ 

 

g d

d g d

g

(4.18)

H7 1 H7

1 2

NH7: = 1

T k k

k k k k k

k

  



 

  _ _ 

 

g d

d g d

g

(4.19) Metode MFR dan Metode MCD memenuhi sufficient descent, g dT_{k k}   g_k 2 yang telah dibuktikan oleh Zhang-Zhou (2008) dan Zhou et al. (2011) sedangkan metode NH6 dan metode NH7 yang diusulkan dalam penelitian ini akan dilakukan pengujian keseuaian konsidi sufficient descent pada sub-sub bab selanjutnya.

Algortma 4.1 NH6

Step 0. Pilih titik awal ₀ , 0 1, 0 1 dan 1 2

n

R    

      

x . Tetapkan

0   k,

d g k 0. Step 1. Jika gk , berhenti.

Step 2. Tentukan ukuran langkah _k dengan aturan pencarian garis Wolfe pada persamaan (4.4).

Step 3. Misalkan x_k1 x_k_kd_k. Jika g_k1  maka berhenti.

Step 4. Tentukan pencarian arah d_k1 dengan menggunakan rumus pada persamaan (4.18).

Step 5. Beri nilai k k 1, dan lanjutkan ke Step 2.

Algortma 4.2 NH7

Step 0. Pilih titik awal. Tetapkand₀  g_k, k 0. ₀ , 0 1, 0 1 2

n

R  

    

x

dan   1

Step 1. Jika gk , berhenti.

Step 2. Tentukan ukuran langkah _k dengan aturan pencarian garis Wolfe pada persamaan (4.4).

Step 3. Misalkan x_k1 x_k_kd_k. Jika g_k1  maka berhenti.

Step 4. Tentukan pencarian arah d_k1 dengan menggunakan rumus pada persamaan (4.19).

9

Analisis Kekonvergen Global Metode NH6 dan NH7

Asumsi A

1. Himpunan level   {x Rn | ( )f x  f(x₀)} terbatas.

2. Dalam beberapa persekitaran N yang terkandung , f terdiferensial kontinu dan gradien gkontinu Lipschitz, terdapat konstanta L0, sehingga

( ) ( ) , ,

g x g y L xy x yN . (4.20) (Nocedal dan Wright 1999)

Dapat dilihat bahwa barisan { (f xk)}menurun maka jelaslah bahwa barisan { }xk pada algoritme 1 dan algoritme 2 yang terkandung dalam .

Dibawah asumsi A pada fungsi f maka digunakan lemma kondisi Zountendijk untuk membuktikan kekonvergenan global metode konjugat gradien tak linear, yaitu:

Lemma 4.1

Misalkan asumsi A terpenuhi. Diberikan { }xk yang dibentuk oleh persamaan (4.1) dan dkadalah arah descent pada persamaan (4.3). Jika k ditentukan dengan pencarian garis Wolfe (4.4) maka diperoleh





2

2 0

T k k k _k





 



g d

d (4.21)

Bukti

Dari kondisi Wolfe pada persamaan (4.4)

( )

T T

k k k k k k

d g d g x  d

dimana g_k g x( _k) maka

( ) ( )

T T

k k k k k k

d g x d g x  d (4.22)





( ) ( ) ( )

T T T T

k k k k k k k k k k

d g x d g x d g x  d d g x









1 T ( ) T( ( ))

k k dk g k k k k

  d g x  x  d g x



_k _{k k}



( _k) _k

 g x d g x d . (4.23) Digunakan kontinu Lipschitz pada persamaan (4.23), maka diperoleh



 1



d g xT_k ( _k)L x_k _kd_k x_k d_k

k k k L 

 d d

k k k L

 d d

2

k k L

 d (4.24)





2

1 T_k ( _k) L _{k k}

  d g x   d





2

1 T_k ( _k)

k k

L 







d g x

d .

10





2 1 T k k k k L 

   d g

d

. (4.25) Digunakan persamaan pencarian garis kondisi Wolfe (4.4)





 

T

k k k k k k k

f x  d  f x  g d

 





T

k k k k k k k

f x  f x  d   g d . (4.26) Disubstitusi persamaan (4.25) ke persamaan (4.26), maka diperoleh

 









2

1

, T

k k T

k k k k k k

k f f L                d g

x x d g d

d

(4.27) sehingga dapat disimpulkan

 









2

1 2

T k k

k k k k

k f x  f x  d C g d

d

(4.28)

dimana C₁ (1 ) 0

L

 

  . Sekarang,

untuk k 0

 









2 0 0

0 0 0 0 1 2

0

T f x  f x  d C g d

d . Karena x₁ x₀₀d₀, maka

 

 





2 0 0 0 1 0 1 2 T f x  f x C g d

d . Untuk k1

 

 





2 1 1

1 2 1 2

1

T f x  f x C g d

d . Untuk k 2

 

 





2 2 2

2 3 1 2

2

T f x  f x C g d

d

.

Untuk k  n 1





 





2

1 1

1 1 2

1 T n n n n n

f _ f C  



  g d

x x

d

.

Dijumlahkan semua pertidaksamaan di atas dan diperoleh

 

 





2 1

0 1 2

0 T n k k k k n

f f C





 



g d

x x

d

11

 





2 *

0 1 2

0 k T k k k

f f C





 



g d

x

d (4.30)

dimana

*

lim ( _k) k

f f



 x . (4.31)

Jadi diperoleh bahwa





2 2 0 T k k k _k    



g d

d

. ∎

Lemma 4.2

Misalkan x_k1 x_k_kd_k diberikan oleh algoritme 4.1 maka d_k yang diberikan oleh persamaan (4.18) memenuhi kondisi sufficient descent

2

, 0

T

k k   k  k

d g g (4.32)

Bukti

Misalkan _k _k*.Untuk d₀  g₀ maka diperoleh

2

0 0 0 0 0

T   T  

g d g g g (4.33)

yang berlaku untuk k 0. Untuk k 1, diperoleh

* 1

k   k k k

d g d . (4.34)

Sekarang untuk _k _k*, diperoleh

* 1 *

1 2

1

T k k

k k k k k

k         _ _    g d

d g d

g

* * 1

1 1 2

T k k

k k k k

k                g d d g g

. (4.35) Kedua ruas dikalikan dengan gT_k , diperoleh

* * 1

1 1 2

T

T T k k T

k k k k k k k k

k          _ _   g d

g d g d g g

g

* 2 * 1 2

1 2

T

T T k k

k k k k k k k k

k

  



   g d

g d g d g g

g

(4.36)

2

T

k k k

d g   g . (4.37) Oleh karena itu, persamaan (4.32) dipenuhi untuk semua k1. ∎

Lemma 4.3

Misalkan x_k1x_k _kd_k diberikan algoritme 4.2 maka d_k yang diberikan oleh persamaan (4.19) memenuhi kondisi sufficient descent

2

, 0

T

k k   k  k

d g g (4.38)

Bukti

Misalkan _k _k**. Untuk d₀  g₀ maka diperoleh

2

0 0 0 0 0

T _{ } T _{ }

12

yang berlaku untuk k 0. Untuk k1, diperoleh

** 1

k   k k k

d g d (4.40)

Sekarang untuk _kH7 _k**, diperoleh

** 1 **

1 2

1

T k k

k k k k k

k         _ _    g d

d g d

g

** ** 1

1 1 2

T k k

k k k k

k          _ _   g d d g g

. (4.41) Kedua ruas dikalikan dengan gT_k, diperoleh

** ** 1

1 1 2

T

T T k k T

k k k k k k k k

k                g d

g d g d g g

g

2

** ** 1 2

1 2

T

T T k k

k k k k k k k k

k d

  



   g d

g d g g g

g

(4.42)

2

T

k k k

d g   g . (4.43) Oleh karena itu, persamaan (4.38) dipenuhi untuk semua k 1. ∎

Teorema 4.1 (Kekonvergenan Global Metode NH6)

Misalkan asumsi A terpenuhi. Diberikan barisan { }x_k yang dihasilkan oleh metode NH6 pada algoritme 4.1. Jika _kditentukan oleh pencarian garis Wolfe dan

k

d memenuhi persamaan (4.18), maka diperoleh liminf k 0

x g  (4.44)

Bukti:

Pembuktian dilakukan dengan pembuktian kontradiksi yaitu persamaan (4.44) salah maka ada sebuah konstanta  0sehingga

g_k   , k 0. (4.45) Dari persamaan (4.18),

H6 1

k  hk kk k

d g d (4.46)

dengan H6 1

2 1 T k k k k k h   g d 

g

dan diperoleh _kH6gT_kd_k1h_k g_k 2  g_k 2. Kedua ruas persamaan (4.46) dikuadratkan, diperoleh

2

H6 2

2

1

k  k k hk k

d d g

 

_H6 2 2 _{H6 2} 2

1 2 1

T

k k hk k k k hk k

 _  _

 d  d g  g

 

_H6 2 2



2 2



₂ 2

1 2

k k h hk k k k hk k

 _

 d  g  g  g

 

_H6 2 2 ₂ 2 2 ₂ 2

1 2 2

k k hk k hk k hk k

 _

 d  g  g  g

 

_H6 2 2 2 ₂ 2

1 2

k k hk k hk k

 _

13 Digunakan persamaan (4.32), maka

 

2

2 _H6 2 _{T 2} 2

1 2

k  k k  hk k k hk k

d d d g g . (4.47) Dilihat bahwa













H6

max 0, min WYL, FR max 0, WYL FR , 0

k k k k k k

         . (4.48)

Dibagi kedua ruas pada persamaan (4.47) dengan



g dTk k



2 dan digunakan persamaan (4.48), (4.32) serta definisi _kFR, maka diperoleh





2 2

4 2

k k

T k _{k k}



d d

g g d





 









2 2 ₂ 2

2 ₁

H6

2 2 2

2

k k k k k

k T

T T T

k k

k k k k k k

h h

 

  

d d g

g d

g d g d g d

 









2 2 2

2 ₁

2 2

2

k k k

FR k

k _T T _T

k k

k k k k

h h

 

 d   g

g d

g d g d

2

2 2 ₂

1

2 4 2 2

1

2

k k k k

k k k k

h h      _ _     g d

g g g g





2 1 2 4 2 1 1

2 1 1

k k k k k h h  

 d    

g g





2 2

1

4 2 2

1

1 1

k k

k k k

h 





 d  

g g g

2 1 4 2 1 1 k k k  

 d 

g g 2 1 2 1 1 2 1 ( Tk )

k k k     

g d g

d

. (4.49) Akan diselesaikan persamaan (4.29) sebagai berikut:

Dari persamaan (4.3), untuk k 0, d₀  g₀ dan digunakan persamaan (4.32), diperoleh

2

0 0 0 0 0

T   T  

g d g g g . (4.50)

Dari persamaan (4.49) dan (4.50), maka untuk k 1





2 2

1 0

2

0 0 1

1 1

2 2

( )

1

T  T 

d d

d g d g

14

1 2 0

1

k _i





g , untuk k 2





2 2

2 1

2

1 1 ₂

2 2

2 2

( )

1

T  T 

d d

d g d g

g 2 2 2 0 2 1 1 1 1   

g g g

2 2 0

1

k _i





g ,

untuk k n





2

2 2 2

1 1 2 1 ( ) 1 n n T

n n _n

n n T      g d d g

g d d

1 2 2 0 2 2 2

1 1 1

1

n

    

g g g g

2 0

1

n

k _k





g , sehingga diperoleh





2 2 2 0 1 n k n n n T k 



d g g d

. (4.51)

Dari persamaan (4.45), diperoleh

2 2 0 1 1 n k k n    



g (4.52) 2 2 0 1 1 n k k n    



g





2 2 2 1 n T n n n    d g d





2

2 2 1 n n n T n    g d d





2

2 2

0 0 1

n n

n n

n T

k k k



 







g d



d





2

2 2 0 0 1 1 n n n T

k k k



 

 







g d



d

.

15 4 2 2 0 0 1 1 k

i _k k k

        





g d (4.53) yang kontradiksi dengan persamaan (4.21). ∎

Teorema 4.2 (Kekonvergenan Global Metode NH7)

Misalkan asumsi A terpenuhi. Diberikan barisan { }x_k yang dihasilkan oleh metode NH7 pada algoritme 4.2 dan d_k memenuhi persamaan (4.19) dengan _k memenuhi pencarian garis Wolfe, maka diperoleh

liminf _k 0

x g  (4.54)

Bukti:

Misalkan dengan pembuktian kontradiksi yaitu persamaan (4.54) tidak terpenuhi maka ada sebuah konstanta  0 sehingga

, 0

k    k

g . (4.55) Dari persamaan (4.19), diperoleh

H7 1

k  hk k k k

d g d (4.56)

dimana H7 1

2 1 T k k k k k h   g d 

g dan

2 2

H7 1

T

k k k hk k k

 g d _  g  g .

Dari persamaan (4.56) dan persaman (4.38), diperoleh

2 H7

1

2

k  k k hk k

d d g

 

2

2 H7 2 H7 2 2

1 2 1

T

k  k k  hkk k k  hk k

d d d g g

 

2





2 _H7 2 2 2 ₂ 2

1 2

k  k k  h hk k k  k  hk k

d d g g g

 

2

2 H7 2 2 2 2 2 2

1 2 2

k  k k  hk k  hk k  hk k

d d g g g

 

2

2 H7 2 2 2 2

1 2

k  k k  hk k  hk k

d d g g . (4.57)

Digunakan persamaan (4.38)

 

2

2 _H7 2 _{T 2} 2

1 2

k  k k  hk k k hk k

d d d g g . (4.58)

Dilihat bahwa

H5

0k  kCD ,  k 0. (4.59)

Kedua ruas pada persamaan (4.58) dibagi dengan



g dTk k



2 . Setelah itu, digunakan persamaan (4.59), (4.38) dan definisi _kCD, maka diperoleh





 









2 2 2 ₂ 2

2 ₁

H7

4 2 2 2

2

k k k k k k

k T

T T T

k k

k k k k k k k

h h

 

   

d d d g

g d

g g d g d g d

(4.60)

 









2 ₂ 2

2 ₁

2 2

2

k k k

CD k

k _T T _T

k k

k k k k

h h

 

 d   g

g d

g d g d









2 2 2 2

2

1

2 2 2

1

2

k k k

k k

T

T T

k _{k k} k k _{k k} h h     _{ }     d g g

16

2

2 2 ₂

1

2 4 2 2

1

2

k k k k

k k k k

h h              g d

g g g g





2 1 2 4 2 1 1

2 1 1

k k k k k h h  

 d    

g g





2 2

1

4 2 2

1

1 ₁

k k

k k k

h 





 d  

g g g

2 1 4 2 1 1 k k k  

 d 

g g

. (4.61)

Akan diselesaikan persamaan (4.61) sebagai berikut:

Dari persamaan (4.61) di atas dan persamaan (4.3), untuk k 0maka d0  g0

dan diperoleh

2

0 0 0 0 0

T   T  

g d g g g , (4.62)

untuk k1

1 0

2 2

4 4

1 0 1

2

1

 

d d

g g g

1 2 2 0 1 1   g g 1 2 0 1

k _i





g , untuk k 2

2 1

2 2

4 4

2 1 2

2

1

 

d d

g g g

2 2 2 0 2 1 1 1 1   

g g g

2 2 0

1

k _i





g , untuk k n





2

2 2 2

1 1 2 1 ( ) 1 n n T

n n _n

n n T      g d d g

g d d

1 2 2 0 2 2 2

1 1 1

1

n

    

g g g g

2 0

1

n

k _k





17 sehingga diperoleh,





2 2 2 0 1 n k n n n T k 



d g g d

. (4.63)

Dari persamaan (4.55), diperoleh

2 2 0 1 1 n k k n    



g (4.64) 2 2 0 1 1 n k k n    



g





2 2 2 1 n T n n n    d g d





2

2 2 1 n n n T n    g d d





2

2 2

0 0 1

n n

n n

n T

k k k



 

 



g d



d





2

2 2 0 0 1 1 n n n T

k k k



 

 







g d



d

.

Pertidaksamaan terakhir di atas dapat disimpulkan bahwa

4 0 2 2 0 1 1 k

i _k k k

        



g



d

(4.65) yang kontradiksi dengan persamaan (4.21). ∎

Hasil Numerik

Pada sub-bab ini dilakukan perbandingan hasil numerik dari metode-metode yang diusulkan dalam penelitian ini yaitu NH6 (algoritme 4.1) dan NH7 (algoritme 4.2) dengan metode-metode yang telah diusulkan pada penelitian-penelitian sebelumnya yaitu NH1, NH2 dan NH3. Algoritme setiap metode ditulis dalam bahasa pemograman. Ukuran langkah _k 0 untuk metode-metode ini menggunakan pencarian garis kondisi Wolfe dengan parameter  0.3 dan

0.8.

[image:30.595.111.471.98.798.2]

18

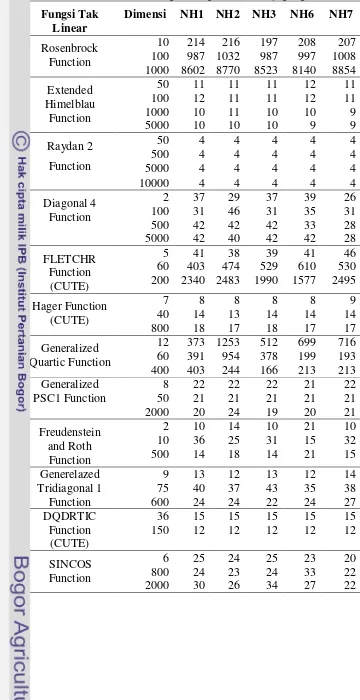
Tabel 1 Jumlah iterasi dari masing-masing metode konjugat gradien

No. Fungsi Tak

Linear

Dimensi NH1 NH2 NH3 NH6 NH7

1 Rosenbrock Function

10 214 216 197 208 207 100 987 1032 987 997 1008 1000 8602 8770 8523 8140 8854 2 Extended

Himelblau Function

50 11 11 11 12 11

100 12 11 11 12 11

1000 10 11 10 10 9

5000 10 10 10 9 9

3 Raydan 2 Function

50 4 4 4 4 4

500 4 4 4 4 4

5000 4 4 4 4 4

10000 4 4 4 4 4

4 Diagonal 4 Function

2 37 29 37 39 26

100 31 46 31 35 31

500 42 42 42 33 28

5000 42 40 42 42 28

5 FLETCHR

Function (CUTE)

5 41 38 39 41 46

60 403 474 529 610 530 200 2340 2483 1990 1577 2495 6 Hager Function

(CUTE)

7 8 8 8 8 9

40 14 13 14 14 14

800 18 17 18 17 17

7 Generalized Quartic Function

12 373 1253 512 699 716 60 391 954 378 199 193 400 403 244 166 213 213 8

Generalized PSC1 Function

8 22 22 22 21 22

50 21 21 21 21 21

2000 20 24 19 20 21

9 Freudenstein and Roth Function

2 10 14 10 21 10

10 36 25 31 15 32

500 14 18 14 21 15

10

Generelazed Tridiagonal 1

Function

9 13 12 13 12 14

75 40 37 43 35 38

600 24 24 22 24 27

11

DQDRTIC Function

(CUTE)

36 15 15 15 15 15

150 12 12 12 12 12

12 SINCOS

Function

6 25 24 25 23 20

800 24 23 24 33 22

[image:31.595.124.545.104.730.2]

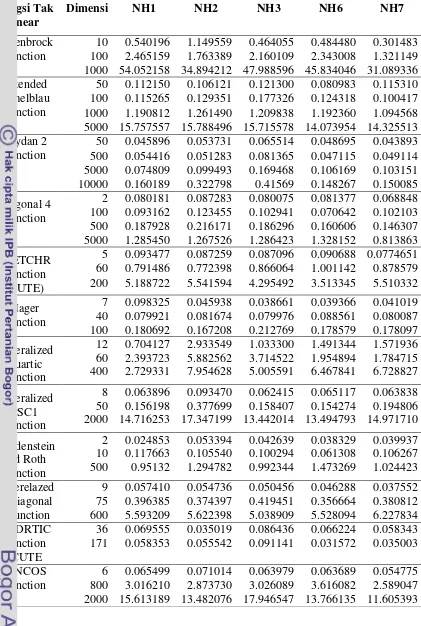
19 Tabel 2 Hasil running time dari masing-masing metode konjugat gradien

No. Fungsi Tak linear

Dimensi NH1 NH2 NH3 NH6 NH7

1

Rosenbrock Function

10 0.540196 1.149559 0.464055 0.484480 0.301483 100 2.465159 1.763389 2.160109 2.343008 1.321149 1000 54.052158 34.894212 47.988596 45.834046 31.089336 2

Extended Himelblau

Function

50 0.112150 0.106121 0.121300 0.080983 0.115310 100 0.115265 0.129351 0.177326 0.124318 0.100417 1000 1.190812 1.261490 1.209838 1.192360 1.094568 5000 15.757557 15.788496 15.715578 14.073954 14.325513 3

Raydan 2 Function

50 0.045896 0.053731 0.065514 0.048695 0.043893 500 0.054416 0.051283 0.081365 0.047115 0.049114 5000 0.074809 0.099493 0.169468 0.106169 0.103151 10000 0.160189 0.322798 0.41569 0.148267 0.150085 4 Diagonal 4

Function

2 0.080181 0.087283 0.080075 0.081377 0.068848 100 0.093162 0.123455 0.102941 0.070642 0.102103 500 0.187928 0.216171 0.186296 0.160606 0.146307 5000 1.285450 1.267526 1.286423 1.328152 0.813863 5 FLETCHR

Function (CUTE)

5 0.093477 0.087259 0.087096 0.090688 0.0774651 60 0.791486 0.772398 0.866064 1.001142 0.878579 200 5.188722 5.541594 4.295492 3.513345 5.510332

6 Hager

Function

7 0.098325 0.045938 0.038661 0.039366 0.041019 40 0.079921 0.081674 0.079976 0.088561 0.080087 100 0.180692 0.167208 0.212769 0.178579 0.178097 7 Generalized

Quartic Function

12 0.704127 2.933549 1.033300 1.491344 1.571936 60 2.393723 5.882562 3.714522 1.954894 1.784715 400 2.729331 7.954628 5.005591 6.467841 6.728827 8 Generalized

PSC1 Function

8 0.063896 0.093470 0.062415 0.065117 0.063838 50 0.156198 0.377699 0.158407 0.154274 0.194806 2000 14.716253 17.347199 13.442014 13.494793 14.971710 9 Freudenstein

and Roth Function

2 0.024853 0.053394 0.042639 0.038329 0.039937 10 0.117663 0.105540 0.100294 0.061308 0.106267 500 0.95132 1.294782 0.992344 1.473269 1.024423 10

Generelazed Tridiagonal

1 Function

9 0.057410 0.054736 0.050456 0.046288 0.037552 75 0.396385 0.374397 0.419451 0.356664 0.380812 600 5.593209 5.622398 5.038909 5.528094 6.227834 11

DQDRTIC Function

(CUTE

36 0.069555 0.035019 0.086436 0.066224 0.058343 171 0.058353 0.055542 0.091141 0.031572 0.035003

12

SINCOS Function

20

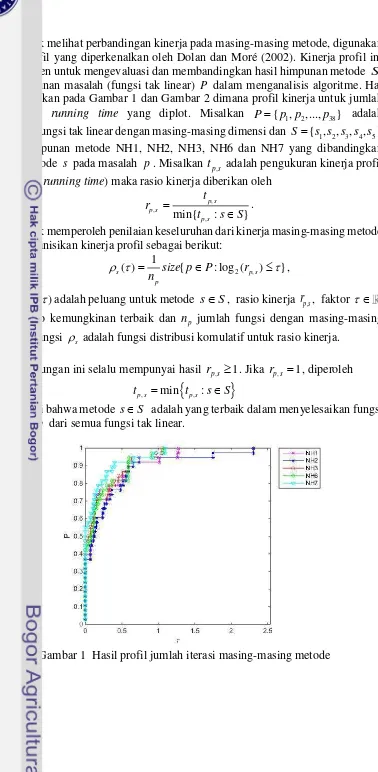
Untuk melihat perbandingan kinerja pada masing-masing metode, digunakan kinerja profil yang diperkenalkan oleh Dolan dan Moré (2002). Kinerja profil ini sangat efisien untuk mengevaluasi dan membandingkan hasil himpunan metode S pada himpunan masalah (fungsi tak linear) P dalam menganalisis algoritme. Hal ini ditunjukkan pada Gambar 1 dan Gambar 2 dimana profil kinerja untuk jumlah iterasi dan running time yang diplot. Misalkan P{p p₁, ₂,...,p₃₈} adalah himpunan fungsi tak linear dengan masing-masing dimensi dan S { , , , , }s₁ s s s s_{2 3 4 5} adalah himpunan metode NH1, NH2, NH3, NH6 dan NH7 yang dibandingkan kinerja metode s pada masalah p. Misalkan t_{p s,} adalah pengukuran kinerja profil (iterasi dan running time) maka rasio kinerja diberikan oleh

, ,

,

min{ : }

p s p s

p s t r

t s S



 .

Untuk memperoleh penilaian keseluruhan dari kinerja masing-masing metode maka didefinisikan kinerja profil sebagai berikut:

2 ,

1

( ) { : log ( ) }

s p s

p

size p P r n

     ,

dimana  _s( )adalah peluang untuk metode sS, rasio kinerja

r

_{p s,} , faktor  adalah rasio kemungkinan terbaik dan n_p jumlah fungsi dengan masing-masing dimensi. Fungsi _s adalah fungsi distribusi komulatif untuk rasio kinerja.

Catatan:

Pada perhitungan ini selalu mempunyai hasil r_{p s,} 1. Jika r_{p s,} 1, diperoleh





, min , :

p s p s t  t sS

[image:32.595.99.477.49.821.2]

yang berarti bahwa metode sS adalah yang terbaik dalam menyelesaikan fungsi tak linear p dari semua fungsi tak linear.

[image:33.595.187.455.95.296.2]

21

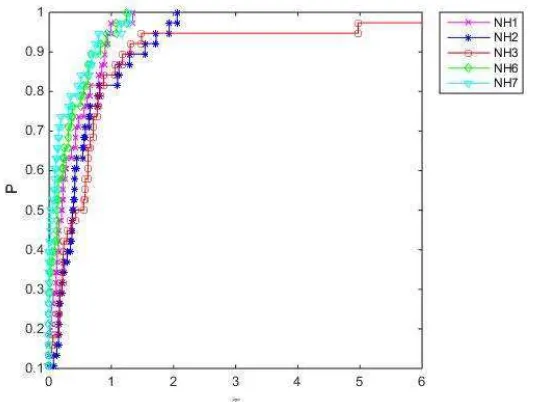
Gambar 2 Hasil profil running time masing-masing metode

Gambar 1 dan 2, masing-masing menunjukkan kinerja dari lima metode konjugat gradien hibrid baru NH1, NH2, NH3 NH6 dan NH7 yang relatif terhadap iterasi dan running time. Semua metode yang diusulkan berhasil menyelesaikan semua masalah optimasi fungsi tak linear tanpa kendala yang diberikan. Dari Gambar 1, dilihat metode NH6 dan NH7 kompetitif dengan metode NH1, NH2 dan NH3 dalam profil iterasi. Metode NH6, NH7 dan NH1 lebih baik dalam profil iterasi dari metode NH2 dan NH3. Sedangkan pada Gambar 2, dalam profil running time-nya metode NH6 dan NH7 yang diusulkan juga kompetitif dengan metode NH1, NH2 dan NH3. Metode NH6, NH7 dan NH1 lebih baik dalam profil running time-nya dari pada metode NH2 dan NH3. Dengan demikian, metode hibrid baru NH6 dan NH7 yang diusulkan kompetitif dan efisien serta menambah koleksi metode hibrid yang sudah tersedia dalam mencari solusi untuk masalah optimasi.

5

SIMPULAN

22

DAFTAR PUSTAKA

Argyros IK. 2008. Convergence and Applications of Newton-type Iterations. New York: Springer.

Andrei N. 2008. An Unconstrained Optimization Test Functions Collection. Advanced Modeling and Optimization. 10(1):147-161.

Bartle R, Sherbert DR. 2011. Introduction to Real Analysis. USA: Jhon Wiley & Sons Inc.

Bazara MS, Sherali HD, Shetty CM. 2006. Nonlinear Programming: Theory and Algorithms. USA: Wiley-Interescience.

Chapman SJ. 2008. Matlab Programming for Enggineers, 4th ed. Ontario (CA): Thomson Learning.

Cormen TH, Leiserson CE, Rivest RL, Stein C. 2009. Introduction to Algorithms: Third Edition. England: The MIT Press.

Dai YH, Yuan Y. 1999. A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property. SIAM Journal on Optimization. 10(1):177-82.doi:10.1137/S1052623497318992.

Dai YH, Yuan Y. 2001. An Efficient Hybrid Conjugate Gradient Method for Unconstrained Optimization. Annals of Operations Research. 103(1-4):33-47. Dolan ED, Moré JJ. 2002. Benchmarking optimization software with performance

profiles. Mathematical Programming. 912(2):201–213.doi: 10.1007/s1010-70100263.

Fletcher R. 1987. Practical Methods of Optimization, Unconstrained Optimization. New York: Wiley.

Fletcher R, Reeves C. 1964. Function Minimization by Conjugate Gradients. The Computer Journal. 7(2):149-154.doi:10.1093/comjnl/7.2.149.

Hestenes MR, Stiefel EL. 1952. Methods of Conjugate Gradients for Solving Linear Systems. Journal of Research of the National Bureau of Standards. 49(6): 409-432.

Liu YL, Storey CS. 1991. Efficient Generalized Conjugate Gradient Algorithms, Part 1: Theory. Journal of Optimization Theory and Applications. 69(1):129-137.doi:10.1007/BF00940464.

Meyer CD. 2000. Matrix Analysis and Apllied Linear Algeb