SKRIPSI
MIZWAR ARIFIN SRG
070803030
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2011
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MIZWAR ARIFIN SRG
070803030
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : PENGARUH PERUBAHAN PARAMETER
TERHADAP NILAI ERROR PADAMETODE RUNGE-KUTTA ORDO-2
Kategori : SKRIPSI
Nama : MIZWAR ARIFIN SRG
Nomor Induk Mahasiswa : 070803030
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juli 2011
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Marihat Situmorang, M.Kom. Prof. Dr. Tulus M.Si.
NIP. 19631214 198903 1 001 NIP : 19620901 198803 1 002
Diketahui/Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
Prof. Dr. Tulus M.Si.
PERNYATAAN
PENGARUH PERUBAHAN PARAMETER TERHADAP NILAI ERROR PADA METODE RUNGE-KUTTA ORDO-2
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2011
PENGHARGAAN
Puji dan syukur penulis panjatkan kehadirat Allah SWT Yang Maha Pemurah dan Maha Penyayang, dengan limpahan kurnia-Nya skripsi ini berhasil diselesaikan dalam waktu yang telah ditetapkan. Shalawat beriring salam kepada Baginda Rasulullah SAW, sebagai rahmatan lil’alamin.
Ucapan terima kasih penulis sampaikan kepada Bapak Prof. Dr. Tulus, M.Si. dan Bapak Drs. Marihat Situmorang, M. Kom. selaku pembimbing yang telah memberikan panduan dan penuh kepercayaan kepada penulis untuk menyempurnakan kajian ini. Bapak Drs. Sawaluddin, M. Kom, M.Si. dan Bapak Syahril Efendi, S.Si., M.IT. selaku penguji yang telah memberikan kritikan dan saran yang membangun dalam penyempurnaan skripsi ini. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara. Ketua dan Sekretaris Departemen Matematika Bapak Prof. Dr. Tulus, M.Si. dan Ibu Dra. Mardiningsih, M.Si.. Seluruh staf pengajar dan staf administrasi di lingkungan Departemen Matematika, serta seluruh civitas akademika di lingkungan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
Ucapan terima kasih juga ditujukan kepada kedua orang tua penulis tercinta, Ayahanda Sahman Siregar dan Ibunda Nur Ayumi Harahap yang telah memberikan banyak bantuan baik materi, moral maupun spiritual. Kepada saudara-saudara penulis, Adinda Nadhira Dwi Sabrina S dan Adinda Azzahra Tri Najla. Teristimewa untuk Affan H. Siregar, S.H dan Hardi Alamsyah Siregar, S.E sebagai sosok pengganti ayah dan juga tempat untuk berbagi cerita yang tak henti-hentinya memberikan bantuan, semangat dan motivasi kepada penulis dalam menyelesaikan skripsi ini dan menyelesaikan studi di Departemen Matematika FMIPA USU.
Tidak terlupakan, ucapan terima kasih kepada sahabat penulis, Sylvia Ria Berlian S, Trinita Hanum dan Yazeni Diana Putri, Ika Ayu Kartika Lbs, Mohammad Ramzi, Aghni Syahmarani, Muhammad Iqbal Pradipta serta rekan-rekan stambuk 2007 Departeman Matematika FMIPA USU, MW Family (Tracy Baumgardner, Károly Kajo Tóth, Pamela Karakula, John Patrick, Sharon Sullivan Delano dan lain-lain). Sahabat-sahabat di Ikatan Mahasiswa Matematika Muslim FMIPA USU, rekan-rekan di Himpunan Mahasiswa Matematika FMIPA USU dan kepada semua pihak yang telah memberikan bantuan dan dorongan yang tidak dapat disebutkan satu per satu.
PERNYATAAN
PENGARUH PERUBAHAN PARAMETER TERHADAP NILAI ERROR PADA METODE RUNGE-KUTTA ORDO-2
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2011
ABSTRAK
THE EFFECT OF CHANGING PARAMETERS ON THE VALUE OF ERROR IN THE RUNGE-KUTTA METHOD OF ORDER-2
ABSTRACT
DAFTAR ISI
2.2 Persamaan Diferensial Biasa Linier 10
2.2.1 Persamaan Diferensial Linier Tingkat Satu 10 2.2.2 Persamaan Diferensial Linier Tingakt Dua 13
2.2.2.1 Persamaan Diferensial Linier Tingkat Dua
Homogen 14
2.2.2.2 Persamaan Diferensial Linier Tingkat Dua
Tidak Homogen Dengan Koefisien Konstan 17 2.2.3 Persamaan Diferensial Linier Tingkat Tinggi 17 2.3 Masalah Nilai Awal (Initial Value Problem) 17
2.4 Kesalahan (Error) 19
2.6.4 Metode Runge-Kutta Ordo Tinggi 32
BAB 3 PEMBAHASAN 34
3.1 Penyelesaian Analitik Persamaan Diferensial Linier Tingkat
Dua 34
3.1.1 Persamaan Dengan Koefisien Konstan 34 3.1.1.1 H x( ) Adalah Polinomial Berderajat n
3.1.1.2 Jika H x( ) P x en( ) x 37 3.1.1.3 Jika H x( ) e x P xn( ) cos x Q xn( )sin x 41
3.1.1.4 Jika H x( ) Mcos x Nsin x 44
3.1.2 Persamaan Diferensial Linier Tingkat Dua dengan
Koefisien Peubah 47
3.1.2.1 Persamaan Tidak Memuat Varialbel y 47 3.1.2.2 Persamaan Diferensial Euler Tingkat Dua 51 3.2 Penyelesaian Numerik Persamaan Diferensial Linier
Tingkat Dua 55
3.3 Perbandingan Nilai Error Menggunakan Nilai Parameter
Yang Berbeda 61
3.4 Analisis Error 79
BAB 4 KESIMPULAN DAN SARAN 87
4.1 Kesimpulan 87
4.2 Saran 88
DAFTAR PUSTAKA 89
LAMPIRAN A 90
DAFTAR TABEL
Halaman
Tabel 3.1a Perbandingan Nilai Error Persamaan Contoh 1 Pada
Nilai Parameter 0.0 a1 0.4 62
Tabel 3.1b Perbandingan Nilai Error Persamaan Contoh 1 Pada
Nilai Parameter 0.5 a1 0.9 63
Tabel 3.2a Perbandingan Nilai Error Persamaan Contoh 2 Pada
Nilai Parameter 0.0 a1 0.4 65
Tabel 3.2b Perbandingan Nilai Error Persamaan Contoh 2 Pada
Nilai Parameter 0.5 a1 0.9 66
Tabel 3.3a Perbandingan Nilai Error Persamaan Contoh 3 Pada
Nilai Parameter 0.0 a1 0.4 68
Tabel 3.3b Perbandingan Nilai Error Persamaan Contoh 3 Pada
Nilai Parameter 0.5 a1 0.9 69
Tabel 3.4a Perbandingan Nilai Error Persamaan Contoh 4 Pada
Nilai Parameter 0.0 a1 0.4 71
Tabel 3.4b Perbandingan Nilai Error Persamaan Contoh 4 Pada
Nilai Parameter 0.5 a1 0.9 72
Tabel 3.5a Perbandingan Nilai Error Persamaan Contoh 5 Pada
Nilai Parameter 0.0 a1 0.4 74
Tabel 3.5b Perbandingan Nilai Error Persamaan Contoh 5 Pada
Nilai Parameter 0.5 a1 0.9 75
Tabel 3.6a Perbandingan Nilai Error Persamaan Contoh 6 Pada
Nilai Parameter 0.0 a1 0.4 77
Tabel 3.6b Perbandingan Nilai Error Persamaan Contoh 6 Pada
ABSTRAK
THE EFFECT OF CHANGING PARAMETERS ON THE VALUE OF ERROR IN THE RUNGE-KUTTA METHOD OF ORDER-2
ABSTRACT
BAB 1
PENDAHULUAN
1.1Latar Belakang
Persamaan diferensial berperan penting dalam kehidupan, sebab banyak permasalahan pada dunia nyata dapat dimodelkan dengan bentuk persamaan diferensial. Ada dua jenis persamaan diferensial yang kita kenal, yaitu persamaan diferensial biasa dan persamaan diferensial parsial. Yang akan dibahas dalam tulisan ini adalah persamaan diferensial biasa. Pesamaan diferensial biasa adalah sebuah persamaan yang melibatkan satu atau lebih turunan dari sebuah unknown function dan hanya memiliki satu variabel bebas. Solusi dari persamaan diferensial adalah fungsi spesifik yang memenuhi persamaan. Persamaan dibawah ini merupakan contoh dari persamaan diferensial biasa yang memiliki solusi. Pada persamaan dibawah ini, x merupkan variabel bebas dan y merupakan variabel tetap. y merupakan nama unknown function
dari variabel x.
Tidak semua permasalahan yang dimodelkan ke bentuk persamaan diferensial biasa dapat diselesaikan dengan mudah, bahkan terdapat suatu persamaan diferensial
3
' x 2
yang tidak dapat diselesaikan secara analitik. Oleh kerena itu, metode numerik digunakan untuk menyelesaikan persoalan dimana perhitungan secara analitik tidak dapat digunakan. Metode numerik ini berangkat dari pemikiran bahwa permasalahan dapat diselesaikan dengan menggunakan pendekatan-pendekatan yang dapat dipertanggungjawabkan secara analitik.
Dengan menggunakan metode pendekatan, tentu setiap nilai hasil perhitungan akan mempunyai nilai error (nilai kesalahan). Dalam analisa metode numerik, kesalahan ini menjadi penting. Karena kesalahan dalam pemakaian algoritma pendekatan akan menyebabkan nilai kesalahan yang besar, tentunya ini tidak diharapkan. Sehingga pendekatan metode analitik selalu membahas tingkat kesalahan dan tingkat kecepatan proses yang akan terjadi.
Ada banyak metode secara numerik yang digunakan untuk menyelesaikan persamaan diferensial salah satunya adalah metode Kutta. Metode Runge-Kutta merupakan metode yang sangat praktis dan sering digunakan dalam menyelesaikan persamaan diferensial biasa karena metode Runge-Kutta tidak membutuhkan perhitungan turunan. Selain itu metode Runge-Kuta juga memiliki nilai kesalahan (error) yang sangat kecil dibandingkan dengan metode-metode yang lain.
Namun metode ini memiliki ordo suku lebih tinggi yang mengakibatkan
perhitungan-perhitungan yang lebih rumit dan lebih mendalam.
Metode Runge-Kutta banyak digunakan orang sebagai alat bantu untuk perhitungan metode numerik dan juga aplikasi komputer. N. Anggriani, A.K. Supriatna dan Widudung mengembangan software penentuan vaksinasi optimal penyakit menular menggunakan metode Runge-Kutta. Banyak aplikasi persamaan-persamaan diferensial yang diselesaikan orang menggunakan metode Runge-Kutta, seperti penyelesaian persamaan suspensi mobil, rangkaian listrik dan gerak pendulum.
metode Runge-Kutta tidak memiliki solusi yang unik. Solusi metode Runge-Kutta bergantung pada pemilihan nilai parameter yang diberikan. Pemilihan nilai parameter juga mempengaruhi besar-kecilnya nilai error. Oleh karena itu penulis mengambil
judul “PENGARUH PERUBAHAN PARAMETER TERHADAP NILAI ERROR
PADAMETODE RUNGE-KUTTA ORDO-2”.
1.2Perumusan Masalah
Dari latar belakang ada beberapa masalah yaitu :
1. Bagaimana solusi persamaan diferensial biasa secara analitik dan numerik yaitu menggunakan metode Runge-Kutta Ordo-2.
2. Bagaimana nilai kesalahan metode Runge-Kutta terhadap perubahan nilai parameter yang diberikan.
3. Bagaimana pengaruh perubahan nilai salah satu parameter secara increament terhadap nilai kesalahan yang diperoleh.
1.3Batasan Masalah
Adapun batasan-batasan masalah dalam melakukan penelitian ini antara lain : 1. Metode Runge Kutta yang digunakan adalah Metode Runge-Kutta Ordo-2. 2. Persamaan diferensial yang diselesaikan pada tulisan ini adalah persamaan
diferensial biasa yaitu persamaan diferensial linier tingkat dua yang memiliki solusi eksak.
3. Aplikasi yang digunakan pada penulisan program mencari solusi persamaan diferensial adalah aplikasi Matlab 6.1
4. Karena nilai parameter a1 adalah bialangan rill yang memenuhi persamaan
1 2 1
a a , maka ada banyak bilangan rill yang memenuhi persamaan tersebut. Oleh Karen itu, penulis membatasi nilai parameter a1 pada interval 0 a1 1
1.4Tinjauan Pustaka
Persamaan diferensial adalah suatu persamaan diantara derivatif-derivatif yang dispesifikasikan pada suatu fungsi yang tidak diketahui, nilainya, dan diketahui jumlah serta fungsinya (Birkhoff, 1978). Persamaan diferensial biasa (PDB) adalah suatu persamaan diferensial yang terdiri dari satu variabel bebas saja (Setiawan, 2006).
Penyelesaian suatu model matematika secara numerik memberikan hasil aproksimasi/pendekatan yang berbeda dengan penyelesaian secara analitis. Adanya perbedaan inilah yang sering disebut sebagai error (kesalahan). Hubungan antara nilai eksak, nilai perkiraan dan error dapat dirumuskan sebagai berikut:
Nilai eksak = aproksimasi + error
Dengan menyusun kembali persamaan di atas, diperoleh definisi dari kesalahan absolut (absolute error), yaitu :
Kesalahan absolut = nilai eksak – aproksimasi
Metode deret Taylor adalah metode yang umum untuk menurunkan rumus-rumus solusi PDB. Deret Taylor dapat digunakan untuk memperoleh Metode ini pada dasarnya adalah merepresentasikan solusinya dengan beberapa suku deret Taylor.
( )
Metode Runge Kutta memperoleh akurasi dari pendekatan deret Taylor tanpa memerlukan perhitungan derivatif yang lebih tinggi. Metode Runge-Kutta
dikembangkan oleh dua ahli matematika Jerman. Mereka adalah Runge dan Kutta. Metode ini juga dibedakan dengan ordo-ordonya.
Banyak variasi dari metode Runge-Kutta, namun secara umum bentuknya adalah :
1
Adapun tujuan dari penelitian yaitu menentukan nilai parameter yang menghasilkan nilai error terkecil pada penyelesaian persamaan diferensial biasa linier tingkat dua menggunakan metode Runge-Kutta.
1.6Manfaat Penelitian
Selain menambah literatur dalam bidang komputasi, tulisan ini juga dapat menambah wawasan bagi masyarakat terutama mahasiswa tentang penyelesaian persamaan diferensial biasa menggunakan metode Runge-Kutta khususnya metode Runge-Kutta Ordo-2 dan penggunaan parameter yang paling efisien pada Runge-Kutta sehingga mendapatkan nilai error yanglebih kecil.
1.7Metodologi Penelitian
Metode penelitian ini bersifat literatur dan kepustakaan dengan langkah-langkah sebagai berikut:
1. Mengumpulkan dan memaparkan beberapa bahan yang berkaitan dengan Metode Runge-Kutta.
2. Membuat program Runge-Kutta menggunakan Matlab 6.1 dimana didalam program tersebut parameter-parameter yang memenuhi syarat metode Runge-Kutta dieksekusi satu per satu.
3. Menguji program dan membandingkan output program sesuai dengan parameter-parameter yang dieksekusi.
BAB 2
LANDASAN TEORI
2.1 Persamaan Diferensial
Definisi 2.1
Persamaan diferensial adalah suatu persamaan diantara derivatif-derivatif yang dispesifikasikan pada suatu fungsi yang tidak diketahui, nilainya, dan diketahui jumlah serta fungsinya (Birkhoff, 1978).
Berdasarkan jumlah variabel bebasnya persamaan diferensial dibagi dalam dua kelas yaitu persamaan diferensial biasa (PDB) dan persamaan diferensial parsial (PDP).
Definisi 2.2
Persamaan diferensial parsial (PDP) adalah persamaan diferensial yang menyangkut turunan parsial dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas. (Ross, 1984: 4)
Contoh :
1)
2 2
2 2 ,
u u u
x y t
2) x z y z z 0
Definisi 2.3
Persamaan diferensial biasa (PDB) adalah persamaan diferensial yang menyangkut turunan biasa dari satu atau lebih variabel tak bebas terhadap satu variabel bebas. (Ross, 1984: 4)
Contoh :
1) dy ex sin( )x
dx
2) (1 y dx) (1 x dy) 0
Definisi 2.4
Tingkat (order) dari persamaan diferensial didefinisikan sebagai tingkat dari derivatif tertinggi yang muncul dalam persamaan diferensial. (Nugroho, D.B, 2011: 2)
Contoh : derivatif tertinggi yang muncul dalam persamaan diferensial. (Nugroho, D.B, 2011: 2)
Istilah persamaan diferensial pertama kali digunakan oleh Leibniz pada tahun 1676 untuk menunjukkan sebuah hubungan antara diferensial dx dan dy dari dua variabel x dan y.
Suatu persamaan diferensial biasa ordo satu adalah suatu persamaan yang memuat satu variabel bebas, biasanya dinamakan x, satu variabel tak bebas, biasanya dinamakan y, dan derivatif
dy
dx. Suatu persamaan diferensial biasa ordo satu tersebut
dapat dinyatakan dalam bentuk
Jika diambil y(x) sebagai suatu fungsi satu varibel, dengan x dinamakan varibel bebas dan y dinamakan variabel tak bebas, maka secara umum sebuah persamaan diferensial biasa linier dan non-linier dapat dituliskan sebagai :
2.2 Persamaan Diferensial Biasa Linier
Definisi 2.6
Suatu persamaan diferensial dikatakan linier jika tidak ada perkalian antara
varibel-variabel tak bebas dan turunan-turunannya. Dengan kata lain, semua koefisiennya
adalah fungsi dari variabel-variabel bebas. (Nugroho, D.B, 2011: 3)
Persamaan diferensial linier dapat diklasifikasikan berdasarkan tingkat (ordo) tertinggi dari turunan yang terkandung dalam persamaan diferensial. Pada setiap persaman diferensial yang sudah diklasifikasikan berdasarkan ordo, persaman diferensial tersebut juga dapat diklasifikasikan menjadi persamaan diferensial linier homogen dan persamaan diferensial linier tak homogen.
2.2.1 Persamaan Diferensial Linier Tingkat Satu
Suatu persamaan diferensial tingkat satu dikatakan linier dalam y jika persamaan tidak dapat memuat hasil kali, pangkat atau kombinasi non-linier lainnya dari y atau y’. Dipunyai bentuk yang paling umum yaitu
( )dy ( ) ( )
F x G x y H x
dx
Atau muncul dalam bentuk yang lebih biasa dengan membagikan setiap fungsi dengan
F(x) sehingga diperoleh
F x adalah adalah fungsi kontinu atau konstanta
langsung, atau jika Q x( ) 0, maka persmaan adalah terpisahkan dan juga merupakan persamaan diferensial linier yang homogen. Persamaan (2.5) memiliki beberapa kemungkinan penyelesaian yang terjadi, yaitu :
1. Untuk P x( ) 0 maka persamaan (2.5) menjadi persamaan
( ) dy
Q x
dx (2.6)
Persamaan (2.6) dapat diselesaikan dengan integrasi langsung sehingga penyelesainnya diperoleh
Persamaan (2.8) adalah persamaan diferensial terpisahkan. Persamaan diferensial terpisahkan (separable differential equation) adalah suatu persamaan diferensial biasa tingkat satu yang secara aljabar dapat direduksi ke suatu bentuk diferensial baku dengan setiap suku tak nol memuat secara tepat satu variabel.
Subtitusikan persamaan (2.10) ke persamaan (2.5) maka
Dari persamaan (2.11) dapat diambil dua persamaan yaitu :
1. dV x( ) P x V x( ) ( ) 0
dengan mengintegralkan kedua sisi persamaan (2.12)
( )
Subtitusikan persamaan (2.13) ke persamaan (2.14) diperoleh
( )
subtitusikan persamaan (2.13) dan (2.16) ke persamaan (2.9)
( ) ( )
Berikut merupakan contoh persamaan diferensial linier tingkat satu
1. y'xe3x2y
2. dy ytan( )x sec( )x
x
2.2.2 Persamaan Diferensial Linier Tingkat Dua
Definisi 2.7
dengan P x( ),Q x( )dan H x( )adalah fungsi dari peubah bebas x. (Munzir, said dan Marwan, 2009).
2.2.2.1Persamaan Diferensial Linier Tingkat Dua Homogen
Secara khusus, persamaan diferensial linier tingkat dua homogen mempunyai bentuk
2
2 ( ) ( ) 0
d y dy
P x Q x y
dx dx (2.19)
Persamaan diferensial tingkat dua homogen selalu mempunyai dua penyelesaian yang bebas linier. Jika y x1( ) dan y x2( ) adalah dua penyelesaian yang bebas linier untuk persamaan (2.19), maka
1 1 2 2
( ) ( ) ( )
y x c y x c y x
adalah penyelesaian umum untuk persamaan (2.19)
Persamaan Diferensial Linier Homogen Dengan Koefisien Konstan
Suatu persamaan diferensial dikatakan persamaan diferensial linier tingkat dua homogen dengan koefisien konstanta apabila H x( ) 0, berarti bentuknya menjadi
2
persamaan (2.20) dalam bentuk y emx dengan m adalah suatu konstanta. Didiferensialkan penyelesaian y emx diperoleh
mx
Persamaan (2.21a),(2.21b) dan (2.21c) disubtitusikan ke persaamaan (2.20) diperoleh akar-akar karakteristik sebagai berikut :
2
Ada beberapa variasi dari akar-akar karakteristik yang diperoleh dari penyelesaian homogen tergantung pada jenis persamaan yang diselesaikan. Berikut variasi akar-akar karakteristik yang akan dibahas cara penyelesaiannya.
1 2
Persamaan Diferensial Linier Homogen Dengan Koefisien Peubah
Suatu persamaan diferensial dikatakan persamaan diferensial linier tingkat dua homogen dengan koefisien peubah apabila H x( ) 0, berarti bentuknya menjdi
2
Pada umumnya tidak ada cara untuk menyelesaikan persamaan diferensial linier homogen dengan koefisien peubah secara eksplisit, kecuali persamaan diferensial yang berbentuk khusus, misalnya persamaan dfierensial tipe Euler dan persamaan diferensial tingkat dua yang telah diketahui salah satu penyelesaiannya. Pada bagian ini yang akan dibicarakan adalah persamaan diferensial Euler khususnya persamaan diferensial Euler tingkat dua.
Suatu persamaan diferensial Euler adalah suatu persamaan diferensial berbentuk
( ) 1 ( 1) ...
' 0
n n n n
dimana an, an 1, . . . , a1, a0 merupakan konstanta-konstanta dan an 0. Karena koefisien pertama a xn n tidak akan pernah nol, selang definisi persamaan diferensial (2.22) ialah salah satu dari dua selang terbuka (0, ) atau ( , 0). Ini berarti, persamaan diferensial itu akan diselesaikan untuk x 0 atau x 0. Persamaan diferensial Euler mungkin merupakan tipe termudah dari persamaan diferensial linier dengan koefisien peubah. Alasan untuk ini ialah bahwa perubahan peubah bebas
0
menghasilkan suatu persamaan diferensial dengan koefisien konstanta. Fakta ini dilukiskan untuk kasus tingkat dua.
Jika n 2 maka pada persamaan (2.22) akan diperoleh
2
2 '' 1 ' 0 0
a x y a xy x y (2.23)
Pada persamaan (2.23) merupakan suatu bentuk dari persamaan diferensial tingkat dua dimana a a2, 1 dan a0 adalah konstanta.
2.2.2.2Persamaan Diferensial Linier Tingkat Dua Tidak Homogen Dengan Koefisien Konstan
1. p dan q adalah konstanta dan H x( ) 0
2. Linier dalam y
3. Turunan tingkat dua
Untuk menyelesaiakan persamaan (2.24), dapat dicari penyelesaian umum y
dengan jalan menjumlahkan penyelesaian homogen yh dan penyelesaian partikuler p
y . Tetapi dalam menyelesaikan persamaan (2.24) terlebih dahulu mencari penyelesaaian homogen. Dari persamaan (2.24) terdapat berbagai bentuk kasus H x( )
yang mungkin terjadi diantaranya adalah :
1. H x( ) P xn( ), dimana P xn( ) adalah suatu polynomial berpangkat n.
2. ( ) ( ) x
n
H x P x e , dimana adalah kostanta.
3. H x( ) e x P xn( ) cos x Q xn( )sin x , dimana P xn( )dan Q xn( ) adalah suatu polynomial berpangkat n sedangkan dan adalah konstanta. 4. H x( ) Mcos x Nsin x, dimana M, N dan adalah konstanta.
2.2.3 Persamaan Diferensial Linier Tingkat Tinggi
Definisi 2.6
2.3 Masalah Nilai Awal ( Initial Value Problem)
Suatu persamaan diferensial biasa dengan syarat tambahan pada fungsi yang tidak diketahui dan derivatif-derivatifnya, semua diberikan nilai yang sama untuk variabel bebas, merupakan suatu masalah nilai awal (initial value problem). Syarat tambahan tersebut dinamakan syarat awal (initial condition). Jika syarat tambahan diberikan pada lebih dari satu varibel bebas, dinamakan masalah nilai batas (boundary value problem) dan syaratnya dinamakan syarat batas.
Secara umum, problem persamaan diferensial biasa selalu melibatkan nilai awal (initial-value), yang dapat ditulis sebagai berikut :
(2.26)
dengan kondisi awal y x( )0 y0 yang dipanggil sebuah masalah nilai awal (initial value problem).(Verner, 2010).
2.4 Kesalahan (Error)
Dalam suatu perhitungan matematik, kita selalu berusaha untuk memperoleh jawaban yang eksak, misalnya untuk menghitung suatu variabel tertentu dari suatu persamaan matematik. Akan tetapi, jawaban yang demikian jarang kita peroleh, maka sebagai solusinya digunakan metode numerik. Dalam metode numerik pada tiap langkah penyelesaiannya dari formulasi hingga komputasinya hanya akan menghasilkan solusi pendekatan (bukan solusi eksak). Oleh karena itu penyelesaian secara numerik memberikan hasil pendekatan yang berbeda dengan penyelesaian secara analitis. Adanya perbedaan inilah yang sering disebut sebagai error. Dalam metode numerik
error sering juga disebut dengan istilah error.
Nilai eksak = pendekatan + error
Error absolut suatu bilangan adalah selisih antara nilai sebenarnya dengan nilai pendekatan. Secara matematis, jika y adalah solusi hampiran dan ya adalah solusi eksak, error dinyatakan oleh
a
y y
error dapat bernilai positif atau negatif. Jika tanda error tidak dipertimbangkan, error
absolut didefinisikan sebagai
| | ya y (2.27)
dengan : ya = nilai sebenarnya
y = nilai perkiraan
= kesalahan absolut (kesalahan terhadap nilai sebenarnya)
Ungkapan kesalahan menggunakan rumus di atas kurang begitu bermakna karena tidak menunjukkan secara langsung seberapa besar error itu dibandingkan dengan nilai eksaknya. Sebagai contoh, jika nilai eksaknya ya = 10 dan nilai hampirannya y = 10,2, error absolutnya adalah 0,2. Error yang sama akan diperoleh jika ya = 8 dan y = 7,8. Ketika seseorang melaporkan hasil perhitungannya 0,2, tanpa menyebutkan nilai eksaknya, kita tidak mendapatkan informasi yang lengkap.
Istilah kesalahan relatif muncul untuk menghindari salah interpretasi terhadap nilai error. Kesalahan relatif didefinisikan sebagai
r a
Akan tetapi, dalam metode numerik, kita tidak mengetahui nilai sejatinya sehingga sulit untuk mendapatkan error relatif ini. Untuk mengatasi hal tersebut,
error dibandingkan dengan nilai hampirannya (disebut error relatif hampiran), yaitu
100%
Di dalam metode numerik sering dilakukan pendekatan secara iteratif. Pada pendekatan tersebut perkiraan sekarang dibuat berdasarkan perkiraan sebelumnya. Dalam hal ini, kesalahan adalah perbedaan antara perkiraan sebelumnya dan perkiraan sekarang, dan kesalahan relatif dapat dituliskan dalam bentuk :
1
yn : nilai perkiraan pada iterasi ke n 1
n
y : nilai perkiraan pada iterasi ke n+1
2.4.1 Pembagian Kesalahan
Kesalahan dalam metode numerik disebabkan oleh hal-hal berikut, yaitu :
1. KesalahanPemotongan (Truncation Error)
berhingga. Kesalahan ini timbul akibat penggunaan hampiran sebagai pengganti formula eksak. Biasanya sering terjadi dalam penyelesaian numerik dengan menggunakan deret Taylor. Untuk penyederhanaan permasalahan biasanya perhatian hanya ditujukan pada beberapa suku dari deret Taylor tersebut, sedangkan suku yang lainnya diabaikan. Pengabaian inilah yang menyebabkan terjadinya kesalahan.
Contohnya, hampiran fungsi cos(x) dengan Deret Taylor : Cos(x) = 1 – x2/2! + x4/4! + x6/6! + x8/8! + x10/10! + . . .
Pemotongan
nilai hampiran error pemotongan
2. KesalahanPembulatan (Round-off Error)
Kesalahan pembulatan merupakan suatu keharusan pada batas ketilitian (batas/titik ambang) aritmatika yang biasanya digunakan dalam metode yang diimplementasikan terhadap komputer. Kesalahan tersebut bergantung pada bilangan dan tipe dari operasi aritmatika yang digunakan pada sebuah langkah.
Kesalahan pembulatan yaitu kesalahan yang disebabkan oleh keterbatasan jumlah digit komputer dalam menyatakan bilangan riil. Bilangan riil yang panjangnya melebihi jumlah digit komputer dibulatkan ke bilangan terdekat. Secara normal, kesalahan pembulatan tidak begitu diperhitungkan pada algoritma analisis numerik, karena bergantung pada komputer yang algoritma diimplementasikan dan merupakan algoritma numerik eksternal.
Contohnya, bilangan riil tanpa akhir 0.666666…., pada komputer 7 digit dinyatakan sebagai 0.6666667.
3. Kesalahan pada data masukan (error in original data)
Merupakan kesalahan yang terjadi akibat dari gangguan yang ada pada data masukan yang akan diproses, atau adanya informasi tertentu yang tidak diketahui
kebanyakan pemodelan matematika suatu sistem fisik, biasanya ada suatu faktor yang tidak kelihatan pengaruhnya terikut dalam proses. Hal ini akan menyebabkan kesalahan pada outputnya.
4. Blunders (gross error)
Merupakan kesalahan yang terjadi akibat kesalahan manusia atau mesin hitung yang digunakan, Kesalahan jenis ini bisa dikurangi dengan melakukan pekerjaan yang berulang-ulang dan memilih mesin hitung yang baik kualitasnya.
2.5 Metode Deret Taylor
Metode deret Taylor adalah metode yang umum untuk menurunkan rumus-rumus solusi PDB. Metode ini pada dasarnya adalah merepresentasikan solusinya dengan beberapa suku deret Taylor. Metode deret taylor juga berkaitan dengan masalah nilai awal yaitu :
adalah solusi eksak dari persamaan (2.29), kita dapat memperluas y x( ) dengan deret Taylor pada titik xx0 dan memperoleh
Jika kita diberikan h x x0, kita dapat menuliskan deret sebagai berikut:
Persamaan (2.30) menyiratkan bahwa untuk menghitung hampiran y x( ), kita perlu menghitung '( ), ''( ), '''( ),0 0 0 IV( ),...,0 n( ),...0
yang dalam hal ini k adalah ordo danP adalah operator turunan yaitu,
P f
Sehingga dengan menggunakan persamaan diferensial parsial diperoleh
y x'( ) f x y( , ) (2.33a)
dan seterusnya. Melanjutkan cara ini, kita dapat menyatakan turunan apa saja dari y
2.6 Metode Runge Kutta
Secara perhitungan komputer, metode yang paling efisien yang berkenaan dengan keakuratan dari solusi persamaan diferensial biasa dikembangkan oleh dua orang ahli matematika Jerman sekitar tahun 1900. Mereka adalah Carl David Tolmé Runge dan Martin Wilhelm Kutta. Metode tesebut dikenal sebagai Metode Runge-Kutta (RK). Metode ini juga dibedakan dengan ordo-ordonya. Metode Runge-Kutta memperoleh akurasi dari pendekatan deret Taylor tanpa memerlukan perhitungan derivatif yang lebih tinggi. Penyelesaian PDB dengan metode deret Taylor tidak praktis karena metode tersebut membutuhkan perhitungan turunan f x y( , ). Lagi pula, tidak semua fungsi mudah dihitung turunannya, terutama bagi fungsi yang bentuknya rumit. Semakin tinggi ordo metode deret Taylor, semakin tinggi turunan fungsi yang harus dihitung. Karena pertimbangan ini, metode deret Taylor yang berordo tinggi pun tidak dapat diterima dalam masalah praktek.
Metode RK adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan tingkat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f x y( , ) pada titik terpilih dalam setiap selang langkah. Metode RK adalah metode PDB yang paling popular karena banyak dipakai dalam masalah dunia nyata.
Sehingga diperoleh
Persamaan (2.35) merupakan rumus metode Runge-Kutta Ordo-n untuk mencari solusi dari suatu persamaan diferensial, dimana k adalah
1 ditulis dalam bentuk array Jagal :
Untuk lebih jelasnya array jagal diperlihatkan sebagai berikut
dimana p p p1, 2,...,pn T, a a a1, 2,...,an T dan q qjl .
Nilai aj,p qj, jl dipilih sedemikian rupa sehingga meminimumkan error per langkah, dan persamaan (2.35) akan sama dengan metode deret Taylor dari ordo setinggi mungkin. Perhatikan bahwa k adalah hubungan yang selalu berulang, k1 hadir dalam persamaan untuk k2, k2 hadir dalam persamaan k3, dan seterusnya. aj,p qj, jl
merupakan parameter-parameter yang digunakan pada metode Runge Kutta.
2.6.1 Metode Runge Kutta Ordo-2
Dengan mengambil n =2 pada persamaan (2.35) maka metode Runge Kutta ordo-2 dapat dituliskan dalam bentuk umum sebagai berikut :
yi 1 yi (a k1 1 a k2 2) h (2.37)
dimana fungsi f x y'( ,i i) harus ditentukan melalui aturan rantai diferensiasi :
f x y'( ,i i) f f dy
x y dx (2.40)
Subtitusikan persamaan (2.39) ke persamaan (2.40), diperoleh :
Strategi dasar yang menggarisbawahi meode Runge-Kutta ialah bahwa metode tersebut menggunakan manipulasi aljabar untuk menyelesaikan harga-harga a a1, 2,p2
dan q21, yang menjadikan persamaan (2.37) dan persamaan (2.41) ekuivalen.
Untuk melakukan ini, pertama-tama kita menggunakan sebuah Deret Taylor untuk memperluas persamaan (2.39). Deret Taylor untuk suatu fungsi dua variabel didefinisikan sebagai :
g x( r y, s) g x y( , ) r g s g ...
x y (2.42)
Dengan menerapkan metode ini untuk memperluas persamaan (2.38.b) akan memberikan :
Dengan mengelompokkan suku-sukunya diperoleh :
Sekarang bandingkan persamaan (2.44) dengan persamaan (2.45), sehingga akan diperoleh :
Karena ada empat parameter dalam tiga persamaan, maka harus diasumsikan satu nilai parameter untuk menentukan tiga parameter lainnya. Misalnya ditentukan suatu nilai parameter a1, maka diperoleh :
2 1 1
a. Metode Heun dengan Korektor Tunggal
Perhatikan bahwa k1 adalah slope pada awal interval, dan k2 adalah slope pada akhir interval.
b. Metode Poligon yang Diperbaiki (Improve Polygon Method)
c. Metode Ralston
Ralston (1962) dan Ralston & Rabinowitz (1978) menyatakan bahwa pemilihan
1 13
a akan memberikan batas minimum truncation error untuk Runge Kutta ordo dua. Jika 1 1
2.6.2 Metode Runge Kutta Ordo-3
Seperti halnya versi orde dua, maka versi Runge-Kutta ordo-3 pun ada banyak macamnya. Salah satu versi Runge Kutta ordo-3 yang dapat dipakai adalah :
2.6.3 Metode Runge Kutta Ordo-4
Metode Runge Kutta ordo-4 ini juga terdapat dalam banyak versi, namun persamaan berikut ini yang sering dipakai, dan disebut sebagai metode Runge-Kutta ordo-4 klasik :
2.6.4 Metode Runge Kutta Ordo Tinggi
Metode Runge Kutta ordo-5 diturunkan oleh Butcher (1964) sebagai berikut :
3 1 2
1 1 1
( , )
4 8 8
i i
k f x h y h k h k
4 2 3
1 1
( , )
2 2
i i
k f x h y h k h k 5 1 4
3 3 9
( , )
4 16 16
i i
k f x h y h k h k
5 1 2 3 4 5
3 2 12 12 8
( , )
7 7 7 7 7
i i
BAB 3
PEMBAHASAN
3.1 Penyelesaian Analitik Persamaan Diferensial Linier Tingkat Dua
Penyelesaian persamaan diferensial linier biasa yang akan dibahas pada tugas akhir ini adalah persamaan diferensial linier tingkat dua yang mempunyai bentuk:
2
2 ( ) ( ) ( )
d y dy
P x Q x y G x
dx dx (3.1)
dengan syarat awal y(0) y0 dan dimanaP x( ), Q x( ) dan G x( ) adalah fungsi kontinu atau konstanta sembarang.
3.1.1 Persamaan Dengan Koefisien Konstan
Bentuk umum persamaan diferensial linier tingkat dua dengan koefisien konstanta adalah
2
2 ( )
d y dy
p qy H x
dx dx (3.2)
dimana p dan q adalah konstanta, linier dalam y dan turunannya tingkat dua.
Untuk menyelesaikan persamaan (3.2) dapat dicari penyelesaian umum y
Akan tetapi, dalam menyelesaikan persamaan (3.2) terlebih dahulu kita mencari penyelesaian homogennya.
3.1.1.1 H x( ) Adalah Polinomial Berderajat n (P xn( ))
Jika H x( ) merupakan suatu polinomial berderajat n yang disimbolkan dengan P xn( )
maka dimisalkan penyelesaian partikuler suatu polinomial berderajat n yaitu
( )
p n
y P x (3.3a)
'p ' ( )n
y P x (3.3b)
''p '' ( )n
y P x (3.3c)
Subtitusikan persamaan (3.3a), (3,3b) dan (3.3c) ke persamaan (3.2). Dengan demikian dapat dicari koefisien dari polinomial P xn( ).
Kasus 1
Cari solusi dari persamaan berikut
'' 4 ' 4 10
y y y x
Dengan nilai x0 0, y(0) 1 dan y'(0) 2
Penyelesaian :
Persamaan diferensial homogen :y'' 4 ' 4y y 0
Persamaan karakteristk :m2 4m 4 0
Akar-akar karakteristik : m 2 m 2 0
Sehingga diperoleh penyelesaian homogen untuk akar karakteristik sama :
Untuk mencari penyelesaian partikuler adalah dengan memisalkan
( )
Dengan diperolehnya nilai dari penyelesaian homogen dan penyelesaian partikuler maka penyelesaian umum adalah
h p
2
Untuk mencari penyelesaian partikulernya dilakukan ketentuan-ketentuan sebagai berikut :
( ) x
c. Apabila adalah kedua-duanya merupakan akar karakteristik, maka penyelesaian partikulernya adalah
2 x
p n
y x P e
Dimana P xn( ) adalah polinomial berderajat n. Untuk nilai yp, 'y p dan y''p
disubtitusikan pada persamaan semula sehingga koefisien dari P xn( ) dapat diperoleh.
1 2 1
Untuk mencari penyelesaian partikulernya dilakukan dengan ketentuan-ketentuan sebagai berikut :
a. Apabila i tidak merupakan akar karakteristik maka
( ) cos ( )sin
b. Apabila i merupakan akar karakteristik maka
( ) cos ( )sin x
p
Selanjutnya dengan mensubtitusiakan yp, y'p dan y''p ke dalam dalam persamaan
Sehingga diperoleh dua persamaan yaitu
10A 2B 8 2A 10B 0
Eliminasikan kedua persamaan diatas sehingga diperoleh
2 13
B dan 10
13 A
Dari nilai A dan B yang diperoleh maka penyelesaian partikulernya adalah
4(0) (0) (0) (0)
Sehingga diperoleh penyelesaian khusus pada kondisi x0 0, (0)y 0 dan y'(0) 1
adalah
Untuk mencari penyelesaian partikulernya dilakukan dengan ketentuan-ketentuan sebagai berikut :
a. Apabila i bukan merupakan akar karakteristik maka penyelesaian partikulernya adalah
cos sin
p
b. Apabila i merupakan akar karakteristik, maka penyelesaian partikulernya
''p 3 sin 3 3 cos 3 3 cos 3 9 sin 3 3 sin 3 9 cos 3
Dari nilai A dan B yang diperoleh maka penyelesaian partikulernya adalah
1 2
3.1.2 Persamaan Diferensial Linier Tingkat Dua dengan Koefisien Peubah
3.1.2.1Persamaan Tidak Memuat Variabel y
Bila persmaaan diferensial linier tingkat dua tidak memuat variabel y maka dari persamaan (2.18) diperoleh bentuk umum persamaan adalah
2
2 ( ) ( )
d y dy
P x G x
dengan P x( )dan G x( ) adalah konstanta atau fungsi kontinu.
Untuk menyelesaikan persaman diferensial jenis tersebut dilakukan langkah-langkah sebagai berikut :
Persamaan (3.5) disubtitusikan pada persamaan (3.4) diperoleh :
( ) ( )
dz
P x z G x
dx
(3.6)
Persamaan (3.6) merupakan persamaan diferensial tingkat satu yang dapat diselesaikan dengan metode penyelesaian persamaan linier tingkat satu.
dy
Persamaan (3.7) disubtitusikan persamaan kasus maka diperoleh
tan sin 2
dz
z x x
dx (3.8)
Persamaan (3.8) sudah merupakan bentuk persamaan diferensial linier tingkat satu yang mana variabel-variabelnya adalah fungsi kontinu. Oleh karena itu berdasarkan subbab sebelumnya solusi persamaan diferensial yang demikian adalah
( ) ( )
Persamaan (3.10) disubtitusikan ke persamaan (3.8) diperoleh:
( ) ( )
Dari persamaan (3.11) dapat diambil dua persamaan yaitu:
( )
Subtitusikan persamaan (3.12) ke persamaan (3.13)
Untuk nilai y'(0) 1 maka persamaan (3.15) adalah
3.1.2.2Persamaan Diferensial Euler Tingkat Dua
Bentuk umum persamaan diferensial Euler Tingkat dua adalah
2
0 '' 1 ' 2 0
a x y a xy a y (3.17)
Dimana a a0, 1 dan a2 adalah konstanta dan pangkat dari x sesuai dengan tingkat turunan.
Dalam suatu interval yang tidak memuat titik asal, persamaan (3.17) memiliki solusi umum yang dituliskan dalam bentuk
1 1( ) 2 2( )
Dengan y1 dan y2 saling bebas linier. Untuk memudahkan, pandang interval x 0. Asumsikan bahwa persamaan (3.17) memiliki penyelesaian dalam bentuk :
m
y x
1 2
Akibatnya y1 dan y2 adalah bebas linier, sehingga menurut persamaan (3.18) diperoleh penyelesaian umum
1 2
Karena akar persamaan bernilai rill dan berbeda maka diperoleh penyelesaian umum dari kasus adalah
Dengan menggunakan metode elminasi maka diperoleh
2 1
c dan c1 2
1 2
y x
x
3.2 Penyelesaian Numerik Persamaan Diferensial Linier Tingkat Dua
Persamaan diferensial linier tingkat dua sesuai kasus-kasus pada subbab diatas akan dibahas dengan menggunakan metode numerik yaitu metode Runge-Kutta ordo-2. Penyelesaian persamaan diferensial linier tingkat dua tersebut menggunakan program dalam bahasa Matlab. Aplikasi yang digunakan untuk menjalankan program yaitu aplikasi Matlab 6.1. Secara umum, algoritma atau langkah-langkah dalam menyelesaikan persamaan diferensial linier tingkat dua dengan metode Runge-Kutta Ordo-2 adalah:
1. Menentukan persamaan diferensial tingkat dua yang akan dicari penyelesaiannya.
2. Memberikan nilai awal variabel bebas x dan variabel terikat y dan z. 3. Menentukan nilai (x) yang akan ditentukan penyelesaiannya.
4. Menentukan besarnya ukuran langkah (h). 5. Menentukan nilai parameter a1.
6. Menghitung parameter-parameter a2,p2 dan q21 dengan mensubtitusikan nilai
a1 ke persamaan rumus yang ditentukan untuk menghitung parameter-parameter tersebut.
7. Menuliskan Rumus Persamaan Metode Runge-Kutta ordo-2
8. Menghitung variabel-variabel Runge-Kutta yang terdapat dalam rumus dengan menggunakan formulasi rumus yang telah ditentukan, dalam hal ini variabel
k1,k2 dan m1,m2.
9. Menghitung yi+1 dan zi+1 dengan mensubtitusikan variabel k1, k2 dan m1,m2. Dimana variabel k1 dan k2 disubtitusikan ke persamaan yi+1 dan variabel m1 dan
m2 disubtitusikan ke persamaan zi+1.
Berdasarkan algoritma diatas, ada beberapa variabel dan parameter yang harus diketahui besar nilainya agar suapaya program yang akan ditulis berdasarkan algoritma dapat berjalan dengan baik . Adapun variabel yang dimaksud adalah nilai x
langkah (h). Dalam hal ini, nilai (x0), (y0) dan (xn) bergantung pada kasus yang diberikan sedangkan ukuran langkah (h) untuk semua kasus adalah sama yaitu 0.01. Hal ini disebabkan untuk mengetahui perbandingan error terhadap setiap kasus dengan ukuran langkah yang sama. Parameter yang diketahui nilainya yaitu parameter
a1 dimana dengan diberikannya nilai parameter a1 akan memberikan nilai juga kepada parameter-parameter yang lain sesuai persamaan (2.46a) dan (2.46b). Berdasarkan (2.46a) nilai a1 harus berada pada interval 0 a1 1 dimana a1 adalah bilangan rill. Oleh karena itu, penulis akan menggunakan parameter a1dengan rentang 0.0001 untuk menyelesaiakan semua kasus yang diperoleh solusi analitiknya pada subbab 3.1.
Berikut merupakan salah satu penyelesaian kasus dengan menggunakan metode Runge-Kutta Ordo-2 berdasarkan algoritma diatas. Kasus yang akan diselesaikan pada pembahasan subbab ini yaitu kasus 1 . Kasus 1 akan diselesaikan dengan menggunakan parameter awal a1 = 0.
Kasus 1
Cari solusi dari persamaan berikut pada x = 2.
'' 4 ' 4 10
y y y x
Dengan nilai x0 0, y(0) 1 dan y'(0) 2
Penyelesaian
Diketahui persamaan diferensial linier soal adalah :
Maka z' y'' g x y y( , , ') g x y z( , , )
Subtitusikan persamaan diatas ke persamaan kasus sehingga diperoleh persamaan diferensiaal tingkat satu
Penyelesaian yang dicari pada soal yaitu pada saat x = 2 dengan menggunakan ukuran langkah h = 0.1
Metode yang digunakan untuk menyelesaikan kasus yaitu metode Runge-Kutta Ordo-2 dimana rumus yang digunakan adalah
2 16.45
Sehingga untuk x = 0 diperoleh solusi
2 ( 2 0.05, 2 0.05 ,1 2 0.05 )1
Sehingga untuk x = 0.1 diperoleh solusi
y = 1.7325
Proses perhitungan terus dilakukan sampai nilai x = 2. Melalui alat bantuk program matlab maka solusi pada nilai x = 2 dengan nilai a1 = 0 dan h = 0.1 diperoleh pada iterasi 21 yaitu y = 460.944839. Output untuk nilai parameter a1 yang lain yaitu
1
3.3 Perbandingan Nilai Error Menggunakan Nilai Parameter Yang Berbeda
Pada pembahasan ini, penulis akan membandingkan nilai error pada setiap perubahan parameter. Tetapi sebelum itu, penulis akan membandingkan terlebih dahulu solusi analitik dan solusi numerik dalam setiap iterasi dengan nilai parameter a1 yang berbeda dalam bentuk grafik kurva. Hal ini dikarenakan nilai error yang diperoleh pada pembahasan ini merupakan hasil perbandingan antara solusi numerik dengan solusi analitik. akan diuji pada interval tersebut dengan pertambahan nilai a1 sebesar 0.1 untuk iterasi pertama, 0.01 untuk iterasi kedua dan seterusnya. Perbandingan nilai Error dilakukan pada kasus yang sama. Dengan melihat hasil yang diperoleh , maka akan dicari pada saat berapakah nilai a1 akan diperoleh nilai error paling minimum pada suatu kasus yang sama.
Kasus-kasus yang dibahas adalah kasus-kasus soal pada sub bab diatas. Oleh karena itu berikut merupakan hasil dari proses perhitungan persamaan diferensial linier tingkat dua dengan menggunakan metode Runge-Kutta ordo-2. Untuk mempermudah penulis, untuk semua kasus pada subbab 3.1 akan diselesaikan menggunakan alat bantu program matlab. Hasil perhitungan akan diperlihatkan dengan tabel dan grafik sesuai kasus yang akan diselesaikan.
Kasus 1
'' 4 ' 4 10
Dengan nilai x0 0, y(0) 1 dan y'(0) 2
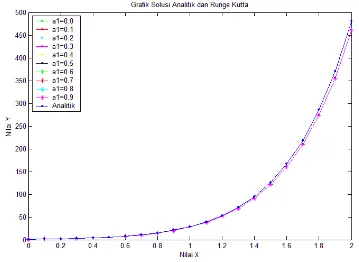
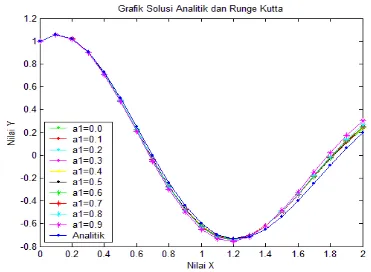
Hasil perhitungan dengan menggunakan program matlab untuk mencari solusi numerik dan solusi analitik dengan ukuran langkah h = 0.1 diperlihatkan dengan grafik sebagai berikut.
Gambar 3.1 Grafik Solusi Analitik dan Solusi Numerik Kasus 1 dengan nilai parameter a1 yang Berbeda
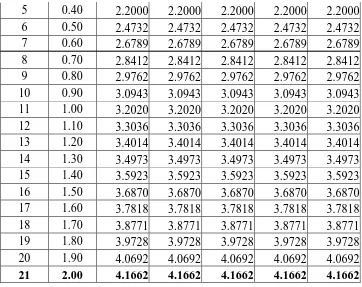
sedangkan nilai error pada kasus 1 untuk setiap parameter a1 dengan ukuran langkah
h = 0.1 dapat diperlihatkan dengan tabel berikut.
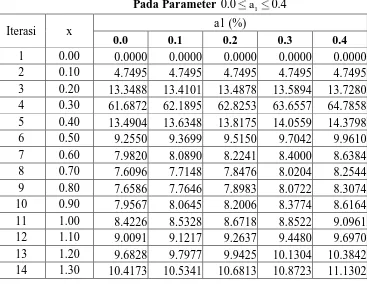
Tabel 3.1a Nilai Error Persamaan Kasus 1 Pada Parameter 0.0 a1 0.4
Iterasi x a1
0.0 0.1 0.2 0.3 0.4
5 0.40 2.2000 2.2000 2.2000 2.2000 2.2000
19 1.80 3.9728 3.9728 3.9728 3.9728 3.9728 20 1.90 4.0692 4.0692 4.0692 4.0692 4.0692 21 2.00 4.1662 4.1662 4.1662 4.1662 4.1662
Pada tabel 3.1a dan 3.1b, perhitungan menggunakan ukuran langkah h =0.1 dan menghasilkan nilai error yang cukup besar untuk metode Runge-Kutta. Oleh karena itu pada grafik dibawah dilakukan perhitungan dengan menggunakan ukuran langkah yang lebih kecil lagi yaitu h = 0.01. Untuk lebih jelasnya dapat dilihat grafik berikut.
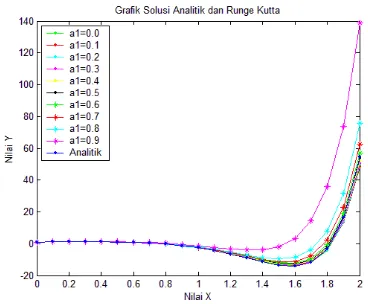
Gambar 3.2 Grafik nilai error kasus 1 untuk setiap nilai parameter a1
Dari gambar 3.2 nilai error yang dihasilkan lebih kecil dibandingkan dengan nilai
Kurva nilai error pada parameter a1 = 0 sampai a1 = 0.8 ditutupi oleh kurva nilai error parameter a1 = 0.9.
Kasus 2
3
'' 5 ' 6 x
y y y xe
Dengan nilai x0 0, y(0) 1 dan y'(0) 1
Hasil perhitungan dengan menggunakan program matlab untuk mencari solusi numerik dan solusi analitik dengan ukuran langkah h = 0.1 diperlihatkan dengan grafik sebagai berikut.
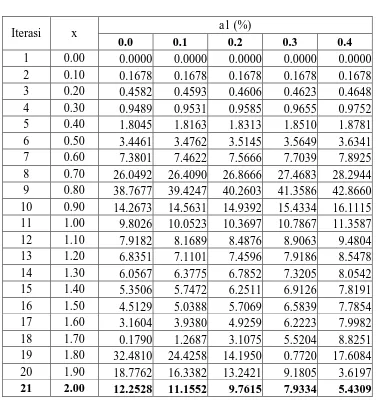
sedangkan nilai error pada kasus 2 untuk setiap parameter a1 dengan ukuran langkah
h = 0.1 dapat diperlihatkan dengan tabel berikut.
Tabel 3.2a Nilai Error Persamaan Kasus 2 Pada Parameter 0.0 a1 0.4
6 0.50 3.7351 3.8960 4.1912 4.9001 8.4218 7 0.60 8.1676 8.6053 9.4081 11.3314 20.8405 8 0.70 29.4984 31.4137 34.9220 43.3121 84.6035 9 0.80 45.0620 48.5532 54.9418 70.1935 144.9311 10 0.90 17.0989 18.6679 21.5363 28.3730 61.7379 11 1.00 12.1913 13.5136 15.9289 21.6767 49.6190 12 1.10 10.3159 11.6418 14.0621 19.8130 47.6686 13 1.20 9.4631 10.9152 13.5635 19.8479 50.1812 14 1.30 9.1211 10.8130 13.8964 21.2035 56.3575 15 1.40 9.1370 11.2258 15.0302 24.0348 67.2189 16 1.50 9.5317 12.2983 17.3340 29.2391 86.1630 17 1.60 10.5784 14.6649 22.0982 39.6521 123.3473 18 1.70 13.6253 21.2248 35.0405 67.6324 222.6061 19 1.80 44.3009 86.5450 163.3017 344.1924 1202.1045 20 1.90 4.4539 17.2273 40.4242 95.0399 353.4279 21 2.00 1.7983 3.9471 14.3757 38.9070 154.6924
Pada grafik dibawah ini dilakukan perhitungan dengan menggunakan ukuran langkah yang lebih kecil lagi, yaitu h = 0.01. Untuk lebih jelasnya dapat dilihat grafik berikut.
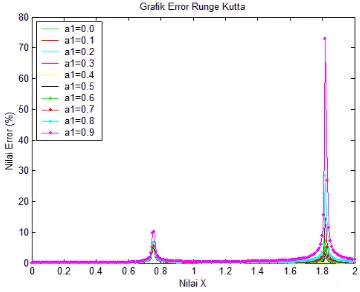
Nilai error terbesar berada pada parameter a1 = 0.9 tepatnya di titik x = 1.82 yaitu 72.78536% . Nilai error pada interval tersebut terus meningkat dengan nilai yang tinggi sampai titik x = 1.82 dan kembali menurun secara normal. Terjadinya nilai
error yang cukup tinggi pada x = 1.82 dipengaruhi oleh nilai koefisien dari fungsi polinomial berderajat satu pada H(x). Semakin kecil nilai koefisien maka lonjakan nilai error pada kurva akan semakin runcing dan posisi lonjakan akan berpindah ke kiri sumbu x. Sedangkan apabila koefisien nilainya diperbesar maka bentuk kurva
error akan semakin tumpul dan nilai error juga akan semakin kecil untuk semua parameter. Pemberian nilai awal x, y, dan y’ yang tepat juga mempengaruhi bentuk kurva error pada kasus 2.
Kasus 3
'' 3 ' 4 8 xcos 2
y y y e x
Dengan nilai x0 0, y(0) 0 dan y'(0) 1
Gambar 3.5 Grafik Solusi Analitik dan Solusi Numerik Kasus 3 dengan nilai parameter a1 yang Berbeda
sedangkan nilai error pada kasus 3 untuk setiap parameter a1 dengan ukuran langkah
h = 0.1 dapat diperlihatkan dengan tabel berikut.
Tabel 3.3a Nilai Error Persamaan Kasus 3 Pada Parameter 0.0 a1 0.4
Iterasi x a1 (%)
0.0 0.1 0.2 0.3 0.4
15 1.40 11.1900 11.3084 11.4575 11.6510 11.9121
Tabel 3.3b Nilai Error Persamaan Kasus 3 Pada Parameter 0.5 a1 0.9
Gambar 3.6 Grafik nilai error kasus 3 untuk setiap nilai parameter a1
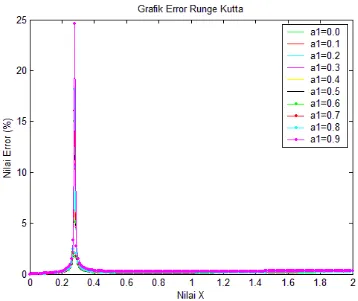
Pada kasus 3 nilai error terbesar pada interval 0 x 2 berada pada parameter a1 = 0.9 yaitu pada titik x = 0.27. Pada titik tersebut nilai error mencapai 24.63 %. Untuk parameter lain, nilai error pada titik x =0.27 juga mengalami kenaikan yang cukup tinggi dibandingkan denga nilai error pada nilai x yang lain. Terjadinya nilai error
yang sangat tinggi pada x = 0.27 dipengaruhi oleh bentuk fungsi H(x) dari suatu persamaan diferensial. Pada kasus 3 fungsi H(x) merupakan kombinasi dari fungsi trigonometri dan fungsi eksponensial natural. Apabila koefisien dari fungsi eksponensial natural pada kasus 3 diperbesar maka kurva error akan semakin cembung dan apabila koefisiennya diperkecil maka kurva error akan semakin lancip atau runcing dan mengalami pergeseran arah kiri sumbu x.
Kasus 4
'' 9 2sin 3
y y x
Hasil perhitungan solusi numerik dan solusi analitik dengan ukuran langkah h = 0.1 diperlihatkan dengan grafik sebagai berikut.
Gambar 3.7 Grafik Solusi Analitik dan Solusi Numerik Kasus 4 dengan nilai parameter a1 yang Berbeda
sedangkan nilai error pada kasus 4 untuk setiap parameter a1 dengan ukuran langkah
h = 0.1 dapat diperlihatkan dengan tabel berikut.
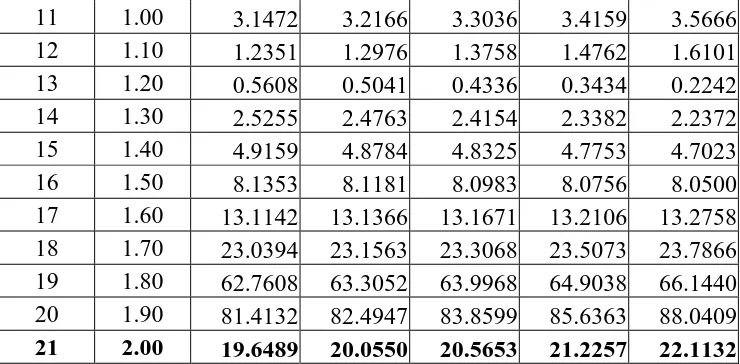
Tabel 3.4a Nilai Error Persamaan Kasus 4 Pada Parameter 0.0 a1 0.4
Iterasi x a1 (%)
0.0 0.1 0.2 0.3 0.4
11 1.00 3.1472 3.2166 3.3036 3.4159 3.5666
Untuk lebih jelasnya, tabel 3.4a dan 3.4b akan diperlihatkan grafik dibawah dengan menggunakan ukuran langkah yang lebih kecil, yaitu h = 0.01.
Gambar 3. 8 Grafik nilai error kasus 4 untuk setiap nilai parameter a1
Pada kasus 4 nilai error terbesar pada interval 0 x 2 berada pada parameter a1 = 0.9 yaitu pada titik x = 1.86. Pada titik tersebut nilai error mencapai 42.07%. Untuk parameter lain, nilai error pada titik x =0.27 juga mengalami kenaikan yang cukup tinggi dibandingkan dengan nilai error pada nilai x yang lain.
Kasus 5
'' ' tan sin 2
y y x x
Dengan nilai x0 0, y(0) 0 dan y'(0) 1
Gambar 3.9 Grafik Solusi Analitik dan Solusi Numerik Kasus 5 dengan nilai parameter a1 yang Berbeda
sedangkan perbandingan nilai error pada kasus 5 untuk setiap parameter a1 dapat diperlihatkan dengan tabel dan grafik berikut dimana perhitungan dilakukan dengan ukuran langkah h = 0.1.
Tabel 3.5a Nilai Error Persamaan Kasus 5 Pada Parameter 0.0 a1 0.4
Iterasi x a1 (%)
0.0 0.1 0.2 0.3 0.4
13 1.20 0.2104 0.1878 0.1591 0.1217 0.0707
Gambar 3. 10 Grafik nilai error kasus 5 untuk setiap nilai parameter a1
Kasus 6
2
2x y'' xy' y 0
Dengan nilai x0 1, y(1) 1 dan y'(1) 2
Gambar 3.11 Grafik Solusi Analitik dan Solusi Numerik Kasus 6 dengan nilai parameter a1 yang Berbeda
sedangkan perbandingan nilai error pada kasus 6 untuk setiap parameter a1 dapat diperlihatkan dengan tabel dan grafik berikut dimana perhitungan dilakukan dengan ukuran langkah h = 0.1.
Tabel 3.6a Nilai Error Persamaan Kasus 6 Pada Parameter 0.0 a1 0.4
Iterasi x a1 (%)
0.0 0.1 0.2 0.3 0.4
9 1.80 12.0146 12.0152 12.0159 12.0169 12.0183 10 1.90 12.9413 12.9421 12.9432 12.9446 12.9464 11 2.00 13.6364 13.6375 13.6388 13.6406 13.6430
Tabel 3.6b Nilai Error Persamaan Kasus 6 Pada Parameter 0.5 a1 0.9
Iterasi x a1 (%)
0.5 0.6 0.7 0.8 0.9
1 1.00 0.0000 0.0000 0.0000 0.0000 0.0000 2 1.10 0.7550 0.7550 0.7550 0.7550 0.7550 3 1.20 2.3338 2.3337 2.3336 2.3337 2.3348 4 1.30 4.1933 4.1933 4.1935 4.1941 4.1980 5 1.40 6.0788 6.0791 6.0797 6.0815 6.0901 6 1.50 7.8592 7.8599 7.8613 7.8650 7.8799 7 1.60 9.4642 9.4655 9.4681 9.4742 9.4969 8 1.70 10.8570 10.8591 10.8631 10.8721 10.9041 9 1.80 12.0203 12.0234 12.0290 12.0413 12.0838 10 1.90 12.9491 12.9534 12.9608 12.9768 13.0306 11 2.00 13.6465 13.6519 13.6613 13.6812 13.7472
Gambar 3. 12 Grafik nilai error kasus 6 untuk setiap nilai parameter a1
3.4Analisis Error
Menganalisis Error sangat penting di dalam perhitungan menggunakan metode numerik. Error berasosiasi dengan seberapa dekat solusi hampiran terhadap solusi sejatinya. Semakin kecil error-nya, semakin teliti solusi numerik yang didapatkan. Dalam menganalisa error, ada dua hal yang harus dipahami yaitu, bagaimana error
timbul dan bagaimana menghitung error.
Misalkan y adalah hampiran (solusi numerik) terhadap nilai sejati ya (solusi analitik), maka selisih
a
disebut error. Jika tanda Error (positif atau negatif) tidak dipertimbangkan, maka muncul istilah error mutlak yang didefinisikan sebagai
| | ya y
Sayangnya, ukuran kurang bermakna sebab tidak menceritakan seberapa besar
error itu dibandingkan dengan solusi analitiknya. Oleh karena itu, error harus dinormalkan terhadap solusi analitiknya. Gagasan ini melahirkan apa yang dinamakan error relatif. Error relatif didefinisikan sebagai
r
Karena error dinormalkan terhadap nilai sejati (solusi analitik), maka error
relatif tersebut dinamakan juga errorrelatif sejati. Pada pembahasan ini, penulis menjadikan error relatif berbentuk persentase.
Pada bab ini akan dicari nilai nilai parameter yang memiliki error terkecil pada interval 0 a1 0.9. Karena a1 adalah bilangan riil, maka ada banyak bilangan yang berada pada interval tersebut. Maka dari itu dibatasi nilai a1 terkecil adalah 10-4. Untuk mencari nilai error terkecil pada interval tersebut maka dilakukan metode pencarian dengan algoritma berikut :
2. Uji nilai error apakah nilai error selalu mengalami kenaikan atau pertambahan dalam arti kurva nilai error menaik pada interval b a1 c. a. Jika iya, maka nilai error terkecil berada pada parameter a1 = b dan
Berdasarkan pengamatan dari subbab 3.3, dan dengan menggunakan algoritma diatas maka diperoleh hasil sebagai berikut.
Gambar 3.13 Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 1
2. Berdasarkan algoritma pencarian nilai error terkecil maka pada kasus 2 diperoleh nilai error relatif terkecil pada x = 2 berada pada a1 =0.5661 yaitu
0%
r . Karena bentuk kurva tidak kurva yang selalu menaik atau kurva yang selalu turun maka proses pencarian nilai error terkecil sampai pada iterasi yang terakhir yaitu iterasi ke-4. Pada iterasi pertama yaitu pencarian nilai error terkecil pada interval 0 a1 1 dimana ukuran langkah parameter adalah 0.1. Dari hasil perhitungan diperoleh nilai error terkecil pada a1 = 0.6. (lihat gambar 3.14a). Pada iterasi kedua yaitu pencari nilai error terkecil pada interval 0.5 a1 0.7 dimana ukuran langkah parameter menjadi 0.01. Dari hasil perhitungan diperoleh nilai error terkecil pada a1 = 0.57. (lihat gambar 3.14b). Pada iterasi ketiga yaitu pencarian nilai error terkecil pada interval
1
0.56 a 0.58 dimana ukuran langkah parameter menjadi 0.001. Dari hasil perhitungan diperoleh nilai error terkecil pada a1 = 0.566. (lihat gambar 3.14c) Pada iterasi keempat yaitu pencarian nilai error terkecil pada interval
1
0.565 a 0.567 dengan ukuran langkah menjadi 0.0001. Dari hasil
yaitu r 0%. (lihat gambar 3.14d). Untuk lebih jelasnya lihat gambar dibawah ini.
Gambar 3.14a Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 2 (ukuran langkah = 0.1)
Gambar 3.14c Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 2 (ukuran langkah = 0.001)
Pada Gambar 3.14c diperoleh error minimum berada pada a1 = 0.566 dengan nilai error yaitu r 0.000071%
Gambar 3.14d Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 2 (ukuran langkah = 0.0001)
3. Pada kasus 3, nilai error relatif terkecil untuk x = 2 diperoleh pada nilai parameter a1 = 0.0. adapun persentase error relatif terkecil yaitu
0.222685%.
r . Sedangkan error relatif terbesar berada pada nilai a1 = 0.9 yaitu dengan persentase r 0.361192%. Setiap nilai parameter a1 memiliki perbedaan nilai error yang berbeda. Nilai error relatif terus meningkat mulai dari parameter a1 = 0.0 sampai parameter a1 = 0.9. Pada kasus 3 nilai parameter juga mempengaruhi besar kecilnya nilai error. Adapun grafik kurva
error relatif pada x =2 untuk setiap parameter a1 adalah sebagai berikut.
Gambar 3.15 Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 3
4. Pada kasus 4, nilai error relatif terkecil untuk x = 2 diperoleh pada nilai parameter a1 = 0.0. Adapun persentase error relatif terkecil yaitu
0.153582 %
Gambar 3.16 Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 4
5. Pada kasus 5, nilai error relatif terkecil untuk x = 2 diperoleh pada nilai parameter a1 = 0.9. Adapun persentase error relatif terkecil yaitu
0.059706%.
r Sedangkan error relatif terbesar berada pada nilai a1 = 0.3 yaitu dengan persentase r 13.268341%. Setiap nilai parameter a1 memiliki perbedaan nilai error yang berbeda terutama pada nilai a1 = 0.6 dan a1 = 0.4. Pada saat tersebut nilai error memiliki perbedaan yang cukup tinggi dibandingkan dengan nilai parameter a1 yang lainnya. Kurva nilai error relatif tidak beraturan mulai dari parameter a1 = 0.0 sampai kepada parameter a1 = 0.9. Pada kasus 5 nilai parameter juga mempengaruhi besar kecilnya nilai
Gambar 3.17a Grafik Eror Berdasarkan Nilai Parameter Pada Kasus 5 (ukuran langkah = 0.1)
6. Pada kasus 5, nilai error relatif terkecil untuk x = 2 diperoleh pada nilai parameter a1 = 0.0. Adapun persentase error relatif terkecil yaitu
13.613585%.
r Sedangkan error relatif terbesar berada pada nilai a1 = 0.9 yaitu dengan persentase r 13.614747%. Setiap nilai parameter a1 memiliki perbedaan nilai error yang cukup kecil mulai dari a1 = 0.0 sampai kepada parameter a1 = 0.9. Semakin besar nilai parameter a1, semakin besar pula nilai
error yang dihasilkan. Selisih nilai error parameter ai dengan ai+ 1 juga semakin besar apabila i besar. Kurva nilai error relatif berbentuk kurva cenderung meningkat dari a1 = 0.0 sampai a1 = 0.9. Pada kasus 6 nilai parameter juga mempengaruhi besar kecilnya nilai error. Adapun grafik kurva
error relatif pada x =2 untuk setiap parameter a1 adalah sebagai berikut.
BAB 4
KESIMPULAN DAN SARAN
5.1Kesimpulan
Dari penelitian yang telah dilakukan ini dapat diambil beberapa kesimpulan mengenai penyelesaian persamaan diferensial menggunakan metode Runge-Kutta Ordo-2.
1. Penyelesaian persamaan diferensial linier tingkat dua menggunakan metode Runge-Kutta yaitu dengan menjadikan persamaan diferensial linier tingkat dua menjadi suatu sistem persamaan diferensial. Dimana didalam sistem tersebut terdapat dua buah persamaan yang memiliki saling keterkaitan, yaitu persamaan diferensial linier tingkat dua yang dirubah menjadi dua persamaan diferensial tingkat satu.
2. Pada pembahasan skripsi ini, tidak diperoleh nilai parameter yang tetap untuk mendapatkan nilai error yang paling minimum pada setiap penyelesaian persamaan diferensial linier tingkat dua secara umum. Setiap parameter memiliki nilai error yang bervariasi pada masing-masing persamaan.
ukuran langkah yang diberikan maka semakin kecil nilai error yang dihasilkan. Selain itu, penentuan nilai awal x0, y0, dan y’0 juga mempengaruhi besar kecilnya nilai error.
5.2Saran