SIMULASI SISTEM MANGSA-PEMANGSA PADA PEMANGSA YANG
HANYA BERADA PADA ZONA TIDAK DILINDUNGI
SRI SEPTIANA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
SRI SEPTIANA. Simulasi Sistem Mangsa-Pemangsa pada Pemangsa yang Hanya Berada pada Zona Tidak Dilindungi. Dibimbing oleh ALI KUSNANTO dan ENDAR HASAFAH NUGRAHANI.
Dalam tulisan ini dipelajari model populasi mangsa-pemangsa yang habitatnya dibagi menjadi dua zona, yaitu zona dilindungi dan zona tidak dilindungi dimana pada zona dilindungi pemangsa tidak dapat masuk ke dalamnya, sedangkan pada zona tidak dilindungi mangsa dan pemangsa dapat hidup secara bersamaan. Dalam pembahasan ini permasalahan dibagi menjadi dua model, yaitu model mangsa-pemangsa pada saat pemangsa sangat bergantung pada mangsanya (model 1) dan pada saat pemangsa tidak sangat bergantung pada mangsanya (model 2). Analisis pada kedua model tersebut dilakukan dengan membandingkan laju interaksi antara mangsa dan pemangsa. Dari hasil analisis tersebut diperoleh tiga titik tetap pada model 1 dan empat titik tetap pada model 2.
Dinamika model digambarkan dengan bantuan software Mathematica 7.0. Secara keseluruhan dari setiap kasus yang diamati, kestabilan populasi mangsa pada zona dilindungi dan zona tidak dilindungi bergantung pada laju interaksi antara mangsa dan pemangsa. Jika besarnya interaksi antara mangsa dan pemangsa diperbesar, maka populasi mangsa pada zona tidak dilindungi dapat berada pada ambang kepunahan, sedangkan untuk populasi mangsa pada zona dilindungi akan mengalami peningkatan populasi. Dalam model 1, banyaknya populasi mangsa pada zona dilindungi mengalami peningkatan populasi lebih banyak dibandingkan model 2.
ABSTRACT
SRI SEPTIANA. Simulation on Prey-Predator System with Predators Present Only in the Unreserved Area. Supervised by ALI KUSNANTO and ENDAR HASAFAH NUGRAHANI.
This paper studied the prey-predator population models that divide the habitat into two areas, namely reserved area and unreserved area. In the reserved area, it is assumed that predators cannot enter into it, while in the unreserved area prey and predators can live simultaneously. In the discussion, two models are being considered namely the prey-predator model when predator depends on prey (first model) and when predators have a choice of prey (second model). Analysis on both models is done by comparing the interaction between prey and predator. The results of the analysis give three fixed points on the first model and four fixed points on the second model.
The simulation study is carried out using Mathematica 7.0 software. In every case, the stability of prey populations in reserved area and unreserved area depend on the interaction rate between prey and predator. If the magnitude of the prey-predator interaction is enlarged, then the prey population in the unreserved area tends to extinct, but the prey population in reserved area tends to increase. Moreover, population increase in reserved area of the first model is larger than that of the second model.
SIMULASI SISTEM MANGSA-PEMANGSA PADA PEMANGSA YANG
HANYA BERADA PADA ZONA TIDAK DILINDUNGI
SRI SEPTIANA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul
: Simulasi Sistem Mangsa-Pemangsa pada Pemangsa yang Hanya Berada
pada Zona Tidak Dilindungi
Nama : Sri Septiana
NRP
: G54070042
Menyetujui,
Pembimbing I
Pembimbing II
Drs. Ali Kusnanto, M.Si
Dr. Ir. Endar Hasafah Nugrahani, MS
NIP. 19650820 199003 1 001
NIP. 19631228 198903 2 001
Mengetahui,
Ketua Departemen Matematika
Dr. Berlian Setiawaty, MS
NIP. 19650505 198903 2 004
KATA PENGANTAR
Puji dan syukur penulis panjatkan kehadirat Allah SWT atas segala nikmat, karunia, izin, dan pertolongan-Nya sehingga penulisan skripsi ini berhasil diselesaikan. Tema yang dipilih adalah Pemodelan Matematika dengan judul Simulasi Sistem Mangsa-Pemangsa pada Pemangsa yang Hanya Berada pada Zona Tidak Dilindungi. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor. Terima kasih penulis ucapkan kepada :
1. Bapak Drs. Ali Kusnanto, M.Si dan Ibu Endar Hasafah Nugrahani, MS. selaku dosen pembimbing atas segala kesabaran dan masukannya selama membimbing penulis; kepada Bapak Dr. Paian Sianturi selaku penguji;
2. Ayahanda Kastowo dan Ibunda Mariyam yang banyak memberi nasihat dan dukungan
serta do’a yang tak terkira, Kakakku Elis Citrawati dan Adikku Imam Nugroho yang
selalu memberi semangat belajar dan mengingatkan tiada henti, serta Margono atas
segenap perhatian dan semangat, kesabaran serta do’anya selama penyusunan skrispi; 3. keluarga besar dan staf Departemen MatematikaFMIPA IPB: Bu Susi, Pak Yono, Bu
Ade, Mas Heri, Mas Deni, Pak Bono, dkk yang telah banyak membantu dalam penyusunan skripsi;
4. teman-teman satu bimbingan: Fajar, Rahma, dan Aje yang selalu saling mengingatkan dan membantu dalam penyusunan skripsi;
5. teman-teman terbaikku di kampus: Melon, Ayung, Rahma, Della, Tyas, Fajar, Denda, Rofi, Pandi, Dian, dan Rizky yang selalu memberikan semangat dan bantuan serta mengingatkan penulis dalam penyusunan skripsi;
6. teman-teman mahasiswa matematika angkatan 44: Melon, Ayung, Rahma, Tyas, Della, Fajar, Rofi, Denda, Dian, Pandi, Rizky, Ruhiyat, Wahyu, Iam, Lingga, Ima, Dora, Lugina, Yuyun, Nunuy, Ucu, Wenti, Ndep, Pepi, Ali, Aje, Deva, Eka, Titi, Lilis, Aqil, Ikhsan, Vianey, Yuli, Masayu, Diana, Yanti, Indin, Sari, Lukman, Olih, Cepi, Aswin, Imam, Ririh, Iresa, Anis, Tita, Arina, Tanti, Lili, Nurus, Nadiroh, Naim, Endro atas segenap dukungan, suka-duka dan kebahagiaan selama penulis menempuh studi di Departemen Matematika;
7. kakak-kakak mahasiswa angkatan 43: kak nia, kak wira, kak copi, kak arum, kak tami, kak apri, kak supri, kak slamet dkk yang telah memberikan banyak informasi dan motivasinya; adik-adik mahasiswa matematika angkatan 45: Dono, Feni, Aci, Yunda, Bolo, Isna dkk yang telah mendukung penulis dalam menyusun skripsi;
8. keluarga besar kosan Puri 9: Nuning, Riska, Susan, Fitri, Ivon, Lia, Ines, Nita, Omi, Anis, Ibu Yanti, dan Nela yang telah memberikan bantuan, informasi, do’a dan motivasinya kepada penulis dalam penyusunan skripsi;
9. pihak-pihak lain yang telah membantu penyusunan skripsi ini, yang tidak dapat disebutkan satu per satu.
Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan. Oleh karena itu, penulis mengharapkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat bagi semua pihak yang memerlukan.
Bogor, Agustus 2011
RIWAYAT HIDUP
Penulis lahir di Tangerang pada tanggal 16 September 1989 sebagai anak ke dua dari tiga bersaudara, anak dari pasangan Kastowo dan Mariyam. Tahun 2001 penulis lulus dari SDS Kuncup Mekar. Tahun 2004 penulis lulus dari SMPN 1 Tangerang. Tahun 2007 penulis lulus dari SMAN 6 Tangerang dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI), Tingkat Persiapan Bersama. Pada tahun 2008, penulis memilih mayor Matematika pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
vii
DAFTAR ISI
Halaman
DAFTAR ISI ... vii
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN ... viii
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Linear ... 2
2.2 Titik Tetap... 2
2.3 Pelinearan ... 2
2.4 Nilai Eigen dan Vektor Eigen ... 2
2.5 Analisis Kestabilan Titik Tetap ... 2
III PEMODELAN 3.1 Model Mangsa-Pemangsa ... 4
3.2 Model Mangsa-Pemangsa pada Saat Pemangsa Sangat Bergantung pada Mangsanya (Model 1) ... 4
3.3 Model Mangsa-Pemangsa pada Saat Pemangsa Tidak Sangat Bergantung pada Mangsanya (Model 2) ... 5
IV PEMBAHASAN 4.1 Analisis Model 1 ... 6
4.2 Analisis Model 2 ... 7
4.3 Simulasi Model 1... 8
4.4 Simulasi Model 2 ... 12
V KESIMPULAN ... 18
DAFTAR PUSTAKA ... 19
viii
DAFTAR GAMBAR
Halaman
1 Jenis kestabilan titik tetap ... 3
2 Skema model mangsa-pemangsa pada model 1 ... 4
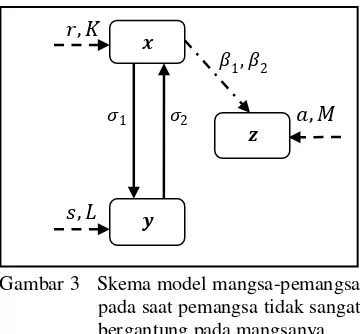
3 Skema model mangsa-pemangsa pada model 2 ... 5
4 Orbit kestabilan di sekitar ( , , ), dengan �2= 0.7 pada model 1 ... 9
5 Orbit kestabilan di sekitar ( , ), dengan �2= 0.7 pada model 1 ... 9
6 Orbit kestabilan di sekitar ( , ), dengan �2= 0.7 pada model 1... 9
7 Orbit kestabilan di sekitar ( , ), dengan �2= 0.7 pada model 1 ... 9
8 Dinamika populasi dari ketiga model terhadap � dengan �2= 0.7 pada model 1 ... 9
9 Orbit kestabilan di sekitar ( , , ), dengan �2= 0.4 pada model 1 ... 10
10 Orbit kestabilan di sekitar ( , ), dengan �2= 0.4 pada model 1 ... 10
11 Orbit kestabilan di sekitar ( , ), dengan �2= 0.4 pada model 1... 10
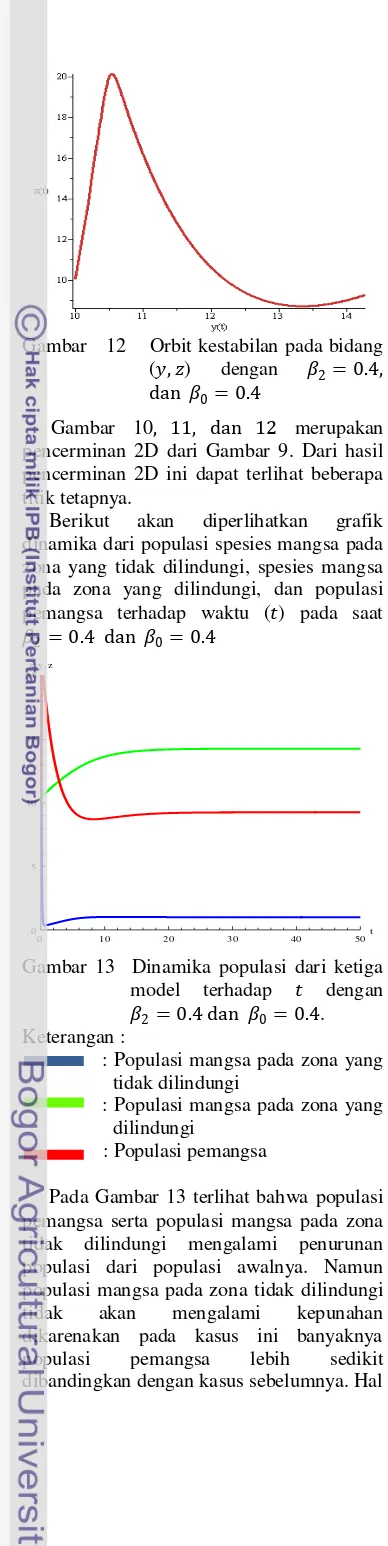
12 Orbit kestabilan di sekitar ( , ), dengan �2= 0.4 pada model 1 ... 11
13 Dinamika populasi dari ketiga model terhadap � dengan �2= 0.4 pada model 1 ... 11
14 Orbit kestabilan di sekitar ( , , ), dengan �2= 0.1 pada model 1 ... 11
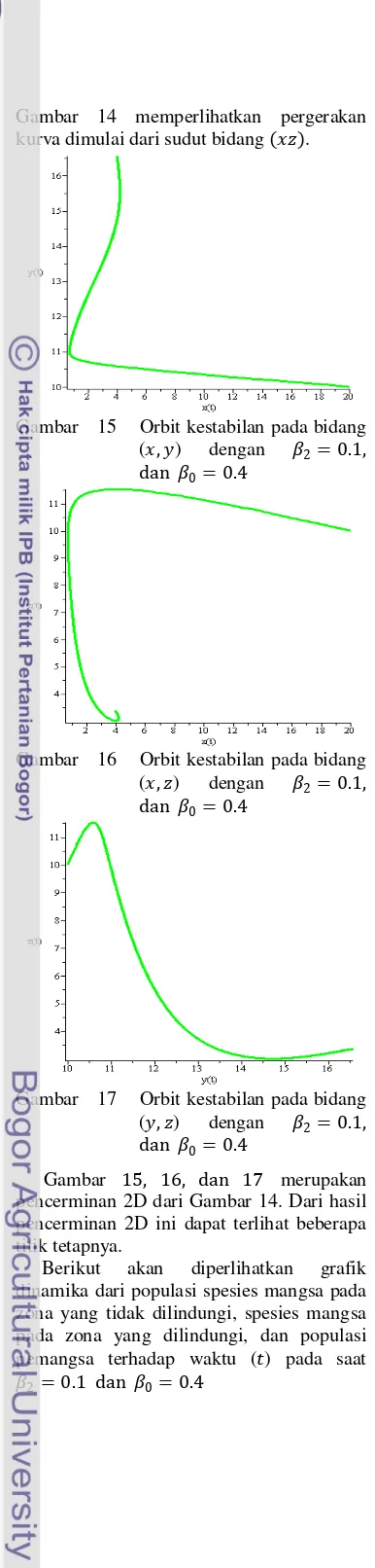
15 Orbit kestabilan di sekitar ( , ), dengan �2= 0.1 pada model 1 ... 12
16 Orbit kestabilan di sekitar ( , ), dengan �2= 0.1 pada model 1... 12
17 Orbit kestabilan di sekitar ( , ), dengan �2= 0.1 pada model 1 ... 12
18 Dinamika populasi dari ketiga model terhadap � dengan �2= 0.1 pada model 1 ... 12
19 Orbit kestabilan di sekitar ( , , ), dengan �2= 0.7 pada model 2 ... 13
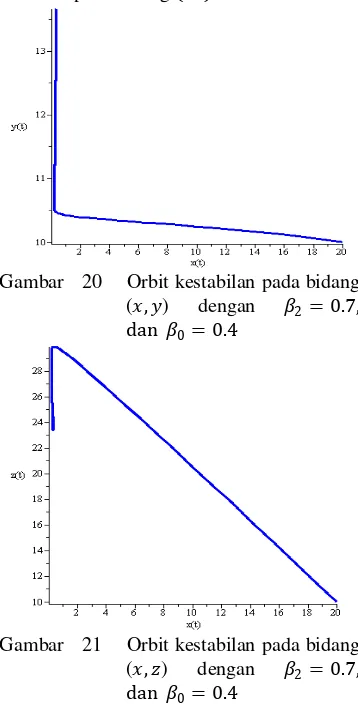
20 Orbit kestabilan di sekitar ( , ), dengan �2= 0.7 pada model 2 ... 13
21 Orbit kestabilan di sekitar ( , ), dengan �2= 0.7 pada model 2... 13
22 Orbit kestabilan di sekitar ( , ), dengan �2= 0.7 pada model 2 ... 14
23 Dinamika populasi dari ketiga model terhadap � dengan �2= 0.7 pada model 2 ... 14
24 Orbit kestabilan di sekitar ( , , ), dengan �2= 0.4 pada model 2 ... 15
25 Orbit kestabilan di sekitar ( , ), dengan �2= 0.4 pada model 2 ... 15
26 Orbit kestabilan di sekitar ( , ), dengan �2= 0.4 pada model 2... 15
27 Orbit kestabilan di sekitar ( , ), dengan �2= 0.4 pada model 2 ... 15
28 Dinamika populasi dari ketiga model terhadap � dengan �2= 0.4 pada model 2 ... 15
29 Orbit kestabilan di sekitar ( , , ), dengan �2= 0.1 pada model 2 ... 16
30 Orbit kestabilan di sekitar ( , ), dengan �2= 0.1 pada model 2 ... 17
31 Orbit kestabilan di sekitar ( , ), dengan �2= 0.1 pada model 2... 17
32 Orbit kestabilan di sekitar ( , ), dengan �2= 0.1 pada model 2 ... 17
33 Dinamika populasi dari ketiga model terhadap � dengan �2= 0.1 pada model 2 ... 17
DAFTAR LAMPIRAN
Halaman 1 Penentuan Titik Tetap Model 1 ... 212 Penentuan Nilai Eigen Model 1 ... 23
3 Penentuan Titik Tetap Model 2 ... 28
4 Penentuan Nilai Eigen Model 2 ... 31
5 Program Penentuan Orbit Kestabilan dan Solusi Model 1 ... 36
I PENDAHULUAN
1.1 Latar BelakangMakhluk hidup pada hakekatnya tidak dapat hidup sendirian, sehingga diperlukan adanya suatu interaksi antar berbagai populasi dan berbagai spesies yang hidup secara bersamaan. Pada populasi tersebut akan terjadi suatu interaksi antar spesies, di mana kedua spesies berinteraksi dalam suatu rantai makanan.
Biosfer merupakan suatu zona yang penting untuk kegiatan biologi terutama terhadap perubahan ekologi dan lingkungan yang ada. Perubahan ekologi dan lingkungan seperti eksploitasi berlebihan, banyaknya pemangsa, dan pencemaran lingkungan dapat menyebabkan banyaknya spesies didorong untuk punah dan masih banyak yang lainnya berada pada ambang kepunahan. Untuk melindungi spesies-spesies tersebut harus dilakukan suatu tindakan, salah satu tindakannya adalah dengan menciptakan zona dilindungi yang dapat mengurangi interaksi dari spesies-spesies tersebut terhadap perubahan ekologi dan lingkungan yang ada. (Dubey 2006).
Model mangsa-pemangsa ini menggambarkan tentang adanya suatu interaksi antar spesies yang hidup secara bersamaan. Spesies mangsa yang dilestarikan dapat dilindungi dari pemangsa dengan menciptakan suatu batas buatan yang ukurannya dibuat agar mangsa saja yang dapat bergerak lalu lalang tetapi pemangsa tidak dapat memakan mangsa pada saat berada pada zona dilindungi. Oleh karena itu, pemangsa yang berada di luar zona dilindungi tidak dapat memasuki batas yang telah dibuat tersebut sehingga aman untuk mangsa yang hidup pada zona dilindungi dan juga dapat membuat habitat terbagi menjadi dua zona, yaitu zona dilindungi dan zona tidak dilindungi.
Simulasi sistem mangsa-pemangsa pada pemangsa yang hanya berada pada zona tidak dilindungi memiliki dua tipe model kasus, yaitu pada saat pemangsa sangat bergantung pada mangsanya dan pada saat pemangsa tidak sangat bergantung pada mangsanya. Dalam pembahasan dinamika sistem mangsa-pemangsa ini juga mempertimbangkan dua tipe zona yang akan digunakan, yaitu zona dilindungi dimana pemangsa tidak dapat memasuki zona ini dan zona tidak dilindungi dimana mangsa maupun pemangsa dapat bergerak atau hidup secara bersamaan.
Dalam karya ilmiah ini akan dibahas model mangsa-pemangsa yang dimodelkan oleh Dubey (2006). Kedua model kasus yang akan dibahas akan menghasilkan suatu model baru yang dapat dianalisis dinamika populasi mangsa pada zona dilindungi dan zona tidak dilindungi ketika terdapat pemangsa pada zona tidak dilindungi, dinamika populasi pemangsa terhadap perubahan laju interaksi antara mangsa dan pemangsa, dan perbandingan model pemangsa pada kedua model kasus yang akan dibahas. Dalam pembahasan ini, akan dilakukan beberapa tahapan untuk dapat menganalisis model tersebut. Pertama, akan ditentukan titik tetap pada setiap model dari kedua kasus tersebut. Selanjutnya ditentukan matriks Jacobi dengan melakukan pelinearan pada setiap persamaan model yang ada terhadap setiap variabel. Kemudian akan ditentukan nilai eigen yang dapat digunakan untuk menganalisis kestabilan titik tetap yang dihasilkan pada setiap model dalam kedua model kasus tersebut.
1.2 Tujuan
Tujuan dari penulisan karya ilmiah ini adalah untuk :
1. Menggambarkan dinamika populasi mangsa pada zona dilindungi dan zona tidak dilindungi ketika terdapat pemangsa pada zona tidak dilindungi. 2. Menggambarkan dinamika populasi
pemangsa dengan adanya perubahan terhadap laju interaksi antara mangsa dan pemangsa.
II LANDASAN TEORI
2.1 Sistem Persamaan Diferensial LinearSuatu sistem persamaan diferensial orde
1 dinyatakan sebagai berikut akan diperoleh bentuk sistem persamaan diferensial linear sebagai berikut
�
�� ≡ =� + , 0 = 0 (2) (Farlow 1994)
2.2 Titik Tetap
Diberikan sistem persamaan diferensial sebagai berikut
=� 1, 2,… , 1, 2,… R� (3) suatu titik yang memenuhi � ∗ = 0 disebut titik keseimbangan atau titik tetap
dari sistem. dapat diabaikan sehingga didapatkan persamaan linear
2.4 Nilai Eigen dan Vektor Eigen
� adalah matriks � x �, maka suatu ditulis kembali sebagai berikut :
� − �I = 0 (7) dengan I adalah matriks identitas. Persamaan (7) mempunyai solusi taknol jika dan hanya jika,
� � � − �� = � − �I = 0 (8) Persamaan (8) disebut persamaan karakteristik dari matriks �.
(Anton 1995)
2.5 Analisis Kestabilan Titik Tetap Diberikan sistem persamaan diferensial sembarang
=� , R� (9) Analisis kestabilan titik tetap dilakukan melalui matriks Jacobi, yaitu matriks �.
Penentuan kestabilan titik tetap diperoleh dengan melihat nilai-nilai eigennya, yaitu � dengan = 1,2,3, . . ,� yang diperoleh dari
� � � − �I = 0. Secara umum, kestabilan titik tetap mempunyai tiga perilaku sebagai berikut :
1.Stabil, jika
Setiap nilai eigen real bernilai negatif (� < 0) untuk semua ,
3
sama dengan nol (� (�)≥0) untuk semua .
3.Sadel, jika perkalian dari kedua nilai eigen real sembarang adalah negatif (�, �� < 0) untuk semua dan � sembarang. Titik tetap sadel ini bersifat tak stabil.
(Tu 1994)
Misalkan diberikan matriks � berukuran 2 2 sebagai berikut
�= � �
dengan persamaan karakteristik � �(� −
�I) = 0 dan I adalah matriks identitas, maka persamaan karakteristiknya menjadi
� � � − � � − � = 0 sedemikian Terdapat tiga kasus untuk nilai Δ:
Kasus Δ< 0. eigen real bernilai positif (�1> 0,�2> 0), maka titik tetap bersifat “simpul tidak stabil”.
Jika �< 0 dan kedua nilai eigen real bernilai negatif (�1< 0,�2< 0), maka titik tetap bersifat “simpul stabil”. �2−4Δ< 0.
Jika �> 0 dan kedua nilai eigen imajiner (�1,2= ± �), maka titik tetap bersifat “spiral tidak stabil”.
Jika �< 0 dan kedua nilai eigen imajiner (�1,2= ± �), maka titik tetap bersifat “spiral stabil”.
Jika �= 0 dan kedua nilai eigen imajiner murni
(�1,2 = ±�), maka titik tetap degenerate nodes yang terletak pada parabola ini. Jika kedua nilai eigen bernilai sama, maka titik tetap tersebut bersifat “simpul sejati”.
Kasus ∆= 0.
Jika salah satu nilai eigen bernilai nol, maka titik asal bersifat “titik tetap tak terisolasi”.
(Strogatz 1994)
Gambar jenis-jenis kestabilan titik tetap seperti yang dijelaskan di atas dapat dilihat dalam Gambar 1.
Simpul Stabil Simpul Tak Stabil Sadel Spiral Tak Stabil
Simpul Terisolasi Spiral Stabil Simpul Sejati Center
III PEMODELAN
3.1 Model Mangsa-PemangsaModel yang akan dianalisis merupakan suatu model yang dibangun berdasarkan interaksi antar spesies yang hidup secara bersamaan pada suatu habitat. Dalam model sistem mangsa-pemangsa yang dikenalkan oleh Dubey (2006) ini membagi habitat menjadi dua zona, yaitu zona dilindungi dan zona tidak dilindungi dan juga membagi permasalahan yang ada menjadi dua model, yaitu pada saat pemangsa sangat bergantung pada mangsanya dan pada saat pemangsa tidak sangat bergantung pada mangsanya.
Konstruksi model matematika untuk model mangsa-pemangsa ini menggunakan asumsi :
1. Pemangsa tidak dapat memasuki zona dilindungi.
2. Semua parameter dan variabel yang digunakan pada masing-masing kasus bernilai positif.
3. Nilai parameter �>�1, >�2,
dan �>�1+�1
Secara umum, model simulasi sistem mangsa-pemangsa pada pemangsa yang hanya berada pada zona tidak dilindungi adalah sebagai berikut :
� tidak dilindungi ke zona dilindungi �2 laju perpindahan mangsa dari zona
dilindungi ke zona tidak dilindungi � laju pertumbuhan intrinsik mangsa
pada zona tidak dilindungi
laju pertumbuhan intrinsik mangsa pada zona dilindungi
besarnya daya dukung lingkungan pada zona tidak dilindungi
besarnya daya dukung lingkungan model sistem mangsa-pemangsa ini merupakan laju interaksi antara mangsa dan pemangsa. Laju interaksi antara mangsa dan pemangsa tersebut akan dianalisis dalam dua model permasalahan yang akan dibahas, yaitu pada saat pemangsa sangat bergantung pada mangsanya dan pada saat pemangsa tidak sangat bergantung pada mangsanya.
3.2 Model Sistem Mangsa - Pemangsa Pada Saat Pemangsa Sangat Bergantung Pada Mangsanya (Model 1).
Pada suatu populasi akan terjadi interaksi antar spesies yang hidup secara bersamaan dalam populasi tersebut, di mana spesies-spesies ini akan berinteraksi dalam suatu rantai makanan. Dalam rantai makanan tersebut, mangsa merupakan sumber makanan bagi pemangsa. Oleh karena itu, mangsa akan menjadi sasaran utama bagi pemangsa dalam mencari makan demi kelangsungan hidupnya.
Pada Gambar 2 dapat dilihat skema diagram model matematika untuk model sistem mangsa-pemangsa pada saat pemangsa sangat bergantung pada mangsanya.
�0
Gambar 2 Skema model mangsa-pemangsa pada saat pemangsa sangat bergantung pada mangsanya Dari Gambar 2 terlihat bahwa, perubahan laju populasi mangsa yang ada pada zona tidak dilindungi dipengaruhi oleh laju pertumbuhan intrinsik dari mangsa pada zona tidak dilindungi � dengan daya dukung
lingkungannya serta dipengaruhi dengan adanya laju perpindahan mangsa dari zona dilindungi ke zona tidak dilindungi �2, kemudian populasi mangsa pada zona tidak dilindungi ini akan mengalami penurunan populasi dengan adanya perpindahan mangsa dari zona tidak dilindungi ke zona dilindungi �1 dan dengan adanya interaksi antara mangsa pada zona tidak dilindungi dengan pemangsa yang dapat menyebabkan kematian dari mangsa pada zona tidak dilindungi �1. Perubahan laju populasi mangsa yang ada pada zona dilindungi dipengaruhi oleh laju pertumbuhan intrinsik dari mangsa tersebut dengan daya dukung lingkungannya serta dipengaruhi dengan laju perpindahan mangsa dari zona tidak dilindungi ke zona dilindungi �1, kemudian populasi mangsa pada zona ini akan mengalami penurunan populasi dengan adanya perpindahan mangsa dari zona dilindungi ke zona tidak dilindungi �2. Sedangkan untuk perubahan laju populasi pemangsa dipengaruhi oleh besarnya laju interaksi antara mangsa dan pemangsa �2, kemudian populasi dari pemangsa akan mengalami kematian secara alami �0.
Sehingga model persamaan untuk pemangsa sangat bergantung pada mangsanya adalah sebagai berikut :
�
Spesies mangsa merupakan sumber makanan bagi pemangsa. Namun pada kasus ini, pemangsa tidak begitu bergantung pada mangsa yang ada dikarenakan pada model ini terdapat jenis spesies mangsa lain yang dapat dijadikan sumber makanan lain bagi pemangsa demi kelangsungan hidupnya.
Pada Gambar 3 dapat dilihat skema diagram model matematika untuk model mangsa-pemangsa pada saat pemangsa tidak sangat bergantung pada mangsanya.
Gambar 3 Skema model mangsa-pemangsa pada saat pemangsa tidak sangat bergantung pada mangsanya Dari Gambar 3 terlihat bahwa, perubahan laju populasi mangsa yang ada pada zona tidak dilindungi dipengaruhi oleh laju pertumbuhan intrinsik dari mangsa pada zona tidak dilindungi � dengan daya dukung lingkungannya serta dipengaruhi dengan adanya laju perpindahan mangsa dari zona dilindungi ke zona tidak dilindungi �2, kemudian populasi mangsa pada zona ini akan mengalami penurunan populasi dengan adanya perpindahan mangsa dari zona tidak dilindungi ke zona dilindungi �1 dan dengan adanya interaksi antara mangsa pada zona tidak dilindungi dan pemangsa yang dapat menyebabkan kematian dari mangsa pada zona tidak dilindungi �1. Perubahan laju populasi mangsa pada zona dilindungi dipengaruhi oleh laju pertumbuhan intrinsik dari mangsa tersebut dengan daya dukung lingkungannya serta dipengaruhi dengan laju perpindahan mangsa dari zona tidak dilindungi ke zona dilindungi �1, kemudian populasi mangsa pada zona ini akan mengalami penurunan populasi dengan adanya perpindahan mangsa dari zona dilindungi ke zona tidak dilindungi �2. Sedangkan untuk laju pertumbuhan populasi pemangsa dipengaruhi dengan adanya laju pertumbuhan pemangsa � serta dengan adanya laju interaksi antara mangsa dan pemangsa �2, serta daya dukung lingkungannya .
Sehingga model persamaan untuk pemangsa tidak sangat bergantung pada mangsanya adalah sebagai berikut :
IV PEMBAHASAN
sehingga diperoleh tiga titik tetap non-negatif sebagai berikut :
0= 0,0,0
(bukti dapat dilihat pada Lampiran 1)
Selanjutnya akan dianalisis kestabilan titik tetap dari model persamaan (3.2). Untuk itu, persamaan (3.2) akan dilinearkan ke dalam bentuk =� , dengan =
( , , ) dan � merupakan matriks Jacobi
yang dapat digunakan untuk menganalisis kestabilan titik tetap yang telah diperoleh pada model persamaan ini.
�= disubstitusikan ke dalam persamaan (4.1),
sehingga diperoleh matriks Jacobi dari setiap titik tetap sebagai berikut :
�10,0,0 =
Untuk memperoleh nilai eigen digunakan persamaan karakteristik � − �� = 0,
7
Pada saat kondisi �2>�0, �2=�0,
dan �2<�0 nilai parameter yang
digunakan akan menghasilkan nilai eigen
�1> 0, �2< 0 dan �3< 0 sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetap untuk 1 pada ketiga kondisi tersebut bersifat sadel.
Kestabilan Sistem di Titik Tetap 2 ∗, ∗, ∗
Kestabilan titik tetap 2 diperoleh dengan mengamati nilai eigen dari matriks
�3, yaitu �3+�1�2+�2�+�3= 0 dengan nilai �1, �2, �3 terdapat pada Lampiran 2. Kemudian bentuk dari nilai eigen tersebut akan diberikan nilai parameter untuk dapat ditentukan jenis kestabilan dari titik tetap 2. (bukti dapat dilihat pada Lampiran 2)
Untuk mengetahui jenis kestabilan titik tetap pada ketiga titik tetap yang terdapat pada model 1, dapat dilihat pada Tabel 1.
Titik Tabel 1 Kestabilan Titik Tetap
4.2 Analisis Model 2
Titik tetap pada model persamaan (3.3) diperoleh dengan menentukan �
�� = 0,
(bukti dapat dilihat pada Lampiran 3)
Selanjutnya akan dianalisis kestabilan titik tetap yang terdapat pada model persamaan (3.3). Untuk itu, persamaan (3.3) akan dilinearkan ke dalam bentuk =� , dengan = ( , , ) dan � merupakan matriks Jacobi yang dapat digunakan untuk
menganalisis kestabilan titik tetap yang telah diperoleh pada persamaan ini.
�= diperoleh matriks Jacobi dari setiap titik tetap sebagai berikut :
10,0,0 =
8
Karena semua parameter bernilai positif dan nilai parameter �>�1 dan >�2, maka �1> 0, �2> 0, dan �3> 0. Dengan demikian menurut jenis kestabilannya titik tetap 0 bersifat tak stabil.
Kestabilan Sistem di Titik Tetap 1 0,0,
Untuk memperoleh nilai eigen digunakan persamaan karakteristik � − �� = 0, Karena semua parameter bernilai positif dan nilai parameter �>�1+�1 dan
>�2, maka �1< 0, �2> 0, dan �3< 0 sehingga menurut jenis kestabilannya titik tetap 1 bersifat sadel.
Kestabilan Sistem di Titik Tetap 2 , , 0
Seperti pada model 1, dalam proses mencari nilai eigen untuk titik tetap ini akan menghasilkan suatu bentuk persamaan aljabar � 3+ 2+ +�= 0 dengan aljabar tersebut akan menghasilkan tiga nilai yang berbeda. Ketiga nilai tersebut akan ditunjukkan pada simulasi.
Titik tetap 2pada saat kondisi �2>�0,
�2=�0, dan �2<�0, nilai parameter yang
digunakan akan menghasilkan nilai eigen
�1> 0, �2< 0, dan �3< 0 sehingga dari nilai-nilai eigen yang diperoleh titik tetap 2 pada ketiga kondisi tersebut bersifat sadel.
Kestabilan Sistem di Titik Tetap aljabar tersebut akan menghasilkan tiga nilai
∗ yang berbeda. Ketiga nilai ∗ tersebut
akan ditunjukkan pada simulasi.
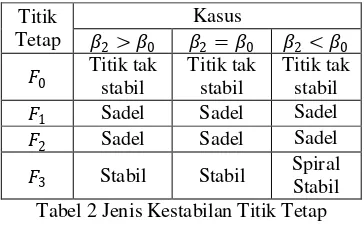
Titik tetap 3 pada saat kondisi �2 >
�0 dan �2=�0, nilai parameter yang
digunakan akan menghasilkan nilai eigen
�1< 0, �2< 0, dan �3< 0 sehingga dari nilai-nilai eigen yang diperoleh titik tetap 3 bersifat stabil. Sedangkan pada saat kondisi
�2<�0, nilai parameter yang digunakan akan menghasilkan nilai eigen �1< 0,
�2 dan �3 kompleks dengan bagian real
bernilai negatif sehingga dari nilai-nilai eigen yang diperoleh titik tetap 3 pada kondisi ini bersifat spiral stabil.
(bukti dapat dilihat pada Lampiran 4)
Untuk mengetahui jenis kestabilan titik tetap pada keempat titik tetap pada kasus 2 dapat dilihat pada Tabel 2.
Titik Tabel 2 Jenis Kestabilan Titik Tetap
4.3 Simulasi Model 1 >> Kasus ��>��
Nilai parameter yang digunakan dalam kondisi ini adalah = 0.6, �= 1, = 40,
= 40, �1= 0.2,�2= 0.4,�0= 0.4,�1=
0.7, �2= 0.7, dengan nilai awal 0 = 20,
0 = 10, dan 0 = 10.
Dari nilai parameter yang digunakan diperoleh titik tetap 0= (0,0,0) yang bersifat sadel serta titik tetap 2=
(0.5714285714, 13.88217026,
15.00461924) yang memiliki jenis
9 nilai titik tetapnya sehingga dari persamaan aljabar tersebut akan diperoleh tiga nilai
yang berbeda, yaitu
1= 23.68146140, 2= 43.62267459,
dan 3=−3.304135986. Ketiga nilai
tersebut jika disubstitusi ke dalam persamaan akan menghasilkan nilai
1=−12.31219692, 2= 31.68825945,
dan 3= 7.290604135. Terlihat bahwa
nilai yang dihasilkan untuk 1 serta nilai 2 yang dihasilkan bernilai negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada kedua zona bernilai positif. Sehingga pada kasus
�2>�0 terdapat tiga titik tetap, yaitu
0, 1, dan 2 dengan nilai titik tetap
1= 43.62267459, 31.68825945, 0
yang memiliki jenis kestabilan berupa sadel. Berikut akan diberikan gambar orbit 3 dimensinya pada sistem persamaan (3.2)
Gambar 4 Orbit Kestabilan di sekitar ( , , ) dengan �2 = 0.7,
dan �0 = 0.4.
Gambar 4 memperlihatkan pergerakan kurva dimulai pada sudut bawah dari titik terendah pada bidang ( ). pencerminan 2D ini dapat terlihat beberapa titik tetapnya.
10 dibandingkan dengan populasi mangsa pada kedua zona. Hal ini dapat membuat ancaman bagi mangsa untuk menuju kepunahan khususnya untuk mangsa yang ada pada zona tidak dilindungi karena mangsa pada zona ini hidup secara bersamaan dengan banyaknya pemangsa tersebut dan merupakan sumber makanan bagi pemangsa. Namun mangsa yang ada pada zona dilindungi akan mengalami kenaikan populasinya dikarenakan pada zona dilindungi tidak terdapat pemangsa yang hidup dalam zona ini.
>> Kasus ��=��
Nilai parameter yang digunakan dalam kondisi ini adalah = 0.6, �= 1, = 40,
= 40, �1= 0.2, �2= 0.4, �0 = 0.4,
�1= 0.7, �2= 0.4, dengan nilai awal
0 = 20, 0 = 10, dan 0 = 10.
Dari nilai parameter yang digunakan diperoleh titik tetap 0= (0,0,0) yang bersifat sadel serta titik tetap 2= (1,
14.26783617, 9.260192096) yang bersifat
stabil, sedangkan untuk titik tetap 1 yang dalam proses mencari nilai titik tetapnya akan menghasilkan suatu bentuk persamaan aljabar � 3+ 2+ +�= 0 dengan
sehingga diperoleh tiga nilai yang berbeda nilainya, yaitu 1= 23.68146140, 2=
43.62267459, dan 3=−3.304135986.
Ketiga nilai tersebut jika disubstitusi ke dalam persamaan akan menghasilkan nilai
1=−12.31219692, 2= 31.68825945,
dan 3= 7.290604135. Terlihat bahwa
nilai yang dihasilkan untuk 1 serta nilai 3 yang dihasilkan bernilai negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada kedua zona bernilai positif. Sehingga pada kasus
�2=�0 terdapat tiga titik tetap, yaitu
0, 1, dan 2 dengan nilai titik tetap
1= 43.62267459, 31.68825945, 0
yang memiliki jenis kestabilan berupa sadel.
Berikut akan diberikan gambar orbit 3 dimensinya pada sistem persamaan (3.3)
Gambar 9 Orbit kestabilan pada bidang ( , , ) dengan �2= 0.4,
dan �0= 0.4
11 pencerminan 2D ini dapat terlihat beberapa titik tetapnya.
Berikut akan diperlihatkan grafik dinamika dari populasi spesies mangsa pada zona yang tidak dilindungi, spesies mangsa pada zona yang dilindungi, dan populasi
Pada Gambar 13 terlihat bahwa populasi pemangsa serta populasi mangsa pada zona tidak dilindungi mengalami penurunan populasi dari populasi awalnya. Namun populasi mangsa pada zona tidak dilindungi tidak akan mengalami kepunahan dikarenakan pada kasus ini banyaknya populasi pemangsa lebih sedikit dibandingkan dengan kasus sebelumnya. Hal
ini dikarenakan besarnya laju interaksi antara mangsa dan pemangsa diperkecil nilainya sehingga dapat membuat populasi pemangsa mengalami penurunan populasi dan dapat membuat populasi mangsa pada kedua zona tetap dapat bertahan hidup.
>> Kasus ��<��
Nilai parameter yang digunakan dalam kondisi ini adalah = 0.6, �= 1, = 40,
= 40, �1= 0.2, �2= 0.4, �0= 0.4,
�1 = 0.7, �2 = 0.1, dengan nilai awal
0 = 20, 0 = 10, dan 0 = 10.
Dari nilai parameter yang digunakan diperoleh titik tetap 0= (0,0,0) yang bersifat sadel serta titik tetap 2= (4,
16.55493132, 3.364990188) yang bersifat
spiral stabil, sedangkan untuk titik tetap 1 yang dalam proses mencari nilai titik tetapnya akan menghasilkan suatu bentuk persamaan aljabar � 3+ 2+ +�= 0
43.62267459, dan 3=−3.304135986.
Ketiga nilai tersebut jika disubstitusi ke dalam persamaan akan menghasilkan nilai
1=−12.31219692, 2= 31.68825945,
dan 3= 7.290604135. Terlihat bahwa,
nilai yang dihasilkan untuk 1 serta nilai 3 yang dihasilkan bernilai negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada kedua zona bernilai positif. Sehingga pada kasus
�2<�0 terdapat tiga titik tetap, yaitu
0, 1, dan 2 dengan nilai titik tetap
1= 43.62267459, 31.68825945, 0
yang memiliki jenis kestabilan berupa sadel. Berikut akan diberikan gambar orbit 3 dimensinya pada sistem persamaan (3.3)
12
Gambar 14 memperlihatkan pergerakan kurva dimulai dari sudut bidang ( ). pencerminan 2D dari Gambar 14. Dari hasil pencerminan 2D ini dapat terlihat beberapa titik tetapnya.
Berikut akan diperlihatkan grafik dinamika dari populasi spesies mangsa pada zona yang tidak dilindungi, spesies mangsa pada zona yang dilindungi, dan populasi
Pada Gambar 18 terlihat bahwa populasi pemangsa yang ada lebih sedikit dibandingkan dengan populasi mangsa pada kedua zona serta populasi pemangsa tersebut akan mengalami penurunan populasi yang cukup drastis dibandingkan dengan kedua kasus sebelumnya. Hal ini dikarenakan besarnya laju interaksi antara mangsa dan pemangsa diperkecil lagi nilainya. Dengan adanya populasi pemangsa yang lebih sedikit dari populasi mangsanya dapat membuat populasi mangsa pada kedua zona dapat tetap bertahan hidup, namun populasi mangsa pada zona tidak dilindungi akan tetap mengalami penurunan populasi dengan adanya sedikit populasi pemangsa tersebut karena pada model ini pemangsa sangat bergantung dengan mangsanya.
4.4 Simulasi Model 2 >> Kasus ��> ��
Nilai parameter yang digunakan dalam keadaan ini adalah = 0.6, �= 1, �=
0.01, = 40, = 40, = 1, �1=
0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2=
0.7 dengan nilai awal 0 = 20, 0 =
10, dan 0 = 10.
13
31.68825945, dan 3= 7.290604135.
Terlihat bahwa nilai yang dihasilkan untuk 1 serta nilai 3 yang dihasilkan bernilai negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada kedua zona bernilai positif, sehingga untuk nilai titik tetap 2= 43.62267459,
31.68825945, 0 memiliki jenis kestabilan
berupa sadel.
0.3348700583. Ketiga nilai ∗ tersebut jika
disubstitusi ke dalam persamaan ∗ dan ∗ dan populasi pemangsa bernilai positif, sehingga dalam kasus �2>�0 terdapat empat titik tetap non-negatif, yaitu 0, 1,
2, dan 3 dengan titik tetap 3=
0.3348700583, 13.00035006,
24.44090408 yang bersifat stabil.
Berikut akan diberikan gambar orbit 3 dimensinya pada sistem persamaan (3.2)
Gambar 19 Orbit kestabilan pada bidang ( , , ) dengan �2= 0.7,
dan �0= 0.4
14
Gambar 22 Orbit kestabilan pada bidang (y, ) dengan �2= 0.7,
dan �0= 0.4
Gambar 20, 21, dan 22 merupakan pencerminan 2D dari Gambar 19. Dari hasil pencerminan 2D ini dapat terlihat beberapa titik tetapnya.
Berikut akan diperlihatkan grafik dinamika dari populasi spesies mangsa pada zona yang tidak dilindungi, spesies mangsa pada zona yang dilindungi, dan populasi pemangsa terhadap waktu (�) pada saat
�2= 0.7 dan �0= 0.4
Gambar 23 Dinamika populasi dari ketiga model terhadap � dengan
Pada Gambar 23 terlihat bahwa populasi pemangsa yang ada lebih banyak dari populasi mangsa pada kedua zona. Populasi pemangsa dalam model ini lebih banyak dari populasi awal mangsa pada zona tidak dilindungi sehingga dapat membuat populasi mangsa pada zona tidak dilindungi dapat berada pada ambang kepunahan dengan banyaknya populasi pemangsa tersebut.
Banyaknya populasi pemangsa dalam model ini dikarenakan dengan adanya laju interaksi antara mangsa dan pemangsa yang diperbesar nilainya dan dikarenakan dengan tidak adanya faktor kematian secara alami dari model pemangsa tersebut.
>> Kasus ��= ��
Nilai parameter yang digunakan dalam keadaan ini adalah = 0.6, �= 1, �=
0.01, = 40, = 40, = 1, �1=
0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2=
0.4 dengan nilai awal 0 = 20, 0 =
10, dan 0 = 10.
Dari nilai parameter yang digunakan diperoleh titik tetap 0= 0,0,0 yang bersifat tak stabil, titik tetap 1= 0,0,1 yang bersifat sadel, sedangkan untuk titik tetap 2 dan 3 akan menghasilkan suatu
31.68825945, dan 3= 7.290604135.
Terlihat bahwa nilai yang dihasilkan untuk 1 serta nilai 3 yang dihasilkan bernilai negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada kedua zona bernilai positif, sehingga untuk nilai titik tetap 2= 43.62267459,
31.68825945, 0 memiliki jenis kestabilan
berupa sadel.
0.4450248589. Ketiga nilai ∗ tersebut jika
15
akan menghasilkan ∗1= 0.01072484449,
∗
2= 12.89152134, dan ∗3=
14.76442048 serta ∗1= 0.5713512873,
∗
2=−16.08688623, dan ∗3=
18.80099436. Terlihat bahwa, nilai ∗1 dan
∗
2 yang dihasilkan serta nilai ∗2 yang dihasilkan untuk ∗2 bernilai negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada zona yang tidak dilindungi dan populasi pemangsa bernilai positif, sehingga dalam keadaan �2 =�0 terdapat empat titik tetap non-negatif, yaitu 0, 1, 2, dan 3 dengan nilai titik tetap
3= 0.4450248589, 14.76442048,
18.80099436 yang memiliki jenis
kestabilan bersifat stabil.
Berikut akan diberikan gambar orbit 3 dimensinya pada sistem persamaan (3.2)
Gambar 24 Orbit kestabilan pada bidang ( , , ) dengan �2= 0.4,
dan �0= 0.4
Gambar 24 memperlihatkan pergerakan kurva dimulai pada sudut bawah dari titik terendah pada bidang ( ).
Gambar 25 Orbit kestabilan pada bidang ( , ) dengan �2 = 0.4,
dan �0= 0.4
Gambar 26 Orbit kestabilan pada bidang ( , ) dengan �2= 0.4,
dan �0= 0.4
Gambar 27 Orbit kestabilan pada bidang (y, ) dengan �2= 0.4,
dan �0= 0.4
Gambar 25, 26, dan 27 merupakan pencerminan 2D dari Gambar 24. Dari hasil pencerminan 2D ini dapat terlihat beberapa titik tetapnya.
Berikut akan diperlihatkan grafik dinamika dari populasi spesies mangsa pada zona yang tidak dilindungi, spesies mangsa pada zona yang dilindungi, dan populasi pemangsa terhadap waktu (�) pada saat
�2= 0.4 dan �0= 0.4
Gambar 28 Dinamika populasi dari ketiga model terhadap � dengan
�2= 0.4 dan �0= 0.4.
0 10 20 30 40 50 t 0
16
Pada Gambar 28 terlihat bahwa populasi pemangsa lebih banyak dibandingkan dengan populasi mangsa pada kedua zona. Seperti pada kasus sebelumnya populasi pemangsa yang ada lebih banyak dari populasi mangsanya, namun pada kasus ini banyaknya populasi pemangsa lebih sedikit dibandingkan dengan populasi pemangsa yang ada pada kasus sebelumnya. Hal ini dikarenakan laju interaksi antara mangsa dan pemangsa diperkecil nilainya sehingga dapat membuat populasi pemangsa mengalami penurunan. Pada kasus ini dibuat nilai dari laju kematian pemangsa sama dengan laju interaksi antara mangsa dan pemangsanya dikarenakan ingin melihat populasi antara mangsa dan pemangsa ketika laju kematian pemangsa sama dengan laju interaksi antara mangsa dan pemangsa.
>> Kasus ��< ��
Nilai parameter yang digunakan dalam keadaan ini adalah = 0.6, �= 1, �=
0.01, = 40, = 40, = 1, �1=
0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2=
0.1 dengan nilai awal 0 = 20, 0 =
10, dan 0 = 10.
Dari nilai parameter yang digunakan diperoleh titik tetap 0= 0,0,0 yang bersifat tak stabil, titik tetap 1= 0,0,1 yang bersifat sadel, sedangkan untuk titik tetap 2 dan 3 akan menghasilkan suatu
31.68825945, dan 3= 7.290604135.
Terlihat bahwa nilai yang dihasilkan untuk 1 serta nilai 3 yang dihasilkan bernilai
negatif. Hal ini tidak bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada kedua zona bernilai positif, sehingga untuk nilai titik tetap 2= 43.62267459,
31.68825945, 0 memiliki jenis kestabilan
berupa sadel.
0.9058536189. Ketiga nilai ∗ tersebut jika
disubstitusi ke dalam persamaan ∗ dan ∗ akan menghasilkan ∗1= 0.04302782447,
∗ bersesuaian dengan asumsi bahwa populasi mangsa yang berada pada zona yang tidak dilindungi dan populasi pemangsa bernilai positif, sehingga dalam keadaan �2<�0 terdapat empat titik tetap non-negatif, yaitu
0, 1, 2, dan 3 dengan nilai titik tetap
3= 0.9058536189,14.18481090,
10.05853619 yang memiliki jenis
kestabilan bersifat spiral stabil.
Berikut akan diberikan gambar orbit 3 dimensinya pada sistem persamaan (3.2)
Gambar 29 Orbit kestabilan pada bidang ( , , ) dengan �2= 0.1,
dan �0= 0.4
17
Gambar 30 Orbit kestabilan pada bidang ( , ) dengan �2 = 0.1,
dan �0= 0.4
Gambar 31 Orbit kestabilan pada bidang ( , ) dengan �2 = 0.1,
dan �0= 0.4
Gambar 32 Orbit kestabilan pada bidang (y, ) dengan �2= 0.1,
dan �0= 0.4
Gambar 30, 31, dan 32 merupakan pencerminan 2D dari Gambar 29. Dari hasil pencerminan 2D ini dapat terlihat beberapa titik tetapnya.
Berikut akan diperlihatkan grafik dinamika dari populasi spesies mangsa pada zona yang tidak dilindungi, spesies mangsa pada zona yang dilindungi, dan populasi pemangsa terhadap waktu (�) pada saat
�2= 0.1 dan �0= 0.4
Gambar 33 Dinamika populasi dari ketiga model terhadap � dengan
�2= 0.1 dan �0= 0.4.
Keterangan :
: Populasi mangsa pada zona yang tidak dilindungi
: Populasi mangsa pada zona yang dilindungi
: Populasi pemangsa
Pada Gambar 33 terlihat bahwa populasi pemangsa lebih banyak dari populasi mangsa pada zona tidak dilindungi. Namun pada kasus ini banyaknya populasi pemangsa lebih sedikit dari populasi pemangsa pada kedua kasus sebelumnya sehingga dapat membuat mangsa pada kedua zona tetap dapat bertahan hidup walaupun banyaknya populasi mangsa pada zona tidak dilindungi hanya sedikit dan mengalami penurunan yang cukup drastis dari populasi awalnya.
0 10 20 30 40 50t 0
V KESIMPULAN
Simulasi sistem mangsa-pemangsa padapemangsa yang hanya berada pada zona tidak dilindungi digambarkan dengan menggunakan bantuan software Mathematica 7.0. Secara keseluruhan dinamika sistem mangsa-pemangsa ini dapat dilihat dari besarnya laju interaksi antara mangsa dan pemangsa. Dari hasil simulasi yang diperoleh dengan adanya perubahan terhadap besarnya laju interaksi antara mangsa dan pemangsa dapat dilihat dinamika populasi mangsa pada kedua zona ketika terdapat pemangsa pada zona tidak dilindungi, dinamika populasi pemangsa terhadap perubahan laju interaksi antara mangsa dan pemangsa, dan perbandingan dari model pemangsa yang terdapat dalam kedua model yang dibahas.
Dinamika populasi mangsa yang berada pada kedua zona ketika terdapat pemangsa pada zona tidak dilindungi akan tetap bertahan hidup. Namun pada saat besarnya laju interaksi antara mangsa dan pemangsa diperbesar nilainya dapat membuat banyaknya populasi mangsa pada zona tidak dilindungi mengalami penurunan populasi dikarenakan mangsa pada zona ini hidup secara bersamaan dengan banyaknya pemangsa tersebut dan merupakan sumber makanan bagi pemangsa. Sedangkan untuk populasi mangsa pada zona dilindungi akan terus mengalami peningkatan populasi. Hal ini dikarenakan dengan tidak adanya pemangsa yang hidup pada zona dilindungi.
Dinamika populasi pemangsa pada kedua model umumnya memiliki populasi yang lebih banyak dibandingkan dengan populasi mangsa pada kedua zona ketika laju interaksi antara mangsa dan pemangsa diperbesar nilainya sehingga dapat membuat ancaman bagi mangsa untuk berada pada ambang kepunahan. Sedangkan ketika laju interaksi antara mangsa dan pemangsa diperkecil nilainya, maka populasi pemangsa akan mengalami penurunan populasi dari populasi awal pemangsa. Hal ini dapat membuat populasi mangsa pada kedua zona dapat tetap bertahan hidup.
DAFTAR PUSTAKA
Anton H. 1995. Aljabar Linear Elementer.Ed ke-5. Terjemahan Pantur Silaban dan I Nyoman Susila. Erlangga, Jakarta.
Dubey B. 2006. A Prey-Predator Model with a Reserved Area. Mathematics Group, Birla Institute of Technology and Science. Vol 12: 479-494.
Farlow SJ. 1994. An Introduction to Differential Equation and Their Application. Mc Graw-Hill, New York.
Strogatz SH. 1994. Nonlinear Dynamics and Chaos With Application to Physics, Biology, Chemistry, and Engineering. Addison-Wesley Publishing Company, Reading, Massachusets.
Tu PNV. 1994. Dynamical System, An Introduction with Application in Economics and Biology. Springer-Verlag. Heidelberg, Germany.
21
Lampiran 1. Penentuan Titik Tetap Model 1
Model persamaan sistem mangsa-pemangsa pada persamaan (3.2) : �
Untuk menentukan titik tetap dari persamaan (3.2) maka persamaan tersebut dibuat sama dengan nol, yaitu = 0, = 0, dan = 0,sehingga diperoleh tiga titik tetap yang non−negatif.
dengan mensubstitusikan ∗=�0
�2 ke dalam persamaan (2), maka akan diperoleh
dengan menggunakan rumus ABC didapatkan
22
Sehingga dari perhitungan di atas diperoleh satu titik tetap yang pertama, yaitu ∗, ∗, ∗ =
�0
Subsitusi = 0, maka persamaan (3.2) akan menjadi
= 1− − �1 +�2 …(4)
= 1− +�1 − �2 …(5)
dari persamaan (4) didapatkan
= 0 pada simulasi. Dari perhitungan di atas dapat diperoleh dua titik tetap yang kedua dan ketiga, yaitu
23
Lampiran 2. Penentuan Nilai Eigen Model 1
�= =
−2 − �1− �1 �2 −�1
�1 −
2
− �2 0
�2 0 �2 − �0
Pelinearan pada titik tetap 0 0,0,0 akan menghasilkan matriks sebagai berikut
�0,0,0 =
− �1 �2 0
�1 − �2 0
0 0 −�0
kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik � − �� = 0
− �1− � �2 0
�1 − �2− � 0
0 0 −�0− �
= 0
− �1− � − �2− � −�0− � − �2 �1 −�0− � = 0
−�0− � − �1− � − �2− � − �2�1 = 0
−�0− � − �2− � − �1 +�2�1+�1� − �+�2�+�2− �2�1 = 0
−�0− � �2+� �2+�1− − − �2 +�1 − = 0
Jadi, diperoleh nilai eigen sebagai berikut : �1=−�0< 0
�2=
− �2+�1− − + �2+�1− − 2+4(1) �2 +�1 −
2 > 0
�3=
− �2+�1− − − �2+�1− − 2+4(1) �2 +�1 −
2 > 0
Pelinearan pada titik tetap 1 , , 0 . >> Pada kasus �2>�0
Untuk mencari nilai eigen pada saat kondisi ini, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1, = 40, = 40, �1= 0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2= 0.7, yaitu titik tetap
1 43.62267459, 31.68825945, 0 sehingga akan didapatkan matriks Jacobi
�(43.62267459 ,31.68825945 ,0)=
−1.381133730 0.4 −30.53587221
0.2 −0.7506477835 0
0 0 30.13587221
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik � −
�� = 0
−1.381133730− � 0.4 −30.53587221
0.2 −0.7506477835− � 0
0 0 30.13587221− �
= 0
−1.381133730− � −0.7506477835− � 30.13587221− � − 0.4 0.2 30.13587221− � = 0
24
Jadi, diperoleh nilai eigen sebagai berikut :
�1= 30.13587221 > 0
�2=
−2.131781514 + (2.131781514 )2−4(0.956744973 )
2 =−0.6423602004 < 0
�3=
−2.131781514− (2.131781514 )2−4(0.956744973 )
2 =−1.489421313 < 0
>> Pada kasus �2=�0
Untuk mencari nilai eigen pada saat kondisi ini, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1, = 40, = 40, �1= 0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2= 0.4, yaitu titik tetap
1 43.62267459, 31.68825945, 0 sehingga akan didapatkan matriks Jacobi
�(43.62267459 ,31.68825945 ,0)=
−1.381133730 0.4 −30.53587221
0.2 −0.7506477835 0
0 0 17.04906984
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik � −
�� = 0
−1.381133730− � 0.4 −30.53587221
0.2 −0.7506477835− � 0
0 0 17.04906984− �
= 0
−1.381133730− � −0.7506477835− � 17.04906984− � −
0.4 0.2 17.04906984− � = 0
17.04906984− � �2+ 2.131781514 �+ 0.956744973 = 0
Jadi, diperoleh nilai eigen sebagai berikut :
�1= 17.04906984 > 0
�2=
−2.131781514 + (2.131781514 )2−4(0.956744973 )
2 =−0.6423602004 < 0
�3=
−2.131781514− (2.131781514 )2−4(0.956744973 )
2 =−1.489421313 < 0
>> Pada kasus �2<�0
Untuk mencari nilai eigen pada saat kondisi ini, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1, = 40, = 40, �1= 0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2= 0.1, yaitu titik tetap
1 43.62267459, 31.68825945, 0 sehingga akan didapatkan matriks Jacobi
�(43.62267459 ,31.68825945 ,0)=
−1.381133730 0.4 −30.53587221
0.2 −0.7506477835 0
0 0 3.962267459
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik � −
�� = 0
−1.381133730− � 0.4 −30.53587221
0.2 −0.7506477835− � 0
0 0 3.962267459− �
25
−1.381133730− � −0.7506477835− � 3.962267459− � − 0.4 0.2 3.962267459− � = 0
3.962267459− � �2+ 2.131781514 �+ 0.956744973 = 0
Jadi, diperoleh nilai eigen sebagai berikut :
�1= 3.962267459 > 0
�2=
−2.131781514 + (2.131781514 )2−4(0.956744973 )
2 =−0.6423602004 < 0
�3=
−2.131781514− (2.131781514 )2−4(0.956744973 )
2 =−1.489421313 < 0
Pelinearan pada titik tetap 2 ∗, ∗, ∗ akan menghasilkan matriks sebagai berikut
� ∗, ∗, ∗ =
kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik � − �� = 0
−2 �0 Jacobi di atas, maka akan didapatkan
27
>> Pada kasus �2>�0
Untuk mengetahui jenis kestabilan titik tetap 2 pada kasus �2>�0 dapat menggunakan nilai parameter = 0.6, = 1, = 40, = 40, �1= 0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2= 0.7 yang kemudian akan disubstitusi ke dalam nilai
1, 2, dan 3 yang telah diperoleh di atas. Dari nilai parameter tersebut akan diperoleh nilai eigen �3+ 9.948270002�2+ 6.227889581�+ 0.909433425 = 0 dan dengan menggunakan bantuan software Maple13 akan diperoleh nilai eigen �1=−9.288302494, �2=−0.4347577316, dan �3=−0.2252097807.
>> Pada kasus �2=�0
Untuk mengetahui jenis kestabilan titik tetap 2 pada kasus �2=�0 dapat menggunakan nilai parameter = 0.6, = 1, = 40, = 40, �1= 0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2= 0.4 yang kemudian akan disubstitusi ke dalam nilai
1, 2, dan 3 yang telah diperoleh di atas. Dari nilai parameter tersebut akan diperoleh nilai eigen �3+ 5.960169552�2+ 3.824267271�+ 0.591261633 = 0 dan dengan menggunakan bantuan software Maple13 �1=−0.2435459581,�2=−0.4620177120, dan �3=−5.254605882.
>> Pada kasus �2<�0
Untuk mengetahui jenis kestabilan titik tetap 2 pada kasus �2<�0 dapat menggunakan nilai parameter = 0.6, = 1, = 40, = 40, �1= 0.2, �2= 0.4, �0= 0.4, �1= 0.7, �2= 0.1 yang kemudian akan disubstitusi ke dalam nilai
28
Lampiran 3. Penentuan Titik Tetap Model 2
Model persamaan sistem mangsa-pemangsa pada persamaan (3.3) adalah sebagai berikut : �
Untuk menentukan titik tetap dari persamaan (3.3) di atas, maka persamaan tersebut akan dibuat sama dengan nol, yaitu = 0, = 0, dan = 0.
Dari persamaan (3) akan didapat nilai sebagai berikut = 0
Substitusi nilai ∗ ke dalam persamaan (2)
29
Persamaan ini membentuk suatu persamaan aljabar ∗3
+ ∗2+ ∗+ = 0, dengan
Substitusi nilai ∗= 0 ke dalam persamaan (1), (2), dan (3) sehingga diperoleh �
dari persamaan (4) didapatkan
= 0
Substitusi nilai ke dalam persamaan (5)
31
Lampiran 4. Penentuan Nilai Eigen Model 2
�= =
−2 − �1− �1 �2 −�1
�1 −
2
− �2 0
�2 0 −
2 +�2
Pelinearan pada titik tetap 0 0,0,0 akan menghasilkan matriks sebagai berikut
�0,0,0 =
− �1 �2 0
�1 − �2 0
0 0
kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik � − �� = 0
− �1− � �2 0
�1 − �2− � 0
0 0 − �
= 0
− �1− � − �2− � − � − �2 �1 − � = 0
− � − �1− � − �2− � − �2�1 = 0
− � − �2− � − �1 +�2�1+�1� − �+�2�+�2− �2�1 = 0
− � �2+� �
2+�1− − + − �2− �1 = 0
Jadi, diperoleh nilai eigennya sebagai berikut �1= > 0
�2=− �
2+�1− − + �2+�1− − 2−41 − �2−�1
2 > 0
�3=− �
2+�1− − − �2+�1− − 2−41 − �2−�1
2 > 0
Pelinearan pada titik tetap 1 0,0, akan menghasilkan matriks sebagai berikut
�0,0, =
− �1− �1 �2 0
�1 − �2 0
�2 0 −
kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik � − �� = 0
− �1− �1 − � �2 0
�1 − �2− � 0
�2 0 − − �
= 0
− �1− �1 − � − �2− � − − � − �2�1 − − � = 0
− − � − �1− �1 − � − �2− � − �2�1 = 0
− − � − �2− � − �1 +�2�1+�1� − �1 +�1 �2+�1 � − �+�2�+
�2− �
2�1 = 0
− − � �2+� �
32
Jadi nilai eigennya adalah sebagai berikut
�1=− < 0
�2=− �
1 +�2+�1− − + �1 +�2+�1− − 2−41 �1 �2−�1 + − �2−�1
2 > 0
�3=− �
1 +�2+�1− − − �1 +�2+�1− − 2−41 �1 �2−�1 + − �2−�1
2 < 0
Pelinearan untuk titik tetap 2 , , 0 dan 3 ∗, ∗, ∗ dapat dilihat dari tiga kasus, yaitu pada saat kondisi �2> �0, �2= �0, dan �2 < �0
>> Pada saat kondisi �2> �0
Pelinearan pada titik tetap 2 , , 0
Untuk mencari nilai eigen pada saat kondisi �2> �0, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1,
= 0.01, = 40, = 40, = 1, �1= 0.2, �2= 0.4, �0 = 0.4, �1 = 0.7, �2= 0.7 yaitu 2 43.62267459, 31.68825945, 0 sehingga diperoleh matriks Jacobi
�(43.62267459 ,31.68825945 ,0)=
−1.381133730 0.4 −30.53587221
0.2 −0.7506477835 0
0 0 30.54587221
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik det � −
�� = 0
−1.381133730− � 0.4 −30.53587221
0.2 −0.7506477835− � 0
0 0 30.54587221− �
= 0
−1.381133730− � −0.7506477835− � 30.54587221− � − 0.4 0.2 30.54587221− � = 0
30.54587221− � �2+ 2.131781514 �+ 0.956744973 = 0
Jadi, diperoleh nilai eigen sebagai berikut :
�1= 30.54587221 > 0
�2=−
2.131781514 + (2.131781514 )2−4(0.956744973 )
2 =−0.6423602004 < 0
�3=−
2.131781514− (2.131781514 )2−4(0.956744973 )
2 =−1.489421313 < 0
33
Pelinearan pada titik tetap 3 ∗, ∗, ∗
Untuk mencari nilai eigen pada saat kondisi �2> �0, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1, = 0.01, = 40, = 40, = 1, �1= 0.2, �2= 0.4, �0= 0.4, �1 = 0.7, �2= 0.7 yaitu 3 0.3348700583,13.00035006,24.44090408 sehingga diperoleh matriks Jacobi
�0.3348700583 ,13.00035006 ,24.44090408 =
−16.32537636 0.4 −0.2344090408
0.2 −0.2098057213 0
17.10863286 0 −0.2444090408
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik det � −
�� = 0
−16.32537636− � 0.4 −0.2344090408
0.2 −0.2098057213− � 0
17.10863286 0 −0.2444090408− �
= 0
−16.32537636− � −0.2098057213− � −0.2444090408− � − 0.2 0.4 −0.2444090408− � + −0.2344090408 −0.2098057213− � 17.10863286 = 0
3.425157363 + 16.53518208�+�2 −0.2444090408− � − 0.821855963 +
3.930418218� = 0
�3+ 16.77959112�2+ 11.39692357�+ 1.658995389 = 0
dengan menggunakan bantuan software Maple13, didapatkan nilai eigen sebagai berikut : �1=−0.2091902791 < 0
�2=−0.4932822220 < 0
�3=−16.07711862 < 0
>> Pada saat kondisi �2= �0
Pelinearan pada titik tetap 2 , , 0
Untuk mencari nilai eigen pada saat kondisi �2= �0, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1,
= 0.01, = 40, = 40, = 1, �1= 0.2, �2= 0.4, �0 = 0.4, �1 = 0.7, �2= 0.4 yaitu 2 43.62267459, 31.68825945, 0 sehingga diperoleh matriks Jacobi
�(43.62267459 ,31.68825945 ,0)=
−1.381133730 0.4 −30.53587221
0.2 −0.7506477835 0
0 0 17.45906984
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik det � −
�� = 0
−1.381133730− � 0.4 −30.53587221
0.2 −0.7506477835− � 0
0 0 17.45906984− �
= 0
−1.381133730− � −0.7506477835− � 17.45906984− � − 0.4 0.2 17.45906984− � = 0
34
Jadi, diperoleh nilai eigen sebagai berikut :
�1= 17.45906984 > 0
�2=
−2.131781514 + (2.131781514 )2−4(0.956744973 )
2 =−0.6423602004 < 0
�3=
−2.131781514− (2.131781514 )2−4(0.956744973 )
2 =−1.489421313 < 0
Pelinearan pada titik tetap 3 ∗, ∗, ∗
Untuk mencari nilai eigen pada saat kondisi �2= �0, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1, = 0.01, = 40, = 40, = 1, �1= 0.2, �2= 0.4, �0= 0.4, �1 = 0.7, �2= 0.4 yaitu 3 0.4450248589,14.76442048,18.80099436 sehingga diperoleh matriks Jacobi
�0.4450248589 ,14.76442048 ,18.80099436 =
−12.38294729 0.4 −0.3115174012
0.2 −0.2129326144 0
7.520397744 0 −0.1880099436
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik det � −
�� = 0
−12.38294729− � 0.4 −0.3115174012
0.2 −0.2129326144− � 0
7.520397744 0 −0.1880099436− �
= 0
−12.38294729− � −0.2129326144− � −0.1880099436− � −
0.2 0.4 −0.1880099436− � + −0.3115174012 −0.2129326144−
� 7.520397744 = 0
2.63673334 + 12.5958799�+�2 −0.1880099436− � − 0.483803842 + 2.262734761� = 0
�3+ 12.78388984�2+ 7.267618771�+ 0.979535928 = 0
dengan menggunakan bantuan software Maple13, didapatkan nilai eigen sebagai berikut : �1=−0.2139566640 < 0
�2=−0.3754313090 < 0
�3=−12.19450188 < 0
>> Pada saat kondisi �2< �0
Pelinearan pada titik tetap 2 , , 0
Untuk mencari nilai eigen pada saat kondisi �2< �0, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1,
= 0.01, = 40, = 40, = 1, �1= 0.2, �2= 0.4, �0 = 0.4, �1 = 0.7, �2= 0.1 yaitu 2 43.62267459, 31.68825945, 0 sehingga diperoleh matriks Jacobi
�(43.62267459 ,31.68825945 ,0)=
−1.381133730 0.4 −30.53587221
0.2 −0.7506477835 0
0 0 4.372267459
35
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik det � −
�� = 0
−1.381133730− � 0.4 −30.53587221
0.2 −0.7506477835− � 0
0 0 4.372267459− �
= 0
−1.381133730− � −0.7506477835− � 4.372267459− � − 0.4 0.2 4.372267459− � = 0
4.372267459− � �2+ 2.131781514 �+ 0.956744973 = 0
Jadi, diperoleh nilai eigen sebagai berikut :
�1= 4.372267459 > 0
�2=
−2.131781514 + (2.131781514 )2−4(0.956744973 )
2 =−0.6423602004 < 0
�3=
−2.131781514− (2.131781514 )2−4(0.956744973 )
2 =−1.489421313 < 0
Pelinearan pada titik tetap 3 ∗, ∗, ∗
Untuk mencari nilai eigen pada saat kondisi �2< �0, dapat menggunakan nilai titik tetap yang telah diperoleh pada simulasi dengan nilai parameter = 0.6, = 1, = 0.01, = 40, = 40, = 1, �1= 0.2, �2= 0.4, �0= 0.4, �1 = 0.7, �2= 0.1 yaitu 3 0.9058536189,14.18481090, 10.05853619 sehingga diperoleh matriks Jacobi
�0.9058536189 ,14.18481090 ,10.05853619 =
−6.286268014 0.4 −0.6340975332
0.2 −0.2255443270 0
1.005853619 0 −0.1005853619
kemudian mencari nilai eigennya dengan menggunakan persamaan karakteristik det � −
�� = 0
−6.286268014− � 0.4 −0.6340975332
0.2 −0.2255443270− � 0
1.005853619 0 −0.1005853619− �
= 0
−6.286268014− � −0.2255443270− � −0.1005853619− � − 0.2 0.4 −0.1005853619− � + −0.6340975332 −0.2255443270− � 1.005853619 = 0
1.417832089 + 6.511812341�+�2 −0.1005853619− � − 0.13580744 + 0.557809298� = 0
�3+ 6.612397703�2+ 2.630634388�+ 0.278420593 = 0
dengan menggunakan bantuan software Maple13, diperoleh nilai eigen sebagai berikut :
�1=−6.195015069 < 0
�2=−0.2086913169 + 0.03729097084 I
36
Lampiran 5. Program Penentuan Orbit Kestabilan dan Solusi Model 1 Pada keadaan �2 >�0
>> Program gambar 3D ( Gambar 4)
>> Program orbit kestabilan bidang ( Gambar 5)
>> Program orbit kestabilan bidang ( Gambar 6)
>> Program orbit kestabilan bidang ( Gambar 7)