Kajian Pengaruh Ukuran Contoh (n) Terhadap Pemodelan State Space

(1)

bimbingan KUSMAN SADIK. dan BAGUS SARTONO.

Data deret waktu merupakan data yang dikumpulkan mengenai suatu karakteristik tertentu pada suatu periode waktu atau interval. Komponen penyusun data deret waktu adalah trend, siklus, variasi musiman dan fluktuasi tak beraturan. Analisis deret waktu (Time Series Analysis) merupakan metode yang mempelajari deret waktu untuk membuat peramalan. Metode-metode dalam analisis deret waktu antara lain metode pemulusan,Winters maupun ARIMA.

Model State Space adalah suatu pendekatan untuk memodelkan dan memprediksi secara bersamaan beberapa data deret waktu yang saling berhubungan dimana peubah-peubah tersebut mempunyai interaksi yang dinamis. Model State Space dapat digunakan untuk analisis data deret waktu univariate (pubah tunggal) maupun multivariate (peubah ganda).

Dalam membuat suatu model kendala yang mungkin dapat kita hadapi adalah jumlah data yang dimiliki. Dengan jumlah data yang sedikit kita dapat membuat suatu model, akan tetapi mungkin saja model yang dihasilkan kurang tepat. Dan untuk mendapatkan jumlah data yang besar sulit, terutama untuk data deret waktu. Atas dasar tersebut dalam penelitian ini akan dilakukan simulasi pemodelan model State Space dengan berbagai jumlah data dan dilihat pengaruh jumlah data tersebut terhadap ketepatan model yang dihasilkan.

Data yang digunakan dalam penelitian ini adalah data simulasi. Data tersebut dibuat sedemikian rupa sehingga membentuk model AR(1), AR(2), MA(1) dan VAR(1). Kemudian dilakukan pemodelan kembali menggunakan model State Space.

(2)

P U R W A D I

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(3)

bimbingan KUSMAN SADIK. dan BAGUS SARTONO.

Data deret waktu merupakan data yang dikumpulkan mengenai suatu karakteristik tertentu pada suatu periode waktu atau interval. Komponen penyusun data deret waktu adalah trend, siklus, variasi musiman dan fluktuasi tak beraturan. Analisis deret waktu (Time Series Analysis) merupakan metode yang mempelajari deret waktu untuk membuat peramalan. Metode-metode dalam analisis deret waktu antara lain metode pemulusan,Winters maupun ARIMA.

Model State Space adalah suatu pendekatan untuk memodelkan dan memprediksi secara bersamaan beberapa data deret waktu yang saling berhubungan dimana peubah-peubah tersebut mempunyai interaksi yang dinamis. Model State Space dapat digunakan untuk analisis data deret waktu univariate (pubah tunggal) maupun multivariate (peubah ganda).

Dalam membuat suatu model kendala yang mungkin dapat kita hadapi adalah jumlah data yang dimiliki. Dengan jumlah data yang sedikit kita dapat membuat suatu model, akan tetapi mungkin saja model yang dihasilkan kurang tepat. Dan untuk mendapatkan jumlah data yang besar sulit, terutama untuk data deret waktu. Atas dasar tersebut dalam penelitian ini akan dilakukan simulasi pemodelan model State Space dengan berbagai jumlah data dan dilihat pengaruh jumlah data tersebut terhadap ketepatan model yang dihasilkan.

Data yang digunakan dalam penelitian ini adalah data simulasi. Data tersebut dibuat sedemikian rupa sehingga membentuk model AR(1), AR(2), MA(1) dan VAR(1). Kemudian dilakukan pemodelan kembali menggunakan model State Space.

(4)

P U R W A D I

G14103034

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Statistika

DEPARTEMEN STATISTIKA

(5)

Menyetujui :

Pembimbing I,

Kusman Sadik, S.Si M.Si.

NIP. 132 158 751

Pembimbing II,

Bagus Sartono, S.Si M.Si

NIP. 132 311 923

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. Drh. Hasim, DEA

NIP. 131 578 806

(6)

Sumaryani. Penulis adalah anak pertama dari tiga bersaudara. Penulis menempuh pendidikan dasar di SD Negeri VI Cileungsi hingga tahun 1997 dan melanjutkan pendidikan menengah pertama di SLTP Puspanegara Citeureup hingga tahun 2000. Pada tahun 2003 penulis menyelesaikan pendidikan menengah atas di SMU Negeri 3 Bogor dan diterima di Departemen Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB.

(7)

atas segala karunia-Nya sehingga penulis dapat menyelesaikan karya ilmiah ini. Shalawat serta salam semoga selalu tercurahkan kepada Rasulullah SAW, keluarga, sahabat, dan umatnya hingga akhir zaman.

Karya ilmiah ini berjudul “Kajian pengaruh ukuran contoh (n) terhadap pemodelan State Space“. Karya ilmiah ini membahas tentang pengaruh ukuran contoh (n) terhadap model State Space dengan menggunakan simulasi untuk peubah tunggal dan ganda.

Terima kasih penulis ucapkan kepada semua pihak yang telah membantu dalam penyelesaian karya ilmiah ini, terutama kepada :

1. Bapak Kusman Sadik, S.Si M.Si. dan Bapak Bagus Sartono, S.Si M.Si. yang telah memberikan bimbingan dan masukan hingga selesainya karya ilmiah ini.

2. Bapak, Ibu, adik-adik, Kakek dan Nenek yang selalu memberi kasih sayang, do’a, dorongan semangat, dukungan dan perhatian kepada penulis.

3. Seluruh dosen pengajar Departemen Statistika IPB atas ilmu yang telah diberikan selama penulis mengikuti perkuliahan di Departemen Statistika IPB.

4. Bu Dedeh, Bu Mar, Bu Sulis, Bang Soedin, Bu Aat, Mang Dur, Mang Herman, Pak Heri, dan Pak Yan yang telah memberikan bantuan selama masa perkuliahan penulis.

5. Teman satu pembimbing, Muti, atas diskusi, masukan, dan dukungannya selama penyusunan karya ilmiah ini.

6. Ipul, Anto, Apri, Lia, Susan, Harti, Rio, Sari (Kimia’40) atas persahabatan selama ini. 7. Edo atas pinjaman laptop dan printer serta dorongan semangatnya dan Rosyid atas

bantuannya dalam pembuatan program.

8. Daus, Anggoro, Bayu, Arief, Yudi,, Rian, Ali dan Santo (FM Mania), serta teman-teman di Wisma Paladium (Mas Eko, Mas Capung, Mas Aris, Irfan, dkk) untuk hari-hari yang menyenangkan selama di kontrakan dan kosan.

9. Meylinda, Rani, Deni, Rara, Dania, Esi, Rina, Chichi dan seluruh STK’40 atas dukungan, semangat, do’a dan semua keceriaan yang diberikan semasa kuliah.

10. Mbak Ika (STK`39), Rere dan Rizka atas bantuannya serta seluruh rekan Statistika angkatan 41, 42 dan 43 yang telah memberi semangat.

11. Semua pihak yang telah memberikan dukungan kepada penulis yang tidak dapat disebut satu persatu sehingga karya ilmiah ini dapat diselesaikan.

Penulis menyadari bahwa penulisan karya ilmiah ini masih jauh dari sempurna. Oleh karena itu kritik dan saran yang membangun sangat penulis harapkan sebagai pemicu untuk dapat berkarya lebih baik lagi. Semoga karya ilmiah ini bermanfaat bagi pihak yang membutuhkan.

Bogor, Juli 2008

(8)

DAFTAR ISI

Halaman

DAFTAR ISI... v

DAFTAR TABEL ... vi

DAFTAR LAMPIRAN ... vi

PENDAHULUAN Latar Belakang ... 1

Tujuan ... 1

TINJAUAN PUSTAKA Data Deret Waktu ... 1

Model AR (p) dan MA(q) ... 1

Vector Autoregressive (VAR) ... 1

Model State Space... 2

Akaike Information Criterion (AIC) ... 2

Analisis Korelasi Kanonik ... 2

Menentukan state vector ... 2

Pendugaan Parameter ... 3

BAHAN DAN METODE Bahan ... 3

Metode ... 3

HASIL DAN PEMBAHASAN Simulasi Awal ... 4

Simulasi AR(1) ... 5

Simulasi AR(2) ... 6

Simulasi MA(1) ... 6

Simulasi VAR(1) ... 6

SIMPULAN ... 7

SARAN ... 8

(9)

DAFTAR GAMBAR

1. Persentase parameter yang signifikan (S) simulasi AR(1) ... 6

2. Persentase parameter yang signifikan (S) simulasi AR(2) ... 6

3. Perbandingan persentase parameter signifikan (S) dan nilai t=A (A) ... 6

4. Persentase parameter yang signifikan (S) simulasi VAR(1) ... 7

5. Perbandingan Simulasi VAR(1) ... 7

DAFTAR LAMPIRAN

1. Hasil Simulasi Awal ... 9

2. Output SAS Simulasi Awal VAR(1) n=120 ... 9

3. Output SAS Simulasi AR(1) n=12 ... 11

8. Tabel Hasil Simulasi ... 13

9. Output SAS Simulasi VAR(1) n=60 ... 14

(10)

PENDAHULUAN

Latar Belakang

Data deret waktu merupakan salah satu bentuk data yang dikenal dalam pengembangan metodologi analisis. Data deret waktu digunakan untuk memprediksi sesuatu di masa yang akan datang. Analisis deret waktu (Time Series Analysis) merupakan metode yang mempelajari deret waktu untuk membuat peramalan. Metode-metode dalam analisis deret waktu antara lain metode pemulusan,

Winters maupun ARIMA. Metode yang sering digunakan adalah ARIMA.

Semakin berkembangnya waktu, semakin banyak metode-metode baru yang dikembangkan. Metode-metode yang dikembangkan tidak hanya melihat pada satu peubah saja atau peubah tunggal (univariate), melainkan sudah melihat hubungan dengan peubah lain atau peubah ganda (multivariate).

Untuk data peubah ganda salah satu metode yang dapat digunakan dikenal dengan nama

State Space Model. Metode ini dapat digunakan untuk analisis data deret waktu peubah tunggal maupun peubah ganda. Model

State Space sudah banyak digunakan dalam berbagai bidang. Model ini biasa digunakan dikarenakan dapat digunakan pada sistem dinamik linear maupun nonlinear, dapat diterapkan pada sebaran NonGaussian, multi input-multi output. Dalam Shumway dan Stoffer 2000 disebutkan beberapa penggunaan model State Space yaitu dalam bidang fisika khususnya elektro, ekonomi (Harrison dan Stevens, 1976, Harvey and Pierse, 1984), ilmu kedokteran (Jones, 1984), ilmu tanah (Shumway, 1985), dan bidang ilmu lainnya. Dalam ekomomi misalnya, State Space

digunakan untuk menggambarkan pertumbuhan ekonomi di wilayah spanyol (Vargas dan Salido). Sedangkan dalam Seppanen et al. 2000 dibahas bagaimana model

State Space dalam proses Tomography

(rekonstruksi pencitraan).

Dalam membuat suatu model kendala yang mungkin dihadapi adalah ukuran contoh (n) yang dimiliki. Dengan ukuran contoh yang sedikit kita dapat membuat suatu model, akan tetapi mungkin saja model yang dihasilkan kurang tepat, sedangkan untuk mendapatkan ukuran contoh yang besar sulit, terutama untuk data deret waktu. Atas dasar tersebut dalam penelitian ini akan dilakukan simulasi pemodelan model State Space dengan berbagai ukuran contoh dan dilihat pengaruh ukuran

contoh tersebut terhadap ketepatan model yang dihasilkan.

Tujuan

Penelitian ini bertujuan untuk melihat pengaruh ukuran contoh (n) terhadap pemodelan State Space.

TINJAUAN PUSTAKA

Data Deret Waktu

Data deret waktu adalah jenis data yang dikumpulkan menurut urutan waktu dalam suatu rentang waktu tertentu (Rosadi 2006). Komponen penyusun data deret waktu adalah trend, siklus, variasi musiman dan fluktuasi tak beraturan.Rentang waktu dapat berupa tahun, bulan, minggu, hari ataupun lainnya. Contoh data deret waktu antara lain produksi padi tiap tahun, produksi teh per hari, dan masih banyak contoh data deret waktu yang lainnya.

Model AR(p) dan MA(q)

Secara umum bentuk model

Autoregressive(AR) adalah:

t p e

 (B)x_t dengan

) B B B (1

(B) ₁ 1 ₂ 2 _p p

p   

     , dan

= intersep

k

 =koefisien autoregressive (k=1, 2..., p)

t

e = galat acak ke-t

Secara umum model Moving Average

(MA) adalah:

t

t μ (B)

x  _q e

dengan:

) B B B 1 ( ) B

( 2 2

1 1

q q

q   

    

 = intersep

k

 =koefisien moving average(k=1, 2, ..., q)

t

e = galat acak ke-t

Vector Autoregressive (VAR)

Vector Autoregresive adalah suatu sistem persamaan yang memperlihatkan setiap peubah sebagai fungsi linier dari konstanta dan nilai lag (lampau) dari peubah itu sendiri serta nilai lag dari peubah lain yang ada dalam sistem.

VAR dengan ordo p dan n buah peubah observasi (endogen) pada waktu t dapat dimodelkan sebagai berikut (Enders 1995):

t p t p 2 t 2 1 t 1 0

t A y y ... y ε

(11)

yt : vektor peubah respon (y1.t, y2.t, ...,yn.t)

berukuran nx1.

A0 : vektor intersep berukuran n x 1

Ai : matriks parameter berukuran n x n

t : vektor sisaan (1,t, 2,t, ...,k,t)

berukuran n x 1

Asumsi yang harus dipenuhi dalam VAR adalah semua peubah respon bersifat stasioner dan sisaan bersifat white noise.

ModelState Space

Model State Space adalah suatu analisis deret waktu, dimana data deret waktu dijelaskan atau digambarkan melalui beberapa peubah bantu. Peubah bantu tersebut dalam

State Space dinamakan state vector. Dalam SAS User’ Guide, state vector mengandung ringkasan semua informasi dari nilai sebelumnya dan nilai sekarang dari suatu deret waktu yang sesuai dengan prediksi dari nilai yang akan datang.

Model State Space dapat dimodelkan secara metematis sebagai berikut (Wei 1989):

1 t t 1

t Fx Ge

x (2)

dengan persamaan output :

t

t x

z H (3)

dimana:

xt :state vector berdimensi k zt : vektor output berdimensi m

F : matriks koefisien (matriks transisi) berukuran k x k,

G : matriks koefisien (matriks input) berukuran k x m.

H : matriks koefisien (matriks observasi) berukuran m x k

et : vektor sisaan, bersifat acak dan menyebar

normal. Berdimensi m dengan nilai tengah 0 dan matriks kovarian ∑

Persamaan (2) dapat diubah menjadi:









t

1 t t t t 1 -t t 1 1 e e e G FB G FB G F        x x x x

Kemudian persamaan diatas dimasukkan ke persamaan (3), sehingga menjadi:





t

1 t H1 FB Ge

  

z

Langkah-langkah dalam pembentukan model State Space adalah sebagai berikut:

1. Menentukan ordo p optimal. Ordo p

yang optimal memiliki nilai AIC yang terkecil.

2. Menentukan state vector dengan menggunakan analisis korelasi kanonik.

3. Pendugaan parameter menggunakan pendekatan kemungkinan maksimum.

Akaike Information Criterion (AIC)

Akaike Information Criterionadalah suatu ukuran atau nilai yang digunakan untuk mengidentifikasikan model dari suatu dataset (Agusta 2005). Dalam model State Spacenilai AIC digunakan untuk menentukan ordo p

optimal. Nilai AIC dapat dihitung melalui persamaan : 2 m 2 ˆ ln n

AIC_p  _p  p (4) dengan :

n = banyaknya observasi m = dimensi dari vektor proses zt

p



ˆ

_{= determinan dari matriks kovarian}

sisaan, atau white noise dalam pemodelan AR (p)

Analisis Korelasi Kanonik

Analisis korelasi kanonik dapat digunakan untuk melihat hubungan antara segugus peubah respon (y1, y2,...,yp) dengan segugus peubah penjelas (x1, x2,...xq). Analisis ini mirip dengan analisis regresi yang dapat mengukur keeratan hubungan antara segugus peubah respon dan gugus peubah penjelas. Selain itu analisis korelasi kanonik juga mampu menguraikan struktur hubungan dalam gugus peubah respon dan peubah penjelas tersebut (Sartono et al. 2003).

Asumsi yang harus dipenuhi dalam analisis korelasi kanonik yaitu:

a. Korelasi antar peubah didasarkan pada hubungan linear

b. Korelasi kanonik adalah hubungan linear antar peubah

c. Asumsi sebaran normal ganda.

Analisis korelasi kanonik dalam pemodelan State Space digunakan untuk menentukan state vector.

Menetukan State Vector

State vector ditentukan secara unik melalui analisis korelasi kanonik antara sekumpulan nilai observasi sekarang dan observasi lampau (zt, zt-1,..., zt-p) dan sekumpulan nilai observasi

sekarang dan yang akan datang (zt, zt+1|t, ...,

(12)

dibentuk antara data spaceDt = (zt, zt-1, ..., zt-p)

dan predictor space Ft = (zt, zt+1|t, ..., zt+p|t),

dimana Dtadalah vektor dari nilai sekarang dan

waktu lampau, dan Ft adalah vektor dari nilai

sekarang dan waktu yang akan datang. Korelasi kanonik terkecil digunakan untuk menentukan komponen dalam state vector.

Analisis korelasi kanonik didasarkan pada

Block Hankel dari matriks kovarian contoh Dt

dan Ft, yaitu:

                           ) 2 ( ˆ ) 1 ( ˆ ) ( ˆ ) 1 ( ˆ ) 2 ( ˆ ) 1 ( ˆ ) ( ˆ ) 1 ( ˆ ) 0 ( ˆ ˆ p p p p p        dengan



       j t j t t z z z z j n 1 )' )( ( n ) ( ˆ 1

,

dimana

j = 0, 1, 2, …, 2p.

Untuk setiap langkah dari serangkaian analisis korelasi kanonik, korelasi kanonik terkecil yang signifikan (ρmin) dihitung berdasarkan kriteria informasi dari Akaike (1976) dalam Wei (1989):

] 1 q ) 1 ( m [ 2 ) 1 ln( n

IC ρ2min  p  

dimana:

q = dimensi dari F_tj pada langkah sekarang m = dimensi dari vektor proses zt

p = ordo AR optimal

Jika IC≤0, ρmin = 0, sedangkan jika IC>0 maka nilai ρmin > 0. Jika ρmin lebih dari nol, z1,t+1|t

ditambahkan ke dalam state vector. Untuk menguji kesignifikanan korelasi kanonik ρ, salah satu pendekatan yang dapat digunakan adalah uji Khi-Kuadrat (chi-square, χ2). Statistik ujinya adalah:

) 1 ln( ) ] 1 q ) 1 ( m [ 5 . 0 n

( min2

hit

2 __ _ _p_ _ _ __ρ



mendekati sebaran Khi-Kuadrat dengan derajat bebas (db) [m(p+1)-q+1].

Hipotesisnya adalah: H0 : ρ0

H1 : ρ0

Pendugaan Parameter

Setelah didapatkan state vector, kemudian dilakukan pendugaan parameter pada model

State Space. Pendugaan paramater dalam model State Space menggunakan pendekatan kemungkinan maksimum (maximum likelihood) dan dilakukan secara iteratif. Dengan pendekatan kemungkinan maksimum diperoleh penduga yang efisien bagi F, G dan

∑. Pada proses pendugaan ini, salah satu

elemen pada F danG, pasti ada yang bernilai konstan seperti 0 dan 1.

BAHAN DAN METODE

Bahan

Data yang digunakan dalam penelitian ini adalah data simulasi. Data tersebut didapat dari hasil pembangkitan data, kemudian dilakukan transformasi membentuk model AR, MA, dan VAR.

Metode

Langkah-langkah yang dilakukan dalam penelitian ini adalah:

1. Membangkitkan data sebanyak n, data tersebut dinyatakan sebagai et, dimana

et~N(0,1). Ukuran contoh (n) yang

digunakan dalam penelitian ini adalah 12, 36, 60, 120 dan 240. Untuk simulasi AR(1) dan MA(1) ukuran contoh ditambahkan dengan n=24, untuk AR(2) n=24 dan n=84, sedangkan VAR(1) n=96. Hal tersebut dilakukan untuk melihat perubahan peningkatan jumlah parameter yang signifikan.

2. Data hasil langkah ke-1 ditransformasi sehingga membentuk suatu model AR(1), AR(2) MA(1) dan VAR(1). Transformasi yang digunakan dalam penilitian ini adalah:

a) AR(1) : xt = 0.9xt-1 + et

b)AR(2) : xt = 0.4xt-1 + 0.5xt-2 + et

c) MA(1) : xt = et- 0.9et-1

d)VAR(1) :

Terdiri dari 2 buah model, yaitu: VAR_1 : xt = 0.4xt-1 + 0.2yt-1 + ε1,t

yt = 0.15xt-1 + yt-1 + ε2,t

VAR_2 : xt = 0.4xt-1 + 0.2yt-1 + ε1,t

yt = 0.15xt-1 + 0.3yt-1 + ε2,t ε1,t dan ε2,t ~ N(0,1).

3. Membuat model State Space dengan menggunakan data yang dihasilkan pada langkah ke-2.

4. Melihat kesignifikanan parameter yang dihasilkan. Jika nilai |t| > 2, maka parameter yang dihasilkan signifikan. 5. Langkah 1 – 4 diulang sebanyak 1000 kali. 6. Menghitung jumlah parameter yang

signifikan untuk setiap model yang dihasilkan.

Proses pemodelan State Space adalah sebagai berikut:

a. Langkah pertama dalam proses pemodelan

(13)

b. Menentukan state vector dari model State Space dengan menggunakan korelasi kanonik. Dalam simulasi kali ini jumlah komponen dalam state vector sudah ditentukan terlebih dahulu yaitu 1 untuk model AR(1) dan 2 untuk model AR(2), MA(1) dan VAR(1). Pada AR(2) dan MA(2) terdapat nilai parameter yang ditentukan terlebih dahulu, untuk AR(2) parameter F(2,2)=G(2,1) dan untuk MA(2)

F(2,1)=F(2,2)=0. Kedua hal tersebut dilakukan agar model State Space yang dihasilkan sama dengan model sebelumnya (AR(1), AR(2), MA(1) atau VAR(1)).

c. Menduga parameter dari model State Space dengan menggunakan pendekatan kemungkinan maksimum. Dugaan parameter yang signifikan memiliki nilai |t|>2, sebaliknya dugaan parameter yang tidak signifikan memiliki nilai |t| < 2.

Software yang digunakan dalam penelitian ini adalah SAS 9.1.

HASIL DAN PEMBAHASAN

Simulasi Awal

Sebelum dilakukan simulasi secara keseluruhan, dilakukan simulasi awal terlebih dahulu, yang bertujuan untuk melihat model yang dihasilkan jika pada proses pemodelan

State Space tidak dilakukan penentuan jumlah

state vector dan menentukan nilai parameter pada pemodelan. Model yang digunakan untuk simulasi awal adalah AR(1), AR(2) dan MA(1). Jumlah ulangan yang digunakan adalah sebanyak 50. Hasil simulasi awal ini dapat dilihat pada Lampiran 1.

Berdasarkan hasil simulasi dapat dilihat bahwa model yang dihasilkan lebih dari satu. Untuk simulasi AR(1) menghasilkan model xt=et, AR(1), ARMA(2,1), ARMA(3,2) dan

Model Lain. Pada simlulasi ini terlihat pada saat n=12 terdapat 64% model yang dihasilkan adalah AR(1), lalu mengalami kenaikan pada saat simulasi dengan n=36, tetapi turun kembali sejalan dengan bertambahnya ukuran contoh (n). Pada saat simulasi AR(1) dengan n=36 sudah tidak terdapat xt=et.

Model yang dihasilkan pada simulasi AR(2) tidak jauh berbeda dengan AR(1). Tetapi pada simulasi ini sama sekali tidak menghasilkan model AR(2). Pada saat simulasi dengan n=120, ada simulasi yang tidak menghasilkan Fitted model, sehingga tidak

didapatkan model akhir (TAM) pada pemodelan State Space.

Hal serupa dengan AR(2) terjadi pada simulasi awal untuk MA(1). Pada simulasi ini tidak manghasilkan model MA(1) kembali dan ada hasil simulasi yang tidak menghasilkan model akhir (TAM).

Untuk simulasi awal VAR(1) tidak dilakukan pengulangan seperti simulasi pada AR(1), AR(2) dan MA(1), tetapi pada simulasi VAR(1) akan dibahas proses pembentukan modelnya. Model VAR(1) yang akan dijelaskan prosesnya disini adalah model VAR_2 dengan n=120.

Langkah pertama dalam pembentukan model State Space adalah memilih ordo p yang optimal. Dalam kasus ini ordo yang optimal adalah 1, dengan nilai AIC 9.208241 (Lampiran 2). Setelah didapatkan ordo p, kemudian dilakukan analisis korelasi kanonik untuk menentukan state vector. Berdasarkan Lampiran 2 dapat dilihat peubah xt+1|t tidak

dapat dimasukkan kedalamstate vector, hal ini dikarenakan jika peubah xt+1|t dimasukkan

kedalam state vector, maka IC bernilai negatif (-3.36316). Hal yang serupa juga terjadi jika peubah yt+1|t, nilai IC pun negatif, sehingga

peubah yt+1|t tidak dapat dimasukkan kedalam state vector. Maka state vector yang didapat adalah:        t t t y x x

Setelah didapatkan state vector, kemudian dilakukan pendugaan parameter F, G dan ∑ dengan pendekatan kemungkinan maksimum dan dilakukan secara iteratif. Penduga parameter yang didapat adalah:

       198047 . 0 012471 . 0 19205 . 0 350665 . 0 ˆ F        1 0 0 1 ˆ G          955478 . 0 07103 . 0 07103 . 0 062467 . 1 ˆ Σ

Dan model State Space yang didapat adalah (Lampiran 2):

(14)

                  955478 . 0 07103 . 0 07103 . 0 062467 . 1 e e var ˆ 1 t , 2 1 t , 1 Σ

Persamaan matriks diatas dapat diubah menjadi persamaan berikut: 1 t . 1 t t 1

t 0.350665x 0.19205y

x_   e _

1 t . 2 t t 1

t 0.012471x 0.198047y e

y_    _

Persamaan diatas merupakan model VAR(1). Berdasarkan hasil pendugaan parameter (Lampiran 2), nilai paramter yang signifikan adalah F(1,1), F(1,2) dan F(2,2), atau tidak semua pendugaan parameter pada simulasi ini signifikan.

Simulasi AR(1)

Proses pembentukan model State Space

pada simulasi AR(1) akan dijelaskan untuk setiap ukuran contoh (n) dengan ulangan sebanyak satu (1).

 AR(1) dengan n=12

Tahap pertama dalam menyusun model State Space adalah memilih ordo optimal. Ordo p yang optimal dapat dilihat dari nilai AIC yang terkecil. Pada simulasi AR(1) dengan n=12, ordo p yang optimal terdapat pada lag ke 1, dengan nilai AIC = 6.834656 (Lampiran 3). Ordo p ini untuk selanjutnya digunakan dalam analisis korelasi kanonik.

Nilai IC yang diperoleh jika xt+1|t

dimasukkan ke dalam state vector adalah sebesar -1.80482. Karena IC bernilai negatif, maka peubahxt+1|t dikeluarkan dari

state vector, sehingga state vector yang diperoleh adalah xt=[xt]. Hal ini juga dapat

disebabkan karena dalam program banyaknya peubah (komponen) dalam

state vector sudah ditentukan, yaitu sebanyak 1. Setelah didapatkan state vector, langkah selanjutnya adalah pendugaan parameter.

Pendugaan parameter dalam model

State Space menggunakan pendekatan kemungkinan maksimum. Proses pendugaan parameter dilakukan secara iterative, sehingga didapat (Lampiran 3):



0.427313



ˆ_

F Gˆ 

 

1



1.496139



ˆ _

Σ

Model State Space yang diperoleh adalah:





t

  

t 1 1

t ] 0.427313[x ] 1 e

x

[    

dengan et ~ N(0, 1.496139).

Persamaan matiks tersebut dapat dibuat bentuk persamaan:

t 1 t t 0.427313x e

x   

Persamaan diatas merupakan persamaan AR(1), dengan nilai



= 0.427313. Parameter F(1,1) (Lampiran 3) memiliki nilai t=1.64 (|t|<2), sehingga parameter tersebut tidak signifikan dan model yg dihasilkan masih kurang baik.

Pada simulasi dengan n=36, model

State Space yang dihasilkan adalah:





t

  

t1 1

t ] 0.719792[x ] 1e

x

[    

Atau dapat dibentuk persamaan:

t 1 t t 0.719792x e

x   

dengan et ~ N(0, 0.859384).

Model yang diperoleh merupakan model AR(1) dan berdasarkan Lampiran 4, parameter F(1,1) signifikan karena memiliki nilai |t|>2.

Untuk simulasi dengan n=60, model yang dihasilkan adalah:





t

  

t1 1

t ] 0.747179[x ] 1e

x [ _   _ atau 1 t t 1

t 0.747179x e

x   

dengan et ~ N(0, 0.928608).

Model diatas merupakan model AR(1) dan parameternya signifikan (Lampiran 5).

Pada simulasi dengan n=120 menghasilkan model AR(1) yaitu:

1 t t 1

t 0.740535x e

x   

dimana et ~ N(0, 0.934095). Pada simulasi

ini parameternya pun signifikan (Lampiran 6).

Model yang dihasilkan dari simulasi AR(1) dengan n=240 adalah:





t

  

t1 1

t ] 0.888042[x ] 1e

x

[    

dengan et ~ N(0, 1.068884). Model

tersebut merupakan model AR(1). Berdasarkan Lampiran 7 dapat dilihat bahwa parameter F(1,1) signifikan dengan nilai t=29.94.

(15)

parameter signifikan dimulai dari simulasi AR(1) dengan n=60 hingga n=240. Hal tersebut berarti semakin besar ukuran contoh, maka semakin besar kemungkinan parameter yang diduga signifikan sehingga model yang berasal dari model AR(1) dapat dihasilkan model AR(1) kembali.

Hasil Simulasi AR(1) dalam %

49.6

94.7 99.8 100 100 100

0 10 20 30 40 50 60 70 80 90 100

12 24 36 60 120 240 Ukuran contoh (n)

S

Gambar 1 Persentase parameter yang signifikan (S) simulasi AR(1)

Simulasi AR(2)

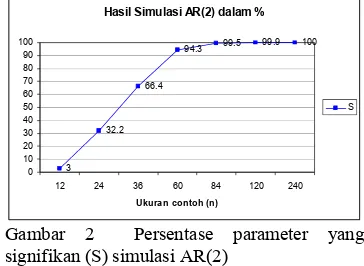
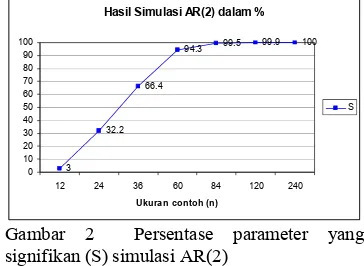
Proses yang sama pada simulasi AR(1) dilakukan pada AR(2), hal yang membedakan hanya jumlah state vector yang ditentukan dalam proses pemodelan. Pada simulasi AR(2) jumlah state vector ditentukan sebanyak 2. Hasil yang diperoleh dari simulasi AR(2) dapat dilihat pada Gambar 2. Berdasarkan hasil simulasi, pada saat ukuran contoh sebesar 12, jumlah parameter yang signifikan hanya sebesar 3% saja. Hal ini berarti hanya sebesar 3% model yang dihasilkan tepat atau menghasilkan model AR(2) kembali. Peningkatan jumlah parameter yang signifikan cukup pesat terjadi pada saat simulasi AR(2) dengan n=12 sampai n=36.

Hasil Simulasi AR(2) dalam %

3 32.2

66.4

94.3 99.5 99.9 100

0 10 20 30 40 50 60 70 80 90 100

12 24 36 60 84 120 240 Ukuran contoh (n)

S

Gambar 2 Persentase parameter yang signifikan (S) simulasi AR(2)

Peningkatan jumlah parameter yang signifikan pada simulasi AR(2) cenderung lebih lambat dari simulasi AR(1) dan MA(1). Pada simulasi AR(2) dengan n=36, parameter yang signifikan baru mencapai 66.4%,

sedangkan simulasi dengan AR(1) dan MA(1) sudah mencapai diatas 90%.

Simulasi MA(1)

Proses simulasi MA(1) tidak jauh berbeda dengan simulasi AR(1) atau AR(2). Hasil simulasi MA(1) dapat dilihat pada Gambar 3. Dari hasil tersebut dapat kita lihat terdapat nilai

t yang bernilai A (tidak memiliki nilai t). Hal ini berarti tidak dapat disimpulkan parameter yang diduga signifikan atau tidak. Hal tersebut dapat terjadi jika jumlah parameter yang diduga sama dengan ukuran contoh yang kita miliki, sehingga eror tidak ada dan nilai t tidak dapat dihitung.

Hasil Simulasi MA(1) dalam %

14.3 64.6

94.2 97.6 99.6 99.8

68.6

33.8

5.7 2.3 0.4 0.2 0

10 20 30 40 50 60 70 80 90 100

12 24 36 60 120 240 Ukuran contoh (n)

S A

Gambar 3 Perbandingan persentase parameter signifikan (S) dan nilai t=A (A)

Pada simulasi dengan n=12 terdapat 68.6% nilai t yang bernilai A, hal ini berarti sebesar 68.6% tidak dapat disimpulkan dugaan parameter signifikan atau tidak, sehingga tidak diketahui apakah hasil simulasi menghasilkan model MA(1) kembali atau tidak. Sama seperti pada AR(1), simulasi MA(1) sudah mencapai diatas 90% pada simulasi MA(1) dengan n=36. Pada simulasi MA(1) dengan n=240 masih terdapat nilai t yang bernilai A atau tidak memiliki nilai t, tetapi pada simulasi ini sudah tidak terdapat lagi parameter yang tidak signifikan.

Simulasi VAR(1)

Contoh proses pembentukan model State Space untuk VAR(1) dengan n=60 adalah sebagai berikut:

Proses awal dalam pembentukan model

State Space adalah pemilihan ordo p. Ordo p

yang optimal adalah p=1 dengan nilai AIC=186.5949. Setelah didapatkan ordo p, kemudian mencari state vector.

(16)

state vector. Begitu pula dengan peubah yt+1|t, jika peubah tersebut dimasukkan ke dalam

state vector nilai IC yang didapat bernilai negatif (Lampiran 9) maka peubah yt+1|t

dikeluarkan dari state vector. Maka diperoleh

state vector:

       t t t y x x

Setelah didapatkan state vector, kemudian dilakukan pendugaan parameter F, G dan ∑.

Dugaan parameter yang didapat adalah:

        012624 . 1 21754 . 0 234551 . 0 207059 . 0 ˆ F        1 0 0 1 ˆ G        7507 . 15 042688 . 5 042688 . 5 860147 . 2 ˆ Σ

sehingga model State Space yang dihasilkan adalah:                                      1 t , 2 1 t , 1 t t 1 t 1 t e e 1 0 0 1 y x 012624 . 1 21754 . 0 234551 . 0 207059 . 0 y x

atau dapat dituliskan sebagai berikut:

1 t . 1 t t 1

t 0.207059x 0.234551y e

x    

1 t . 2 t t 1

t 0.21754x 1.012624y e

y_    _

dengan                 7507 . 15 042688 . 5 042688 . 5 860147 . 2 var 1 , 2 1 , 1 t t e e Σ .

Model diatas merupakan model VAR(1). Berdasarkan hasil pendugaan parameter, tidak semua parameter yang diduga signifikan (Lampiran 9), parameter yang signifikan adalah

F(1,2) dan F(2,2).

Hasil Simulasi VAR(1) dalam %

0.2 0.5 3.3 25.3 60.6 99.8 0 10 20 30 40 50 60 70 80 90 100

12 36 60 96 120 240 Ukuran contoh (n)

S

Gambar 4 Persentase parameter yang signifikan (S) simulasi VAR(1)

Setelah dilakukan ulangan sebanyak 1000 kali, hasil simulasi dapat dilihat pada Gambar 4. Berdasarkan hasil simulasi dapat dilihat bahwa meningkatnya jumlah parameter yang

signifikan dari simulasi VAR(1) dengan n=12 sampai n=60 sangat lambat dibandingkan dengan simulasi AR(1), AR(2) dan MA(1). Pada simulasi VAR(1) dengan n=96, jumlah parameter yang signifikan mencapai 25.3%, dan terus bertambah sejalan dengan bertambahnya data. Pada simulasi VAR(1) dengan n=240, pendugaan parameter yang signifikan belum mencapai 100%, hal ini berarti pada simulasi ini masih terdapat pendugaan model yang kurang tepat.

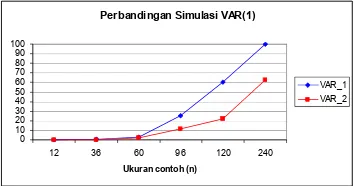
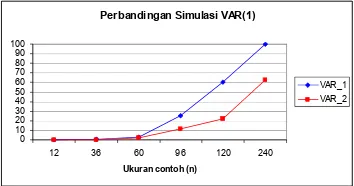
Perbandingan Simulasi VAR(1)

0 10 20 30 40 50 60 70 80 90 100

12 36 60 96 120 240 Ukuran contoh (n)

VAR_1 VAR_2

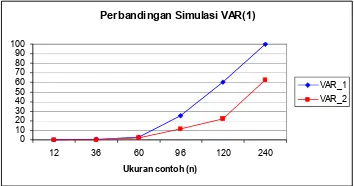
Gambar 5 Perbandingan Simulasi VAR(1) Perbandingan antara dua simulasi VAR(1), VAR_1 dengan VAR_2, dapat dilihat pada Gambar 5. Berdasarkan hasil tersebut dapat dilihat bahwa peningkatan jumlah parameter yang signifikan pada simulasi VAR(1) model kedua (VAR_2) lebih lambat daripada simulasi VAR(1) model pertama (VAR_1). Untuk VAR_2 pada ukuran contoh 240 hanya terdapat 62.4% parameter yang signifikan, sedangkan VAR_1 mencapai 99.8%.

SIMPULAN

Semakin besar ukuran contoh yang dimiliki maka model yang dihasilkan akan semakin tepat. Hal tersebut dapat dilihat dari semakin bertambahnya parameter yang signifikan sejalan dengan semakin besarnya data yang dibangkitkan. Karena jika data yang kita miliki sedikit, maka untuk mencari pola dari data tersebut akan lebih sulit dibandingkan dengan data yang besar.

(17)

suatu model VAR(1) sehingga menghasilkan model yang tepat. Berdasarkan hasil penelitian dapat dilihat batas minimal ukuran contoh yang baik untuk memodelkan AR(1), AR(2) dan MA(1) adalah 60. Sedangkan ukuran contoh yang baik digunakan untuk memodelkan VAR(1) adalah 240.

SARAN

Untuk penelitian selanjutnya sebaiknya jumlah ulangan ditambahkan, ukuran contoh lebih bervariasi, misalkan n=132, n=180, dan sebagainya. Serta model simulasi sebaiknya ditambahkan dengan model lain seperti ARMA.

DAFTAR PUSTAKA

Agusta, Y. 2005. Mixture Modelling

Menggunakan Prinsip Minimum Message Length. J Sistem dan Informatika; 1: 1-16.

Cryer, JD. 1986. Time Series Analysis.

Boston: Duxbury Press.

Enders, W. 1995. Applied Econometric Time Series. Ed ke-8. New York: Wiley and Sons, Inc.

Montgomery, DC, Johnson LA, Gardiner JS. 1990. Forecasting and time Series Analysis. Singapore: Mc Graw Hill, Inc.

Rosadi, D. 2006. Pengantar Analisa Runtun Waktu. Statistika Universitas Gadjah Mada.

Sartono, B, Affendi FM, Syafitri UD,

Sumertajaya IM, Angraeni Y. 2003.

Modul Teori Analisis Peubah Ganda.

Statistika Institut Pertanian Bogor.

SAS Institute Inc. 2002. SAS User’s Guide. Version 9.1 SAS Institute Inc., Cary, NC, USA.

Seppanen, A, Vauhkonen M, Somersalo E, Kaipio JP. State Space Models in Process Tomography – Approximation of State Noise Covariance. 2000. Finland: Department of Applied Physics, University of Kuopio.

Shumway, RH dan Stoffer DS. Time Series an its Application. New York: Springer.

Vargas, MV dan Salido RM. A State-Space Modelization of Economic Growth Among Spanish Regions.

http://www.uclm.es/AB/fcee/documentostr abajo.asp. [05 Mei 2008]

Wei, WWS. 1989. Time Series Analysis:

(18)

(19)

Lampiran 1 Hasil Simulasi Awal

Hasil Model

Bangkitan

Ukuran contoh

(n) xt=et AR(1) ARMA(2,1) ARMA(3,2) Model Lain TAM

12 30% 64% 4% 2% 0% 0% 36 0% 96% 2% 2% 0% 0% 60 0% 92% 4% 0% 4% 0% 120 0% 84% 12% 2% 2% 0%

A

R

(1

)

240 0% 80% 18% 2% 0% 0% 12 62% 30% 6% 2% 0% 0% 36 6% 28% 56% 10% 0% 0% 60 8% 88% 2% 2% 0% 0% 120 0% 0% 82% 8% 8% 2%

A

R

(2

)

240 0% 0% 92% 4% 4% 0% 12 32% 46% 12% 0% 0% 10% 36 0% 20% 60% 10% 2% 8% 60 0% 2% 84% 6% 4% 4% 120 0% 0% 82% 6% 8% 4%

M

A

(1

)

240 0% 0% 74% 2% 8% 16%

Keterangan:

TAM : Tidak ada model akhir (Fitted model) Lampiran 2 Output SAS Simulasi Awal VAR(1) n=120

The STATESPACE Procedure

Number of Observations 120

Standard Variable Mean Error

X 0.206513 1.117438 Y 0.026371 0.997263

Information Criterion for Autoregressive Models

Lag=0 Lag=1 Lag=2 Lag=3 Lag=4 Lag=5 Lag=6 Lag=7 Lag=8 25.90501 9.208241 16.21565 20.36134 21.98143 28.50604 32.26929 35.82196 42.61469

Information Criterion for Autoregressive Models Lag=9 Lag=10

47.81303 50.93209

The STATESPACE Procedure Canonical Correlations Analysis

Information Chi

X(T;T) Y(T;T) X(T+1;T) Criterion Square DF 1 1 0.072753 -3.36316 0.631533 2

Information Chi

(20)

Selected Statespace Form and Preliminary Estimates

State Vector X(T;T) Y(T;T)

Estimate of Transition Matrix 0.350665 0.19205 0.012471 0.198047

Input Matrix for Innovation 1 0 0 1

Variance Matrix for Innovation 1.062467 -0.07103 -0.07103 0.955478

Iterative Fitting: Maximum Likelihood Estimation

Iter Half Determinant Lambda F(1,1) F(1,2) F(2,1) F(2,2) Sigma(1,1) 0 0 1.01012 0.1 0.35066527 0.19205002 0.01247083 0.19804659 1.0624673 1 0 1.01012 0.01 0.35066527 0.19205002 0.01247083 0.19804659 1.0624673

Iter Half Sigma(2,1) Sigma(2,2) 0 0 -0.0710258 0.95547806 1 0 -0.0710258 0.95547806

Maximum likelihood estimation has converged.

Selected Statespace Form and Fitted Model

Estimate of Transition Matrix 0.350665 0.19205 0.012471 0.198047

Variance Matrix for Innovation 1.062467 -0.07103 -0.07103 0.955478

Parameter Estimates

Standard

(21)

Lampiran 3 Output SAS Simulasi AR(1) n=12

Standard Variable Mean Error

X -1.24974 1.352907

17.56094 19.46843

The STATESPACE Procedure Canonical Correlations Analysis

Information Chi

X(T;T) X(T+1;T) Criterion Square DF 1 0.127019 -1.80482 0.187052 1

Selected Statespace Form and Preliminary Estimates

State Vector X(T;T)

Estimate of Transition Matrix 0.427313

Input Matrix for Innovation 1

Variance Matrix for Innovation 1.496139

Iter Half Determinant Lambda F(1,1) Sigma(1,1) 0 0 1.496139 0.1 0.42731336 1.49613929 1 0 1.496139 0.01 0.42731336 1.49613929

Maximum likelihood estimation has converged.

State Vector X(T;T)

(22)

Parameter Estimates

Standard

Parameter Estimate Error t Value F(1,1) 0.427313 0.260755 1.64

State Vector X(T;T)

Parameter Estimates

Standard

State Vector X(T;T)

Parameter Estimates

Standard

(23)

Parameter Estimates

Standard

Parameter Estimates

Standard

Lampiran 8 Tabel Hasil Simulasi

Keterangan: TS : Parameter tidak signifikan

S : Parameter signifikan

A : Nilai t = A (tidak memiliki nilai t)

Parameter Model

Bangkitan

Ukuran contoh

(n) _TS _S _A

12 504 496 0

24 53 947 0

36 2 998 0

60 0 1000 0

120 0 1000 0

A

R

(1

)

240 0 1000 0

12 970 30 0

24 678 322 0

36 336 664 0

60 57 943 0

84 5 995 0

120 1 999 0

A

R

(2

)

240 0 1000 0

12 171 143 686

24 16 646 338

36 1 942 57

60 1 976 23

120 0 996 4

M

A

(1

)

240 0 998 2

12 998 2 0

36 995 5 0

60 967 33 0

96 747 253 0

120 394 606 0

V

A

R

_

1

240 2 998 0

12 998 2 0

36 999 1 0

60 974 26 0

96 889 111 0

120 777 223 0

V

A

R

_

2

(24)

Lampiran 9 Output SAS Simulasi VAR(1) n=60

Standard Variable Mean Error X 4.549138 3.987512 Y 14.24175 11.99416

236.0508 239.3411

Canonical Correlations Analysis

Information Chi

X(T;T) Y(T;T) X(T+1;T) Criterion Square DF 1 1 0.045403 -3.87618 0.121752 2

Information Chi

X(T;T) Y(T;T) Y(T+1;T) Criterion Square DF 1 1 0.088583 -3.52733 0.464794 2

Estimate of Transition Matrix 0.207059 0.234551 -0.21754 1.012624

Variance Matrix for Innovation 2.860147 5.042688 5.042688 15.7507

Parameter Estimates

Standard

Parameter Estimate Error t Value

(25)

Lampiran 10 Program yang Digunakan

AR(1)

%macro coba; %do i = 1 %to 1000; data awal;

do t=1 to 12;

a=rand('normal',0,1); output;

end; keep a ; run; proc iml; use awal;

read all var{a} into a; x=a;

n=nrow(a); do i=2 to n;

x[i]=0.9*x[i-1]+a[i]; end;

create akhir var{x}; append;

quit;

ods select ParameterEstimates; ods trace on;

ods output ParameterEstimates=tes; run;

proc statespace data=akhir cancorr out=output itprint; var x;

form x 1; run;

proc append base=gabung data=tes; run;

%end; %mend; %coba;

AR(2)

do t=1 to 12; a=rand('normal',0,1); output;

read all var{a} into a;

(26)

x=a; n=nrow(a); do i=2 to n;

if i=2 then

x[i]=0.4*x[i-1]+a[i]; else

x[i]=0.5*x[i-2]+0.4*x[i-1]+a[i]; end;

quit;

form x 2;

restrict f(2,2)=0.4 g(2,1)=0.4; run;

%end; %mend; %coba;

MA(1)

do t=1 to 12;

a=rand('normal',0,1); output;

read all var{a} into a; x=a;

n=nrow(a);

do i=2 to n; x[i]=a[i]-0.9*a[i-1]; end;

quit;

(27)

form x 2;

restrict f(2,1)=0 f(2,2)=0; run;

%end; %mend; %coba;

VAR(1)

do t=1 to 12;

a=rand('normal',0,1); b=rand('normal',0,1); output;

end; keep a b; run; proc iml; use awal;

read all var{a} into a; read all var{b} into b; x=a;

y=b; n=nrow(a); do i=2 to n;

x[i]=0.4*x[i-1]+0.2*y[i-1]+a[i]; y[i]=0.15*x[i-1]+y[i-1]+b[i]; end;

create akhir var{x y}; append;

quit;

proc statespace data=akhir cancorr out=output itprint; var x y;

form x 1 y 1; run;

%end; %mend; %coba;

(Pada simulasi awal syntax ini tidak dipakai)

(28)

P U R W A D I

DEPARTEMEN STATISTIKA

(29)

PENDAHULUAN

Latar Belakang

Tujuan

TINJAUAN PUSTAKA

Data Deret Waktu

t p e

 (B)x_t dengan

) B B B (1

(B) ₁ 1 ₂ 2 _p p

p   

     , dan

= intersep

k

t

e = galat acak ke-t

(MA) adalah:

t

t μ (B)

x  _q e

dengan:

) B B B 1 ( ) B

( 2 2

1 1

q q

q   

    

 = intersep

k

t

e = galat acak ke-t

Vector Autoregressive (VAR)

t p t p 2 t 2 1 t 1 0

t A y y ... y ε

(30)

PENDAHULUAN

Latar Belakang

Tujuan

TINJAUAN PUSTAKA

Data Deret Waktu

t p e

 (B)x_t dengan

) B B B (1

(B) ₁ 1 ₂ 2 _p p

p   

     , dan

= intersep

k

t

e = galat acak ke-t

(MA) adalah:

t

t μ (B)

x  _q e

dengan:

) B B B 1 ( ) B

( 2 2

1 1

q q

q   

    

 = intersep

k

t

e = galat acak ke-t

Vector Autoregressive (VAR)

t p t p 2 t 2 1 t 1 0

t A y y ... y ε

(31)

yt : vektor peubah respon (y1.t, y2.t, ...,yn.t)

berukuran nx1.

A0 : vektor intersep berukuran n x 1

Ai : matriks parameter berukuran n x n

t : vektor sisaan (1,t, 2,t, ...,k,t)

berukuran n x 1

Asumsi yang harus dipenuhi dalam VAR adalah semua peubah respon bersifat stasioner dan sisaan bersifat white noise.

ModelState Space

Model State Space adalah suatu analisis deret waktu, dimana data deret waktu dijelaskan atau digambarkan melalui beberapa peubah bantu. Peubah bantu tersebut dalam

State Space dinamakan state vector. Dalam SAS User’ Guide, state vector mengandung ringkasan semua informasi dari nilai sebelumnya dan nilai sekarang dari suatu deret waktu yang sesuai dengan prediksi dari nilai yang akan datang.

Model State Space dapat dimodelkan secara metematis sebagai berikut (Wei 1989):

1 t t 1

t Fx Ge

x (2)

dengan persamaan output :

t

t x

z H (3)

dimana:

xt :state vector berdimensi k zt : vektor output berdimensi m

F : matriks koefisien (matriks transisi) berukuran k x k,

G : matriks koefisien (matriks input) berukuran k x m.

H : matriks koefisien (matriks observasi) berukuran m x k

et : vektor sisaan, bersifat acak dan menyebar

normal. Berdimensi m dengan nilai tengah 0 dan matriks kovarian ∑

Persamaan (2) dapat diubah menjadi:









t

1 t t t t 1 -t t 1 1 e e e G FB G FB G F        x x x x

Kemudian persamaan diatas dimasukkan ke persamaan (3), sehingga menjadi:





t

1 t H1 FB Ge

  

z

Langkah-langkah dalam pembentukan model State Space adalah sebagai berikut:

1. Menentukan ordo p optimal. Ordo p

yang optimal memiliki nilai AIC yang terkecil.

2. Menentukan state vector dengan menggunakan analisis korelasi kanonik.

3. Pendugaan parameter menggunakan pendekatan kemungkinan maksimum.

Akaike Information Criterion (AIC)

Akaike Information Criterionadalah suatu ukuran atau nilai yang digunakan untuk mengidentifikasikan model dari suatu dataset (Agusta 2005). Dalam model State Spacenilai AIC digunakan untuk menentukan ordo p

optimal. Nilai AIC dapat dihitung melalui persamaan : 2 m 2 ˆ ln n

AIC_p  _p  p (4) dengan :

n = banyaknya observasi m = dimensi dari vektor proses zt

p



ˆ

_{= determinan dari matriks kovarian}

sisaan, atau white noise dalam pemodelan AR (p)

Analisis Korelasi Kanonik

Analisis korelasi kanonik dapat digunakan untuk melihat hubungan antara segugus peubah respon (y1, y2,...,yp) dengan segugus peubah penjelas (x1, x2,...xq). Analisis ini mirip dengan analisis regresi yang dapat mengukur keeratan hubungan antara segugus peubah respon dan gugus peubah penjelas. Selain itu analisis korelasi kanonik juga mampu menguraikan struktur hubungan dalam gugus peubah respon dan peubah penjelas tersebut (Sartono et al. 2003).

Asumsi yang harus dipenuhi dalam analisis korelasi kanonik yaitu:

a. Korelasi antar peubah didasarkan pada hubungan linear

b. Korelasi kanonik adalah hubungan linear antar peubah

c. Asumsi sebaran normal ganda.

Analisis korelasi kanonik dalam pemodelan State Space digunakan untuk menentukan state vector.

Menetukan State Vector

State vector ditentukan secara unik melalui analisis korelasi kanonik antara sekumpulan nilai observasi sekarang dan observasi lampau (zt, zt-1,..., zt-p) dan sekumpulan nilai observasi

sekarang dan yang akan datang (zt, zt+1|t, ...,

(32)

dan Ft, yaitu:



       j t j t t z z z z j n 1 )' )( ( n ) ( ˆ 1

,

dimana

j = 0, 1, 2, …, 2p.

] 1 q ) 1 ( m [ 2 ) 1 ln( n

IC ρ2min  p  

dimana:

p = ordo AR optimal

) 1 ln( ) ] 1 q ) 1 ( m [ 5 . 0 n

( min2

hit

2 __ _ _p_ _ _ __ρ



H1 : ρ0

Pendugaan Parameter

BAHAN DAN METODE

Bahan

Metode

1. Membangkitkan data sebanyak n, data tersebut dinyatakan sebagai et, dimana

et~N(0,1). Ukuran contoh (n) yang

digunakan dalam penelitian ini adalah 12, 36, 60, 120 dan 240. Untuk simulasi AR(1) dan MA(1) ukuran contoh ditambahkan dengan n=24, untuk AR(2) n=24 dan n=84, sedangkan VAR(1) n=96. Hal tersebut dilakukan untuk melihat perubahan peningkatan jumlah parameter yang signifikan.

2. Data hasil langkah ke-1 ditransformasi sehingga membentuk suatu model AR(1), AR(2) MA(1) dan VAR(1). Transformasi yang digunakan dalam penilitian ini adalah:

a) AR(1) : xt = 0.9xt-1 + et

b)AR(2) : xt = 0.4xt-1 + 0.5xt-2 + et

c) MA(1) : xt = et- 0.9et-1

d)VAR(1) :

Terdiri dari 2 buah model, yaitu: VAR_1 : xt = 0.4xt-1 + 0.2yt-1 + ε1,t

yt = 0.15xt-1 + yt-1 + ε2,t

VAR_2 : xt = 0.4xt-1 + 0.2yt-1 + ε1,t

yt = 0.15xt-1 + 0.3yt-1 + ε2,t ε1,t dan ε2,t ~ N(0,1).

3. Membuat model State Space dengan menggunakan data yang dihasilkan pada langkah ke-2.

4. Melihat kesignifikanan parameter yang dihasilkan. Jika nilai |t| > 2, maka parameter yang dihasilkan signifikan. 5. Langkah 1 – 4 diulang sebanyak 1000 kali. 6. Menghitung jumlah parameter yang

signifikan untuk setiap model yang dihasilkan.

Proses pemodelan State Space adalah sebagai berikut:

a. Langkah pertama dalam proses pemodelan

(33)

dan Ft, yaitu:



       j t j t t z z z z j n 1 )' )( ( n ) ( ˆ 1

,

dimana

j = 0, 1, 2, …, 2p.

] 1 q ) 1 ( m [ 2 ) 1 ln( n

IC ρ2min  p  

dimana:

p = ordo AR optimal

) 1 ln( ) ] 1 q ) 1 ( m [ 5 . 0 n

( min2

hit

2 __ _ _p_ _ _ __ρ



H1 : ρ0

Pendugaan Parameter

BAHAN DAN METODE

Bahan

Metode

1.