SATU-FAKTORISASI BEBAS K-CYCLE DARI GRAPH
LENGKAP
TESIS
Oleh
ASTRI SYAFRIANTY 097021003/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MAGISTER MATEMATIKA
UNIVERSITAS SUMATERA UTARA MEDAN
SATU-FAKTORISASI BEBAS K-CYCLE DARI GRAPH
LENGKAP
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam
Program Studi Magister Matematika pada Sekolah Pascasarjana
Universitas Sumatera Utara
Oleh
ASTRI SYAFRIANTY
097021003/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM PROGRAM STUDI MAGISTER MATEMATIKA
UNIVERSITAS SUMATERA UTARA MEDAN
2011
Judul Tesis : SATU-FAKTORISASI BEBAS K-CYCLE DARI GRAPH LENGKAP Nama Mahasiswa : Astri Syafrianty
Nomor Pokok : 097021003 Program Studi : Matematika
Menyetujui, Komisi Pembimbing
(Dr. Saib Suwilo, M.Sc) (Dr. Marwan Ramli, M.Scı)
Ketua Anggota
Ketua Program Studi Direktur
(Prof. Dr. Herman Mawengkang) (Prof. Dr. Ir. T.Chairun Nisa. B,M.Sc)
Telah diuji pada
Tanggal
PANITIA PENGUJI TESIS
Ketua : Dr. Saib Suwilo, M.Sc Anggota : 1. Dr. Marwan Ramli, M.Si
2. 3.
ABSTRAK
jhgadj
ABSTRACT
ajdb
Keyword:
KATA PENGANTAR
Dengan segala kerendahan hati dan penuh sukacita, penulis mengucapkan puji syukur ke hadirat Tuhan Yang Maha Kuasa atas segala anugrah dan berkat-Nya yang telah diberikan, sehingga penulis dapat menyelesaikan tesis dengan judul: SATU-FAKTORISASI BEBAS K-CYCLE DARI GRAPH LENGKAP. Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Studi Magister Matematika SPs Universitas Sumatera Utara.
Pada kesempatan ini, penulis menyampaikan terimakasih sebesar-besarnya kepada :
Prof. Dr. dr. Syahril Pasaribu, DTMH, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara
Prof. Dr. Ir. T. Chairun Nisa, B, M.Sc selaku Direktur Pascasarjana Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Magister Matematika di Sekolah Pascasarjana Universitas Sumatera Utara Medan.
Prof. Dr. Herman Mawengkangselaku Ketua Program Studi Magister Mate-matika SPs Universitas Sumatera Utara yang telah banyak memberikan bantuan
dalam penulisan tesis ini.
Dr. Saib Suwilo, M.Sc selaku Sekretaris Program Studi Magister Matemati-ka SPs Universitas Sumatera Utara dan selaku Pembimbing Utama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.
Dr. Marwan Ramli, M.Scselaku Pembimbing Kedua yang juga telah banyak memberikan bimbingan kepada penulis dalam penulisan tesis ini
Seluruh Staf Pengajarpada Program Studi Magister Matematika SPs Univer-sitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan.
Saudari Misiani, S.Siselaku Staf Administrasi Program Studi Magister Mate-matika SPs Universitas Sumatera Utara yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
Tak lupa penulis mengucapkan terimakasih sebesar-besarnya dan penghar-gaan setinggi-tingginya kepada ibunda tercinta Armaini Lubis dan ayahanda Buyung Damanikyang telah mencurahkan kasih sayang dan dukungan kepada penulis, terlebi yang dengan setia mendampingi dan membantu penulis selama mengikuti perkuliahan hingga sampai penulisan tesis ini. yang telah memberikan semangat dan dorongan kepada penulis dalam penulisan tesis ini.
Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya. Terimakasih.
Medan, Penulis,
Astri Syafrianty
RIWAYAT HIDUP
Alfred Hasiholan Silalahi dilahirkan di Batu V Pematangsiantar pada tang-gal 31 Oktober 1969 dari pasangan Bapak St. Maruli Silalhi, BA & Ibu Tiomina br. Simanjuntak dan merupakan anak ke empat dari delapan bersaudara. Penulis menamatkan pendidikan Sekolah Dasar (SD) HKBP Batu IV Pematangsiantar tahun 1981, Sekolah Menengah Pertama (SMP) HKBP Batu IV Pematangsiantar tahun 1984, Sekolah Menengah Atas (SMA) PGRI 29 Perumnas Batu VI Pe-matangsiantar tahun 1987. Pada tahun 1987 memasuki Perguruan Tinggi Uni-versitas HKBP Nommensen Pematangsiantar jurusan PMIPA Program Studi Ma-tematika pada Jenjang Diploma III Proyek Pengembangan Pendidikan Tenaga Kependidikan (P 3TK) dan lulus tahun 1990. Kemudian pada tahun 1990 penulis melanjutkan perkuliahan ke jenjang Strata Satu (S-1) pada Universitas HKBP Nommensen Pematangsiantar dan lulus tahun 1991.
Pada tahun 1990 1993, penulis menjadi guru honorer pada SMP HKBP Batu IV Pematangsiantar. Kemudian pada tahun 1993 1995, penulis bekerja sebagai Mechanic - A pada PT. Budi Bora Jaya Duri Riau. Pada tahun 1995 1997, penulis bekerja sebagai Lead Mechanic pada PT. Timbul Permata Jaya Duri
Riau. Pada tahun 1997 1999, penulis merantau ke Jakarta dan bekerja sebagai guru honorer pada SMP Negeri 70 Tanah Abang, SMK Negeri 9 Pinangsia Jakarta Barat, SMK Corpotarin Jakarta Timur, SMK TIO Bekasi, dan part time sebagai Debt Collector pada Astra Credit Company (ACC) Jakarta. Pada tahun 1998, penulis mengikuti Test CPNS di Jakarta dan Lulus, kemudian pada tanggal 1 Maret 1998, penulis diangkat menjadi CPNS dan ditempatkan pada SLTP Negeri 1 Sabu Barat Kabupaten Kupang Nusa Tenggara Timur, tetapi penulis baru pergi ke NTT untuk melaksanakan tugas pada bulan Juli 1999 dan langsung mendapat nota tugas sebagai guru pada SMA Negeri 1 Atambua Kabupaten Belu NTT untuk mengatasi jumlah siswa pengungsi yang membludak akibat korban jajak pendapat di Timor-Timur. Pada Tahun 2000, penulis pulang ke Medan untuk menikah dengan isteri tercinta Delima Christin Rajagukguk, SE. Tuhan mengaruniakan 2 anak perempuan bernama Gracia Monica Silalahi & Anasthasya Silalahi dan 1 anak laki-laki bernama Yehezkiel Silalahi.
tahun 2006 sekarang, penulis menjabat sebagai Wakil Kepala Sekolah Urusan Kurikulum pada SMA Negeri 2 Bandar Kabupaten Simalungun. Selama melak-sanakan tugas, penulis telah banyak mengikuti Pendidikan dan Pelatihan (Diklat) yang berhubungan dengan peningkatan kompetensi Guru baik pada tingkat kabu-paten maupun provinsi. Pada tahun 2008, penulis mendapat beasiswa dari Pe-merintah Provinsi Sumatera Utara untuk melanjutkan pendidikan pada Program Studi Magister Matematika SPs Universitas Sumatera Utara.
DAFTAR ISI
Halaman
ABSTRAK . . . i
ABSTRACT . . . ii
KATA PENGANTAR . . . iii
RIWAYAT HIDUP . . . v
DAFTAR ISI . . . vii
BAB 1 PENDAHULUAN . . . 1
1.1 Latar Belakang . . . 1
1.2 Perumusan Masalah . . . 2
1.3 Tujuan Penelitian . . . 2
1.4 Manfaat Penelitian . . . 2
1.5 Metode Penelitian . . . 2
BAB 2 TINJAUAN PUSTAKA . . . 4
BAB 3 SATU-FAKTORISASI DARI GRAPH LENGKAP DAN PERKEM-BANGANNYA . . . 6
3.1 Graph . . . 6
3.2 Graph Lengkap dan Graph Regular . . . 8
3.3 Subgraph dan Spanning Subgraph . . . 9
3.4 Satu-Faktorisasi dan Graph Lengkap . . . 10
3.5 Satu-Faktorisasi K2r, r >1 . . . 12
3.5.1 Strategi Shift and Rotate (S-R) . . . 13
3.5.2 Strategi Butterfly . . . 13
3.5.3 Metode Lain untuk Menghitung Satu-Faktorisasi K2r, r >1 . . . 13
3.5.5 Metode RAND . . . 15
3.6 Satu-Faktorisasi Bebas k-cycle . . . 15
BAB 4 HASIL UTAMA . . . 23
4.1 Satu-faktorisasi dari K2m untuk m= 2r, r ≥2 . . . 23
4.1.1 Metode Silang . . . 23
BAB 5 KESIMPULAN DAN SARAN . . . 27
5.1 Kesimpulan . . . 27
5.2 Saran . . . 28
DAFTAR PUSTAKA . . . 29
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Suatu graph G adalah suatu objek yang terdiri dari himpunan titik-titik berhingga tak kosong V yang disebut verteks dari G dan himpunan garis E
yang menghubungkan verteks-verteks yang anggotanya disebut edge dari G dan dinotasikan dengan G(V, E), (Gross dan Yellen, 2006). Suatu edge dari verteksu
kev dinotasikan dengan (u, v). Suatu walk dari ukev dengan panjang m adalah barisan edge dalam bentuk
u=v0−v1−v2−. . .−vm−1−vm =v
dengan v0 =udan vm =v. Suatu walk dari ukev disingkat sebagaiuv-walk. Su-atuuv−walkdikatakanterbuka bilau6=vdan dikatakantertutup bila sebaliknya. Suatuuv−pathadalah suatuuv−walkyang tidak mengandung verteks berulang kecuali mungkin u=v. Suatu uv−pathtertutup disebut cycle.
Graph Lengkap Kn adalah suatu graph dengan n verteks, yang setiap dua verteks berbeda dihubungkan oleh satu edge. Graph lengkap Kn mempunyai edge sebanyak E(Kn) = 1
2n(n − 1) dan setiap verteksnya mempunyai derajat (n−1), (Deo N, 1986). Graph Regular adalah suatu graph yang semua verteksnya berderajat sama. Graph regular yang semua verteksnya berderajat k disebut
k−regular. Graph lengkap Kn disebut juga (n−1)−regular.
Suatu graphG1dikatakansubgraphdari graphGjika semua verteks dan edge dari G1 ada dalam graph G, dan setiap edge dari G1 mempunyai verteks ujung yang sama dengan edge dari graph G. Suatu subgraph G1 yang memuat semua verteks disebut spanning subgraph dari G. Suatu spanning subgraph k−regular
dari graph G disebutk−f aktor dari graph G, (Gross dan Yellen, 2006).
Satu−f aktor dari suatu graph G adalah suatu spanning subgraph regu-lar berderajat satu. Satu−f aktorisasi dari graph G adalah suatu himpunan
F = {F1, F2, ..., Fn} dari edge-disjoint satu-faktor sedemikian hingga E(G) =
Sn
2
dua-faktor yang terdiri dari cycle-cycle dengan panjang genap, (Gross dan Yellen, 2006).
Satu-faktorisasi F = {F1, F2, ..., Fn} dari G dikatakan bebas k-cycle jika gabungan dari dua satu-faktor tidak memuat panjang-panjang cycle dari him-punan S, khususnya jika S = {4,6, ..., k}maka F disebut bebas k-cycle. Dengan perkataan lain, F mempunyai cycle dengan panjang k jika ada dua satu-faktor padaF, (Meszka M, 2009). Penelitian ini menentukan untuk setiapm= 2r, r≥2
dan setiap k ≥ 4 genap sedemikian hingga 4 ≤ k ≤ 2m adalah satu-faktorisasi bebas k-cycle dengan satu edge persekutuan.
1.2 Perumusan Masalah
Andaikan graph lengkap K2m untuk setiap m = 2r, r≥ 2 dan setiap k ≥ 4
genap sedemikian hingga 4≤k≤2madalah satu-faktorisasi bebask-cycle dengan satu edge persekutuan. Masalah dalam penelitian ini apa syarat perlu atau syarat cukup dari graph yang demikian.
1.3 Tujuan Penelitian
Adapun yang menjadi tujuan dari penelitian ini adalah menentukan syarat perlu atau syarat cukup dari graph lengkap K2m untuk setiapm= 2r,r ≥2 dan
setiap k ≥4 genap sedemikian hingga 4≤ k ≤2m adalah satu-faktorisasi bebas
k-cycle dengan satu edge persekutuan.
1.4 Manfaat Penelitian
Penelitian ini bermanfaat untuk memperkaya literatur tentang satu faktorisasi bebas k-cycle dari graph lengkap.
1.5 Metode Penelitian
Metode penelitian ini bersifat literatur dan kepustakaan. Untuk mencari syarat perlu atau syarat cukup dari graph lengkapK2muntuk setiapm = 2r,r≥2
dan setiap k ≥ 4 genap sedemikian hingga 4 ≤ k ≤ 2m adalah satu-faktorisasi bebask-cycle dengan satu edge persekutuan dilakukan dengan pendekatan sebagai berikut :
3
1. Mencari bentuk satu-faktorisasi dari suatu graph lengkap
2. Mencari satu atau lebih satu-faktorisasi yang lain dari suatu graph lengkap sedemikian hingga mempunyai mempunyai satu edge persekutuan dengan satu-faktorisasi sebelumnya.
3. Membuat metode yang tepat untuk membentuk satu-faktorisasi
4. Menggabungkan dua satu-faktor dari satu-faktorisasi yang pertama dan ke-dua yang mempunyai satu edge persekutuan sedemikian hingga bebas k -cycle.
BAB 2
TINJAUAN PUSTAKA
Istilah-istilah baku graph dalam tulisan ini diambil dari Gross dan Yellen (2006). Mendelsohn dan Rosa (1985) menemukan jumlah tepat N(2m) untuk 2m≤14, antara lainN(4) =N(6) = 1,N(8) = 6,N(10) = 396 denganN adalah semua pasangan berurut dari satu-faktorisasi tak-isomorfik pada graph lengkap
K2m dan m adalah banyaknya edge dari graph lengkap. Kemudian Dinitz, et. al.
(1994) menemukan untuk N(12) = 526, 915, 620. Oleh karena itu, banyak in-vestigasi (termasuk enumerasi) berkenaan dengan satu-faktorisasi padaK2myang
dianggap layak jika dibatasi suatu subclass yang memenuhi beberapa sifat tamba-han. Suatu pertanyaan timbul berkenaan dengan keberadaan dari keseragaman (sempurna) satu-faktorisasi. Satu-faktorisasi dikatakan sempurna jika gabungan dari dua satu-faktor adalah isomorfik dengan cycle Hamilton.
Satu-faktorisasi sempurna dari graph lengkap diperkenalkan oleh Kotzig (1964). Kemudian Anderson (1973) menemukan class dari satu-faktorisasi sem-purna ketika m prima. Hal yang sama juga ditemukan oleh Bryant, et. al. (2006) ketika 2m − 1 adalah prima. Satu-faktorisasi sempurna sangat jarang ditemukan diantara semua satu-faktorisasi. Pernyataan ini didukung oleh hasil penelitian yang dilakukan oleh Seah (1991) yang menemukan P(2m), yaitu un-tuk P(4) = P(6) = P(8) = P(10) = 1, P(12) = 5 dengan P adalah pasangan berurut dari satu-faktorisasi sempurna tak-isomorfik. Meszka dan Rosa (2003) melakukan penelitian yang sama dan menemukan P(16) ≥ 88. Faktanya, hanya ada tiga klasifikasi tak berhingga dari satu-faktorisasi dan contoh-contoh yang jarang dari satu-faktorisasi seragam tidak-sempurna. Gopal, et. al. (2007)
mene-mukan metode untuk menghitung satu-faktorisasi dari graph lengkap dengan jum-lah verteks merupakan perpangkatan 2. Metode tersebut juga dapat digunakan untuk memperoleh satu-faktorisasi dari graph lengkap dengan jumlah verteks ke-lipatan 4 atau graph lengkap denganmnverteks jika satu-faktorisasi dariKm dan satu-faktorisasi dariKn diketahui.
Dinitz, et. al. (2005) menginvestigasi panjang-panjang cycle yang mungkin muncul dari gabungan sebarang dua satu-faktor pada graph lengkap. Dalam penelitian tersebut ditemukan untuk m ≥ 3 dan k genap sedemikian hingga
5
4 ≤ k ≤ 2m, satu faktorisasi dari graph lengkap terdiri dari cycle dengan pan-jang k jika dan hanya jika k/2 | 2m−1 atau k−1 | 2m−1. Oleh karena itu, diperoleh beberapa klasifikasi tak berhingga dari satu-faktorisasi bebas k-cycle. Selanjutnya Meszka (2009) menentukan untuk setiap m ≥ 3 dan untuk setiap
k ≥ 4 dengan k 6= 2m, maka terdapat satu-faktorisasi dari graph lengkap K2m
sedemikian hingga sebarang dua satu-faktor dariK2m bebas dari k−cycle. Untuk
2m6=p+ 1,p prima atau 2m6≡6,12,18(mod24), maka satu-faktorisasi dariK2m
BAB 3
SATU-FAKTORISASI DARI GRAPH LENGKAP DAN PERKEMBANGANNYA
Pada bab ini akan dipaparkan mengenai materi-materi yang berhubungan dan mendukung untuk satu-faktorisasi bebas k-cycle dari graph lengkap. Materi tersebut akan dijadikan sebagai landasan berfikir dalam melakukan penelitian ini sehingga mempermudah dalam hal pembahasan hasil utama pada bab berikut-nya. Adapun materi-materi tersebut mencakup pengertian graph, contoh graph, pengertian graph lengkap, pengertian satu-faktorisasi, beberapa metode untuk membangun faktorisasi dari graph lengkap, dan fakta-fakta tentang satu-faktorisasi bebask-cycle dari graph lengkap.
3.1 Graph
Secara sederhana suatu graph adalah kumpulan titik-titik yang dihubungkan oleh garis. Secara matematis suatu graph Gadalah suatu objek yang terdiri atas dua himpunan, yakni :
• Himpunan berhingga tak kosong V. Unsur dari V disebut verteksdari G.
• HimpunanE yang merupakan himpunan bagian dari pasangan tak berurut dari unsur-unsur diV. Unsur dari E disebut edge dari G.
GraphGdengan himpunan verteksV dan himpunan edgeE dinotasikan de-nganG(V,E). Andaikanudanv adalah dua verteks diG. Suatu edge (u, v) atau juga dapat dinotasikan denganu−vadalah suatu edge diGyang menghubungkan verteksu dan v.
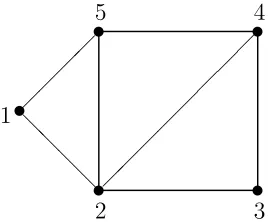
Contoh 1 : Himpunan verteksV ={1,2,3,4,5}bersama dengan himpunan edge
E ={1−5,5−4,5−2,4−2,2−1,2−3,4−3,3−3}adalah suatu graph dengan 5 verteks dan 8 edge.
Sesuai dengan namanya, suatu graph biasanya direpresentasikan secara grafis dengan cara setiap verteks pada graph tersebut direpresentasikan sebagai suatu titik atau lingkaran kecil dan setiap edgeu−v yang terdapat dalam graph itu
7
representasikan sebagai garis berarah dariukev. Representasi graph pada contoh 1 diperlihatkan pada Gambar 3.1.
Gambar 3.1 : Graph dengan 5 verteks dan 7 edge
AndaikanG(V,E) adalah suatu graph danu,v ∈V. Suatu walk dariu kev
dinotasikan denganuv-walk atauwuv (untuk selanjutnya dipakai notasiuv-walk). Suatu walk dari u ke v yang panjangnya m adalah suatu barisan edge dalam bentuk
u=v0−v1−v2−. . .−vm−1−vm =v
Suatu walk dikatakan terbuka jika verteks u 6= v dan dikatakan tertutup jikau =v. Panjang dari suatu walk wuv adalah banyaknya edge yang menyusun walk tersebut dan dinotasikan denganℓ(uv-walk). Suatu path adalah suatu walk tanpa ada perulangan verteks kecuali mungkin verteks awal dan verteks akhir. Suatu path yang menghubungkan verteks u dan v dinotasikan dengan uv-path dan panjangnya dinotasikan dengan ℓ(uv-path). Suatu cycle adalah suatu path tertutup. Cycle yang panjangnya k dinotasikan dengank−cycle
Perhatikan graph pada Gambar 3.1 yang terdiri dari 5 verteks dan 7 edge. Berikut ini diperlihatkan contoh dari walk, path, dan cycle.
1. 2−1−5−2−3 adalah suatu uv-walk dengan panjang 4. Walk ini bukan merupakan suatu path karena verteksv2 berulang.
2. 5−4−3−2 adalah suatu uv-path dengan panjang 3.
3. 5−4−3−2−1 adalah suatu uv-path tertutup atau cycle dengan panjang 5.
ko-8
respondensi satu-satu antara verteks-verteks dan edge-edgenya sedemikian hing-ga sifat insident tetap terpelihara atau denhing-gan perkataan lain graph G1 dan
G2 dikatakan isomorfik jika terdapat pemetaan bijektif θ : V1 → V2 sehingga memenuhi u−v ∈ E1 ⇔ θ(v) ∈ E2 untuk sebarang verteksu, v ∈ V1 dan dino-tasikan dengan E1 ∼=E2.
Syarat perlu agar dua buah graph G1 dan G2 isomorfik , yaitu jika G1 dan
G2 isomorfik, maka G1 dan G2 harus memenuhi :
1. Banyak verteks di G1 dan G2 sama
2. Banyak edge di G1 dan G2 sama
3. Derajat setiap verteks yang berkorespodensi sama
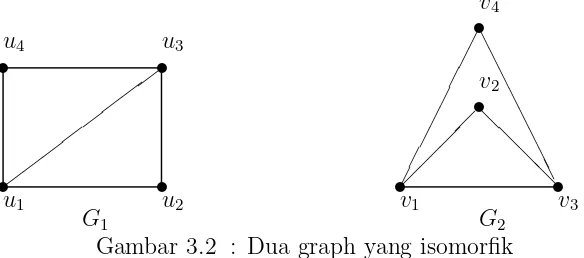
Contoh 2 : Berikut ini akan diberikan satu contoh dari dua buah graph yang isomorfik. Gambar 3.2 : Dua graph yang isomorfik
Perhatikan graphG1 danG2. Berikut ini diperlihatkan pemetaan bijektifθ , yaitu : θ(u1) =v1, θ(u2) =v4, θ(u3) =v3, dan θ(u4) =v2 dan memenuhi u1−u2 ∈E1
⇔ v1 −v4 ∈ E2 , u1 −u3 ∈ E1 ⇔ v1−v3 ∈ E2, u1 −u4 ∈ E1 ⇔ v1−v2 ∈ E2,
u2−u3 ∈E1 ⇔v4−v3 ∈E2, dan u3−u4 ∈E1 ⇔v3−v2 ∈E2. Jadi G1 ∼=G2.
3.2 Graph Lengkap dan Graph Regular
Suatu graph lengkapKn adalah suatu graph dengan n verteks, yang setiap dua verteks berbeda dihubungkan oleh satu edge. Pada Gambar 3.3 berikut akan diperlihatkan graph lengkap atas satu, dua, tiga, empat, lima, dan enam verteks.
Contoh 3 : Gambar di samping merupakan contoh dari graph lengkap
9
Gambar 3.3 : Graph Lengkap
Teorema 3.2.1 Banyaknya edge dari suatu graph lengkap dengannverteks adalah E(Kn) = 1
2n(n−1).
Bukti. Andaikan G adalah suatu graph lengkap dengan n verteks 1,2,3, ..., n. Ambil sebarang verteks 1, karenaGmerupakan graph lengkap maka 1 dihubungkan dengan (n−1) verteks lainnya (2,3, ..., n). Dengan demikian terdapat (n−1) edge. Selanjutnya, ambil sebarang verteks kedua 2. Karena G adalah graph lengkap, maka 2 juga dihubungkan dengan verteks lainnya (1,3, ..., n), sehingga terdapat (n−1) edge yang terhubung dengan 2. Salah satu edge tersebut menghubungkan 2 dan 1. Edge ini sudah dihitung ketika menghitung banyaknya edge yang ter-hubung dengan 1. Jadi, terdapat (n−2) edge yang belum dihitung. Proses dilan-jutkan dengan menghitung banyaknya edge yang terhubung dengan 3,4, ..., ndan yang belum dihitung sebelumnya. Banyaknya edge yang diperoleh berturut-turut adalah (n−3),(n −4), ...,3,2,1. Oleh karena itu, secara keseluruhan terdapat (n−1 + (n−2) + (n−3) +...+ 3 + 2 + 1 = 1
2n(n−1) edge.
Derajat pada suatu verteksuadalah banyaknya edge yang terhubung dengan verteks tersebut dan dinotasikan dengandu. Graph lengkapKn mempunyai edge sebanyak E(Kn) = 1
2n(n−1) dan setiap verteksnya mempunyai derajat (n−1).
GraphRegularadalah suatu graph yang semua verteksnya berderajat sama. Graph regular yang semua verteksnya berderajat k disebut k-regular. Graph lengkap Kn disebut juga (n−1)-regular.
3.3 Subgraph dan Spanning Subgraph
10
verteks ujung sama dengan edge dari graphG. Spanning subgraphdari G adalah suatu subraph G2 yang memuat semua verteks dari graph G.
Contoh 4 : Gambar berikut ini merupakan contoh graph regular
s s
1-regular 2-regular 5-regular
Gambar 3.4 : Graph Regular
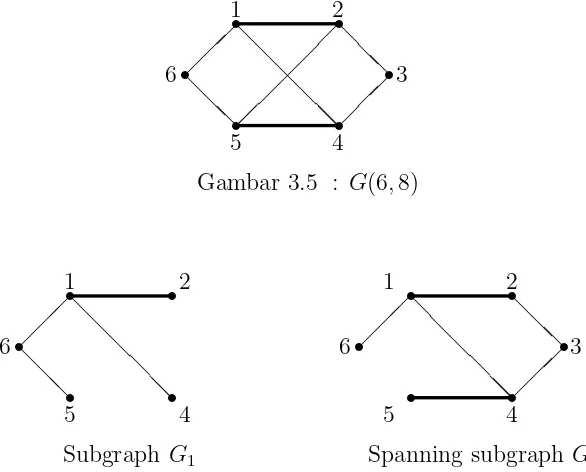
Contoh 5 : Berikut ini diberikan graph G(6,8) kemudian diperlihatkan juga subgraph dan spanning subgraph dari G.
s s
Subgraph G1 Spanning subgraph G2
Gambar 3.6 : Subgraph dan Spanning subgraph dari graph G(6,8)
3.4 Satu-Faktorisasi dan Graph Lengkap
Suatu f aktor dari graph G adalah suatu spanning subgraph dari graph
G. Suatu f aktorisasi dari graph G adalah suatu himpunan faktor-faktor yang
11
himpunan-himpunan edge nya membentuk suatu partisi dari himpunan edge pa-da graph G. k-faktor dari graph G adalah suatu spanning subgraph k-regular dari graph G. Satu-faktor dari graph G adalah suatu spanning subgraph regu-lar berderajat satu. Satu-faktorisasi dari graph G adalah suatu himpunan F =
{F1, F2, ..., Fn}dari edge disjoint satu-faktor sedemikian hinggaE(G) =
n
S
i=1
E(Fi).
Satu-faktorisasi dari graph lengkap K2m mempunyai 2m−1 satu-faktor,
masing-masing satu-faktor mempunyai m edge. F mempunyai cycle dengan panjang k
jika terdapat dua satu-faktor di F.
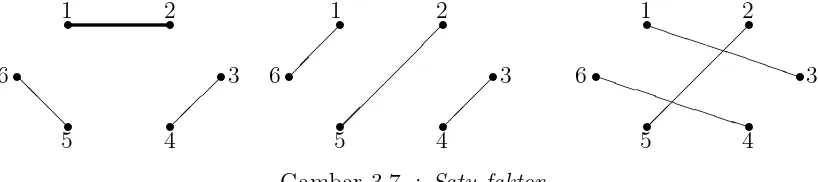
Contoh 6 : Gambar 3.6 berikut adalah contoh satu-faktor dari K6.
s s
Contoh 7 : Satu-Faktorisasi dari K6 diperlihatkan oleh Gambar 3.8 berikut :
1,2 3,4 5,6
1,3 2,6 4,5
1,4 2,5 3,6
1,5 2,3 4,6
1,6 2,4 3,5
Gambar 3.8 : Satu-faktorisasi K6
Dari gambar di atas diketahui graph mempunyai edge m = 3, dan
satu-faktor sebanyak 2m−1 = 2(3)−1 = 5. Maka,E(K6) =S6i=1E(Fi) = 15
Satu-faktorisasi{F1, F2, ..., F2m−1}dariK2madalah sequentially uniformjika
satu-faktor dapat diurutkan menjadi {F1, F2, ..., F2m−1}sedemikian hingga graph dengan himpunan edge Fi∪Fi+1 isomorfik untuk semua 1≤i≤2m−1. Karena gabungan dua satu-faktor adalah suatu graph 2-regular dengan 2-edge-colorable, isomorfik dengan gabungan saling lepas dari cycle-cycle genap. Dikatakan mul-tiset T = (k1, k2, kr) adalah jenis dari satu-faktorisasi sequentially uniform jika
12
k1, k2, ..., kr, dengank1+k2+...+kr = 2m. Jika gabungan setiap dua satu-faktor berurutan adalah suatu cycle Hamilton, satu-faktorisasi dikatakan sequentially perfect (Dinitz, et. al. , 2005).
Suatu ide yang mempertimbangkan pengurutan faktor dalam satu-faktorisasiK2mtidak sepenuhnya akademik. Faktanya, pengurutan satu-faktorisasi K2m telah diperlihatkan sebelumnya pada penjadwalan permainan untuk round-robin tournament yang dimainkan dalam 2m−1 babak.
Definisi di atas adalah suatu relaksasi dari definisi uniform (perfect) satu-faktorisasi K2m yang mengharuskan gabungan sebarang dua satu-faktor
isomor-fik dengan cycle Hamilton. Variasi uniform satu-faktorisai telah dibangun dari
Steiner triple system. Sebagai contoh, ketika m = 2r untuk sebarang r
bi-langan bulat positif memberikan suatu konstruksi dari uniform satu-faktorisasi
K2m jenis (4,4, ...,4). Selain itu contoh lain diberikan untuk perfect Steiner triple
system yaitu uniform satu-faktorisasi jenis (2m −4,4). Jika m = 3r, uniform
satu-faktorisai jenis (4,6, ...,6) dan ketika terdapat suatu p dengan padalah pri-ma ganjil pri-maka terdapat suatu uniform satu-faktorisasi jenis (p + 1,2p, ...,2p), (Mendelsohn dan Rosa, 1985).
3.5 Satu-Faktorisasi K2r, r >1
Graph lengkap atas 2m verteks secara umum dapat direpresentasikan seba-gai gabungan dari tiga graph yaitu dua Km yang diberi indeks dengan verteks 1 sampai m dan m+ 1 sampai 2m, dan graph bipartit komplit Km,m dengan m
verteks yang masing-masing sisi dipartisi. Andaikan 2mmerupakan perpangkatan dua. Satu-faktorisasi dari Km terdiri darim−1 satu-faktor yang masing-masing terdiri dari m/2 edge. Maka dengan menempatkan satu-faktorisasi diantara Km
secara bersamaan akan menghasilkan (m−1) satu-faktor masing-masing terdiri dari m edge. Satu-faktorisasi dari Km,m mempunyai m satu-faktor yang masing-masing terdiri dari m edge. Maka jumlah total adalah m − 1 + 1 = 2m − 1 satu-faktor terdiri dari totalm(2m−1) edge, yang merupakan jumlah edgeK2m.
Karena masing-masing edge K2m mempunyai tepat satu satu-faktor, metode ini
menghasilkan satu-faktorisasi K2m.
Berikut diberikan beberapa metode untuk membangun satu-faktorisasi dari
K2m dengan 2m merupakan perpangkatan dua (Gopal, et. al. 2007).
13
3.5.1 Strategi Shift and Rotate (S-R)
Pada strategi ini untuk membangun satu-faktorisasi Km,m dicatat bahwa untuk setiap satu-faktor mempunyai 1,2,3, ..., m sebagai titik-akhir yang perta-ma dari m edge dan m + 1 sampai 2m sebagai titik-akhir yang kedua. Titik akhir yang kedua berurut berbeda untuk setiap faktor dimulai dengan satu-faktor (1, m+ 1),(2, m+ 2), ...,(m,2m). Untuk membangun satu-faktor ke-i, shift and rotate barisan m+ 1, m+ 2, ...,2m dengan i berpindah ke kiri memberikan penambahan ke-i faktor (1, m+i+ 1),(2, m+i+ 2), ...,(m,2m+i−m).
Untuk menunjukkan hasil satu-faktor pembentuk satu-faktorisasi, bentuk formalnya adalah sebagai berikut. Satu-faktor berkorespondensi ke edge Km,m, masing-masing edge Km,m muncul tepat satu kali pada satu-faktor. Diberikan edge (i, j) dengan 1 ≤i≤m dan m+ 1≤j ≤2m dengan order dari satu-faktor edge (i, j) muncul ke j−i+ 1 satu-faktor sebagai titik-akhir i.
3.5.2 Strategi Butterfly
Dengan ketentuan mendaftarkan masing-masing satu-faktor sebagai medge dengan titik-akhir pertama 1 sampaim, sehingga jenis satu-faktor dapat ditulis,
(1, v1),(2, v2), ...,(m, vm) dengan m+ 1≤v1, v2, ..., vm≤2m.
Untukl = 0, satu-faktor F0 disebut faktor identitas yaitu :
{(1, m),(2, m+ 1),(3, m+ 2), ...,(m,2m)}.
Untukl = 1,2, ..., m−1 satu-faktor ke-l , Fi dihitung sebagai berikut :
Jika l merupakan perpangkatan dua, maka Fl adalah edge (i, j) ∈ Fl jika edge (i′, j′) ∈ F
3.5.3 Metode Lain untuk Menghitung Satu-Faktorisasi K2r, r >1
Selain dari dua metode di atas, ada pendekatan lain untuk mendirikan satu-faktorisasi sempurna untuk Km,m dan K2m dengan m perpangkatan dari
14
{(u1, v1)}mi=1yang mana semuaui pada partisi yang sama danvi pada partisi yang lain.
Andaikan ui sebagai titik-akhir pertama dan vi sebagai titik-akhir kedua. Himpunan lain dari titik-akhir, misalkan{u1, u2, ..., um}ditukar dengan memutar untuk mendapatkan satu-faktor yang lain. Akibat operasi shift pada{u1, u2, ..., um} adalah {u2, u3, ..., um, u1} jika ditukar ke kiri (dengan operasi rotate). Pada class strategi Shift and Rotate, tukar titik-akhir pertama atau titik-akhir kedua dari edge pada F1 untuk memperoleh F2 hingga Fm−1.
Contoh 8 : Satu-faktorisasi dengan m = 4, maka K2m = K8. Titik-pertama 4 faktor dari K4,4 adalah 1 hingga 4 dan titik-akhir kedua 8 menurun ke 5. Maka satu-faktorisasi Km,m dibangun mulai dari faktor identitas
F0 = (1,8),(2,7),(3,6),(4,5).
Selanjutnya shift and rotate titik-akhir pertama ke kiri untuk mendapatkan (m−
1)-faktor yang lain, hingga diperoleh satu-faktorisasi dari K8.
1,8 2,7 3,6 4,5
Gambar 3.9 : Satu-faktorisasi K8 dengan strategi Shift and Rotate
Selanjutnya akan diberikan metode lain untuk membangun satu-faktorisasi dariK2m menggunakan heuristik. Dengan cara ini dibuktikan bahwa satu-faktorisasi F dari K2m mempunyai 2m−1 matching sempurna di dalamnya. Setiap
match-ing sempuna mempunyai m edge. Ambil (1, i) sebagai edge awal dan kemu-dian diperpanjang menaik sedemikian hingga Fi menjadi matching sempurna. Tahap selanjutnya jika ingin membangun edge kej, (uj, vj) untuk matching keFi
memilih edge tambahan hanya dari himpunanE\{F1∪F2...∪Fi−1∪Ei} dengan
Ei =
ei1, ei2, ei3, ..., eij−1 dan eik adalah edge kek yang dipilih untuk matching keFi. Untuk efisiensi waktu pilih verteks pertamauj sebagai verteks yang paling
15
terkeci dari verteks V′ = {v
1, v2, v3, ..., vi} dengan vi ∈ V′ jika dan hanya jika
vi tidak dimuat oleh Fi. Verteks kedua vj dapat dipilih dengan menggunakan metode MINatau RAND.
3.5.4 Metode MIN
Pada metode ini untuk memilih edge ke j, (uj, vj) untuk matching ke Fi, verteks terkecil dari semua verteks yang tidak dimuat Fi dipilih sebagai verteks
uj. Untuk mengambil verteks kedua, lakukan strategi yang sama seperti pada pengambilan pertama. Jika edge (uj, vj) sudah digunakan pada satu-faktorisasi
F, maka verteks terkecil selanjutnyavj ∈V′ dipilih sebagaivj. Proses ini
berlan-jut hingga edge yang cocok diperoleh sehingga Fi diperluas. Jika tidak berhasil memperluas Fi menggunakan semua verteks, maka kembali dan susun kembali edge sebelumnya (uj−1, vj−1) pada matching. Jika j = 0 maka susun kembali edge sebelumnya pada faktorFi−1.
3.5.5 Metode RAND
Pada metode ini, untuk menambah edge ke-j (uj, vj) untuk matching ke
Fi, verteksuj dipilih sebagai verteks terkecil pada V′. Verteksvj kemudian
dipi-lih seragam secara acak dari himpunan V′\{uj}. Jika (uj, vj) tidak dapat
digu-nakan pada perluasanFi, maka tetap memilih verteksvj seragam secara acak dari
V′\{uj} hingga ditemukan edge yang dapat digunakan pada perluasan Fi. Jika
tidak sukses pada perluasan Fi menggunakan semua verteks, maka kembali dan susun kembali edge sebelumnnya (uj−1, vj−1) pada matching. Jika j = 0 maka susun kembali edge sebelumnya pada faktorFi−1. metodeRANDtidak memenuhi sebarang satu-faktorisasi melalui pemilihan acak yang sesuai selama tahapan.
3.6 Satu-Faktorisasi Bebas k-cycle
Satu-faktorisasi F = {F1, F2, ..., Fn} dari G dikatakan bebas k-cycle jika gabungan dua satu-faktor tidak memuat cycle dengan panjang k. F adalah be-bas S-cycle jika gabungan sebarang dua satu-faktor tidak memuat cycle dengan panjang diambil dari himpunan S. Jika S = {4,6, ..., k} maka F disebut bebas k <−cycle.
sedemi-16
kian hingga gcd(l, n) > 1, maka gcd(l, n) = l. Meskipun untuk n′ ≥ 3, jika
l′ adalah bilangan bulat positif genap terkecil sedemikian hingga gcd(l′, n′) > 1,
maka gcd(l′, n′) =l′/2.
Klaim 3.6.2 Jika k > 2m ≥ 4, maka satu-fasktorisasi dari K2m adalah bebas k-cycle.
Hasil investigasi yang dilakukan oleh Dinitz, et. al. (2005) terhadap panjang-panjang cycle yang mungkin muncul dari gabungan sebarang dua satu-faktor pada graph lengkap diberikan pada lemma berikut.
Lemma 3.6.3 Untuk m ≥3 dan k genap sedemikian hingga 4≤ k ≤2m, satu-faktorisasi dari K2m terdiri dari cycle dengan panjang k jika dan hanya jika k/2
| 2m−1atau k−1 | 2m−1.
Bukti. Andaikan p = 2m−1. Asumsikan bahwa satu-faktorisasi terdiri dari cycleCk dengan panjangk yang terdapat pada gabungan dua satu-faktorFh dan
Fi, untuk h < i dan h, i ∈ {0,1, ..., p−1}. Andaikan z =i−h, dibagi menjadi dua kasus.
Kasus 1 : Ck terdiri dari verteks ∞. Tetangga dari∞ adalah h dan i. Verteks konsekutif sepanjang cycleCkadalah : ∞, i, h−z, i+2z, h−3z, i+4z, h−5z, ..., i+ (k −2)z,∞, dengan k adalah bilangan bulat positif genap terkecil sedemikian hingga i+ (k −2)z ≡ h (mod p) (ekiuvalen ke (k −1)z ≡ 0 (mod p). Karena dengan kasus 1, karena 0< z < pdan Klaim 3.6.1 oleh sifat ekiuvalen darikz ≡0 (mod p) maka gcd(k, p) =k/2.
Untuk membuktikan syarat cukup, pertama anggap bahwa k < 2n dan k/2|p. Maka k ≡ 2(mod 4). Untuk menemukan suatu cycle dengan panjang k, ambil dua satu-faktor F0 dan Fi, dengan i =
p
k/2. Andaikan l adalah panjang dari cycle yang tidak terdiri dari ∞pada gabungan F0 dan Fi. Hitung kembali Kasus 2, l adalah bilangan bulat positif genap terkecil sedemikian hingga li ≡ 0 (mod
17
p). Maka lp
k/2 ≡ 0 (mod p), selanjutnya karena k/2 ganjil, l = k. Hal yang sama untuk sebarang k ≤ 2m genap dengan k −1|p, dua satu-faktor F0 dan Fi diperoleh, dengan j = p
k−1. Jika l adalah panjang dari suatu cycle yang terdiri dari ∞, oleh Kasus 1, l adalah bilangan bulat positif genap terkecil sedemikian hingga (l−1)j ≡0 (mod p). Maka l=k.
Berikut ini diberikan hasil yang ekiuvalen dengan Lemma 3.6.1 di atas.
Akibat 3.6.4 Untuk m ≥ 3 dan k ≥ 4 genap, satu-faktorisai K2m adalah bebas k-cycle jika dan hanya jika k/2 6 | 2m−1 atau k−1 6 | 2m−1.
Akibat 3.6.5 Andaikan r adalah faktor prima terkecil dari 2m−1. Jika r≥5, maka satu-faktorisasi dariK2m adalah (r−1)<− cycle bebas.
Diketahui bahwa satu-faktorisasi dariK2m adalah sempurna jika dan hanya
jikam bilangan prima, (Anderson, 1973). Lemma berikut merupakan sifat satu-faktorisasi dari K2m.
Lemma 3.6.6 Untuk m≥3 ganjil dan k genap sedemikian hingga 4≤k ≤2m, satu-faktorisasi dariK2m terdiri dari cycle dengan panjangk jika dan hanya jika k/2 | m.
Bukti. Asumsikan satu-faktorisasi terdiri dari cycle dengan panjang k yang merupakan gabungan dari dua satu faktor Fi dan Fh, dengan h < i dan h, i ∈ {0,1, ...,2m−2}. Anggap dibagi menjadi tiga kasus.
Kasus 1 : h < i < m−1. Jika konstruksi satu-faktorisasi Km+1verteks himpunan bagianV(Km+1)\{∞}ditempatkan denganVp, untukp= 0,1, dan selain itu satu-faktorisasi Km+1 dibatasi untuk verteks Vp, maka satu-faktorisasi dekat dengan
Km menjadi dekat satu-faktor Fip ={{(i−j)p,(i+j)p}:j = 1,2, ...,(m−1)/2}
diperoleh, dengan i= 0,1, ..., m−1. Oleh karena itu, Fm
i ⊂Fi (satu-faktor K2m
18
panjangnya k/2 + 1 (terdiri dari verteks ∞) melalui induksi satu-faktor dengan memberi indeks pada h dan i pada satu-faktorisasi Km+1. Maka oleh Kasus I pada Lemma 3.6.3, gcd(k/2, m) =k/2.
Kasus 2 : h < m≤i, anggap dibagi menjadi dua subkasus.
2.A :h0 bukan verteks pada k−cycle. Makah1 juga bukan verteks padak−cycle. Diketahui bahwa panjang k−cycle merupakan pembagi 4. Andaikan (h+x)0 merupakan verteks pada k−cycle untuk x 6= 0. Maka tetangga (h+x)0 adalah halnya dengan kasus sebelumnya, karenam < i+ 1<2m, oleh Klaim 3.6.1 maka gcd(k/2, m) =k/2.
Untuk syarat cukup, anggap bahwak ≤2mdan k/2|m. Untuk menemukan cycle dengan panjang k, ambil satu-faktor Fm dan Fi sedemikian hingga i = m+ k/m2. Jika l adalah panjang cycle dari gabungan Fm dan Fi, maka l adalah bilangan bulat genap terkecil sedemikian hingga l
2(i−m) ≡ 0 (mod m). Maka
lm
2k/2 ≡ 0 (mod m),l =k.
Berikut ini diberikan hasil yang ekiuvalen dengan Lemma 3.6.6.
Akibat 3.6.7 Untuk m ≥ 3 ganjil dan k ≥4 genap, satu-faktorisai K2m adalah bebas k-cycle jika dan hanya jika k/2 6 | m.
19
Akibat 3.6.8 Andaikan m ≥ 3 ganjil. Andaikan r adalah faktor prima terkecil dari m. Maka satu-faktorisasi dari K2m adalah (2r−2)<− cycle bebas.
Hasil di atas memenuhi untuk membangun satu-faktorisasiK2mbebask−cycle
dengan m genap dan k6≡4 (mod 8).
Lemma 3.6.9 Untuk m ≥ 4 genap dan k ≥ 6 genap sedemikian hingga k 6≡
4(mod 8), jika terdapat satu-faktorisai bebask-cycle padaKm, maka satu-faktorisasi bebas k-cycle pada K2m memenuhi.
Bukti. Asumsikan bahwa satu-faktorisasi F bebas k-cycle dari Km diberikan. andaikan H adalah gabungan dua satu-faktor Fh dan Fi pada satu-faktorisasi
K2m, dengan h < idan h, i∈ {0,1, ...,2m−2}. Jika keduanyah, i < m−1, maka H tidak mempunyai cycle dengan panjang k karena semua cycle di H meru-pakan penggandaan dari cycle-cycle yang diperoleh dari satu-faktorisasi F pada
Km yang merupakan bebas k-cycle. Jika i = m −1 atau h = m − 1, maka setiap cycle di H mempunyai panjang 4. Selanjutnya asumsikan i ≥ m. Jika
i− h = m, maka setiap cycle di H juga mempunyai cycle dengan panjang 4. Sebaliknyai−h 6= m. Dicatat bahwa setiap cycle di H terhubung ke suatu cy-cle pada gabungan satu-faktor Fh dan Fi−m pada Km. Andaikan l dinotasikan
sebagai cycle dengan panjang l pada Fh ∪Fi−m dengan verteks v1, v2, v3, ..., vl.
Anggap bahwa h < m−1. Cycle dengan panjang l terhubung ke l′-cycle (jika
l ≡ 0 (mod 4)) dengan panjang l atau ke l”-cycle (jika l ≡ 2 (mod 4)) de-clelm-cycle diH dengan panjang sama denganl. MakaKm adalah bebask-cycle, k 6=l pernyataan memenuhi.
Lemma 3.6.10 Untukm≥4genap dank ≥12 sedemikian hinggak ≡4(mod 8), jika terdapat satu-faktorisasi bebas {k/2, k}-cycle padaKm, maka satu-faktorisasi
{k/2, k}-cycle pada K2m memenuhi.
20
hingga l ≡ 2 (mod 4). Maka oleh pembuktian Lemma 3.6.6, setiap cycle dalam satu-faktorisasi K2m mempunyai panjang 4 atau sama dengan panjang cycle yang
terhubung pada satu-faktorisasi pada Km.
Dari hasil yang diperoleh sebelumnya, maka teorema berikut memberikan syarat perlu dari satu-faktorisasi K2m bebas k−cycle.
Teorema 3.6.11 Untuk setiap m dan setiap k ≥ 4 genap sedemikian hingga k 6= 2m, graph lengkap K2m mempunyai satu-faktorisasi bebas k−cycle.
Bukti. Andaikan 2λ0pλ1
1 p
λ2
2 ...pλww adalah faktorisasi prima dari k ke faktor
non-trivial, λj ≥1 untuk setiap pj dan p1 < p2 < ... < pw. Karena k genap, λ0 ≥ 1. Jikak≥2m, oleh Klaim 3.6.2 pernyataan benar. Maka, hasil trivial untukm= 4. Andaikank <2m, untuk induksi asumsikan bahwa satu-faktorisasi bebask−cycle dari K2m ada untuk setiap r sedemikian hingga 2 ≤ r < m dan 2r 6 k. Anggap
dibagi menjadi dua kasus.
Kasus 1 : k/2 6 | m. Untuk m ganjil oleh Akibat 3.6.7, satu-faktorisasi adalah bebas k−cycle. Asumsikan m genap. Jikaλ0 6= 2, maka untuk menemukan satu-faktorisasi K2m gunakan Lemma 3.6.9. Anggap kasus λ0 = 2. Diketahui bahwa
k > 4 karena sebaliknya k/2 = 2 |m. Andaikan x =max{y : gcd(2y, m) = 2y}. faktorisasi K2m adalah bebas k−cycle. Anggap kasus sebaliknya gcd(k−1, m−
1) = k −1. Andaikan f faktor nontrivial faktor dari 2m−1 dan e = 2m−1
2 untuk beberapa bilanga bulat z,
k(f−z) =f−1. Makak adalah pembagi darif−1 yang manaf ≥k+ 1 =e+ 2, kontradiksi dengan fakta bahwaf adalah faktor terkecil dari 2m−1. Oleh induksi diasumsikan terdapat satu-faktorisasi bebas k−cycle dariKe+1.
21
Teorema 3.6.12 Andaikan 2m 6= p+ 1, dengan p prima, atau 2m 6≡ 6,12,18
(mod 24). Maka graph lengkap K2m mempunyai satu-faktorisasi bebas 2m−cycle.
Bukti. Andaikan 2m 6=p+1 untuk setiappprima. Andaikanf faktor prima dari 2m−1 dane= 2m−1
f . Jika 2m ≡2,4 (mod 6), maka diperoleh satu-faktorisasi
dengan orde 2m adalah bebas 2m−cycle. Faktanya gabungan sebarang dua satu-faktor terdiri dari cycle dengan panjangk. Jika 2m≡0 (mod 8), maka m genap. Oleh Klaim 3.6.2 satu-faktorisasi dari Km adalah bebas 2m−cycle.
Pada kenyataannya permasalahan satu-faktorisasiK2mbebask−cycle ketika k = 2m hanya sebagian saja yang dapat diselesaikan. Sebaliknya untuk satu-faktorisasi sempurna, jika 2m =p+1 denganpprima merupakan yang paling sulit untuk membentuk satu-faktorisasi K2m bebas 2m−cycle. Namun untuk setiap
orde 2n 6≡ 2 (mod 4), satu-faktorisasi K2m bebas 6 < −cycle dapat dibentuk,
(Meszka, 2009).
Teorema 3.6.13 Untuk setiap m ≥ 5 ganjil, terdapat satu-faktorisasi dari K2m bebas 6<−cycle.
Bukti. Andaikan q adalah faktor prima terkecil dari m. Jikaq ≥ 5, maka satu-faktorisasi dari K2m oleh Akibat 3.6.8 adalah bebas 8 < −cycle. Oleh karena
itu, asumsikan q = 3 diperoleh 3 6 |2m−1. Jika 5 bukan faktor dari 2m −1, maka satu-faktorisasiK2m, oleh Akibat 3.6.5 adalah bebas 6 <−cycle. Andaikan
2m −1 = r1r2...rv adalah faktorisasi prima dari 2m −1 ke faktor non-trivial dengan 5 = r1 ≤ r2 ≤ ... ≤ rv dan v ≥ 2. Diketahui bahwa untuk rv ≥ 7 terdapat satu-faktorisasi dari Krv+1 bebas 6 < −cycle, oleh Akibat 3.6.5 satu-faktorisasi tersebut dapat disubstitusikan untuk memperoleh satu-satu-faktorisasi dari
Kv+1. Sebaliknya jika rv = 5 dan 2m−1 = 5x untuk x ≥ 2. Andaikan satu-faktorisasi dariK52
+1 sempurna, maka pada tahap selanjutnya jikarv = 5 dengan induksi diperoleh satu-faktorisasi bebas 6<−cycle untuk graph dengan orde 2m.
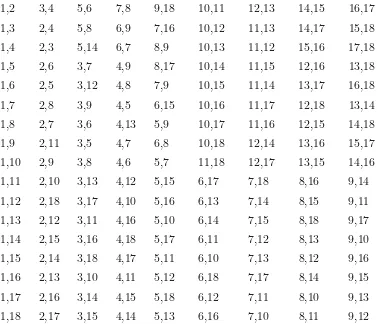
Berikut diberikan contoh satu-faktor dari satu-faktorisasi bebas 18-cycle dari
K18.
22
1,2 3,4 5,6 7,8 9,18 10,11 12,13 14,15 16,17
1,3 2,4 5,8 6,9 7,16 10,12 11,13 14,17 15,18
1,4 2,3 5,14 6,7 8,9 10,13 11,12 15,16 17,18
1,5 2,6 3,7 4,9 8,17 10,14 11,15 12,16 13,18
1,6 2,5 3,12 4,8 7,9 10,15 11,14 13,17 16,18
1,7 2,8 3,9 4,5 6,15 10,16 11,17 12,18 13,14
1,8 2,7 3,6 4,13 5,9 10,17 11,16 12,15 14,18
1,9 2,11 3,5 4,7 6,8 10,18 12,14 13,16 15,17
1,10 2,9 3,8 4,6 5,7 11,18 12,17 13,15 14,16
1,11 2,10 3,13 4,12 5,15 6,17 7,18 8,16 9,14
1,12 2,18 3,17 4,10 5,16 6,13 7,14 8,15 9,11
1,13 2,12 3,11 4,16 5,10 6,14 7,15 8,18 9,17
1,14 2,15 3,16 4,18 5,17 6,11 7,12 8,13 9,10
1,15 2,14 3,18 4,17 5,11 6,10 7,13 8,12 9,16
1,16 2,13 3,10 4,11 5,12 6,18 7,17 8,14 9,15
1,17 2,16 3,14 4,15 5,18 6,12 7,11 8,10 9,13
1,18 2,17 3,15 4,14 5,13 6,16 7,10 8,11 9,12
Gambar 3.10 : Satu-faktorisasi K18 bebas 18−cycle
Dari penelitian-penelitian yang telah dilakukan sebelumnya diperoleh bahwa tidak mungkin untuk membangun satu-faktorisasi bebask < −cycle untuk semua orde 2m ≥ k ≥ 6. Namun oleh Akibat 3.6.5, satu-faktorisasi dari K2m adalah
bebas k < −cycle untuk setiap orde 2m sedemikian hingga faktorisasi prima dari 2m−1 tidak terdiri dari suatu faktor lebih kecil dari k. Andaikan m ≥ 3 dan
r ≥5,l =max{r1−1,2r2−2}dengan r adalah faktor prima terkecil dari 2m−1,
r1 adalah faktor prima terkecil dari
2m−1
r dan r2 adalah faktor prima terkecil
dari m, maka terdapat satu-faktorisasi bebasl < −cycle dari K2m.
BAB 4
HASIL UTAMA
Pada bab ini akan diperlihatkan hasil utama dari penelitian ini. Hasil utama yang diperoleh berdasarkan penjelasan-penjelasan yang telah dipaparkan pada bab-bab sebelumnya. Hasil utama dari penelitian ini yaitu syarat perlu atau syarat cukup dari graph lengkap K2m untuk setiap m = 2r, r ≥ 2 dan setiap k ≥4 genap sedemikian hingga 4≤k ≤2m adalah satu-faktorisasi bebas k-cycle dengan satu edge persekutuan.
4.1 Satu-faktorisasi dari K2m untuk m = 2r, r ≥2
Seperti yang diketahui sebelumnya bahwa satu-faktor merupakan matching sempurna. Oleh karena itu setiap satu-faktor juga terdiri dari m edge.
Satu-faktorisasi F dari K2m terdiri dari (2m−1) satu-faktor. JikaF ={F1, F2, F3, ...,
F2m−2, F2m−1}, dengan {Fi ∩ Fj} = ∅ ∀i, j ∈ [1,2m − 1] dan i 6= j, maka
|F1 ∪F2∪F3...∪F2m−1|= (2m−1)(m). Suatu satu-faktor Fi selalu mempunyai (1, v) sebagai edge awal dan kemudian diperpanjang menaik sedemikian hingga
Fi menjadi matching sempurna. Proses dilakukan terus hingga F2m−1 dan ter-bentuklah satu-faktorisasi dari K2m. Berdasarkan dari pengalaman sebelumnya,
berikut ini diberikan suatu metoda dengan sedikit penggabungan dan perbaikan dari metoda-metoda sebelumnya yang mungkin metoda ini akan terlihat lebih mudah.
4.1.1 Metode Silang
Asumsikan satu-faktor terdiri dari m edge. Satu-faktorisasi F mempunyai 2m−1 satu-faktor. Satu-faktor Fi selalu mempunyai (1, v) sebagai edge awal. Andaikan faktor identitasF1 mempunyai verteks pertama dari setiap edge adalah 1 sampai n, sehingga type satu-faktor terlihat
F1 ={(1, v1),(2, v2),(3, v3), ...,(n, vn)}.
Jika n+ 1 ≤v1, v2, ..., vn≤n, maka
24
Untuk membentuk satu-faktor berikutnya pindahkan secara silang verteks kedua dari setiap edge kej dan j+ 1, j ∈[1, m] pada F1 sehingga diperoleh :
F2 ={(1, n+ 2),(2, n+ 1), ...,(n−1,2n),(n,2n−1)}.
Lakukan proses hingga diperoleh F2m−1. Jika {Fi ∩Fj} = ∅ ∀i, j ∈ [1,2m−1] dan i 6= j, maka proses berlanjut. Dalam hal ini urutan verteks dari edge pada setiap Fi tidak diperhatikan kecuali mungkin verteks pada edge awal. Proses penyilangan yang sama terjadi pada Fi, untuk setiapi jika 2m ≡i (mod 2).
Bukti. Asumsikan satu-faktor terdiri dari m edge. Satu-faktorisasi F dari K2m
mempunyai 2m −1 satu-faktor. Ambil (1, v) sebagai edge awal dari setiap Fi. Selanjutnya tentukan edge yang lain sedemikian hinggaFimenjadi matching sem-purna. Andaikan faktor identitasF1 mempunyai verteks pertama dari setiap edge adalah 1 sampai n, sehingga type satu-faktor terlihat
F1 ={(1, v1),(2, v2),(3, v3), ...,(n, vn)}.
Jika n+ 1 ≤v1, v2, ..., vn≤n, maka
F1 ={(1, n+ 1),(2, n+ 2), ...,(n,2n)}.
Untuk membentuk satu-faktor berikutnya pindahkan secara silang verteks kedua dari setiap edge kej dan j+ 1, j ∈[1, m] pada F1 sehingga diperoleh :
F2 ={(1, n+ 2),(2, n+ 1), ...,(n−1,2n),(n,2n−1)}.
Jika{F1∩F2}=∅, lakukan proses selanjutnya untuk mendapatkanF3. F3 diben-tuk dengan memindahkan secara silang verteks kedua pada edge pertama dan edge m pada F2. Kemudian pindahkan verteks kedua pada edge kedua dan edge (m−1) pada F2, dan seterusnya sehingga diperoleh :
F3 ={(1,2n−1),(2,2n), ...,(n−1, n+ 1),(n, n+ 2)}.
Jika {F1∩F3} = ∅ dan {F2∩F3} = ∅, lakukan proses selanjutnya untuk men-dapatkan F4. F4 dibentuk dengan memindahkan secara silang verteks kedua dari setiap kej dan j+ 1 pada F3, sehingga diperoleh :
F3 ={(1,2n),(2,2n−1), ...,(n−1, n+ 2),(n, n+ 1)}.
Proses penyilangan yang sama terjadi ketika memperoleh F2, F4, F6, ..., F2m−2. Sehingga penyilangan Fi sama untuk setiap i jika 2m ≡ i (mod 2). Karena
25
{Fi ∩Fj} = ∅ ∀i, j ∈ [1,2m −1] dan i 6= j, maka |F1∪F2 ∪F3...∪F2m−1| = (2m−1)(m). Oleh karena itu, terbentuklah satu-faktorisasiF dari K2m.
Dalam penelitian ini akan ditentukan satu-faktorisasi bebas k−cycle dari
K2m dengan satu edge persekutuan. Oleh karena itu, dibutuhkan sedikitnya dua
satu-faktor dari K2m dengan syarat satu-edge persekutuan. Dari pengalaman
sebelumnya diketahui bahwa satu-faktorisasi tak isomorfik dariK2m tidaklah
sedi-kit. Sebaliknya untuk membentuk satu-faktorisasi dari K2m dengan syarat
satu-edge persekutuan diketahui cukup sulit, sehingga dalam penelitian ini satu-satu-edge persekutuan dibatasi untuk edge awal saja yaitu edge (1, v). Sementara itu, untuk edge lainnya dapat dilakukan penelitian lanjutan.
Untuk membentuk satu-faktorisasi yang lain dari K2m dengan satu edge
persekutuan dapat dilakukan mula-mula dengan memindahkan secara acak verteks-verteks dari setiap edge pada faktor identitas F1 sehingga terbentuk satu-faktor identitas F21 yang baru. Selanjutnya gunakan kembali Metoda Silang sedemikian hingga diperoleh satu-faktorisasi yang baru dari K2m. Namun ada beberapa hal
yang perlu diperhatikan yaitu :
1. Satu-faktor identitasF21dibentuk dari faktor identitasF1 dengan cara me-mindahkan verteks-verteks dari masing-masing edge pada F1 secara acak sedemikian hingga {F1∩F21}= (1, n+ 1)
2. Satu-faktor F22 dibentuk dengan memindahkan verteks-verteks dari edge pada F21 dengan Metoda Silang sedemikian hingga {F21∩F22} =∅.
Proses dilakukan hingga diperoleh 2m − 1 faktor, dan terbentuklah satu-faktorisasi yang baru dari K2m.
Contoh 10 : Satu-faktorisasi denganr= 2 makam = 4 danK2m =K8. Verteks pertama dari setiap edge pada satu-faktor dariK8 adalah (1, v),v ∈[2,8]. Faktor identitas dari K8 adalah
F1 = (1,5),(2,6),(3,7),(4,8).
26
1,6 2,5 3,8 4,7
1,7 2,8 3,5 4,6
1,8 2,7 3,6 4,5
1,4 2,3 6,7 5,8
1,3 2,4 6,8 5,7
1,2 3,4 5,6 7,8
Gambar 4.1 : Satu-faktorisasi K8 dengan Metode Silang
Selanjutnya akan ditentukan satu-faktorisasi yang lain dari K8. Untuk memperoleh faktor identitas yang baru F21, ambil faktor identitas F1 dari satu-faktorisasi sebelumnya, kemudian pindahkan verteks-verteksnya secara acak de-ngan syarat satu edge persekutuan.
F1 = (1,5),(2,6),(3,7),(4,8) Faktor identitas yang baru
F21= (1,5),(2,3),(4,6),(7,8)
Oleh karena itu, satu-faktorisasi yang baru dariK8 diperoleh :
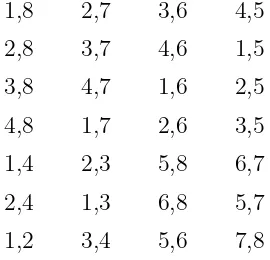
1,3 2,5 4,8 7,6
1,6 2,8 4,5 7,3
1,8 2,6 4,3 7,5
1,7 2,4 6,3 8,5
1,4 2,7 6,5 8,3
1,2 4,7 6,8 5,3
Gambar 4.2 : Satu-faktorisasi baru K8 dengan Metode Silang
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
28
5.2 Saran
Untuk penelitian masa mendatang, penulis menyarankan agar :
1. Pertimbangan tentang model yang memasukkan kelas ongkos yang berbeda-beda, isu penangkapan kembali, routing pemeliharaan dan variasi menu-rut hari. Walaupun model yang ditingkatkan ini bisa lebih sejalan dengan operasi perusahaan penerbangan di dalam praktek, padanan stokastiknya mungkin terlalu sulit diselesaikan. Mungkin lebih cocok menyelesaikan mo-del program stokastik yang lebih relatip sederhana, namun menantang, yang diajukan dalam tulisan ini untuk mengambil keputusan penugasan kelompok-ke-leg, dan kemudian menyelesaikan variant deterministik dari model yang ditingkatkan untuk melakukan penugasan tingkat-tipe pesawat di dalam kelompok yang dirancang.
2. Topik lainnya untuk penelitian masa mendatang adalah mengkaji peningka-tan optimisasi kuat pada model stokastik dan untuk merancang pendekapeningka-tan penyelesaian yang sesuai untuk menangani nonlinieritas fungsi tujuan yang dihasilkan. Akan menarik untuk dikaji apakah mekanisme ini bisa meng-hasilkan peningkatan lebih lanjut dalam kualitas penyelesaian yang dihasil-kan dibanding yang dihasildihasil-kan SPFAM. Juga, dengan saling ketergantungan penugasan armada perusahaan penerbangan dengan operasi lainnya seper-ti perencanaan jadwal, rouseper-ting pesawat dan penjadwalan awak, diperlukan lebih banyak penelitian tentang pemaduan (sebagian) fitur-fitur ini dalam model tunggal untuk membantu perusahaan penerbangan dalam proses pe-ngambilan keputusan mereka secara keseluruhan.
DAFTAR PUSTAKA
Anderson, A. B. 1973. Finite topologies and Hamiltonian paths.J. Combin. Theory Ser. B 14 : hal. 87-93.
Bryant, D., Maenhaut, B. dan Wanless, M. I. 2006. New families of atomic Latin squares and perfect 1-factorizations. J. Combin. Theory Ser. A 113 : hal. 608-624.
Deo, N. 1986. Graph Theory with Applications to Engineering and Computer Sci-ence. Prentice-Hall of India Private Limited.
Dinitz, H. J., Dukes, P dan Stinson, R. D. 2005. Sequentially perfect and uniform one-factorizations of the complete graph. Electron. J. Combin. 12 : #R1.
Dinitz, H. J., Garnick, K. D dan McKay, D. B. 1994. There are 526, 915, 620 nonisomorphic one-factorizations of K12. J. Combin. Theory Ser. 2 : hal. 273-285.
Gopal, P., Kothapalli. K., dan Venkaiah, Ch. 2007. Various one-factorization of complete graph.
Gross, L. J dan Yellen, J. 2006. Graph Theory and Its Applications. Chapman & Hall/CRC.
Kotzig, A. 1964. Hamilton graphs and Hamilton circuits. Theory of Graphs and Its Applications. : hal. 63-82.
Mendelsohn, E. dan Rosa, A. 1985. One-factorizations of the complete graph. J. Graph Theory.9 : hal. 43-65.
Meszka, M. dan Rosa, A. 2003. Perfect 1-factorizations of K16 with nontrivial automorphism group. J. Combin. Math. Combin. Comput 47 : hal. 97-111.
Meszka, M. 2009. k-cycle free one-factorizations of complete graph. Electron. J. Combin. 16.