NAMA : EKO SUPRIYANI
NIM : 04610248
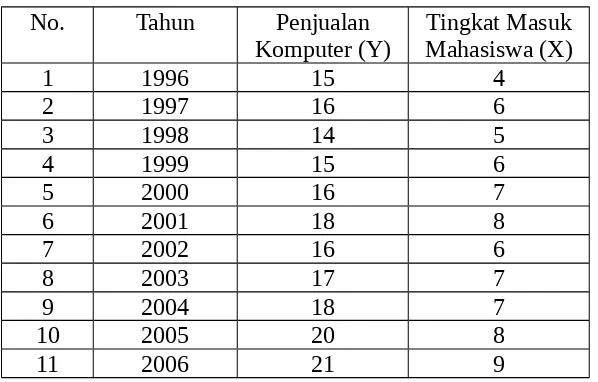
PT ZANIE MANIEZ TAHUN 1996 – 2006
(dalam ribuan)
No. Tahun Penjualan
Komputer (Y) Mahasiswa (X)Tingkat Masuk
1 1996 15 4
2 1997 16 6
3 1998 14 5
4 1999 15 6
5 2000 16 7
6 2001 18 8
7 2002 16 6
8 2003 17 7
9 2004 18 7
10 2005 20 8
11 2006 21 9
[image:1.595.150.449.191.382.2]REGRESI SEDERHANA
Tabel lanjutan agar lebih mudah dalam penyelesaiannya:
No. Tahun Penjualan (Y) TKM (X) X2 Y2 XY
1 1996 15 4 16 225 60
2 1997 16 6 36 256 96
3 1998 14 5 25 196 70
4 1999 15 6 36 225 90
5 2000 16 7 49 256 112
6 2001 18 8 64 324 144
7 2002 16 6 36 256 96
8 2003 17 7 49 289 119
9 2004 18 7 49 289 126
10 2005 20 8 64 400 160
11 2006 21 9 81 441 189
Jumlah 11 186 73 505 3192 1262
Dari tabel di atas maka dapat kita cari koefisien regresinya adalah sebagai berikut: B = [ N ΣXY – ((ΣX) (ΣY)) ]
[ N ΣX2 – ((ΣX)2 ]
[ 11(505) – (73)2 ]
B = 13882 – 13578 5555 – 5329
B = 304
226 B = 1.35
A = [ΣY] – B [ΣX] N N A = 186 – (1.35) (73)
11 11 A = 16.91- 8.96 A = 7.95
Maka persamaan regresinya adalah: Y’ = A + BX
Y’ = 7.95 + 1.35X
Misalkan, perusahaan ini meramalkan penjualannya untuk tahun 2007 dengan X yang sudah ditentukan, misalkan X = 8 (8000 mahasiswa)
Y’ = 7.95 + 1.35 (8) Y’ = 7.95 + 10.8 Y’ = 18.75
Y’ = 18.75 dibulatkan menjadi 19. Jadi ramalan penjualan untuk tahun 2007 adalah sebesar 19000 unit (19 dikalikan 1000), demikian juga untuk ramalan penjualan periode-periode yang lain caranya sama.
KOEFISIEN KORELASI
r = [N.(ΣXY)] – [(ΣY) . (ΣX)]________ [N.(ΣX2)] – [ΣX)2] [N.(ΣY2)] – [(ΣY)2]1/2
r = [11(1262) – (186) (73)]_______ 11(505) – (73)2(11(3192)) – ((186)2)1/2
r = 13882 – 13578_________ 5555 – (5329)(35112) – (34596)1/2
(226) (516)1/2
r = 304__ 5134.72
r = 0.05920 dibulatkan menjadi 0.06