Pertemuan 15 Bilangan Kompleks 15.1 Pendahuluan - 15 Bilangan Kompleks

(1)

Pertemuan 15 Bilangan Kompleks

15.1 Pendahuluan

Bilangan kompleks adalah bilangan dengan bentuk a ib , dimana a dan b adalah

bilangan-bilangan real dan i merupakan simbol untuk 1. Bagian pertama dari suatu bilangan kompleks (yang diwakili dengan a) disebut bagian real, sedangkan bagian kedua bilangan kompleks (yang ditandai dengan b) disebut bagian imajiner. Bagian kedua bilangan kompleks disebut demikian karena bagian itulah yang mencirikan suatu bilangan kompleks tidak nyata, dan tidak dapat diwakili dengan sistem bilangan real yang telah ada.

Pada pembahasan bab ini, kita akan mengenal sistem bilangan kompleks sebagai pengembangan dari sistem bilangan yang telah ada sebelumnya. Pembahasan dilanjutkan dengan operasi dasar bilangan kompleks, argand diagram, dan rumus Euler dalam sistem bilangan kompleks.

15.2 Sistem Bilangan

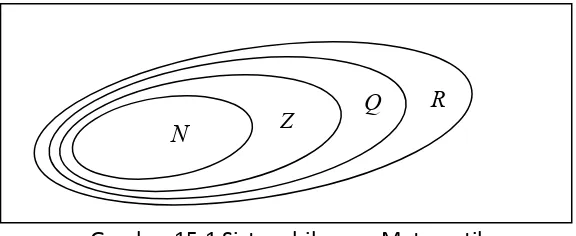
Sebelum pembahasan mengenai sistem bilangan kompleks dimulai, ada baiknya kita mengingat kembali beberapa sistem bilangan umum yang telah ada, seperti sistem bilangan asli, sistem bilangan bulat, sistem bilangan rasional, dan sistem bilangan real.

15.2.1 Sistem Bilangan Umum

Sistem bilangan adalah suatu sistem yang mendefinisikan dan mencirikan karakteristik suatu kelompok bilangan tertentu. Perkembangan sistem bilangan di Matematika dimulai dari

sistem bilangan asli (natural numbers, N), yang mewakili bilangan-bilangan



1, 2,3,



, dan sistem bilangan cacah, yang mewakili bilangan-bilangan dalam sistem bilangan asli ditambah bilangan 0. Dalam perkembangan selanjutnya, dikenal sistem bilangan bulat (integers, Z), yang mewakili semua bilangan dalam sistem bilangan cacah ditambah bilangan-bilangan

negatif,



, 2, 1, 0,1, 2, 



. Selanjutnya, sistem bilangan rasional atau pecahan (rational numbers, Q) dikembangkan dari sistem bilangan bulat, yang berarti mewakili seluruh bilangan dalam sistem bilangan bulat ditambah bilangan-bilangan pecahan,

2 1 1 2

, , , 0, , ,

3 5 3 4

 _ _ 

 

 . Dari sistem bilangan pecahan, kemudian dikembangkan sistem

bilangan real yang paling umum digunakan dalam pemecahan masalah perhitungan, dimana selain mewakili sistem bilangan pecahan yang telah ada sebelumnya, sistem bilangan real (biasa disimbolkan dengan R) juga mewakili bilangan-bilangan yang tidak dapat diwakili

(2)

Gambar 15.1 Sistem bilangan Matematika

15.2.2 Sistem Bilangan Kompleks

Sebelum sistem bilangan kompleks dibangun, setidaknya ada tiga sistem bilangan yang telah dibangun dan dikembangkan, yakni:

1. Sistem bilangan bulat (integers), yang dibangun dari sistem bilangan cacah.

2. Sistem bilangan pecahan (rational) m

n , yang dibangun dari sistem bilangan bulat. 3. Sistem bilangan real x, yang dibangun dari sistem bilangan rasional.

Setiap sistem bilangan di atas memiliki hirarki, dimana sistem bilangan yang dibangun selalu lebih luas dibandingkan sistem bilangan sebelumnya, yang berarti mengizinkan operasi-operasi tambahan dilakukan tanpa keluar dari sistem.

1. Pada sistem bilangan bulat, kita dapat menyelesaikan seluruh persamaan dengan bentuk 0

x a  ,

dimana a adalah sembarang bilangan bulat.

2. Pada sistem bilangan rasional, kita dapat menyelesaikan seluruh persamaan dengan bentuk

0 ax b  ,

dimana a dan b adalah bilangan rasional dan a0.

3. Pada sistem bilangan real, kita dapat menyelesaikan persamaan-persamaan di atas ditambah seluruh persamaan kuadrat

2

0 ax bx c  , dimana a0 dan 2

4 0

b  ac .

Untuk menyelesaikan persamaan kuadrat, kita dapat menggunakan rumus

2 4 2

b b ac

x

a

  



dimana diskriminan, Db24ac, tidak boleh negatif. Jika diperoleh D0, maka solusi persamaan kuadrat tersebut tidak ada dalam ketiga sistem bilangan yang disebutkan di atas. Bahkan persamaan kuadrat sederhana, seperti

2

1 0 x   ,

tidak dapat diselesaikan jika kita hanya menggunakan ketiga sistem bilangan di atas.

Karena itu, diperkenalkan sistem bilangan kompleks yang lebih luas dari sistem bilangan real. Sistem bilangan kompleks terdiri atas bilangan-bilangan kompleks a ib , atau biasa

N Z

(3)

disingkat sebagai

 

a b, , dimana a disebut bagian real dan b disebut bagian imajiner dari bilangan kompleks

 

a b, . Notasi i adalah simbol untuk menyatakan 1.

15.3 Operasi Dasar Bilangan Kompleks

Berikut beberapa operasi dasar bilangan kompleks yang perlu diketahui: 1. Persamaan

a ib  c id jika dan hanya jika ac dan bd

Dua bilangan kompleks

 

a b, dan

 

c d, dikatakan sama atau sebanding jika dan hanya jika ac dan bd .

2. Penjumlahan



a ib

 

 c id

 

 a c 

 

i b d



Jumlahan dua bilangan kompleks

 

a b, dan

 

c d, adalah bilangan kompleks



a c b d , 



.

3. Perkalian

i.



a ib

 

 c id

 

 ac bd

 

i adbc



Hasil kali dua bilangan kompleks

 

a b, dan

 

c d, adalah bilangan kompleks



ac bd ad , bc



.

ii. c a ib







ac i bc

 

Hasil kali suatu bilangan real c dengan bilangan kompleks

 

a b, adalah bilangan kompleks



ac bc,



.

Bilangan kompleks

 

0, 0 adalah bernilai 0 pada sistem bilangan kompleks, dan bilangan kompleks

 

1, 0 merupakan elemen satuannya.

Bilangan kompleks

 

0,1    0 i 1 i menghasilkan bilangan imajiner i, dan bilangan kompleks

 

0,1 2   i2 1.

Untuk menyederhanakan bentuk pecahan bilangan kompleks menjadi satu bilangan kompleks, dapat digunakan operasi aljabar sederhana, seperti perkalian dengan sekawannya berikut



 





 





_

2 2

_

 





c id a ib ac bd i ad bc c id

a ib a ib a ib a b i ab ab

     



 

       .

Hasilnya adalah bilangan kompleks x iy , dengan

2 2

ac bd x

a b

 

 dan 2 2 ad bc y

a b

 

 ,

serta a2b2 0 karena a ib 

   

a b,  0, 0 .

Bilangan kompleks a ib disebut kompleks konjugat dari a ib . Untuk menyatakan

kompleks konjugat dari bilangan kompleks z digunakan notasi z (dibaca z bar).

(4)

Contoh 15.1 Operasi aritmatika dengan bilangan kompleks

i.



2 3 i

 

 6 2i

 

 2 6 

 

i 3 2



 8 i.□ ii.



2 3 i

 

 6 2i

 

 2 6 

 

i 3 2



  4 5i.□ iii.



2 3 i

 

 6 2i



    



2 6 3

 

2



i



2  2



3 6





12 6

 

i 4 18



18 14i

       .□

iv.



 











2 6 3 2 2 2 3 6

2 3 2 3 6 2

6 2 6 2 6 2 6 6 2 2

i

i i i

      

 _  _  _

      



12 6

 

4 18



6 22 3 11

36 4 40 40 20 20

i

i i

  

    

 .□

15.3.1 Argand Diagram

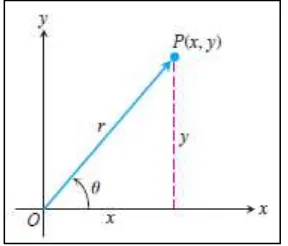
Terdapat dua representasi geometri dari suatu bilangan kompleks z x iy, yakni:

1. sebagai titik P x y

 

, dalam bidang-xy. 2. sebagai vektor OP dari titik pusat O ke P.

Dalam tiap representasi, sumbu-x disebut sebagai sumbu real dan sumbu-y disebut

sebagai sumbu imajiner. Kedua representasi tersebut merupakan Argand Diagram untuk bilangan kompleks x iy .

Gambar 15.2 Argand diagram di atas menunjukkan z x iy, baik sebagai titik P x y

 

, maupun sebuah vektor OP

(Thomas’s Calculus, 11th

ed, p.AP-16)

Dalam bidang koordinat kutub (akan dibahas pada sub bab 15.4 di bawah), diperoleh cos

xr  dan yrsin sehingga z  x iy r



cosisin



.

Kita definisikan nilai mutlak dari suatu bilangan kompleks x iy sebagai panjang r dari

vektor OP (dari titik pusat O ke titik P x y

 

, ), sehingga

2 2

x iy  x y .

Jika dipilih koordinat kutub dengan r dan  tertentu sehingga r non negatif, maka r x iy .

(5)

Perhatikan bahwa,

Rumus Euler memberikan aturan-aturan baru yang dapat digunakan untuk menghitung perkalian, pembagian, perpangkatan, dan akar pangkat dari bilangan kompleks.

Perkalian

Untuk mengalikan dua bilangan kompleks, kita kalikan nilai absolut-nya dan jumlahkan sudutnya. Misal, panjangnya merupakan hasil kali dari panjang kedua faktor dan argumennya merupakan jumlahan dari argumen-argumen kedua faktor (bilangan kompleks) tersebut.

Contoh 15.2 Hasil kali bilangan kompleks

Misal z1 1 i dan z2  3i. Kita menggambar bilangan-bilangan kompleks ini dalam Argand Diagram, dimana dapat ditemukan

(6)

1

Contoh 15.3 Hasil bagi bilangan kompleks

Misal z₁ 1 i dan z₂  3i, maka

Jika n adalah bilangan bulat positif, kita dapat menerapkan rumus perkalian untuk mencari

n

Jika diambil r1, diperoleh De Moivre’s Theorem, yakni



cosisin



n cosnisinn.

Contoh 15.4 Pangkat bilangan kompleks

Jika n3 dan r1, dengan De Moivre’s Theorem diperoleh





3

cosisin cos 3isin 3.

Ruas kiri persamaan di atas diperluas dengan menggunakan teorema Binomial menjadi

3 2 2 3

Jika zrei adalah bilangan kompleks tidak nol dan n bilangan bulat positif, maka terdapat n bilangan kompleks berbeda w w₀, ₁, ,w_n_₁, yang merupakan akar-akar dari z. dapat dinyatakan bahwa n dan  harus sama, namun dapat dinyatakan bahwa kedua nilai tersebut berbeda hanya dengan kelipatan 2 .

2

(7)

Oleh karena itu,

Contoh 15.5 Akar pangkat bilangan kompleks

Tentukan keempat akar pangkat 4 dari -16 dalam sistem bilangan kompleks! Jawaban

Pertama, kita gambarkan Argand Diagram bilangan -16 dan menentukan koordinat kutubnya. Diperoleh untuk z 16, maka r16 dan   .

Salah satu akar dari 16 i

e adalah ₂_ei4_.

Selanjutnya kita peroleh akar-akar lainnya dengan penjumlahan berulang 2

4 2

dan keempat akar dari -16 adalah