Vektor di Bidang dan di Ruang
4.1. Pengertian, notasi ,dan operasi pada vektor
Vektor merupakan istilah untuk menyatakan besaran yang mempunyai arah. Secara
geometris, vektor dinyakan dengan segmen-segmen garis yang terarah atau panah
di dalam bidang atau di ruang. Vektor biasanya dinyatakan dengan huruf kecil
tebal atau hurus kecil bergaris di atasnya (overbars), misal v atau v atau
dinotasikan dengan .
Dalam bidang koordinat, kita dapat menyatakan titik v = (a, b) dengan vektor
kolom v = atau dalam bentuk v . Dalam hal ini a dan b adalah
bilangan real adalah komponen- komponen dari vektor tersebut (elemen/entri dari
matriks). Himpunan semua vector dengan dua komponen ini dinamakan R2
Gambar 4.1. vektor di R2
z
Gambar 4.2. vektor di R3
Dua vektor dikatakan sama jika elemen-elemen yang bersesuaian sama, jadi
Panjang vektor v = adalah v √ . Vektor dengan panjang atau
norm sama dengan satu disebut vektor satuan.
Operasi pada vektor
Operasi vektor meliputi:
1. Penjumlahan
2. Perkalian :
- Perkalian vektor dengan skalar
- Perkalian vektor dengan vektor lain: perkalian titik dan
perkalian silang.
Penjumlahan vektor
Misalkan u dan v adalah vektor-vektor di R2, maka jumlah kedua vektor tersebut
adalah u + v, yang komponennya merupakan jumlah dari
komponen-komponen yang bersesuaian dari u dan v. Secara geometri vektor u + v ini
berkorespondensi dengan titik keempat suatu jajaran genjang yang tiga titik
lainnya adalah ketiga vektor u, v, dan 0.
berikut
v
u + v
u
Gambar 4.3. penjumlahan vektor
Contoh 4.1.: Misalkan u = 2
u + v
u
v
0
Gambar 4.4. Contoh penjumlahan vektor
Perkalian vektor dengan skalar ( perkalian skalar)
Misalkan v vektor dan k scalar ( bilangan real), maka hasil perkalian skalar dari
vektor v adalah vektor yang diperoleh dengan mengalikan setiap elemen dari v
dengan k.
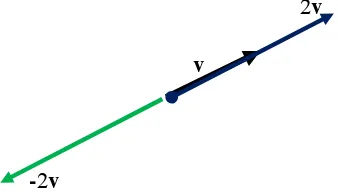
Jika k > 0 , maka kv searah dengan v, dan jika k < 0 maka kv berlawanan arah
dengan v.
2v
v
-2v
Gambar 4.5. Perkalian vektor dengan skalar
Contoh 4.2: Misal v = 0.5
1 dan k = 3, maka
kv = 3 0.5
Sebagai catatan, kadang-kadang vektor kolom v ditulis dalam bentuk (a,b) dan
bukan (a b). Ini adalah kesepakatan, untuk menghindari salah tafsir, seperti
misalnya
2
1 2 1 .
Secara analitis, kedua operasi vektor diatas dapat dijelaskan sebagai berikut:
Misal u = , , dan v = , , vektor di R3, dan k bilangan real, maka
- u + v = , ,
- u - v = , ,
- k u = , ,
Terkadang, vektor muncul dengan tidak dimulai di titik asal. Misalnya vektor P P
mempunyai titik permulaaan P1 = , , dan P2 = , , , maka
P P , , .
Contoh 4.3:
Komponen-komponen dari vektor v = P P dengan titik permulaan P1 = 2, 2,1
dan titik akhir P2 = 7,5, 5 adalah
v = 7 2,5 2 , 5 1 5,7, 6 ,
Secara sama untuk vektor di R2 dapat ditentukan dengan menghilangkan
komponen ketiga.
Perkalian antara dua vektor
Ada dua macam, yaitu:
- Hasil kali titik (dot product)
Dot Product
Dot product merupakan operasi antara dua buah vektor pada ruang yang sama
yang hasilnya berupa skalar. Sering disebut juga perkalian dalam, didefinisikan
sebagai berikut:
Misal, u dan v dua vektor pada ruang yang sama, maka hasil kali titik antara u dan
v adalah:
u.v = u v ,
dimana:
u : panjang vektor u
v : panjang vektor v
: sudut antara u dan v
Contoh 4.4:
Misal u = (2,2) dan v = (2,0) maka tentukan u.v
Penyelesaian :
Pertama kita harus mengetahui besarnya sudut .
Perhatikan bahwa u dan v membentuk sudut , sehingga
u.v = u . v cos ,
= 4√2 cos 4 .
Sering, tidak mudah untuk dapat mengetahui besar sudut antara dua vektor,
Selanjutnya mengingat aturan cosinus:
c
a
b
Gambar 4.6. Aturan cosinus pada segitiga
Pada segitiga seperti gambar 4.6 di atas dipunyai
2 cos .
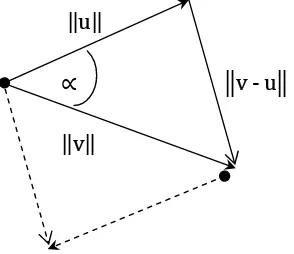
Sekarang perhatikan vektor berikut
u
v ‐ u
v
Gambar 4.7. Aturan cosinus pada vektor
v ‐ u v u 2 u v cos
Dengan demikian dipunyai,
u v cos v u v ‐ u
Misal u = , , dan v = , , vektor di R3, maka
u , v , dan
= 2 2 2
Sehingga diperoleh
u v cos
2 2 2
2 2 2
.
Dengan demikian hasil kali titik dapat dituliskan sebagai:
u.v .
Dari formula ini diperoleh,
cos u v .
Contoh 4.5:
Tentukan kembali hasil kali titik dari dua vektor pada contoh 4.4, kemudian
tentukan besar sudut yang dibentuk oleh kedua vektor tersebut!
Penyelesaian:
u.v
= 2 (2) + 2 (0)
= 4.
cos u v 4
√8 2 1 2 √2.
Jadi besar sudut yang dibentuk oleh vektor u dan v adalah
Contoh 4.6:
Tentukan besar sudut yang dibentuk oleh vektor u = ( 4 ,0,3) dan v = (1,2, – 2).
Penyelesaian:
cos u v 4 1 0 25 3 3 2 15.2
Jadi besar sudut yang dibentuk oleh vektor u dan v adalah
arc cos 15.2
Sifat-sifat perkalian titik:
Jika u,v, dan w vektor-vektor di R2 atau R3 dan k skalar, maka:
(i) u.v = v.u
(ii) u.(v + w) = u.v + u.w
(iii) k(u.v) = (ku).v = u. kv
Sekarang perhatikan gambar berikut:
u
O
v
Gambar 4.8. Dua vektor saling tegak lurus
Pada gambar 4.8, vektor u dan v saling tegak lurus, besar sudut antara keduanya
adalah . jadi u.v = u . v cos 0.
Dengan demikian, dua buah vektor u dan v yang berada pada ruang yang sama,
hal ini dapat dikatakan u ortogonal terhadap v dan sebaliknya, v ortogonal
terhadap u, sering ditulis u ┴v.
Contoh 4.7:
Vektor u = ( 2, – 3) dan v = (3,2) saling ortogonal, karena
u.v = 2(3) + (-3)(2) = 0.
Proyeksi orthogonal
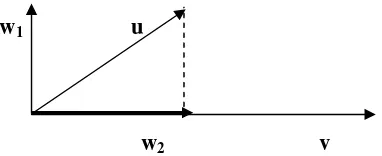
Perhatikan bahwa sebarang vektor u selalu dapat dinyatakan sebagai jumlah dua
vektor lainnya, seperti pada gambar 4.9, u = w1 + w2
w1 u
w2 v
Gambar 4.9. vektor u sebagai jumlah dua vektor
Pada gambar 4.9, vektor w1 adalah komponen vektor u yang orthogonal terhadap
v, sedangkan vektor w2 adalah proyeksi orthogonal u pada v.
Pada gambar 4.9, terlihat bahwa
w2 = k v.
di lain pihak dipunyai,
u = w1 +w2
sehingga
u . v = (w1 +w2).v
= w1 . v + k v. v
= kv . v
= k v .
Jadi
u.v v
Dengan demikian dipeoleh rumus proyeksi orthogonal vektor u terhadap v adalah
w2 Proyv u u.vv v.
Sedangkan komponen u yang orthogonal terhadap v adalah
w1 u w2 u u.vv v.
Contoh 4.8:
Tentukan proyeksi orthogonal vektor u = (1, 2,– 1) terhadap vektor v = ( 1, 3, 4),
dan tentukan komponen vektor u yang orthogonal terhadap v.
Penyelesaian:
Proyeksi orthogonal u pada v adalah
w2 Proyv u u.vv v
1 1 2 3 ‐1 4
26 1,3,4
3 26 ,
9 26 ,
12 26 .
Sedangkan komponen u yang orthogonal terhadap v adalah
Cross Product
Cross Product atau hasil kali silang merupakan hasil kali antara dua vektor di R3
yang menghasilkan vektor yang tegak lurus ( orthogonal) terhadap kedua vektor
yang dikalikan tersebut.
Misalkan u = , , dan v = , , vektor di R3, maka hasil kali silang
u dan v didefinisikan sebagai:
u v
, , .
Contoh 4.9:
Tentukan vektor w yang orthogonal terhadap dua vektor u = 1,2, 1 dan
v = 2,3,1 .
Penyelesaian:
Vektor yang tegak lurus terhadap dua vektor lain adalah hasil kali silang dari kedua
vektor tersebut, jadi
w = u v
1 2 1
2 3 1
2 1 1 3 , 1 2 1 1 , 1 3 2 2
5,1,7 .
w . u 5 1 1 2 7 1 0
dan
w . v 5 2 1 3 7 1 0.
Beberapa sifat cross product:
(i) u . (u x v) = 0
(ii) v . (u x v) = 0
(iii) . .
Dari sifat (iii) diperoleh:
.
cos cos cos
sin .
Dengan demikian dipunyai,
sin .
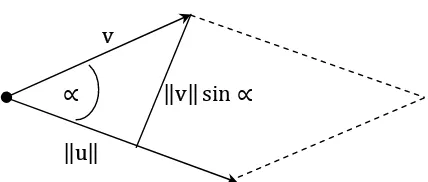
Sekarang perhatikan vektor berikut
v
v sin
u
Luas jajaran genjang pada gambar 4.10. adalah sin . Jadi
luas segitiga yang dibentuk oleh kedua vektor u dan v adalah setengah luas jajaran
genjang, yaitu:
Luaas segitiga = .
Contoh 4.10:
Diketahui titik-titik di R3, yaitu: A (1,2,3), B ( 0,1,4), dan C (2,– 1,1). Tentukan
luas segitiga ABC!
Penyelesaian:
Misalkan u = AB = ( – 1, – 1, 1) dan v = AC = (1, – 3, – 2).
Untuk menghitung luas segitiga ABC terlebih dahulu hitung hasil kali silang antara
u dan v, yaitu:
1 2 1 3 , 1 1 1 2 , 1 3 1 1
5, 1,4)
dan
√25 1 16 √42
Maka luas segitiga ABC = √42 .
(Pembaca silakan mencoba dengan memisalkan u = BC dan v = BA atau u = CA
dan v = CB ).
Soal Latihan 4.1:
1. Misalkan u = 1,2, 1 , v = 2,3,1 , dan w = 3,4, 5 , maka carilah
komponen-komponen dari
(a) u + v (c) 2u + 3w
2. Diketahui titk P1 = 1, 2, 1 .
(a) Carilah sebuah vektor dengan titik permulaan P1 yang searah dengan
vektor v = (6,4,- 1).
(b) Carilah sebuah vektor yang berlawanan arah dengan vektor v = ( -2, 4,
1), yang mempunyai titik terminal P1.
3. Carilah semua skalar , , dan sehingga
2,7,8 1, 1,3 3,6,11 0,0,0 .
4. Tentukan sudut yang dibentuk oleh dua vektor u dan v berikut:
(a) u = (1, 2) dan v = (3, – 4)
(b) u = (1, 2, – 2) dan v = (8, – 2, 2)
5. Tentukan k sehingga vektor u dan v berikut orthogonal
(a) u = (k, 2) dan v = (3, – 6)
(b) u = (1, k, – 2) dan v = (8, – 2, k)
6. Tentukan proyeksi orthogonal vektor u pada v dan carilah komponen
vektor u yang orthogonal terhadap v, jika:
(a) u = (1, – 2) dan v = (– 3, 2)
(b) u = ( 2, –1, 3) dan v = (1, 2, 2)
7. Tentukan vektor w yang tegak lurus terhadap vektor u dan v, jika:
(c) u = (2, 1, – 2) dan v = (4, – 1, 2)
(d) u = (2, 0, 4) dan v = (– 7, 1, 3)
8. Tentukan luas segitiga yang ketiga titik sudutnya adalah A (2, 0, –3),