Textbook INF206 Text Book Turunan Fungsi 1

TURUNAN FUNGSI (3)

Turunan Fungsi Implisit

Fungsi implisit adalah fungsi yang berbentuk f (x,y)= 0 atau f(x,y)=c. Maka cara mencari dy/dx dari fungsi implicit adalah sebagai berikut:

Untuk memudahkan pemahaman , maka akan langsung diberikan beberapa contoh.

Contoh:

1) x2 _{+ y}2_{= 25 (fungsi Implisit)}

dy

dx=2x+2y dy dx=0 2x+2ydy

dx=0 2ydy

dx=−2x

dy

dx

=−

2

x

2

y

dy

dx

=−

x

y

2) jika x2 _{+ y}2 _{– 2x – 6y + 5 = 0}

tentukan dy dxdan

d2y dx2

di titik

x

=

3

y

=

2

Jawab :

 x2 _{+ y}2 _{– 2x – 6y + 5 =0}

2x + 2y dy dx−2−6

dy dx=0

(2y - 6) dy

2 (y-3) dy

dx _=2(1-x)

dy dx ₌

1

−

x

y

−

3

di (3,2)

dy dx=

−2

−1=2



d

2

y

dx

2

=

d

dx

(

1

−

x

y

−

3

)

=(y−3)(−1)−(1−x)(1)

dy dx

(y−3)2

¿(3−y)−(1−x)

dy dx

(2−3)2

¿(3−2)−(1−3).2

(2−3)2

¿1−(−2)

2

1 =5

3) f(x,y)= x + xy2 _{– x sin y}

(atau, x + xy2 _{= x sin y)}

cari dy dx _dan

d2y dx2

Jawab : (Coba sendiri yah, buat latihan .... )

Penurunan dengan Bantuan Logaritma

Untuk menurunkan Fungsi yang berpangkat Fungsi, dapat digunakan penurunan dengan bantuan logaritma.

Jika diketahui z = f(u,v)= uv_{, dimana u,v adalah fungsi dalam x maka}

df

dx _dapat

ln z = ln uv

ln z = v ln u diturunkan ke-x: 1 z dz dx= dv

dx . lnu+ v u

du dx dz

dx=u

v

(

dv dx lnu+

v u

du dx

)

2. z = uv

z = elnu

v

=evlnu

dz dx=e

vlnu

(

dv dxlnu

v u

du dx

)

uv

(

dv dxlnu+

v u

du dx

)

contoh:

Diketahui z = xx

Cara pertama: z = xx

ln z = ln xx

ln = x ln x 1

z dz

dx=1 . lnx+ x x dz

dx _=xx _{(ln x +1)}

Cara kedua: z = xx

z = elnX

X

=exlnx

dz dx=e

xlnx

(

1 lnx+x

x

)

e

xlnx

(

ln

x

+1)

TURUNAN FUNGSI (4)

Mendeferensialkan Persamaan Bentuk Parameter

x

=

f

(

t

)

y

=

g

(

t

)

_{t = parameter}

dy

dx

=

Δx

lim

−0

Δy

Δx

=

Δt

lim

−0

Δy

/

Δ t

Δx

/

Δ t

=

lim Δt−0

Δy/Δt

lim Δt−0Δx/Δt

=dy/dt

dx/dt

Jika

dy

dx

=

y'

dy

dt

=

Y

¿

dx

dt

=

X

¿

y’=

Y

¿

X

¿ _maka

d2y dx2=

d dx

(

dy dt dx dt

)

=d dt

(

dy dt dx dt

)

.dt dx = dx dt

d2y dt2−

dy dt

d2x dt2 1 dx dt (dx dt) 2 =

y

= { { {x} cSup { size 8{ cdot } } {y - {}} cSup { size 8{ cdot cdot } } {y} cSup { size 8{ cdot } } {x} cSup { size 8{ cdot cdot } } } over { left ( {x} cSup { size 8{ cdot } } right ) rSup { size 8{3} } } } } {

¿

y'

=

y

¿

x

¿

Contoh:

maka y’ =

dy

dx

=

y

¿

x

¿

dx

dt

=

y

¿

=

2

t

−

6

dx

dt

=

x

∘

=−

1

y'

=

dy

dx

=

2

t

−

6

−

1

=

6

−

2

t

=

2

(

2

−

t

)+

2

= 2x+2

= 2(x+1)

Mendeferensialkan Fungsi dengan Peubah Lebih Dari Satu

Secara umum jika diketahui z adalah funsi dari u1, u2, u3, …, un, dan u1, u2,

u3, …, un adalah fungsi dari x, maka

dz dx=

∂z

∂u₁.

du₁ dx +

∂z

∂u₂.

du₂ dx +. ..+

∂z

∂u_n.

du_n dx

∂z

∂u _{= derifatif parsiil pertama dari z ke u}

artinya peubah lain kecuali u dianggap konstan.

Contoh:

z = x2_+y3_+x2_y3

dz

dx

=

z '

=

2

x

+

3

y

2

dy

dx

+

2

xy

3

+

3

y

2

x

2

dy

dx

∂

z

∂

x

=

z

x

=

2

x

+

2

xy

3

∂

z

∂

y

=

zy

=

3

y

2)

x

=

t

−

sin

t

y

=

1

−

cos

t

_0<t<

x

∘

=

dx

dt

=

1

−

cos

t

y

∘

=

dy

dt

=

sin

t

y'

=

sin

t

1

−

cos

t

=

sin

t

y

sin t dinyatakan dalam y y= 1 – cos t

cos t = 1 – y (sin2_{t + cos}2_{t = 1)}

sin t =

√

1

−

cos

2

t

√

1

−(

1

−

y

)

2 ₌

√

1

−(

1

−

2

y

+

y

2

)

√

1

−

1

+

2

y

−

y

2 ₌

√

2

y

−

y

2

y’=

1

y

√

2

y

−

y

TURUNAN FUNGSI: BEBERAPA APLIKASI (5)

FUNGSI NAIK DAN TURUN

Definisi :

Suatu fungsi f(x) dikatakan naik di titik x = x0 , jika dapat ditunjukkan

bilangan pos kecil h sedemikian, sehingga untuk setiap titik tertentu x1 < x2 yang

terletak dalam interval (x0-h , x0+h) berlaku : f(x1) < f(x2) .

Suatu fungsi f(x) dikatakan turun di titik x = x0 , jika dapat ditunjukkan

bilangan pos kecil h sedemikian, sehingga untuk setiap titik tertentu x1 > x2 yang

terletak dalam interval (x0-h , x0+h) berlaku : f(x1) > f(x2) .

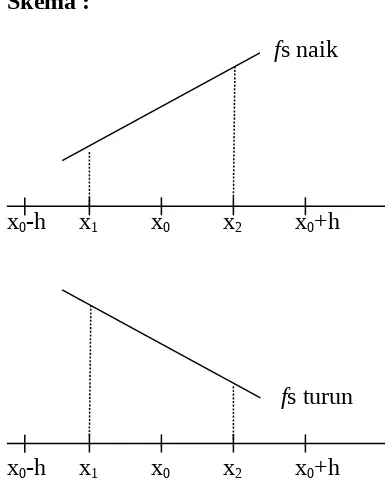
Untuk pemudahkan pemahamannyad diberikan skema pada gambar 3.1.

Skema :

x0-h x1 x0 x2 x0+h

x0-h x1 x0 x2 x0+h

Gambar 3.1. Skema Fungsi Naik dan Fungsi Turun

Dalil :

fs naik

Jika f'(x0) >0  _{y = f (x) naik di x = x0}

f'(x₀) <0 _{ y = f (x) turun di x = x}

0

f'(x₀) =0 _{ titik stasioner dari fungsi f tercapai}

} } \( x rSub { size 8{0} } \) `<`0} {

¿

f¿

¿  maka titik (x₀ , f(x₀)) titik maksimum

} } \( x rSub { size 8{0} } \) `>`0} {

¿

f¿

¿  maka titik (x₀ , f(x₀)) titik minimum

Contoh :

f

(

x

)=

2

x

4

−

4

x

2

+

3

Tentukan semua ekstrim relatif dari fungsi f

Jawab :

f (x) = 2x4 _{– 4x}2 _{+ 3}

f’ (x) = 8x3 _{– 8x}

= 8x (x2 _{– 1)}

f” (x) = 24x2 _{– 8}

Titik stasioner tercapai jika f’’_{(x) = 0}

f’ (x) = 8x (x2 _{– 1) = 0}

= 8x (x+1) (x-1) = 0 x1 = 0 ; x2 = 1 ; x3 = -1

f(0) = 3 ; f(1) = 1 ; f(-1) = 1

-1 0 1

f” (0) = -8 < 0 maka (0, 3) titik maksimum f” (1) = 16 > 0 maka (1, 1) titik minimum

+

-f” (-1) = 16 > 0 maka (-1, 1) titik minimum

Sebelum mempelajari soal-soal lebih lanjut, akan diberikan terlebih dahulu teorema-teorema yang mendukung fungsi naik maupun fungsi turun.

Teorema Uji Keturunan Kedua untuk Kecekungan

Misal f fungsi yang mempunyai turunan kedua pada selang I (terbuka)

1. Jika

} } \( x \) `>`0} {

¿

f¿

¿  Grafik f cekung ke atas pada I

2. Jika

} } \( x \) `<`0} {

¿

f¿

¿  Grafik f cekung ke bawah pada I

Definisi Titik Belok (Ekstrim)

f fungsi kontinu pada selang terbuka I

a

∈

I

. Titik ( a _{, f (} a _{)) dikatakan}

titik belok jika dipenuhi 2 syarat berikut :

1. Terdapat perubahan kecekungan dari grafik fungsi f disekitar x = a

2. Terdapat garis singgung pada grafik fs f di ( a _{, f (} a ₎₎

Contoh :

f

(

x

)=

5

x

3

−

3

x

5

+

2

f

'

(

x

)=−

15

x

4

+

15

x

2

=

0

x

2

(

15

−

15

x

2

)

(a) Tentukan selang f cekung ke atas dan f cekung ke bawah (b) Tentukan semua titik ekstrimnya

Jawab :

f

(

x

)=

5

x

3

−

3

x

5

+

2

, x

∈

R

f

'

(

x

)=

15

x

2

−

15

x

4

, x

∈

R

} } \( x \) ``= 30 x - 60 x rSup { size 8{3} } ~,`x` in `R} {

¿

f¿

¿

= −60x(x

2₋1

= −60x(x+ 1

2

√

2) (x− 1 2

√

2

x₁=0 x2=−

1

2

√

2 x3=

1 2

√

2

f(0)=2 _; f (− 1

2

√

2)=2− 7

8

√

2 _; f ( 1

2

√

2)=2+ 7 8

√

2

0

−1

2

√

2

1 2

√

2 x<−1

2

√

2 −

1

2

√

2<x<0 x> 1 2

√

2

(a) f cekung ke atas :

(

−n , −1

2

√

2

)

;

(

0 , 1 2

√

2

)

f cekung ke bawah :

(

−1

2

√

2 , 0

)

;

(

1

2

√

2 , n

)

(b) Karena f”(x) ada di

x

∈

R

dan disekitar

x=−1

2

√

2 , x=0 , x= 1

2

√

2 _{ada perubahan kecekungan, maka titik}

ekstrimnya

(

−1

2

√

2 ,2− 7

8

√

2

)

; (0 ,2) ;

(

1

-Garis singgung dan -Garis Normal

Untuk menentukan garis singgung suatu kurva, dapat menggunakan teorema-teorema berikut ini :

a. Teorema Rolle

Misalkan f memenuhi syarat :

a) Kontinu pada selang tertutup (a, b)

b) Mempunyai turunan pada selang terbuka (a, b) c) f (a) = f (b)

Maka terdapat suatu c∈ (a , b) Э f’ (c) = 0

(Teorema ini menjamin adanya titik-titik pada grafik f(x) dimana f’ (x) = 0 atau garis singgung mendatar).

Skema :

f’(c) = 0 f (c)

f

f (a) = f (b)

a c b

Gambar 3.2. Skema Teorema Rolle.

b. Teorema Nilai Rata-rata

Misalkan f memenuhi syarat :

d) Kontinu pada selang tertutup (a, b)

e) Mempunyai turunan pada selang terbuka (a, b)

Maka terdapat suatu c∈ (a , b) sehingga f '(c)=

f(b)−f(a)

(b, f (b))

Skema :

f’(c) f (c)

f (b) f (a)

a c b b – a

Gambar 3.3 Skema Teorema Nilai Rata-rata.

c. Teorema, Rumus Tayor

Misal fungsi f mempunyai turunan ke-(n+1) pada selang terbuka I yang memuat titik x dan x0 , maka f(x) dapat diuraikan dalam bentuk :

f(x)=

f \( x rSub { size 8{0} } \) } over {2!} } \( x - x rSub { size 8{0} } \) rSup { size 8{2} } +~ dotsaxis ~+{}} { ¿

f(x0)+

f '(x0)

1! (x−x0)+¿ ¿

f(n)

(x₀)

n ! (x−x0)n+

f(n+1)(c)

(n+1)! (x−x0)n+1

c terletak antara x dan x0 .

Dapat ditulis :

f(x)=P_n(x)+R_n(x)

Dimana :

Pn(x) = suku banyak Taylor berderajad n

Rn(x) =

f(n+1)(c)

(n+1)! (x−x0)

n+1

= suku sisa uraian Taylor

Contoh :

Jawab :

f(x) = sin x f (0) = 0 f’(x) = cos x f’(0) = 1 f”(x) = -sin x f”(0) = 0 f3_{(x) = -cos x f}3_{(0) = -1}

f4_{(x) = sin x f}4_{(0) = 0}

f5_{(x) = cos x f}5_{(0) = 1}

f(x) =

f \( 0 \) } over {2!} } x rSup { size 8{2} } +~ dotsaxis } { ¿

f(0)+f '(0)

1! x+¿

¿

= 0+1 .x+0+

(−1)

3! x

3_{+ ⋯}

= x− x3 3!+

x5 5!− ⋯

Deret Taylor dimana x0 = 0 dinamakan Deret Mac Laurin.

Contoh :

Diket : f(x)=x3_-9x2_+15x-5

Tentukan semua titik ekstrimnya.

Jawab:

f'(x) = 3x2_-18x+15

Stasioner jika f'(x) = 0, maka 3x2_{-18x+15=0 atau x}2_{-6x+5 = 0.}

Sehingga (x-5)(x-1)=0, x1 = 5, x2 = 1.

f''(x) = 6x – 18 , maka f''(5) > 0, dan f''(1) < 0.

Bentuk-bentuk Tidak Tertentu

Yang dinamakan bentuk-bentuk tak tertentu adalah bentuk-bentuk berikut: 0

0 ; ∞∞ ; 0 .∞ ; ∞−∞ ; 1

∞ _{; 0}0 _{; ∞}0

Aturan dari de l’ Hospital :

1. Diketahui f(x) dan g(x) kontinu dan dapat dideferensialkan sebanyak n kali disekitar x = a.

f(a)=f '(a)=f \( a \) =` dotsaxis `=f rSup { size 8{ \( n - 1 \) } } \( a \) =0} { ¿

g(a)=g'(a)=g \( a \) =` dotsaxis `=g rSup { size 8{ \( n - 1 \) } } \( a \) =0} { ¿

Sedang f (n) _{(a) dan g} (n) _{(a) salah satu atau keduanya tidak nol, maka :}

lim

x→a

f(x)

g(x) =

f(n)(a)

g(n)(a)

2. Kecuali untuk bentuk 0

0 _{, aturan dari de l’ hospital bisa juga dipakai untuk}

bentuk

∞

∞

.

f

(

a

)=

f'

(

a

)=

f

\( a \) = dotsaxis =f rSup { size 8{n - 1} } \( a \) = infinity } {} # g \( a \) =g' \( a \) =g

(

a

)=⋯=

g

n−1

(

a

)=∞

¿

Sedang f (n) _{(a) dan g} (n) _{(a) salah satu atau keduanya tidak tak berhingga, maka}

:

lim

x→a

f(x)

g(x) =

f(n)(a)

g(n)

(a)

Contoh:

1.

lim

x→2

x2−x−2

2−x →

0 0

=

lim

x→2

2x−1 −1 =−3

2.

lim

x→0

sinx2

sin2_x→

=

lim

x→0

2x cosx2

2sinx cosx→

0 0

=

lim

x→0

2x cosx2

sin 2x →

0 0

=

lim

x→0

2cosx2−(2x) (2x)sinx2

2 cos 2x

= 2.1

2 =1

3.

lim

x→∞

x2+x

3x2₊₁→∞∞

=

lim

x→∞

2x+1

6x →∞∞ =

lim

x→∞ 2 6= 1 3 =

lim

x→∞ 2x x + 1 x 6x x =2 6= 1 3 Contoh: 1.

lim

x→Π 2

ln(x−Π 2) tanx

= lim

x→π

2

1 x−π/2 sec2_x

= lim

x→π

2

cos2x x−π/2 ₌ lim

x→π

2

1/2(cos 2x+1)

x−π/2 ₌ lim

x→π

2

1/2(−2sin 2x)

1 _{= 0}

2. limx→0

ex−1

x2 ₌ limx→0

ex 2x=limx→0

ex 2 =1/2

3.

lim

x→∞ x2 ℓx₋₁

= xlim→ ∞

2x

ex ₌ xlim→ ∞

DAFTAR PUSTAKA

[1] Yusuf Yahya, D. Suryadi H.S., Agus S., Matematika Dasar untuk Perguruan Tinggi, Ghalia Indonesia, Jakarta, 1995

[2] Frank Ayres, Differential and Integral Calculus 2/ed, McGraw-Hill Book Company, NewYork, 1978.

[3] Leithold, L ., 1972, The Calculus with Analitic Geometry, Harper International Edition, Harper and Row, Publishers, New York, Hagerstown, San Francisco, London.

[4] Martono, K., 1970, Modern Control Engineering, Prentice-Hall., Englewood Cliffs, New Jersey.