MODUL 2
TABEL KONTINGENSI RXC dan TABEL KONTINGENSI 2X2
Tabel kontingensi atau yang sering disebut tabulasi silang (cross tabulation atau cross classification) adalah tabel yang berisi data jumlah atau frekuensi atau beberapa klasifikasi (kategori). Cross tabulation yaitu suatu metode statistik yang menggambarkan dua atau lebih variabel secara simultan dan hasilnya ditampilkan dalam bentuk tabel yang merefleksikan distribusi bersama dua atau lebih variabel dengan jumlah kategori yang terbatas (Agresti, 1990). Metode cross tabulation dapat menjawab hubungan antara dua atau lebih variabel penelitian tetapi bukan hubungan sebab akibat. Semakin bertambah jumlah variabel yang di tabulasikan maka semakin kompleks interpretasinya
Keuntungan Menggunakan Cross Tabulation
1. Mudah diinterpretasikan dan dimengerti oleh si pengambil keputusan yang tidak mengerti statistik
2. Kejelasan informasi dapat mempermudah si pengambil keputusan untuk melakukan sesuatu dengan benar
3. Dapat menginformasikan fenomena-fenomena yang ada secara lebih kompleks daripada hanya menggunakan analisis variabel secara terpisah
Dua Variabel Cross Tabulation
1. Dapat disebut sebagai bivariate cross tabulation
2. Isi sel dari tabelnya dapat berupa count ataupun persentase kolom maupun baris tergantung variabel mana yang menjadi variabel independennya
3. Jika variabel independennya pada kolom maka prosentasenya ke arah kolom 4. Apabila dua variabel tidak berposisi sebagai variabel independen maupun
dependen maka lebih baik menggunakan total prosentase.
Jika kedua variabel berskala diskret maka peneliti bisa membuat tabel kontingensi untuk menguji apakah kedua variabel tsb independen. Tabel Kontingensi RXC adalah sebagai berikut
Tabel 2.1 (a) Tabel Kontingensi rxc
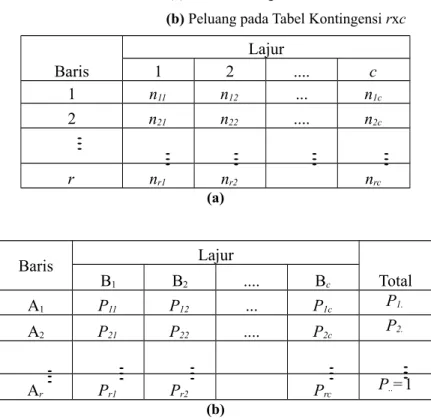
(b) Peluang pada Tabel Kontingensi rxc
Baris Lajur 1 2 .... c 1 n11 n12 ... n1c 2 n21 n22 .... n2c r nr1 nr2 nrc (a) Baris Lajur Total B1 B2 .... Bc A1 P11 P12 ... P1c P1. A2 P21 P22 .... P2c P2. Ar Pr1 Pr2 Prc P..=1 (b)
Tabel 2.1 sering disebut Tabel 2 Dimensi
nij = banyaknya individu yang termasuk dalam sel i,j, (total pengamatan pada sel ke-i,j, ) dengan i=1,2,...r dan j= 1, 2, ... c
Baris dan lajur mencerminkan 2 kejadian, misal : baris = kebiasaan merokok,
lajur = penyakit jantung.
2.1 Uji Independensi
Uji independensi digunakan untuk mengetahui hubungan antara dua variabel (Agresti, 1990). Setiap level atau kelas dari variabel – variabel tersebut harus memenuhi syarat sebagai berikut:
1. Homogen
Homogen adalah dalam setiap sel tersebut harus merupakan obyek yang sama. Sehingga jika datanya heterogen tidak bisa dianalisis menggunakan tabel kontingensi. 2. Mutually Exclusive dan Mutually Exhaustive
Mutually exclusive (saling asing) adalah antara level satu dengan level yang lain harus saling lepas (independen).
Mutually exhaustive merupakan dekomposisi secara lengkap sampai pada unit terkecil. Sehingga jika mengklasifikasikan satu unsur, maka hanya dapat diklasifikasikan dalam satu unit saja, atau dengan kata lain semua nilai harus masuk dalam klasifikasi yang dilakukan.
3. Skala Nominal dan Skala Ordinal
Skala nominal adalah merupakan skala yang bersifat kategorikal atau klasifikasi, skala tersebut dapat berfungsi untuk membedakan tetapi tidak merupakan hubungan kuantitatif dan tingkatan. Jadi anggota dari kelas yang satu berbeda dengan anggota dari kelas yang lainnya. Ciri – ciri dari skala ini adalah posisi data setara dan tidak bisa dilakukan operasi matematik. Contoh skala nominal yaitu laki-laki dan perempuan, cacat dan tidak cacat, baik dan jelek, ya dan tidak. Skala ordinal adalah merupakan skala yang bersifat kategorikal atau klasifikasi, skala ordinal ini berfungsi membedakan dan berfungsi untuk menunjukkan adanya suatu urutan atau tingkatan. Jadi skala menyatakan besaran yang berbeda atau membedakan urutan bahwa yang satu lebih besar dari atau lebih kecil dari yang lainnya. Contoh dari data ordinal yaitu (sangat memuaskan, memuaskan, biasa, tidak memuaskan, sangat tidak memuaskan), (sangat setuju, setuju, biasa, tidak setuju, sangat tidak setuju), (Sangat penting, penting, cukup, tidak penting, sangat tidak penting).
Hipotesis
H0 : Tidak ada hubungan antara dua variabel yang diamati
H1 : Ada hubungan antara dua variabel yang diamati
Uji statistik
n i n j ij ij ij E E O X 1 1 2 2 Dimana :Oij = Nilai observasi/pengamatan baris ke-i kolom ke-j
Eij = Nilai ekspektasi baris ke-i kolom ke-j
Tabel Kontingensi 2 x 2
Adalah kasus khusus dari Tabel kontingensi r x c. Jika terdapat 2 kejadian, yaitu A dan B, dimana kejadian A terdiri dari A1 dan A2 serta kejadian B terdiri atas B1 dan B2.
Dengan demikian, setiap individu mungkin termasuk ke dalam salah satu dari 4 kategori: A1B1 A1B2 A2B1 A2B2
Tabel 2.2 (a) Kejadian Populasi (b) Kejadian Sampel Individu A B 1 A1 B1 2 A1 B2 3 A2 B1 4 A2 B1 N A1 B2 (a) Individu A B 1 A1 B1 2 A1 B2 3 A2 B1 4 A2 B1
n A1 B2 (b)
Jika x dan y saling bebas maka P (x
y) = P(x) P(y) Jika x dan y tidak bebas maka P (x
y) = P(x) P(y x)Tabel Kontingensi 2x2 untuk Populasi dan Sampel adalah sebagai berikut
Tabel 2.3 (a) Tabel Kontingensi 2x2 untuk Populasi (b) Tabel Kontingensi 2x2 untuk Sampel
Kejadian B1 B2 Total A1 A2 N11 N12 N21 N22 N1. N2. Total N.1 N.2 N.. (a) Kejadian B1 B2 Total A1 A2 n11 n12 n21 n22 n1. n2. Total n.1 n.2 n.. (b)
Tabel kontingensi untuk populasi hampir tidak pernah diperoleh karena dilakukan dengan mencacah semua anggota populasi. Sedangkan Tabel Kontingensi untuk sampel dapat diperoleh. Tabel 2.3 (b) adalah rerpresentasi dari Tabel 2.3 (a) . Tabel 2.3 (b) dapat digunakan untuk menarik kesimpulan tentang Tabel 2.3 (a). Jika Tabel 2.3 (b) diperoleh, pertanyaan apa yang bisa dijawab? Tergantung pada bagaiman cara memperoleh Tabel 2.3 (b).
Cara memperoleh Tabel 2.3 (b):
1. Mengambil sampel acak individu sebanyak n.. kemudian setiap individu dikelaskan ke dalam 4 kategori tadi (fixed total).
2. Mengambil sampel acak sebanyak (n1. dan n2. ) atau (n.1 dan n.2 ) kemudian setiap individu dikelaskan ke dalam kategori (B1/B2) atau (A1/A2) {fixed margin}.
Jika Tabel 2.3 (b) berasal dari cara 1, maka akan menjawab hubungan antara kejadian A dan B, apakah A dan B bebas. Namun, jika Tabel 2.3 (b) berasal dari cara 2 menjawab perbedaan proporsi Bi pada kondisi A1 dan A2 , atau perbedaan proporsi Ai
pada kondisi B1 dan B2 (tergantung margin mana yang ditetapkan).
Pendekatan statistika keduanya persis sama. Perhatikan jika n.. ditetapkan, maka
pertanyaan selanjutnya apakah A dan B bebas?. Pertanyaan ini tidak dapat dijawab dengan pasti jika kita tidak mengamati Tabel 2.3 (a). Jika A dan B bebas maka:
p11 = p1. x p.1 p12 = p1. x p.2
p21 = p2. x p.1 dan
p22 = p2. x p.2 , atau secara umum
Pij = pi. x p.j (2.3) .. . .. . .. N N x N N N Nij i j
, dengan catatan harus diketahui banyaknya populasi Pij = pi. x p.j tidak dapat diperoleh jika Tabel 2.3 (a) tidak diperoleh.
Pada Tabel 2.3 (b) : .. ˆ n n p ij ij , .. . . ˆ n n p i i , .. . . ˆ n n p j j
Sehingga jika A dan B bebas maka seharusnya: pˆij pˆi.x pˆ.j. Untuk menilai
”hampir sama” perlu dilakukan pengujian, dengan Hipotesis: H0: tidak ada hubungan antara A dan B (bebas) atau ( pij = pi. x p.j )
H1 : tada hubungan antara A dan B (bebas) atau ( pij
pi. x p.j )Jika H0 benar, maka isi sel (i,j) diharapkan
eij = n.. x pˆij = n.. x pˆi.xpˆ.j = n.. x .. . n ni x .. . n n j = .. . .* n n ni j (2.4) eij disebut frekuensi harapan.
Dasar pengujian adalah jika eij (harapan) ”tidak terlalu berbeda” dengan nij
(kenyataan) maka H0 diterima, jika sebaliknya maka H0 ditolak. Perlu statistik uji untuk
menilai perbedaaan itu. Statistik uji yang dapat digunakan:
a. Pearson2 2 =
J
J
I
I
1
1
ij ij ij m m n )2 ( = 2 . 1 . . 2 . 1 2 21 12 22 11 ..( ) n n n n n n n n n (2.5)Sebaran dari Pearson 2 tidak pasti. Hanya saja bisa dibuktikan.
Jika nij, maka2 atau dapat disebut 2
hit
akan berdistribusi (21)
Jika nij sedang , maka hit2 akan dihampiri oleh
2 ) 1 (
Jika nij kecil sekali, maka 2hit ?? maka digunakan Uji Yates. b. Yates (1934) 2 hit = 2 . 1 . . 2 . 1 2 .. 21 12 22 11 .. 2 ) 1 | (| n n n n n n n n n n berdistribusi 2 (1) (2.6) Jika ada sel (i,j) yang kecil, misal 5 maka 2
hit dan
*
2hitung perlu dihindari (karena hampirannya terlalu kasar).c. Fisher
Fisher adalah Pengujian Eksak untuk menilai kebebasan ( H0: Pij = pi. x p.j ), dengan cara sebagai berikut:
1. Mencari konfigurasi-konfigurasi tabel yang lebih ekstrim dari tabel yang kita amati.
2. Menghitung nilai p dari tabel-tabel itu, sebut saja sebagai p1, p2, ..., pk. p = ! ! ! ! !! !! ! .. 22 21 12 11 2 . 1 . . 2 . 1 n n n n n n n n n dimana n! = n(n-1)(n-2)...(1) (2.7) 3. Nilai p dari tabel yang kita amati adalah penjumlahan nilai p1p2...pk
nilai pdaritabelyangdiamati
Seberapa jauh keeratan dari hubungan antara 2 kejadian (jika ada)?. Beberapa ukuran yang dapat digunakan adalah sebagai berikut:
1. Yule Q = 21 12 22 11 21 12 22 11 n n n n n n n n
untuk
n
, dengan Q berdistribusi Normal. (2.8)Var (Q) =
22 21 12 11 2 1 1 1 1 1 4 1 n n n n Q (2.9) Nilai Q berkisar antara -1 sampai 1 , jika Q = 0 maka tidak ada hubungan.2. Nisbah Odds (Odds Ratio)
21 11 21 11 P P N N
adalah odds dari A1 terhadap A2 pada kategori B1
22 12 22 12 P P N N
22 12 21 11 / / P P P P = 21 12 22 11 22 12 12 11 / / N N N N N N N N , dengan 0 < <
(2.10) jika = 1 maka 22 12 21 11 P P P P P11 = .. 22 21 12 22 21 12 .. * * N N N N P P P Pij=Pi. x P.j = .. .. N Ni * .. . N N j =
.. 2 1 N N Ni i x
.. 2 1 N N N j j (2.11) loge odds = loge , dengan -
< <
Pertanyaan selanjutnya ialah:
1. Seberapa jauh sebaran 2hit mendekati
2(1)demikian pula *2hit ?2. Dapatkah kita menghindari penggunan 2hitatau *2hit dalam pengujian?
3. Bagaimana sebaran dari ?
Mungkinkah dilakukan simulasi? (untuk menjawab 3 hal di atas) dapat dilakukan Bootstrap
2.2 Bootstrap (Efron, 1979)
1. Misalkan Fˆ adalah sebaran empirik dari segugus data D = {x1,x2,...,xn}, Fˆ memberikan bobot sama sebesar 1/n bagi masing-masing data xi.
2. Menggunakan bilangan acak (random numbers) untuk menarik contoh berukuran n dari D dengan pemulihan, sehingga setiap pengamatan pada contoh ini merupakan unsur dari D dan bersifat bebas satu sama lain.
3. Menghitung statistik yang diperlukan, misal ˆ*, dari contoh yang baru ini.
4. Mengulang langkah (2) dan (3) sebanyak N kali. Catat hasilnya sebagai ˆ*1, 2
*
ˆ
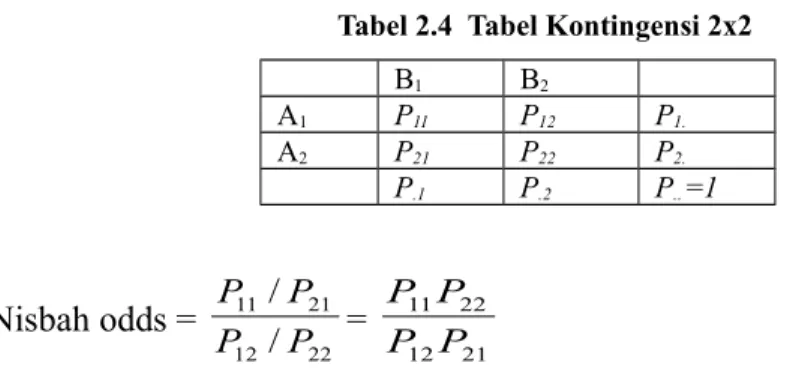
Tabel 2.4 Tabel Kontingensi 2x2 B1 B2 A1 P11 P12 P1. A2 P21 P22 P2. P.1 P.2 P.. =1 Nisbah odds = 22 12 21 11 / / P P P P = 21 12 22 11 P P P P
Jika A dan B bebas, maka untuk setiap i dan j, Pij = P1. P.j
Sehingga P11 = P1. P.1 dan P12 = P1. P.2 , Jadi, jika A dan B bebas maka nisbah odds = 1
2.3 Risiko Nisbi (Relative Risk)
Adalah Perbandingan antara proporsi individu yang termasuk kategori A1, jika
diketahui termasuk kategori B1 dengan proporsi A1 jika diketahui termasuk kategori B2
atau perbandingan antara proporsi individu yang termasuk kategori B1 jika diketahui A1
dengan proporsi B1 jika diketahui A2
Risiko Nisbi = 2 1 1 1 P P atau 2 2 1 2 P P (2.12) R ˆN = 2 1 1 1 ˆ ˆ P P atau 2 2 1 2 ˆ ˆ P P (2.13) Pada Tabel 2.4, peluang suatu individu termasuk ke dalam kategori A1B1, A1B2,
A2B1 atau A2B2 masing-masing berturut-turut P11, P12, P21, P22. Secara Teoritis akan mengikuti model multinomial.
Jika X = individu maka P(x
A1B1 ) = P11P(x
A2 B2 ) = P22nij = banyaknya individu yang termasuk dalam kategori AiBj
Maka nij Multinomial (n.. ; P11,P12,P21,P22)
Peluang kita mengamati sebanyak nij individu pada kategori AiBj adalah ij
P
ij
n
L( ) = n i 1 f(x; ) = n 1 i P(Xi=x, ) (2.14) Untuk Tabel 2.4 L(Pij) =
11 11
12 n12 21 n21 22 n22 n P P P P = 2 1 i 2 1 j
P
ij
ij nJika fungsi L(Pij) atau ln L(Pij) dimaksimumkan terhadap Pij kita dapatkan penduga
kemungkinan maksimum dari Pij. Pˆij=
..
n nij
Kebebasan antara baris dengan lajur pada Tabel 2.4, dapat di uji pula (selain uji
hit 2
=
ij ij ij e e n 22.5 Uji Nisbah Kemungkinan (Likelihood Ratio Test)
Prinsip:
Untuk H0 dan H1 tertentu maksimum Fungsi Kemungkinan (FK) dalam 2
keadaan, yaitu dalam keadaan H0 benar dan dalam sembarang keadaan
(apakah H0 benar atau tidak)
Ambil nisbah dari 2 nilai maksimum tersebut, sebut sebagai (0< <1) Besaran disebut nisbah kemungkinan dan -2 log
2(db) Jika -2 log ada di daerah penolakan maka H0 ditolak.
Db adalah selisih antara par bebas pada keadaan H0 benar dengan par bebas pada
keadaan umum (H0 benar atau salah)
Pada Tabel 2.4, Jika H0 benar maka Pˆij= Pˆi. Pˆ.j= . 2.
.. n n ni j , sehingga Fungsi Kemungkinannya adalah L(Pˆij H0 benar) = 22 21 12 11 22 21 12 11 n n n n P P P P = 11 2 .. 1 . . 1 n n n n 12 2 .. 2 . . 1 n n n n 21 2 .. 1 . . 2 n n n n 22 2 .. 2 . . 2 n n n n (2.15) Secara umum Fungsi Kemungkinan adalah sebagai berikut
FK :
11
12
21
22
22 21 12 11 2 . . 2 1 . . 2 2 . . 1 1 . . 1 2 .. 1 n n n n n n n n n n n n n n n n n (2.16) L(Pij ) = 22 21 12 11 22 21 12 11 n n n n P P P P = 11 .. 11 n n n 12 .. 12 n n n 21 .. 21 n n n 22 .. 22 n n n =
11
12 21 22
22 21 12 11 2 2 1 2 2 1 11 .. 1 n n n n n n n n n n n n n . Nisbah Kemungkinannya adalah sebagai berikut = ) ( 0 ij ij P L benar H P L
11 12 21 22
.. 22 21 12 11 22 21 12 1 1 .. 2 . . 2 1 . . 2 2 . . 1 1 . . 1 n n n n n n n n nn
n
n
n
n
n
n
n
n
n
n
n
n
=
2 1 2 1 .. 2 1 2 1 . . .. i j n ij n i j n j i ij ij n n n n (2.17) -2 log λ = 2
2 1 2 1 2 1 2 1 ln ln i j i j n ij n ij ij e ij n = 2
i i j ij ij j ij ij n n e n ln ln = 2
i j ij ij ij e n n ln ~ χ2 (db) derajat bebas db umum (3 bebas) db H0 benar (2 bebas) Sehingga db = 1 Statistik uji kemungkinan maksimum (G2)
G2 = -2 log λ ~ χ2 (1) = 2
i j ij ij ij e n n ln = 2 i j i j j j i i ij ij n n n n n n n n ln .ln . . ln . ..ln .. (2.18)2.6 Pemecahan Sumber-sumber Ketakbebasan
Jika pada Tabel kontingensi r x c (Tabel 2.1), didapatkan hasil bahwa antara baris dan lajur tidak bebas, maka penyebabnya ada 2 kemungkinan, yakni:
1. Seluruhnya (sebagian besar) sel i , j 2. Satu atau dua sel i, j saja
oleh karena itu seringkali diperlukan pemecahan sumber-sumber ketakbebasan.
Prinsip : jika peubah acak x ~ χ2
(a) dan y~ χ2(b) , x dan y bebas maka (x+y) ~ χ2(a+b)
Tabel asal dapat dipecah menjadi beberapa sub tabel yang bebas satu sama lain. Cara memecahnya tidak unik (bermacam-macam). Ada patokan yang bisa diikuti agar subtabel-subtabel itu bebas, sebagai berikut:
1. Jika db dari tabel asal sebesar c maka banyaknya subtabel yang bisa dibuat tidak mungkin lebih besar dari dari c.
2. Frekuensi pada setiap sel hanya ada pada satu sub tabel saja; artinya jika isi sel (i,j) pada subtabel x maka nilai x ini tidak akan ditemui pada sub tabel yang lain 3. Setiap total marginal dari subtabel pasti muncul sebagai frekuensi sel pada
subtabel lainnya atau sebagai total marginal dari tabel asal.
Artinya setelah kita pecah, secara umum antara A dan B bebas, kecuali jika A1 dan
B1 dipertimbangkan. Dengan kata lain jika diketahui individu termasuk B2, B3 atau B4
maka kemungkinan bahwa individu ini juga termasuk ke dalam kategori A2 atau A3
memiliki peluang yang sama. Tetapi jika diketahui suatu individu masuk kategori B1
maka ia berpeluang besar untuk juga masuk ke dalam kategori A1
2.7 Ukuran Keeratan
1. Statistik λb
Digunakan untuk membandingkan keadaan sebagai berikut: ”jika suatu individu dipilih secara acak dari populasi dan kita diminta untuk menebak termasuk kategori B (B1, B2, ...), manakah individu tersebut .
a. Tanpa keterangan tambahan, atau
b. Dengan keterangan mengenai kategori dari A.
Dari kedua hal tersebut, yang mana yang terbaik, tergantung apakah A dan B saling bebas atau tidak. Jika A dan B bebas, maka tebakan kita sama saja kualitasnya pada keadaan (a) atau (b). Jika A dan B tidak bebas maka tebakan kita kualitasnya akan meningkat pada keadaan (b).
Statistik λb mengukur seberapa besar peningkatan kualitas tebakan pada keadaan (b).
λb = m m im n n n n . .. 1 .
(2.19) dimana nim = maksimum nij pada baris ke –in.m = maksimum n.j
2. Statistik λa
Serupa dengan λb , kecuali merupakan perbaikan kualitas tebakan terhadap kategori
A1, A2,... jika kategori B nya (B1, B2,...) diketahui.
λa = . .. . m j m mj n n n n
(2.20) dimana nmj = maksimum nij pada lajur ke –jnm. = maksimum ni.
Contoh :
1. Dalam suatu penelitian perusahaan, sejumlah data dikumpulkan untuk menentukan apakah proporsi barang yang cacat (A) yang dhasilkan oleh karyawan sama untuk giliran shift pagi, sore atau malam (B). data berikut menggambarkan barang yang diproduksi yang cacat untuk shift pagi, sore atau malam. Berikan kesimpulan anda. Tuliskan H0 dan H1 serta statistik ujinya
dengan Likelihood ratio (G2), gunakan 0.025.
Tabel 2.5 Hubungan Shift dan Proporsi Cacatan
shift pagi sore malam
cacat 45 55 70
tidak cacat 905 890 870
Penyelesaian:
H0 : Tidak ada hubungan antara proporsi barang yang cacat dengan shift
H1 : Ada hubungan antara proporsi barang yang cacat dengan shift
Shift Pagi Sore Malam Cacat 46 (56.97) 55 (56.67) 70 (56.37) 170 Tidak cacat 905 (893.03) 890 (888.33) 870 (883.63) 2665 950 945 940
i j ij ij e n G2 2 ln 63 . 883 870 ln 870 ... 67 . 56 55 ln 55 97 . 56 45 ln 45 2
3.097
2 194 . 6 378 . 3 2 ) 2 ( 025 . 0 Kesimpulan: Karena 02.025(2) 2 G , maka terima H0 artinya tidak ada hubungan antara proporsi barang yang cacat dengan shift. Dengan kata lain, proporsi barang yang cacat yang dihasilkan karyawan adalah sama untuk giliran shift pagi, sore, atau malam.
2. Tunjukkan bahwa jika odds ratio=1 maka hubungan antara dua kejadian tidak nyata.
Misalkan Pada Tabel 2x2 1 B B2 1 A P11 P12 P1. 2 A P21 P22 P2. 1 . P P.2 P.. OR=1 1 / / 22 12 21 11 P P P P 22 12 21 11 P P PP 22 21 12 11 P P P P
.. 22 21 12 .. 22 .. 21 .. 12 11 N N N N N N N N N N P x (1) Jika 1, maka berlaku pula
22 12 21 11 / / N N N N 22 12 21 11 / / 1 N N N N 21 11 22 12 N N N N 11 21 12 22 N N N N (2) Jika persamaan (2) disubtitusikan ke persamaan (1) maka diperoleh
1 . . 1 11 .. 1 . .. . 1 .. 21 11 .. 12 11 2 .. 22 11 21 11 12 11 11 11 2 .. 22 21 12 11 11 .. .. .. 11 .. 11 .. 11 21 12 21 12 11 P P P N N x N N N N N x N N N N N N N N N N N N N N N N N N N N N N N N N N N N N N P Jadi, jika odds ratio =1 maka hubungan antara dua kejadian tidak nyata (saling bebas).
3. Apa beda statistik uji Pearson, Yates, dan Fisher untuk Tabel Kontingensi 2x2? Penyelesaian:
Statistik Uji Pearson dan Yates sama-sama diturunkan dari konsep probabilitas dan berdistribusi 2. Namun statistik uji Yates lebih cepat
konvergen menuju 2 ) 1 (
karena adanya koreksi terhadap statistik uji Pearson.. Sedangkan Fisher adalah uji eksak, sehingga langsung dapat diperoleh nilai P-value untuk mengambil keputusan menerima atau menolak H0. Selain itu
statistik uji Fisher digunakan jika ada sel (i,j) yang frekuensinya kecil
nij 5
2.8 Latihan Soal
1. Apa perbedaan dan persamaan antara statistik uji χ2 dan G2?
2. Apa yang dimaksud dengan Risiko Nisbi? dan Apa bedanya dengan Odds Ratio? 3. Diberikan tabel kontingensi sebagai berikut:
Tabel 2.6 Hubungaan Penderita Kanker dan Pemakaian Pil KB
Pil KB Mengidap Kanker
Total
Ya Tidak
Ya 23 34 57
Tidak 35 132 167
Total 58 166 224
Apakah ada hubungan antara minum PIL KB dengan penyakit Kanker? 4. Diberikan tabel kontingensi sebagai berikut:
Tabel 2.7 Kebiasaan meminum aspirin dan gangguan jantung
Pil (Tablet) Terkena SeranganJantung (B 1)
Tidak Terkena
Serangan Jantung (B2) Total
Aspirin 104 10933 11037
Netral/Placeto 189 10845 11034
Total 293 21778 22071
5. Diberikan Tabel Kontingensi sebagai berikut.
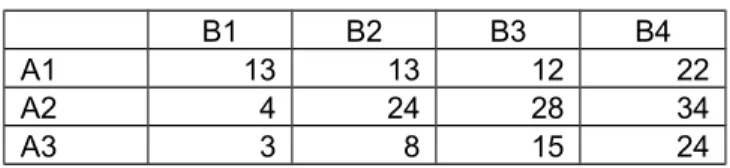
Tabel 2.8 Hubungan Variabel A dan B
B1 B2 B3 B4
A1 13 13 12 22
A2 4 24 28 34
A3 3 8 15 24
Lakukan pemecahan sumber-sumber penyebab ketakbebasan kemudian interpretasikan hasilnya.
10. Seorang manager perusahaan ingin melihat apakah ada hubungan atau pengaruh antara income dan kepuasan seorang karyawan perusahaannya. Kemudian ia juga ingin tahu pula kategori mana yang menyebabkan berpengaruh. Gunakan
1 . 0
Tabel 2.9 Hubungan Income dan Tingkat Kepuasan
Income tidak puas biasa puas
x<6000 45 15 23
6000<x<15000 10 12 10
15.000<x<25.000 10 11 13
x>25000 22 15 46
11. Penelitian terhadap 12 perusahaan dengan fasilitas di suatu propinsi ternyata 10 melunasi pajak tepat waktu, sedangkan dari 15 perusahaan tanpa fasilitas, terdapat 6 perusahaan yang tidak tepat waktu dalam melunasi pajaknya.
Tabel 2.10 Hubungan Income dan Tingkat Kepuasan
Pemberian Fasilitas Tepat Waktu Ya Tidak Dengan Fasilitas 10 2 Tanpa Fasilitas 9 6
Gunakan 0.05, apakah ada hubungan antara pemberian fasilitas ke perusahaan terhadap ketepatan dalam melunasi pajak.
Supplement
I. Tabel Kontingensi 2 x 2
Variabel katagorik yang hanya meliputi dua katagori dinamakan variabel biner,
misalnya terserangnya kanker paru-paru seperti pada ilustrasi tabel dibawah (terserang atau tidak), hasil dari suatu tindakan (berhasil atau tidak) atau kebiasaan merokok malam dan yang tidak memiliki kebiasaan merokok malam. Sehubungan dengan variabel biner ini seringkali diperbandingkan antara beberapa kelompok individu; pada ilustrasi tsb misalnya, ingin dibandingkan antara proporsi serangan kanker pada
kelompok yang memiliki kebiasaan merokok malam dan yang tidak memiliki kebiasaan tersebut. Jika ada dua kelompok, distribusi nilai variabel biner ini dapat disajikan pada suatu tabel kontingensi 2 x 2. Nilai variabel biner (Q=kanker paru-paru) dapat
dinyatakan sebagai 1 untuk nilai katagori yang satu, dan 2 untuk nilai katagori lainnya; misalnya 1 untuk terserang kanker paru-paru dan 2 untuk tidak terserang, variabel biner lainnya (P= kebiasaan merokok) 1 untuk kelompok yang memiliki kebiasaan merokok malam dan 2 untuk kelompok yang tidak memiliki kebiasaan tersebut. Selanjutnya tabel 2x2 dapat disusun menjadi 4 sel seperti Tabel 1.
Tabel 1: Tabel 2 x 2 Secara Umum
P Q Total
1 2
1 a = n11 b = n21 a + b = n1
2 c = n21 d = n22 c + d = n2
Total a + c = n1 b + d = n2 a + b + c + d = N
Untuk tabel kontingensi 2 x 2, statistik uji x2 (digunakan untuk menguji hipotesis bahwa tidak ada keterkaitan antara terserang kanker paru-paru, variabel Q dengan kebiasaan merokok malam hari, variabel P ) dapat dihitung dengan persamaan :
) )( )( )( ( ) ( 2 2 d c b a d b c a bc ad N
Hasil ini nantinya dibandingkan dengan tabel distribusi x2 jika nilai x2 hitung > x2 tabel maka hipotesis ditolak artinya ada hubungan antara variabel Q (kanker paru-paru) dengan variabel P (kebiasaan merokok)
Seandainya setelah diambil sampel sebanyak 56 orang dengan rincian yang merokok malam 36 orang sisanya 20 orang tidak punya kebiasaan tsb sedangkan yang terserang kanker ada 26 orang yang tidak kena kanker 30 orang, diperoleh data nilai frekuensi sampel masing-masing sel adalah sbb :
Tabel 2 : Tabel Hubungan antara Terserang Kanker Paru-Paru dengan Kebiasaan Merokok di Malam Hari
P 1=terserang kanker paru2 Q 2=tidak terserang kanker Total 1= kebiasaan merokok malam hari a = n11=20 b = n21=16 36 2=tidak biasa merokok malam hari c = n21=6 d = n22=14 20 Total 26 30 56
Nilai statistik uji untuk tabel kontingensi 2 x 2 pada ilustrasi pada tabel 2 dapat dihitung dengan persamaan yang lebih sederhana :
3376 20 36 30 26 6 16 14 20 56 2 2 2 . ) )( )( )( ( ) )( ( ) )( ( ) d c )( b a )( d b )( c a ( ) bc ad ( N 1.1 Nilai Q-YuleUntuk tabel kontingensi 2 x 2, nilai Q menunjukkan kuatnya keterkaitan. Nilai Q ini dikenal juga sebagai nilai Q-Yule, diajukan oleh Yule (1900; dalam Daniel,1990).
bc ad bc ad Q
Nilai Q-Yule merentang dari -1 sampai +1, dengan nol berarti antara kedua variabel saling bebas. Nilai Q-Yule yang semakin dekat dengan -1 atau +1 menunjukkan keterkaitan yang semakin kuat.
Contoh :
Nilai Q-Yule untuk tabel kontingensi 2 x 2 pada ilustrasi tabel 2 :
489 0 6 16 14 20 6 16 14 20 . ) )( ( ) )( ( ) )( ( ) )( ( bc ad bc ad Q
1.2. Angka Odds
Untuk individu-individu yang berada pada baris i, menyatakan 1i sebagai peluang bahwa individu tersebut terkatagori 1, dan ((1i,2i )(1i,11i)) sebagai
distribusi peluang bersyarat variabel biner tersebut. Pembandingan antara kedua baris, baris 1 dengan baris 2, dapat dinyatakan sebagai selisih katagori 1, 11-12.
Pembandingan proporsi katagori 2 adalah ekuivalen, yaitu
2 1 1 1 2 1 1 1 2 2 1 2 1 1 ( ) ( )
Selisih proporsi ini nilainya akan berkisar antar -1 dan +1, bernilai 0 jika baris 1 dan baris 2 identik. Variabel katagorik tersebut dikatakan bebas sehubungan dengan pengelompokan menurut baris jika 1112= 0.
Rasio Odds. Odds adalah ukuran yang menunjukkan perbandingan peluang munculnya
suatu kejadian dengan peluang tidak munculnya kejadian tersebut. Odds suatu kejadian A misalnya dihitung dengan membagi peluang kejadian A dengan peluang kejadian bukan A. ) A ( P ) A ( P ) A ( P ) A ( P ) A ( 1
Untuk tabel kontingensi 2 x 2, Odds katagori 1 pada baris 1 dan baris 2 masing-masing dihitung sebagai 2 2 2 1 2 1 2 1 2 1 2 1 1 1 1 1 1 1 1 1 dan
Apabila kedua katagori, baris dan kolom, berupa variabel acak, odds katagori 1 pada baris 1 dan baris 2 masing-masing adalah
22 21 2 12 11 1 dan
Selanjutnya, rasio antara odds 1 dan odds 2,
12 21 22 11 22 21 12 11 2 1
Nilai rasio odds berkisar antara 0 dan
. Apabila katagori baris dan katagori kolom saling bebas, maka nilai rasio odds adalah 1. Apabila nilai rasio odds lebih dari 1, 1<θ<
, berarti individu-individu pada baris pertama lebih besar kemungkinannya bernilai katagori 1 daripada individu-individu pada baris kedua; yaitu 1112. Apabila rasioodds kurang dari 1, 0<θ<1, berarti individu-individu pada baris pertama lebih kecil kemungkinannya bernilai katagori 1 daripada individu-individu pada baris kedua; yaitu
2 1 1
1
. Rasio odds tidak berubah apabila baris dan kolom tabel kontingensi
dipertukarkan.
Semakin jauh nilai rasio odds, θ, dari angka 1 pada arah tertentu berarti
keterkaitan antara katagori baris dan kolom semakin kuat. Dua nilai rasio odds, θ1 dan
θ2, menunjukkan tingkat keterkaitan yang sama apabila nilai yang satu merupakan
kebalikan dari nilai kedua, θ1 = 1/θ2 ; θ1=0.25 dan θ2= 4.0 misalnya menunjukkan
tingkat keterkaitan yang sama. Jika urutan baris atau kolom dipertukarkan, nilai rasio odds yang baru akan sama dengan seper nilai rasio odds yang lama. Jika diambil logaritma dari rasio odds, ln (θ), logaritma rasio odds untuk 2 rasio odds yang memiliki tingkat keterkaitan yang sama ini memiliki angka yang sama hanya berbeda tanda; ln(0.25) = -1.39, ln(4) = 1.39, ln(1) = 0 menunjukkan kebebasan antara katagori baris dan katagori kolom.
Untuk frekuensi sampel, statistik rasio odds dihitung sebagai ˆ n11n22 n12n21.
Rasio odds ini tidak berubah apabila kedua sel dalam baris dikalikan dengan suatu bilangan tidak nol. Demikian pula apabila kedua sel dalam kolom dikalikan dengan bilangan tak nol.
Hal ini menunjukkan sifat invarian atas perkalian, sehingga rasio odds sampel tetap merupakan penduga bagi parameter θ meskipun sampel yang digunakan tidak proporsional. Untuk persampelan retrospektif untuk keterkaitan antara aplikasi vaksin dengan keterserangan penyakit misalnya, rasio odds tetap merupakan penduga bagi θ, meskipun misalnya untuk keperluan tersebut dipilih masing-masing 100 orang yang mendapat serangan dan tidak mendapat serangan untuk kemudian diketetapkan
memakai atau tidak memakai vaksin, atau dipilih 150 pengamatan untuk yang terserang dan 50 untuk yang tidak terserang. Selanjutnya, rasio odds sama baiknya, baik
persampelannya retrospektif, atau prospektif, yaitu dengan memiliki 100 yang menggunakan vaksin dan 100 yang tidak menggunakan untuk kemudian diperiksa apakah terserang atau tidak terserang, atau kros seksi, yaitu dengan memilih 200 orang yang kemudian diperiksa apakah ia menggunakan vaksin dan apakah ia terserang penyakit.
Contoh :
Untuk tabel kontingensi pada tabel 2, odds baris 1, odds baris 2, dan rasio odds baris 1 pada odds baris 2 masing-masing adalah :
92 2 16 6 14 20 43 0 14 6 25 1 16 20 12 21 22 11 2 1 22 21 2 12 11 1 . ) )( ( ) )( ( n n n n . n n ˆ . n n ˆ 1
= 1.25 menunjukkan bahwa pada kelompok yang merokok malam hari, peluang terserang kanker paru-paru adalah 1.25 kali peluang tidak terserang. 2 = 0.43
menunjukkan bahwa pada kelompok yang tidak merokok malam hari, peluang terserang kanker paru-paru adalah 0.43 kali peluang tidak terserang.
Dengan nilai rasio odds 1/2 lebih dari 1, menunjukkan bahwa individu-individu
yang biasa merokok malam hari lebih besar kemungkinannya bernilai terserang kanker paru-paru dari pada individu-individu yang tidak biasa merokok malam hari.
072 1 92 2. ) . ln( ln .