KAJIAN METODE LEAST ABSOLUTE SELECTION AND
SHRINKAGE OPERATOR (LASSO) PADA DATA YANG
MENGANDUNG HETEROSKEDASTISITAS
MEIRA MAWATI
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2015
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Kajian Metode LeastAbsolute Selection and Shrinkage Operator (LASSO) pada Data yang
Mengandung Heteroskedastisitas adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Maret 2015
Meira Mawati
ABSTRAK
MEIRA MAWATI. Kajian Metode Least Absolute Selection and Shrinkage
Operator (LASSO) pada Data yang Mengandung Heteroskedastisitas. Dibimbing
oleh KUSMAN SADIK dan BAGUS SARTONO.
Metode Least Absolute Selection and Shrinkage Operator (LASSO) telah banyak digunakan dalam regresi berdimensi besar untuk menyeleksi peubah maupun menduga parameter. Solusi LASSO diperoleh dengan meminimumkan jumlah kuadrat sisaan terhadap suatu kendala, yaitu jumlah dari nilai mutlak penduga MKT (Metode Kuadrat Terkecil) lebih kecil daripada suatu konstanta. Jia et al. (2010) melakukan analisis terhadap data aplikasi medical imaging menggunakan metode LASSO dimana ragam galat data tersebut menyebar Poisson-like. Penelitian ini melakukan hal serupa. LASSO dievaluasi menggunakan data regresi yang heteroskedastis. Berdasarkan pendekatan simulasi, terungkap bahwa LASSO tidak selektif pada data regresi yang banyak mengandung penduga yang tidak signifikan (sparse). LASSO tidak lebih baik dibandingkan dengan MKT dan Best
Subset dalam menangani data yang mempunyai ragam galat yang heterogen.
Kata kunci: heteroskedastisitas, LARS, LASSO
ABSTRACT
MEIRA MAWATI. Study of Least Absolute Selection and Shrinkage Operator (LASSO) Method Under Heteroscedasticity. Under the supervision of KUSMAN SADIK and BAGUS SARTONO.
Least Absolute Selection and Shrinkage Operator (LASSO) has been
acknowledged to analyse high dimention data to select variables and to estimate parameters. LASSO estimators obtained by minimizing the residual sum of squares subject to the sum of the absolute value of the coefficients being less than a constant. Jia et al. (2010), in his research, conducted an analysis on a medical imaging application data using LASSO when error variance of the data suffered heteroscedasticity problem, which is Poisson-like distributed. This research aimed to study the similar problem. LASSO is evaluated by using heteroscedastic regression data. By conducting simulation approach, the result showed that LASSO encountered difficulties. In regression data that has too many zero-coefficients estimator, LASSO is not selective. Compared to OLS (Ordinary Least Square) and Best Subset, LASSO doesn’t offer better solution.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Statistika
pada
Departemen Statistika
KAJIAN METODE LEAST ABSOLUTE SELECTION AND
SHRINKAGE OPERATOR (LASSO) PADA DATA YANG
MENGANDUNG HETEROSKEDASTISITAS
MEIRA MAWATI
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2015
Judul Skripsi : Kajian Metode Least Absolute Selection and Shrinkage Operator (LASSO) pada Data yang Mengandung Heteroskedastisitas
Nama : Meira Mawati NIM : G14100084
Disetujui oleh
Dr Kusman Sadik, MSi Pembimbing I
Dr Bagus Sartono, MSi Pembimbing II
Diketahui oleh
Dr Anang Kurnia, MSi Ketua Departemen
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2014 ini ialah Metode LASSO, dengan judul Kajian Metode Least Absolute Selection and
Shrinkage Operator (LASSO) pada Data yang Mengandung Heteroskedastisitas.
Terima kasih penulis ucapkan kepada Bapak Dr Kusman Sadik, MSi dan Bapak Dr Bagus Sartono, MSi selaku pembimbing. Di samping itu ungkapan terima kasih juga penulis sampaikan kepada ayah, ibu, kakak, serta rekan-rekan, atas doa, kasih sayang, dan segala bentuk dukungan yang telah diberikan.
Semoga karya ilmiah ini bermanfaat.
Bogor, Maret 2015
DAFTAR ISI
DAFTAR TABEL x DAFTAR GAMBAR x DAFTAR LAMPIRAN x PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 2 TINJAUAN PUSTAKA 2 LASSO 2 Algoritma LAR 3Validasi Silang Lipat-K 4
Heteroskedastisitas pada Regresi Linier 4
LASSO pada Kasus Heteroskedastisitas 6
DATA DAN METODE 6
Data 6
Metode 8
HASIL DAN PEMBAHASAN 9
SIMPULAN DAN SARAN 13
Simpulan 13
Saran 13
DAFTAR PUSTAKA 14
LAMPIRAN 15
DAFTAR TABEL
1. Sebaran peubah penjelas (X1, X2, X3, dan X4) dan nilai parameter (βi)
data simulasi contoh kasus 2 6
2. Nilai ragam galat data simulasi contoh kasus 1 7
3. Sebaran peubah penjelas (X1, X2, …, X8) dan nilai parameter (βi) data
simulasi contoh kasus 2 7
4. Beberapa contoh Uji Breusch-Pagan pada contoh kasus 1 dan 2 9
5. Hasil simulasi contoh kasus 1 12
6. Jumlah kemunculan setiap peubah penjelas pada contoh kasus 2 13
DAFTAR GAMBAR
1. Contoh validasi silang lipat-5 saat anak gugus data ke-3 dijadikan anak
gugus data pengujian model 4
2. Plot objek yang dihasilkan oleh algoritma LARS untuk menduga
koefisien LASSO 10
3. Nilai KTG validasi silang mode fraction (a) dan mode step (b) pada
salah satu gugus data di contoh kasus 1 10
4. Nilai KTG validasi silang mode fraction (a) dan mode step (b) gugus
data ke-53 pada contoh kasus 2 11
DAFTAR LAMPIRAN
1. Model yang terpilih pada simulasi contoh kasus 2 15
PENDAHULUAN
Latar BelakangLeast Absolute Selection and Shrinkage Operator (LASSO) adalah suatu
metode yang telah banyak digunakan dalam regresi berdimensi besar untuk menyeleksi peubah maupun menduga parameter. Dalam aplikasi keilmuan, berbagai macam percobaan sering kali melibatkan banyak peubah. Peubah-peubah tersebut diekspresikan menjadi pengaruh-pengaruh yang dapat memberikan efek terhadap respon, baik efek dari pengaruh tunggal, maupun efek dari interaksi antarpeubah. Banyaknya pengaruh menyebabkan penyeleksian peubah menjadi sulit untuk dilakukan sehingga model yang efisien sulit didapat.
LASSO ditemukan oleh Tibshirani (1996) pertama kali sebagai alternatif dari solusi permasalahan penduga parameter model MKT yang kurang akurat dalam prediksi dan sulit diinterpretasi. Penelitian telah menunjukkan bahwa pada data yang mengandung jumlah peubah penjelas lebih banyak dari jumlah amatan, metode LASSO menunjukkan hasil yang baik dalam memilih model yang tepat (Jia et al. 2010). LASSO mengadaptasi konsep pemilihan peubah dan pendugaan parameter yang dikenal lebih dulu dengan nama subset selection dan ridge
regression. Oleh karena itu, LASSO menyeleksi peubah dan menduga parameter
secara simultan (Chand dan Kamal 2011).
Pemilihan model dan pendugaan parameter LASSO sudah dikenal dengan baik dalam kondisi data yang memenuhi asumsi standar, salah satunya dalam kondisi data yang homoskedastis (Jia at al. 2010). Walaupun demikian, masalah homoskedastisitas atau kehomogenan ragam galat sering kali tidak dideskripsikan dengan jelas. Homoskedastisitas mengindikasikan setiap pengamatan mengandung informasi yang sama penting (Rawlings et al. 1998). Kondisi ini penting untuk diperhatikan karena keabsahan uji hipotesis yang dilakukan terhadap data tersebut bergantung pada terpenuhinya asumsi homoskedastisitas. Inferensia yang dilakukan terhadap data yang tidak memenuhi asumsi homoskedastisitas menyebabkan simpulan menyimpang, serta penduga dan model yang diperoleh tidak meyakinkan karena mengandung bias yang tinggi.
Jia et al. (2010) melakukan analisis terhadap data aplikasi medical imaging menggunakan metode LASSO. Data yang digunakan tidak memenuhi asumsi homoskedastisitas, yaitu ragam galat data tersebut menyebar Poisson-like. Penelitian ini melakukan hal serupa, yaitu evaluasi akan dilakukan terhadap metode LASSO dengan mengaplikasikannya terhadap data yang heteroskedastis. Perbedaannya adalah ragam galat pada simulasi dijadikan sebagai fungsi dari peubah penjelas yang terdapat dalam model. Dengan demikian akan didapat galat yang tidak saling bebas terhadap peubah penjelas, dan kondisi heteroskedastisitas diperoleh. Proses pengecekan kondisi heteroskedastisitas data dilakukan dengan Uji Breusch-Pagan pada taraf nyata 0.05. Perbandingan antara LASSO dengan MKT dan Metode Best Subset dilakukan untuk mengetahui keunggulan LASSO dibandingkan dengan keduanya.
2
Tujuan Penelitian
Tujuan penelitian ini adalah mengkaji metode LASSO dalam melakukan pemilihan peubah dan pendugaan parameter pada data yang mengandung heteroskedastisitas.
TINJAUAN PUSTAKA
LASSOTibshirani (1996) pertama kali memperkenalkan LASSO sebagai metode penyeleksian peubah dan pendugaan parameter. Metode LASSO mulai dikenal setelah Efron menemukan algoritma LAR pada tahun 2004. Penduga LASSO tidak dapat diperoleh dalam bentuk tertutup seperti pada MKT ataupun ridge
regression, tetapi dengan pemrograman kuadratik (Hastie et al. 2008). Penduga
koefisien LASSO ( ̂LASSO diperoleh dengan meminimumkan jumlah kuadrat sisaan dengan suatu kendala L1 (Tibshirani 1996), sebagai berikut:
̂LASSO argmin ∑ ( i - β - ∑ ijβj p j ) N i L ∑ |βj| p j t (Hastie et al. 2008). Dalam persamaan di atas, jumlah kuadrat sisaan diminimumkan terhadap parameter β dengan s arat kendala L1 sehingga dapat diperoleh solusi LASSO.
Nilai t dalam L1 merupakan parameter kontrol yang mengendalikan banyaknya
penyusutan yang dilakukan terhadap nilai penduga, dengan t > 0. Nilai t yang kecil menyebabkan beberapa koefisien regresi menjadi bernilai nol sehingga peubah-peubah yang berpengaruh besar dalam model terpilih dan peubah-peubah yang berpengaruh kecil tereliminasi. Hai ini mengakibatkan solusi LASSO menghasilkan model yang efisien. Jika β̂jmerupakan penduga MKT dan t0 =
∑ |β̂p j| maka nilai t < t0 menyebabkan penduga solusi MKT susut ke arah nol. Jika
nilai t yang dipilih lebih besar daripada t0 maka penduga LASSO yang diperoleh
akan sama dengan penduga MKT model penuh (Tibshirani 1996).
Penduga koefisien LASSO dievaluasi dengan menentukan parameter baku s t
∑ |β̂p j|, dengan t = ∑ |β̂j|
p
dan β̂jmerupakan penduga MKT model penuh atau pada gambar output algoritma LARS ditulis sebagai |beta|/max|beta| (Dewi 2010). Plot antara penduga galat LASSO versus nilai s dibuat untuk mempermudah interpretasi. Penentuan nilai optimal s dapat diperoleh dengan melakukan validasi silang (Tibshirani 1996). Hastie et al. (2008) melakukan validasi silang lipat 10 untuk menentukan nilai s optimum pada LASSO.
Perbedaan antara ridge regression dengan LASSO adalah terletak pada nilai kendala yang digunakan untuk memperoleh penduga parameter regresi. Kendala pada ridge regression adalah ∑pj βj t, sedangkan pada LASSO adalah
3 ∑ |βpj j| t. Perbedaan tersebut menyebabkan penduga parameter LASSO cenderung lebih kecil dibandingkan dengan penduga parameter ridge regression. Penduga parameter regresi yang diperoleh dari ridge regression hanya disusutkan ke arah nol, sedangkan pada solusi LASSO beberapa penduga parameter regresi disusutkan tepat menjadi nol. Dengan demikian metode LASSO juga berfungsi sebagai seleksi peubah seperti pada subset selection.
Algoritma LAR
Least Angle Regression (LAR) adalah metode klasik yang berkaitan dengan
metode pemilihan model yang dahulu dikenal dengan nama forward selection atau
forward stepwise regression (Efron et al. 2004). Seperti halnya pada forward selection, dalam algoritma LAR model terbaik diperoleh dengan cara
memasukkan peubah penjelas satu persatu. Modifikasi algoritma LAR untuk LASSO menghasilkan efisiensi algoritma dalam menduga koefisien LASSO dengan komputasi yang lebih cepat dibandingkan pemrograman kuadratik (Pusporini 2012). Algoritma LAR selalu mengambil p langkah untuk mendapatkan penduga kuadrat terkecil secara penuh, sedangkan modifikasi LAR untuk LASSO, disebut LARS, dapat memiliki lebih dari p langkah untuk mendapatkannya. Algoritma LASSO dengan memodifikasi LAR merupakan cara yang efisien dalam komputasi solusi masalah LASSO, terutama ketika jumlah peubah penjelas yang digunakan jauh lebih banyak daripada jumlah amatan. Tahapan algoritma LARS adalah sebagai berikut (Hastie et al. 2008):
1. Membakukan peubah penjelas { i: i = 1, ..., p } sehingga rata-ratanya bernilai nol dan ragamnya bernilai 1. Mulai dengan sisaan r - ̅ , β , ..., βp= 0. Jika nilai terbakukan dinyatakan dengan i* maka pembakuan yang dilakukan yaitu : i* i - X̅
√ ar(X) Proses pembakuan dilakukan agar dapat membandingkan
dugaan koefisien regresi yang berbeda ragam dalam suatu model. 2. Mencari peubah penjelas xa yang paling berkorelasi dengan r.
3. Mengubah nilai βa dari 0 menuju nilai koefisien regresi yang diperoleh dari
proses MKT sampai suatu xb mempunyai korelasi sama besarnya dengan
korelasi antara xa dengan sisaan sekarang.
4. Mengubah nilai βa dan βb bergerak dalam arah koefisien kuadrat terkecil
bersama dari sisaan sekarang dalam (xa, xb) sampai suatu kompetitor lain,
misalnya xc, memiliki korelasi yang cukup dengan sisaan akibat (xa, xb). Mengeluarkan peubah tersebut dari gugus peubah aktif jika koefisien
bukan nol mencapai nilai nol, dan menghitung kembali arah kuadrat terkecil bersama.
5. Meneruskan langkah nomor 4 sampai semua p peubah penjelas telah masuk. Setelah min(N-1,p) langkah, solusi model penuh untuk kuadrat terkecil diperoleh.
4
Validasi Silang Lipat-K
Validasi silang merupakan metode yang paling sederhana dan banyak dipakai secara luas untuk menduga galat prediksi. Idealnya, ketika data yang dimiliki memadai, akan dapat ditentukan suatu anak gugus data validasi dan digunakan untuk mengukur ketepatan model yang dimiliki. Namun sering kali data yang dimiliki terlalu sedikit sehingga tidak memungkinkan untuk dilakukan validasi secara langsung. Solusinya adalah melakukan validasi silang yang menggunakan sebagian data yang tersedia untuk mengepaskan model (validasi model), dan sebagian data yang lain untuk digunakan sebagai data pengujian model (Hastie et al. 2008).
Salah satu jenis validasi silang adalah validasi silang lipat-K. Metode ini baik digunakan ketika jumlah data amatan sedikit. Dalam validasi silang lipat-K, amatan dibagi ke dalam K anak gugus data sama rata secara acak.
Sebagai contoh, jika K = 5 maka salah satu contoh skenario pembagian data yang terjadi akan terlihat seperti pada Gambar 1. Pada ilustrasi ini, anak gugus data ke-3 menjadi gugus data validasi, model dibangun menggunakan keempat anak gugus data lain, yaitu anak gugus data ke-1, 2, 4 dan 5. Lalu dihitung nilai dugaan galat prediksi dari model terbaik ketika memprediksi anak gugus data ke-3. Hal ini dilakukan untuk k = 1, 2, 3, 4, 5, lalu semua 5 penduga galat prediksi dikombinasikan.
Nilai galat prediksi ( ̂) validasi silang lipat-K diduga oleh persamaan berikut:
P ̂ C ∑ ∑ ( i - ̂-k( i )
( i, i)
k
dengan ̂-k( i adalah dugaan y untuk xi pada saat lipat ke-k tidak digunakan
dalam menduga model, dan yi adalah nilai respon pada amatan ke-i pada data test
T. Izeman (2008) merekomendasikan validasi silang lipat-5 atau lipat-10 karena menghasilkan nilai ̂ dengan bias tinggi namun ragam rendah.
Heteroskedastisitas pada Regresi Linier
Homoskedastisitas adalah salah satu asumsi dalam regresi linier ketika ragam dari galat menyebar konstan di suatu nilai tertentu. Asumsi ini menunjukkan bahwa setiap amatan pada peubah respon mengandung informasi yang sama pentingnya sehingga seluruh pengamatan di dalam MKT mendapatkan bobot yang sama (Rawlings et al. 1998).
Gambar 1 Contoh validasi silang lipat-5 saat anak gugus data ke-3 dijadikan anak gugus data pengujian model
5 Model umum regresi berganda dapat ditulis sebagai berikut:
i β + ∑ ijβj
p
j + i,
dengan
yi : nilai respon pada amatan ke-i,
β0 : intersep,
xij : nilai peubah penjelas ke-j pada amatan ke-i,
βj : nilai parameter bagi peubah penjelas ke-j, i : nilai galat pada amatan ke-i.
Ragam galat disebut homogen jika Var ( i) σ2, sebaliknya ketika data tidak
homogen dalam ragam, maka setiap amatan mempunyai nilai ragam yang berbeda, atau disimbolkan sebagai: Var ( i) = σi. Akibatnya, setiap amatan
mengandung informasi yang tidak sama karena ragam tidak konstan pada suatu nilai tertentu (Rawlings et al. 1998). Kondisi demikian disebut heteroskedastisitas. Heteroskedastisitas disebabkan beberapa pengamatan mengandung informasi yang lebih dibandingkan dengan yang lain. Dengan demikian pengamatan tersebut seharusnya mendapat bobot yang lebih besar dibandingkan dengan pengamatan lainnya (Rawlings et al. 1998).
Sifat dari penduga MKT yaitu tak bias terbaik (memiliki ragam penduga yang minimum) dan sangat bergantung pada asumsi kehomogenan ragam. Pembobotan yang sama, sebagaimana yang dilakukan pada MKT, tidak akan menghasilkan penduga dengan ragam minimum, apabila ragamnya tidak sama. Oleh karena itu, pengaruh dari tidak terpenuhinya asumsi ini adalah presisi/kecermatan dari penduga MKT menjadi lebih kecil dibandingkan dengan penduga yang mengakomodasi ketidakhomogenan ragam tersebut (Rawlings et al. 1998).
Sejalan dengan Rawlings et al. (2008), Gujarati (2006) menyatakan (tanpa pembuktian) bahwa ada beberapa dampak buruk dari keberadaan heteroskedastisitas, yaitu:
1. Ragam menjadi tidak minimum. Keberadaan heteroskedastisitas mempunyai makna bahwa ragam galat tidak homogen. Asumsi ragam galat yang homogen mengindikasikan bahwa informasi seluruh amatan sama. Namun karena asumsi tersebut tidak terpenuhi maka ragam pendugaan secara keseluruhan tidak lagi efisien. Hal ini berlaku juga dalam analisis menggunakan ukuran sampel yang besar.
2. Rumus-rumus biasa untuk memprediksi ragam penduga MKT umumnya bias. Prediksi ragam penduga MKT bias, namun tidak dapat dikatakan secara tegas bias ke atas (overestimate) atau bias ke bawah (underestimate). Hal ini disebabkan oleh tidak dapat dijelaskannya seberapa besar derajat keheterogenan ragam yang terjadi dalam model regresi yang mendapat gangguan heteroskedastisitas karena belum ada alat ukur yang dapat menghitungnya secara pasti.
3. Bias muncul karena σ̂ (penduga bagi σ2 yaitu ∑ni ei⁄d.b.) tidak lagi merupakan penduga tak bias dari σ2
6
4. Selang kepercayaan dan hipotesis yang didasarkan pada distribusi t dan F tidak meyakinkan. Oleh sebab itu, kemungkinan kesalahan perhitungan dapat terjadi jika dilakukan pengujian hipotesis.
LASSO pada Kasus Heteroskedastisitas
Metode LASSO telah banyak digunakan dalam penyeleksian peubah dan pendugaan parameter pada data regresi berdimensi besar. Proses pemilihan model yang dilakukan oleh LASSO telah baik dikenal dalam kondisi model regresi standard sparse dan homoskedastis (Jia et al. 2010).
Dalam kasus heteroskedastisitas, LASSO memilih model ketika ragam penduga tidak minimum. Dalam masalah kekonsistenan, LASSO kekar terhadap pelanggaran asumsi homoskedastisitas yang galatnya menyebar Poisson-like. Hasil teoritis dari model regresi sparse Poisson-like serupa dengan model regresi standard sparse. Simulasi yang telah dilakukan membuktikan bahwa dalam masalah kualitas pemilihan model, data regresi yang galatnya menyebar
Poisson-like dan data yang homoskedastis menunjukkan hasil yang serupa (Jia et al. 2010).
DATA DAN METODE
DataData yang digunakan dalam penelitian ini adalah data simulasi. Proses pembangkitan data dilakukan pada perangkat lunak R versi 3.1.2. Dalam penelitian ini digunakan dua contoh kasus. Kasus pertama adalah analisis kemampuan LASSO dengan mencobakan beberapa kondisi ragam galat. Kasus yang kedua adalah perbandingan metode LASSO dengan MKT dan Best Subset dalam menganalisis data regresi yang heteroskedastis.
Pada contoh kasus 1 dicobakan 100 gugus data bangkitan (100 ulangan) dengan masing-masing 30 amatan (n=30). Sebanyak empat peubah penjelas X dibangkitkan menurut sebaran peubah acak Seragam, dengan nilai koefisien regresi yang berbeda-beda (Tabel 1).
Peubah respon yang menampung nilai amatan (Y) diperoleh dari model regresi linier berganda tanpa intersep, ditambah galat, + , dengan X merupakan matriks berukuran 30x4 yang menampung nilai-nilai keempat peubah penjelas, merupakan vektor penduga koefisien regresi, dan merupakan vektor
Tabel 1 Sebaran peubah penjelas (X1, X2, X3, dan X4) dan nilai
parameter (βi) data simulasi contoh kasus 2
Peubah
Penjelas Sebaran peubah penjelas Xi Nilai parameter (βi)
X1 Seragam(1, 10) diskrit 10.0
X2 X2 = 2X1 + e, e~Normal(0,1) 10.0
X3 Seragam(1, 20) diskrit 5.0
7 galat. Kondisi heteroskedastisitas dalam data diperoleh dari pembangkitan galat terlebih dahulu yang ragamnya menyebar menurut fungsi dari peubah penjelasnya, yaitu Seragam. Sebagai kontrol dilibatkan satu kali simulasi terhadap data yang homoskedastisitas. Kondisi ragam sisaan yang dicobakan pada contoh kasus 1 dideskripsikan pada Tabel 2.
Tabel 2 Nilai ragam galat data simulasi contoh kasus 1 Simulasi
ke-
Nilai ragam galat
(σ ) Keterangan 1 1 Homoskedastis* 2 X1i Heteroskedastis 3 2X1i Heteroskedastis 4 X Heteroskedastis 5 X2i Heteroskedastis 6 2X2i Heteroskedastis 7 X Heteroskedastis 8 X4i Heteroskedastis 9 2X4i Heteroskedastis 10 X Heteroskedastis *sebagai kontrol
Pada contoh kasus 2 dilakukan simulasi dengan 100 gugus data (100 ulangan) dan 50 jumlah amatan pada masing-masing gugus data (n=50). Sebanyak delapan peubah penjelas dibangkitkan menurut sebaran Normal dengan nilai parameter (μ dan σ2
) beda dan nilai koefisien regresi ditentukan berbeda-beda pula (Tabel 3).
Tabel 3 Sebaran peubah penjelas (X1, X2, …, X8) dan nilai parameter
(βi) data simulasi contoh kasus 2
Peubah Penjelas Sebaran peubah penjelas Xi Nilai parameter (βi) X1 Normal (100,5) 3.0 X2 Normal (10,2) 2.0 X3 Normal (55,7) 0.0 X4 Normal (155,10) 0.0 X5 Normal (65,7) 1.5 X6 Normal (20,3) 0.0 X7 Normal (10,3) 0.0 X8 Normal (40,5) 2.0
Peubah respon yang menampung nilai amatan (Y) diperoleh dari model regresi linier berganda tanpa intersep. Kondisi heteroskedastisitas diperoleh dengan menetapkan Var ( i) = X . Pada contoh kasus ini dilakukan pembandingan antara
LASSO, MKT, dan Best Subset. Dari ketiga metode tersebut diamati model regresi yang diperoleh pada 100 gugus data.
8
Metode
Tahapan metode yang digunakan pada contoh kasus 1 adalah sebagai berikut:
1. Membangkitkan peubah penjelas X sebanyak 4 peubah, X1, X2, X3, dan X4,
dengan X2 merupakan peubah yang berkorelasi kuat dengan X1 (X2i = X ).
2. Membangkitkan peubah respon Y dengan model regresi linier dari sebanyak 4 peubah penjelas yang dihasilkan pada langkah 1 dengan koefisien regresi yang ditentukan terlebih dahulu sesuai dengan Tabel 1, ditambah galat yang memiliki ragam heterogen seperti pada Tabel 2.
3. Menguji keberadaan heteroskedastisitas pada model regresi data simulasi dengan Uji Breusch-Pagan.
Jika heteroskedastisitas terdeteksi maka analisis dilanjutkan ke langkah 4. Sedangkan jika tidak terdeteksi, mengulangi langkah 1 sampai 3.
4. Melakukan seleksi peubah dan pendugaan parameter dengan metode LASSO menggunakan algoritma LARS.
5. Memilih model dengan nilai KTG terkecil yang diperoleh dari proses validasi silang.
6. Mengulang langkah 1 sampai 5 sebanyak 100 kali (100 gugus data). 7. Melakukan evaluasi terhadap penduga LASSO dengan cara:
menghitung banyaknya peubah penjelas yang oleh LASSO diduga memiliki nilai koefisien regresi (βi≠ ) dan yang disusutkan menjadi nol.
8. Melakukan semua langkah tersebut (1 sampai 8) dengan kondisi galat kedua, ketiga, sampai kesepuluh.
Tahapan metode yang digunakan pada contoh kasus 2 adalah sebagai berikut:
1. Membangkitkan peubah penjelas X sebanyak 8 peubah.
2. Membangkitkan peubah respon Y dengan model regresi linier dari sebanyak 8 peubah penjelas yang dihasilkan pada langkah 1 dengan koefisien regresi yang ditentukan terlebih dahulu, ditambah galat yang memiliki ragam heterogen yang merupakan fungsi dari peubah X3 (Var ( i) = X ).
3. Menguji keberadaan heteroskedastisitas pada model regresi data simulasi dengan Uji Breusch-Pagan.
Jika heteroskedastisitas terdeteksi maka analisis dilanjutkan ke langkah 4. Sedangkan jika tidak terdeteksi, mengulangi langkah 1 sampai 3.
4. Melakukan seleksi peubah dan pendugaan parameter dengan metode LASSO menggunakan algoritma LARS.
5. Memilih model dengan nilai KTG terkecil yang diperoleh dari proses validasi silang.
6. Mengulang langkah 1 sampai 5 sebanyak 100 kali (100 gugus data). 7. Melakukan evaluasi terhadap penduga LASSO dengan cara:
menghitung banyaknya peubah penjelas yang oleh LASSO diduga memiliki nilai koefisien (βi≠ ) dan yang disusutkan menjadi nol.
8. Melakukan langkah 1 sampai 3 lalu dilanjutkan dengan:
pemilihan model dan pendugaan parameter menggunakan MKT,
9
HASIL DAN PEMBAHASAN
Dalam penelitian ini dilakukan pembangkitan data regresi yang heteroskedastis. Masalah pertama yang dihadapi adalah cara membuat data yang sesuai dengan kriteria yang diinginkan sehingga dapat dianalisis. Data peubah penjelas dibangkitkan menurut sebaran Seragam untuk contoh kasus 1 dan sebaran Normal untuk contoh kasus 2. Pemilihan sebaran dan nilai parameter bagi peubah penjelas yang digunakan mengandung subjektifitas yang tinggi dan dapat berbeda-beda di setiap percobaan dan pengguna (user).
Setelah melakukan pembangkitan data peubah penjelas, masalah kedua yang dihadapi adalah cara memperoleh model regresi yang galatnya mempunyai ragam yang heterogen. Dalam MKT, asumsi homoskedastisitas mensyaratkan ragam galat menyebar Normal ( , σ2). Dengan demikian jika ingin memperoleh ragam galat yang heterogen dapat dilakukan dengan menentukan fungsi ragam galat dari peubah penjelas yang terlibat (misalnya Var ( i) = X1i untuk contoh kasus 1).
Keberhasilan proses ini dapat diamati dari nilai-p pada Uji Breusch-Pagan. Jika nilai-p pada uji Breusch-Pagan lebih kecil dari taraf nyata (0.05) maka diperoleh data yang heteroskedastis. Uji Breusch-Pagan didekati dengan pengujian statistik uji sebaran Khi-kuadrat dengan derajat bebas (d. b.) sebesar banyaknya peubah penjelas pada model. Berdasarkan beberapa gugus data dalam simulasi (Tabel 4), terlihat bahwa data regresi telah memenuhi kriteria yang diinginkan, yaitu data regresi yang heteroskedastis kecuali bagi kontrol.
Tabel 4 Beberapa contoh Uji Breusch-Pagan pada contoh kasus 1 dan 2 ar ( i) Gugus data ke- Statistik Uji Breusch-Pagan d.b. Nilai-p Keterangan Contoh 1 1 1 6.89050 4 0.14180 Homoskedastis X2i 40 10.68580 4 0.03033 Heteroskedastis X 16 11.85030 4 0.01850 Heteroskedastis 2X4i 9 16.10830 4 0.00288 Heteroskedastis X 63 15.44060 4 0.00387 Heteroskedastis Contoh 2 X 1 15.53450 8 0.04955 Heteroskedastis 25 17.45550 8 0.02570 Heteroskedastis 42 16.93980 8 0.03074 Heteroskedastis 69 17.66080 8 0.02392 Heteroskedastis 95 19.09850 8 0.01434 Heteroskedastis Gambar 2 merupakan grafik hasil proses pemilihan peubah pada algoritma LARS. Peubah penjelas terpilih satu persatu ke dalam model sekaligus diduga (Chand dan Kamal 2011). Garis membujur 0, 1, 2, 3, dan 4 menggambarkan jumlah langkah yang dialami LASSO pada saat pemilihan model. Pada contoh data yang grafiknya tercermin di Gambar 2, peubah penjelas X2 merupakan
peubah yang paling berkorelasi dengan sisaan, oleh karenanya peubah tersebut terpilih di langkah awal pemilihan model. Pada langkah selanjutnya, X3 terpilih,
10 K o ef isi en r eg re si b ak u KTG v ali d asi sil an g KTG v ali d asi sil an g
sampai akhirnya peubah X1 dan X4 juga terseleksi. Setelah semua peubah penjelas
terseleksi, dibuat terlebih dahulu grafik antara nilai s dengan nilai KTG (Kuadrat Tengah Galat) yang diperoleh dari proses validasi silang untuk mengevaluasi model yang terbaik. Model terbaik adalah model ketika langkah tersebut menghasilkan KTG yang minimum. Model terbaik dapat diperoleh dengan menggunakan dua fungsi yang terdapat pada algoritma LARS, yaitu fraction dan
step. Mode fraction berguna untuk mencari nilai KTG minimum pada proses
validasi silang, sedangkan untuk mencari langkah ketika model terbaik bagi solusi LASSO digunakan fungsi pada mode step.
Gambar 2 Plot objek yang dihasilkan oleh algoritma LARS untuk menduga koefisien LASSO
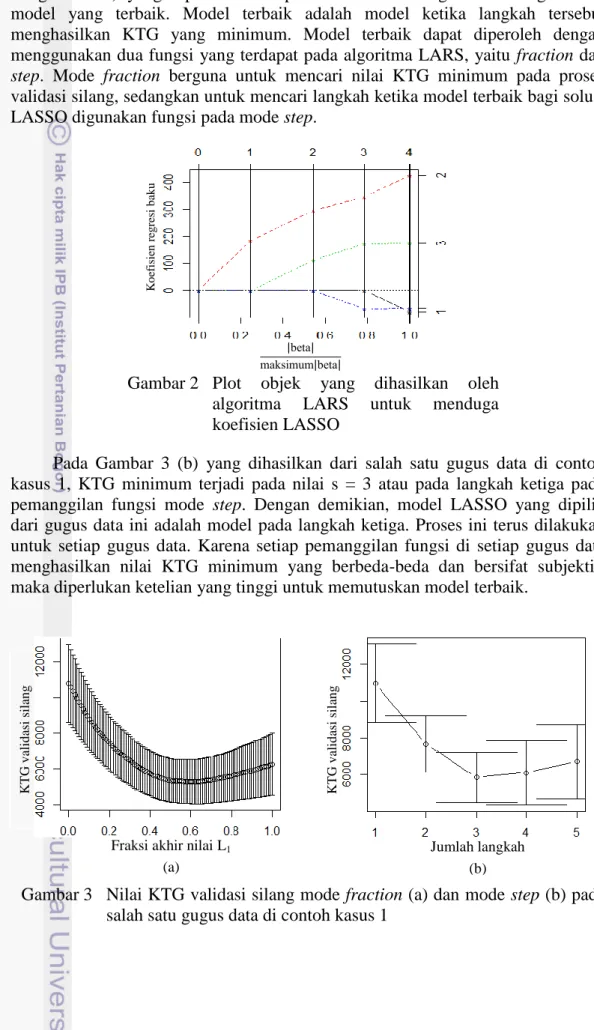
Pada Gambar 3 (b) yang dihasilkan dari salah satu gugus data di contoh kasus 1, KTG minimum terjadi pada nilai s = 3 atau pada langkah ketiga pada pemanggilan fungsi mode step. Dengan demikian, model LASSO yang dipilih dari gugus data ini adalah model pada langkah ketiga. Proses ini terus dilakukan untuk setiap gugus data. Karena setiap pemanggilan fungsi di setiap gugus data menghasilkan nilai KTG minimum yang berbeda-beda dan bersifat subjektif, maka diperlukan ketelian yang tinggi untuk memutuskan model terbaik.
Gambar 3 Nilai KTG validasi silang mode fraction (a) dan mode step (b) pada salah satu gugus data di contoh kasus 1
Jumlah langkah (b) Fraksi akhir nilai L1
(a)
|beta| maksimum|beta|
11 Dalam pemilihan model dan pendugaan parameter LASSO di contoh kasus 2, terdapat beberapa gugus data dimana tidak terpilih sama sekali peubah penjelas, artin a semua βi disusutkan menjadi nol oleh LASSO. Hal ini diidentifikasi dari
grafik yang ditunjukkan pada mode step maupun mode fraction. Trend pada grafik ang dihasilkan dari data dengan semua βi = 0 berbeda dengan trend yang
ditunjukkan pada Gambar 3. Salah satu contoh kasus tidak terpilihnya peubah penjelas sama sekali ada pada gugus data ke-53. Grafik yang dihasilkan gugus data ke-53 pada pemanggilan fungsi mode fraction dan mode step ditunjukkan pada Gambar 4.
Gambar 4 Nilai KTG validasi silang mode fraction (a) dan mode step (b) gugus data ke-53 pada contoh kasus 2
Pada grafik di Gambar 4, KTG minimum terjadi pada langkah pertama. Dengan demikian pada gugus data ini, penduga parameter LASSO yang didapat adalah ̂ = (0, 0, 0, 0, 0, 0, 0, 0)T. Pada gugus data ini heteroskedastisitas mempengaruhi LASSO dalam menduga parameter sehingga tidak terpilih model yang baik. Peubah yang berpengaruh maupun yang tidak berpengaruh disusutkan semua menjadi nol oleh LASSO. Selain gugus data ke-53, terdapat 28 gugus data lain yang juga mengalami hal serupa.
Evaluasi dilakukan terhadap metode LASSO dengan menghitung ketepatan LASSO dalam menyeleksi peubah penjelas yang berkoefisien regresi tidak nol/berpengaruh dan berkoefisien regresi nol/tidak berpengaruh. Tabel 5 menunjukkan hasil evaluasi dari simulasi pada contoh kasus 1.
Tabel 5 mengungkap bahwa dalam kasus data regresi heteroskedastis dengan ragam galat yang merupakan fungsi dari peubah penjelas berpengaruh ( ar ( i) = f(Xi); βi≠ ), heteroskedastisitas tidak mempengaruhi LASSO ketika
ukuran sampel kecil (n<30). Hasil pada kasus tersebut sama dengan hasil dari proses pendugaan parameter dan pemilihan model pada data homoskedastis (Var ( i) = 1). Hal ini menunjukkan bahwa LASSO menghasilkan solusi yang
memuaskan untuk ragam galat yang merupakan fungsi dari peubah penjelas yang berpengaruh. KT G v alid asi s ila n g
Fraksi akhir nilai L1
(a) KT G v alid asi s ila n g Jumlah langkah (b)
12
Tabel 5 Hasil simulasi contoh kasus 1 ar ( i) Keterangan Persentase (%) terdeteksi berpengaruh (βi≠ ) X1 X2 X3 X4 1 Homoskedastis 100 100 100 0 X1i Heteroskedastis 100 100 100 0 2X1i Heteroskedastis 100 100 100 0 X Heteroskedastis 100 100 100 0 X2i Heteroskedastis 100 100 100 0 2X2i Heteroskedastis 100 100 100 0 X Heteroskedastis 100 100 100 0 X4i Heteroskedastis 100 100 100 0 2X4i Heteroskedastis 98 100 100 7 X Heteroskedastis 67 78 81 44
Sebaliknya, pada data regresi dengan nilai ragam galat yang merupakan fungsi dari peubah penjelas ang tidak berpengaruh ( ar ( i) = f(X4i); β4 = 0),
LASSO menghasilkan model yang tidak memuaskan dengan semakin membesarnya intensitas keheterogenan ragam galat (Xi < 2Xi < Xi) bagi ukuran
sampel kecil (n<30). Ketelitian LASSO menurun dengan semakin besarnya intenstas keheterogenan ragam galat. Hal ini terbukti dengan semakin memburuknya ketepatan LASSO ketika Var ( i) = X . Peubah penjelas dengan
βi≠ tidak 100% terdeteksi benar bahwa peubah penjelas tersebut mempunyai
nilai koefisien regresi tidak sama dengan nol, dan peubah penjelas dengan βi=0,
terdeteksi 44 kali berpengaruh dari 100 kali simulasi data. Hasil simulasi contoh kasus 1 menunjukkan bukti bahwa LASSO kurang selektif dalam menyeleksi peubah penjelas. Contoh kasus 2 dilakukan untuk mengetahui keunggulan LASSO dibandingkan dengan dua metode lain (MKT dan Metode Best Subset).
Contoh kasus 2 menganalisis 100 gugus data (100 ulangan) dengan masing-masing gugus data terdiri atas 50 amatan (n=50). Koefisien regresi yang digunakan adalah = (3, 2, 0, 0, 1.5, 0, 0, 2)T. Dalam contoh kasus ini digunakan banyak koefisien regresi yang tidak berpengaruh agar terlihat selektivitas setiap metode terhadap keberadaan peubah penjelas yang berkoefisien regresi nol. Dengan menggunakan peubah acak Normal bagi delapan peubah penjelas dan ar ( i) = X , hasil secara keseluruhan dapat diamati pada Lampiran 1.
Lampiran 1 menunjukkan bahwa setiap metode mempunyai karakter yang berbeda, model yang dihasilkan pun beragam. Keberagaman ini merupakan indikasi bahwa ketiga metode belum mampu menghadapi model regresi yang heteroskedastis dengan baik. Belum terlihat adanya kestabilan pemilihan model dari 100 gugus data pada simulasi. Terutama LASSO, yang dijadikan perhatian utama, memperlihatkan bahwa model yang terpilih banyak. Oleh karena itu, dapat dikatakan bahwa pemilihan model LASSO sangat terpengaruh oleh keberadaan heteroskedastisitas. Dari 100 gugus data simulasi, ada 29 gugus data yang tidak terpilih model sama sekali atau semua koefisien regresi dari delapan peubah penjelas susut menjadi nol (β̂LASSO= ... = β̂LASSO = 0).
13 Tabel 6 Jumlah kemunculan setiap peubah penjelas pada contoh kasus 2
Peubah penjelas Jumlah kemunculan (kali) pada 100 gugus data
LASSO MKT Best Subset
* X1 62 81 88 * X2 29 11 42 X3 27 10 42 X4 30 9 40 * X5 46 28 56 X6 28 8 47 X7 23 14 41 * X8 46 33 64
* Xi dengan nilai parameter βi≠
Secara ringkas, jumlah kemunculan setiap peubah penjelas pada 100 gugus data simulasi pada contoh kasus 2 dapat diamati pada Tabel 6. Dari ketiga metode, terlihat bahwa pada data regresi yang mengandung banyak koefisien regresi bernilai nol, LASSO masih banyak mendeteteksi peubah-peubah tersebut sebagai peubah yang berpengaruh. Tabel 6 memperlihatkan bahwa peubah penjelas yang tidak berpengaruh masih banyak muncul dalam model, baik model yang dihasilkan oleh metode LASSO, maupun MKT atau Best Subset.
Dengan demikian, contoh kasus 2 memperlihatkan bahwa heteroskedastisitas dalam regresi linier mempengaruhi LASSO. Metode LASSO belum mampu menggambarkan seleksi model dan pendugaan parameter yang ideal dan unggul dalam menghadapi data yang heteroskedastis, terutama ketika ragam galatnya merupakan fungsi dari peubah penjelas yang tidak berpengaruh.
SIMPULAN DAN SARAN
SimpulanMelalui pendekatan simulasi dapat disimpulkan bahwa heteroskedastisitas mempengaruhi LASSO dalam menyeleksi peubah dan menduga parameter ketika ragam galat merupakan fungsi dari peubah yang tidak berpengaruh (βi=0).
LASSO tidak selektif terhadap model yang mengandung banyak peubah penjelas dengan berkoefisien regresi nol (βi=0) karena pada simulasi beberapa peubah
tersebut terseleksi oleh LASSO. Dibandingkan dengan MKT dan Best Subset, LASSO tidak lebih unggul dalam menangani data regresi yang heteroskedastis ketika galatnya berkorelasi kuat dengan peubah penjelas yang tidak berpengaruh.
Saran
Dapat digunakan jenis data lain untuk mengkaji LASSO dalam menyeleksi peubah dan pendugaan parameter, serta dapat dilakukan kajian lebih jauh mengenai LASSO dalam menangani data heteroskedastis yang keheterogenan ragam galatnya bersumber dari sebab lain.
14
DAFTAR PUSTAKA
Chand S, Kamal S. 2011. Variable Selection by LASSO-type Methods, Journal of
Statistics and Operation Research, 7(2): 451-464.
Dewi YS. 2010. OLS, LASSO, dan PLS pada Data Mengandung Multikolinieritas. Jurnal Ilmu Dasar 11(1): 83-91.
Efron B, Hastie T, Johnstone I, Tibshirani R. 2004. Least Angle Regression.
Annals of Statistics, 32(2): 407-499.
Gujarati DN. 2006. Dasar-dasar Ekonometrika Jilid 2. Ed ke-3. Mulyadi JA, Andri Y, penerjemah; Barnadi D, Hardani W, editor. Jakarta (ID): Penerbit Erlangga. Terjemahan dari: Essentials of Econometrics. Ed ke-3. Hastie T, Tibshirani R, Friedman J. 2008. The Elements of Statistical Learning.
Data Mining, Inference, and Prediction. Ed ke-2. New York (US):
Springer.
Izeman AJ. 2008. Modern Multivariate Statistical Techniques: Regression,
Classification, and Manifold Learning. New York (US): Springer.
Jia J, Rohe K, Yu B. 2010. The LASSO under Heteroscedasticity. Department of Statistics and Department of EECS. Barkeley (US): University of California.
Pusporini A. 2012. Penerapan Regresi Gulud dan Least Absolute Shrinkage and
Selection Operator (LASSO) dalam Penyusutan Koefisien Regresi
[skripsi]. Bogor (ID): Institut Pertanian Bogor.
Rawlings JO, Pantula SG, Dickey DA. 1998. Applied Regression Analysis: A
Research Tool. Ed ke-2. New York (US): Springer.
Tibshirani R. 1996. Regression Shrinkage and Selection via the LASSO. Journal
15 Lampiran 1 Model yang terpilih pada simulasi contoh kasus 2
Gugus data ke- Model
LASSO MKT Best Subset
1 146 156 12456 2 124568 158 268 3 - 1 1348 4 - 17 1457 5 18 18 138 6 48 8 13458 7 134578 - 13458 8 - 1 3458 9 - 18 12478 10 124568 - 12568 11 - 15 145 12 13578 1378 1378 13 1358 1358 13568 14 4 1 1248 15 56 15 1256 16 - 14 14678 17 - 1 178 18 - 8 568 19 1234578 138 123478 20 15 1 158 21 18 18 1256 22 13678 178 12567 23 78 178 14678 24 1 1 128 25 - 15 125 26 - 18 1378 27 1 1 147 28 - 1 356 29 14568 1 13568 30 18 1 168 31 235 25 2357 32 12578 18 1578 33 123458 18 1258 34 - 1 136 35 58 8 358 36 1 1 168 37 1578 1578 1578 38 123468 126 12368 39 - - 2578 40 - 145 134567 41 1235678 1567 123567 42 13 134 1348 43 167 17 167 44 14578 158 14578
16
Lampiran 1 Model yang terpilih pada simulasi contoh kasus 2
Gugus data ke- Model
LASSO MKT Best Subset
45 145 1 134578 46 1234578 35 1234578 47 125 5 125 48 12468 1 1268 49 - 1 1268 50 - 1 168 51 12345678 357 23458 52 12345678 1678 13678 53 - - 178 54 12678 17 1267 55 15 15 168 56 123678 278 12678 57 12345678 5 12456 58 - 1 1257 59 25 125 12357 60 1368 13 1368 61 58 18 13578 62 - 168 1268 63 134568 134 13468 64 1235678 568 13568 65 12457 14 1457 66 1234567 17 1467 67 - 158 1458 68 1234567 1 1234567 69 13568 18 12368 70 145 4 145 71 18 1 1238 72 128 128 128 73 1278 278 1278 74 - 12 468 75 1458 18 158 76 1235 15 12356 77 124568 126 12456 78 - 1 3456 79 - 1 367 80 - 1 1247 81 12456 1245 1245 82 13458 15 13458 83 14568 58 1458 84 123568 15 12356 85 - 1356 134567 86 - 1 1578 87 16 145 1234578
17 Lampiran 1 Model yang terpilih pada simulasi contoh kasus 2
Gugus data ke- Model
LASSO MKT Best Subset
88 1348 14 1348 89 14 1 145 90 5 5 3567 91 1358 158 13458 92 - 18 178 93 125 12 1256 94 14 1 147 95 - 12 12367 96 - 1 1248 97 12578 17 12578 98 158 16 1568 99 15678 8 1568 100 13568 138 1368
Lampiran 2 Model yang muncul pada simulasi contoh kasus 2 Model Jumlah terdeteksi (kali) pada 100 gugus data
LASSO MKT Best Subset
* - 29 4 0 ** 1258 0 0 1 1 3 26 0 4 1 1 0 5 1 3 0 8 0 4 0 12 0 3 0 13 1 1 0 14 2 3 0 15 2 7 0 16 1 0 0 17 0 5 0 18 4 11 0 25 1 1 0 35 0 1 0 48 1 0 0 56 1 0 0 58 2 1 0 78 1 0 0 125 2 1 2 126 0 2 0 128 1 1 2 134 0 2 0 136 0 0 1 138 0 2 1 145 2 2 3
18
Lampiran 2 Model yang muncul pada simulasi contoh kasus 2 Model Jumlah terdeteksi (kali) pada 100 gugus data
LASSO MKT Best Subset
146 1 0 0 147 0 0 2 156 0 1 0 158 1 4 2 167 1 0 1 168 0 1 4 178 0 2 3 235 1 0 0 268 0 0 1 278 0 2 0 356 0 0 1 357 0 1 0 358 0 0 1 367 0 0 1 468 0 0 1 568 0 1 1 1235 1 0 0 1238 0 0 1 1245 0 1 1 1247 0 0 1 1248 0 0 2 1256 0 0 3 1257 0 0 1 1267 0 0 1 1268 0 0 3 1278 1 0 1 1348 1 0 3 1356 0 1 0 1358 2 1 0 1368 1 0 2 1378 0 1 2 1457 0 0 2 1458 1 0 2 1467 0 0 1 1567 0 1 0 1568 0 0 2 1578 1 1 3 1678 0 1 0 2357 0 0 1 2578 0 0 1 3456 0 0 1 3458 0 0 1 3567 0 0 1 12356 0 0 2
19 Lampiran 2 Model yang muncul pada simulasi contoh kasus 2
Model Jumlah terdeteksi (kali) pada 100 gugus data
LASSO MKT Best Subset
12357 0 0 1 12367 0 0 1 12368 0 0 2 12456 1 0 3 12457 1 0 0 12468 1 0 0 12478 0 0 1 12567 0 0 1 12568 0 0 1 12578 2 0 1 12678 1 0 1 13458 1 0 4 13468 0 0 1 13568 2 0 3 13578 1 0 1 13678 1 0 1 14568 2 0 0 14578 1 0 1 14678 0 0 2 15678 1 0 0 23458 0 0 1 123458 1 0 0 123468 1 0 0 123568 1 0 0 124568 3 0 0 123478 0 0 1 123567 0 0 1 123678 1 0 0 134567 0 0 2 134568 1 0 0 134578 1 0 1 1234567 2 0 1 1234578 2 0 2 1235678 2 0 0 12345678 3 0 0 Total 100 100 100
20
RIWAYAT HIDUP
Penulis dilahirkan di Bogor, 27 Mei 1991 dari pasangan Yayan Milyani dan Noni Muryani. Penulis merupakan anak kedua dari dua bersaudara.
Tahun 2003 penulis terdaftar sebagai siswi di SMPN 1 Bogor. Lalu, masa-masa SMA penulis habiskan di sekolah kejuruan analisis kimia SMK-SMAK Bogor dari 2006 sampai 2010. Pada 2010, penulis terseleksi melalui seleksi penerimaan mahasiswa baru UTMI pada Mayor Statistika.
Selama mengikuti perkuliahan penulis juga aktif dalam kegiatan rohis kelas dan selain itu sempat menjadi anggota dari komunitas debat IPB, IPB Debating Club (IDC). Selain itu, penulis juga aktif di himpunan profesi mahasiswa statistika, Gamma Sigma Beta (GSB) selama 2 periode. Selain kegiatan keorganisasian, penulis juga aktif dalam kepanitiaan acara, antara lain Statistika Ria 2012, G-FORCE 48 (2012), Porstat (Pekan Olahraga Statistika) 2011, dan MPKMB angkatan 48 (2011).
Pada transisi dari semester enam menuju semester tujuh tepatnya Juli 2013 sampai Agustus 2013 penulis melaksanakan praktik lapang di Balai Tanaman Rempah dan Obat (BALITTRO), Bogor, Jawa Barat, dan bergabung bersama peneliti di Kelompok Peneliti Hama dan Penyakit Tanaman.