PROSIDING SEMINAR NASIONAL MATEMATIKA DAN PENDIDIKAN MATEMATIKA

ISBN : 978-979-16353-3-2

“P

P

e

e

n

n

e

e

l

l

i

i

t

t

i

i

a

a

n

n

d

d

a

a

n

n

P

P

e

e

n

n

d

d

i

i

d

d

i

i

k

k

a

a

n

n

M

M

a

a

t

t

e

e

m

m

a

a

t

t

i

i

k

k

a

a

s

s

e

e

r

r

t

t

a

a

k

k

o

o

n

n

t

t

r

r

i

i

b

b

u

u

s

s

i

i

n

n

y

y

a

a

d

d

a

a

l

l

a

a

m

m

U

U

p

p

a

a

y

y

a

a

P

P

e

e

n

n

c

c

a

a

p

p

a

a

i

i

a

a

n

n

W

W

C

C

U

U

(

(

W

W

o

o

r

r

l

l

d

d

C

C

l

l

a

a

s

s

s

s

U

U

n

n

i

i

v

v

e

e

r

r

s

s

i

i

t

t

y

y

)

)

”

”

Yogyakarta, 5 Desember 2009

Jurusan Pendidikan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta

2009

PROSIDING

SEMINAR NASIONAL

MATEMATIKA DAN PENDIDIKAN

MATEMATIKA

Penyelenggara :

Jurusan Pendidikan Matematika FMIPA UNY

Kerjasama dengan

Himpunan Matematika Indonesia (Indo-MS)

wilayah Jateng dan DIY

PROSIDING SEMINAR NASIONAL

MATEMATIKA DAN PENDIDIKAN MATEMATIKA

5 Desember 2009 FMIPA Universitas Negeri Yogyakarta

Artikel‐artikel dalam prosiding ini telah dipresentasikan pada

Seminar Nasional Matematika dan Pendidikan Matematika

pada tanggal 5 Desember 2009

di Jurusan Pendidikan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta

Tim Penyunting Artikel Seminar :

1. Prof. Dr. Rusgianto

2. Dr. Hartono

3. Dr. Jailani

4. Sahid, M.Sc

Jurusan Pendidikan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta

1

DAFTAR MAKALAH

kode Nama pemakalah Judul Hal

A.1 Imam Fahcruddin _{Spectrum Pada Graf Star ( ) Dan Graf Bipartisi Komplit ( )} Dengan

1 A.2 M.V.Any Herawati,S.Si.,M.Si. TEOREMA GOURSAT Konstruksi subgrup dari grup darab langsung 12 A.3 Lucia Ratnasari/ Y.D. Sumanto KOMPLEMEN GRAF FUZZY 22 An.1 Muslim Ansori _{RUANG LINEAR BERNORMA}

(

(

)

)

2

,

[ , ]

ESS

C

H L

a b

31

An.2 Drajad Maknawi /Drs. Mulich, M.Si

Definisi Tipe Riemann untuk Integral Lebesgue 38 An.3 Rudianto Artiono Discounted Feynman Kac Untuk Mencari PDP Pada Penentuan Harga Opsi

Saham Karyawan Setelah Vesting Period 49 An.4 Sujito, S.T., M.T Implementasi Lagrange Equation Pada Optimasi Incremental Fuel Cost

Pembangkit Energi Guna Penjadwalan Pembangkit Berbasis Metode Dynamic Programming

57 An.5 Hairur Rahman Globally Small Riemann Sums (Gsrs) Integral Henstock-Pettis Pada Ruang

Euclide Rn

72 P.1 Drs. M. Nur Yadil, M.Si Penerapan Model Pembelajaran Van Hiele Untuk Meningkatkan

Pemahaman Siswa SMP Karunadipa Palu Terhadap Konsep Bangun- Bangun Segiempat

81 P.2 Drs. Syaiful, M.Pd Model Pengajaran Untuk Meningkatkan Kemampuan Pemecahan Masalah

Matematika Pada Guru SMP 92

P.3 Dra. Dwi Astuti, M.Si/ Bambang

Hudiono Perilaku Metakognisi Anak Dalam Matematika: Kajian Berdasarkan Etnis _{Dan Gender Pada Siswa SMP Di Kalimantan Barat} 107 P.4 Budiyono Kompetensi Guru Sekolah Dasar

Dalam Memahami Matematika SD 119 P.5 Budiyono /Wanti Guspriati Jenis-Jenis Kesalahan Dalam Menyelesaikan Soal Persamaan Differensial

Biasa (PDB) Studi Kasus Pada Mahasiswa Semester V Program Studi Pendidikan Matematika

Universitas Muhammadiyah Purworejo

131

P.6 Drs. Abusyafik, M. Pd./ Siti Khanifah, S.

Pd PEMBELAJARAN FPB DAN KPK DENGAN DAN TANPA ALAT PERAGA _{PADA SISWA KELAS V SD NEGERI BLENGORKULON KECAMATAN} AMBAL KABUPATEN KEBUMEN TAHUN PELAJARAN 2008/2009

141

P.7 Dra. Sulis Janu Hartati, M.T Karakteristik Proses Berpikir Siswa Kelas III Sekolah Dasar Pada Saat

Melakukan Aktivitas Membagi 153 P.8 Drs. Hamdani, M.Pd. Pengembangan Pembelajaran Dengan Mathematical Discourse Dalam

Meningkatkan Kemampuan Komunikasi Matematik Pada Siswa Sekolah Menengah Pertama

163

P.9 Dra. Tina Yunarti, M.Si Fungsi Dan Pentingnya Pertanyaan

Dalam Pembelajaran 174

P.10 Supratman Membandingkan Hasil Belajar Matematika Siswa Yang Pembelajarannya Menggunakan Model Kooperatif Tipe Jigsaw Dengan Tipe Stad Pada Materi Lingkaran

185 P.11 Akhmad Jazuli Berfikir Kreatif Dalam Kemampuan Komunikasi Matematika 209 P.12 Agustin Ernawati, S.Pd./

2

P.13 Alfath Famela Rokhim/ Sitti Maesuri

Patahuddin Penggunaan Permainan Online Dalam Belajar Matematika 234 P.14 Darmadi, S.Si, M.Pd.

Spektrum Hasil Belajar Analisis Real Mahasiswa Program Studi Pendidikan Matematika IKIP PGRI Madiun

Tahun Akademik 2008/2009

247 P.15 Endang Rahayu, S.Si, M.Pd. Pembelajaran Konstruktivisme

Ditinjau Dari Gaya Belajar Siswa 252 P.16 Armiati Komunikasi Matematis dan Kecerdasan Emosional 270 P.17 Sitti Maesuri Patahuddin/ Siti Rokhmah/

Mohamad Nur Pengembangan LKS berbasis ICT pada Pembelajaran Matematika SMP RSBI 281 P.18 Drs. Mustangin, M.Pd / Agustin Debora

MS Penerapan Global Learning Dan Mind Mapping Dalam Pembelajaran Matematika Sebagai Jaringan Konsep 295 P.19 Drs.Dwikoranto,M.Pd MENINGKATKAN KOMPETENSI

GURU MATEMATIKA DAN IPA SMP MELALUI KEGIATAN LESSON STUDY 310 P.20 Siti Rokhmah/ Siti Maesuri Patahuddin /

Mohamad Nur LKS Matematika Berbasis ICT Untuk Memfasilitasi Siswa Berpikir Kritis 325 P.21 Agustin Debora MS, Drs. Mustangin,

MPd Dra. Santi Irawati, M.Si,Ph.D Mengoptimalkan Memory Jangka Panjang Siswa SMPN1 Pajarakan dalam Memaknai Konsep Garis Singgung Persekutuan Dua Lingkaran Dengan Penyandian

336 P.22 Kartini, S.Pd. M.Si Peranan Representasi dalam Pembelajaran Matematika 361 P.23 Ariyadi Wijaya, M.Sc Hypothetical Learning Trajectory

dan Peningkatan Pemahaman Konsep Pengukuran Panjang 373 P.24 Abdussakir, M.Pd/ Nur Laili Achadiyah,

S.Pd PEMBELAJARAN KELILING DAN LUAS LINGKARAN DENGAN STRATEGI _{REACT PADA SISWA KELAS VIII SMP NEGERI 6 KOTA MOJOKERTO} 388 P.25 Djamilah Bondan Widjajanti, M.Si KEMAMPUAN PEMECAHAN MASALAH MATEMATIS MAHASISWA CALON

GURU MATEMATIKA: APA dan BAGAIMANA MENGEMBANGKANNYA 402 P.26 Sugiman, M.Si PANDANGAN MATEMATIKA SEBAGAI AKTIVITAS INSANI BESERTA

DAMPAK PEMBELAJARANNYA 414

P.28 Kadir, S.Pd., M.Si. Peningkatan Kemampuan Pemecahan Masalah Matematik Siswa SMP

melalui Penerapan Pembelajaran Kontekstual Pesisir 428 P.30 Risnanosanti PENGGUNAAN PEMBELAJARAN INKUIRI DALAM MENGEMBANGKAN

KEMAMPUAN BERPIKIR KREATIF SISWA SMA DI KOTA BENGKULU 441 P.31 Abdul Qohar PEMAHAMAN MATEMATIS SISWA SEKOLAH MENENGAH PERTAMA

PADA PEMBELAJARAN DENGAN MODEL RECIPROCAL TEACHING

453 P.32 Ali Mahmudi, M.Pd Menulis sebagai Strategi Belajar Matematika 466 P.33 Dra. Sri Hastuti Noer, M.Pd. Peningkatan Kemampuan Berpikir Kritis Matematis Siswa SMP Melalui

Pembelajaran Berbasis Masalah 473 P.34 Dra. Nila Kesumawati, M. Si Peningkatan Kemampuan Pemecahan Masalah Matematis Siswa SMP

Melalui Pendekatan Pendidikan Matematika Realistik 484 P.35 Eri Satria Model Pembelajaran Computer Support Collaborative Learning (CSCL) 494 S.1 Pika Silvianti,

Khairil A. Notodiputro, I Made Sumertajaya

Pendekatan Metode Bayes Untuk Pendugaan Pengaruh Interaksi Pada Model Ammi

(Bayesian Approach for Estimating Interaction Effect of AMMI Model)

503 S.2 I Gede Nyoman Mindra Jaya Analisis Interaksi Genotipe Lingkungan Menggunakan Partial Least Square

Path Modeling 514

S.3 H. Bernik Maskun *) _{Pengujian Hipotesis Rata-Rata Berurut} Menggunakan Statistik Chi-Kuadrat Rank (Pendekatan Non Parametrik)

530 S.4 Zulhanif , _{Yadi Suprijadi Perbandingan Mekanisme Data Hilang Pada Model Normal 544}

3

S.5 Mohammad Masjkur

Metode Kemungkinan Maksimum Em Pendugaan Parameter Model Nonlinear Jerapan Fosfor 551 S.6 Enny Supartini Menentukan Statistik Pengujian Untuk Eksperimen Faktorial dengan Dua Kali

Pembatasan Pengacakan 560

S.7 Neneng Sunengsih Seleksi Variabel Dalam Analisis Regresi Multivariat Multipel 567 S.8 Liana Kusuma Ningrum / Winita

Sulandari, M.Si Penerapan Model Arfima (Autoregressive Fractionally Integrated Moving Average) Dalam Peramalan Suku Bunga Sertifikat Bank Indonesia (SBI)

581 S.9 Retno Hestiningtyas / Winita Sulandari,

M.Si Pemodelan Tarch Pada Nilai Tukar Kurs Euro Terhadap Rupiah 591 S.10 Epha Diana Supandi, S.Si., M.Sc./ Dra.

Khurul Wardati, M.Si./ Iwan Kuswidi, S.Pd.I., M.Sc.

Aplikasi Multidimensional Scalling

(Studi Kasus : Analisis Segmentasi dan Peta Posisi UIN Sunan Kalijaga terhadap Perguruan Tinggi di Yogyakarta)

599 S.11 Anindya Apriliyanti Pravitasari

Penentuan Banyak Kelompok dalam Fuzzy CMeans Cluster Berdasarkan Proporsi Eigen Value Dari Matriks Similarity dan Indeks XB (Xie dan Beni) 623 S.12 Wahyu Wibowo METODE KUADRAT TERKECIL UNTUK ESTIMASI KURVA REGRESI

SEMIPARAMETRIK SPLINE 633

S.13 Achmad Zanbar Soleh / Peris Siregar/

Resa Septiani Pontoh SELEKSI VARIABEL KUALITATIF MELALUI PROPORTIONAL REDUCTION IN UNCERTAINTY (PRU) 646 S.14 Lisnur Wachidah

Uji Kecocokan Chi-Kuadrat Untuk Distribusi Poisson Pada Data Asuransi 653 S.15 Danang Teguh Qoyyimi Model Suku Bunga Multinomial 666 S.16 Hery Tri Sutanto MULTI KOLLINIERITAS DALAM REGRESI MULTIPLE LOGISTIK 676 S.17 Hery Tri Sutanto Cluster Analysis 681 S.18 Anna Chadidjah/ Indra Elfiyan Model Regresi Data Panel untuk Menaksir Realisasi Total Investasi Asing dan

Dalam Negeri .(Studi Kasus di Provinsi Jawa Barat) 690 S.19 Siti Sunendiari Model Regresi Linier Dalam Melihat

Keberhasilan Belajar Siswa SMU 731 S.20 Anik Djuraidah Indeks Kerentanan Sosial Ekonomi

Untuk Bencana Alam Di Wilayah Indonesia 746 S.21 Anik Djuraidah Evaluasi Status Ketertinggalan Daerah Dengan Analisis Diskriminan 756 S.22 Isnani, M.Si Penggunaan Bootstrap Untuk Mendeteksi Keakuratanan Kriging 772 S.23 Dr.rer.nat. Dedi Rosadi, M.Sc Pemanfaatan Software Open Source R dalam pemodelan ARIMA 786 S.24 Indahwati / Dian Kusumaningrum /

Wiwid Widiyani APLIKASI REGRESI DUA LEVEL TERHADAP NILAI AKHIR METODE STATISTIKA 796 S.25 Indahwati / Yenni Angraeni /Tri Wuri

Sastuti PEMODELAN REGRESI TIGA LEVEL PADA DATA PENGAMATAN BERULANG 816 S.26 Yusep Suparman Perlukah Cross Validation dilakukan?

Perbandingan antara Mean Square Prediction Error dan Mean Square Error sebagai Penaksir Harapan Kuadrat Kekeliruan Model

833 S.27 Ridha Ferdhiana, M.Sc

Uji Alternatif Data Terurut

4

S.28 Bertho Tantular Pelanggaran Asumsi Normalitas Model Multilevel

Pada Galat Level yang Lebih Tinggi 849 S.30 Dien Sukardinah SENSITIFITAS INDIKATOR KESELURUHAN MULTIKOLINEARITAS

DALAM MODEL REGRESI LINEAR MULTIPEL 862 S.31 Lienda Noviyanti SUATU MODEL HARGA OBLIGASI 871 S.32 Kismiantini / Dhoriva Urwatul Wutsqa DAMPAK PENURUNAN HARGA BBM JENIS PREMIUM TERHADAP

ANGKA INFLASI DI KOTA YOGYAKARTA (Studi Aplikasi Model Intervensi dengan Step Function)

879 S.33 Iqbal Kharisudin Koefisien Determinasi Regresi Fuzzy Simetris Untuk Pemilihan Model Terbaik 895 S.35 Heri Retnawati Pengaruh Kemampuan Awal dan Kemampuan Berfikir Logis/penalaran

terhadap Kemampuan Matematika (Studi Komparasi Sensitivitas Program Lisrel 8.51 dan Amos 6.0)

910 S.36 Dhoriva Urwatul Wutsqa /Suhartono PERAMALAN DERET WAKTU MULTIVARIAT SEASONAL PADA DATA

PARIWISATA DENGAN MODEL VAR-GSTAR 933 T.1 Muhammad Wakhid Musthofa, M.Si Desain Linear Quadratic Regulator pada Sistem Inverted Pendulum 950 T.2 Gumgum Darmawan, Okira Mapanta ,

Trifandi Lasalewo Membangun Software Aplikasi pada Antrian Jaringan Jackson untuk menentukan Performansi Optimal 960 T.3 Totok Yulianto Simulasi Pengendalian Struktur berbasis pada Material Cerdas 979 T.4 John Maspupu

ESTIMASI EKSPONEN SPEKTRAL DAN KEMUNCULAN DERAU KEDIP

(FLICKER NOISE) PADA SINYAL ULF GEOMAGNET 993 T.5 John Maspupu

PENENTUAN HUBUNGAN EKSPONEN SPEKTRAL DAN DIMENSI

FRAKTAL SINYAL ULF GEOMAGNET 1000 T.6 Gatot Riwi Setyanto, Drs., M.Si. RISIKO PENDANAAN PENSIUN ACCRUED BENEFIT COST METHOD

DENGAN MEMPERTIMBANGKAN PENGARUH KURS VALUTA ASING 1010 T.7 Bachtiar Anwar Analyzing Coronal Mass Ejection of July 10, 2005 and Its Effect on the Earth’s

Magnetosphere 1021

T.8 Sangadji FORMULA HERON:

TINJAUAN DI GEOMETRI EUKLID DAN GEOMETRI SFERIK

1033 T.9 Dwi Lestari / Atmini Dhoruri, MS _{Model Epidemi Berdasarkan Umur dan Kriteria Threshold} 1040 T.10 Renny, M.Si MODEL MATEMATIKA

DALAM KASUS EPIDEMIK KOLERA DENGAN POPULASI KONSTAN 1051 T.11 Rubono Setiawan Analisa Kestabilan Ekuilibrium

Model Matematika Berbentuk Sistim Persamaan Diferensial Tundaan dengan Waktu Tundaan Diskrit

1064 T.12 I Made Sulandra Algoritma Groebner Walk Lambat? 1078 T.13 Dwi Ertiningsih, Widodo Optimalisasi dan Pemodelan Inventory dengan Dua Gudang Penyimpanan

untuk Barang yang Mengalami Penyusutan dengan Backlog Shortage dan Waktu Tunggu (Lead Time) Fuzzy

1093 T.14 M. Navi’ Jauhari Ulinnuha Perancangan Software Batik Berbasis Geometri Fraktal 1109 T.15 Habirun ANALISIS MODEL VARIASI HARIAN KOMPONEN GEOMAGNET

BERDASARKAN POSISI MATAHARI 1116 T.16 Dr. Hanna Arini Parhusip, MSc.nat /

Sulistyono _PEMETAAN α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

DAN HASIL PEMETAANNYA

1127

T.17 Dr. Hanna Arini Parhusip, MSc.nat /

Siska Ayunani METODEFINALTIUNTUKMENENTUKANBERATSAPIOPTIMAL 1139 T.18 Lusia Krismiyati Budiasih, S.Si., M.Si. Metode Levenberg-Marquardt

5

T.19 Dra. Asmara Iriani Tarigan, M.Si Optimasi Jadwal Ujian di Perguruan Tinggi dengan Metode Branch and Bound 1162 T.20 Fitriana Yuli Saptaningtyas Metode Volume Hingga Untuk Mengetahui Pengaruh Sudut Pertemuan

Saluran Terhadap Profil Perubahan Sedimen Pasir Pada Pertemuan Sungai 1174 T.21 Nikenasih Binatari Model SIR untuk Ketahanan Behavioural 1187 T.22 Kuswari Hernawati Optimalisasi SEO (Search Engine Optimizer) sebagai upaya meningkatkan

unsur Visibility dalam Webometric 1198 T.23 Isnaini Rosyida PENENTUAN BILANGAN KROMATIK FUZZY PADA GRAF FUZZY GF(V,EF)

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1127 

T-16

PEMETAAN 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

 DAN HASIL PEMETAANNYA 

Oleh : 

H. A. Parhusip

1

 dan Sulistyono

2

 

Program Studi Matematika Industri dan Statistika  

Fakultas Sains dan Matematika (FSM) 

Universitas Kristen Satya Wacana (UKSW) (www.uksw.edu) 

1

pressure1733@hotmail.com

 

2

mahasiswa S1, matematika –FSM‐UKSW 

 

Abstrak : Pemetaan 

w

=

( z

1

/

)

α

 , dengan  α

∈ Z (himpunan bulat negatif) dan 

−

α

∈

(

0

,

1

)

  serta  hasil  pemetaannya  ditunjukkan  pada  makalah  ini.  Dapat  ditunjukkan 

pemetaan  ini  konformal.  Hasil  pemetaan  diperoleh  dengan  melakukan  transformasi 

geometri.  

 

Kata kunci : pemetaan konformal, fungsi analitik, persegi 

 

1.

Pendahuluan 

Pemetaan  konformal  adalah  pemetaan  yang  mempertahankan  besaran  dan 

arah sudut diantara sebarang dua kurva yang berpotongan di suatu titik tertentu. Pada 

makalah  terdahulu  (Parhusip  dan  Sulisyono,  2009)  ditunjukkan  hasil  pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

untuk 

α

=

1

dan 

α

=

2

. Hasil pemetaan ditunjukkan dengan terlebih dahulu 

ditunjukkan  untuk  pemetaan  garis  vertikal  dan  garis  horizontal  secara  terpisah. 

Selanjutnya  dilakukan  pemetaan  untuk  1  bidang  persegi.  Untuk  persegi  lebih  dari  1 

dilakukan  dengan  menggunakan  transformasi  geometri  seperti  pencerminan.    Pada 

makalah ini akan ditunjukkan pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

untuk berbagai nilai α .  

Pada  Bab  II  ditunjukkan  pemetaan  konformal  w=1/z    dan  hasil  pemetaannya 

yang merupakan hasil penelitian sebelum ini (Parhusip dan Sulisyono, 2009) . Pada Bab 

III  dijelaskan  cara  melakukan  penelitian  ini.  Hasil  dan  Pembahasan  ditunjukkan  pada 

Bab IV. Selanjutnya kesimpulan ditunjukkan pada Bab terakhir.  

 

2.

Pemetaan konformal  w=1/z  dan hasil pemetaannya  

Pemetaan garis vertikal dan garis horizontal 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1128 

 

Telah diketahui bahwa  pemetaan garis vertikal dan haris horisontal oleh w=1/z 

merupakan  persamaan  lingkaran  (Parhusip  dan  Sulisyono,  2009).  Beberapa  hasil 

pemetaan  untuk  garis  vertikal  dan  horizontal  ditunjukkan  pada  Gambar  1‐3.  

Sedangkan untuk y = a dan garis x = b  (a,b 

≠

0

 ) dengan fungsi pemetaan w = 1/z 

untuk berbagai nilai a dan b yang berbeda, yaitu a,b > 0, a > 0 dan b <0, a < 0 dan b 

> 0 dan a,b < 0 berturut‐turut ditunjukkan pada Gambar 4. 

 

 

 

Gambar 1. Persamaan garis x=c, x=d 

dipetakkan dengan w=1/z  

menjadi lingkaran , c,d > 0  

 

Gambar 2. Persamaan garis x=c, x=d 

dipetakkan dengan w=1/z  

menjadi lingkaran ,c,d < 0.  

 

Gambar 3. Persamaan garis x=c dan  x=d dan bayangannya untuk c>0 dan d<0 

 

Gambar 4. Persamaan garis y=a, x=b dipetakkan dengan w=1/z menjadi lingkaran 

dengan a,b > 0, a > 0 dan b <0, a < 0 dan b > 0 dan a,b < 0. 

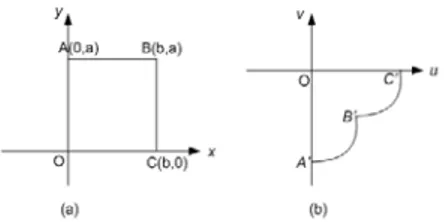
Bayangan persegí  untuk 1 persegi  

 

Gambar  4a  menunjukkan  bahwa  a,b  >  0  dan  bayangan  digambarkan  dalam 

lingkaran penuh. Bayangan pada Gambar 4a ini dapat dibatasi (tidak sebagai lingkaran 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1129 

penuh)  jika  kita  juga  membatasi  persegí  yang  terbentuk  pada  Gambar  4a,  yaitu 

Gambar 4a diubah sedemikian sehingga terbentuk Gambar 5. 

 

Gambar 5.  Persegi ABCO dan bayangannya dengan pemetaan w=1/z. 

Bayangan  pada  Gambar  5b  diperoleh  pertama  kali  mencari  batas  dari  bayangannya 

yaitu titik  '

A ,  '

B dan 

C

'

dan kemudian menghubungkan titik‐titik tersebut. Untuk titik 

asal  tetap  dipetakkan  ke  titik  asal,  karena  titik  asal  O(0,0)  adalah  titik  singular  atau 

kesingularan dari w=1/z. Untuk titik A(0,a) pada bidang z akan dipetakkan oleh fungsi 

w=1/z ke titik  

'

(

0

,

1

)

a

A

−

pada bidang w. Hal ini karena titik A(0,a) pada bidang z dapat 

ditulis  sebagai  z  =  0+ia,  sehingga 

a

ia

z

w

1

0

1

1

−

=

+

=

=

  dan  karena  w  =  u  +  iv  maka 

diperoleh titik 

'

(

0

,

1

)

a

A

−

. 

 

Untuk titik B(b,a) pada bidang z akan dipetakkan oleh fungsi pemetaan w=1/z 

ke titik 

⎟

⎠

⎞

⎜

⎝

⎛

+

−

+

2 2 2 2

,

'

b

a

a

b

a

b

B

 pada bidang w. Titik  '

B diperoleh dengan menuliskan titik 

B sebagai z = b + ia , sehingga diperoleh 

_{2 2}

b

a

ia

b

w

+

−

=

 sehingga diperoleh koordinat  '

B  

tersebut.  Untuk  selanjutnya  titik  C(b,0)  pada  bidang  z  dipetakkan  ke  titik 

⎟

⎠

⎞

⎜

⎝

⎛

1

_,

₀

'

b

C

 

pada bidang w oleh fungsi pemetaan w=1/z Kemudian titik‐titik tersebut dihubungkan 

untuk  memperoleh  Gambar  5b.    Untuk  selanjutnya  kita  dapat  menyusun  hasil 

pemetaan  untuk  tiap  persegi  pada  kuadran  yang  lain  dengan  cara  melakukan 

pencerminan.  

 

Matriks  transformasi  untuk  pencerminan  terhadap  sumbu  x  dan  sumbu  u 

adalah  

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1130 

⎥

⎦

⎤

⎢

⎣

⎡

−

=

1

0

0

1

R

X

 

 

 

 

 

(3) 

sehingga  jika  koordinat  suatu  titik  A  dinyatakan  dalam  notasi  vektor  posisi 

_⎥

⎦

⎤

⎢

⎣

⎡

A A

y

x

 

dengan  koordinat  bayangannya  adalah   

A sebagai  vektor  posisi 

'

_⎥

⎦

⎤

⎢

⎣

⎡

'

' A A

y

x

  maka  dapat 

ditulis 

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

A A R A A

y

x

X

y

x

' '

. 

 

 

 

 

  

Kita  dapat  melakukan  transformasi  pencerminan  untuk  titik  B  dan  C  untuk 

mendapatkan  koordinat  pencerminannya  berturut‐turut '

B   dan 

C

'

.  Kita  dapat 

melakukan pencerminan dengan cara serupa sehingga dapat diperoleh berbagai hasil 

pemetaan  yang  ditunjukkan  pada  Gambar  6.  Gambar  6  diperoleh  dengan  melakukan 

pencerminan  Gambar  5a  dan  Gambar  5b  terhadap  Sumbu  y  dan  sumbu  v  secara 

berturut‐turut 

menggunakan 

matriks 

transformasi 

_⎥

⎦

⎤

⎢

⎣

⎡

−

=

1

0

0

1

R

X

 

dan 

⎥

⎦

⎤

⎢

⎣

⎡

−

−

=

1

0

0

1

R

X

.  

 

Gambar 6. Pemetaan 1 persegi dan hasil pemetaannya melalui pencerminan. 

 

2.3 Bayangan persegí  untuk n x n persegi 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1131 

 

Dengan  menggabungkan  hasil  gambar‐gambar  yang  diperoleh  pada  subbab 

sebelum  ini  beserta  bayangannya,  diperoleh  beberapa  hasil  pemetaan  sebagaimana 

ditunjukkan  pada  Gambar  7.  Untuk  persegi  dengan  jumlah  yang  lebih  banyak, 

bayangannya dapat diperoleh dengan langkah‐langkah yang sama.   

 

 

Gambar  7a.  Ilustrasi  perseguí  4  x  4  

yang  dipetakkan  (kiri)  dan  hasil 

pemetaannya (kanan) oleh w=1/z.  

 

Gambar 7b. Ilustrasi perseguí 14 x 14 

yang  dipetakkan  (kiri)  dan  hasil 

pemetaannya (kanan) oleh w=1/z.  

 

 

Modifikasi pemetaan w=1/z dan hasil pemetaannya 

 

Modifikasi  yang  ditunjukkan  pada  makalah  ini  adalah  menyusun  pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dan 

α

∈

N

 (himpunan bilangan asli). Dapat ditunjukkan bahwa pemetaan ini 

merupakan  pemetaan  konformal  dengan  menyatakan  w  dalam  koordinat  polar  dan 

memenuhi persamaan Cauchy‐Riemann. Untuk persegi yang dibentuk dari persegi 14 

x14 yang dipetakkan oleh 

2

1

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

ditunjukkan pada Gambar 10.  

 

Gambar 10. Pemetaan persegi 14 x 14 (kiri) oleh 

2 1

1

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

dan hasil pemetaannya 

(kanan). 

3. METODE PENELITIAN  

Dalam tahap ini dibagi dalam beberapa kasus, yaitu: 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1132 

3.1 Menunjukkan bahwa pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dengan 

α

∈ Z

−

 (himpunan bulat negatif) 

adalah pemetaan konformal 

3.2  Mengilustrasikan  hasil  pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

, 

α

=

−

β

  dan 

β

=

2

  untuk  bidang 

persegi yang dipetakkan. 

3.3  Menunjukkan  bahwa  pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dengan 

α

∈

(

0

,

1

)

  adalah  pemetaan 

konformal. 

3.4  Mengilustrasikan  hasil  pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

,

α

=

0

.

5

  untuk  bidang  persegi  yang 

dipetakkan. 

 

4. HASIL & PEMBAHASAN 

4.1 Pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dengan 

α

∈ Z

−

 (himpunan bulat negatif)  

Untuk 

α

∈ Z

−

maka  dapat  dituliskan  sebagai 

α

=

−

β

  dengan 

β

∈

N

  (himpunan 

bilangan asli) sehingga  

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

= 

β β

z

z

⎟

⎠

=

⎞

⎜

⎝

⎛

1

−

. Sebutlah 

w

=

z

β

=

w

1

dengan 

w

1

=

u

+

iv

.  

 

 

(4.1) 

Teorema 4.1. Pemetaan 

β β

z

z

⎟

⎠

=

⎞

⎜

⎝

⎛

1

−

dengan 

β

∈

N

merupakan pemetaan konformal. 

Bukti. Perlu ditunjukkan bahwa 

w

=

z

β

=

w

1

 merupakan pemetaan analitik yang dapat 

ditunjukkan 2 cara yaitu dengan Koefisien Binomial (cara I) dan koordinat kutub (cara 

II). Pada bagian ini ditunjukkan kedua cara. 

Cara 1.  

Karena  z  =  x  +  iy  maka 

w

1

=

z

β

=

(

x

+

iy

)

β

.  Dengan  menggunakan  koefisien  Binomial 

diperoleh  

β

z

w

₁

=

=

(

x

+

iy

)

β

=

j j j j

iy

x

C

(

)

0 − =

∑

β β β

 

=

C

₀β

x

β

+

iC

₁β

x

β−1

y

−

C

₂β

x

β−2

y

2

−

iC

₃β

x

β−3

y

3

+

C

₄β

x

β−4

y

4

+

iC

₅β

x

β−5

y

5

+

...

 . 

(4.a) 

Dengan  menuliskan  bagian  riil  dan  bagian  khayal  dari  persamaan  (4.a)  berturut‐turut 

diperoleh 

j j j k j j

_C

_x

_y

y

x

C

y

x

C

y

x

C

x

u

2 2 2 0 6 6 6 4 4 4 2 2 2

...

(

1

)

− = − − −

₊

₋

₊

₌

∑

₋

−

=

β β β β β β β β β

, 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1133 

1 2 ) 1 2 ( 1 2 0 5 5 5 5 5 5 3 3 3 1

_...

₍

₁

₎

− + + + = − − − −

₋

₊

₊

₊

₌

∑

₋

=

j j j k j j

_C

_x

_y

y

x

C

y

x

C

y

x

C

y

x

u

β

β β β β β β β β β

       

 

 

Sehingga 

j j j k j j

_j

_C

_x

_y

x

u

2 1 2 2 0

)

2

(

)

1

(

− − =

−

−

=

∂

∂

_∑

_β

β β

   

 

_(5.a) 

1 2 2 2 0

2

)

1

(

− − =

∑

−

=

∂

∂

j j j k j j

_jC

_x

_y

y

u

β β

 

 

 

 (5.b)   

 

1 2 ) 1 ( 2 1 2 0

)

1

2

(

)

1

(

₊ − + + =

−

−

−

=

∂

∂

∑

j j j k j j

_j

_C

_x

_y

x

v

_β

_{β β}

,   

 

(5.c) 

 

j j j k j j

_j

_C

_x

_y

y

v

2( 1) 2 1 2 0

)

1

2

(

)

1

(

− + + =

+

−

=

∂

∂

_∑

β β

 

 

 

 (5.d) 

dengan  

=

_⎢⎣

⎢

_⎥⎦

⎥

2

β

k

. Dari  

persamaan  (5.a)‐(5.b)  belum  terlihat  bahwa 

persamaan 

tersebut 

memenuhi 

persamaan 

Cauchy‐Riemann 

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

−

=

∂

∂

∂

∂

=

∂

∂

x

v

y

u

y

v

x

u

dan

.  

 Oleh  karena  itu  masing‐masing  turuna  parsial 

pada persamaan (5.a)‐(5.d) dijabarkan  diperoleh  

(

2

)

(

4

)

5 4

...,

4 2 3 2 1 0

−

−

+

−

+

=

∂

∂

_C

_x

−

_C

_x

−

_y

_C

_x

−

_y

x

u

_β

β β

_β

β β

_β

β β

   

(6.a) 

...,

6

4

2

0

6 5 6 3 4 4 2 2

+

+

+

−

=

∂

∂

_C

_x

−

_y

_C

_x

−

_y

_C

_x

−

_y

y

u

β β β β β β

 

 

(6.b) 

...,

)

5

(

)

3

(

)

1

(

6 5 5 3 4 3 2 1

−

−

+

−

+

−

=

∂

∂

_C

_x

−

_y

_C

_x

−

_y

_C

_x

−

_y

x

v

_β

β β

_β

β β

_β

β β

   

(6.c) 

...,

5

3

5 4 5 2 3 3 1 1

−

+

+

=

∂

∂

_C

_x

−

_C

_x

−

_y

_C

_x

−

_y

y

v

β β β β β β

 

 

(6.d) 

Dengan  menggunakan  identitas  0!=1,  maka 

C

0a

=

C

aa

=

1

, 

C

1a

=

a

dan 

C

ba

=

C

aa−b

. 

Selain itu  

 

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

−

−

−

−

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

=

)!

(

!

)!

))(

1

(

)...(

2

)(

1

(

)!

(

!

!

b

a

b

b

a

b

a

a

a

a

b

b

a

b

a

b

bC

a b

 

 

 

 

 

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

−

−

−

−

=

)!

1

(

!

))

1

(

)...(

3

)(

2

)(

1

(

b

b

b

a

a

a

a

a

b

 

 

 

 

 

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

−

−

−

−

−

−

=

)!

1

(

))

1

(

)...(

3

)(

2

)(

1

(

))

1

(

(

b

b

a

a

a

a

a

b

a

 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1134 

Maka 

didapatkan 

2

C

₂β

=

(

β

−

1

)

C

₁β

,

3

C

₃β

=

(

β

−

2

)

C

₂β

,

4

C

₄β

=

(

β

−

3

)

C

₃β

 

dan 

seterusnya  sehingga  persamaan  (6.a)‐(6.d)  diperoleh 

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

−

=

∂

∂

∂

∂

=

∂

∂

x

v

y

u

y

v

x

u

dan

. 

Yang berarti 

w

₁

 memenuhi persamaan Cauchy‐Riemann. 

 

Cara 

2. 

Dalam 

koordinat 

polar 

w

1

 

dapat 

ditulis 

sebagai 

)

sin

(cos

1

z

β

r

β

βθ

i

βθ

w

=

=

+

.  Denan  menuliskan  bagian  riil  dan  bagian  khayal 

w

1

 

diperoleh 

u

(

r

,

θ

)

=

r

β

cos

βθ

 

dan 

v

(

r

,

θ

)

=

r

β

sin

βθ

. 

Sehingga 

θ

βθ

β

βθ

β

β β

∂

∂

=

=

=

∂

∂

−

v

r

r

r

r

r

u

1

cos

1

cos

1

  

dan 

r

u

r

r

r

r

r

v

∂

∂

−

=

−

=

=

∂

∂

_β

β−1

_sin

_βθ

_β

β

_sin

_βθ

.  Jadi  memenuhi  persamaan  Cauchy‐

Riemann.  

Karena 

w

₁

  merupakan  polinom  berderajat 

β

  atau  dapat  juga  disebut  sebagai  fungsi 

pangkat,  maka  turunan 

w

₁

  yaitu 

w

₁'

=

β

z

β−1

ada  untuk  setiap 

z

≠ 0

∈

C

.  Jadi 

w

₁

 

merupakan pemetaan konformal.  

 

Untuk 

β

=

1

 maka diperoleh

w

1

= z . Hasil pemetaan adalah gambar yang sama 

karena fungsi pemetaan ini tidak mengubah bentuk gambar tetapi hanya menggantu 

sumbu‐sumbu koordinat, yaitu sumbu x menjadi sumbu u dan sumbu y menjadi sumbu 

v  berturut‐turut  untuk  bidang  z  dan  bidang  w.    Pada  bagian  selanjutnya  ditunjukkan 

untuk 

β

=

2

.  

4.2 Hasil pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

, 

α

=

−

β

 dan 

β

=

2

 

 

Untuk  nilai 

β

=

2

  diperoleh 

w

₁

=

z

2

  dan  ini  merupakan  fungsi  parabolik  atau 

fungsi  kuadrat.  Berdasarkan  persamaan  (4.1)  maka 

w

₁

=

x

2

+

2

ixy

−

y

2

.  Dengan 

menuliskan bagian riil dan bagian khayal dari 

w

₁

 berturut‐turut diperoleh  

2 2

_y

x

u

=

−

 dan 

v 2

=

xy

.  

 

 

 

 

(7) 

Berdasarkan persamaan (7) maka persamaan garis 

x

=

±

a

pada bidang –z dipetakkan 

sebagai keluarga parabola pada bidang‐w, yang ditunjukkan oleh persamaan (8.). Yaitu 

karena  

ay

v

=

±

2

 sehingga 

a

v

y

2

±

=

 dan 

u

=

a

2

−

y

2

 maka 

₂ 2 2 2 2

4

2

a

v

a

a

v

a

u

⎟

=

−

⎠

⎞

⎜

⎝

⎛±

−

=

. 

 

(8.a) 

Untuk  persamaan  garis 

y

=

±

b

  pada  bidang‐z  dipetakkan  sebagai  suatu  keluarga 

parabola pada bidang‐w, yaitu  

bx

v

=

±

2

 sehingga 

b

v

x

2

±

=

 dan 

u

=

x

2

−

b

2

 maka 

2 2 2 2 2

4

2

b

b

v

b

b

v

u

⎟

−

=

−

⎠

⎞

⎜

⎝

⎛±

=

.   (8.b) 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1135 

Keluarga parabola persamaan (8.a)‐(8.b) merupakan sistem ortogonal (Gordon,1963). 

Masing‐masing dari bayangan garis 

x

=

±

a

 dan 

y

=

±

b

 dan persegi ditunjukkan pada 

Gambar 4.1‐4.3. 

 

 

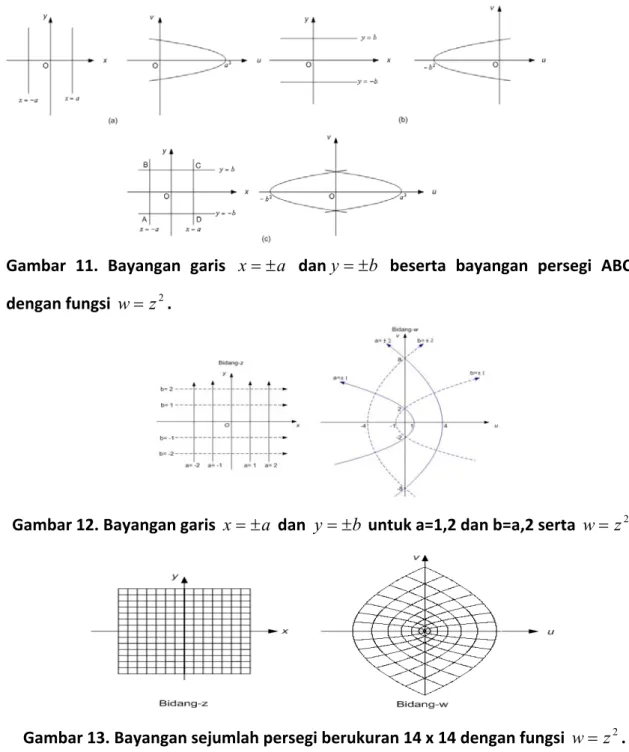
Gambar  11.  Bayangan  garis 

x

=

±

a

  dan

y

=

±

b

  beserta  bayangan  persegi  ABCD 

dengan fungsi 

w

=

z

2

. 

 

Gambar 12. Bayangan garis 

x

=

±

a

 dan 

y

=

±

b

 untuk a=1,2 dan b=a,2 serta 

w

=

z

2

. 

 

Gambar 13. Bayangan sejumlah persegi berukuran 14 x 14 dengan fungsi 

w

=

z

2

. 

4.3 Pemetaan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dengan 

α

∈

(

0

,

1

)

  

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1136 

 

Karena 

α

∈

(

0

,

1

)

, maka dapat dituliskan 

b

a

=

α

 dengan a,b

∈

N

, a<b, sehingga 

diperoleh  

b a

z

z

w

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

1

1

α

. 

Dalam koordinat polar dapat diperoleh 

⎟

⎠

⎞

⎜

⎝

⎛

₋

=

⎟

⎠

⎞

⎜

⎝

⎛

=

_θ −

θ

θ

b

a

i

b

a

r

re

w

b a b a i

cos

sin

1

. Dengan 

menuliskan  bagian  riil  dan  khayalnya  diperoleh 

θ

b

a

r

u

b a

cos

−

=

,   

θ

b

a

r

v

b a

sin

−

−

=

.  

Sehingga  

θ

b

a

r

b

a

r

u

_ba

cos

1 − −

−

=

∂

∂

;  

θ

θ

b

a

r

b

a

u

_ba

sin

−

−

=

∂

∂

;   

 

 

(9.a) 

θ

b

a

r

b

a

r

v

_ba

sin

1 − −

=

∂

∂

; 

θ

θ

b

a

r

b

a

v

_ba

cos

−

−

=

∂

∂

.  

 

 

 (9.b) 

Jadi  persamaan  Cauchy‐Riemann  dipenuhi.  Karena 

z

C

z

b

a

w

b a

∈

∀

≠

⎟

⎠

⎞

⎜

⎝

⎛

=

−

,

0

1

'

1

maka 

terbukti 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dengan 

α

∈

(

0

,

1

)

 merupakan pemetaan konformal.  

  

Untuk 

2

1

=

α

,  maka  diperoleh  bentuk  pemetaan 

z

w

=

1

.  Dengan 

menggunakan koordinat polar diperoleh  

( )

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = = − 2 2 sin 2 2 cos 1 2 / 1 θ π θ π θ k _i k r re w i

_{,  k = 0,1.} 

 

 ₍₁₀₎ 

Sehingga  untuk  k  =  0  diperoleh  nilai  utama

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

=

=

2

sin

2

cos

1

0

θ

θ

i

r

w

_k

dan  untuk 

nilai  k  =  1  diperoleh

( )

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛ +

−

⎟

⎠

⎞

⎜

⎝

⎛ +

=

=

− =

2

2

sin

2

2

cos

1

2 / 1 1

π

θ

π

θ

θ

_i

r

re

w

i k

.  Dengan 

mengingat bahwa  

sin (a + b) = sin a cos b + cos a sin b dan cos(a+b)=cos a cos b – sin a sin b , maka  

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

−

=

=

2

sin

2

cos

1

1

θ

θ

i

r

w

_k

= 

−

w

k=0

. 

Dengan  menuliskan 

w

_k=0

=

u

+

iv

  ,  maka  bagian  riil  dan  bagian  khayal  dapat  ditulis 

sebagai  

 

2

cos

1

θ

r

u

=

 dan 

2

sin

1

θ

r

v

=

−

.   

 

 

(11) 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1137 

Dengan  menuliskan  persamaan  (11)  dalam  x  dan  y  diperoleh 

2

cos

1

1

+

θ

=

r

u

. 

Karena 

2

2

cos

1

cos

2

_θ

₌

+

θ

 _diperoleh  

2

1

2

1

2

1

2

1

1

2 2 2 2

x

y

x

y

x

x

r

r

r

x

r

r

r

x

r

u

+

+

+

=

+

=

+

=

+

=

. 

Secara sama, karena 

2

2

cos

1

sin

2

_θ

₌

−

θ

 diperoleh  

2 1 2 1 2 1 2 1 1 2 2 2 2 x y x y x x r r r x r r r x r v + − + − = − − = − − = − − =

. 

Sehingga  untuk  setiap  titik  (a,b)  pada  bidang‐z  akan  dipetakkan  menjadi  titik 

⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ _{+ −} + − + + + 2 1 , 2 1 2 2 2 2 2 2 2 2 a b a b a b b a b a

  pada  bidang‐w.  Dengan  mengambil 

nilai utama 

w

k=₀

 yaitu 

0

≤

θ

<

2

π

 maka bayangan sejumlah persegi berukuran 14 x 14 

ditunjukkan pada Gambar 14 pada dua cabang.  

 

Gambar 14 Hasil pemetaan 

w

k=0

=

z

1

 untuk 14 x14 persegi. 

Kita dapat melakukan pemetaan untuk berbagai nilai 

α

 yang lain dan menyusun aspek 

matematis sebagaimana di atas. Untuk nilai 

2

1

−

=

α

dapat ditunjukkan hasil pemetaan 

yang ditunjukkan pada Gambar 15. 

 

Gambar 15. Hasil pemetaan persegi 14x14 dengan 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

dengan 

2

1

−

=

α

. 

5 KESIMPULAN DAN SARAN 

PROSIDING    ISBN : 978‐979‐16353‐3‐2 

Seminar Nasional Matematika dan Pendidikan Matematika

Jurusan Pendidikan Matematika FMIPA UNY, 5 Desember 2009

  1138 

 

Pada  makalah  ini  telah  ditunjukkan  hasil  pemetaan  persegi  n  x  n  dari 

α

⎟

⎠

⎞

⎜

⎝

⎛

=

z

w

1

untuk 

α

∈ Z

−

(himpunan  bilangan  bulat  negatif)  dan 

α

∈

(

0

,

1

)

. 

Diperoleh  bahwa  hasil  pemetaan  persegi  n  x  n  untuk 

α

=

2

  merupakan  keluarga 

parabola.  Sedangkan  pemetaan  persegi  n  x  n    dengan 

2

1

=

α

  merupakan  bentuk 

lemniscate  yang  terpotong‐potong.  Beberapa  pengembangan  dapat  dilakukan 

dengan melakukan pemetaan tak konformal untuk bidang persegi. 

 

 

DAFTAR PUSTAKA 

Churchill,  R.  V.  1960.  Complex  Variables  and  Applications,2nd  Edition.  McGraw‐Hill 

Book Company. New York. 

Gordon, L. I dan Sim Lasher.  1963. Elements of Complex Variables.  Holt, Rinehart and 

Winston, Inc. 

Parhusip H. A., dan Sulistyono,  Pemetaaan Konformal dan Modifikasinya untuk suatu 

Bidang  Persegi,  Prosiding  Seminar  Nasioanal  Matematika  UNPAR  5  September  2009, 

hal.MT 250‐259, Vol 4. Th. 2009, ISSN 1907‐3909. 

 

 Pustaka Web 

web1. http://mathworld.wolfram.com/ConformalMapping.html