BAB III METODE NUMERIK

19

BAB III

METODE NUMERIK

3.1. Definisi High Order Compact Finite Difference

HOC merupakan salah satu metode skema FD yang mampu menghasilkan komputasi numerik dengan orde yang lebih dari dua serta melibatkan titik grid yang berdekatan sehingga jumlah operasi aritmatik dapat diminimalisir namun tetap menghasilkan akurasi dengan orde tinggi ^[18].

3.2. Diskritisasi Ruang HOC20

Pada model geometri 2D yang memiliki lebar a ≤ x ≤ b dan c ≤ y ≤ d akan dibagi menjadi grid-grid sebanyak N x M titik. Jarak antar titik ∆𝑥 =^𝑏−𝑎

𝑁 , ∆𝑦 =

𝑑−𝑐

𝑀 dan posisi 𝑥_𝑖 ketika i = 0, 1, 2, …, N dan 𝑦_𝑗 ketika j = 0, 1, 2, …, M adalah:

𝑥_𝑖 = 𝑎 + 𝑖 . ∆𝑥 ... (20a) 𝑦_𝑗 = 𝑐 + 𝑗 . ∆𝑦 ... (20b) sehingga ketika 𝑥₀ = 𝑎 dan 𝑥_𝑁 = 𝑏 serta 𝑦₀ = 𝑐 dan 𝑦_𝑁= 𝑑.

Diferensiasi terhadap fungsi ruang satu dimensi 𝑢(𝑥) pada high order compact finite difference akan didapatkan dari solusi solusi SPL triangular

menggunakan algoritma Thomas.

Untuk turunan pertama 𝑢(𝑥, 𝑡), diskritisasi numerik di titik interior dari grid seperti pada persamaan (21-23).

1. Untuk 𝑖 = 2, 3, … , 𝑁 − 2, 𝑢_𝑖−1^′ + 4𝑢_𝑖^′+ 𝑢_𝑖+1^′ = ³

ℎ(−𝑢_𝑖−1+ 𝑢_𝑖+1) ... (21)

20 2. Untuk 𝑖 = 1,

4𝑢₁^′ + 𝑢₂^′ = ¹

ℎ(−¹¹

12𝑢₀− 4𝑢₁+ 6𝑢₂ −⁴

3𝑢₃+¹

4𝑢₄) ... (22) 3. Untuk 𝑖 = 𝑁 − 1

𝑢_𝑁−2^′ + 4𝑢_𝑁−1^′ = ¹

ℎ(−¹

4𝑢_𝑁−4+⁴

3𝑢_𝑁−3− 6𝑢_𝑁−2+ 4𝑢_𝑁−1+¹¹

12𝑢_𝑁).... (23) Untuk turunan kedua 𝑢(𝑥, 𝑡), diskritisasi numerik di titik interior dari grid seperti pada persamaan (24-26).

4. Untuk 𝑖 = 2, 3, … , 𝑁 − 2, 𝑢_𝑖−1^′′ + 10𝑢_𝑖^′′+ 𝑢_𝑖+1^′′ =¹²

ℎ²(𝑢_𝑖−1− 2𝑢_𝑖 + 𝑢_𝑖+1) ... (24) 5. Untuk 𝑖 = 1,

10𝑢₁^′′+ 𝑢₂^′′ = ¹

ℎ²(³³

4 𝑢₀−⁶⁷

6 𝑢₁ −³⁵

6 𝑢₂+ 13𝑢₃−⁶¹

12𝑢₄+⁵

6𝑢₅) ... (25) 6. Untuk 𝑖 = 𝑁 − 1,

𝑢_𝑁−2^′′ + 10𝑢_𝑁−1^′′ = ¹

ℎ²(⁵

6𝑢_𝑁−5−⁶¹

12𝑢_𝑁−4+ 13𝑢_𝑁−3−³⁵

6 𝑢_𝑁−2−⁶⁷

6 𝑢_𝑁−1+

33

4 𝑢_𝑁) ... (26) Jika 𝑢₀ dan 𝑢_𝑛 diketahui, maka persamaan turunan pertama dan kedua dari 𝑢(𝑥, 𝑡) membentuk matriks triangular SPL untuk 𝑢^′(𝑖 = 1, … , 𝑁) dan 𝑢^′′(𝑖 = 1, … , 𝑁) yang dapat secara efektif diselesaikan dengan algoritma Thomas.

[

𝑑₁ 𝑎_𝟏 0 0 ⋯ 0

𝑏₂ 𝑑₂ 𝑎₂ 0 ⋯ 0

0 𝑏₃ 𝑑₃ 𝑎₃ ⋯ 0

⋮ ⋱ ⋱ ⋱

0 ⋯ 0 𝑏_𝑁−1 𝑑_𝑁−1 𝑎_𝑁−1

0 ⋯ 0 0 𝑏_𝑁 𝑑_𝑁 ]

[ 𝑋₁ 𝑋₂

⋮ 𝑋_𝑁

] = [ 𝑐₁ 𝑐₂

⋮ 𝑐_𝑁

]

Forward substitution (k = 2, 3, …, N)

21 𝑑′_𝑘 = 𝑑_𝑘− ^𝑏𝑘

𝑑^′𝑘−1𝑎_𝑘−1 ... (27) 𝑐′_𝑘 = 𝑐_𝑘− ^𝑏𝑘

𝑑^′_𝑘−1𝑐′_𝑘−1 ... (28) Backward substitution (k = N-1, N-2, …, 1)

𝑋_𝑁 = ^𝑐′𝑁

𝑑^′𝑁 ... (29) 𝑋_𝑘 =^{𝑐′𝑘−𝑎𝑘𝑋𝑘+1}

𝑑′𝑘 ... (30) 3.3. Diskritisasi Waktu Runge-Kutta Orde 4

Runge-Kutta orde 4 merupakan salah satu metode diskritisasi PDB.

Penggunaan RK4 umum digunakan karena dari segi kestabilan komputasi numerik jauh lebih baik. Jika suatu fungsi turunan pertama ^𝑑𝑥

𝑑𝑡 = 𝑥^′= 𝑓(𝑥, 𝑡), maka solusi diskritisasi waktu dengan metode RK4 ditunjukkan pada persamaan (31) dengan 𝑛 adalah langkah waktu.

𝑥_𝑛+1 = 𝑥_𝑛 +¹

6(𝑘₀+ 2𝑘₁+ 2𝑘₂+ 𝑘₃)∆𝑡, ... (31) dimana k0 hingga k3 harus dihitung secara berurut seperti yang diberikan oleh persamaan (32a – 32d).

𝑘₀ = 𝑓(𝑥_𝑛, 𝑡_𝑛) ... (32a) 𝑘₁ = 𝑓(𝑥_𝑛+¹

2𝑘₀∆𝑡, 𝑡_𝑛 +¹

2∆𝑡) ... (32b) 𝑘₂ = 𝑓(𝑥_𝑛+¹

2𝑘₁∆𝑡, 𝑡_𝑛 +¹

2∆𝑡) ... (32c) 𝑘₃ = 𝑓(𝑥_𝑛+ 𝑘₂∆𝑡, 𝑡_𝑛+ ∆𝑡) ... (32d)

22 Gambar 3.1. Penggambaran grafikal metode RK4 (Cuplikan layar dari Chapra

dan Canale^[29]).

Pada Gambar 3.1 merupakan ilustrasi metode RK4. Metode ini menggunakan empat kali pendekatan gradien nilai fungsi pada langkah waktu selanjutnya (t + ∆t). Hal tersebut berfungsi untuk menghasilkan estimasi nilai fungsi yang semakin mendekati pada nilai eksak untuk t + ∆t.

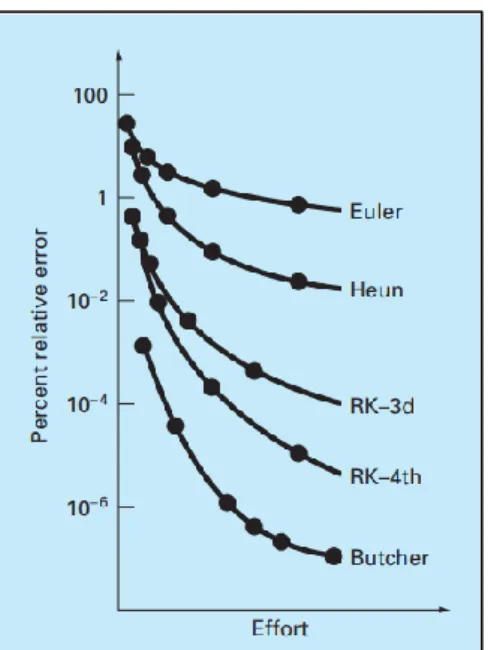
Metode untuk menyelesaikan PDB lain adalah forward euler, predictor- corrector (RK2), RK3, dan butcher (RK5). Gambar 3.2 merupakan penggambaran

persentase galat relatif yang dihasilkan dan usaha komputasi yang diperlukan pada tiap metode. Terlihat bahwa metode forward euler hingga RK3 memiliki galat relatif yang lebih tinggi daripada RK4. Penggunaan butcher memiliki galat relatif yang lebih rendah dari RK4, tetapi dari segi usaha komputasi memerlukan memori dan waktu yang lebih banyak karena perlu enam kali perhitungan aproksimasi gradien sehingga dalam aplikasi komputasi numerik dengan jumlah grid yang besar akan kurang efisien dari segi waktu.

23 Gambar 3.2. Perbandingan galat relatif dan usaha komputasi pada tiap metode

(Cuplikan layar dari Chapra dan Canale^[29]).

3.4. Skema Numerik Kondisi Batas Vorticity dengan HOC20

Misal terdapat sebuah dinding tanpa celah pada batas kiri yang dapat bergerak atau diam seperti pada Gambar 3.3. Kondisi tanpa celah memiliki arti kecepatan 𝑢_0,𝑗 = 𝜕𝛹_0,𝑗⁄𝜕𝑦= 0 atau stream function sepanjang dinding adalah konstan serta kecepatan 𝑉_0,𝑗 = −𝜕𝛹_0,𝑗⁄𝜕𝑥 = ±𝑉_{𝑤𝑎𝑙𝑙} dengan 𝑉_{𝑤𝑎𝑙𝑙} merupakan kecepatan pergerakan dinding.

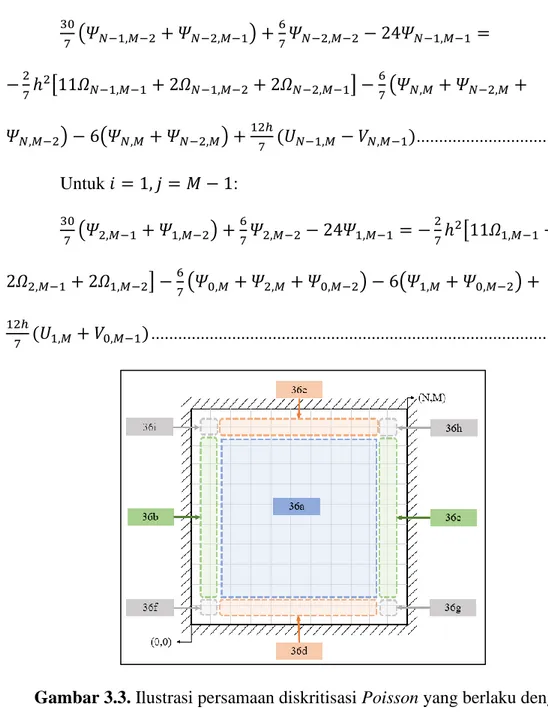
Gambar 3.3. Titik pada batas dinding kiri

24 Pendekatan orde 4 vorticity pada batas kiri didapatkan dengan melakukan ekspansi deret Taylor:

𝛹_1,𝑗 = 𝛹_0,𝑗+ ℎ𝜕𝛹_0,𝑗

𝜕𝑥 +ℎ² 2

𝜕²𝛹_0,𝑗

𝜕𝑥² +ℎ³ 6

𝜕³𝛹_0,𝑗

𝜕𝑥³ +ℎ⁴ 24

𝜕⁴𝛹_0,𝑗

𝜕𝑥⁴ + 𝑂(ℎ⁵) sehingga 𝑉_0,𝑗 = −𝜕𝛹_0,𝑗⁄𝜕𝑥 dapat diaproksimasikan menjadi akurasi orde 4:

𝑉_0,𝑗 = −(𝛹_1,𝑗− 𝛹_0,𝑗)

ℎ +ℎ

2

𝜕²𝛹_0,𝑗

𝜕𝑥² +ℎ² 6

𝜕³𝛹_0,𝑗

𝜕𝑥³ +ℎ³ 24

𝜕⁴𝛹_0,𝑗

𝜕𝑥⁴ + 𝑂(ℎ⁴) dengan melakukan substitusi persamaan Poisson sendiri, didapatkan:

𝑉_0,𝑗 = −(𝛹_1,𝑗− 𝛹_0,𝑗)

ℎ −ℎ

2𝛺_0,𝑗−ℎ² 6

𝜕𝛺_0,𝑗

𝜕𝑥 −ℎ³

24(𝜕²𝛺_0,𝑗

𝜕𝑥² + 𝜕⁴𝛹

𝜕𝑥²𝜕𝑦²) Dengan melakukan substitusi formulasi mengacu pada Tabel 2.2 sehingga didapatkan persamaan vorticity pada batas kiri (33a).

𝛺_0,𝑗 = ¹

7ℎ²(−24ℎ𝑉_0,𝑗− 𝛹_0,𝑗−1+ 26𝛹_0,𝑗− 𝛹_0,𝑗+1+ 2𝛹_1,𝑗−1− 28𝛹_1,𝑗+ 2𝛹_1,𝑗+1− 𝛹_2,𝑗−1+ 2𝛹_2,𝑗 − 𝛹_2,𝑗+1) −⁶

7𝛺_1,𝑗+¹

7𝛺_2,𝑗 ... (33a) Metode yang sama juga dilakukan pada batas dinding bawah, kanan, dan atas secara berurutan ditunjukkan pada persamaan (33b – 33d).

𝛺_𝑖,0 = ¹

7ℎ²(24ℎ𝑈_𝑖,0− 𝛹_𝑖−1,0+ 26𝛹_𝑖,0− 𝛹_𝑖+1,0+ 2𝛹_𝑖−1,1− 28𝛹_𝑖,1+ 2𝛹_𝑖+1,1− 𝛹_𝑖−1,2+ 2𝛹_𝑖,2− 𝛹_𝑖+1,2) −⁶

7𝛺_𝑖,1+¹

7𝛺_𝑖,2 ... (33b) 𝛺_𝑁,𝑗 = ¹

7ℎ²(24ℎ𝑉_𝑁,𝑗− 𝛹_{𝑁,𝑗−1}+ 26𝛹_𝑁,𝑗− 𝛹_𝑁,𝑗+1+ 2𝛹_{𝑁−1,𝑗−1} − 28𝛹_{𝑁−1,𝑗}+ 2𝛹_{𝑁−1,𝑗+1}− 𝛹_{𝑁−2,𝑗−1}+ 2𝛹_{𝑁−2,𝑗}− 𝛹_{𝑁−2,𝑗+1}) −⁶

7𝛺_{𝑁−1,𝑗}+¹

7𝛺_{𝑁−2,𝑗} ... (33c)

25 𝛺_𝑖,𝑀 = ¹

7ℎ²(−24ℎ𝑈_𝑖,𝑀− 𝛹_{𝑖−1,𝑀}+ 26𝛹_𝑖,𝑀− 𝛹_𝑖+1,𝑀+ 2𝛹_{𝑖−1,𝑀−1}− 28𝛹_{𝑖,𝑀−1}+ 2𝛹_{𝑖+1,𝑀−1}− 𝛹_{𝑖−1,𝑀−2}+ 2𝛹_{𝑖,𝑀−2}− 𝛹_{𝑖+1,𝑀−2}) −⁶

7𝛺_{𝑖,𝑀−1}+¹

7𝛺_{𝑖,𝑀−2} ... (33d) 3.5. Skema Numerik Persamaan Poisson Orde 4

Persamaan Poisson (15) diaproksimasikan secara orde 4 pada persamaan (34)^[30].

𝜕²𝛹

𝜕𝑋² +^𝜕2𝛹

𝜕𝑌² −^ℎ2

12(^𝜕4𝛹

𝜕𝑋⁴ +^𝜕4𝛹

𝜕𝑌⁴) + 𝑂(ℎ⁴) = −𝛺 ... (34) Diskritisasi persamaan Poisson orde 4 dilakukan dengan mengubah turunan orde 4 menjadi turunan orde 2 sehingga suku ketiga sisi kiri persamaan (34) didekatkan berdasarkan persamaan (15).

𝜕²𝛹

𝜕𝑋² = −^𝜕2𝛹

𝜕𝑌² − 𝛺

Dengan mengali seluruh suku dengan ^𝜕

2

𝜕𝑋² didapatkan turunan orde 4 terhadap x dan turunan orde 4 terhadap y.

𝜕⁴𝛹

𝜕𝑋⁴ = − ^𝜕4𝛹

𝜕𝑋²𝜕𝑌²−^𝜕2𝛺

𝜕𝑋²+ 𝑂(ℎ²)

𝜕⁴𝛹

𝜕𝑋⁴ = − ^𝜕4𝛹

𝜕𝑋²𝜕𝑌²−^𝜕2𝛺

𝜕𝑋²+ 𝑂(ℎ²)

Kedua persamaan tersebut disubstitusikan ke persamaan (34) sehingga didapatkan aproksimasi persamaan Poisson orde 4.

−^𝜕2𝛹

𝜕𝑋²−^𝜕2𝛹

𝜕𝑌²−^ℎ2

6

𝜕⁴𝛹

𝜕𝑋²𝜕𝑌² = 𝛺 +^ℎ2

12(^𝜕2𝛺

𝜕𝑋²+^𝜕2𝛺

𝜕𝑌²) ... (35) Diskritisasi persamaan (36) dilakukan dengan formulasi central finite difference yang ditunjukkan pada Tabel 3.1. Formulasi tersebut disubstitusikan

26 pada persamaan (35) dan didapatkan diskritisasi persamaan Poisson orde 4 pada persamaan (36a) untuk 𝑖 = 2, 3, 4, … , 𝑁 − 2 dan 𝑗 = 2, 3, 4, … , 𝑀 − 2.

Tabel 3.1. Formulasi turunan diferensial dengan central finite difference

Turunan diferensial Formula

𝜕²𝑈

𝜕𝑥²

(𝑈_𝑖+1,𝑗− 2𝑈_𝑖,𝑗+ 𝑈_{𝑖−1,𝑗}) ℎ²

𝜕²𝑈

𝜕𝑦²

(𝑈_𝑖,𝑗+1− 2𝑈_𝑖,𝑗+ 𝑈_{𝑖,𝑗−1}) ℎ²

𝜕⁴𝑈

𝜕𝑥²𝜕𝑦²

4𝑈_𝑖,𝑗− 2(𝑈_𝑖+1,𝑗+ 𝑈_{𝑖−1,𝑗}+ 𝑈_𝑖,𝑗+1+ 𝑈_{𝑖,𝑗−1}) ℎ⁴

+ 𝑈_{𝑖+1,𝑗+1}+ 𝑈_{𝑖+1,𝑗−1}+ 𝑈_{𝑖−1,𝑗+1}+ 𝑈_{𝑖−1,𝑗−1} ℎ⁴

4(𝛹_𝑖+1,𝑗+ 𝛹_𝑖,𝑗+1+ 𝛹_{𝑖−1,𝑗}+ 𝛹_{𝑖,𝑗−1}) + 𝛹_{𝑖+1,𝑗+1}+ 𝛹_{𝑖−1,𝑗+1}+ 𝛹_{𝑖−1,𝑗−1}+ 𝛹_{𝑖+1,𝑗−1}− 20𝛹_𝑖,𝑗 = −¹

2ℎ²[8𝛺_𝑖,𝑗+ 𝛺_𝑖+1,𝑗+ 𝛺_𝑖,𝑗+1+ 𝛺_{𝑖−1,𝑗} + 𝛺_{𝑖,𝑗−1}] ... (36a) Persamaan (36a) memerlukan nilai vorticity pada kondisi batas dengan langkah waktu yang sama ketika 𝑖 = 1, 𝑗 = 1, 𝑖 = 𝑁, 𝑗 = 𝑀. Oleh karena itu, khusus pada titik grid tersebut memerlukan solusi vorticity pada batas secara paralel untuk mendapatkan solusi stream function dari persamaan (36a). Hal tersebut perlu dilakukan untuk mendapatkan SPL untuk Ψ secara eksplisit. Dengan mensubstitusi vorticity pada batas yang diberikan oleh persamaan (34a – 34d), didapatkan SPL

untuk Ψ seperti diberikan oleh persamaan (36b – 36i).

Untuk 𝑖 = 1; 𝑗 = 2, 3, … , 𝑀 − 2:

29

7 (𝛹_2,𝑗 + 𝛹_1,𝑗+1+ 𝛹_1,𝑗−1) +¹³

14(𝛹_2,𝑗+1+ 𝛹_2,𝑗−1) − 22𝛹_1,𝑗 =

−¹

2ℎ²[⁵⁰

7 𝛺_1,𝑗+⁸

7𝛺_2,𝑗+ 𝛺_1,𝑗+1+ 𝛺_1,𝑗−1] −¹³

14(𝛹_0,𝑗+1+ 𝛹_0,𝑗−1) −⁴¹

7 𝛹_0,𝑗+

12

7 𝑉_0,𝑗ℎ ... (36b)

27 Untuk 𝑖 = 𝑁 − 1; 𝑗 = 2, 3, … , 𝑀 − 2:

29

7 (𝛹_{𝑁−2,𝑗} + 𝛹_{𝑁−1,𝑗+1}+ 𝛹_{𝑁−1,𝑗−1}) +¹³

14(𝛹_{𝑁−2,𝑗+1}+ 𝛹_{𝑁−2,𝑗−1}) − 22𝛹_{𝑁−1,𝑗} = −¹

2ℎ²[⁵⁰

7 𝛺_{𝑁−1,𝑗}+⁸

7𝛺_{𝑁−2,𝑗} + 𝛺_{𝑁−1,𝑗+1}+ 𝛺_{𝑁−1,𝑗−1}] −¹³

14(𝛹_𝑁,𝑗+1+ 𝛹_{𝑁,𝑗−1}) −⁴¹

7 𝛹_𝑁,𝑗−¹²

7 𝑉_𝑁,𝑗ℎ ... (36c) Untuk 𝑖 = 2, 3, … , 𝑁 − 2; 𝑗 = 1:

29

7 (𝛹_𝑖+1,1+ 𝛹_𝑖,2+ 𝛹_𝑖−1,1) +¹³

14(𝛹_𝑖+1,2+ 𝛹_𝑖−1,2) − 22𝛹_𝑖,1 =

−¹

2ℎ²[⁵⁰

7 𝛺_𝑖,1+⁸

7𝛺_𝑖,2+ 𝛺_𝑖+1,1+ 𝛺_𝑖−1,1] −¹³

14(𝛹_𝑖+1,0+ 𝛹_𝑖−1,0) −⁴¹

7 𝛹_𝑖,0−

12

7 𝑈_𝑖,0ℎ ... (36d) Untuk 𝑖 = 2, 3, … , 𝑁 − 2, 𝑗 = 𝑀 − 1:

29

7 (𝛹_{𝑖,𝑀−2}+ 𝛹_{𝑖+1,𝑀−1}+ 𝛹_{𝑖−1,𝑀−1}) +¹³

14(𝛹_{𝑖+1,𝑀−2}+ 𝛹_{𝑖−1,𝑀−2}) − 22𝛹_{𝑖,𝑀−1}= −¹

2ℎ²[⁵⁰

7 𝛺_{𝑖,𝑀−1}+⁸

7𝛺_{𝑖,𝑀−2}+ 𝛺_{𝑖+1,𝑀−1}+ 𝛺_{𝑖−1,𝑀−1}] −¹³

14(𝛹_𝑖+1,𝑀+ 𝛹_{𝑖−1,𝑀}) −⁴¹

7 𝛹_𝑖,𝑀+¹²

7 𝑈_𝑖,𝑀ℎ ... (36e) Untuk 𝑖 = 1, 𝑗 = 1:

30

7 (𝛹_2,1+ 𝛹_1,2) +⁶

7𝛹_2,2− 24𝛹_1,1 = −²

7ℎ²[11𝛺_1,1+ 2𝛺_2,1+ 2𝛺_1,2] −

6

7(𝛹_0,0+ 𝛹_0,2 + 𝛹_2,0) − 6(𝛹_0,1+ 𝛹_1,0) +^12ℎ

7 (𝑉_0,1− 𝑈_1,0) ... (36f) Untuk 𝑖 = 𝑁 − 1, 𝑗 = 1:

30

7 (𝛹_𝑁−1,2+ 𝛹_𝑁−1,2) +⁶

7𝛹_𝑁−2,2− 24𝛹_𝑁−1,1 = −²

7ℎ²[11𝛺_𝑁−1,1+ 2𝛺_𝑁−1,2+ 2𝛺_𝑁−2,1] −⁶

7(𝛹_𝑁,0+ 𝛹_𝑁−2,0+ 𝛹_𝑁,2) − 6(𝛹_𝑁,1+ 𝛹_𝑁−1,0) −

12ℎ

7 (𝑉_𝑁,1+ 𝑈_𝑁−1,0) ... (36g) Untuk 𝑖 = 𝑁 − 1, 𝑗 = 𝑀 − 1:

28

30

7 (𝛹_{𝑁−1,𝑀−2}+ 𝛹_{𝑁−2,𝑀−1}) +⁶

7𝛹_{𝑁−2,𝑀−2}− 24𝛹_{𝑁−1,𝑀−1}=

−²

7ℎ²[11𝛺_{𝑁−1,𝑀−1}+ 2𝛺_{𝑁−1,𝑀−2}+ 2𝛺_{𝑁−2,𝑀−1}] −⁶

7(𝛹_𝑁,𝑀+ 𝛹_{𝑁−2,𝑀}+ 𝛹_{𝑁,𝑀−2}) − 6(𝛹_𝑁,𝑀+ 𝛹_{𝑁−2,𝑀}) +^12ℎ

7 (𝑈_{𝑁−1,𝑀}− 𝑉_{𝑁,𝑀−1}) ... (36h) Untuk 𝑖 = 1, 𝑗 = 𝑀 − 1:

30

7 (𝛹_2,𝑀−1+ 𝛹_1,𝑀−2) +⁶

7𝛹_2,𝑀−2− 24𝛹_1,𝑀−1 = −²

7ℎ²[11𝛺_1,𝑀−1+ 2𝛺_2,𝑀−1+ 2𝛺_1,𝑀−2] −⁶

7(𝛹_0,𝑀+ 𝛹_2,𝑀+ 𝛹_0,𝑀−2) − 6(𝛹_1,𝑀 + 𝛹_0,𝑀−2) +

12ℎ

7 (𝑈_1,𝑀+ 𝑉_0,𝑀−1) ... (36i)

Gambar 3.3. Ilustrasi persamaan diskritisasi Poisson yang berlaku dengan mengacu pada lokasi titik grid

Seluruh SPL pada persamaan (36a – 36i) dapat diselesaikan dengan metode iterasi SOR. Dengan metode tersebut, penyelesaian sistem persamaan linear mampu diselesaikan dengan memperbaharui nilai stream function pada tiap iterasi hingga mencapai konvergensi. Jika k merupakan suatu langkah iterasi pada 𝛹_𝑖,𝑗 atau 𝛹_𝑖,𝑗^𝑘,

29 maka untuk persamaan (36a) didapatkan formulasi iterasi untuk 𝑖 = 2, 3, 4, … , 𝑁 − 2 dan 𝑗 = 2, 3, 4, … , 𝑀 − 2

𝛿_𝑖,𝑗^𝑘+1= ¹

20(𝛹_{𝑖+1,𝑗+1}^𝑘 + 𝛹_{𝑖+1,𝑗−1}^𝑘 + 𝛹_{𝑖−1,𝑗+1}^𝑘+1 + 𝛹_{𝑖−1,𝑗−1}^𝑘+1 + 4(𝛹_𝑖+1,𝑗^𝑘 + 𝛹_𝑖,𝑗+1^𝑘 + 𝛹_{𝑖,𝑗−1}^𝑘+1 + 𝛹_{𝑖−1,𝑗}^𝑘+1) +¹

2ℎ²(𝛺_𝑖,𝑗+ 𝛺_𝑖+1,𝑗+ 𝛺_𝑖,𝑗+1+ 𝛺_{𝑖−1,𝑗}+ 𝛺_{𝑖,𝑗−1}) − 𝛹_𝑖,𝑗^𝑘 ... (37)

𝛹_𝑖,𝑗^𝑘+1= 𝛹_𝑖,𝑗^𝑘 + 𝛾𝛿_𝑖,𝑗^𝑘+1 ... (38) dengan 𝛾 merupakan koefisien relaxation yang tipikal diantara 1 ≤ 𝛾 ≤ 2. Hal yang sama juga dapat dilakukan pada kasus lokasi 𝑖 dan 𝑗 lain.

Konvergensi dari metode SOR didapatkan ketika ‖𝛿^𝑘+1‖ < 𝜖‖𝛹⁰‖, dengan

‖𝛹^𝑘‖merupakan I-norm2 dari 𝛹_𝑖,𝑗^𝑘.

‖𝛹_𝑖,𝑗^𝑘‖ = √∑^𝑁,𝑀_{𝑖=0,𝑗=0}(𝛹_𝑖,𝑗)² ... (39)

3.6. Skema Numerik Kondisi Batas Dinding Adiabatik

Dinding adiabatik merupakan dinding yang tidak menerima, melepas, atau transfer energi kalor sehingga definisi matematis dinding adiabatik adalah

𝜕𝜃 𝜕𝑋⁄ = 0 untuk dinding vertikal dan 𝜕𝜃 𝜕𝑌⁄ = 0 untuk dinding horizontal.

Contoh sebuah dinding adiabatik horizontal sisi bawah, nilai temperatur pada posisi tepat di dinding adiabatik dapat ditentukan dengan penurunan persamaan (21). Jika 𝑢_𝑖,𝑗 = 𝜃_𝑖,𝑗 dan 𝑢_𝑖,𝑗^′ =^𝜕𝜃

𝜕𝑌|

𝑖,𝑗,

𝜕𝜃

𝜕𝑌|

𝑖,𝑗−1

+ 4𝜕𝜃

𝜕𝑌|

𝑖,𝑗

+𝜕𝜃

𝜕𝑌|

𝑖,𝑗+1

= 3

ℎ(−𝜃_{𝑖,𝑗−1}+ 𝜃_𝑖,𝑗+1)

maka ketika 𝑗 = 1,

30

𝜕𝜃

𝜕𝑌|

𝑖,0

+ 4𝜕𝜃

𝜕𝑌|

𝑖,1

+𝜕𝜃

𝜕𝑌|

𝑖,2

= 3

ℎ(−𝜃_𝑖,0+ 𝜃_𝑖,2)

Dari definisi matematis dinding adiabatik, maka ^𝜕𝜃

𝜕𝑌|

𝑖,0= 0. Untuk 4^𝜕𝜃

𝜕𝑌|

𝑖,1+

𝜕𝜃

𝜕𝑌|

𝑖,2dijabarkan dengan persamaan (22) sehingga nilai temperatur tepat pada dinding adiabatik sisi bawah ditunjukkan pada persamaan (40a).

1 ℎ(−11

12𝜃_𝑖,0− 4𝜃_𝑖,1+ 6𝜃_𝑖,2−4

3𝜃_𝑖,3+1

4𝜃_𝑖,4) =3

ℎ(−𝜃_𝑖,0+ 𝜃_𝑖,2) 𝜃_𝑖,0 = ¹²

25(4𝜃_𝑖,1− 3𝜃_𝑖,2+⁴

3𝜃_𝑖,3−¹

4𝜃_𝑖,4) ... (40a) Untuk dinding adiabatik sisi atas dengan 𝑗 = 𝑀 − 1,

𝜃_𝑖,𝑀 = ¹²

25(4𝜃_{𝑖,𝑀−1}− 3𝜃_{𝑖,𝑀−2}+⁴

3𝜃_{𝑖,𝑀−3}−¹

4𝜃_{𝑖,𝑀−4}) ... (40b) Untuk dinding adiabatik sisi kiri dengan 𝑖 = 1,

𝜃_0,𝑗 =¹²

25(4𝜃_1,𝑗− 3𝜃_2,𝑗+⁴

3𝜃_3,𝑗 −¹

4𝜃_4,𝑗) ... (40c) Untuk dinding adiabatik sisi kanan dengan 𝑖 = 𝑁 − 1,

𝜃_𝑁,𝑗 = ¹²

25(4𝜃_{𝑁−1,𝑗}− 3𝜃_{𝑁−2,𝑗}+⁴

3𝜃_{𝑁−3,𝑗}−¹

4𝜃_{𝑁−4,𝑗}) ... (40d) 3.7. Konvergensi dan Stabilitas

Hasil simulasi numerik pada sistem persamaan diferensial merupakan aproksimasi solusi numerik pada solusi eksak. Untuk menghasilkan aproksimasi yang mendekati, diperlukan indikator yang menunjukkan aproksimasi tersebut sudah cukup atau mendekati solusi eksak yang disebut konvergensi serta kestabilan solusi numerik.

31 Galat absolut merupakan galat yang menggambarkan perbedaan solusi aproksimasi dengan solusi eksak. Jika dalam satu dimensi, maka dapat didefinisikan pada persamaan (41).

𝑒_𝑖^𝑛 = 𝑓_𝑖^𝑛− 𝑓(𝑥_𝑖, 𝑡_𝑛) ... (41) Pendekatan solusi dinyatakan konvergen ketika 𝑒_𝑖^𝑛 → 0 selama ∆𝑥, ∆𝑡 → 0. Pengukuran bahwa solusi galat dapat ditoleransi, digunakan I-norm2 seperti pada persamaan (39) untuk vorticity.

‖𝛺_𝑖,𝑗^𝑛+

1

2‖ < 𝜖‖𝛺_𝑖,𝑗^𝑛+1‖ ... (42)

Stabilitas numerik menjadi faktor penting dalam solusi numerik. Jika solusi numerik tidak stabil, maka pendekatan numerik tidak dapat dilakukan atau hasil dari solusi numerik tidak mendekati solusi eksak. Suatu solusi numerik dinyatakan stabil jika ukuran galat berangsur mengecil terhadap berjalan waktu.

|^𝑔𝑛+1

𝑔^𝑛 | ≤ 1 ... (43) Dengan perbandingan 𝑔^𝑛+1⁄𝑔^𝑛 merupakan faktor amplifikasi.

Permasalahan murni difusi pada satu dimensi (u = 0), kondisi stabil ditentukan pada persamaan (44).

∆𝑡 ≤¹

2

∆𝑥²

𝐷 ... (44) Jika permasalahan murni konveksi pada satu dimensi (D = 0), persamaan (44) tidak dapat digunakan sehingga kondisi stabil tidak dapat tercapai. Oleh karena itu, kondisi stabil pada bagian konveksi berlaku persamaan (45) yang disebut sebagai kondisi Courant-Friedrichs-Lewy.

𝑢^∆𝑡

∆𝑥 ≤ 1 ... (45)

32 Permasalahan pada tugas akhir ini merupakan penggabungan dari fenomena konveksi dan difusi sehingga besar ∆t menggunakan nilai terkecil dari kedua persamaan (44-45).

3.8. Implementasi Skema Numerik

Skema numerik diimplementasikan pada program komputer C++

menggunakan perangkat lunak CodeBlock. Untuk pengembangan program dan visualisasi data menggunakan program komputer python pada perangkat lunak spyder.

Program dengan bahasa C++ digunakan untuk variasi data dan program yang sudah pada tahap akhir karena keunggulan dari bahasa C++ yang mampu menghasilkan komputasi numerik yang lebih cepat dari bahasa python. Sedangkan bahasa python lebih mudah dari segi analisis data-data tiap variabel dan visualisasi.

Kedua perangkat lunak tersebut merupakan open source dan digunakan dalam implementasi skema numerik. Komputasi dilakukan pada sebuah Virtual Private Server dengan CPU E5-2620 v4 8 core dan RAM 8 GB.

3.9. Variabel pada Tugas Akhir 3.9.1. Variabel Bebas

Variabel bebas pada tugas akhir ini adalah bilangan Rayleigh, aspek rasio geometri model ruang tertutup persegi panjang, serta kondisi batas transien.

3.9.2. Variabel Terikat

Variabel terikat pada tugas akhir ini adalah pola aliran sirkulasi stream function dan isotermal, serta bilangan Nusselt.

33 3.9.3. Variabel Terkendali

Variabel terkendali pada tugas akhir ini adalah kombinasi skema HOC20 untuk diskritisasi ruang dan metode RK4, parameter temperatur pada model, kondisi awal dan batas dari permodelan.

3.10. Metode Pelaksanaan Tugas Akhir

Pada pelaksanaan tugas akhir ini, dilakukan langkah-langkah sebagai berikut:

1. Permodelan dari permasalahan konveksi alami pada geometri ruang tertutup persegi panjang (Gambar 3.4.) dengan kondisi batas berupa sisi kiri merupakan dinding dengan temperatur tinggi yang tidak konstan dan sisi kanan ruang merupakan dinding dengan temperatur rendah yang konstan. Sedangkan sisi atas dan bawah ruang merupakan adiabatik.

2. Melakukan pengujian akurasi dan konvergensi metode HOC20 secara DNS dengan tiga tahapan besar sebagai berikut:

a. Tahap 1:

i. Melakukan pengujian dengan membandingkan hasil komputasi numerik dengan solusi eksak pada tiga contoh permasalahan ^[31].

ii. Melakukan validasi akurasi dan konvergensi skema solusi Poisson^[32] untuk memecahkan persamaan Poisson yang diketahui solusi eksaknya^[33-34].

b. Tahap 2: melakukan pengujian akurasi dan konvergensi gabungan skema solusi Poisson^[30] untuk persamaan Poisson

34 dengan skema numerik pada tugas akhir ini untuk persamaan Burgers dan kondisi batas pada permasalahan lid dirven cavity

keadaan transien.

c. Tahap 3: melakukan pengujian akurasi pada permasalahan konveksi alami tunak dengan ruang geometri tertutup berbentuk persegi.

3. Menguji dan memvariasikan variabel bebas berupa bilangan Rayleigh dan aspek rasio geometri ruang untuk permasalahan

konveksi alami transien. Selain itu melakukan variasi Pr pada konveksi alami tunak untuk melihat pengaruh perubahan Pr terhadap variabel terikat.

4. Hasil perubahan variabel bebas dalam simulasi numerik merupakan variasi distribusi stream function dan isotermal dalam bentuk plot grafik. Plot tersebut akan dibandingkan untuk meneliti pengaruh variable bebas terhadap variable terikat pada ruang tertutup berbentuk persegi panjang.

35 Gambar 3.4. Permodelan masalah konveksi alami pada ruang tertutup berbentuk

persegi panjang

Skema numerik yang digunakan adalah skema baru yang dikembangkan oleh pembimbing dan penulis serta validasi skema dengan eksperimen dan analisis tidak digunakan dengan alasan berikut:

1. Permasalahan konveksi alami dan lid driven cavity merupakan permasalahan dua dimensi sehingga validasi eksperimen sulit dilakukan karena secara eksperimen pengaruh aliran tiga dimensi sulit diabaikan. Selain itu, eksperimen juga tidak bisa menghasilkan sebaran kecepatan pada tiap titik yang relevan karena keterbatasan alat ukur yang digunakan dan terdapat potensi terganggunya aliran fluida oleh pengukuran.

2. Solusi persamaan Navier-Stokes, persamaan poisson, hingga persamaan energi pada contoh kasus konveksi alami belum memiliki solusi analitis pada suatu permasalahan spesifik dan penelitian yang

36 ada masih mengacu pada solusi numerik berupa benchmark sehingga pada tahap 2 dan tahap 3 dari pengujian akurasi dilakukan perbandingan nilai data pada beberapa penelitian dengan contoh kasus yang sama.

Dari alasan tersebut, tahapan-tahapan pengujian akurasi dan konvergensi menjadi penting untuk menjadi landasan data yang dapat dipercaya dan diandalkan ketika melibatkan variabel bebas pada eksperimen numerik.

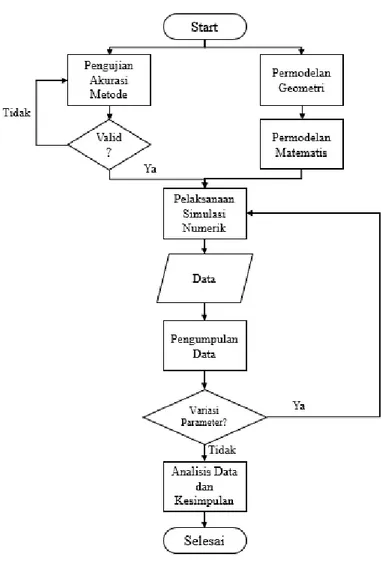
Gambar 3.1 merupakan flowchart dari langkah-langkah tugas akhir ini.

Grafik 3.1. Flowchart alur metode yang dilakukan pada tugas akhir.

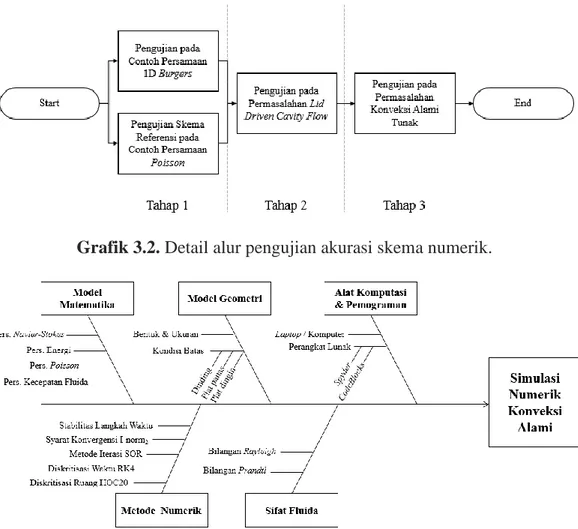
37 Gambar 3.2 merupakan flowchart detail dari pengujian akurasi skema numerik HOC20 pada permasalahan burgers hingga benchmark konveksi alami tunak pada ruang tertutup. Selain itu, Gambar 3.3 merupakan diagram fishbone yang secara detail membagi kategori-kategori untuk melaksanakan kegiatan simulasi numerik konveksi alami pada ruang tertutup persegi panjang.

Grafik 3.2. Detail alur pengujian akurasi skema numerik.

Grafik 3.3. Pembagian kategori untuk melakukan simulasi numerik konveksi alami pada ruang tertutup persegi panjang.