PEMBELAJARAN DENGAN SCIENTIFIC DEBATE
UNTUK MENINGKATKAN KEMAMPUAN KOMUNIKASI,
PENALARAN, DAN KONEKSI MATEMATIS MAHASISWA
DALAM KONSEP INTEGRAL
DISERTASI
Diajukan untuk Memenuhi Sebagian dari Persyaratan Memperoleh
Gelar Doktor Pendidikan dalam Pendidikan Matematika
Promovenda
Yani Ramdani
NIM. 0907657
SEKOLAH PASCASARJANA
PERNYATAAN
Dengan ini saya menyatakan bahwa disertasi dengan judul “Pembelajaran dengan
Scientific Debate untuk Meningkatkan Kemampuan Komunikasi, Penalaran, dan
Koneksi Matematis Mahasiswa dalam Konsep Integral” ini beserta seluruh isinya
adalah benar-benar karya saya sendiri, dan saya tidak melakukan penjiplakan atau
pengutipan dengan cara-cara yang tidak sesuai dengan etika keilmuan yang berlaku
dalam masyarakat keilmuan. Atas pernyataan ini, saya siap menanggung risiko/sanksi
yang dijatuhkan kepada saya apabila kemudian ditemukan adanya pelanggaran
terhadap etika keilmuan dalam karya saya ini, atau ada klaim dari pihak lain terhadap
keaslian karya saya ini.
Bandung, 11 Januari 2013
Yang membuat pernyataan
ABSTRAK
Yani Ramdani (2012). Pembelajaran dengan Scientific Debate untuk Meningkatkan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa dalam Konsep Integral.
Penelitian ini mengkaji pengaruh pembelajaran dengan scientific debate terhadap peningkatan kemampuan komunikasi, penalaran, dan koneksi matematis mahasiswa. Desain penelitian adalah kuasi eksperimen dengan perbandingan kelompok statis yang melibatkan 96 mahasiswa Jurusan Pendidikan Matematika di kota Bandung. Instrumen penelitian meliputi pengetahuan awal mahasiswa (PAM), tes kemampuan komunikasi, penalaran, dan koneksi matematis serta bahan ajar. Data dianalisis dengan Mann-Whitney U, ANAVA dua jalur, dan Kruskal Wallis. Hasil penelitian menunjukkan bahwa peningkatan kemampuan komunikasi dan penalaran matematis mahasiswa dengan scientific debate tidak berbeda secara signifikan dibandingkan dengan konvensional dan peningkatan kemampuan koneksi matematis berbeda secara signifikan. Ini berarti bahwa mahasiswa yang mengikuti pembelajaran dengan scientific debate memiliki peningkatan kemampuan koneksi matematis lebih baik dibandingkan secara konvensional. Tidak terdapat perbedaan rata-rata peningkatan kemampuan komunikasi dan koneksi matematis antara mahasiswa yang mengikuti pembelajaran dengan scientific debate dengan mahasiswa yang mengikuti pembelajaran secara konvensional yang didasarkan pada PAM. Tidak terdapat interaksi antara PAM dengan pendekatan pembelajaran terhadap peningkatan kemampuan komunikasi dan koneksi matematis. Rata-rata peningkatan kemampuan penalaran matematis pada mahasiswa dengan scientific debate yang didasarkan pada PAM tidak berbeda secara signifikan. Rata-rata peningkatan kemampuan penalaran matematis pada kelas konvensional yang didasarkan pada PAM berbeda secara signifikan. Pada pembelajaran scientific debate, perbedaan latar belakang pendidikan mahasiswa tidak memberikan efek yang signifikan terhadap peningkatan kemampuan komunikasi, penalaran, dan koneksi matematis. Pada pembelajaran konvensional perbedaan latar belakang pendidikan mahasiswa memberikan efek yang signifikan. Mahasiswa yang berlatar belakang Sekolah Menengah Umum memiliki peningkatan kemampuan komunikasi, penalaran, dan koneksi matematis yang lebih baik dibandingkan dengan mahasiswa yang berlatar belakang yang berlatar belakang Madrasah Aliyah. Strategi pemecahan masalah yang dilakukan mahasiswa adalah menyelesaikan masalah secara algoritmik, memberikan argumen dengan: mendefinisikan simbol matematika; menguraikan alasan model matematika yang digunakan; menjelaskan ide, situasi, dan relasi matematika dari tabel atau grafik; menguraikan perubahan model matematika menjadi bentuk representasi matematis lainnya; menggambarkan masalah dalam bentuk tabel atau grafik; menyebutkan bidang ilmu lain yang terkait dengan masalah; menjelaskan konsep-konsep yang digunakan; dan membuat generalisasi. Kekeliruan mahasiswa tergolong: (1) Structural errors; (2) Arbitrary errors; atau (3) Executive errors.
ABSTRACT
Yani Ramdani (2012). Scientific Debate Instructional to Enhance Students’ Mathematical Communication, Reasoning, and Connection Ability in the Concept of Integral.
This study examines the effect of scientific debate instructional strategy on the enhancement of students’ mathematical communication, reasoning, and connections ability in the concept of Integral. This quasi-experimental study with a static group comparison design involves 96 students from Department of Mathematics Education in Bandung. Research instruments include student’ prior knowledge (PAM), a test of mathematical communication, reasoning and connection ability as well as teaching materials. The data are analyzed by using Mann-Whitney U test, two-way ANOVA and Kruskal-Wallis Test. The study finds that the students’ enhancement in mathematical communication and reasoning abilities in students with the scientific debate is not significantly different from that of the conventional instruction. Students’ mathematical connection ability that follows instruction with scientific debate strategy is better than that of students who follow the conventional instruction. There was no difference in the average rate of the increasing mathematical communication and connection skills of students between the interactions of PAM with learning approach. There is no interaction between instructional factors and PAM factors on the increasing mathematical communication and connection skills. The enhancement of student’ mathematical reasoning abilities with a scientific debate based on the PAM, it is not completely distinctive. On the other hand, the enhancement of students’ mathematical reasoning abilities with a conventional instruction based on the PAM was considerably different. On the scientific debate, students’ educational background differences do not give major effect on the enhancement mathematical communication, reasoning and connection ability but on the conventional instruction provides a better effect. This means that, the students with background of Senior High School have enhanced mathematical communication, reasoning, and connections ability better than compare to the students of the Islamic Senior High School. There are several strategies that the students take to solve the problem; first, the students elucidate the algorithmic problems and then they give the answer as an argument like defining mathematical symbols, mathematical models and describing the reason why they use it; explaining ideas, situations, and mathematical relationships of tables or graphs; portraying the mathematical model into other forms of mathematical representation; depicting the problem in the form of tables or graphs, mentioning other disciplines related to the matter, illustrating the concepts used and make generalizations. There are three major errors of students in this research. The researcher classified them into three groups (1) structural errors, (2) arbitrary errors, (3) executive errors.
DAFTAR ISI
Halaman HALAMAN PENGESAHAN
RIWAYAT HIDUP
PERNYATAAN……….
KATA PENGANTAR ………..
ABSTRAK ………
ABSTRACT ………..
DAFTAR ISI ……….
DAFTAR TABEL ……….
DAFTAR LAMPIRAN ……….
i ii vi vii x xi xii xiv xvii
BAB I PENDAHULUAN
A. Latar Belakang Masalah ………. B. Rumusan Masalah ……….. C. Tujuan Penelitian ……… D. Manfaat Penelitian ……….. E. Definisi Operasional ………...
1 12 13 15 16 BAB II KAJIAN PUSTAKA
A. Aliran Konstruktivisme (Constructivism) ……….. B. Teori Belajar yang Mendukung Penelitian ………. C. Kemampuan Berfikir Matematis Tingkat Tinggi ……… D. Mengembangkan Kemampuan Berfikir Matematis Tingkat
Tinggi ………..
E. Pendekatan Pembelajaran untuk Meningkatan Kemampuan Berfikir Matematis Tingkat Tinggi ………... F. Model Pembelajaran Scientific Debate ………...
20 22 27 40 42 51 BAB III METODE PENELITIAN
A. Disain Penelitian ……….. B. Populasi dan Sampel ………... C. Variabel Penelitian ……….. D. Teknik Pengumpulan Data dan Teknik Analisis Data ………… E. Waktu Penelitian ………. F. Pengembangan Instrumen ………... G. Pengembangan Bahan Ajar ………. H. Prosedur Penelitian
55 56 57 57 62 62 86 90 BAB IV PEMBAHASAN A. Hasil Penelitian
2. Perbandingan Kemanpuan Komunikasi, Penalaran, dan Koneksi Matematis Manurut Interaksi antara Model Pembelajaran dengan PAM ………... 3. Kemanpuan Komunikasi, Penalaran, dan Koneksi
Matematis Menurut Hubungan antara Model Pembelajaran dengan Latar Belakang Pendidikan Mahasiswa
……….
4. Strategi Penyelesaian Masalah oleh Mahasiswa …………... 5. Analisis Kesalahan, Kekeliruan, atau Kekurangan dan
Kesulitan Mahasiswa dalam Proses Penyelesaian Masalah ...
B. Pembahasan
1. Model Pembelajaran ………... 2. Pengetahuan Awal Matematis ……… 3. Latar Belakang Pendidikan Mahasiswa ……….
96
127 139
142
171 177 182
BAB V
KESIMPULAN DAN SARAN
A. Kesimpulan ……….. B. Implikasi ………...
C. Rekomendasi ………
189 192 197
DAFTAR PUSTAKA ………... 199
DAFTAR TABEL
Halaman
Tabel 3.1 Rancangan Anova Dua Jalur ……….. 60
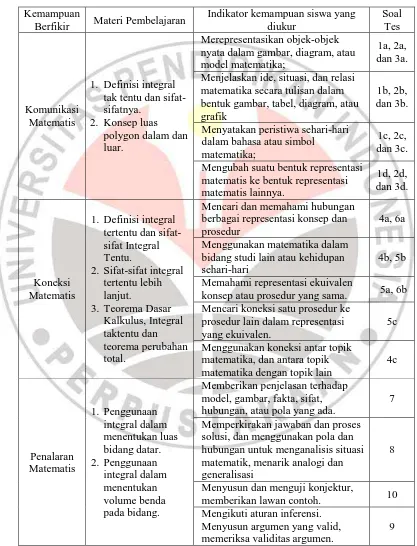
Tabel 3.2 Matriks Rancangan Tes ………. 68
Tabel 3.3 Hasil Pertimbangan Instrumen Tentang Validitas Isi ……… 74
Tabel 3.4 Uji Hasil Pertimbangan Validitas Isi ………. 74
Tabel 3.5 Hasil Pertimbangan Instrumen Tentang Validitas Muka ……….. 75
Tabel 3.6 Uji Hasil Pertimbangan Validitas Muka ……… 75
Tabel 3.7 Pedoman Penskoran ………... 76
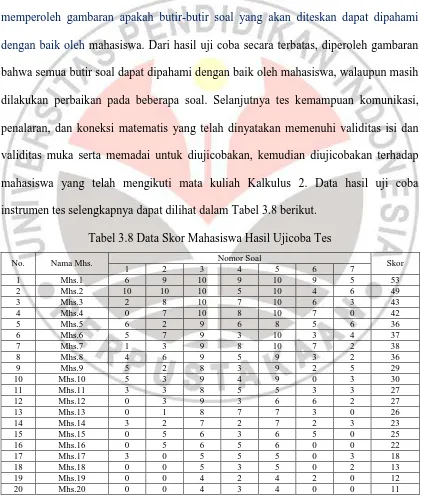
Tabel 3.8 Data Skor Mahasiswa Hasil Ujicoba Instrumen ……… 77
Tabel 3.9 Validitas Butir Soal ……… 79
Tabel 3.10 Tingkat Reliabilitas ……… 80
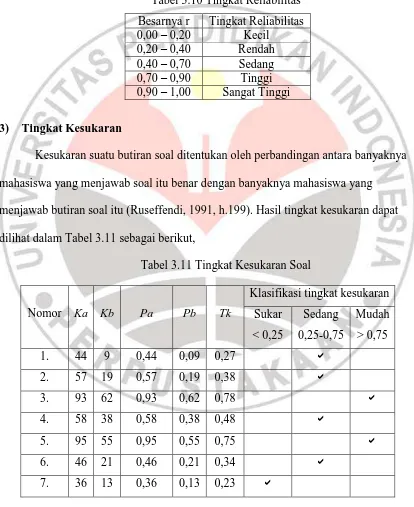
Tabel 3.11 Tingkat Kesukaran Soal ………. 80
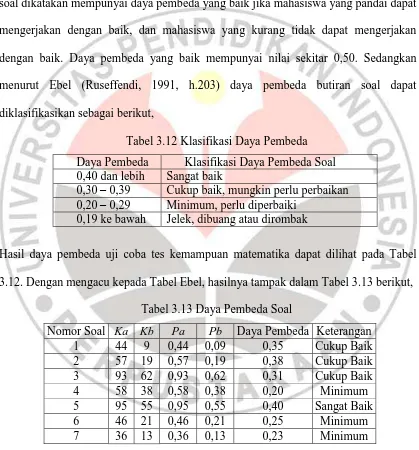
Tabel 3.12 Klasifikasi Daya Pembeda ………. 81
Tabel 3.13 Daya Pembeda Soal ………... 81
Tabel 4.1 Uji Normalitas Skor PAM ………. 93
Tabel 4.2 Uji Homogenitas Varians Populasi Skor PAM ……….. 94
Tabel 4.3 Deskripsi Data PAM Kelas Eksperimen dan Kontrol …………... 94
Tabel 4.4 Uji-t Skor PAM ……….. 95
Tabel 4.5 Kelompok PAM Siswa berdasarkan Asal Sekolah ……… 96
Tabel 4.6 Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa ……… 97
Tabel 4.7 Uji Normalitas Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis ……… 98
Tabel 4.8 Deskripsi Data Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis ……… 101
Tabel 4.10 Uji Mann-Whitney U Skor Peningktan Kemampuan Komuniksi, Penalaran, dan Koneksi Matematis ………
103
Tabel 4.11 Deskripsi Data Peningkatan Kemampuan Komunikasi,
Penalaran, dan Koneksi Matematis Mahasiswa Kelas Eksperimen berdasarkan PAM ……….. 105
Tabel 4.12 Deskripsi Data Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Kontrol
berdasarkan PAM ……….. 106
Tabel 4.13 Uji Normalitas Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Eksperimen berdasarkan PAM ……….. 108
Tabel 4.14 Uji Normalitas Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Kontrol
berdasarkan PAM ……….. 109
Tabel 4.15 Uji Homogenitas Varians Populasi Skor Peningkatan
Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis
Mahasiswa Kelas Eksperimen berdasarkan PAM ………. 113
Tabel 4.16 Kelompok Mahasiswa berdasarkan PAM dan Metode ………….. 115
Tabel 4.17 Deskripsi Data Peningkatan Kemampuan Komunikasi
berdasarkan PAM dan Metode ……….. 115
Tabel 4.18 ANOVA Skor Peningkatan Kemampuan Komunikasi Matematis
berdasarkan PAM dan Metode ……….. 116
Tabel 4.19 Perbandingan Selisih Peningkatan Kemampuan Komunikasi
Matematis berdasarkan Pendekatan Pembelajaran dengan PAM... 117
Tabel 4.20 Homogeneous Subsets Peningkatan Kemampuan Komunikasi
Matematis ………... 118
Tabel 4.21 Deskripsi Data Peningkatan Kemampuan Koneksi Matematis
berdasarkan PAM dan Metode ……….. 120
Tabel 4.22 ANOVA Skor Peningkatan Kemampuan Koneksi Matematis
berdasarkan PAM dan Metode ……….. 122
Tabel 4.23 Perbandingan Selisih Peningkatan Kemampuan Koneksi
Matematis berdasarkan Pendekatan Pembelajaran dengan PAM .. 123
Tabel 4.24 Homogeneous Subsets Peningkatan Kemampuan Koneksi
Matematis ………... 123
Tabel 4.25 Rank Skor Peningkatan Kemampuan Penalaran Matematis Kelas
Tabel 4.26 Uji Kruskal Wallis Skor Peningkatan Kemampuan Penalaran
Matematis Kelas Eksperimen ……… 126
Tabel 4.27 Rank Skor Peningkatan Kemampuan Penalaran Matematis Kelas
Kontrol berdasarkan PAM ………. 126
Tabel 4.28 Uji Kruskal Wallis Skor Peningkatan Kemampuan Penalaran
Matematis Kelas Kontrol ……… 127
Tabel 4.29 Uji Normalitas Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas
Eksperimen berdasakan Latar Belakang Pendidikan ………… 128
Tabel 4.30 Uji Normalitas Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Kontrol
berdasakan Latar Belakang Pendidikan ………. 129
Tabel 4.31 Uji Homogenitas Varian Populasi Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa
Kelas Eksperimen berdasakan Latar Belakang Pendidikan …… 130
Tabel 4.32 Uji Homogenitas Varian Populasi Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa
Kelas Kontrol berdasakan Latar Belakang Pendidikan …………. 131
Tabel 4.33 Deskripsi Data Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas
Eksperimen berdasakan Latar Belakang Pendidikan Mahasiswa. 133
Tabel 4.34 Rank Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Eksperimen
berdasakan Latar Belakang Pendidikan Mahasiswa ……… 134
Tabel 4.35 Uji Mann-Whitney U Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Kontrol berdasakan Latar Belakang Pendidikan
Mahasiswa ……… 135
Tabel 4.36 Deskripsi Data Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Kontrol
berdasakan Latar Belakang Pendidikan Mahasiswa ……… 136
Tabel 4.37 Rank Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa Kelas Kontrol berdasakan
Latar Belakang Pendidikan Mahasiswa ………... 137
Tabel 4.38 Uji Mann-Whitney U Skor Peningkatan Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa
Mahasiswa ……….
Tabel 4.39 Karakteristik Model Pembelajaran ……… 172
DAFTAR LAMPIRAN
Lampiran A Lampiran A-1 Lampiran A-2 Lampiran A-3 Lampiran B Lampiran B-1 Lampiran B-2 Lampiran B-3 Lampiran B-4 Lampiran C Lampiran C-1 Lampiran C-2 Lampiran C-3 Lampiran C-4 Lampiran C-5 Lampiran C-6Lembar Pertimbangan ……….
Hasil Pertimbangan Mengenai Validitas Isi dan Muka Tes Kemampuan Komunikasi, Penalaran, dan Koneksi
Matematis Mahasiswa………..
Data Hasil Uji Coba Soal Tes Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa …………..
Rencana Pembelajaran ………
Lembar Kerja Mahasiswa Pembelajaran Scientific Debate.
Lembar Observasi Pembelajaran Scientific Debate………..
Kisi-kisi dan Soal Kemampuan Komunikasi, Penalaran dan Koneksi Matematis Mahasiswa ………
Skor Pretes dan Postes Kemampuan Komunikasi
Matematis Mahasiswa Kelas Eksperimen ………..
Skor Pretes dan Postes Kemampuan Penalaran Matematis Mahasiswa Kelas Eksperimen ………
Skor Pretes dan Postes Kemampuan Koneksi Matematis Mahasiswa Kelas Eksperimen ………
Skor Pretes dan Postes Kemampuan Komunikasi
Matematis Mahasiswa Kelas Kontrol ……….
Skor Pretes dan Postes Kemampuan Penalaran Matematis Mahasiswa Kelas Kontrol ………...
Skor Pretes dan Postes Kemampuan Koneksi Matematis Mahasiswa Kelas Kontrol ………...
Lampiran C-7
Lampiran C-8
Skor PAM dan Asal Sekolah Kelas Eksperimen …………
Skor PAM dan Asal Sekolah Kelas Kontrol ………...
BAB I
PENDAHULUAN
A.
Latar Belakang Masalah
Integral dan turunan adalah konsep yang penting dalam matematika. Integral
dan turunan merupakan dua operasi utama di dalam kalkulus. Prinsip-prinsip integral
diformulasikan oleh Isaac Newton and Gottfried Leibniz pada abad 17 dengan
memanfaatkan hubungan erat yang ada antara anti turunan dan integral tentu, yaitu
suatu hubungan yang memungkinkan kita untuk menghitung secara mudah nilai yang
sebenarnya dari banyak integral tentu tanpa perlu memakai jumlah Riemann.
Hubungan ini disebut teorema dasar kalkulus. Melalui teorema dasar kalukulus
mereka mengembangkan konsep integral yang dikaitkan dengan turunan. Sehingga
integral dapat didefinisikan sebagai anti turunan.
Definisi secara modern tentang integral dikemukakan oleh Riemann dengan
gagasan pertamanya adalah jumlah Riemann. Gagasan ini memunculkan kaitan antara
integral tentu dengan luas daerah. Secara umum, integral tentu menyatakan batasan
luas daerah yang tercakup di antara kurva y = f(x) dan sumbu-x dalam selang [a,b].
Luas bagian-luas bagian yang berada di bagian atas sumbu-x diberikan tanda positif,
sedangkan luas bagian-luas bagian yang berada di bagian bawah sumbu-x diberikan
tanda negatif.
Integral memiliki aplikasi yang luas dalam bidang sains dan industri. Sebagai
tertentu, penggunaan kecepatan pesawat ulang-alik Endeavour untuk menentukan
ketinggian yang dicapai pada waktu tertentu, penggunaan pengetahuan tentang
konsumsi energi untuk menentukan energi yang digunakan di suatu tempat pada suatu
hari. Selain itu, dalam beberapa bidang, integral juga digunakan untuk memecahkan
persoalan yang berkaitan dengan volume, panjang kurva, perkiraan populasi, keluaran
kardiak, gaya pada bendungan, usaha, surplus konsumen, bisbol, dan lain-lain.
Berdasarkan peta konsep integral, integral tak tentu diperoleh dari konsep
turunan. Turunan digunakan untuk mendefinisikan konsep anti turunan yang
menghasilkan sifat-sifat aljabar integral dan dengan teorema dasar kalkulus digunakan
untuk mendefinisikan integral tentu dan memunculkan sifat-sifat aljabar integral tentu.
Dari integral tentu dapat digunakan untuk mendefinisikan dan menghitung panjang,
luas, volume yang memuat juga konsep volume benda putar, usaha/kerja, momen, dan
pusat masa. Untuk menyelesaikan persoalan pada konsep integral tentu maka muncul
teknik pengintegralan yang bersifat integral parsial dan dengan menggunakan aturan
rantai maka muncul aturan substitusi yang mencakup juga substitusi trigonometri.
Di Perancis, konsep integral diperkenalkan pada siswa secondary education
(17 - 18) tahun, yang disajikan dalam bentuk definisi secara tradisional dalam bentuk
fungsi primitif. Pada tahun 1972, diperkenalkan integral kalkulus yang meliputi:
definisi jumlah Riemann untuk fungsi numerik dari variabel real pada interval
terbatas; teorema terintegrabel dari fungsi kontinu dan fungsi monoton. Setelah
reformasi tahun 1982, kembali lagi melihat integral sebagai fungsi primitif dan
sebagai daerah yang berada dibawah fungsi positif, serta memperkenalkan contoh
Di Indonesia, konsep integral diberikan pada siswa-siswa Sekolah Menengah
Atas (SMA) yang meliputi: (1) pengertian integral; (2) integral tak tentu; (3) integral
tertentu; (4) menentukan luas daerah; dan (5) menentukan volume benda putar. Untuk
tingkat Perguruan Tinggi, kalkulus integral merupakan bagian dari mata kuliah
Kalkulus, materi yang diberikan meliputi: (1) integral tentu sebagai pengabstrakan
berbagai permasalahan nyata; (2) definisi integral fungsi kontinu dengan aturan lima
langkah dan interpretasi setiap langkah; (3) perumusan bentuk integral untuk berbagai
situasi nyata; (4) aljabar integral: sifat kelinearan, integral pada suatu selang dan
integral pada sub selangnya; (5) pengertian fungsi primitif dan sifatnya. Integral suatu
fungsi sebagai fungsi batas atasnya, teorema dasar I dan II dalam kalkulus, primitif
suatu fungsi sebagai integral tak tentu, primitif dan integral tentu fungsi-fungsi
sederhana; (6) sifat kelinearan integral tak tentu, pengintegralan parsial, metode
substitusi sederhana; serta (7) teknik pengintegralan yang meliputi: metode substitusi,
substitusi trigonometri, integral fungsi rasional dengan menguraikan atas fungsi
rasional sederhana (partial fraction), integral fungsi trigonometri yang dijadikan
integral fungsi rasional, pengintegralan parsial.
Kemampuan integral yang diujikan untuk tingkat SMU dan sederajat adalah:
(1) menghitung integral tak tentu; (2) menghitung integral tertentu fungsi aljabar dan
fungsi trigonometri; (3) menghitung luas daerah; dan (4) menghitung volume benda
putar. Kemampuan yang diujikan tersebut, masih berkisar sekitar pemahaman konsep,
dan termasuk dalam kategori tingkat rendah dalam tingkat berfikir matematis tingkat
tinggi. Hal ini dicirikan dengan soal yang berbentuk: mengingat, menerapkan rumus
dalam kasus sederhana atau dalam kasus serupa. Menurut Polya kemampuan yang
diujikan ini termasuk pada: (1) pemahaman mekanikal yang dicirikan oleh mengingat
dan menerapkan rumus secara rutin dan menghitung secara sederhana dan (2)
pemahaman induktif, yaitu menerapkan rumus atau konsep dalam kasus sederhana
atau dalam kasus serupa. Kemampuan ini tergolong pada kemampuan tingkat rendah.
Padahal standar kompetensi lulusan (SKL) yang harus dicapai untuk konsep integral
adalah memahami konsep integral dari fungsi aljabar dan fungsi trigonometri serta
mampu menerapkannya dalam pemecahan masalah.
Walaupun kemampuan yang diujikan masih termasuk dalam kategori tingkat
rendah dan belum sesuai dengan SKL, namun beberapa hasil penelitian membuktikan
bahwa dalam tingkat rendah pun hasil belajar siswa untuk konsep integral ini masih
termasuk dalam kategori rendah dibandingkan dengan materi matematika lainnya.
Rendahnya kemampuan siswa dalam memahami konsep integral dikemukakan oleh
Orton (1983) bahwa nilai rata-rata hasil evaluasi untuk materi integral memiliki nilai
terendah, yaitu 1,895 untuk tingkat persekolahan dan 1,685 untuk tingkat perguruan
tinggi pada skala 0 s.d 4, dibandingkan dengan materi dalam Kalkulus yang lainnya
seperti: barisan, limit, dan turunan. Orton mengklasifikasi kesalahan siswa ke dalam
tiga kategori yaitu: (1) Structural errors: muncul dari beberapa kesalahan dalam
melihat hubungan-hubungan yang terlibat dalam masalah atau pada grafik beberapa
prinsip-prinsip yang penting untuk menyelesaikan masalah. (2) Arbitrary errors:
kesalahan tidak sesuai aturan atau muncul secara kebetulan dan kesalahan pada
mengambil perhitungan dari pembatas. (3) Executive errors: melibatkan
dipahami. Selain itu, kesulitan lain yang muncul melibatkan kesulitan tentang
penggunaan penyajian grafik yang relevan. Siswa biasanya dapat menghitung integral
dari fungsi polinomial secara benar dan berhasil untuk soal-soal yang berbentuk
tentukanlah atau hitunglah, tetapi untuk soal yang berupa aplikasi atau terapan pada
umumnya mereka kesulitan dalam membentuk model matematikanya. Serta sangat
minimnya siswa dalam memahami simbol yang digunakan.
Sabella dan Redish (2011) menyatakan bahwa kebanyakan mahasiswa di
perguruan tinggi pada kelas konvensional memiliki pemahaman yang dangkal dan
tidak lengkap tentang konsep dasar dalam kalkulus. Romberg and Tufte (1987)
menyatakan bahwa para mahasiswa memandang matematika sebagai kumpulan dari
konsep dan teknis yang statis untuk diselesaikan tahap demi tahap. Dalam
pembelajaran matematika, mahasiswa hanya diminta untuk menyelesaikan,
menggambarkan dalam bentuk grafik, menemukan, mengevaluasi, menentukan, dan
menghitung dalam suatu model yang sudah jelas. Mereka jarang ditantang untuk
menyelesaikan masalah-masalah matematika tingkat tinggi (Ferrini-Mundy 627).
Hasil uji coba UN 2010 yang diberikan kepada 879 siswa SMA di kota
Bandung menunjukkan bahwa siswa yang mampu menjawab benar untuk konsep
integral hanya 30,22%. Kondisi ini tentu saja belum mencapai ketuntasan secara
kelompok, artinya suatu pembelajaran dikatakan berhasil bila ketuntasan belajar siswa
secara kelompok mencapai 65%. Sedangkan hasil uji coba UN 2011 yang diikuti oleh
1578 siswa di kota Bandung, juga menunjukkan kemampuan siswa yang masih
rendah dalam konsep integral yaitu hanya 6,7% siswa yang mampu menjawab benar
Hal ini merupakan masalah yang cukup serius tentang pemahaman siswa SMA untuk
konsep integral. Kelemahan ini dapat dipandang dari berbagai aspek seperti: siswa,
guru, materi, dan pendukung lainnya.
Mempelajari kecenderungan pembelajaran matematika saat ini, penerapan
keempat pilar UNESCO, serta pentingnya penguasaan kompetensi matematika untuk
kehidupan peserta didik, tentu saja kondisi di atas sangat memprihatinkan khususnya
bagi siswa yang melanjutkan pendidikannya pada jurusan matematika.
Ketidaktuntasan siswa dalam materi integral tersebut tentu saja akan berdampak pada
perkuliahan Kalkulus. Padahal Kalkulus ini sangat terkait dengan mata kuliah lainnya
dan merupakan pondasi untuk mempelajari mata kuliah selanjutnya seperti: Persamaan
Differensial, Analisis Real, Aljabar, Statistika Matematika, juga untuk mata kuliah
lain yang bersifat aplikasi seperti Fisika dan Kimia. Adapun tujuan yang ingin dicapai
oleh mata kuliah Kalkulus adalah:
1. Pemahaman konsep dengan baik dan benar, meliputi: kemampuan
mengungkapkan konsep dengan benar dengan kata-kata sendiri, mampu
mengidentifikasi penerapan konsep yang benar dan yang salah, serta mampu
menginterpretasikan konsep dalam berbagai situasi sehingga mampu
menggunakannya dengan baik dan benar.
2. Penguasaan keterampilan teknis, yaitu kemampuan dalam berbagai manipulasi
matematika yang tepat.
3. Terbiasa berfikir logis (logical reasoning), meliputi: mampu dan terbiasa
dilakukan serta mampu dan terbiasa mempertanyakan sesuatu yang baru dan
berusaha mencari jawabannya dengan mengemukakan alasan yang logis.
Berdasarkan sasaran yang ingin dicapai tersebut, nampak bahwa kemampuan
mahasiswa untuk materi kalukulus ini harus sampai pada kemampuan berfikir tingkat
tinggi yang meliputi kemampuan pemahaman, pemecahan masalah, komunikasi,
penalaran, dan koneksi matematis. Tetapi proses pembelajaran Kalkulus masih
disajikan dalam bentuk konsep-konsep dasar, penjelasan konsep melalui contoh, dan
latihan penyelesaian soal. Proses pembelajaran tersebut pada umumnya dilaksanakan
sejalan dengan pola sajian seperti yang tersedia dalam buku rujukan. Proses
pembelajaran seperti ini lebih cenderung mendorong proses berfikir reproduktif
sebagai akibat dari proses penalaran yang dikembangkan lebih bersifat imitatif. Situasi
seperti ini kurang memberikan ruang untuk meningkatkan kemampuan berfikir tingkat
tinggi serta berfikir kritis dan kreatif bagi mahasiswa, karena mahasiswa cenderung
untuk menyelesaikan masalah integral dengan melihat contoh yang sudah ada,
sehingga ketika diberikan soal non rutin, mahasiswa kesulitan.
Pengembangan kemampuan berfikir matematika tingkat tinggi ini sangat
penting bagi mahasiswa karena dalam semua disiplin ilmu dan dalam dunia kerja
mensyaratkan seseorang untuk mampu: (1) Mengekrepresikan gagasan melalui bicara,
menulis, mendemonstrasikan, dan menggambarkan secara visual dalam berbagai
penyajian yang berbeda; (2) Memahami, menginterpretasikan, dan mengevaluasi
gagasan yang disajikan secara lisan, dalam bentuk tulisan, atau dalam bentuk visual;
(3) Mengkonstruksi, menginterpretasi, dan menghubungkan representasi yang berbeda
dugaan, memformulasikan pertanyaan, dan menarik kesimpulan serta mengevaluasi
informasi; dan (5) Menghasilkan dan menyajikan argumentasi-argumentasi yang
meyakinkan (Secretary’s Commission on Achieving Necessary Skills, 1991).
Kemampuan-kemampuan di atas erat kaitannya dengan kemampuan
komunikasi, penalaran, dan koneksi matematis. Dengan demikian, kemampuan
mahasiswa dalam berkomunikasi, bernalar, dan kemampuan melakukan koneksi
merupakan kompetensi yang harus dimiliki oleh setiap mahasiswa.
Dalam pendidikan matematika, kemampuan berkomunikasi, bernalar, dan
melakukan koneksi merupakan kemampuan tingkat tinggi yang harus dimiliki oleh
mahasiswa untuk menyelesaikan masalah matematika dan masalah kehidupannya
yang dapat dialihgunakan pada setiap keadaan, seperti berfikir kritis, logis dan
sistematis. Hal ini sesuai dengan karakteristik matematika sebagai ilmu yang bernilai
guna yang tercermin dalam peran matematika sebagai bahasa simbolik serta alat
komunikasi yang tangguh, singkat, padat, cermat, tepat, dan tidak memiliki makna
ganda (Wahyudin, 2003). Pernyataan tersebut menunjukkan bahwa matematika
mempunyai peranan yang sangat penting bagi pengembangan pola berfikir mahasiswa
baik sebagai representasi pemahaman terhadap konsep matematika, alat komunikasi,
maupun sebagai alat yang melayani bidang ilmu lainnya.
Melalui kemampuan komunikasi matematis, mahasiswa dapat saling bertukar
pengetahuan dan mengklarifikasi pemahamannya. Proses komunikasi tersebut
membantu mahasiswa membangun makna dan kelengkapan gagasan serta
menghindari miskonsepsi. Aspek komunikasi juga membantu mahasiswa untuk dapat
mahasiswa ditantang dan diminta berargumentasi untuk mengkomunikasikan hasil
pemikiran mereka kepada orang lain baik secara lisan maupun tertulis, maka
mahasiswa belajar untuk menjelaskan dan meyakinkan orang lain, mendengarkan
gagasan atau penjelasan orang lain, dan memberikan kesempatan kepada dirinya untuk
mengembangkan pengalamannya.
Komunikasi matematis bisa terjadi dua arah di mana gagasan matematika
dieksplorasi dari berbagai sudut pandang untuk membantu mahasiswa mempertajam
pemikiran dan membuat hubungan-hubungan (koneksi) serta menilai kebenaran
penyelesaian suatu masalah. Kondisi ini akan membantu mahasiswa mengembangkan
bahasa untuk mengemukakan gagasan matematika dan apresiasi akan kebutuhan
berbahasa secara tepat.
Selain kemampuan komunikasi, kemampuan lain yang harus dikembangkan
adalah kemampuan bernalar. Kemampuan bernalar seseorang dapat terlihat dari
kemampuannya mengatasi berbagai persoalan hidup. Seseorang dengan kemampuan
bernalar tinggi akan selalu mampu dengan cepat mengambil keputusan dalam
menyelesaikan berbagai persoalan dalam kehidupannya. Kemampuan ini didukung
oleh kekuatan daya nalarnya sehingga mampu menghubungkan fakta dan bukti untuk
sampai pada suatu kesimpulan yang tepat. Dengan demikian, pengembangan
kemampuan bernalar menjadi esensial bagi setiap mahasiswa, sebagai bekal agar
mampu melakukan analisis sebelum membuat keputusan dan mampu membuat
argumen untuk mempertahankan pendapat.
Dalam matematika, penalaran diistilahkan sebagai penalaran matematis yang
penalaran matematis tidak hanya diperlukan untuk menyelesaikan masalah yang
berkaitan dengan bidang matematika, tetapi juga diperlukan dalam menyelesaikan
persoalan yang dihadapi dalam kehidupan. Penalaran matematis diperlukan seseorang
ketika dihadapkan pada persoalan, di mana kita harus mengevaluasi argumen dan
menyeleksi beberapa solusi fisibel. Kondisi ini mengisyaratkan bahwa ketika
seseorang dihadapkan pada sejumlah pernyataan atau argumen yang berkaitan dengan
persoalan yang dihadapinya, kemampuan penalaran matematis diperlukan untuk
membuat pertimbangan atau mengevaluasi pernyataan tersebut sebelum membuat
keputusan. Dengan demikian, kemampuan matematis yang dimiliki seseorang tidak
hanya digunakan untuk tujuan perhitungan tetapi juga untuk memberikan argumentasi
atau mengklaim penyajian yang memerlukan kelogisan untuk meyakinkan bahwa cara
berfikir yang dilakukan adalah benar.
Kemampuan lain yang juga penting untuk dikembangkan bagi mahasiswa
adalah kemampuan untuk melakukan koneksi matematis. Kemampuan koneksi ini
akan nampak pula pada kemampuan mahasiswa dalam melakukan komunikasi dan
penalaran. Kemampuan koneksi matematis (mathematical connection) erat kaitannya
dengan pemahaman relasional. Pemahaman relasional menuntut seseorang untuk dapat
memahami lebih dari satu konsep dan melihat hubungan antara konsep-konsep
tersebut serta mampu merelasikannya. Sedangkan kemampuan koneksi matematis
adalah kemampuan seseorang untuk menghubungkan berbagai macam
gagasan-gagasan atau ide-ide matematis yang ada pada dirinya baik dalam bidang matematika
maupun dalam bidang lain serta dunia nyata. Dengan demikian, agar kemampuan
matematis juga harus dikembangkan. Hal ini didasarkan pada kenyataan bahwa
dengan meningkatnya kemampuan koneksi matematis untuk menghubungkan antar
konsep dan ide-ide matematika maka kemampuan pemahaman relasional siswa
tersebut akan ikut bertambah.
Kemampuan matematika yang dikembangkan di atas, sesuai dengan
kompetensi matematika yang dikemukakan oleh Niss (dalam Kusumah, 2012:3) yaitu:
(1) Berfikir dan bernalar secara matematis (mathematical thinking and reasoning); (2)
Berargumentasi secara matematis (mathematical argumentation); (3) Komunikasi
matematis (mathematical communication); (4) Pemodelan (modeling); (5) Problem
possing dan problem solving; (6) Penyajian (representation); (7) simbol; dan (8) Alat
dan teknologi (tool and technology). NCTM (2000) telah mengidentifikasi bahwa,
kemampuan komunikasi, penalaran (reasoning), dan problem solving merupakan
proses yang penting dalam pembelajaran matematika dalam upaya menyelesaikan
masalah-masalah matematika. Kemampuan-kemampuan yang dimiliki mahasiswa
tersebut selanjutnya akan bermuara pada kemampuannya memecahkan masalah
kehidupan yang dihadapinya.
Kemampuan komunikasi, penalaran, dan koneksi matematis ini, hanya dapat
dicapai melalui pembelajaran yang dapat meningkatkan kemampuan-kemampuan
khususnya dalam domain kognitif di samping kemampuan afektif dan psikomotor.
Penelitian Suryadi (2005) tentang pengembangan berfikir tingkat tinggi melalui
pendekatan tidak langsung, terdapat dua hal mendasar yang perlu mendapat
pengkajian serta penelitian lebih lanjut dan mendalam yaitu hubungan siswa-materi
mendorong terjadinya suatu aksi mental, proses pembelajaran harus diawali oleh
sajian masalah yang memuat tantangan bagi mahasiswa untuk berfikir. Selain itu
proses pembelajaran, juga harus dapat memfasilitasi mahasiswa untuk mengkonstruksi
pengetahuan atau konsep secara mandiri sehingga mahasiswa akan mampu
menemukan kembali pengetahuan (reinvention).
Salah satu model pembelajaran yang dapat memenuhi tuntutan di atas adalah
model pembelajaran scientific debate (debat ilmiah). Hal ini didukung oleh hasil
penelitian Legrand et al. (1986), yang mengungkapkan bahwa pengaruh dari
penerapan pembelajaran scientific debate dalam pembelajaran dapat memperbaiki
pemahaman mahasiswa dalam konsep integral pada saat ujian akhir. Hasil penelitian
lain, ditunjukkan oleh Alibert et al. (1987) bahwa penerapan scientific debate dalam
pembelajaran adalah mayoritas mahasiswa mencapai tingkat ketuntasan dalam
memahami konsep integral, selain itu mahasiswa dapat mengetahui bagaimana
mengeskplorasi pengetahuan mereka di mana penyelesaian secara algoritma tidak
diterapkan.
Model pembelajaran scientific debate mampu menciptakan nuansa
interaktivitas yang diharapkan dapat memunculkan collaborative learning, sehingga
peranan dosen dalam kelas tidak lagi dominan tetapi berfungsi sebagai fasilitor yang
akan berperan untuk mengarahkan dan membantu mahasiswa. Model pembelajaran
scientific debate ini berbasis teori belajar konstruktivisme. Dalam implementasi
pembelajarannya dicirikan antara lain: menganut model pembelajaran berbasis
masalah, berorientasi pada mahasiswa, dosen lebih berperan sebagai fasilitator,
(authentic assessment), serta mahasiswa dan dosen secara bersama-sama membentuk
suatu learning community.
Dalam penerapan model pembelajaran scientific debate, mahasiswa dilatih
untuk mengkomunikasikan pengetahuannya melalui debat, dan mahasiswa harus
mampu mempertahankan argumen yang dimilikinya sesuai dengan kebenaran dalam
konsep matematika. Kemampuan untuk berargumentasi ini akan memacu
mengembangkan kemampuan penalaran dan koneksi matematisnya, karena dengan
sendirinya mahasiswa harus mampu berfikir logis dan sistematis, serta mampu
mengaitkan berbagai konsep untuk mempertahankan argumentasinya. Hal ini sesuai
dengan teori konstruktivisme yang menyatakan bahwa pengetahuan diperoleh
mahasiswa, dimana mahasiswa mengkonstruksi pengetahuan sendiri melalui interaksi,
konflik, dan re-equilibration yang melibatkan pengetahuan matematika, mahasiswa
lain, dan berbagai persoalan. Interaksi diatur oleh dosen untuk mengambil
pilihan-pilihan persoalan yang mendasar. Teori belajar yang mendukung agar mahasiswa
mampu mengkonstruksi sendiri konsep atau pengetahuannya, menemukan kembali
(reinvention) dengan cara diskusi, berdebat, dan berbagi ide dengan temannya baik
pada kelompok kecil maupun dalam seluruh kelas dengan bimbingan dosen,
mengaitkan materi yang sedang dipelajari dengan pengetahuan yang telah ada pada
mahasiswa adalah teori belajar dari Piaget, Vygostky, Bruner, Ausubel, dan Dubinsky.
Untuk menunjang keberhasilan penerapan model pembelajaran scientific
debate dalam upaya meningkatkan kemampuan komunikasi, penalaran, dan koneksi
matematis mahasiswa, maka diperlukan suatu bahan ajar dan rencana pembelajaran
ajar serta rencana pembelajaran diperlukan penekanan-penekanan pada
mempertimbangkan materi matematika yang lebih bersifat pemecahan masalah,
menyadari adanya learning obstacles (hambatan pembelajaran), model pembelajaran
dengan scientific debate.
Berdasarkan kondisi di atas, peneliti tertarik untuk mengkaji dan menganalisis
penerapan model pembelajaran scientific debate serta mengklasifikasi
kesulitan-kesulitan mahasiswa dalam mempelajari konsep integral dalam upaya meningkatkan
kemampuan komunikasi, penalaran, dan koneksi matematis. Adapun judul penelitian
yang dilakukan adalah: “Pembelajaran dengan Scientific Debate untuk Meningkatkan
Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis Mahasiswa dalam
Konsep Integral.
B.
Rumusan Masalah
Berdasarkan latar belakang masalah di atas, peneliti dapat merformulasikan
rumusan masalah penelitian sebagai berikut:
1. Apakah terdapat perbedaan peningkatan kemampuan komunikasi, penalaran,
dan koneksi matematis antara mahasiswa yang pembelajaran matematikanya
dengan model pembelajaran Scientific Debate dengan mahasiswa yang
pembelajaran matematikanya dengan model pembelajaran konvensional?
2. Apakah terdapat perbedaan peningkatan kemampuan komunikasi dan koneksi
matematis menurut interaksi antara mahasiswa yang pembelajaran
mahasiswa yang pembelajaran matematikanya dengan model pembelajaran
konvensional ditinjau dari pengetahuan awal matematika (PAM) mahasiswa?
3. Apakah terdapat perbedaan peningkatan kemampuan penalaran matematis
antara mahasiswa yang pembelajaran matematikanya dengan model
pembelajaran Scientific Debate dengan mahasiswa yang pembelajaran
matematikanya dengan model pembelajaran konvensional ditinjau dari
pengetahuan awal matematika (PAM) mahasiswa?
4. Apakah terdapat perbedaan peningkatan kemampuan komunikasi, penalaran,
dan koneksi matematis antara mahasiswa yang pembelajaran matematikanya
dengan model pembelajaran Scientific Debate dengan mahasiswa yang
pembelajaran matematikanya dengan model pembelajaran konvensional
ditinjau dari latar belakang pendidikan mahasiswa?
5. Bagaimana strategi penyelesaian mahasiswa terhadap
permasalahan-permasalahan yang diberikan terkait dengan materi integral baik mahasiswa
dengan model pembelajaran Scientific Debate maupun mahasiswa yang
pembelajaran matematikanya dengan model pembelajaran konvensional?
6. Kesalahan, kekeliruan, atau kekurangan serta kesulitan apa yang dialami
mahasiswa ditinjau dari proses penyelesaian soal matematika?
C.
Tujuan Penelitian
Berdasarkan rumusan masalah di atas, maka tujuan yang ingin dicapai adalah
1. Menganalisis secara komprehensif perbedaan peningkatan kemampuan
komunikasi, penalaran, dan koneksi matematis antara mahasiswa yang
pembelajaran matematikanya dengan model pembelajaran Scientific Debate
dengan mahasiswa yang pembelajaran matematikanya dengan model
pembelajaran konvensional ditinjau dari keragaman serta sifat berfikir
matematis mahasiswa.
2. Menganalisis perbedaan peningkatan kemampuan komunikasi dan koneksi
matematis menurut interaksi antara mahasiswa yang pembelajaran
matematikanya dengan model pembelajaran Scientific Debate dengan
mahasiswa yang pembelajaran matematikanya dengan model pembelajaran
konvensional ditinjau dari pengetahuan awal matematika (PAM) mahasiswa?
3. Menganalisis perbedaan peningkatan kemampuan penalaran matematis antara
mahasiswa yang pembelajaran matematikanya dengan model pembelajaran
Scientific Debate dengan mahasiswa yang pembelajaran matematikanya
dengan model pembelajaran konvensional ditinjau dari pengetahuan awal
matematika (PAM) mahasiswa?
4. Menganalisis perbedaan peningkatan kemampuan komunikasi, penalaran, dan
koneksi matematis antara mahasiswa yang pembelajaran matematikanya
dengan model pembelajaran Scientific Debate dengan mahasiswa yang
pembelajaran matematikanya dengan model pembelajaran konvensional dilihat
dari latar belakang pendidikan mahasiswa.
5. Menganalisis strategi penyelesaian mahasiswa terhadap
dengan model pembelajaran Scientific Debate maupun mahasiswa yang
pembelajaran matematikanya dengan model pembelajaran konvensional.
6. Mengidentifikasi dan mendeskripsikan secara komprehensip kesalahan,
kekeliruan, atau kekurangan serta kesulitan yang dialami mahasiswa ditinjau
dari proses penyelesaian soal matematika.
D.
Manfaat Penelitian
Adapun manfaat yang diharapkan dari hasil penelitian ini adalah:
1. Dengan penerapan model pembelajaran scientific debate, mahasiswa akan
terlatih untuk mengkomunikasikan pengetahuannya melalui debat, sehingga
mahasiswa akan mampu mempertahankan argumen yang dimilikinya sesuai
dengan kebenaran dalam konsep matematika. Kemampuan untuk
berargumentasi ini akan memacu mengembangkan kemampuan komunikasi,
penalaran dan koneksi matematisnya, karena dengan sendirinya mahasiswa
ditantang untuk mampu mengkomunikasikan pengetahuannya, berfikir logis
dan sistematis, serta mampu mengaitkan berbagai konsep untuk
mempertahankan argumentasinya.
2. Model pembelajaran scientific debate mampu menciptakan nuansa
interaktivitas antara dosen dengan mahasiswa dan antara mahasiswa dengan
mahasiswa, sehingga dapat memunculkan collaborative learning. Dalam
kondisi ini dosen dapat pula memperoleh pengetahuan dari interaksi tersebut.
3. Bagi peneliti, dari hasil analisis terhadap perbedaan kemampuan serta
integral diharapkan dapat mengantisipasinya melalui penerapan model
pembelajaran scientific debate sehingga dapat menyusun dan mengembangkan
bahan ajar serta buku ajar yang dapat digunakan sebagai acuan bagi para
pengajar.
4. Pembuat kebijakan, agar lebih memahami bahwa model pembelajaran
scientific debate dalam matematika merupakan model pembelajaran yang
dapat meningkatkan aspek-aspek kognitif kemampuan matematis seperti
pemahaman, pemecahan masalah, penalaran, komunikasi, dan koneksi
matematis serta dapat meningkatkan aspek-aspek afektif ketika berkomunikasi
dan berdebat dalam kelompok.
E.
Definisi Operasional
Variabel-variabel dalam penelitian, didefinisikan sebagai berikut:
1. Kemampuan berfikir tingkat tinggi matematis adalah pemahaman matematis,
problem solving matematis, komunikasi matematis, penalaran matematis, dan
koneksi matematis. Adapun kemampuan berfikir tingkat tinggi matematis yang
dikembangkan dalam penelitian disertasi ini meliputi: komunikasi matematis,
penalaran matematis, dan koneksi matematis.
a. Komunikasi matematis adalah kemampuan untuk berkomunikasi yang
meliputi kegiatan penggunaan keahlian menulis, menyimak, menelaah,
menginterpretasikan, dan mengevaluasi ide, simbol, istilah, serta informasi
matematika yang diamati melalui proses mendengar, mempresentasi, dan
(1) kemampuan merepresentasikan objek-objek nyata dalam gambar,
diagram, atau model matematika; (2) kemampuan menjelaskan ide, situasi,
dan relasi matematika secara tulisan dalam bentuk gambar, tabel, diagram,
atau grafik; (3) kemampuan menyatakan peristiwa sehari-hari dalam
bahasa atau simbol matematika; (4) kemampuan mengubah suatu bentuk
representasi matematis ke bentuk representasi matematis lainnya.
b. Penalaran diartikan sebagai proses berfikir sebagai upaya penjelasan dalam
upaya memperlihatkan hubungan antara dua atau lebih berdasarkan
sifat-sifat, atau hukum-hukum tertentu yang sudah terbukti kebenarannya
melalui langkah-langkah tertentu dan berakhir dengan sebuah kesimpulan
(Kusumah, 1986). Kemampuan penalaran matematis yang dikembangkan
meliputi: (1) kemampuan memberikan penjelasan terhadap model, gambar,
fakta, sifat, hubungan, atau pola yang ada; (2) kemampuan memperkirakan
jawaban dan proses solusi, dan menggunakan pola dan hubungan untuk
menganalisis situasi matematik, menarik analogi dan generalisasi; (3)
kemampuan menyusun dan menguji konjektur, memberikan lawan contoh;
(4) kemampuan mengikuti aturan inferensi. Menyusun argumen yang valid,
memeriksa validitas argumen.
c. Koneksi matematis adalah keterkaitan antara konsep matematika,
matematika dengan ilmu lain, dan matematika dengan kehidupan
sehari-hari. Kemampuan koneksi matematis yang dikembangkan meliputi: (1)
kemampuan mencari dan memahami hubungan berbagai representasi
bidang studi lain atau kehidupan sehari-hari; (3) kemampuan memahami
representasi ekuivalen konsep atau prosedur yang sama; (4) kemampuan
mencari koneksi satu prosedur ke prosedur lain dalam representasi yang
ekuivalen; (5) kemampuan menggunakan koneksi antar topik matematika,
dan antara topik matematika dengan topik lain.
2. Model pembelajaran scientific debate adalah model pembelajaran yang
implementsinya menganut model pembelajaran berbasis masalah, berorientasi
pada mahasiswa, guru lebih berperan sebagai fasilitator, menganut sistem
asesmen yang bersifat menyatu dengan proses pembelajaran (authentic
assessment), serta mahasiswa dan guru secara bersama-sama membentuk suatu
learning community. Model pembelajaran scientific debate meliputi tiga tahap
yaitu: (1) Guru memulai dan mengorganisir hasil-hasil pernyataan siswa.
Hasil-hasil ini ditulis pada papan tulis tanpa mengevaluasi kebenaran
pernyataan tersebut; (2) Pernyataan diberikan kembali pada siswa untuk
mempertimbangkan dan mendiskusikannya. Kemudian siswa memberikan
kembali kepada guru setelah mereka mendiskusikannya, di mana setiap
persoalan telah didukung oleh beberapa cara, diberikan argumentasinya,
dibuktikan, pembuktian bahwa sesuatu tidak benar, dengan counter-examples,
dan lain-lain; (3) Pernyataan dibenarkan dengan menunjukkan
teorema-teorema atau aturan yang berlaku, sedangkan beberapa yang dibangun sebagai
pernyataan yang tidak benar disajikan sebagai “pernyataan yang salah”,
3. Pengetahuan awal matematika adalah pengetahuan yang dimiliki mahasiswa
sebelum pembelajaran berlangsung, pengetahuan ini diukur melalui hasil akhir
BAB III
METODE PENELITIAN
A.
Disain Penelitian
Penelitian ini adalah eksperimen dengan disain kelompok pretes postes.
Penelitian ini diawali dengan pengembangan perangkat pembelajaran dan instrumen
penelitian. Dalam penelitian ini, terdapat perlakuan terhadap kelompok eksperimen,
yaitu kelompok mahasiswa dengan pendekatan pembelajaran scientific debate (X).
Adapun kelompok kontrol memperoleh pendekatan pembelajaran matematika secara
konvensional. Setelah proses pembelajaran, diberikan tes kemampuan komunikasi,
penalaran dan koneksi matematis (O). Disain penelitiannya adalah disain kelompok
kontrol pretes-postes dengan bentuk:
O X O
O O
Di mana:
O = Pretes dan Postes pada kelompok eksperimen dan kelompok kontrol.
X = Model pembelajaran Scientific Debate.
Data yang dianalisis adalah perbedaan peningkatan kemampuan komunikasi,
penalaran, dan koneksi matematis mahasiswa antara kelompok eksperimen dan
kelompok kontrol. Data dikelompokkan berdasarkan pendekatan pembelajaran
(scientific debate dan konvensional), pengetahuan awal mahasiswa (tinggi, sedang,
B.
Populasi dan Sampel
Populasi dalam penelitian ini adalah mahasiswa Jurusan Pendidikan
Matematika di Indonesia, yang setingkat mutunya dengan Jurusan Pendidikan
Matematika Universitas Islam Negeri (UIN) Bandung. Pemilihan subjek penelitian
mahasiswa dipertimbangkan berdasarkan kemampuan mahasiswa, yang diharapkan
dapat dioptimalkan melalui penerapan pendekatan pembelajaran scientific debate.
Sampel diambil dari mahasiswa Jurusan Pendidikan Matematika Fakultas
Tarbiyah UIN Bandung, yang mengambil Mata Kuliah Kalkulus 2, yaitu mata kuliah
wajib yang diberikan pada semester II. Mata Kuliah Kalkulus 2 dipilih karena sangat
terkait dengan mata kuliah lainnya dan merupakan pondasi untuk pemahaman mata
kuliah selanjutnya seperti: Persamaan Differensial, Analisis Real, Aljabar, juga untuk
mata kuliah lain yang bersifat aplikasi. Dengan penerapan pendekatan scientific debate
diharapkan kemampuan komunikasi, penalaran, dan koneksi matematis mahasiswa ini
dapat meningkat.
Untuk melihat secara lebih mendalam pengaruh penerapan kedua pendekatan
terhadap hasil belajar mahasiswa, maka penelitian ini melibatkan dua faktor yaitu
pengetahuan awal mahasiswa (PAM) dan latar belakang pendidikan mahasiswa. PAM
dikategorikan menjadi tinggi, sedang, dan kurang berdasarkan pada nilai mata kuliah
matematika yang sudah ditempuh oleh mahasiswa. Tingkatan kemampuan awal
mahasiswa ini sangat penting dan juga harus diperhatikan secara serius dalam
pendidikan mahasiswa dikelompokan menjadi SMU (Sekolah Menengah Umum) dan
MA (Madarasah Aliyah).
C.
Variabel Penelitian
Variabel penelitian merupakan suatu kondisi yang dimanipulasi, dikendalikan
atau diobservasi oleh peneliti. Penelitian ini melibatkan tiga jenis variabel: (1) variabel
bebas, yaitu pembelajaran scientific debate dan pembelajaran konvensional; (2)
variabel terikat, yaitu peningkatan kemampuan komunikasi, penalaran, dan koneksi
matematis; dan (3) variabel kontrol, yaitu tingkatan kemampuan awal mahasiswa
dalam matematika yang dikategorikan ke dalam tingkatan pandai, sedang, dan rendah,
serta latar belakang pendidikan mahasiswa.
D.
Teknik Pengumpulan Data dan Teknik Analisis Data
Teknik pengumpulan data diambil dari keluaran instrumen, berupa hasil pretes
dan postes serta data pengetahuan awal matematika (PAM). Sedangkan teknik
pengolahan data dilakukan sesuai dengan tujuan yang ingin dicapai dalam penelitian
ini. Data yang dianalisis untuk tujuan 1, 2, 3, dan 4 adalah skor hasil pretes, postes,
dan PAM.
Untuk menganalisis data PAM yang diperoleh, terlebih dahulu dilakukan uji
normalitas dan homogenitas terhadap data PAM. Berdasarkan uji Shapiro-Wilk
diketahui bahwa skor pengetahuan awal mahasiswa berdistribusi normal dan
bervariansi homogen maka satistik uji yang digunakan untuk menguji apakah terdapat
dilakukan uji t. Pengujian terhadap PAM ini dilakukan dalam upaya ingin mengetahui
kondisi awal dari subyek yang diteliti. Pengujian hipotesis yang dilakukan yaitu:
Ho : 1 =2
H1 : 1 2
1 adalah rata-rata skor PAM kelompok eksperimen, sedangkan 2 adalah rata-rata
skor PAM kelompok kontrol. Adapun statistik uji yang digunakan adalah uji-t dengan
asumsi varians populasi tidak diketahui dan homogen. Rumus yang digunakan adalah:
2 1
2 1
1 1
n n s
x x t
Kriteria pengujian, terima Ho jika –t(1-1/2) t t(1-1/2) dimana t(1-1/2) didapat dari
daftar tabel distribusi t dengan derajat bebas n1 + n2– 2 dan peluang (1-1/2). Untuk
harga-harga t lainnya Ho ditolak.
Data hasil pretes dan postes digunakan untuk menganalisis perbedaan
peningkatan kemampuan hasil pembelajaran scientific debate yang dibandingkan
dengan pendekatan pembelajaran konvensional terhadap kemampuan komunikasi,
penalaran, dan koneksi matematis mahasiswa. Adapun faktor-faktor yang berinteraksi
dalam eksperimen ini adalah pendekatan pembelajaran (scientific debate dan
konvensional), pengetahuan awal mahasiswa (tinggi, sedang, dan rendah),
kemampuan komunikasi, penalaran, dan koneksi matematis, serta latar belakang
pendidikan mahasiswa yang diklasifikasi menjadi dua yaitu SMU dan MA.
Berdasarkan rumusan masalah dan hasil kajian secara teoritis, maka hipotesis
1. Peningkatan kemampuan komunikasi matematis mahasiswa yang
menggunakan model pembelajaran scientific debate lebih baik dari pada
mahasiswa yang menggunakan model pembelajaran konvensional.
2. Peningkatan kemampuan penalaran matematis mahasiswa yang menggunakan
model pembelajaran scientific debate lebih baik dari pada mahasiswa yang
menggunakan model pembelajaran konvensional.
3. Peningkatan kemampuan koneksi matematis mahasiswa yang menggunakan
model pembelajaran scientific debate lebih baik dari pada mahasiswa yang
menggunakan model pembelajaran konvensional.
4. Terdapat interaksi antara model pembelajaran yang digunakan (scientific
debate dan konvensional) dengan pengetahuan awal mahasiswa (PAM)
terhadap peningkatan kemampuan komunikasi matematis.
5. Terdapat perbedaan peningkatan kemampuan penalaran antara mahasiswa
dengan model pembelajaran scientific debate dan mahasiswa dengan model
pembelajaran konvensional yang didasarkan pada pengetahuan awal
mahasiswa (PAM).
6. Terdapat interaksi antara model pembelajaran yang digunakan (scientific
debate dan konvensional) dengan pengetahuan awal mahasiswa (PAM)
terhadap peningkatan kemampuan koneksi matematis.
7. Perbedaan latar belakang pendidikan mahasiswa tidak memberikan efek yang
signifikan terhadap peningkatan kemampuan komunikasi matematis
8. Perbedaan latar belakang pendidikan mahasiswa tidak memberikan efek yang
signifikan terhadap peningkatan kemampuan penalaran matematis mahasiswa.
9. Perbedaan latar belakang pendidikan mahasiswa tidak memberikan efek yang
signifikan terhadap peningkatan kemampuan koneksi matematis mahasiswa.
Untuk tujuan 1 yaitu melihat kategori peningkatan kemampuan komunikasi,
penalaran, dan koneksi matematis antara mahasiswa yang pembelajaran
matematikanya dengan pendekatan Scientific Debate dan mahasiswa yang
pembelajaran matematikanya dengan pembelajaran konvensional digunakan uji gain
ternormalisasi menurut Meltzer (2002) dengan rumus:
.
Dengan kategori gain ternormalisasi (g) adalah: g < 0,3 adalah rendah; 0,3 ≤ g
< 0,7 adalah sedang; dan 0,7 ≤ g adalah tinggi. Selanjutnya, dilakukan uji normalitas
dan homogenitas terhadap data peningkatan kemampuan komunikasi, penalaran, dan
koneksi matematis. Berdasarkan uji Shapiro-Wilk diketahui bahwa data peningkatan
kemampuan komunikasi, penalaran, dan koneksi matematis tidak seluruhnya
berdistribusi normal. Dengan demikian, statistik uji yang digunakan untuk menguji
apakah terdapat perbedaan peningkatan kemampuan komunikasi, penalaran, dan
koneksi matematis antara mahasiswa yang mengikuti pembelajaran dengan scientific
debate dengan mahasiswa yang mengikuti pembelajaran secara konvensional
digunakan uji Mann-Whiney (U).
Untuk tujuan 2, yaitu hipotesis 4 dan 6 adalah melihat perbedaan peningkatan
kemampuan mahasiswa komunikasi dan koneksi matematis menurut interaksi antara
mahasiswa yang pembelajaran matematikanya dengan konvensional ditinjau dari
pengetahuan awal matematika mahasiswa (tinggi, sedang, dan kurang) digunakan
ANOVA dua jalur dan Uji Scheffe karena data berdistribusi normal dan bervariansi
[image:40.612.113.526.182.578.2]homogen. Tabel Anova dua jalur disajikan dalam Tabel 3.1 berikut,
Tabel 3.1 Rancangan Anova Dua Jalur
Kemampuan PAM
Metode Belajar Konvensional
(A1)
Scientific Debate (A2)
Komunikasi (B1)
Tinggi (C1) Sedang (C2) Rendah (C3)
Koneksi (B2)
Tinggi (C1) Sedang (C2) Rendah (C3)
Untuk melihat faktor-faktor mana yang berinteraksi antara pendekatan
pembelajaran dengan PAM terhadap peningkatan kemampuan komunikasi dan
koneksi matematis mahasiswa maka dilanjutkan dengan Uji Scheffe.
Untuk tujuan 3 yaitu melihat perbedaan peningkatan kemampuan penalaran
matematis antara mahasiswa yang pembelajaran matematikanya dengan Scientific
Debate dengan mahasiswa yang pembelajaran matematikanya secara konvensional
ditinjau dari pengetahuan awal matematika mahasiswa (tinggi, sedang, dan kurang)
digunakan satistik uji nonparametrik dengan Uji Kruskal Wallis karena data skor
kemampuan penalaran matematis kelas eksperimen dan kelas kontrol pada level tinggi
tidak berdistribusi normal, sedangkan untuk level lainnya berdistribusi normal.
Untuk tujuan 4 yaitu melihat perbedaan peningkatan kemampuan komunikasi,
penalaran, dan koneksi matematis antara mahasiswa yang pembelajaran
pembelajaran matematikanya secara konvensional ditinjau dari latar belakang
pendidikan mahasiswa (SMU, MA, dan Kejuruan) digunakan uji nonparametrik
dengan uji Mann-Whitney (U). Karena, berdasarkan uji normalitas terhadap data skor
peningkatan kemampuan komunikasi, penalaran, dan koneksi matematis mahasiswa
yang didasarkan pada latar belakang pendidikan mahasiswa, diperoleh hasil bahwa
untuk kelas eksperimen menunjukkan data tersebut tidak berdistribusi normal.
Sedangkan untuk kelas kontrol menunjukkan berdistribusi normal. Sedang untuk uji
homogenitas varians kedua kelompok baik eksperimen maupun kontrol menunjukkan
variansinya homogen.
Sementara untuk tujuan 5 dan 6 dianalisis menggunakan klasifikasi dari Orton,
di mana kesalahan dan kekeliruan mahasiswa dikelompokkan ke dalam tiga kategori
yaitu: (1) Structural errors: muncul dari beberapa kesalahan dalam melihat
hubungan-hubungan yang terlibat dalam masalah atau pada grafik beberapa prinsip-prinsip yang
penting untuk menyelesaikan masalah. (2) Arbitrary errors: kesalahan tidak sesuai
aturan atau muncul secara kebetulan dan kesalahan pada mengambil perhitungan dari
pembatas. (3) Executive errors: melibatkan kesalahan-kesalahan melakukan
manipulasi meskipun prinsip-prinsip yang dilibatkan telah dapat dipahami.
E.
Waktu Penelitian
Penelitian ini dilaksanakan mulai bulan Juni 2011 sampai Juni 2012 dengan
rincian sebagai berikut:
September 2011 – Nopember 2011 : Uji instrumen penelitian dan
analisis
Desember 2011- Desember 2012 : Pretes, pembelajaran, postes.
Pengolahan dan analisis data serta
penulisan laporan.
F.
Pengembangan Instrumen
Instrumen utama yang digunakan dalam penelitian disertasi meliputi: 1) tes
kemampuan komunikasi matematis, penalaran matematis, dan koneksi matematis yang
akan digunakan untuk mengevaluai hasil belajar mahasiswa dan menganalisis
kesulitan-kesulitan mahasiswa dalam menyelesaikan masalah untuk konsep integral;
2) lembar observasi untuk dosen; dan 3) lembar observasi untuk mahasiswa.
1. Tes Kemampuan Komunikasi, Penalaran, dan Koneksi Matematis
Tipe soal tes kemampuan komunikasi, penalaran, dan koneksi matematis
yang dikembangkan berbentuk tes uraian dengan tujuan untuk mengukur higher level
learning outcomes. Alasan digunakannya tes bentuk uraian, karena dengan tes bentuk
uraian diharapkan kemampuan mahasiswa dalam penguasaan materi dapat terlihat
melalui langkah-langkah penyelesaian soal yang diberikan. Hanya mahasiswa yang
telah menguasai dengan benarlah yang dapat memberikan jawaban yang baik dan
benar. Adapun langkah-langkah pelaksanaan yang dilakukan dalam pengembangan
a. Menganalisis tujuan dan sasaran yang ingin dicapai
Pengembangan instrumen penelitian berupa tes harus mengacu pada aspek
kompetensi yang harus dikuasai oleh setiap mahasiswa, sehingga analisis tujuan dan
sasaran yang ingin dicapai mutlak diperlukan. Sebelum instrumen tes dibuat, maka
terlebih dahulu dilakukan analisis terhadap standar kompetensi dan kompetensi dasar
agar setiap item tes sesuai dengan standar kompetensi dan kompetensi dasar yang
sudah ditentukan. Dengan demikian tujuan dan sasaran yang ingin dicapai oleh
instrumen tes tersebut dapat dicapai secara akurat. Disamping itu, analisis terhadap
standar kompetensi dan kompetensi dasar juga ditujukan untuk melihat apakah
instrumen tes tersebut telah memenuhi validitas konstruk sebagai dasar dalam
pengembangan instrumen tes. Validitas konstruk adalah validitas yang diperoleh
melalui penyusunan instrumen yang didasarkan kepada kharakteristik subjek yang
dituju atau perilaku subjek yang diharapkan. Validitas konstruk ditentukan oleh
perhatian terhadap perlakuan psikologis atau susun (konstruk) yang akan diukur oleh
soal tesnya.
Tes yang dikembangkan digunakan untuk dua tujuan utama meliputi: 1)
memberikan umpan balik bagi mahasiswa tentang hasil belajar mahasiswa dalam
setiap tahap proses belajarnya. Tes ini berfungsi juga sebagai tes formatif. Hasil tes ini
dijadikan petunjuk tentang kesulitan mahasiswa dalam bagian-bagian tertentu dari
bahan ajar yang digunakan dan 2) menilai efektifitas sistem pembelajaran secara
keseluruhan. Tes ini akan digunakan sebagai tes awal dan tes akhir dalam ujicoba
Yani Ramdani, 2013
Pembelajaran Dengan Scientific Debate Untuk Meningkatkan Kemampuan Komunikasi, Penalaran, Dan Sasaran yang ingin dicapai dalam mengembangkan tes kemampuan
komunikasi, penalaran, dan komunikasi matematis meliputi: 1) meningkatkan tingkat
kemajuan mahasiswa; 2) mengukur pertumbuhan dan perkembangan mahasiswa; 3)
merangking mahasiswa berdasarkan kemampuannya; 4) mendiagnosis kesulitan
mahasiswa; 5) mengevaluasi hasil pengajaran; 6) mengetahui efektifitas pencapaian
kurikulum; dan 7) memotivasi.
b. Menyusun peta konsep utama berdasarkan tujuan dan sasaran
Instrumen tes yang dikembangkan harus benar-benar mampu mengukur apa
yang harus diukur, seperti berbagai kompetensi yang harus dikuasai oleh mahasiswa.
Untuk itu, diperlukan peta konsep untuk mengelompokkan berbagai kompetensi
tersebut secara esensial. Hal ini sesuai dengan pernyataan Kumaidi (2008) bahwapeta
konsep merupakan pengelompokan kompetensi esensial dan level pemahaman seperti
yang diamanatkan dalam kurikulum, agar tes yang dikembangkan itu benar-benar
mampu mengukur berbagai pencapaian kompetensi yang harus dikuasai mahasiswa.
Formulasi materi pembelajaran dalam bentuk peta konsep akan memudahkan
penyusunan soal tes dan mampu mengidentifikasi keterkaitan kompetensi yang harus
dicapai, sehingga ketika soal tes dirancang kita akan memperoleh gambaran yang jelas
bagaimana sebuah tes harus dikembangkan sesuai dengan kompetensi yang harus
dikuasai oleh setiap mahasiswa. Dengan demikian, untuk mengembangkan bahan ajar
dan intrumen penelitian disusun peta konsep utama yang didasarkan pada tujuan dan
sasaran yang ingin dicapai. Adapun kegiatan penyusunan instrumen disajikan dalam
Diagram 3.1 sebagai berikut:
PERUMUSAN TUJUAN: 1.Menggunakan
KEGIATAN BELAJAR:
Diagram 3.1
Rancangan Penyusunan Instrumen Penelitian
Sedangkan peta konsep untuk integral adalah sebagai berikut, PENGEMBANGAN ALAT
EVALUASI:
1.Menentukan jenis tes yang akan digunakan untuk menilai tercapai tidaknya tujuan.
2.Menyusun tes untuk menilai masing-masing tujuan
PELAKSANAAN: 1. Mengadakan tes awal. 2. Menyampaikan materi
pelajaran.
3. Mengadakan tes akhir. 4. Perbaikan.
PENGEMBANGAN PROGRAM KEGIATAN:
1. Merumuskan materi pelajaran. 2. Menetapkan metode yang dipakai. 3. Memilih alat pelajaran dan sumber
Peta Konsep Integral
c. Menyusun matriks rancangan t