PENYELESAIAN SISTEM PERSAMAAN LINEAR JARANG DENGAN CARA TERPARTISI MENURUT MARSHALL C PEASE

(1)

MENURUT MARSHALL C PEASE

SKRIPSI

Diajukan Untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Teknik Jurusan Teknik Informatika

Disusun Oleh: M Edi Waskito

005314068

JURUSAN TEKNIK INFORMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

(2)

PARTITIONING MATRIX METHOD

A Thesis

Presented as Partial Fulfillment of the Requirements to Obtain the Sarjana Teknik Degree

in Informatic Engineering

by M Edi Waskito

005314068

DEPARTEMENT OF INFORMATIC ENGINEERING

FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY

YOGYAKARTA

(3)

(4)

(5)

PERNYATAAN

Dengan ini saya sebagai penulis tugas akhir menyatakan dengan

sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian

karya orang lain, kecuali pemikiran, metode atau hasil penelitian orang lain yang

diambil disebutkan dengan jelas sebagai acuan.

Yogyakarta, September 2007

M Edi Waskito

Penulis

(6)

v Karyaku ini kupersembahkan untuk :

Yesus Kristus Tuhan dan juru selamatku yang selalu membimbingku dan memberikan apa yang aku butuhkan.

Keluargaku tercinta, khususnya Bapak dan Ibu yang telah memberikan

seluruh kasih dan sayangnya dalam membimbing untuk terus menghangatkan saya. Kedua kakak saya widi dan papih terima kasih atas perhatian dan

dukungannya.

(7)

Ketakutan yang ditakuti adalah ketakutan diri sendiri (Albert Camus)

Kesalahan terbesar yang bisa dibuat oleh seseorang adalah takut membuat kesalahan

(Elbert Hubbard)

Kegagalan adalah kesempatan untuk memulai lebih cerdik (John C Maxwell)

Kalau anda berpikir anda kalah, anda kalah.

Kalau anda berpikir anda tidak berani, anda tidak berani.

Kalau anda ingin menang tetapi berpikir anda tidak bisa,

Hampir dapat dipastikan anda tidak bisa.

Perjuangan hidup tidak selalu dimenangkan

Oleh orang yang lebih kuat atau lebih cepat,

Tetapi cepat atau lambat, orang yang menang

Adalah orang yang berpikir dia bisa menang. (John C Maxwell)

“Kamu adalah garam dunia… kamu adalah terang dunia…” (Matius:5)

(8)

Banyak metode yang dapat digunakan untuk menyelesaikan sistem persamaan

linear. Salah satu cara untuk menyelesaikan sistem persamaan linear yaitu dengan

partisi matriks yang digunakan Marshall C Pease. Cara yang digunakan Marshall C

Pease yaitu metode bordering, dari metode bordering dapat diterapkan metode

updating untuk menyelesaikan sistem persamaan linear.

Dalam tugas akhir ini, penyelesaian sistem persamaan linear diutamakan pada

matriks jarang. Penyelesaian matriks jarang akan menimbulkan banyak permasalahan

tetapi permasalahan itu dapat diselesaikan menggunakan metode updating,

penggunaan metode updating perlu disertai penukaran baris atau penukaran kolom

agar dapat dicapai hasil yang sesuai.

(9)

Many methods are able to be used solve the equation linear system. One of the

way of solving the equation linear system that is by partitioning matrix used by Marshall

C Pease. Way of partition used by Marshall C Pease is bordering method, from bordering

method earn in applied by updating method to finish the equation linear system.

In final project, prefered solving with sparse matrix. Solving the sparse matrix

will generate many problem, but that problems can be solved to use the updating method,

usage of updating method require to be accompanied by the line conversation or column

conversation so that be reachable appropriate result.

(10)

Puji syukur penulis haturkan kepada Tuhan Yang Maha Esa atas segala

karunia yang diberikan, sehingga penulis dapat menyelesaikan tugas akhir yang

berjudul “Penyelesaian Sistem Persamaan Linear Jarang dengan Cara terpartisi Menurut Marshall C Pease” ini dengan baik. Penulisan ini merupakan salah satu syarat untuk memperoleh gelar Sarjana Teknik di

Universitas Sanata Dharma pada program studi Teknik Informatika.

Selama penulisan skripsi ini penulis telah memperoleh bantuan dan

bimbingan dari berbagai pihak. Oleh karena itu penulis mengucapkan terima kasih

kepada:

1. Bapak, Ibu dan kedua kakak saya yang telah memberi dorongan baik moril

maupun spiritual.

2. Bapak Prof. Dr Ir Soesianto Ph. E Bs. C selaku pembimbing I yang telah

banyak membantu dan membimbing selama mengerjakan tugas akhir ini.

3. Ibu Merry, ST. selaku pembimbing II yang telah memberi banyak masukan

dan bimbingan serta perhatian demi terselesaikannya tugas akhir ini.

4. Ibu Agnes Maria Polina, S.Kom., M.Sc. dan Bapak JB. Budi Darmawan, S.T.,

M. Sc. selaku panitia penguji pada ujian pendadaran penulis

5. Seluruh staff dan dosen pengajar di Univeritas Sanata Dharma pada umumnya

dan Jurusan Teknik Informatika pada khususnya

6. Indra, Aang, Wisnu “Jongos”Ari, Toni terima kasih atas dukungannya dan

pemacu semangat.

7. Temen-temen kos : gogon, pram, gusur, sukur, rendi, aming, lukas, agung,

boy, Andi, citro, topan , adi, cemong + erni, arot, serta teman-teman yang

tidak dapat saya sebut satu persatu terima kasih atas bantuan, dukungan,

terutama atas nasehat–nasehat dan kebersamaannya

(11)

9. Temen-temen gua maria kerep : lehek, mas ari, mas eko, mas bambang, heru,

nono, pak moh yang selalu dukungan dan doanya

10.temen-temen yang telah menyediakan pinjaman komputer : seti”kasut” &

yayuk , pinjaman laptop: toni+ponco, linda adikku yang ikut serta

mendukung.

11.Semua pihak yang tidak dapat penulis sebutkan satu persatu, yang telah

memberikan dukungan serta bantuannya guna penyusunan karya tulis ini

Penulis menyadari sepenuhnya bahwa Tugas Akhir ini masih jauh dari

kesempurnaan dan masih banyak kekurangan. Oleh karena itu penulis sangat

mengharapkan kritik dan saran yang bersifat membangun demi perbaikan lebih

lanjut. Penulis berharap semoga Tugas akhir ini dapat bermanfaat dan berguna

bagi pembaca.

Yogyakarta, September 2007

Penulis

(12)

HALAMAN JUDUL ... i

Halaman persetujuan... ii

Halaman pengesahan ... iii

Halaman pernyataan... iv

Motto... v

Halaman persembahan ... vi

Kata pengantar ... vii

Abstraksi ... ix

Abstract ... x

Daftar Isi ... xi

Daftar Gambar ... xv

Daftar Tabel ... xviii

BAB I PENDAHULUAN... 1

1.1 Latar Belakang... 1

1.2 Perumusan Masalah ... 2

1.3 Batasan Sistem... 2

1.4 Tujuan Skripsi... 3

1.5 Metode Penelitian ... 3

1.6 Sistematika Penyusunan Skripsi ... 3

BAB II DASAR TEORI ... 5

2.1. Bentuk matriks dari suatu linear ... 7

(13)

2.3.1. Pengertian matriks ... 10

2.3.2. Jenis-jenis matriks ... 11

2.4. Operasi-operasi atas matriks... 12

2.4.1. Operasi pertambahan ... 12

2.4.2. operasi pengurangan ... 12

2.4.3. Operasi perkalian ... 13

2.4.4. operasi transpose... 14

2.4.5. operasi invers ... 14

2.4.6. operasi penukaran baris dan kolom... 15

2.5. Partisi matriks ... 16

2.6. Penyelesaian sistem persamaan linear dengan cara terpartisi menurut Marshall C Pease ... 18

2.7. Contoh penyelesaian sistem persamaan linear dengan metode updating .... 20

2.7.1. Penyelesaian sistem persamaan linear pada matriks 5x5... 20

2.7.2. Penyelesaian sistem persamaan linear jarang pada matriks 10x10.... 26

2.7.3. Penyelesaian sistem persamaan linear jarang dengan operasi penukaran baris pada matriks 10x10... 29

2.7.4. Penyelesaian sistem persamaan linear jarang dengan operasi penukaran kolom pada matriks 10x10 ... 57

2.8. Handle grafik ... 87

2.9. Obyek yang digunakan dalam handle grafik ... 87

(14)

2.9.2.1. obyek uicontrol frame ... 88

2.9.2.2. obyek uicontol pushbutton... 89

2.9.2.3. obyek uicontol axes dan text... 90

2.9.2.4. obyek uicontrol edit text ... 90

2.9.2.5. obyek open file... 91

2.9.3. Perintah pada matlab... 91

BAB III ANALISA dan PERANCANGAN... 93

3.1. Analisa sistem ... 93

3.2. Masalah yang dihadapi ... 94

3.3. Pemecahan masalah ... 95

3.4. Perancangan... 97

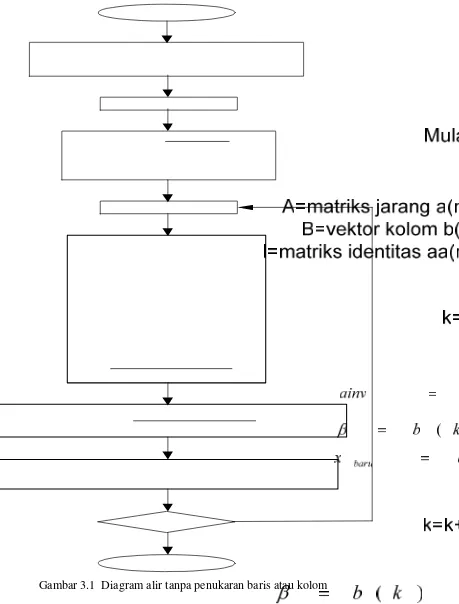
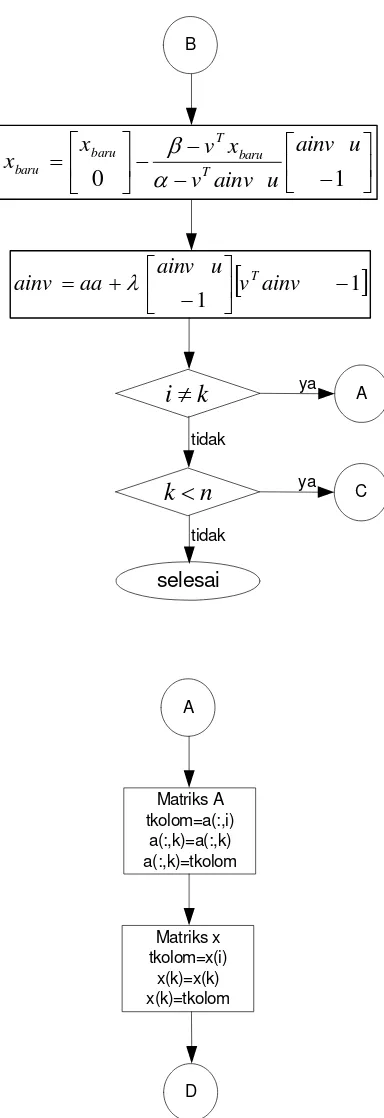
3.4.1 Algoritma dan diagram alir... 98

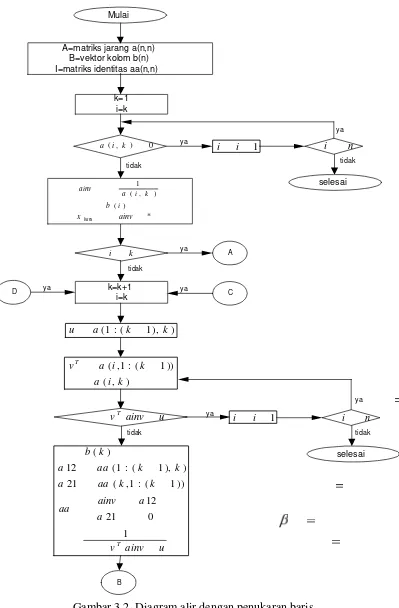
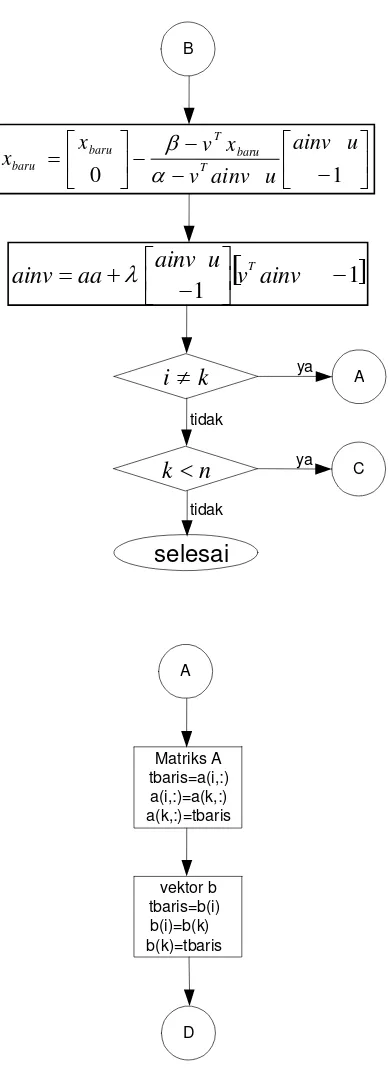
3.4.2.1. Algorima dan diagram alir tanpa penukaran baris atau kolom . 98 3.4.2.2. Algoritma dan diagram alir dengan penukaran baris... 101

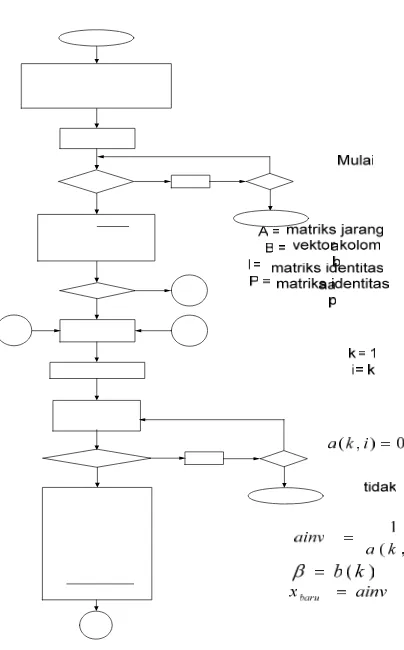
3.4.2.3. Algoritma dan diagram alir dengan penukaran kolom ... 105

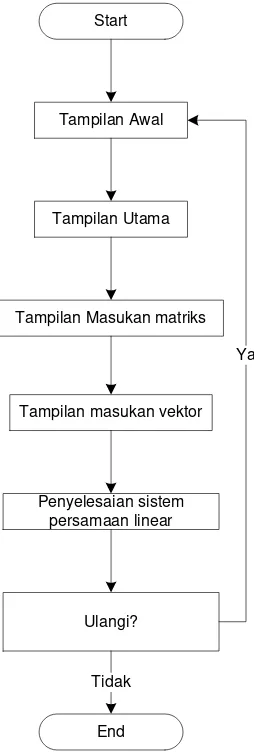
3.4.2 Desain antar muka... 109

3.4.2.1. Desain antar muka star up... 109

3.4.2.2. Desain antar muka utama... 110

3.4.2.3. Desain antar muka info ... 112

3.4.2.4. Desain antar muka otomatis masukan matriks... 112

3.4.2.5. Desain antar muka masukan vektor ... 113

(15)

4.1. Implementasi program ... 116

4.2. Implementasi antar muka... 124

4.2.1 Implementasi tampilan pembuka ... 125

4.2.2 Implementasi tampilan utama ... 126

BAB V Analisa hasil... 140

5.1. Analisa bahasa pemrograman ... 140

5.2. Hasil uji coba program... 140

5.2.1 Matriks uji ... 141

5.2.2 Hasil uji ... 147

5.3. Analisis ... 153

5.4. Kelebihan dan kekurangan program ... 154

5.4.1 Kelebihan... 154

5.4.2 Kekurangan ... 154

BAB VI PENUTUP ... 156

6.1 Kesimpulan ... 156

6.2 Saran ... 156

(16)

berpotongan,(b) kedua garis sejajar, dan (c) kedua garis berhimpit... 7

2. Gambar 3.1 Diagram alir tanpa penukaran baris atau kolom ... 101

3. Gambar 3.2 Diagram alir dengan penukaran baris ... 104

4. Gambar 3.3 Diagram alir dengan penukaran baris(lanjutan) ... 105

5. Gambar 3.4 Diagram alir dengan penukaran kolom. ... 108

6. Gambar 3.5 Diagram alir dengan penukaran kolom(lanjutan) ... 109

7. Gambar 3.6 Desain antar muka star up ... 111

8. Gambar 3.7 Desain antar muka utama ... 111

9. Gambar 3.8 Desain antar muka info... 113

10. Gambar 3.9 Desain antar muka otomatis masukan matriks ... 113

11. Gambar 3.10 Desain antar muka masukan vektor... 114

12. Gambar 3.11 Diagram alir desain antar muka... 115

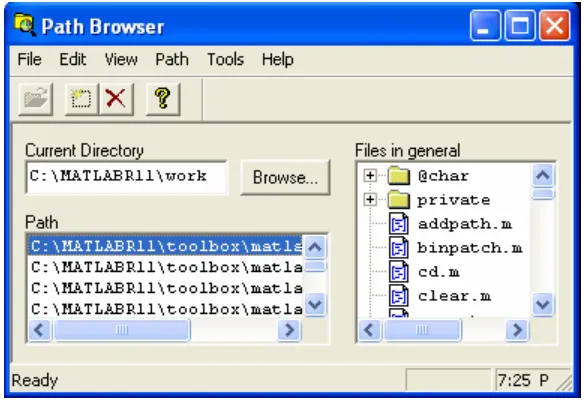
13. Gambar 4.1 Path browse... 124

14. Gambar 4.2 Browse ... 125

15. Gambar 4.3 Tampilan awal ... 125

16. Gambar 4.4 Tampilan utama ... 126

17. Gambar 4.5 Tampilan masukan matriks secara file ... 127

18. Gambar 4.6a Tampilan masukan matriks secara pengguna ... 128

19. Gambar 4.6b Tampilan masukan matriks secara pengguna ... 128

20. Gambar 4.7Tampilan masukan matriks secara otomatis ... 129

21. Gambar 4.8 Tampilan pesan masukan matriks... 129

(17)

24. Gambar 4.10b Tampilan masukan vektor secara pengguna ... 131

25. Gambar 4.11 Tampilan masukan vektor secara file ... 132

26. Gambar 4.12 Tampilan penyelesaian persamaan linear ... 133

27. Gambar 4.13a Tampilan cek slide 1 ... 134

28. Gambar 4.13b Tampilan cek slide 2... 134

29. Gambar 4.13c Tampilan cek slide 3 ... 135

30. Gambar 4.13d Tampilan cek slide 4... 135

31. Gambar 4.13e Tampilan cek slide 5 ... 136

32. Gambar 4.13f Tampilan cek slide 6 ... 136

33. Gambar 4.14 Tampilan pilihan lihat matriks... 137

34. Gambar 4.15 Tampilan lihat matriks... 137

35. Gambar 4.16 Tampilan simpan matriks ... 138

36. Gambar 4.17 Tampilan info ... 138

37. Gambar 4.18 Tampilan info tentang program ... 139

38. Gambar 5.1 Matriks 64x64 dengan unsur-unsur 10% tak nol... 144

(18)

47. Gambar 5.10 Matriks 128x128 dengan unsur-unsur50% tak nol.... 147

(19)

1. Tabel 5.1 keluaran matriks 2x2 ... 148

(20)

BAB I

PENDAHULUAN

1.1. Latar Belakang

Sering kali invers matriks sangat dibutuhkan, seperti halnya pada

penyelesaian sistem persamaan linear. Dalam kenyataannya invers matriks

digunakan sebagai pengganti operasi pembagian, karena pada operasi matriks

tidak dikenal adanya operasi pembagian. Dengan adanya operasi invers

matriks, suatu persamaan linear Ax=b jika matriks A dan vektor b diketahui

maka x dapat dicari penyeleasaiannya dengan mengalikan invers matriks

A(A-1) dengan matriks A dan matriks B. A-1Ax=A-1b menjadi Ix=b karena pada dasarnya perkalian suatu matriks dengan matriks I tidak akan

mempengaruhi matriks tersebut.

Jika dalam penyelesaian suatu sistem persamaan linear pada suatu

matriks jarang, pasti akan membuat kita merasa sulit karena ukurannya relatif

sangat besar. Dalam penyelesaian inversnya pun akan menemui banyak

permasalahan karena mengandung unsur nolnya tersebut.

Dari sekeliling masalah terdapat banyak metode yang digunakan

dalam penyelesaian sistem persamaan linear disamping itu terdapat

komputer yang sangat membantu dalam perhitungan tanpa ada kesalahan,

mengurangi kesalahan pembulatan dan keefesienan waktu dalam

menyelesaikannya (menyelesaikan sistem dengan kecepatan maksimum).

(21)

matriks tersebut menjadi matriks dari ukuran terkecil hingga matriks yang

akan dicari invers matriksnya.

Dari uraian tersebut, maka dalam penulisan tugas akhir ini penulis akan

mengambil topik “ Penyelesaian sistem persamaan linear jarang dengan cara terpartisi menurut Marshall C Pease ”.

1.2. Rumusan Masalah

Dari topik di atas, maka rumusan permasalahan dalam penulisan tugas

akhir ini adalah sebagai berikut :

“ Bagaimana membangun sebuah aplikasi sistem bantu dalam penyelesaian

sistem persamaan linear pada matriks jarang dengan cara terpartisi menurut

Marshall C Pease ?“.

1.3. Batasan Masalah

Dalam penyelesaian persamaan sistem linear invers matriks jarang

dengan cara terpartisi menurut Marshall C. Pease, penulis membatasi

penyelesaian tersebut untuk matriks yang ada invers matriksnya (matriks tak

singular) dan hanya penyelesaian pada sistem persamaan linear dengan cara

terpartisi menurut Marshall C. Pease.

1.Metode yang dipakai untuk menyelesaikan sistem persamaan linear dari

resep Marshall C Pease

2.Yang dibahas dari masalah yang timbul dari sistem persamaan linear

(22)

3.Dari pemecahan masalah yang dipakai dengan hasil keluaran adalah waktu

komputasi dan beban komputasi.

4.Ukuran matriks yang diteliti adalah 2nx2n dimana n adalah bilangan bulat dari 1 sampai 10. ukuran prosentase besarnya elemen tak nol adalah 10%,

20%, 30%, 40%, dan 50%.

1.4. Tujuan Skripsi

Tujuan dari skripsi ini adalah:

Membangun sebuah aplikasi perangkat lunak yang berfungsi sebagai sebuah

sistem bantu yang mampu menyelesaikan sistem persamaan linear jarang

yang mempunyai invers matriks dengan menggunakan metode dari Marshall

C Pease

1.5. Metode Penelitian

Metodologi yang digunakan adalah studi literatur, yaitu antara lain:

1 Mempelajari materi

2 Mempelajari dan memilih teknik yang digunakan

1.6. Sistematika Penyusunan Laporan

Sistematika penulisan laporan ini terbagi atas enam bab dengan garis

besar sebagai berikut :

BAB I. Pendahuluan

(23)

manfaat, dan sistematika penulisan laporan.

BAB II. Dasar teori

Bab ini berisi landasan teori yang dipakai untuk pembahasan

penulisan tugas akhir.

BAB III. Analisa dan perancangan sistem

Bab ini merupakan bab yang membahas tentang gambaran

perancangan sistem aplikasi yang dibuat Berisi analisis dan

perancangan secara umum, dan perancangan tampilan pembuatan

program aplikasi.

BAB IV. implementasi

Membahas tentang pengkonversian rancangan ke dalam bentuk

program dan menganalisa program tersebut

BAB V. Analisa hasil perangkat lunak

Membahas tentang program yang telah dibuat dan menganalisa

program tersebut.

BAB VI. PENUTUP

Berisi tentang kesimpulan dari pembahasan dan implementasi yang

telah dilakukan dalam penulisan tugas akhir ini serta saran-saran

(24)

BAB II

LANDASAN TEORI

Sistem persamaan linear dalam beberapa variabel adalah persamaan dalam

bentuk polinom yang variabelnya berderajat satu atau nol dan tidak terjadi

perkalian antara varibelnya. Contoh persamaan linear dengan tiga variabel x, y, z

adalah 2x− 3y+105z =5. Sedangkan persamaan x2 −2y =5 dan

7 3

2 + =

− x y

xy bukan merupakan persamaan linear. Yang pertama karena

terdapat suku x2 dan yang kedua karena perkalian dari variabelnya. Sedangkan sistem persamaan linear adalah kumpulan dari berhingga banyaknya persamaan

linear.

Sistem persamaan linear ax+by=c, dua varibel dengan dua persamaan mempunyai bentuk umum, berikut persamaan linear tersebut

⎩ ⎨ ⎧

= +

2 2 2

1 1 1

c y b x a

(2.1)

Sistem persamaan linear disebut konsisten, jika sistem persamaan tersebut

mempunyai sedikitnya satu jawaban. Sedangkan sistem persamaan linear tak

konsisten, jika sistem tersebut tidak mempunyai jawaban.

Seperti yang diketahui persamaan linear ax+by=c dapat digambarkan sebagai garis bidang. Jadi dari sistem persamaan (2.1) dapat digambarkan garis

dan di bidang. Ada tiga kemungkinan kedudukan garis tersebut, yaitu (lihat

gambar 2.1)

1 L

(25)

1. Garis L₁ dan L₂ berpotongan, 2. Garis L₁ dan L₂ sejajar, dan

3. Garis L₁ dan L₂ merupakan satu garis(berimpit).

(a) (b) (c)

gambar 2.1 Kemungkinan dari kedudukan kedua garis di bidang. (a) kedua garis berpotongan, (b) kedua garis sejajar, dan (c) kedua garis berimpit.

Pasangan bilangan (x,y) merupakan jawab dari sistem persamaan (2.1) jika dan hanya jika titik (x,y) terletak pada kedua baris. Dalam hal kemungkinan pertama, hanya ada satu titik yang terletak pada kedua baris. Oleh karena itu,

jawab sistem persamaan(2.1) ini tepat satu. Sedangkan dalam hal kedua, tak ada

titik yang terletak pada kedua baris. Ini mengatakan bahwa sistem persamaan

tersebut tidak mempunyai jawab. Yang ketiga, ada banyak titik terletak pada

kedua garis. Ini berarti bahwa sistem persamaan tersebut mempunyai jawab tak

hingga banyaknya. Dengan demikian ada tiga kemungkinan jawab dari sistem

dari sistem persamaan linear(2.1), yaitu :

1. mempunyai tepat satu jawab;

2. tak mempunyai jawab; atau

3. mempunyai jawab banyak.

Ketiga kemungkinan ini berlaku untuk sembarang sistem persamaan linear.

1 L =L₂

1

L

1

L

2

(26)

2.1 Bentuk matriks dari suatu linear

Perkalian matriks mempunyai suatu penerapan penting pada sistem

persamaan linear. Sembarang sistem persamaan linear m dalam n 1

1 2

12 1

11x a x a x b

a + +L+ _n _n =

2 2

2 22 1

21x a x a x b

a + +L+ n n =

M M M M

m n mn

m x amx a x b

a ₁ ₁+ ₂ +L+ =

Karena dua matriks sama jika dan hanya jika unsur-unsurnya yang

padanan sama, maka kita bisa menggantikan persamaan-persamaan m dalam n

pada sistem ini dengan persamaan matriks tunggal.

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

+ + +

m n

mn m

m

n n

b b b

x a x

a x a

x a x

a x a

x a x

a x a

M L

M M

M

L L

2 1

2 2 1 1

2 2

22 1 21

1 2

12 1 11

Matriks m+1 pada ruas kiri pada persamaan ini bisa ditulis

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

m m

mn m

m

n n

b b b

x x x

a a

a

a a

a

a a

a

M M

L M M M

L L

2 1

2 22 21

1 12

11

jika kita menandai matriks-matriks ini masing-masing dengan A,x, dan b, sistem persamaan asli m dan n peubah telah digantikan oleh persamaan matriks

Ax=b

(27)

2.2 Besaran skalar dan besaran vektor

Dalam fisika, besaran-besaran yang hanya memiliki nilai tunggal (angka

real) disebut juga besaran skalar. Besaran yang memiliki nilai jamak disebut

vektor. Misalnya, kecepatan yang terdapat pada sebuah benda yang bergerak.

Besaran ini memiliki sekurang-kurangnya dua nilai, yaitu besarnya kecepatan

(laju) dan arah geraknya. Maka dalam fisika kecepatan dimengerti sebagai

besaran vektor.

Dalam hal ini besaran vektor diberi arti yang lebih luas. Vektor dapatlah

dipandang sebagai himpunan besaran-besaran dengan indeks yang jelas (untuk

menunjukkan lokasinya dalam himpunan itu). Masing-masing besaran disebut

elemen vektor tersebut.

Dalam penulisan skripsi ini vektor lambang huruf alfabet kecil dengan

garis bawah. Misalnya, diberikan vektor a. Elemen (pada lokasi) ke-i dari vektor a dilambangkan oleh ai.

Vektor a dengan cacah elemen n buah ditulis lengkap sebagai deretan nilai

ai, dengan i = 1, 2,…n,membentuk satu kolomseperti dibawah ini:

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

n

a a a a

a M

3 2 1

Vektor seperti itu disebut vektor-kolom. Jika elemen-elemen tersebut ditulis

berderet membentuk satu baris, maka vektor itu disebut vektor-baris. Kecuali

(28)

Untuk menghemat ruangan penulisan, untuk vektor tersebut diatas ditulis

pula a≡

( )

a_i , dengan I = 1,2…n, dan simbol “≡” dapat dibaca sebagai “didefinisikan sebagai”. Jadi misalnya ai∈R, yaitu bahwa ai bernilai real, maka

secara ringkas dapat ditulis pula a≡(a_i)∈Rn. dalam kontek ini Rn dapat dibaca sebagai “semesta angka real berdimensi n”.

Vektor nol dilambangkan oleh 0, adalah vektor dengan semua elemen

bernilai nol. Salah satu jenis vektor yang ternyata penting adalah vektor basis.

Vektor basis ei adalah vektor dengan semua elemen bernilai nol, kecuali elemen

ke-I bernilai 1. misalnya, vektor basis e3∈RT adalah

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

0 0 0 0 1 0 0

3 e

Tentu saja dalam ruangan berdimensi n ada vektor basis n buah, yaitu .

, , , , ₂ ₃

1 e e en

e K Secara singkat: e_i∈Rn dengan dengan

(Soesianto, 2004)

(29)

2.3 Matriks

2.3.1 Pengertian matriks

Jika vektor membentuk larik berdimensi satu, maka matriks adalah larik

berdimensi dua. Karena memiliki dua indeks, yaitu indeks untuk baris dan indeks

untuk kolom. Matriks diberi lambang dengan huruf alfabet besar. Misalnya

diberikan matriks A. Elemen matriks A pada baris i dan kolom j diberi lambang aij. Indeks pertama i senantiasa menyatakan nomor baris, dan indeks kedua j menyatakan nomor kolom. Jika matriks A itu terdiri atas m baris dan n kolom, secara singkat akan ditulis A=(a_ij),i=1,2,K,mdan j=1,2,K,n. Jika

maka . Ditulis secara lengkap:

R a_ij∈

n m

ij R

a ∈ ×

( )

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ≡

1 31 21 11

m ij

a a a a

a A

M

2 32 22 12

m

a a a a

M

3 33 23 13

m

a a a a

M

L K K K

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

mn n n n

a a a a

M 3 2 1

Karena tiap kolom dari matriks membentuk vektor kolom, maka juga

dapat ditulis,

[

1

)

(a a

A≡ _ij = a₂ a₃ K,a_n

]

, dengan a_j∈Rn, j=1,2,K,n. Cara penulisan penulisan lain adalah berdasarkan baris:

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

T n T T T

a a a a

a M

(30)

Superskrip (…)T ditambahkan untuk menunjukkan bahwa lambang yang bersangkutan membentuk vektor baris. Karena itu, agar masih menghemat

tempat, biasanya ditulis pula:

[

T

a

a= ₁ aT₂ aT₃ K,aT_n

]

T

(Soesianto,2004)

2.3.2 Jenis-jenis matriks a Matriks nol (Mnol)

Matriks dengan semua elemennya bernilai nol. Matriks nol diberi

lambang 0 .

b Matriks bujur sangkar (MBS)

Matriks bujur sangkar adalah matriks yang mempunyai cacah baris

sama dengan cacah kolom.

c Matriks satuan

Matriks satuan termasuk matriks diagonal, dilambangkan dengan I, didefinisikan sebagai matriks diagonal dengan semua elemen diagonal

bernilai satu. Matriks satuan juga sering disebut sebagai matriks

identitas

d Matriks jarang

Matriks jarang adalah matriks dengan cacah baris dan cacah kolom

yang relatif besar dengan bagian terbesar dari elemen-elemennya

(31)

e Matriks permutasi

Matriks ini adalah matriks identitas yang baris-baris atau kolomnya

mengalami pertukaran.

(Soesianto,2004)

2.4 Operasi-operasi atas matriks 2.4.1 Operasi pertambahan

Matriks dan matriks hanya dapat dipertambahkan, jika m =

p dan n = q. Artinya, pertambahan dua matriks A dan matriks B

hanya dapat terlaksana jika cacah baris untuk A dan matriks B serta cacah kolom A dan matriks B sesuai (compatible). Hasilnya adalah matriks C dengan sifat, bahwa: c

) (mxn

A B(pxq)

ij : = aij +bij. Operasi ini bersifat

komutatif, artinya A + B = B + A.

2.4.2 Operasi pengurangan

Matriks dan matriks hanya dapat diperkurangkan, jika

m = p dan n = q. Artinya, pengurangan dua matriks A dan matriks B

hanya dapat terlaksana jika cacah baris untuk A dan matriks B serta cacah kolom A dan matriks B sesuai (compatible). Hasilnya adalah matriks C dengan sifat, bahwa: c

) (mxn

A B₍_pxq₎

(32)

2.4.3 Operasi perkalian

a Perkalian sebuah nilai real dengan matriks

Jika matriks A dikalikan dengan sebuah nilai real β∈R, maka baik β A maupun Aβ menghasilkan matriks C yang memiliki dimensi sama dengan A.

) (c_ij

C≡ dengan c_ij:=βa_ij

Artinya, matriks C diperoleh dengan mengalikan tiap elemen dari matriks A dengan nilai real β.

b Perkalian vektor dengan matriks

Perkalian matriks dengan vektor dapat memberikan

hasil vektor. Hasil kali A ) (mxn

A x(n)

x adalah vektor kolom sedangkan xTA adalah vektor baris.

c Perkalian matriks dengan matriks

Operasi perkalian atas matriks A dan matriks B tersebut diatas

menghasilkan matriks C≡(c_ij), dengan

∑

= = n

i ij ij

ij a b

c

1

:

Secara implisit telah diisyaratkan dalam rumus ini bahwa

operasi perkalian tersebut hanya terlaksana jika cacah kolom n dari matriks A sama dengan cacah baris p dari matriks B adalah sama. Sebagai akibatnya, matriks C memiliki cacah baris m dan cacah kolom

(33)

Atas dasar dapatlah dimengerti bahwa pada umumnya operasi

perkalian tidak komutatif. Artinya :

BA AB≠

2.4.4 Operasi transpos

Jika A adalah sembarang matriks m * n, maka transpos A, dinyatakan dengan AT, didefinisikan sebagai matrriks n * m yang didapatkan dengan mempertukarkanbaris dan kolom dari A; yaitu, kolom pertama dari AT

adalah baris pertama dari A, kolom kedua dari AT adalah baris kedua dari

A, dan seterusnya. 2.4.5 Operasi invers

Operasi invers mengganti peran operasi pembagian. Matriks A

disebut invers matriks B, atau matriks B disebut matriks invers matriks A jika dan hanya jika

I BA AB= =

Atas dasar itu digunakan notasi: A = B-1atau B = A-1. Dapat juga dikatakan bahwa:

I A A AA−1 = −1 =

I B B BB−1 = −1 =

Dari kenyataan ini dapat disimpulkan, bahwa matriks satuan I

(34)

Sifat komutatif pada operasi invers harus ditegaskan disini, bahwa

operasi invers hanya terdapat pada matriks bujur sangkar (MBS). Artinya

matriks persegi panjang (MPP) tidak memiliki invers. Sebaliknya,

pastilah bahwa tidak semua matriks bujur sangkar memiliki invers.

Contoh sederhana adalah matriks bujur sangkar dengan semua elemen

nilai nol. Matriks bujur sangkar seperti itu disebut matriks singular.

Lawannya (yaitu yang memiliki invers) disebut matriks tak singular.

(Soesianto,2004)

2.4.6 Operasi penukaran baris dan kolom

Operasi penukaran baris atau kolom merupakan operasi yang

mendasar dari matriks. Operasi penukaran baris atau kolom biasanya

ditujukan untuk sistem persamaan linear guna menghindari operasi yang

buntu ditengah jalan meskipun sistem persamaan linear tersebut

mempunyai penyelesaian.

Syarat yang harus dipenuhi jika menggunakan operasi penukaran

baris yaitu penukaran baris tersebut dengan langkah yang belum

(35)

2.5 Partisi matriks

Matriks dapat ditulis dalam bentuk terpartisi (tersekat). Tiap bagian

matriks disebut submatriks. Tiap submatriks memiliki cacah baris dan kolom

yang lebih kecil. Dibawah ini diberikan sebuah contoh:

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

=

0 2 0 2 4

A =

0 1 2 5 2

−

2 3 5 2 0

−

1 7

3 1 2

− −

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

0 1 2 0 0

⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

0 2 0 2 4

L

0 1 2 5 2

− L

2 3 5 2 0

− L

M M M L M M

1 7

3 1 2

− − L

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

0 1 2 0 0

L

sebelum terpartisi sesudah terpartisi

Sekarang matriks terpartisi A itu dapat ditulis memiliki empat elemen berupa submatriks,

⎢ ⎣ ⎡ =

21 11 A A

A _⎥

⎦ ⎤

22 12 A A

dengan

⎢ ⎣ ⎡ =

2 4

11

A 5

2

⎥ ⎦ ⎤

2 0

⎢ ⎣ ⎡ − =

1 2

12

A _⎥

⎦ ⎤

0 0

⎢ ⎢ ⎢

⎣ ⎡ =

0 2 0

21

A

0 1 2

−

⎥ ⎥ ⎥

⎦ ⎤ −

2 3 5

⎢ ⎢ ⎢

⎣ ⎡− =

1 7

3

22 A

⎥ ⎥ ⎥

⎦ ⎤

6 1 2

Vektor pun dapat dipartisi atas subvektor-subvektor yang lebih kecil

cacah elemennya. Operasi aljabar matriks dapat juga dilaksanakan pada

matriks-matriks dan vektor-vektor terpartisi, dengan catatan, bahwa operasi

(36)

didalamnya juga dapat dilaksanakan. Kesesuaian (compatibility) harus tetap terpenuhi.

Berikut contoh perkalian matriks dalam bentuk terpartisi: misalkan

matriks U dan V terpartisi menurut , dan

Dalam bentuk terpartisi, nyatakan matriks W, hasil perkalian U dan V,

sebagai .

⎢ ⎣ ⎡ =

C A

U _⎥

⎦ ⎤ D B

⎢ ⎣ ⎡ =

G E

V _⎥

⎦ ⎤ H F

⎢ ⎣ ⎡ =

R P

W _⎥

⎦ ⎤ S Q

Menurut aturan operasi perkalian atas matriks,

P = AE + BG Q = AF + BH R = CE + DG S = CF+ DH

Oleh karena itu agar operasi ini dapat dilakukan, haruslah perkalian

A dengan E, B dengan G A dengan F, B dengan H C dengan E, D dengan G C dengan F, D dengan H

Memenuhi syarat yang ditentukan oleh operasi perkalian atas matriks juga.

(37)

2.6 penyelesaian sistem persamaan linear dengan cara partisi menurut Marshall C. Pease

Dalam Journal of the ACM jilid 14 nomor 4 (oktober 1967).

Marshall C. Pease menamplikan relasi matriks dan vektor terpartisi sebagai

berikut:

⎢ ⎣ ⎡

T

v A

⎢ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ α

− −

T

A u

0

1 1

[

1

1 0

0 − ₋

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − λ − ⎥ ⎦ ⎤

A v

A T

−1

]

Disini A sebuah matriks bujur sangkar, u adalah vektor-kolom, vT adalah vektor-baris, dan 0, 0T, serta 0 masing-masing adalah vektor-kolom nol, vektor-baris nol, dan nilai real nol. Ukuran (dimensi) dari matriks dan vektor

harus sesuai (selaras) satu sama lain. Besaran α dan λ adalah besaran real.

Agar hasilnya matriks identitas, haruslah λ

α 1/

1 =

− −

u A vT

atau bahwa

) /(

1 ) /(

1 −vTA−1u+ = −vTA−1u

= α α

λ

Maka syaratagar operasi invers dapat dijalankan adalah bahwa vTA−1u≠α. Dengan kenyataan itu, Pease dalam artikel itu mengusulkan relasi itu

sebagai basis untuk menerapkan invers dari matriks bujur sangkar pada

sembarang dimensi, dengan metode yang disebutnya sebagai “bordering

method”.

Metode bordering menyelesaikan invers matriks secara bertahap.

Dengan mengetahui invers matriks 1x1, maka dapat ditetapkan invers

(38)

invers 3x3, demikian selanjutnya sampai selesai. Matriks akan dapat

ditetapkan jika matriks yang diselesaikan adalah matriks tak singular.

Resep Pease tersebut di atas tidak langsung dapat diterapkan pada

matriks jarang, karena matriks jarang pada umumnya memiliki invers yang

berupa matriks padat (dan itu tidak efesien dari segi memori). Namun resep

itu dapat digunakan untuk menetapkan solusi atas sistem persamaan linear

b x

A = , sekalipun A adalah matriks jarang, dengan menerapkan metode updating di bawah ini.

⎢ ⎣ ⎡ ≡ _T

baru

v A x

1 − ⎥ ⎦ ⎤

α

u

⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣

⎡ −

0 0 0

1

T

A b

β

[

]

⎥_⎦

⎤ ⎢ ⎣ ⎡ − ⎥

⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣

⎡ − ₋

β λ

β

b A

v A

b T

1 1

= ( )

1 0

1 1

1

β

λ _⎥ −

⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣

⎡ − − ₋

b A v u A b

A T

= ( )

1 0

1

β

λ _⎥ −

⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣

⎡ −

lama T lama

x v u A x

Dalam rumusan ini A−1u adalah sebuah vector-kolom. Dengan cara ini tidak ada problem memori sama sekali. Penataan kembali pernyataan di

atas menghasilkan:

⎥ ⎦ ⎤ ⎢ ⎣ ⎡

− −

− − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡

≡ ₋ −

1 0

1

u A u A v

x v x

x _T lama

T lama

baru _α

β

Sekarang dapat disarankan cara elegan untuk mengatasi komplikasi yang

timbul pada sembarang langkah( misalnya dengan cara penukaran baris atau

(39)

(a).penataan elemen-elemen dari vector x sebagai akibat dari operasi penukaran kolom, dan

(b).tidak perlu menghitung kembali A−1u karena hanya vT dan u saja yang berubah.

Jika operasi penukaran baris ini ternyata tidak dapat dijalankan, barulah

ditempuh operasi penukaran kolom. Dalam hal penukaran kolom ini

penghitungan kembali A−1u perlu kiat tersendiri. (Soesianto,2004)

2.7 Contoh penyelesaian sistem persamaan linear dengan metode updating 2.7.1. Penyelesaian sistem persamaan linear pada matriks 5x5

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

5 5 5 5 5

5 4 4 4 4

5 4 3 3 3

5 4 3 2 2

5 4 3 2 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

5 4 3 2 1

x x x x x

=

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

75 61 49 40 35

Penyelesaian:

Matriks A berordo 5x5 maka akan terdapat 5 langkah untuk menyelesaikan

persamaan linear.

• Langkah 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

5 5 5 5 5

5 4 4 4 4

5 4 3 3 3

5 4 3 2 2

5 4 3 2 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

5 4 3 2 1

x x x x x

=

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

(40)

A = 1 A-1 = 1 1 1 1 = =

A β = 35

x = A-1 β

x = 1.35 = 35

• Langkah 2

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 5 5 5 5 5 4 4 4 4 5 4 3 3 3 5 4 3 2 2 5 4 3 2 1 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 4 3 2 1 x x x x x = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 75 61 49 40 35

A = 1 v = 2 u = 2 α =2 β = 40

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 15 30 0 35 1 2 2 30 0 35 1 2 . 1 2 . 1 . 2 2 35 . 2 40 0 35 x ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 15 5 x

[

1

]

1 1

0 0

0 1 ₁

(41)

• Langkah 3 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 5 5 5 5 5 4 4 4 4 5 4 3 3 3 5 4 3 2 2 5 4 3 2 1 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 4 3 2 1 x x x x x = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 75 61 49 40 35 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 2 2 2 1

A v=

[

3 3

]

_⎥

⎦ ⎤ ⎢ ⎣ ⎡ = 3 3 u 3 =

α β = 49

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β [ ] [ ] [ ] ⎥⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 333 , 7 11 0 0 15 5 1 5 , 1 0 5 , 1 11 0 15 5 1 3 3 5 , 0 1 1 1 3 3 5 , 0 1 1 1 3 3 3 15 5 3 3 49 0 15 5 x ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 333 , 7 4 5 x

[

1

]

1 1

0 0

0 1 ₁

(42)

• Langkah 4 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 5 5 5 5 5 4 4 4 4 5 4 3 3 3 5 4 3 2 2 5 4 3 2 1 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 4 3 2 1 x x x x x = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 75 61 49 40 35 ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 3 3 3 3 2 2 3 2 1

A v=

[

4 4 4

]

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 4 4 4 u 4 =

α β =61

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β

[

]

[

]

⎥⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 4 4 4 667 , 0 1 0 1 2 1 0 1 1 4 4 4 667 , 0 1 0 1 2 1 0 1 1 4 4 4 4 333 , 7 4 5 4 4 4 61 0 333 , 7 4 5 x ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 333 , 1 0 0 333 , 1 333 , 4 0 333 , 7 4 5 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 25 , 3 333 , 4 0 0 0 333 , 7 4 5 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 25 , 3 3 4 5 x

[

1

]

1 1

0 0

0 1 ₁

(43)

[

]

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = − ₁ 667 , 0 1 0 1 2 1 0 1 1 4 4 4 1 4 4 4 667 , 0 1 0 1 2 1 0 1 1 333 , 1 1 0 0 0 0 0 667 , 0 1 0 0 1 2 1 0 0 1 1 1 A

[

0 0 1,333 1

]

1 333 , 1 0 0 333 , 1 1 0 0 0 0 0 667 , 0 1 0 0 1 2 1 0 0 1 1 1 − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = − A ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − = − 75 , 0 1 0 0 1 333 , 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 667 , 0 1 0 0 1 2 1 0 0 1 1 1 333 , 1 0 0 333 , 1 778 , 1 0 0 0 0 0 0 0 0 0 0 333 , 1 1 0 0 0 0 0 667 , 0 1 0 0 1 2 1 0 0 1 1 1 A ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − = − 75 , 0 1 0 0 1 2 1 0 0 1 2 1 0 0 1 1 1 A

• Langkah 5

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 5 5 5 5 5 4 4 4 4 5 4 3 3 3 5 4 3 2 2 5 4 3 2 1 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 5 4 3 2 1 x x x x x = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 75 61 49 40 35 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 4 4 4 4 4 3 3 3 4 3 2 2 4 3 2 1 A ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 5 5 5 5

u v=

[

5 5 5 5

]

5

=

α β =75

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

(44)

[ ] [ ] ⎥⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 5 5 5 5 75 , 0 1 0 0 1 2 1 0 0 1 2 1 0 0 1 1 5 5 5 5 75 , 0 1 0 0 1 2 1 0 0 1 2 1 0 0 1 1 5 5 5 5 5 25 , 3 3 4 5 5 5 5 5 75 0 25 , 3 3 4 5 x ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 2 3 4 5 1 25 , 1 0 0 0 0 25 , 3 3 4 5 1 25 , 1 0 0 0 25 , 1 25 , 1 0 25 , 3 3 4 5

[

1

]

1 1

0 0

0 1 ₁

1 1 1 − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − − − − − lama lama lama lama A v u A u A v A A α [ ] ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − + ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − = − 75 , 0 1 0 0 1 2 1 0 0 1 2 1 0 0 1 1 5 5 5 5 1 5 5 5 5 75 , 0 1 0 0 1 2 1 0 0 1 2 1 0 0 1 1 25 , 1 1 0 0 0 0 0 0 75 , 0 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 1 1 A

[0 0 0 1,25 1]

(45)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − − − − = − 8 , 0 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 2 1 0 0 0 1 1 1 A

2.7.2. Penyelesaian sistem persamaan linear jarang pada matriks 10x10

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x

• Langkah 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x

A = 1 β =141

1 1 1 1

1 = = =

(46)

• Langkah 2 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x

A = 1 v = 0 u = 0 α =2 β =16

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 1 0 . 1 0 . 1 . 0 2 141 . 0 16 0 141 x _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 8 0 0 141 1 0 2 16 0 141 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 8 141 x

[

1

]

1 1

0 0

0 1 ₁

(47)

• Langkah 3 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 2 0 0 1

A v=

[

0 0

]

_⎥

⎦ ⎤ ⎢ ⎣ ⎡ = 4 0

u α =0 β =168

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β

[

]

[

]

⎥⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 0 0 5 , 0 0 0 1 0 0 5 , 0 0 0 1 0 0 0 8 141 0 0 168 0 8 141 x ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 1 0 0 0 168 0 8 141 x

(48)

2.7.3. Penyelesaian sistem persamaan linear jarang dengan operasi penukaran baris pada matriks 10x10

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x Penyelesaian:

Matriks berordo 10x10 maka terdapat 10 langkah dalam penyelesaiannya.

Langkah k digunakan untuk langkah dalam partisi dan langkah i digunakan

sebagai penyelesaian jika terjadi pembagian nol.

Langkah k=1 ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x 0 ) 1 , 1 ( ≠

a , pada langkah ini tidak mengalami penukaran baris.

A = 1 β =141

1 1 1 1

1 = = =

−

(49)

141 141 . 1 1 = = = − x A x β

Langkah k = 2

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x ? 1 u vA− = α 1 ) 1 , 1 ( = =a

A v=a(2,1)=0 u=a(1,2)=0 α =a(2,2)=2

16 ) 2 ( = =b β 0 0 . 1 . 0

1 = =

− u A v

u vA−1 ≠

α , tidak mengalami penukaran baris

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 1 0 . 1 0 . 1 . 0 2 141 . 0 16 0 141 x _⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 8 0 0 141 1 0 2 16 0 141 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = 8 141 x

[

1

]

1 1

0 0

0 1 ₁

(50)

[

]

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − 5 , 0 0 0 0 0 0 0 1 1 0 0 0 2 1 0 0 0 1 1 1 . 0 1 0 . 1 2 1 0 0 0 1 1 A ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − 5 , 0 0 0 1 1 A

Langkah k = 3

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 15 144 168 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 0 0 0 5 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 24 0 0 0 0 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = = 2 0 0 1 ) 2 : 1 , 2 : 1 ( a

A v=a(3,1:2)=

[

0 0

]

_⎥

⎦ ⎤ ⎢ ⎣ ⎡ = = 4 0 ) 3 , 2 : 1 ( a u 0 ) 3 , 3 ( = =a

α β =b(3)=168

[

]

0

4 0 5 , 0 0 0 1 0 0 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − u A v u A v −1 =

α , mengalami penukaran baris

• Langkah i = k+1

i = 4 v=a(i,1:2)=

[

0 0

]

α =a(i,3)=0 β =b(i)=168

[

]

0

4 0 5 , 0 0 0 1 0 0 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − u A v u A v −1 =

(51)

• Langkah i = k+2

i = 5 v=a(i,1:2)=

[

0 0

]

α =a(i,3)=5 168

)

( =

=b i

β

[

]

0

4 0 5 , 0 0 0 1 0 0 1 = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − u A v u A v −1 ≠

α , lakukan penyelesaian persamaan linear

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

α β [ ] ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 3 6 0 0 8 141 1 2 0 5 15 0 8 141 1 4 0 5 , 0 0 0 1 0 5 8 141 0 0 15 0 8 141 x ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = 3 2 141 x

[

1

]

1 1

0 0

0 1 ₁

1 1 1 ₋ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − − − − − lama lama lama lama A v u A u A v A A α [ ] ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = − 1 5 , 0 0 0 1 0 0 1 4 0 5 , 0 0 0 1 5 1 0 0 0 0 5 , 0 0 0 0 1 1 A [ ] ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = − 1 0 0 2 0 0 0 0 0 5 1 0 0 0 0 5 , 0 0 0 0 1 1 0 0 1 2 0 5 1 0 0 0 0 5 , 0 0 0 0 1 1 A ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − = − 2 , 0 0 0 4 , 0 5 , 0 0 0 0 1 1 A

Karena adanya penukaran baris maka baris ke – k ditukar dengan baris ke – i. jadi

baris ke – 3 ditukar dengan baris ke – 5. dan dengan adanya penukaran baris maka

(52)

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 128 195 162 66 32 168 144 15 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 24 0 0 0 0 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 ij p x x x x x x x x x x

Langkah k = 4

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 128 195 162 66 32 168 144 15 16 141 0 0 16 0 0 0 0 0 0 0 15 0 0 0 0 9 0 0 0 0 0 18 0 0 0 0 0 0 0 0 0 0 0 0 10 0 0 0 3 0 0 0 0 0 0 0 8 0 0 0 0 0 0 24 0 0 0 0 0 0 12 0 0 0 0 0 6 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 4 2 0 0 0 0 20 0 0 0 0 0 1 10 9 8 7 6 5 4 3 2 1 x x x x x x x x x x ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = − − = 5 0 0 4 2 0 0 0 1 ) 1 : 1 , 1 : 1

( k k

a A ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ = − = 0 0 0 ) , 1 : 1

( k k

a u

[

0 0 0

]

) 1 : 1 , ( − =

=a k k

v α =a(k,k)=6 β =b(k)=144

[

]

0

0 0 0 2 , 0 0 0 4 , 0 5 , 0 0 0 0 1 0 0 0 1 ₌ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − = − u A v u vA−1 ≠

α , tidak mengalami penukaran baris

⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − − − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = ₋ − 1 0 1 1 u A u A v x v x

x lama lama

(53)

[ ] ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 24 0 0 0 0 3 2 141 1 0 0 0 6 144 0 3 2 141 1 0 0 0 2 , 0 0 0 4 , 0 5 , 0 0 0 0 1 0 6 3 2 141 0 0 0 144 0 3 2 141 x ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = 24 3 2 141 x

[

1

]

1 1

0 0

0 1 ₁

1 1 1 − ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − − + ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = − − − − − lama lama lama lama A v u A u A v A A α [ ] ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = − 1 2 , 0 0 0 4 , 0 5 , 0 0 0 0 1 0 0 0 1 0 0 0 2 , 0 0 0 4 , 0 5 , 0 0 0 0 1 6 1 0 0 0 0 0 2 , 0 0 0 0 4 , 0 5 , 0 0 0 0 0 1 1 A [ ] ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = − ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = − 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 6 1 0 0 0 0 0 2 , 0 0 0 0 4 , 0 5 , 0 0 0 0 0 1 1 0 0 0 1 0 0 0 6 1 0 0 0 0 0 2 , 0 0 0 0 4 , 0 5 , 0 0 0 0 0 1 1 A ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ − = − 1667 , 0 0 0 0 0 2 , 0 0 0 0 4 , 0 5 , 0 0 0 0 0 1 1 A

Langkah k = 5

(54)

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡ = − −

=

6 0 0 0

0 5 0 0

0 4 2 0

0 0 0 1

) 1 : 1 , 1 : 1

( k k

a A

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

= − =

0 0 0 0

) , 1 : 1

( k k

a u

[

0 0 0 0

]

) 1 : 1 ,

( − =

=a k k

v α =a(k,k)=0

168 )

( =

=b k

β

[ ] 0

0 0 0 0

1667 , 0 0 0 0

0 2

, 0 0 0

0 4 , 0 5 , 0 0

0 0

0 1

0 0 0 0

1 ₌

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

− u A v

u A v −1 =

α , mengalami penukaran baris

• Langkah i = k+1

i = 6 v=a(i,1:k −1)=

[

0 0 0 8

]

α =a(i,k)=0 32

)

( =

=b i

β

[ ] 0

0 0 0 0

1667 , 0 0 0 0

0 2

, 0 0 0

0 4 , 0 5 , 0 0

0 0

0 1

8 0 0 0

1 ₌

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

−

u A v

u A v −1 =

α , lanjutkan langkah i

• Langkah i = k+2

i = 7 v=a(i,1:k −1)=

[

0 3 0 0

]

α =a(i,k)=0 66

)

( =

=b i

β

[ ] 0

0 0 0 0

1667 , 0 0 0 0

0 2

, 0 0 0

0 4 , 0 5 , 0 0

0 0

0 1

0 0 3 0

1 =

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

−

u A v

u A v −1 =

(55)

• Langkah i = k+3

i = 8 v=a(i,1:k −1)=

[

0 0 0 0

]

α =a(i,k)=0 162

)

( =

=b i

β

[ ] 0

0 0 0 0

1667 , 0 0 0 0

0 2

, 0 0 0

0 4 , 0 5 , 0 0

0 0

0 1

0 0 0 0

1 ₌

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

− u A v

u A v −1 =

α , lanjutkan langkah i

• Langkah i = k+4

i = 9 v=a(i,1:k −1)=

[

0 0 0 0

]

α =a(i,k)=9 195

)

( =

=b i

β

[ ] 0

0 0 0 0

1667 , 0 0 0 0

0 2

, 0 0 0

0 4 , 0 5 , 0 0

0 0

0 1

0 0 0 0

1 ₌

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

− u A v

u A v −1 ≠

α , lakukan penyelesaian persamaan linear

[ ] [0 0 0 0]

1667 , 0 0 0 0

0 2

, 0 0 0

0 4 , 0 5 , 0 0

0 0

0 1

0 0 0 0

1 ₌

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

− A v

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡ = ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

− =

−

0 0 0 0

1667 , 0 0