Contoh Makalah Fisika Tentang Besaran dan Vektor

BAB I PENDAHULUAN

1.1 Latar Belakang

Dalam kehidupan sehari-hari, banyak terjadi peristiwa-peristiwa yang berhubungan dengan pengetahuan baik yang bermanfaat maupun yang tidak bermanfaat. Namun hal tersebut tidak kita sadari bagaimana cara mengembangkan peristiwa-peristiwa yang bermanfaat bagi kehidupan kita. Salah satu dari ilmu pengetahuan tersebut adalah ilmu fisiska, dimana ilmu fisika tersebut sangat bermanfaat bagi kehidupan kita sehari-hari dalam melakukan suatu aktivitas, contoh ilmu fisika yang mempunyai hubungan yang sangat erat dengan usaha manusia untuk mempelajari gejala alam. Setelah gejala alam diketahui, maka dipikirkan bagaimana cara pemanfaatannya di dunia nyata atau kehidupan sehari-hari , kajian ilmu fisika sangat sering muncul dalam terjadinya suatu peristiwa, misalnya sebuah mobil yang melakukan pengereman dan lain-lain, memindahkan sebuah barang/benda ketempat lain. Peristiwa-peristiwa ini tentunya menimbulkan banyak pertanyaan bagi kita jika kita kaitkan dengan ilmu fisika.

Disini kita akan membahas bagaimana caranya kita menerapkan pertanyaan-pertanyaan yang ada dipkiran kita dengan mempelajari materi-materi fisika. Dalam makalah ini kami akan menjelaskan tentang perbedaan besaran pokok dan besaran turunan beserta satuan dan dimensinya serta memprediksi dimensi suatu besaran melakukan analisis, dan melakukan penjumlahan dan perkalian vektor dan menerapakannya dalam kehidupan sehari-hari.

panjang dan masih banyak lagi. Sedangkan besaran vektor adalah besaran yang memiliki nilai dan arah.

Untuk lebih menambah pemahaman kita tentang besaran pokok, besaran turunan, satuan SI, dimensi, analisis dimensi maupun besaran vektor dan besaran skalar, dalam makalah ini penulis akan menjelaskan berbagai kajian-kajian tentang besaran pokok, besaran turunan, satuan SI, dimensi, analisis dimensi, besaran vektor dan besaran skalar lebih lanjut. Kajian-kajian yang dijelaskan diantaranya pengertian besaran pokok dan besaran turunan, menjelaskan penerapan satuan besaran pokok dan besaran turunan dalam SI, cara menentukan dimensi dan pengertian analisis dimensi, pengertian skalar dan vektor, operasi vektor, resultan vektor dengan metode jajar genjang, resultan vektor dengan metoda poligon, resultan vektor dengan metode analisis. Selain dari semua itu, kami juga akan menjelaskan tentang perkalian titik (dot), perkalian silang (cross) dan sifat-sifatnya, dan juga penerapan perkalian skalar dan silang dalam fisika.

1.2 Rumusan Masalah

Berdasarkan latar belakang diatas, maka ada beberapa rumusan masalah yang dapat paparkan sebagai berikut :

1. Apa yang dimaksud besaran pokok, besaran turunan dan contoh-contohnya? 2. Bagaimana cara menerapkan satuan besaran pokok dan besaran turunan dalam SI? 3. Bagaimana caranya menentukan dimensi suatu besaran pokok dan turunan dan apa

yang dimaksud dengan analisis dimensi dalam fisika?

4. Apa pengertian skalar dan vektor, dan bagaimana cara mempresentasikan vektor ? 5. Apa saja jenis operasi vektor, resultan vektor dan metodenya ?

6. Apa saja jenis dari perkalian vektor ?

7. Bagaimana menerapkan konsep perkalian skalar dan perkalian silang dalam pemecahan masalah sehari-hari ?

1.3 Tujuan

Adapun tujuan dari makalah diatas sesuai dengan rumusan masalah di atas sebagai berikut:

1. Mampu membandingakan besaran pokok, besaran turunan dan contoh-contohnya.

3. Mampu menentukan dimensi suatu besaran pokok dan turunan dan kita juga bisa mengetahui pengertian dari analisis dimensi dalam fisika.

4. Mampu mendeskripsikan tentang pengertian skalar dan vektor dan menjelaskan cara menyatakan (merepresentasikan) vektor

5. Mampu menjelaskan tentang operasi – operasi pada vektor, resultan vektor dan metodenya

6. Mampu menjelaskan tentang jenis perkalian vektor

7. Mampu menerapkan konsep perkalian skalar dan perkalian silang dalam pemecahan masalah sehari-hari.

1.4 Manfaat

Adapun manfaat yang diharapkan dari penulisan makalah ini adalah : 1. Bagi Penulis

Dalam penulisan makalah ini manfaat yang kami dapat bagi penulis yaitu memberikan banyak pengalaman dalam penyusunan makalah ini dan juga bisa memberikan informasi tentang besaran pokok dan besaran turunan, dan bisa menjelaskan tentang skalar dan vektor serta hal – hal yang berkaitan dengan vektor.

2. Bagi Pembaca

BAB II

PEMBAHASAN

2.1 Pengertian Besaran Pokok dan Besaran Turunan

Besaran fisis yaitu segala sesuatu yang dapat diukur dan dinyatakan dengan angka. Besaran fisis digunakan untuk menyatakan hukum-hukum fisika, misalnya: panjang, massa, waktu, gaya, kecepatan, temperatur, intensitas cahaya, dan banyak lagi yang lain. Ada banyak besaran fisis, kadang-kadang saling bergantung satu dengan lainnya, sehingga pengaturannya menjadi sulit, misalnya saja laju (speed) adalah perbandingan antara panjang dan waktu. Yang harus kita lakukan adalah memilih sejumlah kecil besaran fisis sebagai besaran pokok. Besaran-besaran fisis lainnya dapat diturunkan dari besaran pokok.

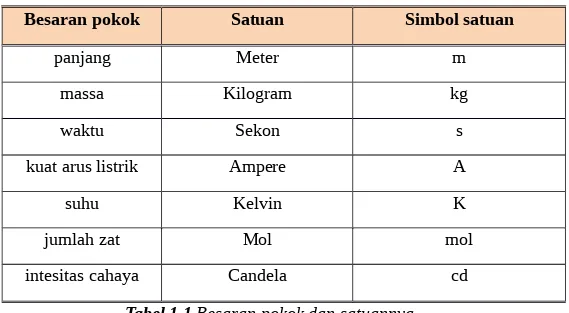
Besaran fisis dikelompokkan menjadi dua, yaitu besaran pokok dan besaran turunan. Besaran pokok adalah besaran yang satuannya telah didefinisikan terlebih dahulu dan tidak dapat dijabarkan dari besaran yang lain. Ada tujuh besaran pokok dalam fisika, seperti ditunjukkan pada Tabel 1.1.

Besaran pokok Satuan Simbol satuan

panjang Meter m

massa Kilogram kg

waktu Sekon s

kuat arus listrik Ampere A

suhu Kelvin K

jumlah zat Mol mol

intesitas cahaya Candela cd

Tabel 1.1 Besaran pokok dan satuannya

besaran-besaran pokok. Berikut contoh beberapa besaran turunan dalam fisika dapat ditunjukkan pada Tabel 1.2.

Besaran turunan Rumus Satuan

luas panjang ∙ lebar m2

volume panjang ∙ lebar ∙

tinggi m

3

massa jenis massa

volume kg m-3

kecepatan pepindahan

waktu m s-1

percepatan kecepatan

waktu m s-2

gaya massa ∙ percepatan kg m s-2 _{= newton (N)} usaha dan energi gaya ∙ perpindahan kg m2 _s-2 _{= joule (J)}

tekanan gaya

luas kg m-1s-2 = pascal (Pa)

daya energi

waktu kg m2 s-3 = watt (W)

impuls dan

momentum gaya ∙ waktu kg m s

-1 _{= N s}

Tabel 1.2 Besaran turunan, rumus dan satuannya

2.2 Sistem Satuan Internasional

Konferensi Umum mengenai Berat dan Ukuran ke-14 (1971), berdasarkan hasil-hasil pertemuan sebelumnya dan hasil-hasil panitia internasional, menetapkan tujuh besaran sebagai dasar. Ketujuh besaran ini merupakan dasar bagi Sistem Satuan Internasional, biasanya disingkat SI, dari bahasa Prancis “Le Systeme International d’Unites.”

Banyak contoh-contoh satuan turunan SI, seperti kecepatan, gaya, hambatan listrik, dan sebagainya. Sebagai contoh, satuan SI untuk gaya disebut newton (disingkat N), yang dalam satuan dasar SI didefinisikan sebagai

1 N = 1 m ∙ kg/s2

Hal ini akan dijelaskan lebih lanjut dalam pasal 5.

Akibat adanya kesukaran yang ditimbulkan oleh penggunaan sistem satuan yang berbeda, maka muncul gagasan untuk menggunakan hanya satu jenis satuan saja untuk besaran-besaran dalam ilmu pengetahuan alam dan teknologi. Suatu perjanjian internasional telah menetapkan satuan internasional (International System of Units) disingkat satuan SI. Satuan SI ini diambil dari sistem metrik yang telah digunakan di Prancis setelah revolusi tahun 1789. Karena ada tujuh besaran pokok, maka juga ada tujuh satuan pokok dalam SI, yaitu: meter (m), kilogram (kg), sekon (s), ampere (A), kelvin (K), candela (cd), dan mol (mol).

2.3 Dimensi suatu Besaran Pokok, Besaran Turunan dan Analisis Dimensi Dimensi suatu besaran menujukkan cara besaran itu tersusun dari besaran-besaran pokok. Dimensi besaran-besaran pokok dinyatakan dengan lambang huruf tertentu (ditulis huruf besar), dan atau diberi kurung persegi. Sebagai contoh, dimensi dari besaran massa ditulis M atau [M]. Dimensi suatu besaran turunan ditentukan oleh rumus besaran turunan tersebut jika dinyatakan dalam besaran-besaran pokok. Sebagai contoh, dimensi dari besaran percepatan yang didefinisikan sebagai hasil bagi dari kecepatan dan waktu adalah sebagai berikut :

[

percepatan

]

=

[

kecepatan

]

[

waktu

]

=

[L

]

[T

]

2 _{= [L][T]}-2

Adapun cara-cara menentukan dimensi besaran turunan dari dimensi besaran pokok yaitu :

Volume (V) p∙ l ∙t [L][L][L] [L]3

Tabel 1.4. Menentukan dimensi besaran turunan dari dimensi besaran pokok

Analisis dimensi dalam fisika adalah alat konseptual yang sering diterapkan dalam fisika, dan teknik untuk memahami keadaan fisis yang melibatkan besaran fisis yang berbeda-beda. Adapun tiga manfaat dimensi dalam fisika, sebagai berikut. 1. Dapat digunakan untuk membuktikan dua besaran fisis setara atau tidak. Dua

besaran fisis yang hanya setara jika keduanya memiliki dimensi yang sama dan keduanya termasuk besaran skalar atau keduanya termasuk besaran vektor. 2. Dapat digunakan untuk menetukan persamaan yang pasti atau mungkin benar. 3. Dapat digunakan untuk menurunkan persamaan suatu besaran fisis jika

kesebandingan besaran fisis tersebut dengan besaran fisis lainnya diketahui.

2.4 Pengertian Skalar , Vektor dan Representasi Vektor

Selain besaran pokok dan turunan, besaran fisika masih dapat dibagi atas dua kelompok lain yaitu besaran skalar dan besaran vektor. Besaran‐besaran seperti massa, jarak, waktu dan volume, termasuk besaran skalar, yakni besaran yang hanya memiliki besar atau nilai saja tetapi tidak memiliki arah. Sedangkan besaran seperti perpindahan, kecepatan, percepatan dan gaya termasuk besaran vektor, yaitu besaran yang memiliki besar (atau nilai) dan juga memiliki arah. Dalam besaran vektor kita hanya mementingkan atau memfokuskan hanya pada nilai suatu besarannya tetapi kita juga akan memperhatikan arah dari besaran vektor tersebut. Beberapa contoh besaran vektor misalnya perpindahan, gaya dan lain-lain. Jika kita menyatakan perpindahan selalu disertai arah, cara menyatakan atau menggambarkan vektor ada 3 cara, yaitu dengan diagram vektor, notasi huruf dan notasi analitis.

1. Besar dan arah vektor dapat kita lihat atau dapat digambarkan melalui diagram vektor. Misalkan diagram vektor di atas, kita dapat melihat besar dan arah vektor A dan B, panjang dari anak panah dapat kita lihat sebagai besar atau nilai vektornya misalnya panjang anak panahnya 1 meter, sedangkan arah dari vektor tersebut dapat kita lihat dari arah kepala anak panah pada diagram vektor.

2. Cara yang kedua adalah dengan notasi huruf. Ada beberapa aturan dalam penulisan vektor menggunakan huruf. Vektor dapat ditulis dengan huruf kapital yang dicetak tebal, huruf kecil yang dicetak tebal, dan dalam penulisan sehari-hari biasanya ditulis dengan menambahkan anak panah di atas huruf yang menyatakan vektor.

Sebagai contohnya vektor AB, dapat ditulis AB, ab, ataupun AB´ dan

⃗

ab

. Vector AB memiliki arti atau dapat diartikan bahwa arah vektornya dari vektor A ke vektor B.

3. Cara yang ketiga adalah dengan notasi analitis. Notasi ini digunakan untuk menganalisa vektor tanpa menggunakan gambar atau diagram. Contoh : vektor a dapat dinyatakan dalam komponen – komponen sebagai berikut :

Gambar 1.2 Menggambarkan vektor dengan cara notasi analitis

Gambar 1.1Vektor AB digambarkan dalam diagram vektor

A B

a ax

ay

x y

x y

z

ay

az

A B

Gambar 1.3 Vektor yang sama

Lebih mudah jika menyatakan vektor menggunakan vektor satuan dalam arah sepanjang sumbu – sumbu koordinat yang dipilih. Dalam koordinat siku – siku biasanya digunakan lambang khusus i, j dan k untuk menyatakan vektor satuan dalam arah sumbu x, y dan z positif berturut – turut.

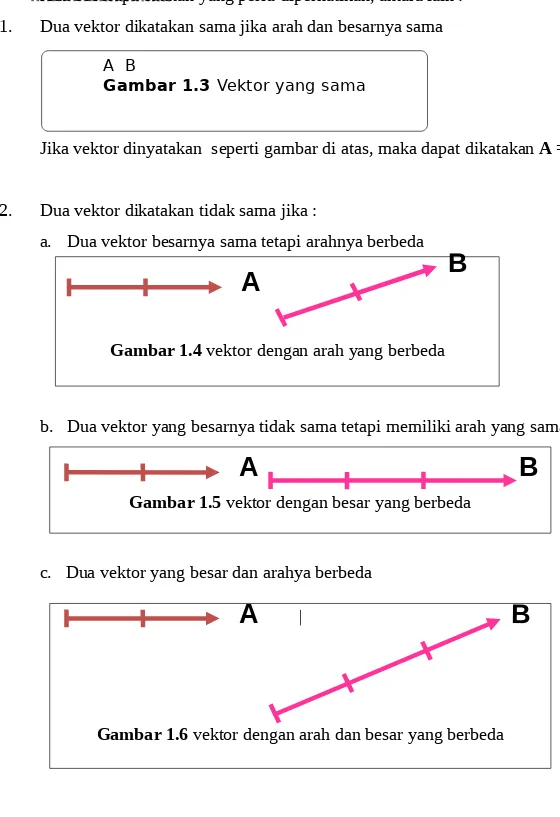
Ada beberapa catatan yang perlu diperhatikan, antara lain : 1. Dua vektor dikatakan sama jika arah dan besarnya sama

Jika vektor dinyatakan seperti gambar di atas, maka dapat dikatakan A = B

2. Dua vektor dikatakan tidak sama jika :

a. Dua vektor besarnya sama tetapi arahnya berbeda

b. Dua vektor yang besarnya tidak sama tetapi memiliki arah yang sama

c. Dua vektor yang besar dan arahya berbeda

Gambar 1.4 vektor dengan arah yang berbeda

Gambar 1.5 vektor dengan besar yang berbeda

Gambar 1.6 vektor dengan arah dan besar yang berbeda

B

A

A

B

2.5 Operasi Vektor, Resultan Vektor dan Metodenya

Dalam kehidupan sehari-hari, besaran – besaran baik besaran skalar maupun vektor juga sering dilibatkan dalam operasi hitung baik penjumlahan, pengurangan dan perkalian. Untuk besaran-besaran skalar dalam operasi hitung mengikuti kaidah berhitung biasa. Sedangkan untuk besaran vektor dalam operasi hitung mengikuti kaidah-kaidah berhitung yang berbeda dengan kaidah berhitung besaran scalar sehingga memerlukan pembahasan tersendiri yang biasanya terangkum dalam kajian analisis vektor.

Dalam vektor, ada beberapa operasi-operasi atau cara-cara yang dapat digunakan dalam menentukan nilai dari sebuah vektor, diantaranya adalah sebagai berikut :

1. Operasi Penjumlahan dan pengurangan

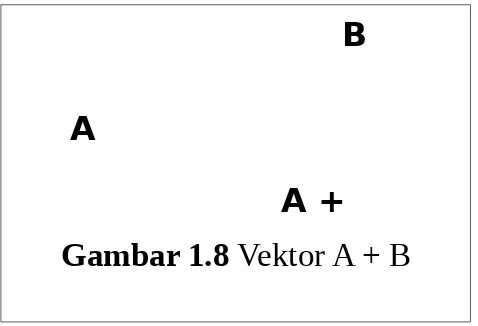
Diberikan 2 buah vektor seperti pada gambar. Tentukan hasil A + B = … ?

Dalam penjumlahan vektor tanda “+” dalam penjumlahan vektor memilki arti dilanjutkan, jadi jika A + B berarti vektor A dilanjutkan oleh vektor B

seperti pada gambar dibawah kita dapat lihat bahwa vector A diteruskan oleh vector B sehingga hasilnya adalah garis panjang yang berwarna merah.

Untuk pengurangan vektor tanda “-“ berarti berlawanan arah misalnya vektor A-B, dapat kita kurangi atau hitung seperti pada gambar dibawah ini.

A

B

A +

A

B −

A - B

Gambar 1.8 Vektor A + B

Gambar 1.9 Vektor A - B

A B

Dalam operasi vektor ini berlaku beberapa hukum, antara lain : a. Hukum Komutatif

A + B = B + A (1.1)

b. Hukum Asosiatif

Kedua hukum ini menyatakan bahwa bagaimanapun urutan atau pengelompokan vektor dalam penjumlahan, hasilnya akan sama.

( A + B ) + C = A + ( B + C ) (1.2)

2. Resultan vektor dan metode mencari resultan

Resultan merupakan hasil penjumlahan dari beberapa vektor. Dalam menentukan resultan dari suatu vector dapat menggunakan beberapa cara atau metode antara lain metode jajar genjang, metode segi banyak atau poligon dan metode analitik.

a. Metode Jajar genjang

Dalam metode jajar genjang resultan vektornya dinyatakan oleh diagonal jajar genjang yang dibentuk oleh dua vector tersebut. Misalkan diberikan dua vector A dan B seperti pada gambar di bawah,

A

A B

B

A

B

C Gambar 1.10

Dalam menentukan resultan vector AB diatas dapat dilakukan dengan beberapa cara yaitu:

1. Titik pangkal vektor B diletakkan berhimpit dengan vektor A

2. Gambar jajar genjang dengan P dan Q sebagai sisinya, lalu tarik garis diagonalnya

Dimana diketahui : AB = P

BC = AD = AC = R

Sehingga persamaan (1.5) dapat ditulis menjadi

R

2

=

P

2

+

Q

2

+

2

(

P

)(

Q

)

cos

α

(1.6)

(1.7)

Catatan :

1. Jika vektor P dan Q searah, maka α = 00 _{dan R =}

_√

_P2

+Q2+2(P) (Q) (1.8) 2. Jika vektor P dan Q berlawanan arah, maka α = 1800 _dan

R=

√

P2+Q2−2(P) (Q) (1.9)

3. Jika vektor P dan Q saling tegak lurus, maka α = 900 _{dan R =}

_√

P2+Q2 (1.10)

b. Metode Segi Banyak (Poligon)

Menghitung nilai resultan juga dapat dilakukan dengan metode polygon (segi banyak). Metode poligon adalah cara meresultankan vektor dengan cara menggambar. Salah satu vektor sebagai acuan dan vektor lain disambungkan dengan pangkal tepat pada ujung vektor sebelumnya. Resultan vektornya dapat dibentuk dengan menggambar anak panah dari pangkal awal hingga ujung akhir. (Sri Handayani : 42)

Pada suatu keadaan tertentu metode polygon dapat mempermudah penyelesaian perhitungan resultan vektor.

Gambar : R=

√

P2

+Q2

+2(P)(Q)cosα

F

H G

E

Jika akan mencari resultannya maka digambar terlebih dahulu

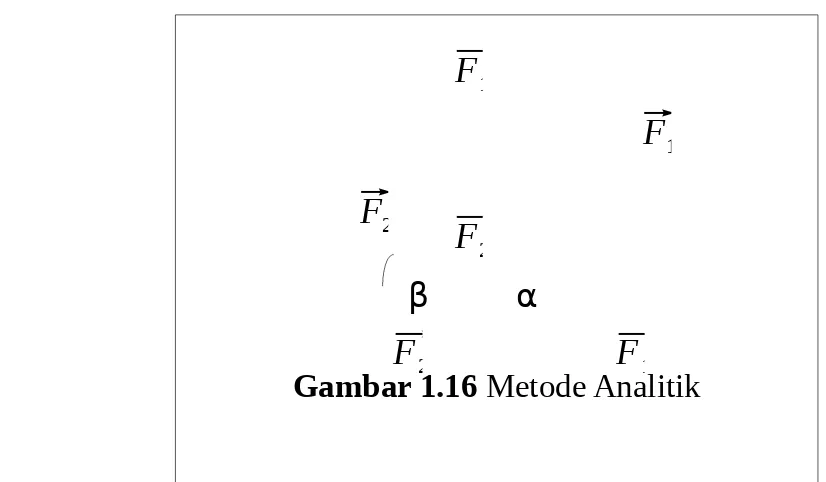
c. Metode Analitik

Jika pada satu titik bekerja lebih dari 1 vektor, maka untuk mencari resultannya dapat digunakan metode analitik (uraian). Dalam metode ini, vektor akan diproyeksikan ke dalam komponen-komponennya dalam suatu system kordinat tertentu. Vektor-vektor tersebut dapat doproyeksikan pada 2 arah (sumbu x dan sumbu y). Vektor-vektor yang sejajar dapat dihitung resultannya dengan cara dijumlahkan atau dikurangkan. 2 resultan pada arah sejajar pasti saling tegak lurus, sehingga resultan akhirnya dapat ditentukan dengan dalil phytagoras

bar :

Resultan proyeksi-proyeksi gaya yang searah memenuhi persamaan berikut :

(1.11) (1.12)

dimana :

F

G E

R

H

⃗_F1y

⃗_F1

⃗_F

2 _⃗F 2y

β α

⃗_F

2x ⃗F1x

∑

F_X=F_1X−F_2X

∑

F_Y=F_1Y+F_2Y

Gambar 1.15 Metode Poligon

1X=¿

Resultan gaya – gaya tersebut dapat memenuhi persamaan berikut :

(1.17)

(1.18) Dengan : R: besar resultan gaya

θ : sudut FR terhadap sumbu x

2.6 Perkalian Vektor

Di atas telah dijelaskan mengenai operasi penjumlahan dan pengurangan vektor, sekarang akan dijabarkan mengenai operasi perkalian vektor. Operasi perkalian vektor ada 2 jenis, yaitu perkalian skalar dengan vektor dan perkalian vektor dengan vektor. Perkalian vektor dengan vektor terdiri dari perkalian titik (dot product) dan perkalian silang (cross product).

1. Perkalian Skalar dengan Vektor

Perkalian ini berarti mengalikan bilangan biasa (skalar) dengan vektor. Hasil perkalian ini adalah vektor baru. Notasi penulisan perkalian ini adalah :

(1.19) Vektor B memiliki besar k kali vektor A. jika nilai k positif (+) maka vektor B akan memiliki arah yang sama dengan vektor A. namun jika k bernilai negative maka vektor B berlawanan arah dengan vektor A.

2. Perkalain Vektor dengan Vektor ada 2 jenis perkalain ini, yaitu a. Perkalain tititk/dot (•)

R=

√

F_1X2+F_2Y2

tgθ=

∑

FY

∑

F_X

Perkalian titik 2 buah vektor, A dan B dapat dituliskan A • B . 2 buah vektor yang dioperasikan dengan perkalian titik menghasilkan bilangan biasa (skalar)

Gambar 1.17

(1.20)

Ada beberapa hal yang perlu diperhatikan dalam perkalian titik, antara lain :

 Dalam perkalian titik berlaku hukum komutatif

A•B = B•A (1.21)

(perklaian dot tidak memperhatikan urutan)

 Perkalian titik juga memenuhi hukum distributif

A•(B+C) = A•B + A•C (1.22)

 Jika vektor A dan B saling tegak lurus (θ = 900_{) maka}

A•B = 0 (1.23)

 Jika kedua vektor memiliki arah yang sama (searah) θ = 0, maka

A•B = AB (1.24)

Jika A=B akan diperoleh

A•A = A2_{atau B•B = B}2 _(1.25)

 Jika θ = 1800 _{maka vektor A dan B akan berlawanan arah}

A•B = −AB (1.26)

b. Perkalian silang/cross (×)

Dengan notasi A×B (dibaca A cross B), perkalian silang 2 vektor ini menghasilkan sebuah vektor baru. Vektor hasil perkalian ini dapat digambarkan sebagai sebuah vektor yang tegak lurus terhadap masing-masing vektor tersebut.

Hal – hal penting yang harus diingat dalam perkalian silang, antara lain :

A

θ B

 Perkalain silang bersifat anti komutatif

A × B = −B × A (1.27)

 Sudut yang dibentuk vektor A dan B 900 _{(tegak lurus) maka}

│A × B│= AB (1.28)

 Jika vektor A dan B segaris dengan θ = 00 _{ataupun θ = 180}0 _{(searah ataupun} berlawanan) maka

│A × B│= 0 (1.29)

2.7 Penerapan Perkalian Vektor

Setelah mengetahui teori tentang perkalian vektor, sekarang kita akan menerapkan operasi perkalian tersebut dalam perumusan – perumusan fisika.

1. Penerapan Perkalian Titik (Dot)

Beberapa contoh penerapan perkalian titik dalam fisika antara lain dalam mencari besarnya usaha. Seperti yang telah diketahui bersama rumus untuk menentukan besarnya usaha yang dilakukan saat sebuah benda dikenai gaya dan benda tersebut mengalami perubahan posisi adalah W = F • s = F (cos θ) • s. Dimana W adalah usaha, F adalah gaya yang bekerja pada benda dan s adalah jarak yang ditempuh benda setelah/selama dikenai gaya.

Gambar 1.19

Hasil dari perkalian ini (usaha) merupakan bilangan skalar (bilangan biasa) tanpa arah. Contoh lain dari penerapan perkalian titik ini adalah saat menghitung fluks listrik.

2. Penerapan Perkalian Silang (Cross)

Masih ingatkah dengan momen gaya ? momen gaya dirumuskan τ = F × r. dimana τ adalah momen gaya, F adalah vektor gaya dan r adalah vektor posisi. Momen gaya ini merupakan besaran vektor karena setelah dioperasikan, momen gaya selain memiliki nilai juga memiliki arah.

s F

θ

θ

Gambar 1.20

Titik O merupakan poros, jika batang tersebut ditarik dengan gaya F, maka batang akan bergerak searah jarum jam. Sehingga momen gaya termasuk salah satu contoh penerapan perkalian silang (cross). Adapun contoh lain yaitu Gaya Lorentz.

BAB III

PENUTUP

3.1 Simpulan

Berdasarkan pembahasan di atas, maka simpulan yang dapat ditarik adalah sebagai berikut :

1. Besaran pokok merupakan besaran yang satuannya telah didefinisikan terlebih dahulu dan tidak dapat dijabarkan dari besaran yang lain. Sedangkan besaran turunan adalah besaran yang diturunkan dari besaran-besaran pokok.

2. Untuk penyamaan persepsi pengukuran di seluruh dunia, diciptakan suatu standar satuan yang disebut dengan satuan Sistem Internasional yang dapat dikonversi ke dalam satuan yang berlaku di negara masing-masing. Misalnya satuan panjang secara internasional adalah meter, dapat dikonversi ke dalam satuan inchi, kaki, mil, dan lain-lain.

3. Dimensi suatu besaran menunjukkan cara besaran itu tersusun dari besaran-besaran pokoknya.

potensial, dan usaha; (b) menentukan satuan dari besaran turunan dengan cara analisis dimensional.

5. Analisis dimensional adalah suatu cara untuk menentukan satuan dari suatu besaran turunan, dengan cara memperhatikan dimensi besaran tersebut. 6. Besaran skalar artinya besaran yang tidak memiliki arah.

7. Besaran vektor merupakan besaran yang selain memiliki nilai juga memiliki arah.

2. Ada 3 cara untuk merepresentasikan vektor, yaitu a. Diagram vektor

b. Notasi huruf c. Notasi analitis

3. Ada beberapa metode untuk mencari nilai resultan vektor, antara lain : a. Metode jajar genjang

R=

√

P2+Q2+2(P)(Q)cosα

b. Metode segi banyak (polygon)

c. Metode analitik (uraian)

4. Perkalian vektor terdiri dari 2 jenis yaitu :

a. Perkalian Titik (dot) yang menghasilkan bilangan skalar (bilangan biasa) b. Perkalian Silang (cross) yang menghasilkan besaran vektor baru.

3.2 Saran

Saran yang ingin kami sampaikan yaitu diharapkan kepada peserta didik agar dapat lebih mengerti dan memahami tentang besaran pokok, besaran turunan, satuan SI, dimensi, analisis dimensi, skalar dan vektor, agar nantinya mampu menjabarkan apa itu besaran pokok, besaran turunan, skalar, vektor dan semua hal – hal yang berkaitan dengan besaran-besaran yang ada di fisika.

F_R2

DAFTAR PUSTAKA

www.ensiklopedia.com

www.google.com

Halliday,Resnick.1999.Fisika Jilid I.Edisi Ketiga. Jakarta: Erlangga Giancoli, D.C.1998. Fisika Jilid I. Edisi ketiga. Jakarta: Erlangga Modul Fisika Dasar 1

Sri Handayani, Ari Damari. 2009. Fisika Untuk SMA dan MA Kelas X. Jakarta: CV Adi Perkasa