PELABELAN TOTAL (a,d)- -ANTIAJAIB SUPER PADA GRAF ULAR

(1)

PELABELAN TOTAL (a,d)-

-ANTIAJAIB SUPER

PADA GRAF ULAR

Lasmanian Rezekina

PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH JAKARTA

(2)

i

PELABELAN TOTAL

-

-ANTIAJAIB SUPER

PADA GRAF ULAR

SKRIPSI

Diajukan kepada

Universitas Islam Negeri Syarif Hidayatullah Jakarta Untuk Memenuhi Salah Satu Persyaratan Dalam

Memperoleh Gelar Sarjana Sains (S.Si)

Oleh:

Lasmanian Rezekina 1111094000025

PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH JAKARTA

(3)

(4)

iii

PERNYATAAN

DENGAN INI SAYA MENYATAKAN BAHWA SKRIPSI INI BENAR-BENAR HASIL KARYA SENDIRI YANG BELUM PERNAH DIAJUKAN SEBAGAI SKRIPSI PADA PERGURUAN TINGGI ATAU LEMBAGA MANAPUN.

Jakarta, Januari 2016

Lasmanian Rezekina 1111094000025

(5)

iv

-PERSEMBAHAN-

Skripsi ini saya persembahkan untuk:

Almarhum Ayah dan Mama tercinta

yang selalu memberikan do’a, dukungan, motivasi dan semangat yang

tiada henti demi kesuksesan anaknya.

MOTTO

(6)

v

ABSTRAK

Suatu pelabelan - -antiajaib adalah suatu fungsi bijektif yang memetakan himpunan titik dan sisi pada graf ke bilangan positif { | | | |} yang memenuhi suatu barisan aritmetika untuk dua bilangan bulat positif dan tertentu serta adalah banyaknya subgraf di Penelitian ini membahas tentang pelabelan total - -antiajaib super pada graf ular untuk . Penelitian ini menghasilkan teorema-teorema yang menyatakan pelabelan total - -antiajaib super pada graf ular , pelabelan total - -antiajaib super pada graf ular dan pelabelan total - -antiajaib super pada graf ular .

Kata Kunci: Pelabelan Total - -Antiajaib, Selimut- , Antiajaib Super, Graf Ular.

(7)

vi

ABSTRACT

An - -antimagic total labeling is a bijective function which is mapping set of vertex and edge in graph to positive integer { | | | |} that constitute an arithmetic progression for two certain positive integers and , and is the amount of subgraph in . This research discusses about super - -antimagic total labeling of snake graph for . This research produced theorems that declare super - -antimagic total labeling of snake graph , super - -antimagic total labeling of snake graph , super - -antimagic total labeling of snake graph .

Keywords: - -Antimagic Total Labeling, -covering, Super Antimagic, Snake Graph

(8)

vii

KATA PENGANTAR

Alhamdulillah, segala puji bagi Allah SWT yang Maha Pengasih lagi Maha Penyayang, Tuhan Semesta Alam, yang senantiasa melimpahkan rahmat dan nikmat-Nya kepada kita semua, tak terkecuali pada penulis hingga penulis dapat menyelesaikan skripsi dengan judul “Pelabelan Total - -Antiajaib Super pada Graf Ular ”. Skripsi ini sebagai salah satu syarat bagi penulis untuk

memperoleh gelar sarjana sains.

Dalam penyusunan skripsi ini, penulis banyak mendapatkan dorongan, semangat, dan bimbingan serta kritikan dan saran dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis ingin mengucapkan terimakasih kepada :

1. Dr. Agus Salim, M.Si selaku Dekan Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta.

2. Dr. Nina Fitiyati, M.Kom selaku Ketua Program Studi Matematika Fakultas Sains dan Teknologi UIN Syarif Hidayatullah Jakarta.

3. Dr. Nur Inayah, M.Si selaku Dosen Pembimbing I yang telah meluangkan waktunya untuk membimbing penulis dan memberikan pengarahan serta saran selama pembuatan skripsi ini.

4. Yanne Irene, M.Si selaku Dosen Pembimbing II yang telah meluangkan waktunya untuk membimbing penulis dan memberikan pengarahan serta saran selama pembuatan skripsi ini.

(9)

viii

5. Kak Edo dan seluruh dosen-dosen Prodi Matematika Fakultas Sains dan Teknologi UIN Jakarta.

6. Kedua orang tua, Alm. Syamsuddin Siregar dan Damsina Harahap, terima kasih atas doa, kasih sayang, serta dukungan moril maupun materil kepada penulis sehingga penulis dapat menyelesaikan skripsi ini.

7. Delvin Raya S. dan Fitriyuni Miralda S., abang dan kakak penulis yang telah memberikan doa, semangat dan motivasi kepada penulis.

8. Likha, Qashi, Dwi, Kokom, Bintang, Tiyo, Ipeng, Laili, Gina, Qori, Dheayu, Safirah, Kak Safti dan Leo selaku Team Hore yang tiada henti-hentinya menyemangati.

9. Seluruh teman-teman Matematika 2011, terima kasih atas kerjasamanya selama masa perkuliahan.

10. Seluruh pihak yang telah membantu penulis dalam mengerjakan skripsi ini yang tidak dapat penulis sebutkan satu-persatu.

Penulis menyadari bahwa dalam penyusunan skripsi ini masih banyak kekurangan. Oleh karean itu, penulis mengharapkan kritik dan saran yang bersifat membangun untuk perbaikan di masa yang akan datang. Dan akhirnya, penulis berharap semoga skripsi ini dapat bermanfaat.

Jakarta, Januari 2016

(10)

ix

DAFTAR ISI

HALAMAN JUDUL ... i

LEMBAR PENGESAHAN ... ii

PERNYATAAN ... iii

PERSEMBAHAN DAN MOTTO ... iv

ABSTRAK ... v

ABSTRACT ... vi

KATA PENGANTAR ... vii

DAFTAR ISI ... ix DAFTAR GAMBAR ... xi BAB I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Perumusan Masalah ... 3 1.3 Pembatasan Masalah ... 3 1.4 Tujuan Penelitian ... 4 1.5 Manfaat Penelitian ... 4

BAB II LANDASAN TEORI 2.1 Fungsi ... 5

2.2 Definisi dan Notasi pada Graf ... 7

2.3 Graf Ular ... 14

2.4 Subgraf ... 15

(11)

x

2.6 Pelabelan Graf ... 17

BAB III HASIL DAN PEMBAHASAN

3.1 Graf Ular ... 22 3.2 Konstruksi Pelabelan Total - -Antiajaib Super

pada Graf Ular ... 23

BAB IV KESIMPULAN DAN SARAN

4.1 Kesimpulan ... 36 4.2 Saran ... 36

(12)

xi

DAFTAR GAMBAR

Gambar 2.1 (a) Fungsi Satu-satu, (b) Fungsi Pada, (c) Fungsi Satu-satu

pada, (d) Bukan Fungsi ... 6

Gambar 2.2 Graf dengan titik dan sisi ... 7

Gambar 2.3 Graf Kosong... 8

Gambar 2.4 Graf ... 8

Gambar 2.5 (a) Graf Terhubung; (b) Graf Tidak terhubung ... 9

Gambar 2.6 Graf Berbobot ... 10

Gambar 2.7 (a) Graf Sederhana; (b) Graf Ganda; (c) Graf Semu ... 11

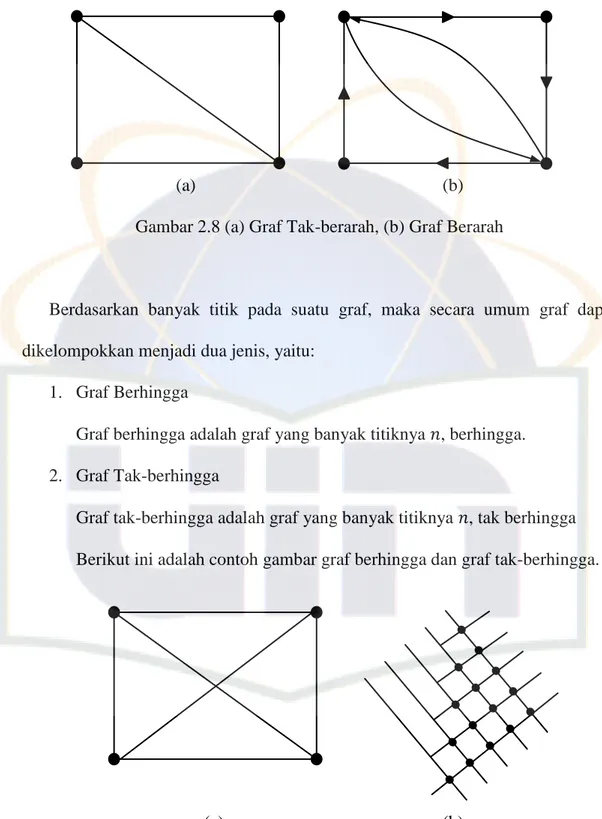
Gambar 2.8 (a) Graf Tak-berarah; (b) Graf Berarah ... 12

Gambar 2.9 (a) Graf Berhingga; (b) Graf Tak-berhingga ... 12

Gambar 2.10 Graf Lengkap ... 13

Gambar 2.11 Graf Lintasan ... 14

Gambar 2.12 Graf Lingkaran... 14

Gambar 2.13 Graf Ular ... 15

Gambar 2.14 Subgraf ... 16

Gambar 2.15 Isomorfisma Graf... 17

Gambar 2.16 Graf dengan Pelabelan Sisi -Titik-Antiajaib ... 18

Gambar 2.17 Graf dengan Pelabelan Titik -Sisi-Antiajaib ... 19

Gambar 2.18 Graf dengan Pelabelan Total -Titik-Antiajaib ... 20

Gambar 2.19 Graf dengan Pelabelan Total -Titik-Antiajaib ... 20

(13)

xii

Gambar 3.2 Pelabelan Total - -Antiajaib Super Graf Ular

dengan ... 27

Gambar 3.3 Pelabelan Total - -Antiajaib Super Graf Ular

dengan ,6. ... 31

Gambar 3.4 Pelabelan Total

- -Antiajaib Super Graf Ular

(14)

1

BAB I PENDAHULUAN

1.1 Latar Belakang

Teori Graf pertama kali diperkenalkan pada tahun 1736 oleh seorang matematikawan Swiss bernama Leonard Euler dalam menyelesaikan masalah jembatan Könisbergh di Jerman. Masalah jembatan Könisbergh muncul ketika Euler dihadapkan pada suatu kasus dimana terdapat tujuh buah jembatan yang menghubungkan daratan yang dibelah oleh sungai. Lalu muncul pertanyaan apakah mungkin melalui ketujuh buah jembatan masing-masing tepat satu kali dan kembali lagi ke tempat semula. Kemudian Euler memodelkan masalah ini ke dalam graf dengan membuktikan bahwa hal tersebut tidaklah mungkin. Pembuktian dari kejadian inilah yang dijadikan sebagai permulaan dari Teori Graf. Sejak saat itu, bidang penelitian dalam teori graf terus berkembang, salah satunya adalah pelabelan graf.

Pelabelan pada graf merupakan pemberian label pada elemen-elemen tertentu dari graf tersebut dengan menggunakan bilangan bulat positif. Secara umum objek kajiannya berupa graf yang direpresentasikan oleh titik, sisi dan himpunan bilangan asli yang disebut label. Pelabelan pertama kali diperkenalkan oleh Sadlàčk (1964), Stewart (1966), Kotzig dan Rosa (1970). Berdasarkan elemen-elemen yang dilabeli, pelabelan dibagi menjadi 3 jenis, yaitu pelabelan titik, pelabelan sisi, dan pelabelan total.

(15)

2

Sejalan dengan era perkembangan pelabelan graf, pelabelan ajaib dan pelabelan antiajaib merupakan jenis pelabelan graf yang sedang banyak diteliti saat ini. Pelabelan ajaib pertama kali diperkenalkan oleh Kotzig dan Rosa pada tahun 1970 yang selanjutnya disebut sebagai pelabelan total sisi ajaib [6]. Kemudian pada tahun 2000, Simanjutak dkk. memperkenalkan pelabelan total -sisi antiajaib.

Pada tahun 2005, pelabelan total sisi ajaib dikembangkan menjadi pelabelan selimut -ajaib oleh Gutiérrez dan Lladó. Dalam pelabelan -ajaib, merupakan selimut sisi dari graf . sebuah selimut sisi dari merupakan subgraf-subgraf berbeda sedemikian sehingga untuk sebarang sisi dari terdapat paling sedikit satu di subgraf untuk . Jika setiap isomorfik dengan suatu graf tertentu, maka memuat suatu selimut .

Pelabelan antiajaib dipelopori oleh Hartsfield dan Ringel pada tahun 1990. Suatu graf dengan sisi dikatakan antiajaib jika setiap sisinya dapat dilabeli dengan sedemikian sehingga didapatkan jumlah label yang berbeda dari setiap sisi yang saling bersisian ke setiap titik dari graf tersebut [4]. Kemudian tahun 2009, Inayah dkk. memperkenalkan pelabelan selimut - -antiajaib. Pelabelan selimut - -antiajaib merupakan pengembangan dari pelabelan total -sisi-antiajaib dan pelabelan selimut.

Dalam teori graf, banyak terdapat jenis-jenis graf salah satunya adalah graf ular. Graf ular merupakan graf yang disusun dengan aturan pengubinan dari graf segitiga dengan panjang . Salah satu masalah utama dalam teori graf adalah

(16)

3

bagaimana cara memberikan label atau menandai suatu titik dan sisi, sedemikian sehingga setiap titik dan sisi yang saling bertetangga memiliki tanda yang berbeda.

Ada beberapa peneliti yang telah membahas tentang pelabelan selimut - -antiajaib pada kelas-kelas graf tertentu. Inayah dkk. telah meneliti tentang Pelabelan Selimut - -Antiajaib Pada Graf Kipas. Melanjutkan penelitian Inayah dkk., pada tahun 2009, Muhammad Iqbal dalam skripsinya telah meneliti tetang Algortima Pelabelan Total - -Antiajaib pada Graf Kipas . Pada tahun 2012, Khorirotuz telah meneliti Pelabelan Selimut- -Ajaib Super pada Graf Roda dan Selimut- -Ajaib Super pada Graf Buku. Kemudian tahun

2015 telah diteliti Pelabelan Total - -Antiajaib (Super) pada Graf Roda

, oleh Husnul. Oleh karena itu, penulis tertarik untuk meneliti tentang

“Pelabelan total - -Antiajaib Super pada Graf Ular ”.

1.2 Perumusan Masalah

Berdasarkan latar belakang yang telah dibahas, perumusan masalah dalam penelitian ini adalah bagaimana mengkonstruksi pelabelan total - -antiajaib super pada graf ular .

1.3 Pembatasan Masalah

Skripsi ini membahas mengenai pelabelan total - -antiajaib super pada graf ular , dengan bilangan bulat positif dan memuat selimut- serta dibatasi oleh graf sederhana dan tak berarah.

(17)

4

1.4 Tujuan Penelitian

Tujuan dari penelitian ini adalah untuk mengkonstruksi pelabelan total - -antiajaib super pada graf ular .

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah untuk menambah wawasan bagi pembaca dan juga penulis dalam mengenal teori graf khususnya mengenai pelabelan antiajaib. Serta untuk memenuhi salah satu syarat penulis dalam menyelesaikan kurikulum tingkat akhir Program Studi Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta.

(18)

5

BAB II

LANDASAN TEORI

Untuk menjelaskan Pelabelan Total - -Antiajaib Super pada Graf Ular , perlu adanya beberapa teori dasar untuk menunjang pembuktian dan mempermudah pemahaman. Beberapa teori dasar meliputi:

2.1 Fungsi

Misalkan dan himpunan. Relasi biner dari ke merupakan suatu fungsi jika setiap elemen di dalam dihubungkan dengan tepat satu elemen di dalam .

Jika adalah fungsi dari ke kita tuliskan yang artinya memetakan ke [9].

Bergantung pada bayangan, fungsi dibedakan menjadi fungsi satu-satu, fungsi pada dan fungsi satu-satu pada.

a. Fungsi Satu-satu

Fungsi dikatakan satu-satu jika tidak ada dua elemen berbeda himpunan yang memiliki bayangan sama. Dengan kata lain, jika dan adalah anggota himpunan , maka bilamana . Jika maka implikasinya adalah [9].

(19)

6

b. Fungsi Pada

Fungsi dikatakan pada jika setiap elemen himpunan merupakan bayangan dari satu atau lebih elemen himpunan . Dengan kata lain, seluruh elemen merupakan jelajah dari [9].

c. Fungsi Satu-satu Pada

Fungsi dikatakan korespondensi satu-satu atau bijektif (satu-satu pada) jika adalah fungsi satu-satu dan fungsi pada [9].

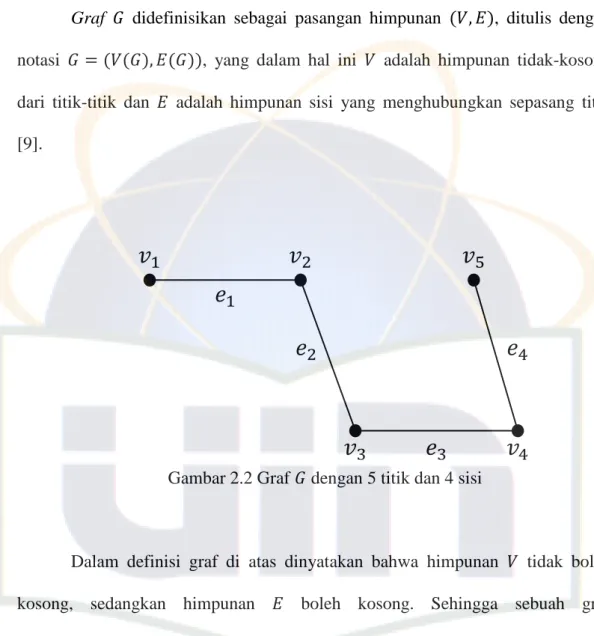
Gambar berikut mengilustrasikan fungsi satu-satu, fungsi pada, fungsi satu-satu pada dan bukan fungsi.

(a) (b)

(c) (d)

Gambar 2.1 (a) Fungsi satu-satu, (b) Fungsi Pada, (c) Fungsi satu-satu pada dan (d) Bukan fungsi

r s t u 1 2 3 4 5 A B r s t u 1 2 3 A B r s t u 1 2 3 4 A B r s t u 1 2 3 4 A B

(20)

7

2.2 Definisi dan Notasi pada Graf

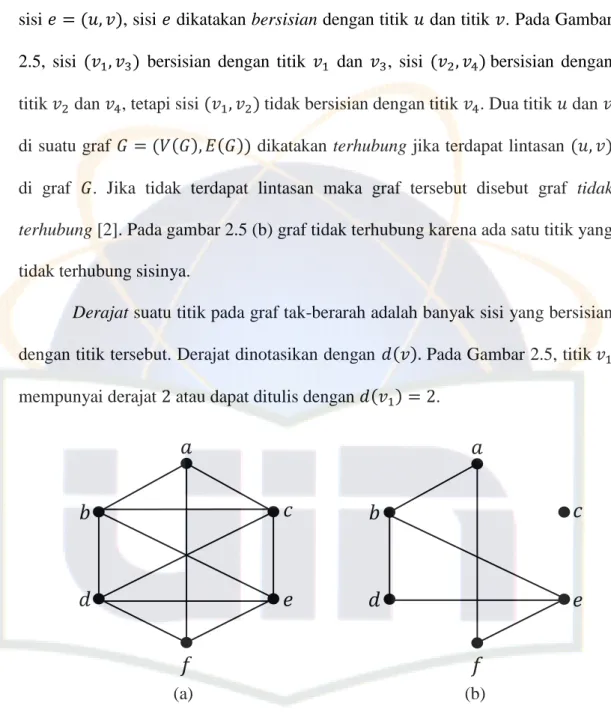
Graf didefinisikan sebagai pasangan himpunan , ditulis dengan

notasi , yang dalam hal ini adalah himpunan tidak-kosong dari titik-titik dan adalah himpunan sisi yang menghubungkan sepasang titik [9].

Dalam definisi graf di atas dinyatakan bahwa himpunan tidak boleh kosong, sedangkan himpunan boleh kosong. Sehingga sebuah graf dimungkinkan tidak mempunyai sisi satu buah pun, tetapi titiknya harus ada minimal satu. Graf yang hanya mempunyai satu buah titik tanpa sebuah sisi dinamakan graf trivial, sedangkan graf yang hanya mempunyai himpunan titik dan tidak memiliki sebuah sisi pun dinamakan graf kosong.

(21)

8

Gambar 2.3 Graf Kosong

Titik adalah titik pada graf yang biasanya dinotasikan dengan huruf, seperti . Sedangkan biasanya dinotasikan dengan sisi yang menghubungkan titik dengan titik , maka dapat ditulis sebagai . Misalkan diberikan graf sebagai berikut:

Gambar 2.4 Graf

Dua titik di graf dikatakan bertetangga bila keduanya terhubung langsung dengan sebuah sisi. Dengan kata lain, bertetangga dengan jika adalah sebuah sisi pada graf . Pada Gambar 2.5, titik bertetangga dengan titik dan tetapi titik tidak bertetangga dengan titik . Untuk sembarang

(22)

9

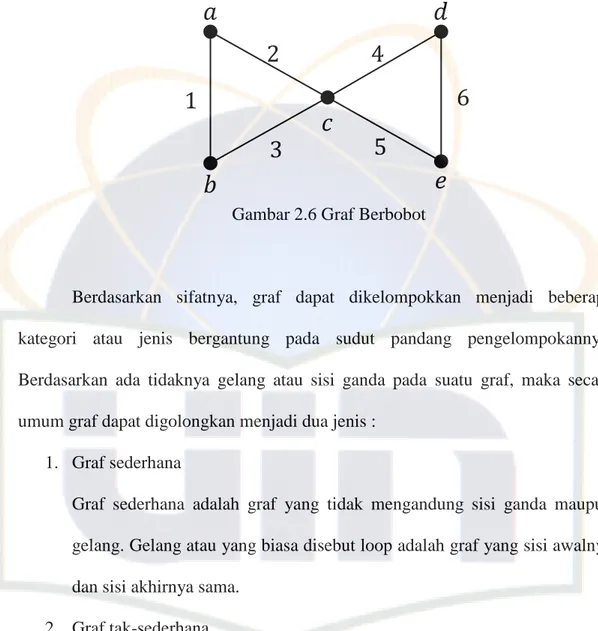
sisi , sisi dikatakan bersisian dengan titik dan titik . Pada Gambar 2.5, sisi bersisian dengan titik dan , sisi bersisian dengan titik dan , tetapi sisi tidak bersisian dengan titik . Dua titik dan di suatu graf dikatakan terhubung jika terdapat lintasan di graf . Jika tidak terdapat lintasan maka graf tersebut disebut graf tidak

terhubung [2]. Pada gambar 2.5 (b) graf tidak terhubung karena ada satu titik yang

tidak terhubung sisinya.

Derajat suatu titik pada graf tak-berarah adalah banyak sisi yang bersisian

dengan titik tersebut. Derajat dinotasikan dengan Pada Gambar 2.5, titik mempunyai derajat atau dapat ditulis dengan .

(a) (b)

(23)

10

Graf berbobot merupakan graf yang setiap sisinya diberi sebuah harga (bobot).

Gambar 2.6 Graf Berbobot

Berdasarkan sifatnya, graf dapat dikelompokkan menjadi beberapa kategori atau jenis bergantung pada sudut pandang pengelompokannya. Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graf, maka secara umum graf dapat digolongkan menjadi dua jenis :

1. Graf sederhana

Graf sederhana adalah graf yang tidak mengandung sisi ganda maupun gelang. Gelang atau yang biasa disebut loop adalah graf yang sisi awalnya dan sisi akhirnya sama.

2. Graf tak-sederhana

Graf tak-sederhana adalah graf yang mengandung sisi ganda maupun loop. Ada dua macam graf tak-sederhana, yaitu graf ganda dan graf semu. Graf ganda adalah graf yang mengandung sisi ganda. Sisi ganda yang menghubungkan sepasang titik bisa lebih dari dua buah. Graf semu adalah graf yang mengandung sisi ganda dan loop.

1

3

2

4

5

(24)

11

Berikut ini adalah contoh gambar graf sederhana, graf ganda dan graf semu.

(a) (b) (c)

Gambar 2.7 (a) Graf Sederhana, (b) Graf ganda dan (c) Graf Semu

Berdasarkan orientasi arah pada sisi, maka secara umum graf dibedakan menjadi dua jenis, yaitu :

1. Graf tak-berarah

Graf tak-berarah adalah graf yang sisinya tidak mempunyai orientasi arah. Pada graf tak-berarah, urutan pasangan titik yang dihubungkan oleh sisi tidak diperhatikan. Jadi, adalah sisi yang sama.

2. Graf berarah

Graf berarah adalah graf yang disetiap sisinya diberikan orientasi arah. Pada graf berarah, dan menyatakan dua buah sisi yang berbeda, dengan kata lain .

Berikut ini adalah contoh graf tak-berarah dan graf berarah. 1

2 3

(25)

12

(a) (b)

Gambar 2.8 (a) Graf Tak-berarah, (b) Graf Berarah

Berdasarkan banyak titik pada suatu graf, maka secara umum graf dapat dikelompokkan menjadi dua jenis, yaitu:

1. Graf Berhingga

Graf berhingga adalah graf yang banyak titiknya , berhingga. 2. Graf Tak-berhingga

Graf tak-berhingga adalah graf yang banyak titiknya , tak berhingga Berikut ini adalah contoh gambar graf berhingga dan graf tak-berhingga.

(a) (b)

(26)

13

Ada beberapa jenis graf sederhana khusus, beberapa di antaranya adalah sebagai berikut :

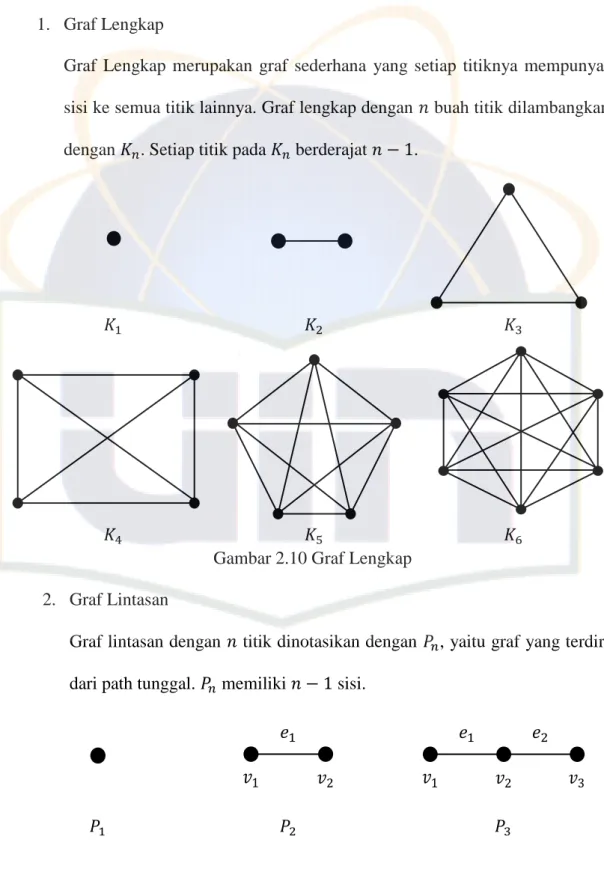
1. Graf Lengkap

Graf Lengkap merupakan graf sederhana yang setiap titiknya mempunyai sisi ke semua titik lainnya. Graf lengkap dengan buah titik dilambangkan dengan . Setiap titik pada berderajat .

Gambar 2.10 Graf Lengkap 2. Graf Lintasan

Graf lintasan dengan titik dinotasikan dengan , yaitu graf yang terdiri dari path tunggal. memiliki sisi.

(27)

(28)

15

adalah kumpulan segitiga-segitiga yang terhubung, maka adalah graf planar terhubung yang terdiri dari kumpulan , dimana setiap segitiga saling terhubung sisinya paling tidak satu sisi. Kumpulan segitiga terhubung disebut triomino. Jadi disebut -triomino jika adalah pengubinan dari segitiga-segitiga yang terhubung.

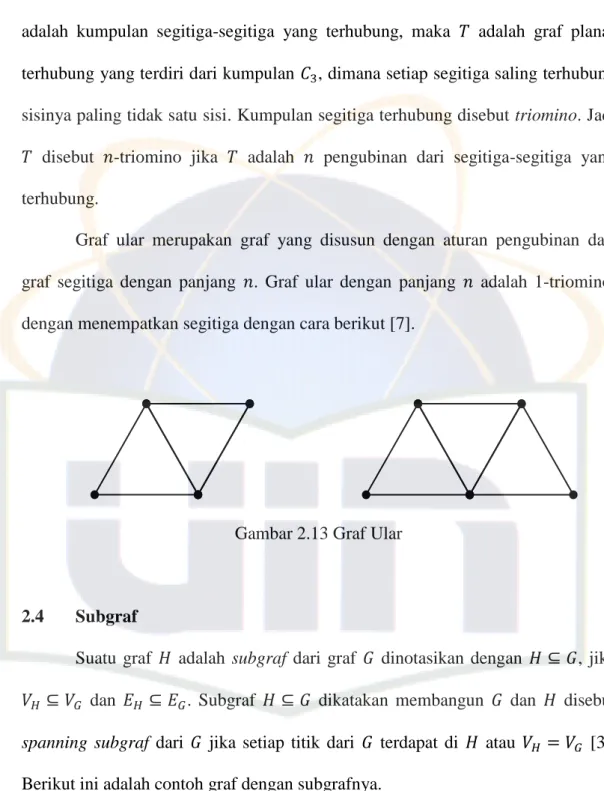
Graf ular merupakan graf yang disusun dengan aturan pengubinan dari graf segitiga dengan panjang . Graf ular dengan panjang adalah 1-triomino, dengan menempatkan segitiga dengan cara berikut [7].

Gambar 2.13 Graf Ular

2.4 Subgraf

Suatu graf adalah subgraf dari graf dinotasikan dengan , jika dan . Subgraf dikatakan membangun dan disebut

spanning subgraf dari jika setiap titik dari terdapat di atau [3]. Berikut ini adalah contoh graf dengan subgrafnya.

(29)

16

2.5 Isomorfisma Graf

Dua graf dan dengan titik disebut isomorfik jika titik dari dan dapat dilabeli dengan bilangan dari 1 sampai sehingga bila titik bertetangga dengan titik di , maka titik bertetangga dengan titik di dan sebaliknya [4]. Dua buah graf dikatakan isomorfik bila memenuhi syarat-syarat berikut:

(a) Mempunyai jumlah titik yang sama, (b) Mempunyai jumlah sisi yang sama, (c) Mempunyai jumlah derajat yang sama.

Graf

Subgraf Subgraf Spanning Subgraf

(30)

17

Berikut ini adalah contoh gambar isomorfisma graf.

Gambar 2.15 Isomorfisma Graf

2.6 Pelabelan Graf

Pelabelan pada suatu graf adalah suatu pemetaan (fungsi) bijektif yang memasangkan unsur-unsur graf (titik atau sisi) dengan bilangan bulat positif [1]. Jika domain dari fungsi adalah titik, maka disebut pelabelan titik (vertex labeling). Jika domainnya adalah sisi, maka disebut pelabelan sisi (edge labeling). Dan jika domainnya adalah titik dan sisi, maka disebut pelabelan total (total labeling) [8].

a. Pelabelan Graf Ajaib

Misalkan dengan | | . Kita katakan ajaib jika sisi-sisi di dapat dilabeli dengan bilangan sehingga jumlah dari label semua insiden sisi-sisi dengan sembarang titik adalah sama [4].

b. Pelabelan Graf Antiajaib

Pelabelan antiajaib pada graf didefinisikan sebagai fungsi yang bersifat bijektif (satu-satu pada) dari kepada himpunan dimana | | dan | | mempunyai karakteristik

(31)

18

bahwa tidak sama atau bobot yang berbeda untuk setiap dengan adalah bobot dari penjumlahan dua titik diantara satu sisi [1].

i. Pelabelan Sisi -Titik-Antiajaib

Pelabelan sisi -titik-antiajaib pada graf adalah sebuah fungsi bijektif yang memetakan himpunan sisi ke bilangan positif sedemikian sehingga himpunan bobot titik dari semua titik di adalah , dimana , dan [1]. Gambar 2. menunjukkan bobot dari setiap sisi pada graf membentuk barisan aritmatika, yaitu dan .

1 2

3

Gambar 2.16 Graf dengan Pelabelan Sisi -Titik-Antiajaib

ii. Pelabelan Titik -Sisi-Antiajaib

Pelabelan titik -sisi-antiajaib pada graf adalah sebuah fungsi bijektif yang memetakan himpunan titik ke bilangan bulat positif sedemikian sehingga himpunan bobot sisi dari semua sisi di adalah , dimana

(32)

19

, dan [1]. Gambar 2. menunjukkan bobot dari setiap titik pada graf membentuk barisan aritmatika, yaitu dan .

1

2

3

Gambar 2.17 Graf dengan Pelabelan Titik -Sisi-Antiajaib

iii. Pelabelan Total -Titik-Antiajaib

Pelabelan total -titik-antiajaib pada graf adalah sebuah fungsi bijektif yang memetakan himpunan titik dan sisi ke bilangan bulat positif sedemikian sehingga himpunan bobot titik dari semua titik di adalah , dimana , dan [1]. Gambar 2. menunjukkan bobot dari setiap titik pada graf membentuk barisan aritmatika, yaitu dan .

(33)

20 1 2 3 4 5 6

Gambar 2.18 Graf dengan Pelabelan Total -Titik-Antiajaib

iv. Pelabelan Total -Sisi-Antiajaib

Pelabelan total -sisi-antiajaib pada graf adalah sebuah fungsi bijektif yang memetakannhimpunan titik dan sisi ke bilangan bulat positif sedemikian sehingga himpunan bobot sisi dari semua sisi di adalah , dimana , dan [1]. Gambar 2. menunjukkan bobot-bobot setiap titik pada graf membentuk barisan aritmatika, yaitu dan .

1 2 3 4 5 6

(34)

21

v. Pelabelan Total - -Antiajaib

Misalkan dan graf. Suatu pelabelan total - -antiajaib dari adalah fungsi bijektif | | | | sedemikian sehingga untuk setiap subgraf isomorfik untuk , himpunan dari bobot-

∑ ∑

merupakan barisan aritmatika dengan jarak , yaitu dengan dan bilangan bulat positif dan adalah suatu bilangan subgraf isomorfik . Dalam hal ini kita katakana bahwa adalah - -antiajaib. Sementara untuk ( ) , kita katakan bahwa adalah pelabelan total - -antiajaib super dan adalah - -antiajaib super.

Catatan jika , maka pelabelan tersebut menjadi pelabelan -ajaib [5].

(35)

22

BAB III

HASIL DAN PEMBAHASAN

3.1 Graf Ular

Graf ular dinotasikan sebagai dengan dimana adalah banyaknya segitiga pada graf ular.

Graf ular mempunyai himpunan titik dan himpunan sisi sebagai berikut, dimana adalah himpunan titik atas dan adalah himpunan titik bawah pada graf ular

.

{ } { }

Dan

(36)

23 { } { } { } { }

3.2 Konstruksi Pelabelan Total - -Antiajaib Super pada Graf Ular

Mengkonstruksi pelabelan dari suatu graf yaitu membangun atau membentuk fungsi bijektif yang memasangkan suatu himpunan unsur-unsur graf yaitu titik dan sisi dengan bilangan bulat.

3.2.1 Teorema 1. Untuk , graf ular mempunyai pelabelan total - -antiajaib super.

Bukti. Misalkan adalah suatu pelabelan - -antiajaib super. Didefinisikan terhadap titik dan sisinya sebagai berikut.

{ {

(37)

24 { { { {

Dapat dilihat bahwa adalah suatu fungsi bijektif dari { } Bobot didefinisikan sebagai bobot total selimut dari pelabelan total pada graf ular. Bilangan dan pada dan bukan pangkat, melainkan bilangan tersebut hanya merupakan kode pembeda bobot total selimut untuk tiap selimut yang berlainan dengan syarat batas yang berbeda. Sehingga dapat dirumuskan sebagai berikut:

(38)

25 ∑ ∑

Karena dan . Berdasarkan hasil diatas, dapat diperhatikan bahwa himpunan bobot total selimut untuk , mempunyai pelabelan total - -antiajaib super. Berikut ini adalah hasil konstruksi pelabelan untuk

35

33

37

6 2 4 7 8 9 11 10 3 12 1 5

(39)

26 6 11 10 9

39

43

7 4 2 15

45

41

8 13 1 12 3 14 5 13 15 17 18

47

51

12 11

45

49

10 9 2 4 6 14 3 16 5 1 7

53

8 5 7 1 10 2 4 6 15 17 12 11 8 21 9

61

16 3 18 20 14 13

51

55

59

19

53

57

9 10 24 69 11 57 61 65 1 18 3 20 5 22 2 19 4 21 6 17 16 15 14 13 7 8 59 63 67 12 23 7 26 9 1 20 3 22 5 24 25 13 12 63 67 71 75 2 21 4 23 6 65 69 73 14 19 18 17 16 15 10 11 27 77 8

(40)

27

Gambar 3.2 Pelabelan Total - -Antiajaib Super pada Graf Ular

dengan

{ { { 29 10 27 8 7 15 14 9 2 23 4 25 6 71 75 79 83 21 20 19 18 17 16 69 73 77 81 1 22 3 24 5 26 28 11 12 30 85 13 77 81 85 89 2 25 4 27 6 29 23 22 21 20 19 75 79 83 87 ₉₁ 28 17 16 15 14 18 1 24 3 26 5 33 12 93 7 30 9 32 11 13 8 31 10

(41)

28 { { {

∑

(42)

29 ∑

Karena dan . Berdasarkan hasil diatas, dapat diperhatikan bahwa himpunan bobot total selimut untuk , mempunyai pelabelan total - -antiajaib super. Berikut ini adalah hasil konstruksi pelabelan untuk .

37

33

41

12 2 4 11 10 9 7 8 3 6 1 5 6 2 3 8 7

51

43

14 15 4 1 9 11 12 13

39

47

5 10

(43)

30 13 11 9 8

49

57

14 15

45

53

16 17 2 4 6 12 3 10 5 1 7

61

18 5 7 1 20 2 4 6 15 13 18 19 8 9 21

71

14 3 12 10 16 17

51

59

67

11

55

63

10 9 2 15 4 13 6 61 69 57 65 73 12 7 11 8 17 18 19 20 21 1 16 3 14 5 77 22 23 24 81 7 12 9 1 18 3 16 5 14 25 26 27 63 71 79 87 24 19 20 21 22 23 8 11 10 67 75 83 91 13 2 17 4 15 6 11 1 20 3 18 5 16 27 28 29 30 26 7 14 9 12 69 77 85 93 101 21 22 23 24 25 8 13 10 73 81 89 97 15 2 19 4 17 6

(44)

31

Gambar 3.3 Pelabelan Total - -Antiajaib Super pada Graf Ular

dengan

{ { { { { 11 1 22 3 20 5 18 29 30 31 32 7 16 9 14 33 75 83 91 99 107 28 23 24 25 26 27 8 15 10 13 12 79 87 95 103 111 17 2 21 4 19 6

(45)

32 {

∑ ∑

(46)

33

Karena dan . Berdasarkan hasil diatas, dapat diperhatikan bahwa himpunan bobot total selimut untuk , mempunyai pelabelan total - -antiajaib super. Berikut ini adalah hasil konstruksi pelabelan untuk .

37

31

43

12 2 4 11 10 9 7 6 3 8 1 5 1 5 6 2 3 9 10

54

42

14 15 4 8 11 12 13

36

48

7 13 9 11 12

47

59

14 15

41

53

16 17 2 4 6 5 8 3 10 1

65

18 7

(47)

34

Gambar 3.4 Pelabelan Total - -Antiajaib Super

Graf Ular dengan

Dilihat dari ketiga teorema yang telah dibahas diatas, didapat bobot dengan masing-masing nilai yang diperoleh. Berikut ini adalah tabel eksistensi pelabelan total - -antiajaib super pada graf ular .

5 7 1 20 2 4 6 15 10 18 19 8 14 21

76

9 3 11 13 16 17

46

58

70

12

52

64

8 57 69 81 17 18 19 20 21 22 2 11 4 13 6 15 23 24 51 63 75 87 7 16 9 1 10 3 12 5 14 2 12 4 14 6 8 18 10 62 74 86 98 16 19 20 21 22 23 25 26 27 56 68 80 92 24 7 17 9 1 11 3 13 5 15 2 13 4 15 6 8 19 10 67 79 91 103 17 21 22 23 24 25 61 73 85 97 109 16 27 28 29 30 26 1 12 3 14 5 7 18 9 20 11 18 2 14 4 16 6 72 84 96 108 120 8 20 10 22 12 23 24 25 26 27 33 66 78 90 102 114 28 17 29 30 31 32 1 13 3 15 5 7 19 9 21 11

(48)

35

Tabel 3.1 Eksistensi Pelabelan Total - -Antiajaib Super pada Graf Ular

(49)

36

BAB IV

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Berdasarkan hasil dan pembahasan, diperoleh kesimpulan bahwa graf ular memuat pelabelan total - -antiajaib super, dan penelitian ini menghasilkan tiga teorema dengan yang berbeda pada masing-masing teorema. Pada Teorema 1, untuk graf ular mempunyai pelabelan total - -antiajaib super. Pada Teorema 2, untuk graf ular mempunyai pelabelan total - -antiajaib super. Dan pada Teorema 3, untuk graf ular mempunyai pelabelan total - -antiajaib super. Berikut adalah tabel pelabelan total - -antiajaib super pada graf ular .

Tabel 4.1 Pelabelan total - -antiajaib super pada graf ular

4.2 Saran

Berdasarkan hasil penelitian mengenai pelabelan total - -antiajaib super pada graf ular , maka saran yang dapat diberikan dari penelitian ini yaitu dapat dilanjutkan mencari konstruksi pelabelan yang lebih umum khususnya

(50)

37

untuk yang lainnya, baik pelabelan tidak super ataupun pelabelan super pada graf ular dengan bilangan bulat positif, serta dapat mencari pola umum pada pelabelan total - -antiajaib untuk kelas-kelas graf yang lainnya.

(51)

38

REFERENSI

[1] Baca, Martin dan Mirka Miller. 2008. Super Edge-Antimagic Graph: A

Wealth of Problems and Solution. Florida: Brown Walker Press.

[2] Bondy, J. A, dan U. S. R Murty. 1976. Graph Theory With Applications. The Macmillan Press.

[3] Harju, Tero. 1994. Lecture Notes on Graph Theory. Department of Mathematics University of Turku, Finland.

[4] Hartsfield, N. dan Gherald Ringel. 1990. Pearls in Graph Theory. San Diego: Academic Press.

[5] Inayah, N., A. N. M. Salman, dan R. Simanjuntak. 2009. On (𝑎,

𝑑)-H-Antimagic Covering of Graph, The Journal of Combinatorial Mathematics and Combinatorial Computing 71, 273-281.

[6] Kotzig, A. dan Rosa, A. 1970. Magic Valuations of Finite Graph. Canada

Mathematics Bulletin 13, 451-461.

[7] Low, Richard M dan Sin-Min Lee. 2004. On the Integer-magic Spectra of

Tessellation Graphs.

[8] Miller, Mirka. 2000. Open Problems in Graph Theory: Labeling Extremal

Graph. Prosiding Konferensi Nasional Himpunan Matematika Indonesia X

di Institut Teknologi Bandung, 17-20 Juli.

[9] Munir, Rinaldi. 2009. Matematika Diskrit, Edisi Ketiga. Bandung: Informatika.