Directory UMM :Journals:Journal_of_mathematics:OTHER:

(1)

THE PLANE ROTATION OPERATOR AS

A MATRIX FUNCTION

by Emil Olteanu

Abstract. Formalism in mathematics can offer many simplifications, but it is an instrument which should be carefully treated as it can easily create confusions. Formalism is an instrument which, together with a programming language that allows abstractions (for instance the C language) can create a very strong programming instrument. One example is realizing the matrix functions in C language using pointers.

The present material refers to an example of matrix functions, the exponential matrix function, used as a plane rotation operator.

A matrix function is a function of the form: Y = F

( )

X , where X and Y are quadratic matrices of order n. The relation can also be written as follows:

















=

nn n n n n nn n n n n

x

F

y

K

2 1 2 22 21 1 12 11 2 1 2 22 21 1 12 11 .

In the case of the plane rotations we shall use matrices of order 2 and for rotations in a three-dimension space we use matrices of order 3.

In order to associate a matrix with a linear transformation of a n-dimensional vectorial space V, we must choose a basis x1, x2, ..., xn. From the equations:

or

( )

∑

=

n

i i ij j

a

x

A

1

(2)

we obtain the matrix which represents the transformation :

nn n

n

n n

a a

a

a a

a

a a

a

A A

K K K K K

K K

2 1

2 22

21

1 12

11

=

→ .

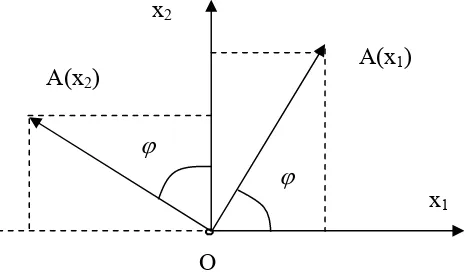
[image:2.595.232.466.299.437.2]

If A is the transformation obtained through the rotation of the plane around the origin O with an angle

ϕ

and if x1 and x2 are two vectors from the basis orthogonal and of length 1, then the representatives of these vectors applied in the origin apply to the representatives of images A(x1) and A(x2).

Figure 1.

A(x1) and A(x2) verify the following equations:

( )

  

× +

× −

=

× +

× =

2 1

2

2 1

1

cos sin

sin cos

x x

x A

x x

x A

ϕ

The operator A is represented by the matrix A :

x

1

x2

A(x

1

)

ϕ

(3)

( )

ϕ

cos

( )

ϕ

sin

cos

−

=

A

The operator A-1 is the rotation of angle

ϕ

in the opposite direction, that is of angle

−

ϕ

.

( )

ϕ

( )

ϕ

sin

( )

ϕ

( )

ϕ

cos

( )

ϕ

sin

cos

sin

cos

1

−

=

−

=

−

A

we verified the relation

A

×

A

−1

=

U

, the unity vector.

( )

×

−

( )

=

−

=

×

−

ϕ

sin

cos

sin

cos

sin

cos

1

A

( )

( ) ( )

( )

= =U

+ −

− +

=

1 0

0 1

cos sin

sin cos cos

sin

cos sin sin

cos sin

cos

2 2

ϕ

Given a vector 

     =

2 1

x x

X in plane we can obtain a vector       =

2 1

Y Y

Y rotated

by an angle

α

towards which we apply the plane rotation operator Y =F

( )

α

×X , where:

( )

=





( )

−

( )





α

cos

sin

cos

F

The product of two angle rotations

α

and

β

is equivalent to an angle rotation

β

α

+

. This is mathematically expressed as follows: F

( ) ( ) (

α

×F

β

= F

α

+

β

)

. The function that verifies this functional equation is the exponential function. This leads us to the conclusion that the rotation operator can be expressed as an exponential. In order to find the exponential function corresponding to this operator we search for a differential equation to verify and then we look for its solutions.

( )

α

=





cos

( )

α

−

sin

( )

α

( )

α





⇒

(4)

( )

α

( )

_αα

( )

_α

( )

α

( )

_α

( )

α

( )

_αα

( )

_αα

( )

_α

( )

α I F

( )

α

F = ×

  

 −

×     − =   



− − −

=   

 −

=

cos sin

sin cos

0 1

1 0 sin

cos

cos sin

cos' sin'

sin' cos'

'

where we noted







 −

=

0

1

0

I

.

We obtained the equation: F'

( )

α

=I×F

( )

α

. This equation can also be written F'

( )

α

= I×F

( )

α

. Generally speaking

A

×

B

≠

B

×

A

, but in this case the multiplication is commutative. From the equation:

( ) ( )

= F ×I ⇒ F'

α

( ) ( )

×

=

⇒

−

F

I

F

1

α

'

α

( ) ( )

×

=

∫

⇒

∫

F

−1

α

F

'

α

d

α

I

d

α

( ) ( )

×

=

∫

⇒

∫

F

−1

α

dF

α

I

d

α

( )

(

F

α

)

=I

α

+C ⇒ ln

( )

I C

e

F

α

=

α+

for

α

=

0

⇒

F

( )

0

=

e

C

⇒

( )

e

F

( )

0

F

α

=

Iα

×

C

=

Iα

×

The formula can also be written:

( )

α

e

Iα

F

=

0

where

( )

C

e

F

0

=

.

We make an assumption

( )









=

1

0

1

0

e

0

U

(5)

⇒

=









      4 3 2 1

1

0

1

_CC _CC

e

⇒       =     4 3 2 1 1 0 0 1 ln C C C C

We calculate









1

0

1

ln

using the development in a series of exponentials.

(

)

∑

∞ =

=

+

⇒

1

ln

n

x

U

, where we noted with









=

1

0

1

U

, the unit matrix and with x

a matrix variable _      4 3 2 1 x x x x . For









=

0

O

x

, where O is zero matrix, results:

(

+

)

=

∑

∞

=









=

0

ln

1

O

n

U

n .

Therefore C = O, meaning Ci = 0, for i

∈

{1, 2, 3, 4}. Thus:

( )

α

I

e

F

=









−

=

cos

sin

cos

.

This formula can also be written in another manner:

( )

α

( )

α

Iα

e

I

U

×

cos

+

×

sin

=

,

which is another way of writing Euler’s formula in the field of matrix functions. We notice that the following relation is true:

U

I

=

−

(6)

References

[1] W. Kecs - Complemente de matematici cu aplicaţii în tehnică (Mathematics Complements with Techical Applications) , Editura Tehnică, Bucureşti, 1981.

[2] I. Gh. Şabac - Matematici speciale (Special Mathematics), Editura Didactică şi Pedagogică, Bucureşti, 1981.

[3] Crstici Borislav (coordonator), ş.a. - Matematici speciale (Special Mathematics) , Editura Didacticăşi Pedagogică, Bucureşti, 1981.

[4] Gheorghe Coman ş.a. - Introducere în teoria ecuaţiilor operatoriale (Introduction to the Theory of Operator Equations) , Editura Dacia, Cluj-Napoca, 1976.

[5] I. M. Gelfand şi G. E. Şilov - Funcţii generalizate (Generalized Functions) , Editura Ştiinţificăşi Enciclopedică, Bucureşti, 1983.

[6] Fazlollah Reza - Spaţii liniare (Linear Spaces) , Editura Didactică şi Pedagogică, Bucureşti, 1973.