BAB 4 ENTROPI PADA PROSES STOKASTIK RANTAI MARKOV

ENTROPI PADA PROSES

STOKASTIK RANTAI MARKOV

4.1 Proses Stokastik

Dalam kehidupan nyata, seringkali orang ingin mengamati keterkaitan satu kejadian dengan kejadian lain dalam suatu interval waktu tertentu, yang merupakan suatu barisan kejadian. Misalnya banyaknya kecelakaan yang terjadi pada ruas jalan yang sama selama 40 hari. Dengan mengetahui kecelakaan hari ini kita dapat memprediksi peluang terjadi kecelakaan esok hari. Hal ini dapat dilakukan dengan proses stokastik. Proses stokastik ini banyak diaplikasikan pada bidang pemasaran (marketing), keuangan dan produksi barang. Proses Stokastik sendiri dapat didefinisikan sebagai berikut.

Definisi 4.1 Proses Stokastik

{

X t_t, ∈T

}

merupakan barisan peubah acak,yaitu untuk setiap t∈T terdapat peubah acak Xt.

Nilai peubah acak Xt dinamakan keadaan (state) pada saat t. Himpunan T disebut ruang parameter atau ruang indeks dari proses stokastik X. Himpunan semua nilai

yang mungkin disebut ruang keadaan dari X.

( )

X t

Proses-proses stokastik dapat diklasifikasikan berdasarkan jenis indeks parameter dan ruang keadaannya.

1. Proses Stokastik dengan ruang keadaan diskrit dan indeks parameternya diskrit atau kontinu.

2. Proses Stokastik dengan ruang keadaan kontinu dan indeks parameternya diskrit atau kontinu.

Proses stokastik dengan indeks parameter diskrit dikatakan stasioner apabila distribusi gabungan hingga tidak berubah terhadap waktu, dapat dituliskan sebagai

(

t1 t 1,..., tm t m

) (

t1 1,..., tm m

)

P X ₊ =x X ₊ =x =P X =x X =x (4.1)

untuk sebarang m∈ dan semua t, , 1Ν ti ≥0 ≤ ≤ . i m

4.1 Laju Entropi dari Proses Stokastik

Ukuran ketidakpastian, entropi juga dapat diterapkan pada proses stokastik. Entropi ini dapat dilihat sebagai laju entropi dan didefinisikan dengan

Definisi 4.2 : Laju entropi dari suatu proses stokastik, {Xt} adalah

( )

H

(

1, 2,...,

)

H lim t t X X X X t →∞ = (4.2)

jika limitnya ada atau dapat pula dituliskan sebagai

( )

(

1 2 1

)

H lim H _{t t} , _t ,..., t X X X ₋ X ₋ X →∞ = (4.3)

Umumnya perhitungan laju entropi diterapkan jika proses stokastik {Xt} stasioner. Untuk {Xt} yang stasioner (saling bebas dan identik), aturan rantai dari entropi menunjukkan

( )

1

( )

( )

1

( )

1 H H H lim lim H t i i t t X t X X X t t = →∞ →∞ =

∑

= = (4.4)

4.2 Rantai Markov

Sebagaimana telah diutarakan pada Sub Bab 4.1, terdapat klasifikasi dalam proses stokastik, dan salah satunya adalah proses stokastik khusus yang mempunyai ruang keadaan diskrit dan indeks parameternya diskrit yaitu rantai Markov. Contoh dalam kehidupan nyata adalah proses perubahan cuaca, dengan keadaan cuaca hari ini dipengaruhi oleh keadaan cuaca satu hari sebelumnya. Secara matematis, rantai Markov didefinisikan sebagai berikut.

Definisi 4.3 Proses stokastik diskrit {Xt, t=1,2,...,m} disebut rantai Markov jika untuk

t>0 berlaku

(

1 1 1 1 1 1

)

(

1 1

)

P X_t+ =i_t+ |X =i,...,X_t− =i_t−,X_t =i_t =P X_t+ =i_t+ |X_t =i_t (4.5)

Dalam memudahkan penulisan dalam bentuk matriks maka persamaan (4.5) dituliskan

(

t 1 | 1 1,..., t 1 t 1, t

)

(

t 1 |

)

P X₊ = j X =i X ₋ =i₋ X = j =P X ₊ = j X_t = j (4.6)

Sehingga diperoleh matriks peluang transisi (satu langkah) dari {Xt,,t=1,2,...,m}dinotasikan P, adalah suatu matriks dengan elemen ke (i, j)nya adalah peluang transisi,pij. Jadi

11 12 1 21 22 2 1 2 m m m m mm p p p p p p p p p ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ P " " # # % # "

Elemen-elemen dari matriks transisi P bernilai non negatif dan jumlah

elemen-elemen pada setiap barisnya sama dengan satu,

1 1 m ij j p = =

∑

, untuk setiap i = 1,2...,m. Definisikan pula qi, peluang awal pada tiap keadaan (state), dengan P(X1=i) = qi. Vektor yang memuat nilai awal dari tiap keadaan, dinamakan distribusi peluang awal,

Dalam kasus ini, fmp dari peubah acak-peubah acak tersebut dituliskan sebagai

(

1, 2,..., t

)

( ) (

1 2| 1

) (

3| 2

) (

... t| t 1

)

p x x x = p x p x x p x x p x x₋ (4.7)

Sehingga jika pmf dari peubah acak pada waktu t adalah p(xt), maka pmf untuk t+1 adalah

( )

1

( )

Pt t₁ t t t x p x₊ =

∑

p x _{x x+} (4.8)

Definisi 4.4: Rantai Markov dikatakan time invariant atau homogen jika peluang

bersyarat p x

(

_t+1|x_t

)

tidak bergantung pada t,

(

1

)

(

2

)

P X_t+ =b X| _t =a =P X =b X| ₁=a , untuk a,b ∈ X. (4.9)

Definisi 4.5 : Suatu distribusi peluang pj, j ≥ 1 dikatakan stasioner untuk suatu rantai

markov jika 1 2 2 1 2 2 ( ) ( ) ( ) _{j ij} i i X i P X j P X j P X i P P ∞ ∞ = = = = =

∑

= = =

∑

(4.10)

dengan induksi dapat diperoleh,

1 1 2 2 ) ( ) ( ( ) t ij t t i i X i _j P X j P X j P X i P P ∞ ∞ = = = = =

∑

= = =

∑

(4.11)

Dengan kata lain, peluang stasioner adalah peluang untuk suatu t → ∞ sehingga terjadinya transisi ke suatu keadaan, baik masuk maupun keluar dari suatu keadaan, nilainya relatif tidak berubah. Jadi, γj merupakan solusi tunggal dari sistem persamaan linear

∑

= = n i ij k j P 1 γ γ , j=1, 2,",n dan 1 1 =

∑

= n i k γ

Penjelasan lebih dalam mengenai rantai Markov dapat dilihat pada buku seperti Taylor dan Karlin (1994).

Contoh 4.1

untuk rantai Markov orde satu, misalkan suatu barisan DNA. Bagian ini dimulai dari kromosom-X

GATCATTGATATGTTGCTAGAACTATGAGTGTTAAAGGTGCTTGTGGTGA GTTATCAGACAGAAACGCAGAAGATGTTATTGGAAGCTTGAGGAAAAGT GATCCTGGATTTACAGTGCCAAGAATTGGCCTGTATTGTGTTCTCAATGTT TTTGAGGAAGGTAGAAACTGTAAGTGATGA

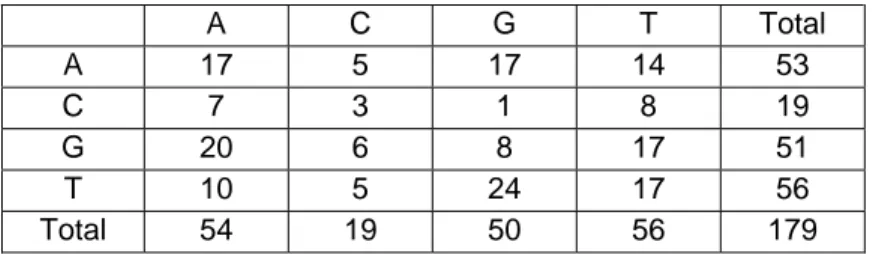
Pada kenyataannya barisan basa DNA ini lebih panjang, hampir mencapai tiga juta barisan. Dalam kasus ini ada empat (4) karakter yaitu basa A, G, C, T. Banyaknya kemunculan basa A pada bagian ini A = 54 kali, C = 19 kali, G = 51 kali, dan T= 56 kali. Dari contoh barisan ini dapat dibuat matriks transisi

Karakter kedua A C G T Total A 17 5 17 14 53 C 7 3 1 8 19 G 20 6 8 17 51 T 10 5 24 17 56 Karakter pertama Total 54 19 50 56 179

Tabel 4.1 : Frekuensi transisi tiap basa

Matriks transisi dapat dibuat menjadi matriks peluang transisi dengan membagi setiap nilai dengan jumlah pada setiap barisnya (frekuensi relatifnya)

Karakter kedua A C G T A 0,32075472 0,09434 0,320755 0,264151 C 0,36842105 0,157895 0,052632 0,421053 G 0,39215686 0,117647 0,156863 0,333333 Karakter pertama T 0,17857143 0,089286 0,428571 0,303571

Terlebih dahulu dihitung taksiran P dan hasilnya 1 0,3207 0, 0943 0, 3208 0, 2642 2 0, 3684 0,1579 0, 0526 0, 4211 ˆ 3 0, 3922 0,1176 0,1569 0, 3333 4 0,1786 0, 0893 0, 4286 0, 3035 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ P

4.3 Entropi pada Rantai Markov

Ukuran entropi juga dapat digunakan pada rantai Markov. Pada tulisan ini dibahas

entropi untuk rantai Markov orde 1. Misalkan berada pada keadaan i, peluang pada

akan berada di keadaan j, dinotasikan pij, dan ketidakpastian memilih keadaan selanjutnya dapat dilihat sebagai entropi yang didefinisikan sebagai

( )

1 H log n i ij j ij p p = = −

∑

(4.12)

Untuk pij = 0, didefinisikan pij log pij = 0. Nilai Hi adalah entropi keadaan ke i.

Apabila rantai Markov stasioner pada keadaan i, yaitu γi, maka entropi state menjadi

(0.1)

( )

1 1 1 H H log n i i i n n i ij ij i j p p γ γ = = = = = −

∑

∑ ∑

Ekspresi ini menyatakan rata-rata jumlah bit yang dibutuhkan untuk menyandikan observasi pada state selanjutnya, dan dinamakan entropi (transisi) rantai Markov, dinyatakan dengan H.

Jadi jika ditetapkan bahwa matriks transisi

1 1 1 3 3 3 1 1 0 2 2 1 3 0 4 4 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ P

maka entropi perbaris dari matriks tersebut adalah

1

H =1, 5849, H₂ =1, H₃ =0,8113.

Apabila dibandingkan dengan matriks transisi yang berbentuk

8 1 1 9 1 8 1 8 1 1 0 2 2 1 3 0 4 4 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ P entropinya menjadi H₁=0, 6144, H₂ = , 1 H₃ =0,8113.

Pandang kembali contoh 4.1 mengenai barisan DNA. Dari matriks peluang transisi ini akan dicari taksiran entropi dari, dengan formula pada persamaan (4.13) dengan basis yang digunakan pada log adalah 2. Hasil yang didapat dengan menggunakan program pada Matlab 7.0 adalah

ˆ H_i

( )

1 1 1 1 ˆ H log 1,881 n j j j p p = = −

∑

= , _{2 2}

( )

₂ 1 ˆ H log 1, 7001 n j j j p p = = −

∑

=

( )

3 3 3 1 ˆ H log 1,8403 n j j j p p = = −

∑

= , _{4 4}

( )

₄ 1 ˆ H log 1,8011 n j j j p p = = −

∑

=

Sehingga entropi ini merupakan matriks berukuran 1 x 4 yaitu

(

)

ˆ

H= 1,881 1,7001 1,8403 1,8011

4.4 Laju Entropi pada Rantai Markov

Pada rantai Markov ini juga dikenal laju entropi sebagai berikut.

Definisi 4.6 : Misalkan rantai Markov tidak tereduksi (irreducible) dengan state yang

hingga, laju entropi dapat dihitung melalui

( )

(

1 2 1

) (

2 1

)

H lim H _{t t} , _t ,..., H t X X X₋ X₋ X X X →∞ = = (4.14)

Rantai Markov yang mempunyai distribusi stasioner, γ dan matriks transisi P, laju entropinya menjadi

( )

( )

1 1 H P l t t i ij ij i j X γ = = = −

∑∑

og P (4.15)

Sama seperti contoh kasus di atas, akan dihitung entropi dari distribusi stasioner rantai Markov, π dan taksiran peluang transisi

1 0,3207 0, 0943 0, 3208 0, 2642 2 0, 3684 0,1579 0, 0526 0, 4211 ˆ 3 0, 3922 0,1176 0,1569 0, 3333 4 0,1786 0, 0893 0, 4286 0, 3035 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ P

dengan γ = [0.3014 0.1060 0.2801 0.3125]. Maka dengan memanfaatkan definisi entropi pada persamaan (2.4) didapat

( ) (

)

H γ = 0.5215 0.34321 0.51426 0.5244 .

Sedangkan laju entropi dari distribusi stasioner dan matriks transisi P diperoleh dengan memasukan nilai-nilai ke persamaan (2.43) sehingga

( )

4 4 2

( )

1 1 H _iP log_ij P_ij 0.15859 i j X γ = = = −

∑∑

=