vii ABSTRAK
Model regresi Poisson secara umum digunakan untuk menganalisis data count yang diasumsikan berdistribusi Poisson dengan nilai rata-rata dan variansinya sama (equidispersion). Namun, seringkali terjadi masalah nilai variansi melebihi nilai rata-rata atau lebih dikenal dengan overdispersi sehingga model regresi Poisson tidak tepat digunakan. Salah satu model yang dapat digunakan untuk mengatasi masalah overdispersi adalah dengan menggunakan model regresi Binomial Negatif. Pendugaan parameter dapat diperoleh dengan metode pendugaan kemungkinan maksimum melalui iterasi Newton-Raphson. Data yang digunakan dalam skripsi ini adalah data banyaknya kematian Ibu hamil di propinsi Jawa Timur tahun 2012. Dari perhitungan mean dan variansi diketahui bahwa terjadi overdispersi sehingga data dimodelkan menggunakan Regresi Binomial negatif. Faktor-faktor yang mempengaruhi banyaknya kematian Ibu adalah jumlah cakupan imunisasi tetanus Toksoid (TT2+) pada Ibu hamil , jumlah ibu hamil yang mendapatkan tablet FE1 (30 tablet) ,jumlah Ibu hamil yang mendapatkan tablet FE3 (90 tablet) ,jumlah cakupan imunisasi Tetanus Toksoid (TT-5) pada Ibu hamil ,cakupan K1 , cakupan K4 , cakupan Ibu hamil yang ditolong nakes , dan jumlah Ibu nifas .
viii ABSTRACT
Poisson regression model is generally used to analyze the count data which is Poisson distributed with equal mean value and variance (equidispersion). However, the problem occurs when the variance exceeds the mean value which we called as overdispersion so that the Poisson regression model is inappropriately used. One model that can be used to solve the overdispersion problem is the negative binomial regression model. The estimation of the parameters can be obtained by the Maximum Likelihood Estimation method through Newton-Raphson iteration. The data used in this thesis is data of the number of maternal mortality of pregnant women in East Java province in 2012. Based on the calculation of mean and variance, it is known that there is an overdispersion problem so that the data is modeled using negative binomial regression. Some factors that affect the number of maternal mortality are the number of tetanus toxoid immunization coverage (TT2 +) in pregnant women , the number of pregnant women who get FE1 tablets (30 tablets) , the number of pregnant women who get Fe3 tablets (90 tablets) , the number of Tetanus toxoid immunization coverage (TT-5) in pregnant women , K1 coverage , K4 coverage , the coverage of pregnant women which is assisted by the health workers , and the number of mother postpartum .
i
PENDUGAAN MODEL REGRESI BINOMIAL NEGATIF DENGAN
METODE KEMUNGKINAN MAKSIMUM
Skripsi
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Program Studi Matematika
Oleh: Maria Ansila Bouk
NIM: 123114019
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
ii
THE ESTIMATION OF NEGATIVE BINOMIAL REGRESSION MODEL USING MAXIMUM LIKELIHOOH METHOD
Thesis
Presented as Partial Fulfillment of the Requirements to Obtain Sarjana Sains Degree in Mathematics
By:
Maria Ansila Bouk Student Number: 123114019
MATHEMATICS STUDY PROGRAM, MATHEMATICS DEPARTMENT
FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY
v
HALAMAN PERSEMBAHAN
Di dalam setiap kejadian dalam kehidupan , Tuhan selalu
mempunyai maksud dan tujuan.
Skripsi ini dipersembahkan untuk
Tuhan Yesus Kristus dan Bunda Maria yang selalu menyertai, memberkati, dan memberikan kemudahan
bagi saya lewat orang-orang yang baik hati dalam setiap perjuangan saya.
Kedua orang tua Bapa Agus dan Mama Siska
Adik-adik tercinta Lista, Nandi, Ory dan Ikun
vii ABSTRAK
Model regresi Poisson secara umum digunakan untuk menganalisis data count yang diasumsikan berdistribusi Poisson dengan nilai rata-rata dan variansinya sama (equidispersion). Namun, seringkali terjadi masalah nilai variansi melebihi nilai rata-rata atau lebih dikenal dengan overdispersi sehingga model regresi Poisson tidak tepat digunakan. Salah satu model yang dapat digunakan untuk mengatasi masalah overdispersi adalah dengan menggunakan model regresi Binomial Negatif. Pendugaan parameter dapat diperoleh dengan metode pendugaan kemungkinan maksimum melalui iterasi Newton-Raphson. Data yang digunakan dalam skripsi ini adalah data banyaknya kematian Ibu hamil di propinsi Jawa Timur tahun 2012. Dari perhitungan mean dan variansi diketahui bahwa terjadi overdispersi sehingga data dimodelkan menggunakan Regresi Binomial negatif. Faktor-faktor yang mempengaruhi banyaknya kematian Ibu adalah jumlah cakupan imunisasi tetanus Toksoid (TT2+) pada Ibu hamil , jumlah ibu hamil yang mendapatkan tablet FE1 (30 tablet) ,jumlah Ibu hamil yang mendapatkan tablet FE3 (90 tablet) ,jumlah cakupan imunisasi Tetanus Toksoid (TT-5) pada Ibu hamil ,cakupan K1 , cakupan K4 , cakupan Ibu hamil yang ditolong nakes , dan jumlah Ibu nifas .
viii ABSTRACT
Poisson regression model is generally used to analyze the count data which is Poisson distributed with equal mean value and variance (equidispersion). However, the problem occurs when the variance exceeds the mean value which we called as overdispersion so that the Poisson regression model is inappropriately used. One model that can be used to solve the overdispersion problem is the negative binomial regression model. The estimation of the parameters can be obtained by the Maximum Likelihood Estimation method through Newton-Raphson iteration. The data used in this thesis is data of the number of maternal mortality of pregnant women in East Java province in 2012. Based on the calculation of mean and variance, it is known that there is an overdispersion problem so that the data is modeled using negative binomial regression. Some factors that affect the number of maternal mortality are the number of tetanus toxoid immunization coverage (TT2 +) in pregnant women , the number of pregnant women who get FE1 tablets (30 tablets) , the number of pregnant women who get Fe3 tablets (90 tablets) , the number of Tetanus toxoid immunization coverage (TT-5) in pregnant women , K1 coverage , K4 coverage , the coverage of pregnant women which is assisted by the health workers , and the number of mother postpartum .
x
KATA PENGANTAR
Puji syukur penulis haturkan ke hadirat Tuhan Yang Maha Kuasa atas segala berkat dan penyertaanNya sehingga penulis dapat menyelesaikan skripsi dengan baik.
Skripsi yang berjudul “Pendugaan Model Regresi Binomial Negatif dengan Metode
Kemungkinan Maksimum” ini adalah salah satu syarat untuk memperoleh gelar sarjana Matematika pada Fakultas Sains dan Teknologi. Dalam penulisan skripsi ini, tentunya penulis telah menerima bantuan baik secara moril maupum materil dari berbagai pihak. Oleh karena itu penulis ingin menyampaikan ucapan terima kasih kepada:
1. Bapak Ir. Ig. Aris Dwiatmoko., M. Sc selaku dosen pembimbing yang dengan penuh kesabaran telah memberikan bimbingan nasihat dan arahan kepada penulis.
2. Bapak Hartono, Ph. D, selaku Ketua Program Studi yang telah memberikan banyak bimbingan dalam hal akademik dan perkuliahan.
3. Serta bapak dan ibu dosen yang telah memberikan banyak ilmu pengetahuan kepada penulis selama menjalani perkuliahan di Universitas Sanata Dharma. 4. Mas Susilo selaku laboran yang telah banyak membantu penulis dalam
perkuliahan terutama dalam penulisan skripsi ini.
xii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PERSEMBAHAN ... v
HALAMAN PERNYATAAN KEASLIAN KARYA ... vi
HALAMAN ABSTRAK ... vii
HALAMAN ABSTRACT ... viii
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... ix
KATA PENGANTAR ... x
E. Manfaat Penulisan ... 5
F. Metode Penulisan ... 5
G. Sistematika Penulisan ... 6
BAB II LANDASAN TEORI ... 8
A. Distribusi Probabilitas ... 8
1. Variabel Random ... 8
2. Fungsi Probabilitas ... 8
a. Distribusi Probabilitas Diskrit ... 8
b. Distribusi Probabilitas Kontinu ... 9
3. Karakteristik Distribusi Probabilitas ... 9
a. Mean ... 9
b. Variansi ... 10
xiii
B. Distribusi Poisson ... 13
C. Distribusi Gamma dan Sifat-sifatnya ... 15
D. Distribusi Binomial Negatif ... 18
E. Distribusi Binomial Negatif sebagai Campuran Distribusi Poisson-Gamma .... 22
F. Metode Maksimum Likelihood ... 25
G. Metode Numerik Newton-Raphson ... 28
H. Keluarga Eksponensial ... 32
1. Distribusi Poisson merupakan keluarga eksponensial ... 33
2. Distribusi Binomial merupakan keluarga eksponensial ... 34
I. Model Regresi Linear Berganda ... 36
J. Jenis Data Penelitian ... 37
1. Data berdasarkan sumbernya ... 37
2. Data berdasarkan bentuk dan sifatnya... 38
K. Model Count Respon ... 41
1. Model Regresi logistik dan Regresi Probit ... 42
2. Model Regresi Poisson dan Regresi Binomial Negatif ... 43
L. Uji Kolmogorov-Smirnov ... 45
BAB III PENDUGAAN MODEL REGRESI BINOMIAL NEGATIF ... 50
A. Model Regresi Poisson Berganda ... 50
B. Overdispersi dan Regresi Binomial Negatif ... 54
C. Binomial Negatif sebagai Keluarga Eksponensial ... 56
D. Model Regresi Binomial Negatif ... 61
E. Pendugaan Parameter untuk Model Regresi Binomial Negatif dengan Metode Maksimum likelihood ... 62
xiv
BAB IV PEMODELAN REGRESI BINOMIAL NEGATIF PADA DATA
BANYAKNYA KEMATIAN IBU DI PROPINSI JAWA TIMUR ... 88
A. Deskripsi Data ... 91
B. Pengolahan Data ... 91
1. Uji Kolmogorov-Smirnov ... 92
2. Pendugaan Model regresi Poisson ... 93
3. Uji Signifikansi Parameter ... 94
4. Uji Overdispersi pada Model Regresi Poisson ... 96
5. Pendugaan Model Regresi Binomial Negatif ... 97
6. Uji Signifikansi Model regresi Binomial Negatif ... 97
BAB V KESIMPULAN DAN SARAN ... 100
A. Kesimpulan ... 100
B. Saran ... 101
DAFTAR PUSTAKA ... 102
xv
DAFTAR TABEL
Tabel 2.1 Data suatu sampel acak untuk contoh 2.4 ... 47
Tabel 2.2 Hasil Pengujian Kolmogorov-Smirnov ... 48
Tabel 3.1 Data banyaknya kasus campak pada kecamatan di kota Semarang ... 81
Tabel 3.2 Hasil Pengujian Kolmogorov-Smirnov ... 83
Tabel 3.3 Parameter , , , , untuk Regresi poisson ... 84
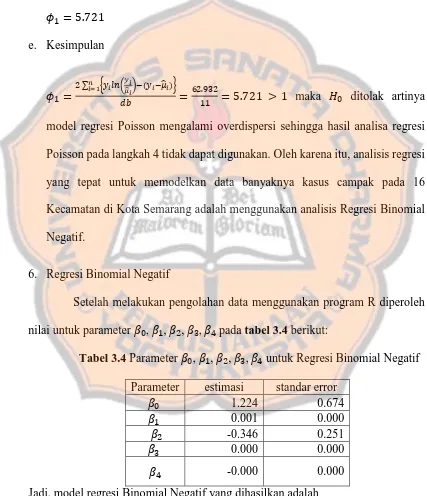
Tabel 3.4 Parameter , , , , untuk Regresi Binomial Negatif ... 86
Tabel 4.1 Deskripsi Data ... 91
Tabel 4.2 Hasil Pengujian Kolmogorov-Smirnov ... 93
Tabel 4.3 Parameter , , , , , , , , untuk Regresi poisson ... 93
1 BAB I
PENDAHULUAN
A.Latar Belakang
Regresi adalah suatu metode yang digunakan untuk menganalisis hubungan antara suatu variabel dependen dengan satu atau lebih variabel independen. Pada umumnya, analisis regresi digunakan untuk menganalisis data variabel dependen yang berupa data kontinu. Namun dalam beberapa aplikasinya, data variabel dependen yang akan dianalisis dapat berupa data diskrit. Variabel dependen diskrit dapat berupa data count yaitu data yang nilainya nonnegatif dan menyatakan banyaknya kejadian dalam interval waktu, ruang, atau volume tertentu. Ketika variabel dependen berupa data count, analisis regresi yang biasa digunakan adalah analisis regresi Poisson. Pada regresi ini variabel dependen diasumsikan berdistribusi Poisson, dengan fungsi probabilitasnya adalah
� � = �!� −�, � = , , , … dengan >
Analisis Regresi Poisson adalah suatu model yang digunakan untuk menganalisis hubungan antara variabel dependen yang berdistribusi Poisson dengan beberapa variabel independen. Pada model Regresi Poisson terdapat asumsi yang harus dipenuhi yaitu nilai variansi dari data yang diperoleh harus sama dengan nilai meannya atau disebut ekuidispersi (equidispersion).
Pada kenyataannya asumsi ini sangat jarang terjadi karena biasanya data count memiliki variansi yang lebih besar dari mean atau disebut kondisi overdispersi ��� � > � � ) atau sebaliknya mean lebih besar dari pada variansi atau disebut underdispersi ��� � < � � . Jika pada data diskrit terjadi overdispersi namun tetap digunakan model regresi Poisson maka estimasi parameter koefisien regresinya tetap konsisten tetapi tidak efisien karena berpengaruh pada nilai standar galat (underestimate). Hal itu dapat mengakibatkan kesimpulan yang akan dihasilkan menjadi tidak tepat atau tidak sesuai dengan data. Alternatif model regresi yang lebih sesuai untuk data overdispersi adalah model regresi Binomial Negatif. Pada regresi ini variabel dependen diasumsikan berdistribusi Binomial Negatif, dengan fungsi probabilitasnya dihasilkan dari distribusi campuran Poisson-Gamma yaitu
� = Γ � + �
Model regresi Binomial Negatif memiliki kegunaan yang sama dengan model regresi Poisson yaitu untuk menganalisis hubungan antara suatu variabel
antara distribusi Poisson dan Gamma. Distribusi Gamma digunakan untuk menyesuaikan kehadiran overdispersi dalam model Poisson.
Dari dua buah model regresi yang digunakan untuk data count, yaitu Poisson dan Binomial Negatif, model Binomial Negatif memiliki bentuk yang lebih umum karena model Poisson dapat dinyatakan dalam model Binomial Negatif ketika parameter dispersinya mendekati nol (k 0) atau dapat dikatakan data dalam keadaan ekuidispersi. Jadi, model Binomial Negatif pada dasarnya dapat digunakan untuk berbagai kasus data count. Dalam penulisan ini akan lebih dikhususkan untuk masalah pendugaan model regresi Binomial Negatif pada kasus overdispersi. Pendugaan parameter dapat diperoleh dengan menggunakan metode pendugaan kemungkinan maksimum melalui iterasi Newton-Raphson.
Adapun beberapa aplikasi dari model Binomial Negatif diantaranya adalah memodelkan kasus terjadinya penyakit demam berdarah dengue (DBD) dan untuk mengetahui besarnya pengaruh variabel-variabel yang mempengaruhi terjadinya penyakit DBD, pemodelan banyaknya kematian Ibu di suatu daerah, model prediksi kecelakaan lalulintas jalan tol, penggolongan resiko jumlah klaim asuransi kendaraan dan lain-lainnya.
B.Rumusan Masalah
Perumusan masalah yang akan dibicarakan dalam skripsi ini adalah:
2. Bagaimana menduga parameter-parameter pada model regresi Binomial Negatif dengan menggunakan metode pendugaan kemungkinan maksimum melalui iterasi Newton-Raphson?
3. Bagaimana menerapkan model regresi Binomial Negatif pada Poisson yang mengalami Overdispersi dengan metode Newton-Raphson dalam masalah nyata?
C.Batasan Masalah
Agar dalam pembahasan tidak terlalu luas dan hasilnya mendekati pokok permasalahan, maka dalam penulisan skripsi ini hanya akan membahas:
1. Model Regresi Binomial Negatif yang merupakan model campuran Distribusi Poisson-Gamma untuk kasus Poisson yang mengalami Overdispersi.
2. Pendugaan parameter dilakukan dengan menggunakan metode pendugaan kemungkinan maksimum melalui iterasi Newton-Raphson.
3. Penulis tidak membahas tentang generalisasi dari Distribusi Binomial Negatif sebagai campuran distribusi Poisson dan Gamma.
4. Penulis hanya membahas tentang distribusi Poisson yang mengalami overdispersi.
5. Dalam perhitungan penulis menggunakan program R dan SPSS. 6. Penulis tidak membahas tentang Prior Natural Conjugate.
D.Tujuan Penulisan
1. Untuk memahami landasan matematis pendugaan model regresi Binomial Negatif dengan metode Newton-Raphson.
2. Untuk dapat menduga parameter-parameter pada model regresi Binomial Negatif menggunakan metode pendugaan kemungkinan maksimum melalui iterasi Newton-Raphson.
3. Untuk dapat menerapkan model regresi Binomial Negatif pada Poisson yang mengalami Overdispersi dengan metode Newton-Raphson dalam masalah nyata.
4. Untuk memenuhi tugas dalam mencapai gelar sarjana.
E.Manfaat Penulisan
Manfaat Penulisan ini adalah untuk memperoleh pengetahuan tentang Regresi Binomial Negatif, membahas dasar-dasar teori yang terkait, dapat menentukan parameter-parameter dari model regresi Binomial Negatif, serta dapat menduga model banyaknya kematian Ibu di propinsi Jawa Timur menggunakan model regresi Binomial Negatif.
F. Metode penulisan
G.Sistematika Penulisan
Sistematika penulisan pada skripsi ini meliputi lima Bab yaitu: BAB I PENDAHULUAN
A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan BAB II LANDASAN TEORI
A. Distribusi Probabilitas B. Distribusi Poisson
C. Distribusi Gamma dan Sifat-sifatnya D. Distribusi Binomial Negatif
E. Distribusi Binomial Negatif sebagai campuran Distribusi Poisson-Gamma
F. Metode Maksimum Likelihood G. Metode numerik Newton-Raphson H. Keluarga Eksponensial
I. Model Regresi Linear Berganda J. Jenis Data Penelitian
L. Uji Kolmogorov-Smirnov
BAB III PENDUGAAN MODEL REGRESI BINOMIAL NEGATIF A. Model Regresi Poisson Berganda
B. Overdispersi dan regresi Binomial Negatif C. Binomial Negatif sebagai keluarga Eksponensial D. Model Regresi Binomial Negatif
E. Pendugaan Parameter untuk Model Regresi Binomial Negatif dengan Metode Maksimum Likelihood
F. Uji Kebaikan Model
BAB IV PEMODELAN REGRESI BINOMIAL NEGATIF PADA DATA BANYAKNYA KEMATIAN IBU DI PROPINSI JAWA TIMUR
A. Deskripsi Data B. Pengolahan Data
BAB V PENUTUP A. Kesimpulan B. Saran
BAB II
LANDASAN TEORI
A. Distribusi Probabilitas 1. Variabel Random
Definisi 2.1
Variabel random adalah fungsi bernilai riil yang domainnya adalah ruang sampel.
Definisi 2.2
Sebuah variabel random dikatakan variabel random diskrit jika himpunan dari kemungkinan hasilnya adalah terbilang. Jika tidak memenuhi definisi di atas maka variabel random di atas disebut variabel random kontinu.
2. Fungsi Probabilitas
a. Distribusi Probabilitas Diskrit Definisi 2.3
Himpunan pasangan terurut , adalah fungsi probabilitas, atau distribusi probabilitas dari suatu variabel random diskrit X jika
1) � = = 2)
Definisi 2.4
Fungsi distribusi kumulatif (cumulative distribution function) dari sebuah variabel random diskrit dengan distribusi probabilitas adalah
= � = ∑ − ∞ < < ∞
�≤
b. Distribusi Probabilitas Kontinu Definisi 2.5
Fungsi adalah fungsi probabilitas (probability function) untuk variabel random kontinu jika
1) , untuk semua ∈ �
2) ∫−∞∞ =
3) � < < = ∫
Definisi 2.6
Fungsi distribusi kumulatif (cumulative distribution function) dari sebuah variabel random kontinu dengan distribusi probabilitas adalah
= � = ∫ , untuk − ∞ < < ∞
−∞
3. Karakteristik Distribusi Probabilitas a. Mean
Misalkan adalah variabel random dengan fungsi probabilitas . Mean atau nilai harapan (expected value) dari adalah
{
= = ∑ , diskrit
= = ∫∞ , kontinu
−∞
b. Variansi Definisi 2.8
Jika adalah variabel random, variansi dari variabel random , maka variansi dari ditulis sebagai � atau � didefinisikan
� = ( − ) .
Teorema 2.1
� � = − ( )
Bukti
� = [ − ]
= − +
= − + ( )
= − ( ) ∎
c. Momen dan Fungsi Pembangkit Momen Definisi 2.9
′ =
Definisi 2.10
Fungsi pembangkit momen dari sebuah variabel random didefinisikan sebagai = � . Fungsi pembangkit momen dari dikatakan ada jika terdapat konstanta positif sedemikian sehingga adalah berhingga untuk | | .
Fungsi pembangkit momen dari variabel acak didefinisikan sebagai
= � =
{
∑ � , diskrit
∫∞ �
−∞ , kontinu
Teorema 2.2
Misalkan variabel acak dengan fungsi pembangkit momen (FPM) maka
|
�=
= ′
Bukti:
Ekspansi Deret maclaurin dari � adalah
� = + +
! + ! + ! +
� = ∑ �
Ketika = untuk semua turunan diperoleh
= ′
Sehingga secara umum
= ′ ∎
Turunan pertama dari fungsi pembangkit momen yaitu
Untuk variabel kontinu, �
� = ′ = ∫ �
∞ −∞
Untuk variabel diskrit, �
� = ′ = ∑ �
Berdasarkan turunan pertama dari FPM diatas, untuk = , diperoleh
= .
Turunan kedua dari fungsi pembangkit momen yaitu:
Untuk variabel kontinu, �
� = ′′ = ∫ �
∞ −∞
Untuk variabel diskrit, �
� = ′′ = ∑ � disebut momen ke- dari variabel acak .
B. Distribusi Poisson Definisi 2.11
= �! − , = , , , …
Berdasarkan Definisi 2.10, diperoleh
= ∑ − ! �
Berdasarkan formulasi Taylor = ∑ �
= ( �− ). �. �+ � ( �− )
= � ( �− )
+ � ( �− )
|�=
= +
Jadi,
� � = − [ ]
= + −
=
C. Distribusi Gamma dan Sifat-sifatnya Definisi 2.12
fungsi Gamma didefinisikan sebagai
Γ = ∫ − −
∞
Untuk > dan nilai dari integral tersebut adalah bilangan positif. Fungsi Gamma memiliki sifat sebagai berikut:
a. Jika = , maka Γ = ∫∞ − = .
b. Jika adalah suatu bilangan bulat positif maka diperoleh Γ = − !. c. Jika > , maka Γ = ∫∞ − − = − Γ −
Definisi 2.14
= { Γ − − ⁄ , ∞
Berasarkan definisi fungsi probabilitas maka
∫ −
= Γ + Γ +
Berdasarkan sifat fungsi Gamma maka Γ + = Γ α , maka diperoleh
= Γ + Γ
= ΓΓ
=
2. Variansi
Berdasarkan teorema 2.1
� = − ( )
= ∫ −
−
Γ
∞
= ∫ +
−
Γ
∞
= Γ ∫∞ + −
Berdasarkan persamaan 2.1 dan definisi sifat fungsi Gamma, maka diperoleh
= Γ + Γ +
= + Γ +Γ
= +Γ Γ
= +
� = − ( )
= + −
= + −
=
D. Distribusi Binomial Negatif
Distribusi Binomial Negatif merupakan distribusi yang memiliki beberapa cara dalam hal pendekatannya. Pendekatan klasik yang sering digunakan adalah Distribusi Binomial Negatif sebagai barisan percobaan Bernoulli yaitu jumlah percobaan Bernoulli yang dibutuhkan sampai terjadi � buah sukses, dengan setiap ulangan saling bebas, dan probabilitas sukses pada setiap percobaan konstan yaitu
sedangkan probabilitas gagal yaitu − .
Misalkan adalah banyaknya kegagalan sebelum sukses ke-�, maka � − sukses dapat terjadi pada sebarang waktu sebelum − ulangan. Misalkan variabel acak menyatakan banyaknya ulangan yang dibutuhkan sampai terjadi � buah sukses, maka berdistribusi Binomial Negatif dengan fungsi probabilitas sebagai berikut
= −− � − −� dengan = , + , + ,
kegagalan sebelum terjadi � buah sukses dengan metode transformasi variabel dengan fungsi transformasinya = − �.
Definisi 2.14
Variabel acak disebut berdistribusi Binomial Negatif jika memiliki fungsi probabilitas sebagai berikut
= + � −� − � − dengan = , , ,
Contoh 2.1
Seorang dokter anak merekrut 5 pasangan untuk berpartisipasi dalam penelitiannya. Masing-masing pasangan berharap untuk melahirkan anak secara normal. Misalkan
= � (pasangan yang dipilih secara acak setuju untuk berpartisipasi). Jika = . , berapakah probabilitas bahwa 15 pasangan harus ditanya sebelum ditemukan 5 pasangan yang setuju untuk berpartisipasi?
Penyelesaian:
Diketahui � = , = . , = sehingga
= + −− . − . = . . = .
Teorema 2.4
Mean dan variansi dari distribusi Binomial Negatif adalah
= =� −
Bukti: 1. Mean
Misalkan = − −�, dalam kalkulus dapat mengikuti ekspansi deret Maclaurin yaitu:
− −� = + ′ +
! + ! + + ! +
Dengan − < < sehingga diperoleh
− −� = + � + � + �
Sehingga Berdasarkan definisi 2.10 diperoleh
= −� − [ −− � �−− ∙ − − .�]� � |
�=
=� − [ + − ]
Sehingga,
� � = − ( )
= � − [ + − ]− −
= � − [ + − − � − ]
= � − ∎
Distribusi Gamma dengan parameter dan dipilih sebagai distribusi dari
Ω karena distribusi Gamma merupakan prior natural conjugate dari distribusi
Poisson. Karena Ω berdistribusi Gamma dengan parameter dan , maka mean
Fungsi probabilitas bersama antara | dan Ω adalah
| ℎ = −
Fungsi probabilitas marginal dari adalah
=
persamaan menjadi
fungsi probabilitas dari Distribusi Binomial Negatif sebagai campuran Poisson-Gamma adalah
; , =Γ +
! Γ ( + ) ( + ) (2.2)
Distribusi Binomial Negatif dengan fungsi probabilitas pada persamaan 2.2 disebut sebagai distribusi campuran Poisson-Gamma. Penurunan distribusi
Binomial Negatif di atas tidak berhubungan dengan penurunan klasik sebagai barisan dari percobaan Bernouli pada subbab sebelumnya.
F. Metode Maksimum Likelihood
Salah satu metode dalam pendugaan parameter adalah metode Pendugaan Kemungkinan Maksimum (Maksimum Likelihood Estimation/MLE). Metode ini pertama kali diperkenalkan oleh R.A Fisher pada tahun 1912. Metode pendugaan ini dapat diterapkan di sebagian besar masalah dan memiliki daya tarik intuitif yang kuat, dan sering menghasilkan penduga yang baik bagi parameter �. Selain itu untuk sampel yang sangat besar, metode ini menghasilkan penduga yang sangat baik bagi �.
Definisi 2.16
Misalkan , , … , adalah variabel random kontinu berukuran dengan fungsi probabilitas , � dan � adalah parameter yang tidak diketahui. Fungsi likelihood dari sampel random adalah fungsi densitas bersama dari variabel random yang merupakan fungsi dari parameter yang tidak diketahui, sehingga fungsi likelihood adalah
� � = ∏ ; � .
Selain itu, karena biasanya sulit untuk mencari turunan fungsi likelihood, maka yang dilakukan adalah menentukan nilai maksimum dari logaritma natural fungsi likelihood tersebut atau disebut dengan fungsi likelihood. Fungsi log-likelihood dapat ditulis dalam bentuk :
= ln � � .
Nilai parameter � dapat diperoleh dengan memaksimumkan fungsi peluang. Hal tersebut dilakukan dengan mencari turunan parsial pertama dari fungsi likelihood-nya terhadap setiap parameterlikelihood-nya. Sehingga, MLE �̂ merupakan penyelesaian dari persamaan berikut :
�
�� =
Misalkan terdapat parameter yang tidak diketahui, maka pendugaan parameter � dengan Metode Kemungkinan Maksimum
� �� =
Contoh 2.2
Misalkan , , … , adalah sampel random berdistribusi eksponensial dengan mean dan variansi . Temukan ̂ dengan menggunakan Metode maksimum likelihood.
Penyelesaian:
, , … , adalah variabel random berdistribusi eksponensial dengan mean dan
variansi maka fungsi probabilitasnya didefinisikan sebagai
= {
−
< ∞
selainnya
Berdasarkan persamaan 2.3 diperoleh fungsi likelihood berikut:
� = , , … , |
= | × | × … × |
= − × − × − × × − �
= ( ) [−∑ ] .
Fungsi log-likelihood dari persamaan diatas adalah
[� ] = [( ) [−∑ ]]
= ( ) −∑
= − −∑
= − −∑
Penduga kemungkinan maksimum dari adalah nilai yang memaksimumkan
ln[� ], dengan mencari nilai turunan parsial terhadap , maka diperoleh
� ln[� ]
−
+∑ =
− + ∑
=
− + ∑ =
̂ =∑
Jadi penduga kemungkinan maksimum untuk adalah
̂ =∑
G. Metode Numerik Newton-Raphson
Pendugaan parameter model regresi Binomial Negatif dilakukan dengan metode pendugaan kemungkinan maksimum. Proses untuk menemukan solusi dari turunan fungsi log-likelihood tidak dapat dilakukan secara langsung karena fungsi log-likelihood tidak linear dalam parameter yang ingin ditaksir sehingga membutuhkan metode numerik Newton-Raphson untuk menyelesaikannya. Metode Newton-Raphson adalah metode yang digunakan untuk mencari akar-akar persamaan dari suatu fungsi non-linear f(x)=0 dengan metode pendekatan yang menggunakan satu titik awal dan mendekatinya dengan memperhatikan slope atau gradien pada titik tersebut. Metode Newton-Rhapson yang diperoleh dari deret Taylor.
Misalkan mempunyai akar pada suatu interval real dan akan dicari nilai pendekatan akarnya. Deret Taylor di sekitar = adalah
= + ′ − + "
Untuk yang cukup dekat dengan maka suku-suku nonlinear dapat diabaikan, maka akan diperoleh pendekatan
= + ′ −
Jika adalah akar dari maka =
= + ′ −
− = ′ −
− = − ′
= − ′
Oleh karena itu diperoleh skema iterasi ke + metode Newton-Raphson adalah
+ = − ′
Contoh 2.2
Selesaikan persamaan − − = dengan menggunakan metode Newton-Raphson yang diketahui = dan toleransi adalah −
Penyelesaian: Diketahui:
= − −
=
Toleransi = −
Oleh karena itu, diperoleh ′ = −
Skema iterasi ke + metode Newton Raphson adalah
Sehingga, Untuk = , diperoleh
+ = − ′
= − − −
−
= − − −− = = .
( ) = .
Untuk = , diperoleh
+ = − ′
= − − −−
= − − −
−
=
= .
( ) = .
Untuk = diperoleh
+ = − ′
= − − − −
= .
. = . × −
Untuk = diperoleh
+ = − ′
= − − −
−
= .
− . . − . − −
= .
. = − . × −
Untuk = diperoleh
+ = − ′
= − − −
−
= .
− . − . −
. −
= .
. = − . × −9
H. Keluarga Eksponensial
Suatu fungsi probabilitas yang tergantung pada suatu parameter � dari suatu variable random dikatakan termasuk dalam keluarga eksponensial apabila dapat dituliskan sebagai
; �, � = exp { � − �� + ; � } 2.6
Dengan:
� adalah parameter kanonik atau fungsi penghubung
� adalah cumulant
� adalah parameter skala, � = jika merupakan model count dan diskrit
; � adalah suku normalisasi untuk menjamin bahwa total nilai fungsi
probabilitas adalah
Bentuk keluarga eksponensial adalah unik karena turunan pertama dan turunan kedua dari cumulant terhadap � akan menghasilkan mean dan variansi. Hal penting yang harus diingat adalah jika seseorang dapat mengkonversi sebuah fungsi probabilitas ke dalam bentuk keluarga eksponensial maka dapat dengan mudah menghitung mean dan variansi. Semua anggota model linear umum dapat dikonversi ke dalam bentuk eksponensial dengan
′ � = mean
" � = variansi
Macam-macam keluarga eksponensial antara lain adalah: 1. Distribusi Binomial Negatif
4. Distribusi Beta, dan 5. Distribusi Normal.
Pada skripsi ini, penulis hanya akan mendeskripsikan bahwa distribusi Poisson dan distribusi Binomial adalah anggota keluarga eksponensial. Berikut akan ditunjukan bahwa
1. Distribusi Poisson merupakan keluarga eksponensial
Variabel random disebut berdistribusi Poisson jika dan hanya jika fungsi probabilitasnya sebagai berikut
= �! − , = , , , … dan >
untuk menunjukkan bahwa distribusi Poisson merupakan keluarga eksponensial maka persamaan di atas ditulis ke dalam bentuk persamaan 2.6 yaitu
; �, � = exp { � − �� + ; � }
Langkah-langkahnya adalah sebagai berikut:
a. Kedua ruas dari fungsi probabilitas distribusi Poisson di ubah dalam bentuk log diperoleh
= log ( ! − )
log( ) = log − − log ! 2.7
b. Persamaan 2.7 diubah dalam bentuk eksponensial diperoleh
= { log − − log ! } 2.8
Sehingga dari persamaan 2.8 diperoleh
Sehingga turunan pertama dan turunan kedua dari � = � terhadap � akan menghasilkan mean dan variansi sebagai berikut:
= �( � )��
= �(���)
= �
=
� � = � � ( � )��
= � (���)
= �
=
2. Distribusi Binomial merupakan keluarga eksponensial
Variabel random yang menyatakan banyaknya sukses pada kali percobaan Bernoulli berdistribusi Binomial yang diberikan dengan yaitu
= − −
untuk menunjukkan bahwa distribusi Binomial merupakan keluarga eksponensial maka persamaan di atas ditulis ke dalam bentuk persamaan 2.6 yaitu
; �, � = exp { � − �� + ; � }
a. Kedua ruas dari fungsi probabilitas distribusi Binomial diubah dalam bentuk log diperoleh
log( ) = + log + − log − 2.9
b. Persamaan 2.9 diubah dalam bentuk eksponensial diperoleh
= { [log − log − ] + log − + }
� terhadap � akan menghasilkan mean dan variansi sebagai berikut:
= −
I. Model Regresi Linear Berganda
Model regresi linear berganda merupakan perluasan dari model regresi linear sederhana. Regresi berganda seringkali digunakan untuk mengatasi permasalahan analisis regresi yang melibatkan hubungan dari dua atau lebih variable independen. Salah satu contoh penggunaan regresi berganda di bidang pertanian di antaranya ilmuwan pertanian menggunakan analisis regresi untuk mengetahui antara hasil pertanian (misal: produksi padi per hektar) dengan jenis pupuk yang digunakan, kualitas pupuk yang diberikan, jumlah hari hujan, suhu, lama penyinaran matahari, dan infeksi serangga. Sebuah model regresi berganda dapat menerangkan hubungan tersebut yaitu
= + + + + + + + �
Dengan menyatakan hasil pertanian, menyatakan jenis pupuk yang digunakan, menyatakan kuantitas pupuk yang diberikan , menyatakan jumlah hari hujan, menyatakan suhu, menyatakan lama penyinaran matahari, dan menyatakan infeksi serangga. Persamaan di atas adalah sebuah model regresi linear berganda dengan enam variable independen.
Pada umumnya, variable dependen dapat dihubungkan pada variabel-variabel independen yang dapat ditulis dalam bentuk:
= + + + + + � � + � 2.11
Persamaan 2.11 merupakan sebuah model regresi linear berganda dengan:
= intersep
� = koefisien regresi dari variabel bebas ke −
� = galat �� �
= , , , ,
� = nilai variabel bebas ke − p pada pengamatan ke − i
Persamaan 2.11 dapat dinayatakan dalam bentuk matriks menjadi:
[ ] =
Matriks tersebut dapat dinyatakan sebagai berikut
= � + �
Dengan:
= vektor kolom dari variabel tak bebas berordo ×
= matriks dari variabel bebas berordo × +
� = vektor kolom dari parameter berordo + ×
� = vektor kolom dari galat berordo ×
J. Jenis Data Penelitian 1. Data berdasarkan sumbernya
Berdasrkan sumbernya, data penelitian dapat dikelompokkan dalam dua jenis, yaitu data primer dan data sekunder.
harus mengumpulkannya secara langsung. Teknik yang dapat digunakan peneliti untuk mengumpulkan data primer antara lain observasi, wawancara, dan penyebaran kuesioner.
b. Data sekunder adalah data yang diperoleh atau dikumpulkan oleh peneliti dari berbagai sumber yang telah ada. Data sekunder dapat diperoleh dari berbagai sumber seperti Biro Pusat statistik (BPS), buku, jurnal, dan lain-lain.
2. Data berdasarkan bentuk dan sifatnya
Berdasarkan bentuk dan sifanya, data penelitian dapat dibedakan dalam dua jenis yaitu data kualitatif dan data kuantitatif. Data kuantitaif dapat dikelompokkan berdasarkan cara untuk mendapatkannya, yaitu data diskrit dan data kontinu. Berdasarkan sifatnya, data kuantitatif terdiri atas data nominal, data ordinal, data interval dan data rasio.
1. Data kualitatif
Data kualitatif adalah data yang berbentuk kata-kata, bukan dalam bentuk angka. Data kualitatif diperoleh melalui berbagai macam teknik pengumpulan data misalnya wawancara, analisis dokumen, dan lainnya. 2. Data kuantitatif
a. Data diskrit adalah data dalam bentuk angka (bilangan) yang diperoleh dengan cara membilang. Contohnya jumlah Sekolah Dasar Negeri di Kecamatan X adalan .
b. Data kontinu adalah data dalam bentuk angka/ bilangan yang diperoleh berdasarkan hasil pengukuran. Data kontinu dapat berbentuk bilangan bulat atau pecahan tergantung jenis skal pengukuran yang digunakan. Contohnya tinggi badan Budi adalah . centimeter.
Berdasarkan tipe skala pengukuran yang digunakan, data kuantitatif dapat dikelompokkan dalam empat jenis yang memiliki sifat berbeda yaitu:
terdiri dari empat kategori yatu belum menikah menikah janda/duda bercerai. Data tersebut memiliki sifat-sifat yang sama dengan data tentang jenis kelamin.
2) Data ordinal adalah data yang berasal dari suatu objek atau kategori yang telah disusun secara berjenjang menurut besarnya. Setiap data ordinal memiliki tingkatan tertentu yang dapat diurutkan mulai dari yang terendah sampai tertinggi ataupun sebaliknya. Namun demikian, jarak atau rentang antar jenjang tidak harus sama. Dibandingkan dengan data nominal, data ordinal memiliki sifat berbeda dalam hal urutan. Data ordinal berlaku perbandingan dengan menggunakan simbol " > " dan " < ". Contohnya peringkat siswa dalam satu kelas yang menunjukkan urutan prestasi belajar tertinggi sampai terendah. Siswa pada peringkat memiliki prestasi belajar lebih tingi dari pada siswa peringkat .
3) Data interval adalah data hasil pengukuran yang dapat diurutkan atas dasar kriteria tertentu serta menunjukan semua sifat yang dimiliki oleh data ordinal. Kelebihan sifat data interval dibandingkan dengan data ordinal adalah memiliki sifat kesamaan jarak. Data interval dapat dilakukan operasi matematik penjumlahan dan pengurangan
+, − . Namun demikian masih terdapat satu sifat yang belum
dimiliki yaitu tidak adanya angka nol mutlak pada data interval. 4) Data rasio adalah data yang berbentuk angka dalam arti
dapat diterapkan semua bentuk operasi matematik +, −, ×, ∶ . Contohnya panjang suatu benda yang dinyatakan dalam ukuran meter adalah data rasio. Benda yang panjangnya meter berbeda secara nyata dengan benda yang panjangnya meter sehingga dapat dibuat kategori benda yang berukuran meter dan meter (sifat data nominal). Ukuran panjang benda dapat diurutkan mulai dari yang terpanjang sampai yang terpendek (sifat data ordinal). Perbedaan antar benda yang panjangnya meter dengan meter memiliki jarak yang sama dengan perbedaan antar benda yang panjangnya meter dengan (sifat data interval). Kelebihan sifat yang dimiliki data rasio ditunjukkan oleh dua hal yaitu: Angka meter menunjukkan nilai mutlak yang artinya tidak ada benda yang diukur; serta benda yang panjangnya meter, kali lebih panjang dibandingkan dengan benda yang panjangnya meter yang menunjukkan berlakunya semua operasi matematik. Kedua hal tersebut tidak berlaku untuk jenis data nominal, data ordianal, maupun data interval.
K. Model Count Respon
Model count respon adalah bagian dari model regresi dengan variabel respon diskrit. Variabel respon diskrit dapat berupa data count yaitu data dengan nilai bilangan bulat non-negatif. Contoh model diskrit adalah sebagai berikut:
Model regresi Poisson dan Regresi Binomial Negatif
1. Model regresi logistik biner dan regresi probit a. Regresi Logistik Biner
Regresi logistik merupakan teknik statistik yang tepat digunakan ketika variabel dependen berbentuk diskrit/kategorial (non-metrik) dan variabel independen dapat berbentuk metrik atau non-metrik. Dengan kata lain, regresi logistik merupakan model yang dapat digunakan untuk menggambarkan hubungan antara beberapa variabel independen dengan sebuah variabel dependen yang bersifat dikotomi. Untuk membedakan antara model regresi logistik dengan model regresi linear dapat dilihat pada variabel dependennya. Pada regresi logistik, variabel dependen berbentuk biner atau dikotomi sedangkan pada regresi linear variabel dependen diasumsikan kontinu. Contoh apakah seseorang akan membeli barang ilegal (ya atau tidak), dengan variabel prediktornya adalah tingkat pendidikan, tingkat pendapatan, dan status perkawinan? Jadi regresi logistik biner digunakan ketika variabel dependen adalah dikotomi sedangkan variabel independen dapat berbagai tipe.
Definisi 2.17
Model regresi logistik dengan variabel bebas adalah sebagai berikut:
� � = +� �� �
b. Regresi Probit
Regresi probit sebenarnya serupa dengan regresi logistik yaitu dapat digunakan untuk menganalisis variabel dependen yang bersifat kategori, namun pada regresi probit variabel dependen diasumsikan berdistribusi normal. Jadi, regresi logitik berdasarkan pada asumsi variabel dependen bersifat kategori (variabel kualitatif ) serta menggunakan distribusi Binomial dan regresi probit mengasumsikan variabel dependen yang bersifat kategori (variabel kuantitatif) dan menggunakan distribusi kumulatif normal.
Definisi 2.18
Model regresi probit dapat dituliskan sebagai berikut:
= + + �
Dengan adalah variabel dependen berdistribusi normal, merupakan intersep yang tidak diketahui, = , , , � adalah parameter koefisien, = , , , � adalah variabel independen dan � adalah galat yang diasumsikan berdistribusi normal dengan mean nol dan variansi
� .
2. Model regresi Poisson dan Regresi Binomial Negatif
Pada umumnya, distribusi Poisson merupakan suatu model yang realistis untuk berbagai macam fenomena acak selama nilai dari peubah acak Poisson berupa bilangan bulat non-negatif. Misalkan banyaknya kecelakaan mobil setiap bulan, banyaknya hujan badai setiap tahun, dan kasus lainnya. Pada model Regresi Poisson terdapat asumsi yang harus dipenuhi yaitu variansi dari variabel responnya sama dengan mean atau disebut ekuidispersi. Pada kenyataannya asumsi ini sangat jarang terjadi karena data count memiliki variansi yang lebih besar dari meannya atau disebut overdispersi. Dalam kondisi seperti ini model regresi Binomial Negatif merupakan salah satu alternatif yang tepat untuk mengatasinya.
Model regresi Binomial Negatif memiliki kegunaan yang sama dengan model regresi Poisson yaitu untuk menganalisis hubungan antara suatu variabel respon data count dengan satu atau lebih variabel independen, tetapi model regresi Binomial Negatif lebih fleksibel dibandingkan dengan model Regresi Poisson karena asumsi mean dan variansi dari model Regresi Binomial Negatif tidak harus sama.
Menurut Hilbe (2011) ada dua pendekatan dasar untuk mengestimasi model data count yaitu
1. Pendugaan Kemungkinan Maksimum 2. Iteratively re-weighted least squares (IRLS)
L. Uji Kolmogorov-Smirnov
Hal yang sangat penting dalam prosedur statistik adalah menentukan distribusi yang mendasari suatu kumpulan data (atau variabel random). Oleh karena itu, dalam skripsi ini untuk mengetahui apakah sampel berdistribusi Poisson akan digunakan uji Kolmogorov-Smirnov. Uji Kolmogorov-Smirnov adalah suatu uji goodness of fit test (kecocokan), artinya yang diperhatikan adalah tingkat kesesuaian antara sebaran dari serangkaian nilai sampel yang diobservasi dengan suatu distribusi teoritis tertentu.
Dalam uji Kolmogorov-Smirnov, pengujian dilakukan pada dua buah fungsi sebaran kumulatif, yaitu sebaran kumulatif yang hipotesiskan dan sebaan kumulatif yang diamati. Misalkan diambil sebuah sampel acak dari suau fungsi sebaran yang belum diketahui, akan dipastikan apakah dapat disimpulkan bahwa =
untuk semua , dengan adalah fungsi distribusi kumulatif yang dihipotesiskan.
Misalkan variabel random , , … , berasal dari distribusi yang tidak diketahui , akan diuji hipotesis bahwa adalah sama dengan suatu distribusi tertentu .
Definisi 2.19
Misalkan , , … , adalah variabel random. Fungsi distribusi empiris ̂ di definisikan sebagai
̂ = ∑ { �≤ }
=
= { , , >
Definisi 2.20
Statistik uji Kolmogorov-Smirnov di definisikan sebagai
= max +, −
+ = max[ ̂ − ]
− = max[ − ̂ − ]
Dengan ̂ adalah fungsi distribusi empiris. Fungsi distribusi empiris berguna sebagai penduga dari fungsi distribusi yang tidak diketahui .
Hipotesis uji Kolmogorov-Smirnov adalah
: =
untuk setiap dengan adalah fungsi distribusi kumulatif yang diketahui, dan
: ≠
Jika lebih dari � yang diberikan oleh tabel Kolmogorov-Smirnov maka ditolak pada tingkat signifikansi .
Langkah-langkah uji Kolmogorov-Smirnov untuk distribusi Poisson adalah sebagai berikut:
1. = data berdistribusi Poisson
=data tidak berdistribusi Poisson
2. Tentukan tingkat signifikansi 3. Statistik uji
= max +, −
5. Berdasarkan Definisi 2.19 hitunglah fungsi distribusi empiris ̂
6. Berdasarkan Definisi 2.20 hitunglah nilai + dan − , dan tentukan maksimum dari ( = maksimum + , − )
7. Daerah keputusan :
ditolak jika
8. Kesimpulan
Untuk memudahkan perhitungan, uji Kolmogorov-Smirnov dapat dilakukan dengan SPSS. Contohnya dapat dilihat dalam contoh 2.4 berikut ini:
Contoh 2.4
Berikut adalah data suatu sampe acak. Akan diuji apakah datanya berdistribusi Poisson?
Table 2.1 Data suatu sampel acak
Data 0 1 2 3 4 5 6
7 8 1 1 1 0 1
Uji hipotesis:
1. = data berdistribusi Poisson
=data tidak berdistribusi Poisson
2. Tingkat signifikansi = . 3. Daerah penolakan
Table 2.2 Hasil Pengujian Kolmogorov-Smirnov
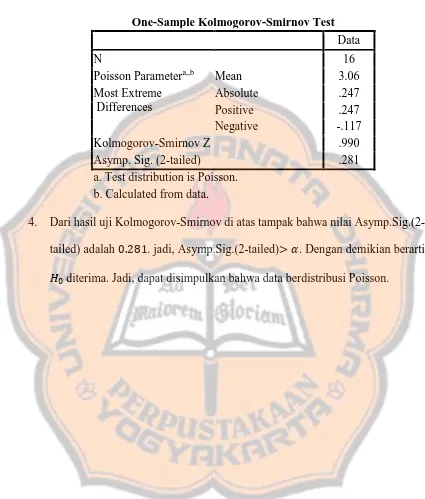
4. Dari hasil uji Kolmogorov-Smirnov di atas tampak bahwa nilai Asymp.Sig.(2-tailed) adalah . . jadi, Asymp.Sig.(2-tailed)> . Dengan demikian berarti
diterima. Jadi, dapat disimpulkan bahwa data berdistribusi Poisson. One-Sample Kolmogorov-Smirnov Test
Data
N 16
Poisson Parametera,,b Mean 3.06 Most Extreme
Differences
Absolute .247 Positive .247 Negative -.117 Kolmogorov-Smirnov Z .990 Asymp. Sig. (2-tailed) .281 a. Test distribution is Poisson.
50 BAB III
PENDUGAAN MODEL REGRESI BINOMIAL NEGATIF
A. Model Regresi Poisson Berganda
Model regresi Poisson Berganda merupakan perluasan dari model regresi Poisson sederhana, dengan model regresi Poisson Berganda akan diketahui hubungan antara sebuah variabel dependen yang bersifat diskrit, bernilai bulat tak negatif dan berdistribusi Poisson dengan buah variabel independen , , , , � yang berjenis diskrit, kontinu atau kategorik. Model regresi Poisson secara umum digunakan untuk menganalisis data diskrit yang variabel dependennya berdistribusi Poisson, yang memiliki rata-rata dan variansi sama dengan > .
Bila diberikan variabel dependen berdistribusi Poisson dengan variabel independen , , , , �, persamaan regresi dengan , , , , � dinyatakan seperti persamaan 2.11,maka nilai harapan dengan = , =
, = , , � = � sebagai berikut
| = , = , = , , � = �
= + + + + + � �
= ( | = , = , = , , � = �
+ ( | = , = , = , , � = � +
+ ( � � | = , = , = , , � = �
+ � | = , = , = , , � = �
dengan asumsi bahwa � | = , maka
= + ( | = , = , = , , � = � +
+ � ( � | = , = , = , , � = � +
= + + + + � � .
Dikarenakan | � berdistribusi Poisson, maka nilai rata-ratanya ( | � = +
+ + + � � = harus bernilai tak negatif (dalam interval , ∞ ),
padahal telah diketahui bahwa nilai regresi + + + + � � ada dalam interval −∞, ∞ . Oleh karena itu, diperlukan fungsi penghubung (link function) yang dapat membuat memiliki nilai dalam interval , ∞ , yaitu dengan fungsi penghubung logaritma (logarithm link), sehingga
= + + + + � � 3.2
merupakan fungsi logaritma, sehingga model regresi Poisson menjadi
ln = + + + + � � 3.3
Atau persamaan 3.3 dapat juga dinyatakan dengan
= exp ��′� 3.4
Parameter � dalam model regresi Poisson dapat diduga dengan salah satu metode penduga yaitu metode penduga kemungkinan maksimum (Maximum Likelihood Estimation).
Fungsi peluang dari distribusi Poisson adalah
| = �!� − , = , , , … dan = exp �
�
′� sehingga
| = exp ��′� �exp − exp �! �′�
=exp −exp ��′� exp �! �′�
Berdasarkan persamaan 2.3 diperoleh fungsi likelihood berikut:
� = ( , , … , �| , , � ; �
= ∑ − exp �′�� dilakukan dari turunan pertama dari fungsi log-likelihood dan turunannya sama dengan nol.
Penduga parameter �̂ dari persamaan diatas dapat diperoleh dengan
� �
Karena persamaan di atas tidak linear, maka persamaan tersebut dapat diselesaikan dengan pendekatan metode numeris misalnya metode Newton-Raphson.
Secara umum, �̂ dari model regresi Poisson dapat diperoleh dengan metode Newton-Raphson sebagai berikut:
�̂�+ = �̂�− [ (�̂� ]− � �̂� 3.6
Dalam skripsi ini, �̂ dapat diduga dengan menggunakan program SPSS atau program R.
B. Overdispersi dan regresi Binomial Negatif
Variabel respon yang berupa data count biasanya dianalisis dengan menggunakan regresi Poisson yang memiliki asumsi mean dan variansi sama. Pada kenyataannya, kondisi seperti ini sangat jarang terjadi karena biasanya data count memiliki variansi yang lebih besar dari mean atau disebut dengan kondisi overdispersi. Overdispersi dalam regresi Poisson dapat mengakibatkan galat standar dari dugaan parameter regresi yang dihasilkan memiliki kecenderungan untuk menjadi lebih rendah dari seharusnya sehingga menghasilkan kesimpulan yang tidak sesuai dengan data.
Overdispersi pada data count dapat diindikasikan dengan nilai devians dan pearson chi-squares yang dibagi dengan derajat bebasnya. Jika kedua nilai tersebut lebih dari , maka dikatakan terjadi overdispersi pada data.
Terdapat dua cara yang dapat digunakan untuk mendeteksi overdispersi, yaitu:
1. Devians Definisi 3.1
Nilai devians dapat ditulis dalam bentuk
= ∑ { ( ̂ ) − − ̂ }
�
� = ;
Dengan = − dengan merupakan banyaknya parameter termasuk konstanta, merupakan banyaknya pengamatan dan adalah nilai Devians. 2. Pearson Chi-squares
Definisi 3.2
Nilai Pearson Chi-squares dapat ditulis dalam bentuk
� = ∑ −
�
=
� = � ;
Dengan = − dengan merupakan banyaknya parameter termasuk konstanta, merupakan banyaknya pengamatan dan � adalah Pearson Chi-squares.
Jadi, jika � atau � bernilai lebih dari maka terjadi overdispersi pada data. Oleh karena itu, Model Binomial negatif merupakan alternatif yang sering digunakan untuk kasus overdispersi pada regresi Poisson.
digunakan adalah Model Binomial Negatif yang merupakan model campuran antara distribusi Poisson dan Gamma. Distribusi Gamma digunakan untuk menyesuaikan kehadiran overdispersi dalam model Poisson.
Definisi 3.3
Fungsi probabilitas dari suatu variabel acak Y yang berdistribusi Binomial Negatif adalah sebagai berikut:
= Γ +
Γ ! ( + )
�
( + ) ⁄ , = , , , …
Jika sama dengan nol, nilai rata-rata dan variansi akan sama, = , akan menjadi distribusi Poisson. Jika > , variansi akan melebihi nilai rata-rata,
> , dan distribusi memungkinkan overdispersi.
C. Binomial Negatif sebagai keluarga Eksponensial
Salah satu keluarga dari beberapa distribusi probabilitas yang sering dijumpai adalah keluarga eksponensial. Keuntungan dari suatu distribusi probabilitas yang termasuk anggota keluarga eksponensial adalah kemudahan dalam mengidentifikasi beberapa ukuran distribusi, salah satunya adalah mean sebagai parameter lokasi dan variansi sebagai nuisance parameter. Berikut adalah definisi dari suatu distribusi yang merupakan anggota keluarga eksponensial.
distribusi dari merupakan anggota dari keluarga eksponensial jika fungsi probabilitasnya memiliki bentuk seperti persamaan 2.6.
Berikut akan ditunjukkan bahwa distribusi Binomial Negatif merupakan salah satu anggota dari keluarga eksponensial. Misalkan adalah suatu varibel acak yang berdistribusi Binomial Negatif dengan parameter dan dengan fungsi
Dengan menganggap sebagai parameter lokasi dan k sebagai nuisance parameter, maka akan diperoleh:
Persamaan 3.7 dapat ditulis kedalam bentuk persamaan 2.6
� = ( + )
� =
; � = � +
� !
� = − ( + )
Sehingga terbukti bahwa distribusi binomial negatif merupakan anggota dari keluarga eksponensial.
Telah disebutkan sebelumnya bahwa salah satu keuntungan dari anggota keluarga eksponensial adalah mean dan variansi dari distribusi tersebut dapat diidentifikasi dengan mudah, sehingga berdasarkan Hilbe (2011) yaitu
a. ′ � akan menghasilkan mean
b. " � � akan menghasilkan variansi
Jadi, akan dicari mean dan variansi dari variabel random yang berdistribusi binomial negatif dengan menggunakan salah satu sifat dari keluarga eksponensial tersebut. Sebelum memperoleh mean dan variansi dari distribusi Binomial Negatif, dapat didefenisikan bahwa:
= �
= ( + )
= − ( + )
− ( + ) = � ⟺ ( + ) = −� ⟺ = −�− ⟺ =
−� −
dan diperoleh
− � =
= −� −
= [ ( −� − ]−
Fungsi cumulant yaitu
� = − ( + )
= ln +
sehingga akan diperoleh mean dan variansi dari binomial negatif sebagai berikut: 1. Mean
′ � =�
� � ��
= + − ( −� − − (− −�
= + ( −�− − ( −�
Karena = [ −�− ]− maka −� = − + sehingga diperoleh
′
� = + − +
2. Variansi
Karena � = , maka variansi dari hanya turunan kedua dari cumulant terhadap � yaitu sebagai berikut:
" � = �
= +− ( + + + + +
= − + +
= +
Jadi, mean dan variansi dari Binomial Negatif secara berturut-turut adalah dan
+ .
D. Model Regresi Binomial Negatif
Dalam berbagai eksperimen, seringkali data count yang merupakan objek penelitian (variabel dependen ) dipengaruhi oleh sejumlah variabel independen. Variabel dependen menyatakan banyaknya kejadian yang diamati pada suatu populasi tertentu. Untuk mengetahui hubungan antara kedua variabel tersebut, maka dapat digunakan suatu model regresi yang didasarkan pada distribusi Binomial Negatif.
Salah satu tujuan dari analisis regresi adalah untuk menentukan pola hubungan antara variabel dependen dengan variable independen , , , , �.Oleh karena itu, dalam regresi Binomial Negatif hubungan tersebut dapat dituliskan dalam bentuk
| = = + + + + � � 3.8
atau dapat dinyatakan dalam notasi matriks
| = = �′� 3.9
dari distribusi Binomial Negatif harus bernilai positif sehingga perlu dilakukan trasformasi sedemikian sehingga bentuk hubungan antara dan �′� menjadi tepat. Hilbe (2011) menyatakan bahwa model Binomial Negatif pada umumnya menggunakan fungsi penghubung logaritma atau log link yaitu
η = ln = �′�
Fungsi η = ln disebut sebagai fungsi link, yaitu fungsi yang menghubungkan dengan prediktor linear �′�. Oleh sebab itu, model regresi Binomial Negatif untuk memodelkan data count yaitu
= exp �′� 3.10
dengan = , , , ,
E. Pendugaan Parameter untuk Model Regresi Binomial Negatif dengan Metode Maksimum Likelihood
Model umum regresi Binomial Negatif dinyatakan dengan:
= exp( + + + + � � + �
Dengan , , , menyatakan parameter yang tidak diketahui dan � menyatakan galat untuk pengamatan ke-i.
Model umum regresi Binomial Negatif dapat diduga dengan
̂ = exp( ̂ + ̂ + ̂ + + ̂� �
� , = ∏ ,
Selanjutnya, dari fungsi likelihood diambil nilai log-nya sehingga diperoleh fungsi log- likelihood dari persamaan diatas sebagai berikut:
Diketahui bahwa Γ �+
Oleh karena itu, log� , bisa ditulis tanpa fungsi Gamma dengan
log Γ +
Likelihood untuk model regresi Binomial Negatif dapat ditulis sebagai,
log� , = ∑ [ ∑ log ( + )
= ∑ [ ∑ +
=
Turunan kedua dari fungsi log-likelihood disebut matriks Hessian.
Karena persamaan-persamaan dalam matriks �∗ tidak linear dalam masing-masing parameternya, maka untuk mencari nilai dari , , , � dan digunakan metode numerik Newton-Raphson sebagai berikut:
F. Uji Kebaikan Model
Uji kebaikan model yang berkaitan dengan model linear umum (GLM) antara lain adalah sebagai berikut:
1. � dan � − � , 2. Statistik deviansi 3. Uji likelihood ratio 4. Uji Wald dan
5. Kriteria informasi Akaike (AIC) dan kriteria informasi Bayessian (BIC). Di dalam skripsi ini, uji kebaikan model regresi yang digunakan adalah
� dan � − � , uji likelihood-ratio, dan uji Wald.
a. � dan � − �
Statistik � biasanya dikenal sebagai koefisien determinasi di dalam model Regresi linear biasa. Statistik � ini biasanya diinterpretasikan sebagai besarnya persentase dari variasi di dalam data yang dijelaskan oleh model. Nilai dari statistik ini berkisar dari 0-1 dengan nilai yang semakin mendekati 1 merepresentasikan model yang terbentuk semakin baik. Namun, statistik ini kurang tepat digunakan untuk model non-linear seperti Regresi Poisson, Regresi Binomial Negatif dan Regresi Logistik.
Statistik � yang biasanya digunakan untuk model Regresi data count adalah statistik � − � . Berdasarkan Hilbe (2011), statistik � − � memiliki formula sebagai berikut:
Dengan: �� = nilai fungsi log-likelihood dari model yang lengkap
� = nilai fungsi log-likelihood dari model yang hanya mengandung intercept
Interpretasi koefisien determinasi � pada Regresi linear tidak dapat diterapkan kepada � − � . Interpretasi yang dapat dibuat adalah nilai yang sangat kecil yang mengindikasikan lack of fit atau model yang diperoleh kurang baik sedangkan nilai yang cukup besar mengindikasikan model yang baik.
b. Uji likelihood -ratio
Uji likelihood-ratio adalah uji yang biasa digunakan untuk uji perbandingan model. Uji ini biasanya digunakan untuk model yang bersarang (nested models), tetapi uji ini juga dapat digunakan untuk uji dua model yang berbeda (misalnya apakah sebuah data lebih baik dimodelkan dengan menggunakan model Binomial Negatif atau Poisson). Formula untuk uji likelihood-ratio adalah sebagai berikut:
�� = − {� � − � � }
Uji likelihood-ratio merupakan uji yang berguna ketika harus diputuskan apakah penambaan satu atau sejumlah variabel penjelas ke dalam model harus dilakukan atau tidak. Selain itu, uji ini digunakan untuk menguji signifikansi dari taksiran model yang telah diperoleh. Berikut ini adalah uji signifikansi model regresi Binomial Negatif, hipotesisnya adalah:
: = = = � =
Statistik uji yang digunakan adalah
�� = − { �̂ − �̂ }
Aturan keputusannya ditolak pada tingkat signifikansi jika �� > ,�
c. Uji Wald
Uji ini digunakan untuk menguji signifikansi dari masing-masing variabel penjelas terhadap model. Hipotesis untuk menguji signifikansi dari sembarang koefisien regresi, misalkan adalah
: =
: ≠
Statistik uji yang digunakan yaitu
= [ ̂̂ ]
Dengan ̂ adalah taksiran parameter dan ( ̂ adalah taksiran galat standar dari yang diperoleh dari matriks taksiran variansi-kovariansi dari �̂. Aturan keputusannya adalah ditolak pada tingkat signifikansi jika > , . Penolakan pada tingkat signifikansi berarti bahwa bariabel penjelas ke-j, untuk suatu tertentu = , , , … , memiliki kontribusi yang signifikan terhadap variabel respon .
matriks Hessian yang disebut matriks variansi-kovariansi dan dinotasikan dengan variansi dari ̂�− , yang dinyatakan dengan �̂(�̂�− dan diperoleh melalui tahapan sebagai berikut:
1. Turunan parsial kedua dari fungsi log-likelihood terhadap ̂ yaitu
� [∑ (+ exp �− exp(��′�
2. Ekspektasi dari minus matriks Hessian akan menghasilkan matriks Fisher Information, sehingga elemen diagonal dari matriks Fisher Information untuk
(
Dalam hal ini, matriks Fisher Information digunakan untuk mengukur seberapa besar informasi dari variabel independen � yang dapat dijelaskan oleh parameter �. Variansi dari � dapat diperoleh dari elemen diagonal matriks � maka variansi dari � adalah:
3. Taksiran galat standar untuk ̂� dalam model regresi Binomial Negatif adalah
( ̂� = √ ̂ ̂� = [∑ � exp(��
Berdasarkan formula taksiran galat standar untuk ̂� pada persamaan diatas, dapat dikatakan bahwa galat standar tersebut dipengaruhi oleh parameter . Hal tersebut memberikan pengertian bahwa pada saat terjadi overdispersi, model Binomial negatif akan menjadi lebih sensitif terhadap signifikansi dari variabel-variabel penjelasnya karena memperhatikan pengaruh dari overdispersi melalui parameter