REKAYASA DAN OPTIMASI PROSES Mata Kuliah

M

a

t

a

K

ul

ia

h

/

M

a

t

e

ri

K

ul

ia

h

Br

a

wi

ja

y

a

U

ni

v

er

si

ty

2

0

1

1

REKAYASA DAN OPTIMASI PROSES

Lagrange Multipliers

Ir. Usman Effendi, MS

Lab. Komputasi Dan Analisis Sistem, FTP, Universitas Brawijaya Email : usman_eff@ub.ac.id

1. PENDAHULUAN 1.1 Pengantar 1.2 Tujuan

2. PENGANTAR METODE KALKULUS

3. METODE LAGRANGE MULTIPLIER

4. METODE LAGRANGE

MULTIPLIER OPTIMASI tidak BERKENDALA

5. OPTIMASI BERKENDALA 6. MASALAH DALAM OPT TIDAK

BERKENDALA

a. Penggunaan Gradien Untuk Optimasi

b. Determination Of Minimum Or Maximum

c. Penentuan Minimum Atau Maksimum d. Konversi Dibatasi

Untuk Masalah Dibatasi

7. MASALAH OPTIMASI BERKENDALA

8. OPTIMASI DENGAN KENDALA KETIMPANGAN: KONDISI KUHN-TUCKER

1. PENDAHULUAN

MODU

L

S

E

L

F-P

R

O

P

A

G

A

TI

N

G

E

N

T

R

E

P

R

E

3

Minggu 3

1.1 PENGANTAR

Jika fungsi ini kontinu dan terdiferensialkan, turunannya menjadi nol pada titik ekstrem tersebut. Untuk fungsi y (x), kondisi ini ditulis sebagai

1.2 TUJUAN

1.2.1 Tujuan Instruksional Umum

Setelah mengikuti mata kuliah ini mahasiswa akan memiliki kemampuan melakukan analisis suatu proses dan melakukan optimasi dengan metode yang telah dipelajarinya

1.2.2 Tujuan Instruksional Khusus

Setelah mempelajari pokok bahasan mahasiswa dapat ;

 Menjelaskan ulang metode optimasi analitik, mampu menentukan kriteria

optimum untuk optimasi variabel tunggal dan ganda.,

 Mengetahui karakteristik Optimasi tidak Berkendala dan Berkendala

 Mampu merubah kondisi berkendala ke dalam tidak berkendala.

 Menguasi Optimasi fungsi non linear dengan kendala persamaan dan ketidak samaan

 Menerapkan metode lagrange multiplier dan Kondisi Kunh Tucker

2. PENGANTAR METODE KALKULUS

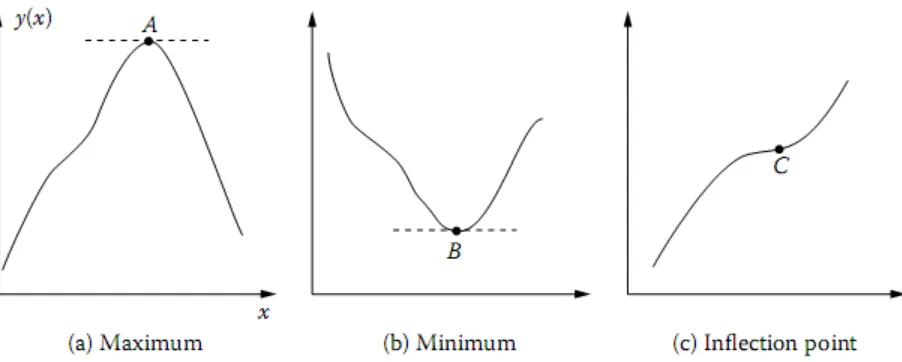
Kondisi yang disampaikan sebelumnya berlaku untuk y fungsi nonlinear (x) dan, karena itu, metode kalkulus berguna untuk sistem termal, yang umumnya diatur oleh nonlinier ekspresi. Namun, baik fungsi dan turunannya harus terus menerus untuk analisis sebelumnya untuk menerapkan.Dengan demikian, dengan menetapkan gradien sama dengan nol, lokasi dari ekstrem dapat diperoleh dan turunan kedua kemudian dapat digunakan untuk menentukan Sifat ekstrem masing-masing. Ada beberapa kasus di mana kedua pertama dan kedua derivatif adalah nol. Hal ini menunjukkan titik perubahan, sebagaimana sketsa di Gambar 1 (c), titik pelana, atau kurva datar, seperti di punggung bukit atau lembah. Ini harus dicatat bahwa kondisi hanya disebutkan menunjukkan hanya ekstrem lokal. Mungkin ada beberapa ekstrem lokal seperti dalam domain yang diberikan. Karena ketertarikan kami terletak pada keseluruhan maksimum atau minimum di seluruh domain untuk mengoptimalkan sistem, kami akan mencari ekstrem global, yang biasanya unik dan merupakan yang terbesar atau terkecil nilai fungsi tujuan. Contoh sederhana berikut menggambarkan penggunaan prosedur sebelumnya untuk optimasi.

Gambar 1. Seketsa memperlihatkan maksimum, minimum dan titik belok fungsi y(x)

Terapkan teknik kalkulus berbasis optimasi hanya diberikan kepada meminimalkan biaya C untuk panas bergulir jumlah yang diberikan dari logam. Biaya ini dinyatakan dalam hal laju aliran massa m � bahan sebagai berikut

di mana istilah pertama di sisi kanan merupakan biaya peralatan, yang meningkat dengan meningkatnya laju alir, dan istilah kedua merupakan operasi biaya, yang turun dengan meningkatnya m.

SOLUSI

Nilai ekstrem diberikan oleh

Karena itu

Turunan kedua diperoleh sebagai berikut

yang bernilai positip karena m adalah positip

3. METODE LAGRANGE MULTIPLIER

Ini adalah metode yang paling penting dan berguna untuk optimasi berdasarkan kalkulus. Hal ini dapat digunakan untuk mengoptimalkan fungsi yang bergantung pada sejumlah independen variabel dan ketika kendala fungsional terlibat. Dengan demikian, dapat diterapkan untuk berbagai situasi praktis disediakan fungsi tujuan dan kendala dapat dinyatakan sebagai fungsi kontinu dan terdiferensialkan. Selain itu, kendala kesetaraan hanya dapat dipertimbangkan dalam proses optimasi.

DASAR PENDEKATAN

tunduk pada kendala

dimana U adalah fungsi tujuan yang akan dioptimalkan dan Gi = 0, dengan i bervariasi dari 1 sampai n, merupakan kendala kesetaraan n. Seperti disebutkan sebelumnya, jika kendala ketimpangan muncul dalam masalah, ini harus diubah menjadi kesetaraan kendala untuk menerapkan metode ini. Selain itu, dalam beberapa kasus, ketidaksetaraan kendala hanya mendefinisikan domain diterima dan tidak digunakan dalam optimasi proses. Namun demikian, solusi yang diperoleh diperiksa untuk memastikan bahwa kendala puas.

Metode Lagrange pada dasarnya mengubah masalah sebelumnya untuk menemukan minimum atau maksimum ke solusi dari sistem aljabar persamaan, sehingga memberikan skema yang nyaman untuk menentukan optimal. Itu fungsi tujuan dan kendala digabungkan menjadi Y fungsi baru, yang dikenal sebagai ekspresi Lagrange dan didefinisikan sebagai

Ketika pembedaan diterapkan pada ekspresi Lagrange, menemukan bahwa optimum diperoleh dengan menyelesaikan sistem persamaan berikut:

Jika U fungsi tujuan dan kendala Gi yang terus menerus dan terdiferensialkan,

sistem persamaan aljabar diperoleh. Karena ada persamaan m untuk kendala dan persamaan tambahan n berasal dari ekspresi Lagrange, total m+ n persamaan simultan diperoleh. Yang tidak diketahui adalah m pengganda, sesuai dengan kendala m, dan variabel independen n. Oleh karena itu, sistem ini dapat diselesaikan untuk mendapatkan nilai-nilai variabel independen, yang menentukan lokasi yang optimum, serta multiplier. Analytical metode untuk memecahkan sistem persamaan aljabar dapat digunakan jika persamaan linier diperoleh dan / atau ketika jumlah persamaan kecil, biasanya sampai dengan sekitar lima. untuk nonlinear persamaan dan untuk set yang lebih besar, metode numerik umumnya lebih tepat. Nilai optimum dari fungsi tujuan ini kemudian ditentukan dengan menggantikan nilai-nilai yang diperoleh untuk variabel independen terhadap ekspresi untuk U. optimum sering diwakili oleh tanda bintang, yaitu, X1*, X2*, …. Xn* dan U*.

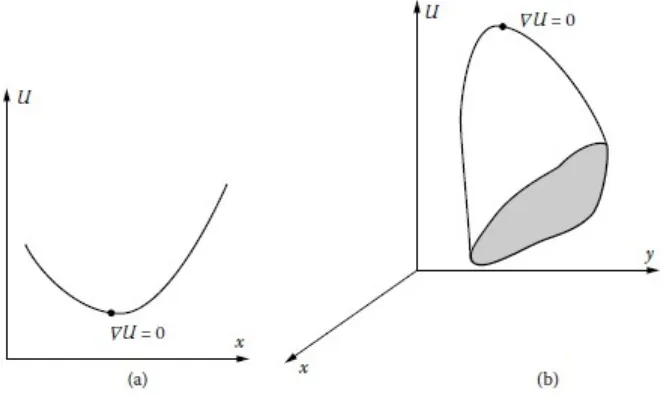
Mari mempertimbangkan masalah tak terbatas untuk dua variabel independen x dan y. Kemudian metode pengali Lagrange menghasilkan lokasi optimal sebagai solusi untuk persamaan

Gambar 2 Minimum dan Maksimum dalam masalah tidak berkendala ∇ U = 0

Oleh karena itu, vektor gradien, yang normal dengan kontur U konstan, adalah nol, menyiratkan bahwa tingkat perubahan U adalah nol sebagai salah satu bergerak menjauh dari titik dimana persamaan ini puas. Ini menunjukkan titik stasioner, atau ekstrem, seperti ditunjukkan secara kualitatif pada Gambar 2 untuk satu atau dua variabel independen. Intinya mungkin minimum atau maksimum. Hal ini juga dapat menjadi titik pelana, ridge, atau lembah (lihat Gambar 2). Informasi tambahan yang diperlukan untuk menentukan sifat stasioner titik, seperti yang dibahas kemudian. Karena Persamaan adalah persamaan vektor, masing-masing komponen dapat ditetapkan sama dengan nol, sehingga menimbulkan dua persamaan berikut:

yang dapat diselesaikan untuk mendapatkan x dan y di optimal, dilambangkan sebagai x* dan y*. Nilai U* optimal kemudian dihitung dari ekspresi untuk U. Jumlah persamaan yang diperoleh adalah sama dengan jumlah variabel independen dan optimal dapat ditentukan dengan memecahkan persamaan.

5. MLM UNTUK OPTIMASI BERKENDALA

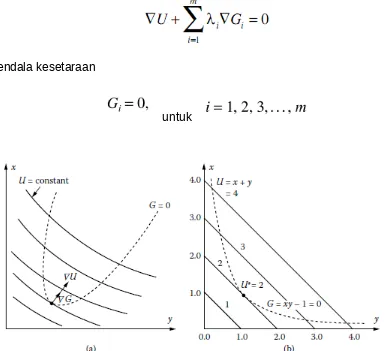
Gambar 3. Interpretasi fisik metode lagrange multiplier untuk dua variabel independen dan kendala tunggal

Gradien vektor ∇ U normal dengan kontur U konstan, sedangkan ∇ G adalah vektor normal terhadap kontur G konstan. Pengganda Lagrange hanya konstan. Oleh karena itu, persamaan ini menyiratkan bahwa dua vektor gradien yang selaras, yaitu, keduanya berada dalam garis lurus yang sama. Besaran dapat berbeda dan dapat disesuaikan untuk memastikan bahwa Persamaan sesuai. Namun, jika dua vektor tidak berada dalam garis yang sama, jumlah itu tidak boleh nol kecuali kedua vektor adalah nol. Hasil ini ditunjukkan secara grafik pada Gambar 3 untuk minimum di U. Sebagai salah satu bergerak di sepanjang kendala, yang diberikan oleh G-0, dalam rangka untuk memastikan bahwa kendala puas, gradien

∇

G bervariasi arah. Titik di mana menjadi collinear dengan ∇ U adalah optimal. Pada titik ini, dua kurva yang tangensial dan dengan demikian menghasilkan nilai minimum U sementara memenuhi kendala.

Kurva U konstan di bawah kurva kendala tidak memenuhi kendala dan yang di atas itu memberikan nilai U lebih besar dari optimum pada lokasi di mana mereka bersinggungan dengan kurva kendala. Jelas, nilai U lebih kecil dari yang di yang optimal ditunjukkan pada gambar bisa diperoleh jika ada kendala tidak ada, dalam hal persamaan yang mengatur akan diperoleh dari Persamaan

∇

U

. Sebagai contoh, mempertimbangkan U fungsi tujuan dalam bentuk

dengan bentuk kendala

Berikut E, koefisien A dan B, dan eksponen a, b, c, dan d diasumsikan menjadi konstanta yang diketahui. Ekspresi seperti yang sering ditemui dalam termal sistem. Misalnya, U mungkin biaya keseluruhan dan x dan y pompa yang dibutuhkan dan diameter pipa, masing-masing, dalam sistem aliran air. Tekanan menurun dengan meningkatnya diameter, sehingga biaya lebih rendah untuk pompa, dan biaya untuk meningkatkan pipa. Hal ini menimbulkan hubungan seperti Persamaan untuk E. Dengan demikian, kontur U konstan dapat ditarik bersama dengan kurva kendala sebuah bidang x - y, seperti sketsa pada Gambar 4 (a). Kemudian optimal ditunjukkan dengan lokasi di mana kontur U konstan menjadi tangensial dengan kendala kurva, sehingga menyelaraskan

∇

U dan

∇

G vektor. Untuk kasus sederhana ketika semua konstanta dalam ekspresi kesatuan, yaitu, U = x+y dan G = xy - 1 = 0, U konstan kontur berupa garis lurus dan kurva kendala diberikan oleh x = 1 / y, seperti sketsa pada Gambar 4 (b). Optimum adalah pada x* = 1,0 dan y* = 1,0, dan nilai U* optimum adalah 2,0 untuk kasus ini.

Meskipun hanya dua variabel independen dianggap sini untuk kemudahan visualisasi dan pemahaman fisik, ide-ide dasar dengan mudah dapat diperpanjang untuk sejumlah besar variabel. Sistem persamaan yang harus diselesaikan untuk mendapatkan optimal diberikan oleh persamaan skalar n berasal dari persamaan vektor

dan m kendala kesetaraan

untuk

Gambar 4. (a). Optimisasi masalah kendala sederhana dan (b) hasil dari semua kendala diberikan oleh ekpresi adalah satu.

Sebagian besar masalah yang dihadapi dalam optimasi desain sistem termal terhambat karena prinsip-prinsip konservasi dan keterbatasan yang ditetapkan oleh bahan yang digunakan peraturan ruang, tersedia, keselamatan dan lingkungan, dll Namun, seringkali kendala yang digunakan untuk mendapatkan hubungan antara berbeda desain variabel. Jika ini kemudian diganti menjadi ekspresi untuk fungsi tujuan, masalah tak terbatas diperoleh karena kendala telah terpenuhi. Kadang-kadang, dalam perumusan masalah optimasi sendiri, kendala bekerja untuk menurunkan ekspresi yang tepat dan kendala tambahan tidak diperlukan. Dengan demikian, suatu hasil masalah tak terbatas. Tentu saja, dalam beberapa kasus, tidak ada kendala yang signifikan, dan masalah diperlakukan sebagai tak terbatas. Dengan demikian, masalah optimasi tidak dibatasi adalah minat banyak sistem termal praktis dan proses.

Penggunaan Gradien Untuk Optimasi

Jika tidak ada kendala dalam masalah, optimal diberikan oleh solusi untuk persamaan berikut vektor untuk U (x1, x2, x3, ..., xn):

Sekali lagi, mudah untuk memvisualisasikan vektor gradien jika hanya dua atau tiga variabel terlibat, seperti yang terlihat di bagian sebelumnya. Namun, konsep-konsep dasar yang sama dan dapat diperpanjang untuk setiap nomor yang sesuai dari variabel. Semua komponen Persamaan vektor persamaan, ∇ U, harus nol agar vektor menjadi nol karena semua variabel diambil sebagai independen satu sama lain. Oleh karena itu, optimal diperoleh dengan memecahkan persamaan

Hal ini mirip dengan kondisi untuk titik stasioner diberikan oleh Persamaan untuk variabel tunggal independen. Fungsi tujuan harus kontinu dan

terdiferensialkan fungsi dari variabel independen dalam masalah dan derivatif harus kontinu.

Sistem persamaan diwakili oleh Persamaan dapat linear atau nonlinier, persamaan nonlinier meskipun lebih sering ditemui untuk termal sistem dan proses. Analisis matematis dapat digunakan dalam kasus-kasus sederhana untuk mendapatkan solusi. Jika tidak, teknik numerik diperlukan. Metode ini sangat berguna untuk sistem yang mungkin ditandai dengan ekspresi aljabar yang dapat dengan mudah dibedakan. Situasi ini biasanya muncul dalam kasus-kasus di mana curve fitting menghasilkan ekspresi seperti untuk karakteristik perilaku sistem dan dalam sistem kecil, ideal, dan sederhana. Kendala diasumsikan absen atau diurus dalam mengembangkan fungsi tujuan, seperti yang dibahas kemudian. Kami sekarang mempertimbangkan menentukan apakah optimal adalah minimum atau maksimum.

PENENTUAN MINIMUM ATAU MAKSIMUM

Dalam kebanyakan kasus, sifat fisik dari masalah akan menunjukkan apakah

lainnya. Sering, diketahui dari pengalaman bahwa minimal atau maksimal ada di domain yang diberikan. Misalnya, hal itu dapat diketahui bahwa minimal dalam energi Konsumsi akan timbul jika tekanan kompresor yang bervariasi atas diterima rentang dalam sistem refrigerasi. Demikian pula, efisiensi termal maksimum diharapkan jika kecepatan, dalam revolusi per menit, dari mesin diesel adalah bervariasi. Namun, dengan tidak adanya informasi tersebut, analisis lebih lanjut dapat dilakukan untuk menentukan karakteristik optimal.

Telah dikenal persamaan-persamaan memberikan kondisi untuk maksimum dan minimum, masing-masing, untuk satu variabel bebas. Jika turunan kedua adalah nol pada titik stasioner, terjadinya titik pelana, titik infleksi, ridge, atau lembah. Kondisi serupa mungkin diturunkan untuk dua atau lebih variabel independen. Untuk kasus dua independen variabel, x1 dan x2, dengan U (x1, x2) dan pertama dua derivatif terus menerus, ini kondisi diberikan sebagai

dimana

Oleh karena itu, untuk dua variabel independen, optimal dapat diperoleh dengan memecahkan ∂U/∂1 = ∂U /∂x2 = 0 dan menerapkan kondisi sebelumnya. Meskipun mirip kondisi dapat diturunkan untuk sejumlah besar variabel, analisis menjadi cukup terlibat. Oleh karena itu, dalam keadaan paling praktis, yang melibatkan tiga atau lebih variabel independen, akan lebih mudah dan efisien bergantung pada sifat fisik dari masalah untuk menentukan apakah maksimum minimum atau memiliki telah diperoleh. Selain itu, variabel independen dapat berubah sedikit dekat optimal untuk menentukan apakah nilai meningkat fungsi objektif atau menurun. Jika nilai berkurang sebagai salah satu bergerak menjauh dari optimal, maksimal diindikasikan, sedangkan jika itu meningkat, minimal telah diperoleh.

CONTOH

Biaya per unit massa dari bahan yang diproses di fasilitas ekstrusi diberikan oleh ekspresi

di mana T adalah temperatur berdimensi dari bahan yang diekstrusi, V adalah laju aliran volume berdimensi, dan C mencakup modal dan biaya operasional. Tentukan biaya minimum.

SOLUSI

Karena baik T dan V adalah jumlah positif, memiliki

Persamaan ini memberikan V* = 1,6930 dan T* = 0,6182. Bila ini diganti dalam ekspresi untuk C, diperoleh C* = 5,1763. Sekarang turunan kedua mungkin diperoleh untuk memastikan sifat dari titik kritis. Dengan demikian,

Mensubstitusikan nilai-nilai dari V dan T pada titik stasioner, menghitung ini tiga derivatif kedua sebagai 1,3544, 23,7023, dan 1,2364, masing-masing. ini memberikan S = 30,57. Oleh karena itu, S = 0 dan ∂2_{C /∂V}2 _{= 0, menunjukkan}

bahwa biaya minimum telah diperoleh.

Konversi Masalah Berkendala manjadi Masalah tidak Berkendala

Hal ini terbukti dari pembahasan sebelumnya bahwa optimasi dibatasi masalah adalah jauh lebih mudah untuk memecahkan, dibandingkan dengan dibatasi sesua salah, karena tidak diketahui jumlah lebih kecil dalam kasus mantan. Setiap kendala memperkenalkan multiplier Lagrange sebagai diketahui dan persamaan tambahan harus puas. Oleh karena itu, diinginkan untuk mengkonversi diberikan dibatasi Masalah menjadi satu tak terbatas bila memungkinkan. Kendala mewakili hubungan antara variabel independen berbagai yang harus dipenuhi. Jika persamaan ini dapat digunakan untuk memperoleh ekspresi eksplisit untuk beberapa variable dalam hal yang lain, ungkapan ini kemudian dapat disubstitusikan ke dalam tujuan berfungsi untuk menghilangkan kendala dan dengan demikian mengubah masalah ke tidak dibatasi satu. Bahkan jika semua kendala tidak dapat dihilangkan, akan lebih bermanfaat untuk menghilangkan sebanyak ini mungkin untuk mengurangi kompleksitas dari masalah. Persamaan dapat digunakan untuk mengekspresikan y dalam x sebagai berikut

Mengganti ini nilai y ke Persamaan

= 1,0 dan U* = 2.0 untuk kasus sederhana ketika semua konstanta dan eksponen adalah kesatuan.

Dengan demikian, hal ini diinginkan untuk mengurangi jumlah kendala, yang juga akan mengurangi jumlah variabel yang tidak diketahui dan pengganda Lagrange, dengan menggunakan kendala persamaan untuk menemukan ekspresi eksplisit berkaitan variabel. Contoh telah menggambarkan solusi dari masalah terkendala dengan mengubahnya menjadi satu tak terkendala. Hal ini kemudian dipecahkan sebagai masalah dibatasi untuk menunjukkan perbedaan antara dua pendekatan.

7. MASALAH OPTIMASI BERKENDALA

Optimasi sistem termal yang paling diatur oleh kendala yang timbul karena hukum konservasi dan keterbatasan yang ditetapkan oleh materi, ruang, biaya, keamanan, dll Seperti yang telah dibahas sebelumnya, jumlah kendala kesetaraan harus kurang dari jumlah variabel independen untuk optimasi menjadi mungkin. Jika jumlah kendala sama dengan jumlah variabel, masalah hanya mungkin diselesaikan untuk menghasilkan set variabel yang memenuhi kendala. Fleksibilitas ada tersedia untuk memilih desain yang terbaik atau optimal.

Jika jumlah kendala lebih besar dari jumlah variabel, masalah ini overconstrained dan beberapa dari kendala harus dibuang, mengakibatkan kesewenang-wenangan dan nonuniqueness dalam solusi. Pertimbangan ini terbukti dari Persamaan, dimana Kondisi m<n diperlukan untuk optimasi sistem. Jika m = n, kendala persamaan dapat digunakan untuk mendapatkan solusi, dan jika m>n, masalah tersebut overconstrained, dan tidak ada solusi yang mungkin kecuali m - n kendala yang dibuang. Mengingat masalah optimisasi, yaitu, m<n, metode pengganda Lagrange dapat diterapkan untuk menentukan desain yang optimal. Persamaan yang perlu dipecahkan diberikan oleh Persamaan Persamaan dapat ditulis ulang di sini sebagai:

dimana

∇

U dan

∇

Gi adalah vektor gradien, yang dapat diperluas dalam hal variabel independen n. Oleh karena itu, m + n persamaan diperoleh untuk n variabel independen dan pengganda m.

Kemudian, metode Lagrange menghasilkan persamaan berikut:

Hal ini dapat menunjukkan bahwa jika salah satu atau x1 x2 bervariasi dari nilai optimal, sekaligus memastikan bahwa kendala puas, U fungsi tujuan meningkat. Oleh karena itu, yang optimum yang diperoleh adalah minimum di U. Dalam kasus sederhana, turunan kedua juga dapat diturunkan untuk mengkonfirmasi bahwa minimal di U telah diperoleh. Itu Koefisien sensitivitas Sc = - λ = 2,027. Hal ini memberi efek santai kendala pada nilai

optimum U. Sebagai contoh, jika x1x2 = 13, bukan 12, U* dapat dihitung menjadi 38,493,

naik dari 2,0. Perbedaan kecil dalam perubahan di U* dari nilai yang dihitung dari Sc adalah hasil dari persamaan nonlinear yang membuat Sc fungsi dari x1 dan tidak konstan. Contoh berikut menggambarkan hal ini untuk masalah tangki dianggap sebelumnya. Memecahkan masalah tangki diberikan sebagai masalah optimasi dibatasi. Solusi Fungsi tujuan adalah Sebuah wilayah, yang harus diminimalkan, dan kendala adalah volume V. Dengan demikian, masalah optimasi dapat ditulis sebagai:

Pemecahan ketiga menghasilkan persamaan

Untuk V = 2 m3: r* = 0,683 m, h* = 1,366 m, A* = 8,793 m2, λ = -2,928. Nilai-nilai ini sama dengan yang diperoleh sebelumnya dengan mengubah satu masalah ke tak terbatas. Sekali lagi, hal itu dapat dikonfirmasikan bahwa minimal di daerah telah diperoleh.

Koefisien sensitivitas Sc, yang sama dengan - λ, diperoleh sebagai tambahan Informasi. Mari berasumsi bahwa kendala pada volume diperlonggar dari 2,0 ke 2.1. Kemudian, dengan mudah dapat ditunjukkan bahwa r* = 0,694 m dan A* = 9,078 m2. Oleh karena itu,∂A /∂V = (9,078-8,793) / 0,1 = 2,85, yang dekat dengan koefisien Sc sensitivitas, yang diberikan oleh - λ dan, dengan demikian, sama dengan 2,928 pada titik optimum. Sekali lagi, perbedaan sedikit antara Sc dan ∂A /∂V adalah karena ketergantungan pada

variabel.

Beberapa kendala

Ruang penyimpangan diciptakan oleh kendala terdiri dari semua poin yang dapat dicapai dengan menambahkan kombinasi linear dari vektor arah penyimpangan-dengan kata lain, semua poin yang "terjangkau" ketika menggunakan arah penyimpangan individu sebagai dasar ruang . Dengan demikian, dapat secara singkat dinyatakan bahwa v berada dalam ruang didefinisikan oleh jika dan hanya jika terdapat satu set "pengganda" sedemikian rupa sehingga:

yang bagi, kami menerjemahkan tujuan untuk menyatakan bahwa arah yang berubah

f pada p adalah di "ruang penyimpangan" didefinisikan oleh kendala jika dan hanya jika:

Seperti sebelumnya, sekarang menambahkan persamaan simultan untuk menjamin bahwa hanya melakukan tes ini ketika berada pada titik yang memenuhi setiap kendala, berakhir dengan persamaan simultan bahwa ketika dipecahkan, mengidentifikasi semua titik stasioner terbatas:

Memecahkan persamaan di atas untuk poin tak terbatas yang stasioner menghasilkan persis titik stasioner sama dengan pemecahan untuk titik stasioner dibatasi dari f di bawah kendala .

Untuk menghormati Lagrange, fungsi di atas disebut Lagrangian, skalar disebut Lagrange Multipliers dan metode optimasi sendiri disebut

Metode pengali Lagrange.

Metode Lagrange adalah umum oleh kondisi Karush-Kuhn-Tucker, yang juga dapat mempertimbangkan kendala ketimpangan bentuk h (x) ≤ c.

Interpretasi pengganda Lagrange

Seringkali pengganda Lagrange memiliki tafsir karena beberapa kuantitas menarik. Misalnya, jika ekspresi adalah Lagrangian

kemudian

Jadi, λk adalah laju perubahan kuantitas yang dioptimalkan sebagai fungsi dari variabel

kendala. Sebagai contoh, dalam mekanika Lagrangian persamaan gerak yang diperoleh dengan mencari titik stasioner dari tindakan , waktu integral dari perbedaan antara energi kinetik dan potensial. Dengan demikian, gaya pada partikel karena potensi skalar, , Dapat diartikan sebagai pengali Lagrange menentukan perubahan dalam tindakan (transfer potensial menjadi energi kinetik) setelah variasi dalam lintasan partikel dibatasi. Dalam teori kontrol ini dirumuskan bukan sebagai persamaan costate.

Selain itu, dengan teorema amplop nilai optimal dari multiplier Lagrange memiliki interpretasi sebagai efek marginal dari kendala yang sesuai konstan pada nilai dicapai optimal dari fungsi tujuan aslinya: jika dapat menunjukkan nilai di optimum dengan tanda bintang, maka dapat ditunjukkan bahwa

Contoh 1

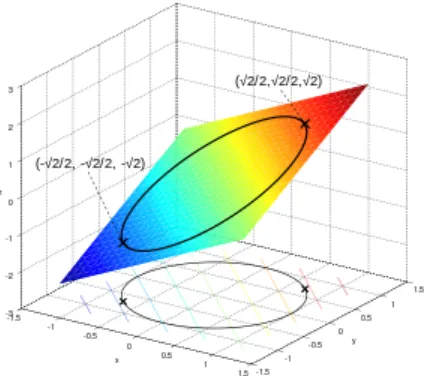
Gambar. 5. Ilustrasi dari masalah optimasi dibatasi

Misalkan ingin memaksimalkan tunduk pada kendala . Set layak adalah lingkaran satuan, dan tingkat set dari f adalah garis diagonal (dengan kemiringan -1), sehingga dapat melihat grafis yang maksimum terjadi pada

, Dan bahwa minimum terjadi pada .

Menggunakan metode pengganda Lagrange, kami telah , Maka

. Mengatur gradien hasil sistem persamaan

di mana persamaan terakhir adalah kendala asli.

Dua yang pertama persamaan hasil dan , Di mana

. Mensubstitusikan ke hasil persamaan terakhir , Sehingga , Yang berarti bahwa titik stasioner yang dan

sehingga maksimum adalah , Yang dicapai pada , Dan minimum adalah , Yang dicapai pada .

Contoh 2

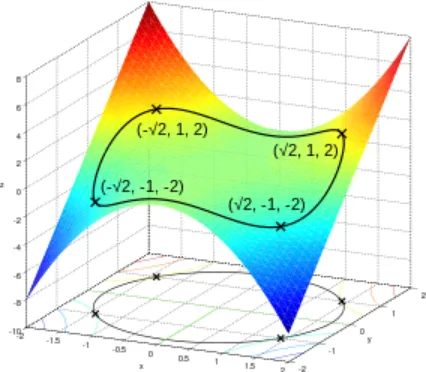
Gambar. 6. Ilustrasi dari masalah optimasi dibatasi Misalkan ingin mencari nilai maksimum

dengan kondisi bahwa x dan y koordinat terletak pada lingkaran di sekitar asal dengan jari-jari, √ 3 yaitu, tunduk pada kendala

Karena hanya ada satu kendala tunggal, akan menggunakan hanya satu multiplier, katakanlah λ.

Kendala g (x, y) -3 sama dengan nol pada lingkaran dengan jari-jari √ 3. Jadi apapun -3 beberapa g (x, y) dapat ditambahkan ke f (x, y) meninggalkan f (x, y) tidak berubah di daerah bunga (di atas lingkaran di mana kendala asli kami puas). Mari

Yang penting nilai-nilai terjadi di mana gradien adalah nol. Derivatif parsial

Persamaan (iii) hanya kendala aslinya. Persamaan (i) menyiratkan atau λ = - y.

kemudian oleh (ii) λ = 0. Dalam kasus kedua, jika λ = - y dan menggantikannya ke dalam persamaan (ii) didapati bahwa,

Kemudian x 2 _{= 2 y} 2. _{Mensubstitusikan ke dalam persamaan (iii) dan memecahkan}

untuk y memberikan ini nilai y:

Jadi ada enam poin penting:

Mengevaluasi tujuan pada titik-titik, ditemukan

Oleh karena itu, fungsi tujuan mencapai yang maksimum global (tunduk pada batasan) pada dan minimum global di Intinya adalah minimum lokal dan adalah sebuah maksimum lokal , sebagaimana ditentukan oleh pertimbangan matriks Hessian dari .

Perhatikan bahwa sementara adalah titik kritis , Itu bukan titik ekstrem lokal. Kami memiliki . Mengingat setiap lingkungan , Dapat memilih positif kecil dan kecil dari salah satu tanda untuk mendapatkan nilai baik besar dan kurang dari .

8.OPTIMASI DENGAN KENDALA KETIMPANGAN:

KONDISI KUHN-TUCKER

Banyak model di bidang ekonomi secara alami dirumuskan sebagai masalah optimasi dengan kendala ketimpangan.

Perhatikan, misalnya, masalah pilihan konsumen. Tidak ada alasan untuk bersikeras bahwa konsumen menghabiskan semua kekayaannya. Untuk memungkinkan dia untuk tidak menghabiskan semuanya, dapat dirumuskan masalah optimasi nya dengan kendala ketimpangan:

max x u (x) tunduk p x ≤ w dan x ≥ 0.

Tergantung pada karakter u fungsi dan nilai-nilai p dan w, mungkin memiliki p x <w

atau p x = w pada solusi dari masalah ini.

Pertimbangkan masalah bentuk berikut

max x f (x) tunduk g j (x) ≤ c j untuk j = 1, ..., m,

dimana f dan g j untuk j = 1, ..., m adalah fungsi dari variabel n, x = (x 1, ..., x n), dan c j

untuk j = 1, ..., m adalah konstanta .

Semua masalah yang telah dipelajari sejauh dapat dimasukkan ke dalam bentuk ini.

Kendala Kesetaraan

Dapat diperkenalkan kendala ketidaksetaraan dua untuk setiap kendala kesetaraan. Misalnya, masalah

max x f (x) tunduk h (x) = 0

dapat ditulis sebagai

max x f (x) tunduk h (x) ≤ 0 dan - h (x) ≤ 0.

Kendala Nonnegativity

Untuk masalah dengan kendala x k ≥ 0 misalkan g j (x) = - x k dan c j = 0 untuk

beberapa j.

Masalah Minimisasi

Untuk masalah minimisasi diperoleh dengan mengalikan fungsi obyektif dengan -1: min x h (x) tunduk g j (x) ≤ c j untuk j = 1, ..., m

adalah sama dengan

max x f (x) tunduk g j (x) ≤ c j untuk j = 1, ..., m,

dimana f (x) = - h (x).

max x f (x) tunduk pada g (x) ≤ c.

Ada dua kemungkinan solusi dari masalah ini. Pada gambar berikut, kurva tertutup hitam kontur f, nilai peningkatan fungsi dalam arah yang ditunjukkan oleh panah biru. Garis miring ke bawah merah adalah himpunan titik-titik x memuaskan g (x) = c,

himpunan poin x memuaskan g (x) ≤ c terletak di bawah dan kiri dari garis, dan mereka g memuaskan (x) ≥ c terletak di atas dan di sebelah kanan baris.

Dalam setiap panel solusi dari masalah adalah titik x*. Pada panel sebelah kiri kendala mengikat pada solusi: perubahan dalam c mengubah solusi. Pada panel sebelah kanan, kendala yang kendur di solusinya: perubahan kecil dalam c tidak berpengaruh pada solusi.

Seperti sebelumnya , menentukan fungsi Lagrangian L oleh L (x) = f (x) - λ (g (x) - c).

Kemudian dari analisis kami sebelumnya masalah dengan kendala kesetaraan dan tanpa kendala,

 jika g (x*) = c (seperti dalam panel kiri) dan kendala memenuhi kondisi

keteraturan, kemudian 'Li (x*) = 0 untuk semua i

 jika g (x*) <c (seperti dalam panel kanan), maka f i '(x*) = 0 untuk semua i.

Sekarang, saya menyatakan bahwa dalam kasus pertama (yaitu, jika g (x*) = c)

dengan memiliki λ ≥ 0. Misalkan, sebaliknya, yang λ <0. Kemudian diketahui bahwa

penurunan kecil di c meningkatkan nilai maksimal f. Artinya, bergerak x* dalam

kendala meningkatkan nilai f, bertentangan dengan fakta bahwa x* adalah solusi dari masalah.

Dalam kasus kedua, nilai λ tidak memasuki kondisi, sehingga dapat memilih nilai untuk itu. Mengingat interpretasi λ, pengaturan λ = 0 masuk akal. Dengan asumsi ini memiliki fi'(x) = L'i (x) untuk semua x, sehingga L'i (x*) = 0 untuk semua i.

Jadi dalam kedua kasus kami memiliki L'i (x*) = 0 untuk semua i, λ ≥ 0, dan g (x*) ≤ c.

Dalam kasus pertama memiliki g (x*) = c dan dalam kasus kedua λ = 0.

Selanjutnya dapat menggabungkan dua kasus dengan menulis kondisi sebagai berikut Li'(x*) = 0 untuk j = 1, ..., n

Sekarang, produk dari dua angka adalah nol jika dan hanya jika setidaknya salah satu dari mereka adalah nol, jadi alternatif bisa menulis kondisi sebagai

L i '(x*) = 0 untuk j = 1, ..., n

λ ≥ 0, g (x*) ≤ c, dan λ [g (x*) - c] = 0.

Argumen diberikan menunjukkan bahwa jika x* memecahkan masalah dan yang memenuhi kendala kondisi keteraturan, maka x* harus memenuhi kondisi ini.

Perhatikan bahwa kondisi tidak mengesampingkan kemungkinan bahwa kedua λ = 0 dan g (x*) = c.

Ketidaksetaraan λ ≥ 0 dan g (x*) ≤ c disebut kondisi kelambanan komplementer; paling banyak satu dari kondisi ini adalah slack (yaitu tidak kesetaraan suatu).

Untuk masalah dengan banyak kendala, maka seperti sebelumnya kami memperkenalkan satu multiplier untuk kendala masing-masing dan mendapatkan

Kuhn-Tucker kondisi, didefinisikan sebagai berikut.

Definisi

Kondisi Kuhn-Tucker untuk masalah

max x f (x) tunduk g j (x) ≤ c j untuk j = 1, ..., m

adalah

L i '(x) = 0 untuk i = 1, ..., n

λ j ≥ 0, j g (x) ≤ c j dan λ j [g j (x) - c j] = 0 untuk j = 1, ..., m,

dimana

L (x) = f (x) - Σ j = 1m λ j (j g (x) - c j).

Kondisi ini dinamai untuk menghormati Harold W. Kuhn, seorang anggota emeritus dari Princeton Matematika Departemen, dan Albert W. Tucker , yang pertama kali merumuskan dan mempelajari kondisi.

Dalam bagian berikut saya mendiskusikan hasil yang menentukan hubungan yang tepat antara solusi dari Kuhn-Tucker kondisi dan solusi dari masalah. Contoh berikut menggambarkan bentuk kondisi dalam kasus tertentu.

Contoh

Pertimbangkan masalah

max x 1, x 2 [- (x 1 - 4) 2 - (x2 - 4) 2] tunduk x1 + x2 ≤ 4 dan 3 x1 + x2 ≤ 9,

Kami memiliki

L (x1, x2) = - (x1 - 4) 2 - (x2 - 4) 2 - λ 1 (x1 + x2 - 4) - λ 2 (3 x1 + x2 - 9) .

Kondisi Kuhn-Tucker

-2 (X1 - 4) - λ 1 - 2 3λ = 0

-2 (X2 - 4) - λ 1 - λ 2 = 0

x1 + x2 ≤ 4, λ 1 ≥ 0, dan λ 1(x 1 + x2 - 4) = 0

3 x1 + x2 ≤ 9, λ 2 ≥ 0, dan λ 2 (3 x1 + x2 - 9) = 0.

Masalah optimasi Nonlinear

Pertimbangkan hal berikut masalah optimasi nonlinear:

di mana x adalah variabel optimasi, adalah tujuan atau fungsi biaya,

adalah ketidaksamaan kendala fungsi, dan

adalah fungsi kesetaraan kendala. Jumlah ketidaksetaraan dan kendala kesetaraan dilambangkan m dan l, masing-masing.

Kondisi Perlu

Misalkan bahwa fungsi tujuan dan fungsi kendala dan yang terus differentiable pada suatu titik . Jika adalah suatu

Stasioneritas

Kelayakan Primal

Kelayakan Ganda

Pelengkap kelambanan (Complementary slackness)

Dalam kasus tertentu , Yaitu, jika tidak ada kendala ketimpangan, kondisi KKT berubah menjadi kondisi Lagrange, dan pengganda KKT disebut Lagrange .

Kondisi Keteraturan (atau kualifikasi kendala)

Agar titik minimum untuk memenuhi kondisi KKT di atas, harus memenuhi beberapa kondisi keteraturan, yang paling banyak digunakan tercantum di bawah ini:

 Linearitas kendala kualifikasi : Jika dan adalah fungsi affine, maka tidak

ada kondisi lain yang diperlukan.

 Kemerdekaan kendala linier kualifikasi (licq): gradien dari kendala ketimpangan

aktif dan gradien dari kendala kesetaraan yang linear di .

 Mangasarian-Fromovitz kendala kualifikasi (MFCQ): gradien dari kendala

ketimpangan aktif dan gradien dari kendala kesetaraan positif-linear independen pada .

 Peringkat Konstan kendala kualifikasi (CRCQ): untuk setiap subset dari gradien

dari kendala ketimpangan aktif dan gradien dari kendala kesetaraan pangkat di sekitar adalah konstan.

 Ketergantungan konstanta positif kualifikasi kendala linear (CPLD): untuk setiap

subset dari gradien dari kendala ketimpangan aktif dan gradien dari kendala kesetaraan, jika hasilnya positif-linear bergantung pada maka positif-linear bergantung pada sekitar .

 Kuasi-normalitas kendala kualifikasi (QNCQ): jika gradien dari kendala

ketimpangan aktif dan gradien dari kendala kesetaraan positif-linear independen pada dengan pengganda terkait untuk kesetaraan dan untuk ketidaksetaraan, maka tidak ada urutan sehingga

dan .

 Kondisi Slater : untuk masalah cembung, terdapat titik sehingga

dan untuk semua aktif dalam .

Hal ini dapat ditunjukkan bahwa licq ⇒ MFCQ ⇒ CPLD ⇒ QNCQ, licq ⇒ CRCQ ⇒ CPLD ⇒ QNCQ (dan converses yang tidak benar), meskipun MFCQ tidak setara dengan CRCQ. Dalam prakteknya kualifikasi kendala lemah lebih disukai karena mereka memberikan kondisi optimalitas kuat.

Kondisi Cukup

Dalam beberapa kasus, kondisi yang diperlukan juga cukup untuk optimalitas. Secara umum, kondisi yang diperlukan tidak cukup untuk optimalitas dan informasi tambahan yang diperlukan, seperti Kondisi Orde Kedua Cukup (SOSC). Untuk fungsi mulus, SOSC melibatkan derivatif kedua, yang menjelaskan namanya.

Kondisi yang diperlukan adalah cukup untuk optimalitas jika fungsi tujuan dan kendala ketimpangan dapat didiferensiasi secara kontinu fungsi cembung dan kendala kesetaraan adalah fungsi affine .

Hal ini ditunjukkan oleh Martin pada tahun 1985 bahwa kelas yang lebih luas dari fungsi di mana kondisi KKT menjamin optimalitas global disebut Tipe 1 fungsi Invex .

Ekonomi

Seringkali dalam matematika ekonomi pendekatan KKT digunakan dalam model teoritis untuk memperoleh hasil kualitatif. Sebagai contoh, pertimbangkan sebuah perusahaan yang memaksimalkan subjek penjualan untuk kendala keuntungan minimum. Membiarkan Q menjadi kuantitas output yang dihasilkan (untuk dipilih), R (Q) akan penjualan dengan turunan pertama positif dan dengan nilai nol nol output, C (Q) menjadi biaya produksi dengan turunan pertama positif dan dengan non-negatif nilai nol pada output, dan menjadi tingkat yang dapat diterima positif minimal keuntungan , maka masalahnya adalah satu bermakna jika tingkat fungsi pendapatan off sehingga akhirnya kurang curam daripada fungsi biaya. Masalah dinyatakan dalam bentuk minimisasi sebelumnya diberikan adalah

Memperkecil tunduk dan dan kondisi KKT yang

Karena itu mengingat bahwa dan secara ketat positif, ketidaksetaraan ini bersama dengan kondisi non-negatif pada jaminan bahwa adalah positif dan sehingga perusahaan pendapatan memaksimalkan beroperasi pada tingkat output di mana penerimaan marjinal kurang dari biaya marjinal - Hasil yang menarik karena kontras dengan perilaku memaksimalkan keuntungan perusahaan, yang beroperasi pada tingkat di mana mereka adalah sama.

Fungsi Nilai

Jika kembali ke masalah optimasi sebagai masalah maksimisasi dengan kendala ketimpangan konstan,

Fungsi nilai didefinisikan sebagai

(Jadi domain V adalah )

REFERENSI

Edgar, T F. And DM Himmelblau. 2001. Optimization Of Chemical Processes, Second Edition. Mcgraw-Hill. New York.

Jaluria, Yogesh. 2008. Design and optimization of thermal systems 2nd ed. CRC Press. USA

Jelen, FC. 1985. Cost and Optimization Engineering. Second edition. McGraw-Hill. New York.

http://www.economics.utoronto.ca/osborne/MathTutorial/MEN.HTM#Lagrangean

http://www.economics.utoronto.ca/osborne/index.html

http://en.wikipedia.org/wiki/ Karush–Kuhn–Tucker conditions

http://en.wikipedia.org/wiki/Lagrange_multiplier.htm. 22 October 2012

PROPAGASI

1. Tugas (Evaluasi mandiri)

1. Gunakan Pengali Lagrange untuk menyelesaikan :

2. Tangki silinder dirancang untuk menyimpan air hangat dari system kolektor surya. Volume diberikan adalah 2 m3 dan luas permukaan diminimalkan untuk meminimasi kelhilangan panas ke sekeliling. Selesaikan maslah optimasi ini dengan keadaan tidak berkendala.

3. Gunakan syarat Kunh-Tucker :

Min f(x, y) = 2x2 _{+ xy + 2y}2 _{– 8x - 6y}

Kendala 2x + y ≤ 1 -x +2y ≤ 4

x ≥ 0 y ≥ 0

Min

2

x

A. QUIZ - (Evaluasi)