Fakultas Ilmu Komputer
Universitas Brawijaya
2459
Clustering Mobilitas Masyarakat Berdasarkan Moda Transportasi
Menggunakan Metode K-Means
Humam Aziz Romdhoni1, M. Tanzil Furqon2, Sigit Adinugroho3
Program Studi Teknik Informatika, Fakultas Ilmu Komputer, Universitas Brawijaya Email: 1[email protected], 2[email protected], 3[email protected]
Abstrak
Mobilitas masyarakat adalah perpindahan masyarakat dari satu tempat ke tempat lain. Mobilitas masyarakat merupakan topik yang patut untuk diteliti. Karena dengan mengetahui mobilitas masyarakat kita dapat mengetahui pola rute yang dilalui, moda transportasi yang dipilih, lama waktu perjalanan, dan lain-lain. Di era modern ini, data lintasan perpindahan seorang individu dapat diketahui melalui GPS (Global Positioning System). Data-data GPS yang diperoleh tersebut dapat diolah menjadi informasi yang berguna, seperti moda transportasi apa saja yang digunakan oleh setiap individu. Untuk melakukan pengolahan data tersebut dapat digunakan salah satu metode data mining, yaitu clustering. Clustering dipilih karena data GPS untuk setiap moda transportasi dianggap mempunyai karakteristik yang hampir sama, sehingga metode pengambilan informasi yang paling tepat adalah dengan cara dikelompokkan. Salah satu metode clustering yang populer adalah k-means. Pada penelitian ini diketahui bahwa hasil
cluster dengan metode k-means memiliki kualitas sedang sampai baik pada nilai k mendekati jumlah
jenis moda transportasi dilihat dari nilai silhouette coefficient. Akan tetapi dari hasil pengujian ketepatan, metode k-means menunjukkan persentase yang baik yaitu sebesar 90%.
Kata kunci: clustering, k-means, lintasan
Abstract
Peoples mobility is the movement of people from one place to another. Peoples mobility is a worthy topic to research. Because by knowing the mobility of society we can know the pattern of the route traversed, the chosen transportation mode, the duration of travel, and others. In this modern era, moving trajectory data of an individual can be known through GPS (Global Positioning System). GPS data obtained can be processed into useful information, such as what each mode of transportation used by each individual. To perform this data processing, we can use one method of data mining, which name is clustering. Clustering is chosen because GPS data for each mode of transport is considered to have almost the same characteristics, so the most appropriate method of information retrieval is by grouping. One of the popular clustering methods is means. In this research we can see that the cluster with k-means method has medium to high quality when k value close to quantity of transportation mode seen from the value of silhouette coefficient. From the results of accuracy testing, k-means method shows a good percentage that is 90%.
Keywords: clustering, k-means, trajectory
1. PENDAHULUAN
Mobilitas masyarakat adalah perpindahan masyarakat dari satu tempat ke tempat lain. Mobilitas masyarakat merupakan topik yang patut untuk diteliti. Karena dengan mengetahui mobilitas masyarakat kita dapat mengetahui pola rute yang dilalui, moda transportasi yang dipilih, lama waktu perjalanan, dan lain-lain. Di era modern ini, data perpindahan seorang individu
dapat diketahui melalui GPS. Salah satu proyek yang mengumpulkan data lintasan GPS adalah
Microsoft GeoLife (Zheng, 2007). Proyek ini
merupakan jejaring sosial berbasis lokasi. Data-data GPS yang diperoleh tersebut dapat diolah menjadi informasi yang berguna, seperti moda transportasi apa saja yang digunakan oleh setiap individu. Dengan mengetahui hal tersebut diharapkan masyarakat mempunyai banyak pilihan yang dapat digunakan sebagai pertimbangan untuk melakukan sebuah
perjalanan. Untuk melakukan pengolahan data tersebut dapat digunakan salah satu metode data
mining, yaitu clustering. Clustering adalah
metode untuk menganalisa data dan bertujuan untuk mengelompokkan data yang mempunyai karakteristik yang sama. Clustering dipilih karena data GPS untuk setiap moda transportasi dianggap mempunyai karakteristik yang hampir sama, sehingga metode pengambilan informasi yang paling tepat adalah dengan cara dikelompokkan. Salah satu metode clustering yang populer adalah k-means. Metode ini memisahkan dan membagi objek ke daerah-daerah yang terpisah sesuai dengan banyaknya k yang telah ditentukan. K-means dipilih karena metode ini mudah untuk diimplementasikan serta mudah untuk diadaptasi.
2. DATA DAN METODE CLUSTERING
2.1. Microsoft GeoLife GPS Trajectory
Data yang digunakan dalam penelitian ini adalah data lintasan GPS yang didapatkan dari proyek Microsoft GeoLife GPS Trajectory. Data GPS ini dikumpulkan oleh 182 pengguna pada proyek GeoLife dalam kurun waktu kurang lebih lima tahun (sejak April 2007 hingga Agustus 2012). Data GPS ini direpresentasikan sebagai rangkaian titik koordinat yang disertai waktu. Titik koordinat tersebut terdiri dari latitude,
longitude, dan altitude. Data ini berisi 17.621
lintasan dengan total jarak mencapai 1.292.951 kilometer dan total durasi selama 50.176 jam. 91,5 persen dari data lintasan diambil dengan representasi yang padat, yaitu setiap 1 – 5 detik atau setiap 5 – 10 meter per poin.
Data yang dibutuhkan untuk diolah adalah data latitude, longitude, dan altitude. Sebanyak 30 titik koordinat dianggap mewakili satu lintasan berdasarkan moda transportasi.
2.2. Metode K-means
Metode k-means merupakan salah satu metode non hirarkial clustering yang populer digunakan. Metode ini pertama kali diperkenalkan oleh MacQueen JB pada tahun 1976. Metode ini membagi atau memisahkan objek ke k kelompok atau golongan bagian yang terpisah. Metode k-means mengharuskan setiap objek masuk ke dalam golongan yang terbentuk, akan tetapi pada suatu tahapan langkah tertentu, objek yang telah menjadi anggota dalam satu golongan tadi akan berpindah ke golongan lain pada tahapan proses berikutnya.
Langkah-langkah metode k-means:
1. Menentukan k sebagai jumlah cluster yang ingin dibentuk.
2. Menentukan nilai secara acak untuk pusat
cluster awal (centroid) sebanyak k.
3. Menghitung jarak setiap data yang dimasukkan terhadap masing-masing
centroid menggunakan rumus Eucledian Distance hingga ditemukan jarak yang
paling dekat antara setiap data dengan
centroid. Berikut ini adalah persamaan Eucledian Distance: 𝑑(𝑥𝑖, 𝑦𝑗) = √(𝑥𝑖− 𝑦𝑗) 2 (2-1) Keterangan: 𝑥𝑖: Data kriteria
𝑦𝑗: Centroid pada cluster j
4. Mengelompokkan setiap data berdasarkan kedekatannya dengan centroid (jarak terkecil).
5. Memperbaharui nilai centroid. Nilai
centroid yang baru didapatkan dari rata-rata cluster yang bersangkutan dengan menggunakan rumus:
𝑦𝑗(𝑡 + 1) = 1
𝑁𝑠𝑗∑𝑗∈𝑠𝑗𝑥𝑗 (2-2)
Keterangan:
𝑦𝑗(𝑡 + 1): Centroid baru pada iterasi ke
t + 1
𝑁𝑠𝑗: Banyaknya data pada cluster j
6. Melakukan perulangan dari langkah 2 hingga 5 sampai anggota tiap cluster tidak ada yang berubah.
7. Jika langkah 6 telah terpenuhi, maka nilai pusat cluster pada perulangan terakhir akan digunakan sebagai parameter untuk menentukan klasifikasi data.
2.3. Sillhouette Coefficient
Metode pengujian yang digunakan dalam penelitian ini adalah metode Silhoutte Coeffisient. Metode ini akan menguji kualitas
dari setiap cluster yang dihasilkan dengan menggabungkan metode cohesion dan
separation.
Ada tiga langkah yang perlu dilakukan untuk menghitung Silhoutte Coeffisient, yaitu: 1. Untuk setiap objek i, hitung rata-rata jarak
objek i dengan seluruh objek yang berada dalam satu cluster. Maka akan didapatkan nilai rata-rata yang disebut dengan ai.
2. Untuk setiap objek i, hitung rata-rata jarak dari objek i dengan objek yang berada di
cluster lainnya. Dari semua jarak rata-rata
tersebut diambil nilai yang paling kecil. Nilai ini disebut dengan bi.
3. Setelah itu maka nilai Silhoutte Coeffisient dari objek i adalah:
𝑆𝑖= (𝑏𝑖− 𝑎𝑖)/𝑚𝑎𝑥(𝑎𝑖, 𝑏𝑖) (2-3)
Keterangan:
𝑎𝑖: Rata-rata jarak objek i terhadap
seluruh objek di dalam cluster
𝑏𝑖: Rata-rata jarak objek i terhadap
seluruh objek di luar cluster
Ukuran nilai Silhoutte Coeffisient
(Kaufman dan Rousseeuw, 2008): • 0,7 < SC <= 1 Strong structure • 0,5 < SC <= 0,7Medium structure • 0,25 < SC <= 0,5Weak structure • SC <= 0,25 No structure 3. PEMBAHASAN 3.1. Proses Clustering
Contoh perhitungan clustering dengan menggunakan metode k-means ini dilakukan terhadap 26 data lintasan. Langkah-langkah proses clustering menggunakan metode k-means dijelaskan secara rinci di bawah ini:
1. Tentukan nilai k, yaitu jumlah cluster yang akan dibentuk. Dalam contoh kali ini akan ditentukan nilai k adalah 3, sehingga akan terbentuk 3 cluster.
2. Tentukan centroid atau pusat cluster. Karena nilai k adalah 3, maka akan dipiplih titik tengah cluster sebanyak 3 titik. Titik pusat cluster ini dipilih secara acak. Nantinya nilai titik pusat cluster (centroid) akan berubah setiap selesai sekali proses
clustering. Setiap sekali proses clustering
anggota cluster yang terbentuk juga tidak akan sama dengan proses clustering sebelumnya. Karena nilai centroid awal ditentukan secara acak, maka ada kemungkinan proses clustering
membutuhkan banyak perulangan apabila nilai awal centroid terlalu jauh dari centroid yang terbentuk pada cluster terbaik. Pada perancangan ini diambil satu contoh percobaan. Dari hasil pemilihan centroid secara acak, maka diperoleh centroid untuk masing-masing cluster sebagai berikut: C1 = (41.765052, 83.34479, -777, 41.765113, 83.345118, -777, …, - 777) C2 = (34.754773, 113.650028, -777, 34.756763, 113.649385, …, -777) C3 = (41.140963, 80.29841, -777, 41.13767, 80.289385, -777, …, -777)
3. Selanjutnya hitung jarak setiap objek data terhadap setiap centroid yang terbentuk. Hasil dari perhitungan ini akan menjadi penentu data tersebut berada pada cluster yang mana. Perhitungan jarak ini dihitung menggunakan rumus Eucledian Distance seperti pada rumus 2.1. Contoh perhitungan data lintasan pertama terhadap centroid pertama adalah sebagai berikut:
d1 =
√(39.893397 − 41.765052)2+ ⋯ + (−777 − (−777))2 = 180.9247425
Contoh perhitungan data lintasan pertama dengan centroid kedua adalah sebagai berikut:
d2 =
√(39.893397 − 34.754773)2+ ⋯ + (−777 − (−777))2 = 31.12279205
Contoh perhitungan data lintasan pertama dengan centroid ketiga adalah sebagai berikut:
d3 =
√(39.893397 − 41.140963)2+ ⋯ + (−777 − (−777))2 = 198.1061559
4. Setelah mengetahui jarak setiap objek data dengan setiap centroid, pilih jarak yang paling dekat dan masukkan data tersebut ke dalam cluster yang di dalamnya terdapat
centroid dengan jarak yang paling dekat
dengan data tersebut. Contohnya pada hasil perhitungan jarak di atas, data nomor 1 memiliki jarak yang paling dekat dengan
centroid 2, maka data nomor dimasukkan
ke dalam cluster 2
5. Setelah semua data masuk ke dalam setiap
cluster, hitung rata-rata atribut pada setiap cluster untuk dijadikan centroid baru pada cluster tersebut. Perhitungan rata-rata ini
menggunakan rumus 2.2. Contoh perhitungan centroid baru adalah sebagai berikut:
Misal pada cluster 1 terdapat 10 anggota. Maka setiap atribut pada tiap-tiap data dijumlahkan kemudian dibagi sebanyak jumlah anggota.
C11 = 41.147205+43.774235+⋯+43.15195 10 = 42.2215328 C12 = 109.619872+95.457762+⋯+95.470535 10 = 88.0972963 ... C190 = −777+(−777)+⋯+(−777) 10 = -777
Pada cluster 2 terdapat 12 anggota, sehingga perhitungan atribut centroid baru: C21 = 39.893397+39.50293+⋯+39.1657 12 = 36.1647855 C22 = 116.313677+116.714948+⋯+117.20348 12 = 114.358932 ... C290 = −777+(−777)+⋯+16 10 = -566.5
Pada cluster 3 terdapat 4 anggota, maka perhitungan atribut centroid baru sebagai berikut: C31 = 41.140963+39.473332+39.471673+39.492748 4 = 39.894679 C32 = 80.29841+75.988222+75.98658+76.047162 4 = 77.0800935 ... C390 = −777+(−777)+⋯+(−777)4 = -777 Keterangan:
C11 = atribut 1 pada centroid cluster 1. C12 = atribut 2 pada centroid cluster 1. C190 = atribut 90 pada centroid cluster
1.
C21= atribut 1 pada centroid cluster 2. C22 = atribut 2 pada centroid cluster 2. C290 = atribut 90 pada centroid cluster
2.
C31 = atribut 1 pada centroid cluster 3. C32 = atribut 2 pada centroid cluster 3. C390 = atribut 90 pada centroid cluster
3.
6. Setelah mendapatkan centroid baru, ulangi langkah 3 sampai 5 hingga setiap anggota
cluster dan centroid tiap cluster tidak
berubah. Pada percobaan kali ini, proses berhenti pada perulangan ke-6.
4. PENGUJIAN DAN ANALISIS
4.1. Pengujian Kualitas Cluster
Kualitas cluster dilihat berdasarkan nilai rata-rata silhouette coefficient. Setiap percobaan
clustering menggunakan nilai k yang
berbeda-beda untuk diketahui nilai k yang paling tepat dan menghasilkan kualitas cluster yang paling baik. Data yang digunakan dalam pengujian
adalah 100 data lintasan dari 5 orang yang berbeda. Masing-masing orang diwakili 20 lintasan.
Pengujian kualitas cluster ini dilakukan sebanyak 10 kali dengan nilai k mulai dari 3 sampai 12. Hasil dari pengujian kualitas cluster ditampilkan tabel 1.
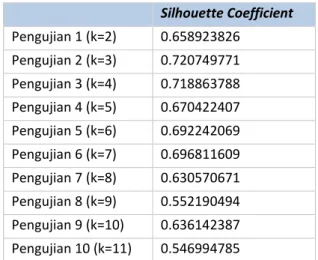
Tabel 1. Hasil Pengujian Kualitas Cluster Silhouette Coefficient Pengujian 1 (k=2) 0.658923826 Pengujian 2 (k=3) 0.720749771 Pengujian 3 (k=4) 0.718863788 Pengujian 4 (k=5) 0.670422407 Pengujian 5 (k=6) 0.692242069 Pengujian 6 (k=7) 0.696811609 Pengujian 7 (k=8) 0.630570671 Pengujian 8 (k=9) 0.552190494 Pengujian 9 (k=10) 0.636142387 Pengujian 10 (k=11) 0.546994785
4.2. Pengujian Ketepatan Cluster
Ketepatan cluster diuji dengan cara mencocokkan hasil cluster dengan data real berdasarkan moda transportasi. Moda transportasi yang ada pada data yang diuji antara lain mobil pribadi, taksi, bus, kereta, dan kereta bawah tanah. Nilai k pada pengujian ketepatan
cluster ini adalah 5 karena disesuaikan dengan
jumlah jenis moda transportasi yang ada pada data lintasan yang diuji.
Jumlah anggota cluster berdasarkan moda transportasi hasil dari pengujian ketepatan
cluster ditampilkan pada tabel 2.
Tabel 2. Hasil Pengujian Ketepatan Cluster
Moda Jumlah C l u s t e r 1 Mobil 0 Bus 0 Kereta 0
Kereta bawah tanah 20
Taksi 0 C l u Mobil 0 Bus 0 Kereta 20
s t e r 2
Kereta bawah tanah 0
Taksi 0 C l u s t e r 3 Mobil 20 Bus 20 Kereta 0
Kereta bawah tanah 0
Taksi 0 C l u s t e r 4 Mobil 0 Bus 0 Kereta 0
Kereta bawah tanah 0
Taksi 10 C l u s t e r 5 Mobil 0 Bus 0 Kereta 0
Kereta bawah tanah 0
Taksi 10
4.3. Analisis Kualitas Cluster
Pada tahap analisis kualitas cluster, tingkat kualitas cluster dilihat dari rata-rata nilai
silhouette coefficient. Nilai tersebut didapatkan
dari rata-rata jarak data terhadap data lain di luar
cluster dikurangi dengan rata-rata jarak data
terhadap data lain di dalam satu cluster. Selanjutnya hasil pengurangan tersebut dibagi dengan nilai terbesar antara kedua nilai yang telah dihitung sebelumnya.
Berdasarkan pengujian clustering yang telah dilakukan terhadap 100 data lintasan dari 5 orang yang berbeda, didapatkan nilai silhouette
coefficient yang berbeda-beda setiap k yang
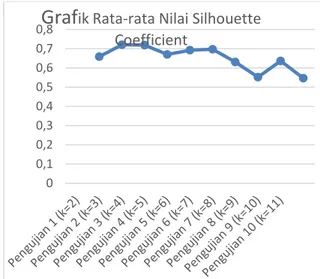
berbeda. Pada gambar 1 adalah grafik nilai rata-rata silhouette coefficient pada pengujian 1 sampai pengujian 10.
Gambar 1. Grafik Rata-rata Nilai Silhouette Coefficient pada Pengujian
Pada gambar 1 diketahui grafik rata-rata nilai silhouette coefficient pada masing-masing pengujian. Terlihat nilai tertinggi ada pada pengujian kedua dengan nilai k = 3. Pada pengujian kedua rata-rata nilai silhouette
coefficient adalah 0,720749771. Hal ini
disebabkan karena ada 3 moda transportasi yang memiliki rute hampir mirip yaitu Bus, Mobil Pribadi, dan Taksi. Sehingga memiliki nilai
silhouette coefficient yang baik jika hanya
membentuk 3 cluster saja. Sedangkan nilai terendah ada pada pengujian kesepuluh dengan nilai k = 11, yaitu 0,546994785.
Sehingga dapat disimpulkan bahwa kualitas
cluster yang dihasilkan adalah medium atau
sedang karena nilai silhouette coefficient berada di antara 0.5 – 0.7.
4.4. Analisis Ketepatan Cluster
Pada tahap analisis ketepatan cluster ini, ketepatan cluster ditentukan dari banyaknya jumlah mayoritas moda transportasi pada tiap
cluster dibanding dengan banyaknya jumlah
anggota pada cluster tersebut.
Berikut perhitungan ketepatan cluster merujuk pada data di tabel 2:
• Cluster 1: Mayoritas moda transportasi adalah Kereta bawah tanah dengan jumlah 20 dan jumlah seluruh anggota cluster
adalah 20.
Maka ketepatan cluster adalah 20
20× 100% = 100%
• Cluster 2: Mayoritas moda transportasi adalah Kereta dengan jumlah 20 dan jumlah seluruh anggota cluster adalah 20.
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7
0,8
Graf
ik Rata-rata Nilai SilhouetteMaka ketepatan cluster adalah 20
20× 100% = 100%
• Cluster 3: Mobil dan Bus sama-sama berjumlah 20 dan anggota cluster adalah 40. Maka ketepatan cluster adalah 2040× 100% = 50%
• Cluster 4: Mayoritas moda transportasi adalah Taksi dengan jumlah 10 dan jumlah seluruh anggota cluster adalah 10. Maka ketepatan cluster adalah 10
10× 100% = 100%
• Cluster 5: Mayoritas moda transportasi adalah Bus dengan jumlah 10 dan jumlah seluruh anggota cluster adalah 10. Maka ketepatan cluster adalah 1010× 100% = 100%
• Rata-rata ketepatan cluster adalah: 100% + 100% + 50% + 100% + 100%
5 = 90%
Bus dan Mobil Pribadi masuk ke dalam
cluster yang sama karena kedua moda
transportasi tersebut memiliki rute lintasan yang hampir mirip. Sedangkan Taksi terbagi ke dua
cluster yang berbeda karena tersisa 2 cluster
setelah Bus dan Mobil Pribadi masuk ke dalam satu cluster.
5. PENUTUP
Kesimpulan yang diambil dari penelititan ini adalah:
1. Metode k-means dapat diimplementasikan untuk clustering mobilitas masyarakat dengan cara menjadikan rangkaian titik koordinat yang terdiri dari latitude,
longitude, dan altitude yang mewakili satu
data lintasan menjadi atribut dalam perhitungan clustering.
2. Kualitas clustering dilihat dari nilai
silhouette coefficient masuk pada kategori
sedang sampai baik pada k yang mendekati jumlah moda transportasi. Sedangkan pada k semakin jauh dari jumlah moda transportasi, semakin buruk kualitas
cluster.
DAFTAR PUSTAKA
Han, J. dan Kamber, M., 2006. Data Mining: Concepts and Techniques, Second Edition. Morgan Kaufmann Publisher.
Irwanto, 2016. Penerapan Data Mining Untuk Mengetahui Pola Pemilihan Program Studi
Mahasiswa Baru UIN Sunan Kalijaga Menggunakan Algoritma K-means Clustering. Universitas Islam Negeri Sunan Kalijaga. Yogyakarta.
Hastuti, N.F. 2013. Pemanfaatan Metode K-means Clustering dalam Penentuan Penerima Beasiswa. Universitas Sebelas Maret. Surakarta.
Zheng, Y., 2007. GeoLife: Building Social Networks Using Human Location History.
https://www.microsoft.com/en- us/research/project/geolife-building-social-networks-using-human-location-history/ Andayani, S. 2007. Pembentukan Cluster dalam
Knowledge Discovery in Database dengan Algoritma KMeans. Seminar Nasional Matematika dan Pendidikan Matematika 2007. Universitas Negeri Yogyakarta. Yogyakarta.
Santosa, B. 2007. Data Mining Teknik Pemanfaatan Data untuk Keperluan Bisnis. Graha Ilmu. Yogyakarta.
Agusta, Y. 2007. K-Means-Penerapan, Permasalahan dan Metode Terkait. Jurnal Sistem dan Informatika Vol.3, 47-60. Nuningsih, S. 2010. K-Means Clustering: Studi
Kasus pada Data Pengujian Kualitas Susu di Koperasi Peternakan Bandung Selatan. Jurusan Matematika FMIPA, Universitas Pendidikan Indonesia. Bandung.
Kaufman, L. dan Rousseeuw, P.J., 2008. Finding Groups in Data: An Introduction to Cluster Analysis. John Wiley & Sons, Inc.