Peramalan banyaknya penabung di Credit Union Sumber Kasih Teraju dengan metode Box-Jenkins

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PERAMALAN BANYAKNYA PENABUNG DI CREDIT UNION SUMBER KASIH TERAJU DENGAN METODE BOX-JENKINS. Tugas Akhir Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika. Oleh: Vinsensia Laura K. NIM: 153114019. PROGRAM STUDI MATEMATIKA, JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2019. i.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. FORECASTING THE NUMBER OF SAVERS IN CREDIT UNION SUMBER KASIH TERAJU WITH THE BOX-JENKINS METHOD. Thesis Presented as a Partial Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains in Mathematics. By: Vinsensia Laura K. NIM: 153114019. MATHEMATICS STUDY PROGRAM, DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY YOGYAKARTA 2019. ii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. iii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. iv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. PERNYATAAN KEASLIAN KARYA Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaimana layaknya karya ilmiah.. Yogyakarta, 19 Juli 2019 Penulis,. Vinsensia Laura K.. v.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama. : Vinsensia Laura K.. Nomor Mahasiswa. : 153114019. Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul: PERAMALAN BANYAKNYA PENABUNG DI CREDIT UNION SUMBER KASIH TERAJU DENGAN METODE BOX-JENKINS beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta izin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis. Demikian pernyataan ini saya buat dengan sebenarnya.. Dibuat di Yogyakarta Pada tanggal: 19 Juli 2019. Yang menyatakan. Vinsensia Laura K.. vi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. MOTTO Tak perlu takut apabila tak ada satu orangpun yang mau melindungi bahkan berteman pun tidak, karena ada Tuhan Yesus yang selalu ada dimanapun kamu berada.. vii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. HALAMAN PERSEMBAHAN Karya ini kupersembahkan untuk: Kemuliaan Tuhan, kedua orangtua dan keluargaku, serta almamaterku.. viii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRAK Pada saat ini kesadaran masyarakat tentang pentingnya menabung semakin membaik, sehingga banyak sekali masyarakat yang telah menabung. Semakin banyak minat masyarakat menabung, semakin banyak juga perusahaan yang berorientasi keuangan didirikan, contohnya ialah Credit Union (CU) dan Bank. Semakin banyaknya CU dan Bank, semakin ketat juga persaingannya. Oleh karena itu diperlukan metode peramalan untuk menduga perkembangan perusahaan tersebut. Salah satu metode yang digunakan untuk peramalan adalah metode BoxJenkins dengan menggunakan model Autoregressive Integrated Moving Average (ARIMA). Metode ini diterapkan untuk peramalan data penabung Pengari di CU Sumber Kasih Teraju berdasarkan data yang diambil dari bulan Januari 2012 sampai dengan bulan Agustus 2018. Berdasarkan hasil peramalan dengan metode Box-Jenkins, diperoleh kesimpulan bahwa jumlah penabung pada buku tabungan Pengari untuk 8 bulan ke depan cenderung tetap atau tidak mengalami kenaikan dan penurunan. Sehingga dapat dikatakan bahwa jumlah penabung dari tabungan Pengari tidak ada pertumbuhan baru. Kata Kunci: peramalan, CU Sumber Kasih, ARIMA.. ix.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRACT At present, public awareness about the importance of saving is getting better, therefore many people have saved money. The more public interest in saving, the more finance companies are set up, for example are Credit Union (CU) and Banks. The increasing number of Cus and Banks, the tighter the competition. Therefore a forecasting method is needed to predict the development of the company. One method used for forecasting is the Box-Jenkins method using the Autoregressive Integrated Moving Average (ARIMA) model. This method is applied to Pengari savers in taken from January 2012 to August 2018. Based on the result of the Box-Jenkins forecasting method, the conclusion is that the number of savers in the passbook for te next 8 months remain unchange. So that it can be concluded that the number of Pengari savers has no new growth.. Keywords: forecasting, CU Sumber Kasih, ARIMA.. x.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. KATA PENGANTAR Ucapan puji syukur kepada Tuhan Yesus dan Bunda Maria tercinta yang dengan murah hati mencurahkan segala kebaikan-Nya melalui orang-orang sekitar dan dari setiap peristiwa yang penulis alami sehingga skripsi ini dapat selesai tepat waktu. Skripsi ini dibuat dengan tujuan memenuhi syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Fakultas Sains dan Teknologi, Univesitas Sanata Dharma. Penulis menyadari bahwa penulis melibatkan banyak pihak yang bersedia membantu dalam menghadapi berbagai macam kesulitan, tantangan dan hambatan. Oleh karena itu pada kesempatan ini penulis mengucapkan terima kasih kepada: 1. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing skripsi yang telah sabar membimbing saya selama saya mengerjakan skripsi. 2. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku Dekan Fakultas Sains dan Teknologi dan selaku Dosen Pembimbing Akademik. 3. Bapak YG. Hartono, S.Si., M.Sc., Ph.D., selaku Kaprodi Matematika. 4. Romo Prof. Dr. Frans Susilo, SJ., Bapak Dr. rer. nat. Herry P. Suryawan, S.Si., M.Si., Bapak Ricky Aditya M.Sc., dan Ibu M. V. Any Herawati, S.Si., M.Si., selaku dosen-dosen Prodi Matematika yang telah memberikan banyak pengetahuan kepada penulis selama proses perkuliahan. 5. Bapak/Ibu dosen/karyawan Fakultas Sains dan Teknologi yang telah berdinamika bersama selama penulis berkuliah. 6. Kedua orang tua, Louis dan keluarga yang telah membantu serta mendukung penulis selama proses pengerjaan skripsi. 7. Teman-teman Prodi Matematika Angkatan 2015 dan teman-teman baik yang mendukung penulis dalam mengerjakan skripsi: Yion, Sasmi, Edi, Watik, Devi, Brigit, Sarah, Acan, Nando, Nerry dan teman-teman statistika lovers. 8. Semua pihak yang tidak dapat disebutkan satu per satu dalam proses penulisan skripsi ini. Semoga segala perhatian, dukungan, bantuan dan cinta yang telah diberikan mendapatkan balasan dari Tuhan Yesus Kristus. Penulis menyadari bahwa masih xi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. banyak kekurangan dalam penulisan skripsi ini. Oleh karena itu, penulis mengharapkan kritik yang membangun dan saran demi penyempurnaan skripsi ini. Harapan penulis, semoga skripsi ini bermanfaat bagi pembaca dan menjadi referensi belajar yang baik.. Yogyakarta, 19 Juli 2019 Penulis,. Vinsensia Laura K.. xii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR ISI. HALAMAN JUDUL................................................................................................ i HALAMAN PERSETUJUAN PEMBIMBING .................................................... iii HALAMAN PENGESAHAN ................................................................................ iv LEMBAR PERNYATAAN KEASLIAN KARYA .................................................v LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI................................. vi MOTTO ................................................................................................................ vii HALAMAN PERSEMBAHAN .......................................................................... viii ABSTRAK ............................................................................................................. ix ABSTRACT .............................................................................................................x KATA PENGANTAR ........................................................................................... xi DAFTAR ISI ........................................................................................................ xiii BAB I PENDAHULUAN ........................................................................................1 A. Latar Belakang ........................................................................................................ 1 B. Rumusan Masalah ................................................................................................... 4 C. Batasan Masalah ..................................................................................................... 4 D. Tujuan Penulisan ..................................................................................................... 4 E. Manfaat Penulisan ................................................................................................... 5 F. Metode Penulisan .................................................................................................... 5 G. Sistematika Penulisan ............................................................................................. 5. BAB II ANALISIS RUNTUN WAKTU DAN METODE BOX-JENKINS ...........7 A. Peramalan Data Runtun Waktu ............................................................................... 7 B. Analisis Runtun Waktu ........................................................................................... 8 C. Nilai Harapan, Variansi dan Kovarian Variabel Random ..................................... 11 D. Kestasioneran ........................................................................................................ 12 E. Transformasi Box-Cox dan Pembedaan (Differencing) ........................................ 15 F. Fungsi Autokovarian, Fungsi Autokorelasi (ACF) dan Fungsi Autokorelasi Parsial (PACF) ................................................................................................................. 21 G. Proses White Noise ............................................................................................... 37 H. Model ARMA ....................................................................................................... 42 I.. Model ARIMA ...................................................................................................... 51 xiii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. J.. Sifat-sifat Model ARIMA Berdasarkan ACF dan PACF ...................................... 54. K. Estimasi Model AR, MA, dan ARMA.................................................................. 58. BAB III METODE BOX-JENKINS ......................................................................68 A. Pendahuluan .......................................................................................................... 68 B. Identifikasi Model ................................................................................................. 69 C. Estimasi Model ..................................................................................................... 70 D. Pemeriksaan Diagnostik........................................................................................ 71 E. Memilih Model yang Terbaik ............................................................................... 74 F. Peramalan.............................................................................................................. 74. BAB IV PERAMALAN DATA PENABUNG DATA PENABUNG CU SUMBER KASIH TERAJU ..................................................................................82 A. CU Sumber Kasih Teraju ...................................................................................... 82 B. Penerapan Metode Box-Jenkins untuk Peramalan Penabung Pengari .................. 83. BAB V PENUTUP .................................................................................................95 A. Kesimpulan ........................................................................................................... 95 B. Saran ..................................................................................................................... 95. DAFTAR PUSTAKA ............................................................................................96 LAMPIRAN ...........................................................................................................98. xiv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB I PENDAHULUAN. A. Latar Belakang Pada saat ini kesadaran masyarakat tentang pentingnya menabung semakin membaik, sehingga banyak sekali masyarakat yang telah menabung. Semakin banyak minat masyarakat untuk menabung, semakin banyak juga perusahaan yang didirikan untuk menabung, contohnya ialah Credit Union (CU) dan Bank. Credit Union atau biasa disingkat CU adalah sebuah lembaga keuangan yang bergerak di bidang simpan pinjam yang dimiliki dan dikelola oleh anggotanya dan yang bertujuan untuk mensejahterakan anggotanya sendiri. Bank adalah sebuah lembaga intermediasi keuangan yang bertugas menghimpun dan menyalurkan dana di masyarakat untuk meningkatkan taraf hidup rakyat. CU dan Bank merupakan perusahaan yang didirikan untuk menabung, namun antara CU dan Bank ada perbedaan, yaitu CU membangun komunitas, aset utama CU adalah manusia, anggota adalah pemilik, keuntungan kembali ke anggota, peduli akan masa depan keuangan anggota, dan tabungan yang dimobilisasi dari anggota kemudian diinvestasikan kembali kepada anggota, sedangkan Bank membangun sektor keuangan, aset utama Bank adalah uang, nasabah hanya pengguna, keuntungan kembali kepada investor, mengutamakan keuntungan yang sebesar-besarnya bagi investor, dan tabungan yang dimobilisasikan dari masyarakat kemudian diinvestasikan ke perusahaan besar serta pasar keuangan. Semakin banyaknya CU dan Bank, semakin ketat juga persaingannya. Oleh karena itu diperlukan metode peramalan untuk menduga perkembangan perusahaan tersebut. Dengan demikian dalam tugas akhir ini, akan diramalkan banyaknya penabung di CU Sumber Kasih Teraju dengan metode Box-Jenkins. CU Sumber Kasih Teraju memiliki 8 macam tabungan, yaitu Tabungan Saham, Tabungan Tembawang, Tabungan Sempurai, Tabungan Pengari, Tabungan Tronong, Tabungan Tanggor, Tabungan Hari Raya, dan Tabungan 1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 2. Kendaraan. Tabungan Saham adalah tabungan yang membuktikan anggota sebagai pemilik yang sah, yang terdiri dari tabungan pokok dan tabungan wajib. Tabungan Tembawang adalah tabungan unggulan CU Sumber Kasih yang memberikan bunga 15 % per tahun, sehingga dalam jangka waktu 5 tahun tabungan tembawang tersebut akan menjadi 2 kali lipat dari saldo awalnya. Tabungan Sempurai adalah produk tabungan masa depan. Tabungan Pengari adalah tabungan yang digunakan untuk kebutuhan makan dan minum seharihari anggota. Tabungan Tronong adalah tabungan untuk biaya pendidikan. Tabungan Tanggor adalah tabungan untuk biaya pendidikan dalam jangka panjang. Tabungan Hari Raya adalah tabungan yang digunakan untuk kebutuhan anggota pada saat merayakan hari raya. Tabungan Kendaraan adalah produk tabungan perencanaan anggota untuk memiliki kendaraan. Peramalan (forecasting) adalah suatu teknik untuk menduga kejadian di masa depan dengan menggunakan referensi data di masa lalu. Data diambil dari data penabung Pengari. Jadi dalam peramalan ini akan diperoleh model matematika. Jika hasil peramalan menunjukkan peminat yang menabung di Tabungan Pengari tersebut hanya sedikit, maka akan dicari solusi dengan cara memperbaiki kebijakan tabungan tersebut atau dengan cara menciptakan terobosan baru untuk buku tabungan CU Sumber Kasih Teraju. Dengan demikian masyarakat akan lebih tertarik untuk menabung di CU Sumber Kasih Teraju dan sekaligus memberi masukan kepada CU Sumber Kasih Teraju untuk evaluasi kinerja. Metode yang digunakan dalam peramalan ini ialah metode Box-Jenkins. Adapun tahapannya adalah identifikasi model, estimasi model, pemeriksaan diagnosa, dan penerapan model untuk peramalan. Runtun waktu adalah himpunan observasi terurut dalam waktu (Wei 2005). Salah satu model yang dapat digunakan untuk peramalan (forecasting) data runtun waktu adalah model Autoregressive Integrated Moving Average (ARIMA). Model Autoregressive Integrated Moving Average (ARIMA) merupakan model Autoregressive Moving Average (ARMA) nonstasioner yang telah diubah (differencing) menjadi model stasioner, sehingga tidak terdapat pertumbuhan atau penurunan pada data (data harus horizontal.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 3. sepanjang sumbu waktu). Dengan kata lain fluktuasi data berada di sekitar suatu nilai rata-rata yang konstan. Model Autoregressive atau AR adalah suatu model yang menjelaskan pergerakan suatu variabel melalui variabel itu sendiri di masa lalu dan dapat ditulis sebagai berikut: Yt    1Yt 1  2Yt 2  ...   pYt  p  et. Model Moving Average atau MA adalah suatu model yang menyatakan pergerakan variabelnya melalui residualnya di masa lalu dan dapat ditulis sebagai berikut: Yt    et  1et 1   2 et 2  ...   q et q. dengan. Yt : variabel dependen pada waktu t,. . : konstanta,. et : nilai residual pada saat t,. j. : parameter autoregressive ke- j , j  1,2,..., p,. j. : parameter moving average ke- j , j  1,2,..., q,. et  k : nilai residual pada saat t  k , k  1,2,..., q. Model Autoregressive Moving Average (ARMA) adalah gabungan antara model Autoregressive atau AR dan model Moving Average atau MA, dan dapat ditulis sebagai berikut: Yt    1Yt 1  2Yt 2  ...   pYt  p  et  1et 1   2et 2  ...   q et q .. Model ARIMA akan diterapkan untuk meramalkan jumlah penabung Pengari di CU Sumber Kasih Teraju dengan menggunakan data dari bulan Januari 2012 sampai dengan bulan Agustus 2018..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 4. B. Rumusan Masalah Berdasarkan latar belakang tersebut, secara garis besar uraian rumusan masalah yang dibahas dalam tugas akhir ini adalah: 1. Bagaimana dasar-dasar teori model ARIMA? 2. Bagaimana model matematika data penabung Pengari di CU Sumber Kasih Teraju? 3. Bagaimana hasil peramalan 8 bulan ke depan untuk data penabung pengari di CU Sumber Kasih Teraju?. C. Batasan Masalah Metode Box-Jenkins yang dibahas dalam tugas akhir ini adalah: 1. Meramalkan data penabung Pengari di CU Sumber Kasih Teraju dengan model Autoregressive Integrated Moving Average (ARIMA). 2. Dasar teori yang digunakan adalah yang berkaitan langsung dengan topik utama analisis runtun waktu, yaitu konsep, nilai harapan, dan kovarians sedangkan teori probabilitas tidak dibahas. 3. Domain waktu yang digunakan adalah diskrit.. D. Tujuan Penulisan Tujuan yang ingin dicapai penulis dalam penulisan tugas akhir ini adalah: 1. Untuk mengetahui dasar-dasar teori model ARIMA. 2. Untuk mengetahui model matematika data penabung Pengari di CU Sumber Kasih Teraju. 3. Untuk mengetahui hasil peramalan 8 bulan ke depan untuk data penabung Pengari di CU Sumber Kasih Teraju..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 5. E. Manfaat Penulisan Manfaat penulisan dari tugas akhir ini adalah sebagai berikut: 1. Memperluas wawasan penulis mengenai peramalan dengan menggunakan metode Box-Jenkins. 2. Menambah. pengetahuan. pembaca. tentang. peramalan. dengan. menggunakan metode Box-Jenkins. 3. Hasil peramalan data penabung CU Sumber Kasih Teraju dalam 8 bulan ke depan dapat digunakan sebagai masukan kepada CU Sumber Kasih Teraju untuk evaluasi kinerja.. F. Metode Penulisan Metode penulisan yang digunakan dalam tugas akhir ini yaitu studi pustaka dengan membaca buku, jurnal-jurnal, makalah ilmiah yang berhubungan dengan metode Box-Jenkins dan menggunakan program R.. G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan BAB II METODE BOX-JENKINS A. Peramalan B. Analisi Runtun Waktu C. Nilai Harapan, Variansi dan Kovariansi Variabel Random D. Kestasioneran.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 6. E. Pembedaan dan Transformasi Box-Cox F. Fungsi Autokovarian, ACF dan PACF G. Model White Noise H. Model ARMA I. Model ARIMA Nonmusiman dan Musiman J. Sifat-sifat Model ARIMA Berdasarkan ACF dan PACF K. Estimasi Model AR, MA, dan ARMA BAB III METODE BOX-JENKINS A. Pendahuluan B. Identifikasi Model C. Estimasi Model D. Pemeriksaan Diagnostik E. Peramalan dengan Model ARIMA BAB IV PERAMALAN DATA PENABUNG CU SUMBER KASIH TERAJU A. CU Sumber Kasih Teraju B. Penerapan Metode Box-Jenkins untuk Peramalan Penabung Pengari BAB V PENUTUP A. Kesimpulan B. Saran LAMPIRAN DAFTAR PUSTAKA.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB II ANALISIS RUNTUN WAKTU DAN METODE BOX JENKINS. A. Peramalan Data Runtun Waktu Peramalan (forecasting) adalah suatu teknik untuk menduga data di masa depan dengan menggunakan referensi data di masa lalu. peramalan merupakan alat bantu yang penting dalam perencanaan yang efektif dan efisien (Makridakis, dkk. 1999). Berdasakan sifat penyusunannya, peramalan dapat dibedakan menjadi dua macam yaitu: 1. Peramalan subjektif Peramalan subjektif adalah peramalan yang didasarkan atas perasaan atau intuisi dari orang yang menyusunnya. 2. Peramalan objektif Peramalan objektif adalah peramalan yang didasarkan atas data yang relevan pada masa lalu, dengan menggunakan teknik-teknik dan metodemetode dalam penganalisaan data tersebut.. Berdasarkan jangka waktunya, peramalan juga dapat dibagi menjadi dua macam yaitu: 1. Peramalan jangka panjang Peramalan jangka panjang adalah peramalan yang dilakukan untuk menyusun hasil ramalan yang jangka waktunya lebih dari satu setengah tahun. 2. Peramalan jangka pendek.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 8. Peramalan jangka pendek adalah peramalan yang digunakan untuk penyusunan hasil ramalan yang jangka waktunya kurang dari satu setengah tahun. Langkah dalam metode peramalan secara umum adalah pengumpulan data, menyeleksi dan memilih data, memilih model peramalan, menerapkan model untuk peramalan, dan evaluasi hasil akhir.. B. Analisis Runtun Waktu Runtun waktu adalah himpunan observasi terurut dalam waktu (Wei 2005). Analisis runtun waktu merupakan salah satu prosedur statistika yang diterapkan untuk menduga struktur probabilitas keadaan yang akan datang dalam rangka pengambilan keputusan. Dasar pemikiran runtun waktu adalah pengamatan sekarang ( Z t ) dipengaruhi oleh satu atau beberapa pengamatan sebelumnya ( Z t k ) . Dengan kata lain, model runtun waktu dibuat karena secara statistik ada korelasi antar deret pengamatan. Tujuan analisis runtun waktu antara lain memahami dan menjelaskan mekanisme tertentu, meramalkan suatu nilai di masa depan, dan mengoptimalkan sistem kendali. Langkah penting dalam memilih suatu metode runtun waktu (time series) yang tepat adalah dengan mempertimbangkan jenis pola data, sehingga metode yang paling tepat dengan pola tersebut dapat diuji. Pola data dapat dibedakan menjadi empat jenis siklis dan trend (Makridakis, dkk, 1999). 1. Pola horizontal (H) terjadi apabila nilai data berfluktuasi di sekitar nilai rata-rata yang konstan. (Deret seperti itu adalah “stasioner” terhadap nilai rata-ratanya). Suatu produk yang penjualannya tidak meningkat atau menurun selama waktu tertentu termasuk jenis ini. Demikian pula, suatu keadaan pengendalian kualitas yang menyangkut pengambilan contoh dari suatu proses produksi kontinyu yang secara teoritis tidak mengalami perubahan juga termasuk jenis ini..

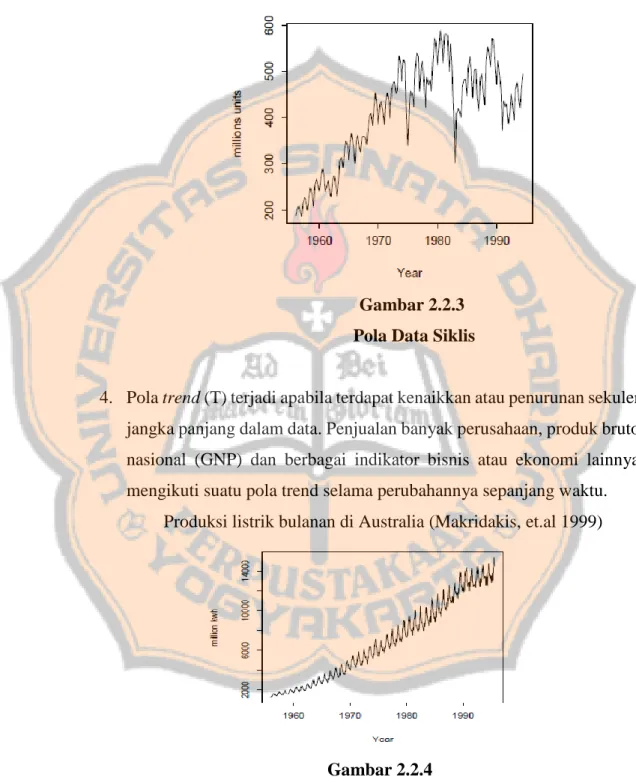
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 9. Penjualan perumahan (Makridakis, et.al 1999). Gambar 2.2.1 Pola Data Horizontal. 2. Pola musiman (S) terjadi apabila suatu deret dipengaruhi oleh faktor musiman (misalnya kuartal tahun tertentu, bulanan, atau hari-hari pada minggu tertentu). Penjualan dari produk seperti minuman ringan, es krim, dan bahan bakar pemanas ruang, semuanya menunjukkan jenis pola ini. Produksi susu per ekor setiap bulan (Makridakis, et.al 1999). Gambar 2.2.2 Pola Data Musiman. 3. Pola siklis (C) terjadi apabila datanya dipengaruhi oleh fluktuasi ekonomi jangka panjang seperti yang berhubungan dengan siklus bisnis..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 10. Penjualan produk seperti mobil, baja, dan peralatan utama lainnya menunjukkan jenis pola ini. Produksi batu bata tanah liat Australia (Makridakis, et.al 1999). Gambar 2.2.3 Pola Data Siklis. 4. Pola trend (T) terjadi apabila terdapat kenaikkan atau penurunan sekuler jangka panjang dalam data. Penjualan banyak perusahaan, produk bruto nasional (GNP) dan berbagai indikator bisnis atau ekonomi lainnya mengikuti suatu pola trend selama perubahannya sepanjang waktu. Produksi listrik bulanan di Australia (Makridakis, et.al 1999). Gambar 2.2.4 Pola Data Trend.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 11. C. Nilai Harapan, Variansi dan Kovarian Variabel Random Berikut akan didefinisikan beberapa konsep yang digunakan dalam analisis runtun waktu. Definisi 2.3.1 Nilai Harapan Misalkan Y variabel acak diskrit dengan fungsi probabilitas p ( y ). Maka nilai harapan dari Y , E (Y ) didefinisikan sebagai E (Y )   yp( y). y. Sedangkan nilai harapan dari variabel acak kontinu Y adalah . E (Y ) .  yf ( y)dy.. . Fungsi ini menyatakan nilai rata-rata dari proses Y pada keseluruhan data runtun waktu.. Definisi 2.32 Variansi Sampel Variansi dari pengukuran sampel y1 , y2 ,..., yn adalah jumlah kuadrat dari perbedaan antara pengukuran dan rata-ratanya, dibagi dengan n  1. Secara simbolis, sampel varians adalah s2 . 1 n ( yt  y) 2 ,  n  1 i 1. i=1,2,...,n. dengan. s 2 = variansi sampel. n = ukuran sampel yt = nilai y ke-i y = rata-rata.. Populasi varians yang sesuai dilambangkan dengan simbol  2 ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 12. Definisi 2.33 Fungsi Kovariansi Jika Yt dan Ys variabel random dengan rata-rata t dan  s , masing-masing kovarian dari Yt dan Ys adalah.  (t , s)  cov(Yt , Ys )  E[(Yt  t )(Ys  s )],. t, s = 1,2,...,n. dengan.  (t , s) = fungsi kovariansi antara data pengamatan Yt dan Ys Yt. = data runtun waktu ke-t. Ys. = data runtun waktu ke-s. t. = rata-rata dari data runtun waktu Yt. s. = rata-rata dari data runtun waktu Ys .. Fungsi kovariansi menyatakan ukuran hubungan antar beberapa data runtun waktu.. D. Kestasioneran Sifat stasioner adalah tidak terdapat pertumbuhan atau penurunan pada data (data horizontal sepanjang sumbu waktu). Dengan kata lain fluktuasi data berada di sekitar suatu nilai rata-rata yang konstan. Sedangkan data yang tidak stasioner adalah sebaliknya. Data runtun waktu stasioner memiliki rata-rata dan variansi yang konstan terhadap waktu. Ada 3 kemungkinan suatu data dikatakan tidak stasioner, yaitu tidak stasioner dalam variansi, tidak stasioner dalam rata-rata, dan tidak stasioner dalam variansi dan rata-rata (Makridakis, et.al, 1999). Untuk melihat data apakah stasioner atau tidak dapat dilihat dari grafik asli dari data atau lebih jelasnya lagi dengan melihat grafik fungsi autokorelasi (ACF) dan grafik fungsi autokorelasi parsial (PACF) yang konsepnya akan dibahas kemudian. Selain itu, stasioner dapat ditentukan berdasarkan pola data runtun waktu yang dapat dilihat dari plot grafiknya. Secara visual, stasioneritas dan tidak stasioner dari data runtun waktu dapat dibagi menjadi 3, yaitu:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 13. 1. Kestasioneran dalam Variansi Stasioner dalam variansi adalah kondisi di mana data deret waktu tidak memperlihatkan adanya perubahan variansi dari waktu ke waktu. Jika data tidak stasioner dalam variansi, maka data dapat diubah menjadi data yang stasioner dengan cara transformasi Box-Cox. Berikut ini adalah ilustrasi dari runtun waktu tidak stasioner dalam variansi (Makridakis, et.al 1999).. Gambar 2.4.1 Runtun Waktu Tidak Stasioner dalam Variansi. Dari gambar 2.4.1 terlihat bahwa data tidak stasioner dalam variansi yang artinya data perlu dilakukan transformasi Box-Cox pada data.. 2. Kestasioneran dalam Rata-rata Stasioner dalam rata-rata adalah kondisi di mana tidak ada perubahan rata-rata yang jelas dari waktu ke waktu. Jika data tidak stasioner dalam rata-rata, maka data diubah menjadi data yang stasioner dengan cara differencing data (mengurangi data di masa lalu). Berikut ini adalah ilustrasi dari grafik runtun waktu stasioner dalam rata-rata dan tidak stasioner dalam rata-rata (Shumway, et.al 2005)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 14. Gambar 2.4.2 Runtun Waktu Stasioner dalam Rata-rata. Gambar 2.4.3 Runtun Waktu Tidak Stasioner dalam Rata-rata. Dari gambar 2.4.2 terlihat bahwa data stasioner dalam rata-rata yang artinya data tidak perlu dilakukan differencing data (mengurangi data di masa lalu). Sedangkan gambar 2.4.3 terlihat bahwa data tidak stasioner dalam rata-rata sehingga diperlukan tindakan. differencing. data. (mengurangi data waktu kini dengan data di masa lalu).. 3. Kestasioneran dalam variansi dan Rata-rata Runtun waktu dikatakan stasioner dalam variansi dan rata-rata adalah kondisi di mana deret waktu tidak memperlihatkan adanya.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 15. perubahan variansi dari waktu ke waktu dan tidak ada perubahan rata-rata. Untuk membuat data stastioner pada data yang tidak stasioner dalam variansi dan rata-rata, dapat dilakukan dengan transformasi data dan differencing (pembedaan) data. Berikut ini adalah ilustrasi dari runtun waktu tidak stasioner dalam rata-rata dan variansi (Makridakis, et.al 1999).. Gambar 2.3.4 Runtun Waktu Tidak Stasioner dalam Variansi dan Rata-rata. Penentuan stasioner ini sangatlah penting. Hal ini berkaitan dengan metode identifikasi model yang digunakan. Seperti yang akan dijelaskan pada bab 3 bahwa jenis data harus stasioner.. E. Transformasi Box-Cox dan Pembedaan (Differencing) Proses transformasi Box-Cox dan proses pembedaan adalah proses untuk mentransformasikan data yang tidak stasioner menjadi data yang stasioner. Berikut ini adalah penjelasan mengenai transformasi Box-Cox dan pembedaan.. 1. Transformasi Box-Cox Transformasi Box-Cox adalah transformasi pangkat pada variabel respon. Box-Cox mempertimbangkan kelas transformasi berparameter tunggal, yaitu  yang dipangkatkan pada variabel respon Y, sehingga transformasinya menjadi Y  ,  adalah parameter yang perlu diduga.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 16. untuk menstasionerkan data. Tabel dibawah adalah beberapa nilai  dengan transformasinya . Transformasi Box-Cox berdasarkan nilai λ ditunjukkan pada Tabel 2.4.1. (Wei 2005).. Tabel 2.4.1 Transformasi Box-Cox. . Bentuk Transformasi. -1. 1 Y. -0,5. 1 Y. 0. ln(Y ) / log(Y ). 0,5. Y. 1. Y. Berikut ini adalah persamaan transformasi Box-Cox..  Yt   1  ,  0 Yt    ln Yt / log(Yt ) ,   0. Contoh 2.4.1 Selidiki apakah data pengiriman bulanan peralatan anti polusi (Makridakis, et.al 1999) stasioner atau tidak. Apabila data tidak stasioner transformasilah data agar model menjadi stasioner. Data pengiriman bulanan peralatan anti polusi terdapat pada lampiran 1. Penyelesaian:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 17. Untuk mengetahui data stasioner atau tidak, penulis melihat grafik data curah hujan dengan menggunakan program R. > plot.ts(data,lag.max=130). Gambar 2.4.1.1 Plot Grafik Data Pengiriman Bulanan Peralatan Anti Polusi. Terlihat dari grafik di atas, bahwa data tidak stasioner dalam variansi dan rata-rata, sehingga perlu dilakukan transformasi Box-Cox data dan differencing data. Di sini penulis melakukan transformasi data menggunakan program R. Dipilih nilai   0. > Yt<-log(data) > plot.ts(Yt,lag.max=130).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 18. Gambar 2.4.1.2 Plot Grafik Data Pengiriman Bulanan Peralatan Anti Polusi Setelah Transformasi Terlihat dari grafik di atas, bahwa data sudah stasioner dalam variansi namun tidak stasioner dalam rata-rata. Agar data menjadi stasioner, langkah selanjutnya adalah menstasionerkan rata-rata dengan cara differencing data yang akan dibahas pada subbab selanjutnya.. 2. Pembedaan (Differencing) Notasi yang sangat bermanfaat adalah operator shift mundur (backward shift) atau ditulis dengan B, yang penggunaannya adalah sebagai berikut:. ( B)Yt  Yt 1 . Dengan kata lain, notasi B yang dipasang pada Yt , mempunyai pengaruh menggeser data 1 periode ke belakang. Dua penerapan B untuk shift Yt akan menggeser data tersebut 2 periode ke belakang, sebagai berikut:. B( BYt )  B 2Yt  Yt 2 . Untuk data bulanan, jika ingin mengalihkan perhatian ke keadaan pada bulan yang sama pada tahun sebelumnya, maka digunakan B12 dan notasinya adalah B12Yt  Yt 12 ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 19. Operator shift mundur tersebut sangat tepat untuk menggambarkan proses pembedaan (differencing). Sebagai contoh, apabila suatu runtun waktu tidak stasioner, maka data tersebut dapat dibuat lebih mendekati stasioner dengan melakukan pembedaan pertama dari deret data. Pembedaan (differencing) pertama. Yt '  Yt  Yt 1 . Menggunakan operator shift mundur, persamaan di atas dapat ditulis menjadi sebagai berikut:. Yt '  Yt  BYt  (1  B)Yt . Perhatikan bahwa pembedaan (differencing) pertama dinyatakan oleh (1  B) . Sama halnya jika perbedaan orde kedua (yaitu perbedaan pertama. dari perbedaan pertama sebelumnya) harus dihitung, maka: Pembedaan (difference) orde kedua. Yt"  Yt '  Yt ' 1.  (Yt  Yt 1 )  (Yt 1  Yt 2 )  Yt  2Yt 1  Yt 2  (1  2B  B 2 )Yt  (1  B) 2 Yt . Perhatikan bahwa pembedaan orde kedua diberi notasi (1  B) 2 . Ini merupakan hal yang penting untuk memperlihatkan bahwa pembedaan orde kedua tidak sama dengan pembedaan kedua, yang diberi notasi 1  B 2 . Demikian pula, pembedaan duabelas adalah 1  B12 , akan tetapi. pembedaan orde ke-12 adalah (1  B)12 . Tujuan menghitung pembedaan adalah untuk mecapai stasioneritas, dan secara umum, pembedaan orde ke-d dapat ditulis sebagai berikut:. (1  B) d Yt . Pembedaan musiman diikuti dari pembedaan pertama dapat ditulis sebagai berikut:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 20. (1  B)(1  B s )Yt . Seluruh faktor dapat dikalikan menjadi sebagai berikut:. (1  B)(1  B s )Yt  (1  B s  B  B s1 )Yt.  Yt  B sYt  BYt  B s1Yt.  Yt  Yt s  Yt 1  Yt s1 untuk data bulanan, s = 12.. Contoh 2.4.2. Berdasarkan contoh 2.4.1 data tidak stasioner dalam variansi dan rata-rata. Berikut adalah cara menstasionerkan rata-rata dengan cara differencing data dengan menggunakan program R. Penyelesaian: Data yang digunakan untuk differencing data adalah data yang sudah ditransformasi. > yt_diff<-diff(Y,n=1). Gambar 2.4.2.1 Plot Grafik Data Pengiriman Bulanan Peralatan Anti Polusi Setelah Differencing data.

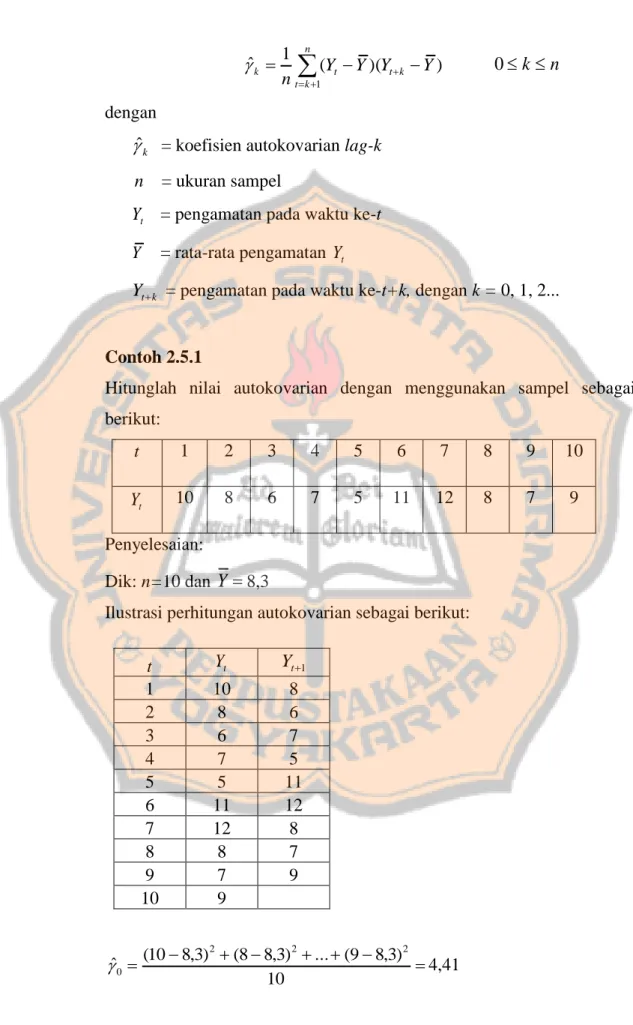
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 21. Grafik di atas sudah menunjukkan bahwa data stasioner dalam variansi dan rata-rata.. F. Fungsi Autokovarian, Fungsi Autokorelasi (ACF) dan Fungsi Autokorelasi Parsial (PACF) Pada subbab ini, akan dibahas beberapa fungsi yang berkaitan langsung dengan analisis data runtun waktu model ARIMA yang akan akan dibahas kemudian. Fungsi-fungsi tersebut adalah fungsi autokovarian, fungsi autokorelasi (ACF) dan fungsi autokorelasi parsial (PACF). Salah satu kegunaan ACF dan PACF adalah untuk mendeteksi apakah suatu data runtun waktu stasioner atau tidak. ACF dan PACF menyediakan informasi yang lebih eksak melalui pengujian signifikansi dari pada penggunaan grafik yang interpretasinya sangat tergantung pada pengamatan visual.. 1. Fungsi Autokovariansi Autokovariansi menunjukkan bagaimana elemen-elemen dari suatu runtun waktu saling bergantung satu dengan yang lainnya. Definisi 2.5.11 Fungsi autokovariansi  t ,s didefinisikan sebagai.  k  cov(Yt , Yt k ),. untuk t,k = 0,  1,  2,.... dengan. cov(Yt , Yt k )  E[(Yt   )(Yt k   )]  E (Yt , Yt k )   2 dengan.  k = autokovariansi pada lag-k Yt. = nilai variable Y pada waktu t. Yt  k = nilai variabel Y pada waktu t+k. . = rata-rata.. Estimator untuk koefisien autokovariansi  k dapat didefinisikan sebagai.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 22. 1 n  (Yt  Y )(Yt k  Y ) n t k 1. ˆk . 0k n. dengan. ˆk = koefisien autokovarian lag-k n. = ukuran sampel. Yt = pengamatan pada waktu ke-t = rata-rata pengamatan Yt. Y. Yt  k = pengamatan pada waktu ke-t+k, dengan k = 0, 1, 2.... Contoh 2.5.1 Hitunglah nilai autokovarian dengan menggunakan sampel sebagai berikut: t. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Yt. 10. 8. 6. 7. 5. 11. 12. 8. 7. 9. Penyelesaian: Dik: n=10 dan Y  8,3 Ilustrasi perhitungan autokovarian sebagai berikut: t 1 2 3 4 5 6 7 8 9 10. ˆ0 . Yt. Yt 1. 10 8 6 7 5 11 12 8 7 9. 8 6 7 5 11 12 8 7 9. (10  8,3) 2  (8  8,3) 2  ...  (9  8,3) 2  4,41 10.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 23. ˆ1 . (10  8,3)(8  8,3)  (8  8,3)(6  8,3)  ...  (7  8,8)(9  8,3)  -4,841 10. 2. Fungsi Autokorelasi (ACF) Fungsi autokorelasi (ACF) menyatakan hubungan antara nilai-nilai dari variabel yang sama tetapi pada periode waktu berbeda. Autokerelasi (ACF) adalah suatu fungsi yang menunjukkan besarnya korelasi (hubungan linear) antara pengamatan pada waktu ke-t (dinotasikan dengan. X t ) dengan pengamatan pada waktu-waktu sebelumnya (dinotasikan dengan X t 1 , X t 2 , ..., X t k ).. Definisi 2.5.21 Autokorelasi merupakan ukuran keeratan hubungan antar pengamatan dalam suatu data runtun waktu. Koefisien autokorelasi untuk lag-k dari data runtun waktu dinyatakan sebagai berikut:. k . Cov(Yt , Yt k ) Cov(Yt , Yt k )  k   , Var(Yt ) 0 Var(Yt )Var(Yt k ). Koefisien fungsi autokorelasi  k di atas dapat diduga dengan koefisien autokorelasi sampel, yaitu: n. . rk . k . 0. .  (Y  Y )(Y. t  k 1. t k. t. Y). n.  (Y  Y ) t 1. 2. t. dengan. rk = koefisien autokorelasi sampel dari lag ke-k, dimana k =1, 2,...,k.  k = koefisien autokorelasi populasi n = ukuran sampel. Yt = nilai Y waktu ke-t. Y  nilai rata-rata.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 24. Yt k  nilai Y waktu ke-t+k, k = 1, 2,..., n.. Contoh 2.5.2 Hitunglah nilai ACF dengan menggunakan sampel sebagai berikut: t. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Yt. 10. 8. 6. 7. 5. 11. 12. 8. 7. 9. Penyelesaian: Dik: n =10 dan Y  8,3 Ilustrasi perhitungan sampel ACF sebagai berikut: t. Yt. Yt 1. Yt 2. Yt 3. 1. 10. 8. 6. 7. 2. 8. 6. 7. 5. 3. 6. 7. 5. 11. 4. 7. 5. 11. 12. 5. 5. 11. 12. 8. 6. 11. 12. 8. 7. 7. 12. 8. 7. 9. 8. 8. 7. 9. 9. 7. 9. 10. 9. .... Yt 9 9. r0 . (10  8,3)(10  8,3)  (8  8,3)(8  8,3)  ...  (9  8,3)(9  8,3) 1 (10  8,3) 2  (8  8,3) 2  ...  (9  8,3) 2. r1 . (10 - 8,3)(8 - 8,3)  (8 - 8,3)(6 - 8,3)  ...  (7 - 8,3)(9 - 8,3)  0,15668934 (10 - 8,3) 2  (8  8,3) 2  ...  (9  8,3) 2. r2 . (10  8,3)(6  8,3)  (8  8,3)(7  8,3)  ...  (8  8,3)(9  8,3)  -0,39637 44,1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 25. r3 . (10  8,3)(7  8,3)  (8  8,3)(5  8,3)  ...  (12  8,3)(9  8,3)  -0,27596 44,1 . r9 . (10  8,3)(9  8,3)  0,026984 44,1. Berikut adalah grafik ACF dengan menggunakan program R. > acf(data). Gambar 2.5.2.1 Plot Grafik ACF. Autokorelasi dapat digunakan untuk mengidentifikasi apakah data bersifat acak, stasioner ataupun musiman. Fungsi autokorelasi (ACF) dibentuk dengan himpunan { k ; k  0,1,2,...} dengan  0  1. Untuk itu akan didefinisikan stasioner yang telah dideskripsikan sebelumnya dengan definisi eksak berikut. 1. Wide-Sense stationary (Stasioner Lemah) Proses Yt , t  T  dengan T    {0,1,2, } disebut proses stasioner W-S jika.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 26. t  . (i). E (| Yt |2 )  . (ii). E (Yt )  konstanta, tidak bergantung pada t, t  . (iii).  (t , s)   (t  h, s  h), t , s, h   .. Jika Yt , t  T  stasioner, maka  (t , s)   (t  s,0), dengan fungsi kovariansi hanya bergantung pada jarak waktu (t – s) (tetapi tidak bergantung pada t atau s secara sendiri-sendiri). Fungsi kovariansi untuk proses stasioner dapat didefinisikan ulang sebagai.  (h)   (h,0)  cov(Yt h , Yt ),. t, h  . dibaca sebagai kovariansi pada lag-h. Secara ekuivalen, fungsi korelasi dari proses. Yt , t  T . stasioner pada lag-h didefinisikan. sebagai.  ( h) .  ( h)  cov(Yt h , Yt )  (0). 2. Strictly Stationary (Stasioner Kuat) Proses Yt , t  T  disebut bersifat stasioner kuat jika fungsi distribusi kumulatif dari (Yt1 , , Ytk )' dan (Yt1h , , Ytk h )' sama untuk semua nilai k    dan untuk semua t1 , , t k , h  . Dengan kata lain, seluruh sifat statistik dari proses stokastik yang bersifat stasioner kuat tidak berubah karena pergeseran waktu.. Grafik ACF yang mencirikan data tidak stasioner adalah penurunan yang lambat dalam ukuran autokorelasi, sedangkan ciri grafik ACF data yang stasioner adalah sebaliknya. Berikut adalah contoh grafik ACF data stasioner dan tidak stasioner..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 27. Contoh 2.5.21 Diberikan data kuartalan yang ditampilkan pada lampiran 2, dapat diperoleh plot grafik ACF, penulis menggunakan program R. Dengan perintah sebagai berikut: > acf(data,lag.max=25). Gambar 2.5.2.2 Plot Grafik ACF Data Kuartalan Grafik ACF di atas menurun secara lambat sehingga data runtun waktu yang diwakilinya dikatakan tidak stasioner. Karena data tidak stasioner, perlu dilakukan differencing data. Berikut adalah grafik data kuartalan yang sudah di-differencing. > acf(Yt_diff,lag.max=25).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 28. Gambar 2.5.2.3 Plot Grafik ACF Data Kuartalan Setelah Differencing Dari grafik ACF yang telah di-differencing di atas, terlihat bahwa data sudah stasioner dan grafik menunjukkan pola musiman yakni dengan periode 4 bulan, yang dapat dilihat dari ACF yang menonjol tiap 4 bulan.. Sifat 2.6 Distribusi Sampel yang Besar dari ACF Dalam kondisi umum, jika xt adalah white noise, maka untuk n yang besar, sampel ACF, ˆ x (h), untuk h = 1, 2,..., H, biasanya berdistribusi dengan rata-rata nol dan standar deviasi.  ˆ. x. (h). . 1 . n. Untuk mengetahui apakah koefisien autokorelasi signifikan atau tidak, perlu dilakukan uji dengan langkah-langkah pengujian hipotesis sebagai berikut: a) H 0 :  k  0 (koefisien autokorelasi tidak signifikan) b) H1 :  k  0 (koefisien autokorelasi signifikan) c) Tetapkan  d) Statistik uji:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 29. t. rk SE(rk ). dengan SE(rk ) . 1 , untuk k = 0,1,2,...,n. n. e) H 0 ditolak jika t hitung > t . dengan derajat bebas df = n-1, n adalah. 2. ,df. banyaknya data. Apabila H 0 ditolak, koefisien autokorelasi signifikan. f) Perhitungan t g) Kesimpulan. Contoh 2.5.22 Diberikan nilai ACF dengan r0  1, r1  0.15668934 , dan r2  1  0.39637 serta n = 10. Ujilah apakah ACF signifikan atau tidak. Penyelesaian: a) H 0 :  k  0 (koefisien autokorelasi tidak signifikan) b) H1 :  k  0 (koefisien autokorelasi signifikan) c)   0,5 d) Statistik uji: t. rk SE(rk ). dengan SE(rk ) . 1 . n. e) H 0 ditolak jika t hitung > t  2. t 2. ,n 1.  t 0.5 2. ,10 1. . ,df.  t0.25 ,9  2.262. f) Perhitungan t SE(rk ) . 1 , untuk k = 0,1,2,...,n. 10.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 30. t1 . r0 1   10  3.1622 SE(r0 ) 1 10. t2 . r1 0.15668934   0.15668934 10  0.4954 SE(r1 ) 1 10. t3 . r2  0.39637   0.3937 10  1.2534 SE(r3 ) 1 10. g) Kesimpulan. H 0 ditolak karena 3.1622 > 2.262 yang artinya r0 signifikan.. H 0 diterima karena 0.4954 < 2.262 yang artinya r1 tidak signifikan. H 0 diterima karena -1.2534 < 2.262 yang artinya r2 tidak signifikan. Hasil uji hipotesis ini konsisten dengan grafik 2.5.1.1. Koefisien otokorelasi yang tidak signifikan akan berada di dalam “pita”, sedangkan yang signifikan (misal r0 ) melewati batas “pita”. Batas pita tersebut sesungguhnya adalah selang kepercayaan bagi koefisien otokorelasi yaitu rk  t 2. ( n 1). SE(rk )  k  rk  t 2. ( n 1). SE(rk ).. 3. Fungsi Autokorelasi Parsial (PACF) Definisi 2.5.31 Fungsi autokorelasi parsial (PACF) pada lag-k adalah hubungan diantara. Z t dan Z t k setelah dependensi linear antara Z t dan Z t k , variabel antara. Z t 1 , Z t  2 , ..., Z t k 1 diabaikan.. Fungsi PACF akan dijabarkan dalam proses berikut. Pertimbangkan model regresi, dengan variabel terikat Z t k dari proses stasioner dengan rata-rata nol pada variabel lag-k, Zt k 1 , Zt  k  2 , ..., dan Zt yaitu:. Zt  k  k1Zt  k 1  k 2 Zt  k  2  ...  kk Zt  et  k.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 31. dengan ki adalah parameter ke-i dari persamaan regresi, dan et  k adalah komponen error yang tidak berkorelasi dengan Zt  k  j , untuk j = 1, 2,..., k. Selanjutnya mengalikan Zt  k  j pada kedua sisi persamaan regresi di atas dan ambil nilai harapannya, diperoleh:. Zt  k Zt  k  j  k1Zt  k 1Zt  k  j  k 2 Zt  k  2 Zt  k  j  ...  kk Zt Zt  k  j  et  k Zt  k  j E (Zt  k Zt  k  j )  E (k1Zt  k 1Zt  k  j )  E (k 2 Zt  k  2 Zt  k  j )  ...  E (kk Zt Zt  k  j )  E (et  k Z t  k  j )  k1E (Zt  k 1Zt  k  j )  k 2 E (Zt  k  2 Zt  k  j )  ... . kk E (Zt Zt  k  j )  E (et  k Zt  k  j ) Dimisalkan E ( Zt  k Zt  k  j )   j , j  0,1,2,..., k dan karena E (et  k Zt  k  j )  0, sehingga diperoleh:.  j  k1 j 1  k 2 j  2  ...  kk j  k oleh karena itu,.  j  k1 j 1  k 2  j  2  ...  kk  j  k . Untuk j  0,1,2,..., k , diperoleh:. 1  k10  k 2 1  ...  kk  j 1 1  k11  k 2 0  ...  kk  j  2 . k  k1k 1  k 2 k  2  ...  kk 0 . Persamaan di atas dapat dibentuk dalam matriks, dengan 0  1 diperoleh:  1    1      k 1. 1 1 . k 2.   k 1  k1   1    k 1  k 2    2                1  kk    k . Dengan menggunakan aturan Cramer, k  1,2,..., diperoleh:. 11  1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 32. 1. 1 2 1. 1. 1. 1. 1. det 1. 1. 2 1. 1 1. det 1. 1. 1 2 3 2 1. 2. 1. 1. det. 22  det. 33 . 1. 1. . det. kk  det. 1. 1. 1. 1 . . 2 1 .  k  2  k 3  .  k 1  k  2 1 1 1 1.  k  3  1 2  k  2 1   k  3. . . .  k 1  k  2. k 3.  . . 1. 1 2 . k  k 1 k 2  1. Sampel PACF ˆkk diperoleh dengan mengganti  j dengan ̂ j dalam persamaan kk . Untuk sampel PACF dapat diduga dengan menggunakan metode rekursif, yang dimulai dengan ˆ11  ˆ1. Berikut ini adalah rumus PACF atau ˆkk . k. ˆk 1, k 1 . ˆ k 1  ˆkj ˆ k 1 j j 1 k. 1  ˆkj ˆ j j 1. dan ˆk 1, j  ˆk j  ˆk 1, k 1ˆk , k 1 j , j  1,..., k..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 33. Contoh 2.5.3 Hitunglah nilai PACF dengan menggunakan sampel sebagai berikut:. t. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Yt. 10. 8. 6. 7. 5. 11. 12. 8. 7. 9. Penyelesaian: Karena sampel ini sama dengan sampel pada contoh ACF dan ̂ j  rk , sehingga untuk nilai ˆ1  r1.. ˆ11  ˆ1  0,15668934 ˆ22 . ˆ 2  ˆ12  0,39637  (0,15668934 )2   0,43152 1  ˆ12 1  (0,15668934 ) 2. ˆ21  ˆ11  ˆ22ˆ11  0,15668934  (0,43152 )(0,15668934 )  0,224304 ˆ33 . . ˆ 3  ˆ21 ˆ 2  ˆ22 ˆ1 1  ˆ21 ˆ1  ˆ22 ˆ 2  0,27596  0,22434 (0,39637 )  (0,43152 )0,15668934 1  0,22434 (0,15668934 )  (0,43152 )(0,39637 ). = -0,15044 Berikut adalah grafik PACF dengan menggunakan program R. > pacf(data).

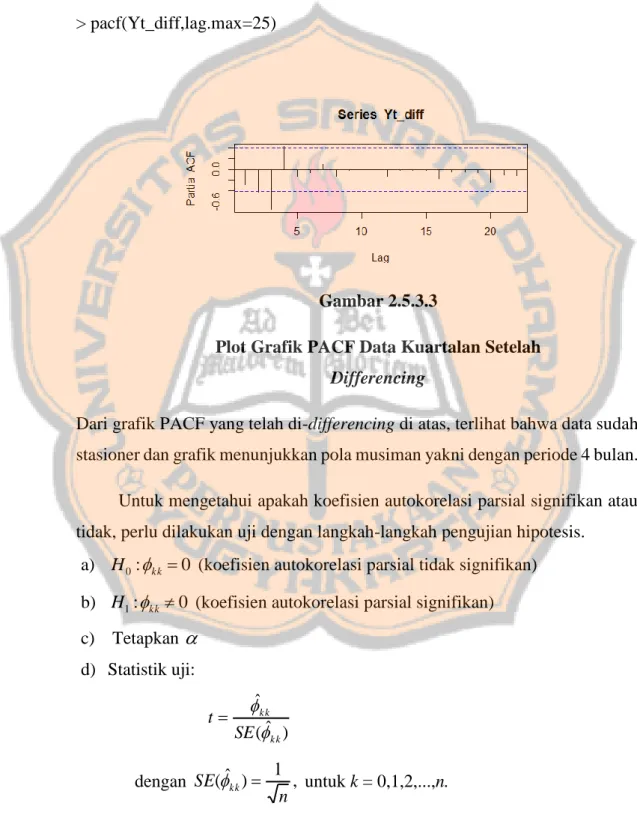
PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 34. Gambar 2.5.3.1 Plot Grafik PACF. Ciri grafik PACF dari data yang tidak stasioner adalah penurunan yang lambat dalam ukuran korelasi parsial, sedangkan ciri grafik PACF data stasioner adalah sebaliknya. Berikut ini adalah contoh grafik PACF data stasioner dan tidak stasioner.. Contoh 2.5.31 Diberikan data kuartalan yang ditampilkan pada lampiran 2 dapat diperoleh plot grafik PACF, penulis menggunakan program R. Dengan perintah sebagai berikut: > pacf(data,lag.max=25). Gambar 2.5.3.2 Plot Grafik PACF Data Kuartalan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 35. Grafik PACF di atas ada yang melewati pita pada lag-5 sehingga data rntun waktu yang diwakilinya dikatakan tidak stasioner. Karena data tidak stasioner, perlu dilakukan differencing data. Berikut adalah grafik data kuartalan yang sudah di-differencing. > pacf(Yt_diff,lag.max=25). Gambar 2.5.3.3 Plot Grafik PACF Data Kuartalan Setelah Differencing Dari grafik PACF yang telah di-differencing di atas, terlihat bahwa data sudah stasioner dan grafik menunjukkan pola musiman yakni dengan periode 4 bulan. Untuk mengetahui apakah koefisien autokorelasi parsial signifikan atau tidak, perlu dilakukan uji dengan langkah-langkah pengujian hipotesis. a) H 0 : kk  0 (koefisien autokorelasi parsial tidak signifikan) b) H1 : kk  0 (koefisien autokorelasi parsial signifikan) c) Tetapkan  d) Statistik uji: t. ˆkk SE (ˆkk ). 1 , untuk k = 0,1,2,...,n. dengan SE(ˆkk )  n.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 36. H 0 ditolak jika t hitung > t  2. , dengan derajat bebas df = n-1, n adalah ,df. banyaknya data. Apabila H 0 ditolak, koefisien autokorelasi parsial signifikan. e) Perhitungan t f) Kesimpulan. Contoh 2.5.32 Diberikan. nilai. PACF. dengan. ˆ11  0.1566,. ˆ22  0.4315,. ˆ33  0.1504 serta n = 10. Ujilah apakah PACF signifikan atau tidak. Penyelesaian: a) H 0 : kk  0 (koefisien autokorelasi parsial tidak signifikan) b) H1 : kk  0 (koefisien autokorelasi parsial signifikan) c)   0,5 d) Statistik uji: t. ˆkk SE (ˆkk ). 1 . dengan SE(ˆkk )  n e) H 0 ditolak jika t hitung > t  2. t 2. ,df.  t 0.5 2. ,10 1. , dengan df = n-1. ,df.  t0.25 ,9  2.262. f) Perhitungan t. 1 1 SE(ˆkk )   . n 10 t1 . ˆ11 0.1566   0.1566 10  0.4952 SE (ˆ11 ) 1 10. t2 . ˆ22  0.4315   0.4315 10  1.3645 1 10 SE (ˆ22 ). dan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 37. t3 . ˆ33  0.1504   0.1504 10  0.4756 1 10 SE (ˆ33 ). g) Kesimpulan. H 0 ditolak karena 0.4952 < 2.262 yang artinya ˆ11 tidak signifikan. H 0 diterima karena - 1.3645 <2.262 yang artinya ˆ22 tidak signifikan. H 0 diterima karena. 0.4756 < 2.262 yang artinya ˆ33 tidak. signifikan. Hasil uji hipotesis ini konsisten dengan grafik 2.5.2.1. Koefisien otokorelasi yang tidak signifikan akan berada di dalam “pita”, sedangkan yang signifikan melewati batas “pita”. Batas pita tersebut sesungguhnya adalah selang kepercayaan bagi koefisien otokorelasi yaitu. ˆkk  t 2. ( n1). SE(ˆkk )  kk  ˆkk  t 2. ( n1). SE(ˆkk ).. G. Proses White Noise Definisi 2.6.11 Proses at disebut proses white noise jika at adalah barisan variabel acak yang independen dan berdistribusi identik dengan rata-rata konstan E (at )  a biasanya diasumsikan 0, variansi konstan var(at )   a2 dan cov(at , at k )  0 untuk semua k  0. Sehingga suatu proses disebut white noise dengan autokovarian  a2 , k    0,. fungsi autokorelasi. k  0, k  0,.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 38. 1, 0,. k  0,. 1, 0,. k  0,. k  . k  0,. dan fungsi autokorelasi parsial. kk  . k  0.. Dengan demikian proses white noise bersifat stasioner. Bila at berdistribusi normal dengan mean 0 dan variansi  a2 , maka runtun waktu disebut white noise Gaussian.. Contoh 2.6.1 Diberikan contoh sebanyak 300 data, dapat diperoleh plot grafik pada gambar di bawah ini, grafik dibuat dengan menggunakan program R. Dengan perintah sebagai berikut: > white_noise<-arima.sim(list(order=c(0,0,0)),300) > plot.ts(white_noise,main="white noise"). Gambar 2.6.1.1 White Noise.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 39. Grafik white noise di atas memiliki rata-rata 0 dan variansi konstan yang ditunjukkan dengan grafik yang cenderung mendatar dan fluktuasi yang relatif konstan. Untuk mengetahui apakah model white noise atau tidak, perlu dilakukan uji dengan langkah-langkah pengujian hipotesis Ljung-Box sebagai berikut: 1. H 0  1   2  ...   k  0 (residual white noise) 2. H1 = minimal ada satu  k  0, untuk k  1,2,..., K (residual tidak white noise) 3. Tetapkan  4. Statistik uji: h. 2  hitung  n(n  2) (n  k ) 1 rk2 k 1. dengan:. n  banyaknya data h  lag-n. rk2  ACF sampel. 2 5. Dengan daerah penolakannya yaitu H 0 ditolak jika  hitung > 2;df atau p-. value <  . 2;df . 2 6. Perhitungan  hitung. 7. Kesimpulan. Contoh 2.6.2 Diketahui n = 36,. r1  0,103 ,. r2  0,099 ,. r3  0,043 , r4  0,031 ,. r5  0,183 , r6  0,025 , r7  0,275 , r8  0,004 , r9  0,011 , r10  0,152 . Ujilah apakah data white noise atau tidak. Jawab: 1. H 0  1   2  ...   k  0 (residual white noise).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 40. 2. H1 = minimal ada satu  k  0, untuk k  1,2,..., K (residual tidak white noise) 3.   0,05 4. Statistik uji: h. 2  hitung  n(n  2) (n  k ) 1 rk2 k 1. dengan:. n  banyaknya data h  lag-n. rk2  ACF sampel. 2 5. Dengan daerah penolakannya yaitu H 0 ditolak jika  hitung > 2;df , atau p-. value <  . 2;df , dengan df  banyaknya k. Diperoleh  02,05;10 = 18,3070 2 6. Perhitungan  hitung. h. 2  hitung  n(n  2) (n  k ) 1 rk2 k 1. 10.  36(38) 1. 1 rk2 36  k. 1 2 1 2 1 2 1  36(38)  r12  r2  r3  ...  r10 34 33 26   35.  7,22. 7. Kesimpulan 2 Diperoleh  hitung =7,22 dan  02,05;10 = 18,3070. H 0 diterima karena 7,22 <. 18,3070. Sehingga dapat disimpulkan bahwa residual white noise.. Model dikatakan white noise apabila grafik ACF dan PACF tidak ada yang melewati pita lag  0. Berikut adalah contoh. white noise dengan. menggunakan uji Ljung-Box, grafik ACF, dan grafik PACF dengan program R. Contoh model ARIMA sebagai berikut:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 41. Data yang digunakan adalah data penjualan kuartalan yang dapat dilihat pada lampiran 2. Model ARIMA (1, 0, 0)(0, 0, 3) > Box.test(residual8,lag=20,type="Ljung-Box"). Box-Ljung test data: residual8 X-squared = 15.736, df = 20, p-value = 0.7329 > acf(residual8). Gambar 3.1 Grafik ACF Residual > pacf(residual8). Gambar 3.2 Grafik PACF Residual.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 42. p-value > α, H 0 diterima sehingga dapat disimpulkan bahwa model ARIMA (1, 0, 0)(0, 0, 3) memiliki residual white noise. Dapat dilihat juga dari grafik ACF residual dan PACF residual, bahwa grafik tersebut tidak ada yang melewati pita pada lag > 0.. H. Model ARMA Model Autoregressive Moving Average (ARMA) adalah gabungan antara model Autoregressive atau AR dan model Moving Average atau MA. Berikut adalah model AR, model MA dan model ARMA. 1. Model AR Model Autoregressive atau AR adalah suatu model yang menjelaskan pergerakan suatu variabel dikaitkan degan nilai variabel itu sendiri di masa lalu. Definisi 2.7.1.1 Suatu model autoregressive dengan orde p, yang dinotasikan AR(p), mempunyai bentuk sebagai berikut:. Yt  1Yt 1  2Yt 2  ...   pYt  p  et dengan Yt stasioner, dan 1 , 2 , ,  p adalah konstanta. Diasumsikan et white noise dengan rata-rata 0 dan variansi  e2 . Lebih lanjut, jika rata-rata. Yt adalah  , substitusikan Yt   akan diperoleh Yt    1 (Yt 1   )  2 (Yt 2   )  ...   p (Yt  p   )  et , atau dapat ditulis. Yt    1Yt 1  2Yt 2  ...   pYt  p  et dengan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 43. . :  (1  1  2     p ),. Yt. : nilai pengamatan variabel dependen pada waktu t,. j. : parameter autoregressive ke- j , j  1,2,..., p,. Yt k. : pengamatan variabel Y pada waktu t  k , k  1,2,... p,. et. : nilai residual pada saat t.. Lebih jauh, dapat juga ditulis dalam bentuk.  ( B)  1  1 B  2 B 2    P B P Contoh 2.7.1.2 1. AR (1). Yt    1Yt 1  et atau. (1  1 B)Yt    et . 2. AR (2). Yt    1Yt 1  2Yt 2  et atau. (1  1 B  2 B 2 )Yt    et .. Contoh 2.7.1.3.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 44. Diberikan contoh model AR orde 2 dengan 1  1 dan 2  0.9 beserta ACF dan PACFnya. Yt  Yt 1  0.9Yt 2  et untuk t=1,2,...,300. Dari persamaan tersebut dibuat simulasi plot grafik dibawah ini yang dibuat dengan menggunakan program R dengan perintah sebagai berikut: > ar<-arima.sim(model=list(ar=c(1,-0.9)),n=300) > plot.ts(ar,main="Autoregressive"). Gambar 2.7.1.1 Plot Grafik AR (2) > ar.acf<-acf(ar,type="correlation",plot=T). Gambar 2.7.1.2 Plot Grafik ACF Model AR (2).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 45. Grafik ACF di atas meluruh menuju nol seperti gelombang sinus teredam. > ar.pacf<-acf(ar,type="partial",plot=T). Gambar 2.7.1.3 Plot Grafik PACF Model AR (2) Grafik PACF di atas signifikan ke lag-2 (terpotong di lag-2), artinya orde dari AR ditentukan oleh lag dimana PACF tersebut signifikan.. 2. Model MA Model Moving Average atau MA adalah suatu model yang menyatakan pergerakan variabelnya melalui residualnya di masa lalu. Definisi 2.7.21 Model Moving Average dengan orde q, atau model MA(q), didefinisikan sebagai. Yt    et  1et 1   2 et 2  ...   q et q dengan. Yt. : nilai pengamatan variabel dependen pada waktu t,.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 46. . : konstanta,. et. : nilai residual pada saat t,. j. : parameter moving average ke- j , j  1,2,..., q,. et  k. : nilai residual pada saat t  k , k  1,2,..., q.. Diasumsikan et white noise dengan rata-rata 0 dan variansi re2 . Jika B adalah operator shift mundur yang dirumuskan sebagai ( B q )et  et q maka model MA di atas dapat disederhanakan menjadi. Yt    et  1et 1   2 et 2  ...   q et q. Yt    et  1 ( B)et   2 ( B 2 )et  ...   q ( B q )et. Yt    (1  1B   2 B 2  ...   q B q )et .. Contoh 2.7.2.1 1. MA (1). Yt    et  1et 1 atau. Yt    (1  1B)et . 2. MA (2). Yt    et  1et 1   2et 2 atau. Yt    (1  1B   2 B 2 )et .. Contoh 2.7.2.2 Diberikan contoh MA orde 2 dengan 1  0.2 dengan ACF dan PACFnya. Yt  et  0,2et 1  0,4et 2 untuk t=1,2,...,300.. dan  2  0.4 beserta.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 47. Dari persamaan tersebut dibuat simulasi plot grafik dibawah ini yang dibuat dengan menggunakan program R dengan perintah sebagai berikut: > ma<-arima.sim(model=list(ma=c(-0.2,0.4)),n=300) > plot.ts(ma,main="Moving Average"). Gambar 2.7.2.1 Plot Grafik MA (2) > ma.acf<-acf(ma,type="correlation",plot=T). Gambar 2.7.2.2 Plot Grafik ACF Model MA (2) Grafik ACF di atas signifikan ke lag-2 (terpotong di lag-2), artinya orde dari MA ditentukan oleh lag dimana ACF tersebut signifikan. > ma.pacf<-acf(ma,type="partial",plot=T).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 48. Gambar 2.7.2.3 Plot Grafik PACF Model MA (2) Grafik PACF di atas meluruh menuju nol seperti gelombang sinus teredam.. 3. Model ARMA Model ARMA adalah gabungan antara model AR dan model MA, sehingga model ARMA dapat ditulis sebagai berikut:. Yt    1Yt 1  2Yt 2  ...   pYt  p  et  1et 1   2et 2  ...   q et q atau. (1  1B  2 B 2  ...   p B p )Yt    (1  1B   2 B 2  ...   q B q )et.  p ( B)Yt     q ( B)et dengan.  p (B) : operator AR.  q (B) : operator MA. Contoh 2.7.3 1. ARMA (1, 1). Yt    1Yt 1  et  1et 1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 49. atau. (1  1B)Yt    (1  1B)et AR (1). MA (1). 2. ARMA (2, 2). Yt    1Yt 1  2Yt 2  et  1et 1   2et 2 atau. (1  1B  2 B 2 )Yt    (1  1B   2 B 2 )et AR (2). MA (2). Contoh 2.7.3.2 Diberikan contoh ARMA (2,2) dengan 1  0.8, 2  0.2, 1  0.6, dan.  2  0.2 beserta ACF dan PACFnya menggunakan persamaan Yt  0,8Yt 1  0,2Yt 2  et  0,6et 1  0,2et 2 untuk t=1,2,...,300. Dari persamaan tersebut dibuat simulasi plot grafik dibawah ini yang dibuat dengan menggunakan program R dengan perintah sebagai berikut: >arma<-arima.sim(model=list(ar=c(0.8,-0.2),ma=c(-0.6,0.2)),n=300) > plot.ts(arma,main="ARMA"). Gambar 2.7.3.1 Plot Grafik ARMA (2,2).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 50. > arma.acf<-acf(arma,type="correlation",plot=T). Gambar 2.7.3.2 Plot Grafik ACF Model ARMA (2,2) Grafik ACF di atas signifikan ke lag-2 (terpotong di lag-2). > arma.pacf<-acf(arma,type="partial",plot=T). Gambar 2.7.3.3 Plot Grafik PACF Model ARMA (2,2) Grafik PACF di atas signifikan ke lag-2 (terpotong di lag-2)..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 51. I. Model ARIMA Model Autoregressive Integrated Moving Average (ARIMA) merupakan model Autoregressive Moving Average (ARMA) nonstasioner yang telah differencing menjadi model stasioner, sehingga tidak terdapat pertumbuhan atau penurunan pada data (data harus horizontal sepanjang sumbu waktu). Dengan kata lain fluktuasi data berada di sekitar suatu nilai rata-rata yang konstan.. 1. Model ARIMA Nonmusiman Jika nonstasioneritas ditambahkan pada proses ARMA , maka model umum ARIMA (p, d, q) terpenuhi. Di sini d adalah orde beda (difference). Tujuan menghitung beda adalah untuk mencapai stasioneritas dan secara umum apabila terdapat pembedaan orde ke-d, untuk mencapai stasioneritas akan ditulis: Pembedaan orde ke-d = (1  B) d Yt Contoh data yang telah stasioner setelah melakukan proses differencing sebagai berikut: 1. ARIMA (0, 1, 0). (1  B)Yt  et 2. ARIMA (0, d, 0). (1  B) d Yt  et. (. pembedaan nilai )( ) orde ke − 𝑑 𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙. Rumus umum untuk model ARIMA (p, d, q) sebagai berikut:.  p ( B)(1  B) d Yt     q ( B)et dengan.  p : koefisien komponen AR dengan orde ke-p, p  1, 2,..., p, B : operator backward,. d : pembedaan (differencing) orde ke-d, d =1, 2,..., d,.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 52. Yt : nilai variabel Y pada waktu t,.  : konstanta,  q : koefisien komponen MA dengan orde ke-q, q =1, 2,..., q, et : residual white noise. Contoh ARIMA (1, 1, 1), adalah sebagai berikut:. (1  B)(1  1 B)Yt    (1  1 B)et. 𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑖𝑛𝑔 ( ) (AR (1)) pertama. (MA (1)). Semua faktor dapat dikalikan dan model umum dapat ditulis sebagai berikut:. (1  1 B  B  1 B 2 )Yt    et  1 Bet Yt  1 BYt  BYt  1 B 2Yt    et  1 Bet Yt    1 BYt  BYt  1 B 2Yt  et  1 Bet Yt    1Yt 1  Yt 1  1Yt 2  et  1et 1. 2.. Model ARIMA Musiman Dengan cara yang persis sama, titik-titik data yang berurutan mungkin memperlihatkan sifat-sifat AR, MA, campuran ARMA, atau campuran ARIMA, sehingga data yang dipisahkan oleh satu musim penuh (yaitu satu tahun) dapat memperlihatkan sifat-sifat yang sama. Sebagai contoh, perhatikan suatu deret data yang dikumpulkan per kuartal. Maka pembedaan (difference) musiman dapat dihitung sebagai berikut:. Yt '  Yt  Yt 4  (1  B 4 )Yt . Deret data yang baru dinyatakan oleh Yt ' , sekarang untuk data yang dikumpulkan bulanan, pembedaan (difference) musiman dalam satu tahun dapat dihitung sebgai berikut:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 53. Yt '  Yt  Yt 12  (1  B12 )Yt . Notasi ARIMA dapat diperluas untuk menangani aspek musiman, notasi umum yang singkat adalah: ARIMA (p, d, q)(P, D, Q)s 𝑠= bagian dari bagian dari ( model ) ( model ) ( periode ) musiman nonmusiman musiman Rumus model umum untuk model ARIMA (p, d, q)(P, D, Q)s.  p ( B) P ( B s )(1  B) d (1  B s ) D Yt   q ( B)Q ( B s )et dengan. p. : koefisien komponen AR dengan orde ke-p,. B. : operator backward non musiman,. P. : koefisien komponen AR musiman dengan orde ke-P,. Bs. : operator backward musiman,. d. : pembedaan (differencing) orde ke-d non musiman,. D. : pembedaan (differencing) orde ke-D non musiman,. Yt. : nilai variabel Y pada waktu t,. q. : koefisien komponen MA dengan orde ke-q,. Q. : koefisien komponen MA musiman dengan orde ke-Q,. et. : residual white noise.. Contoh model ARIMA (1, 1, 1)(1, 1, 1)4 sebagai berikut:. (1  1B)(1  1B4 )(1  B)(1  B4 )Yt  (1  1B)(1  1B4 )et. (. nonmusiman nonmusiman nonmusiman )( ) ( ) AR(1) 𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑒 MA(1) musiman musiman ( ) ( ) AR(1) 𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑒. musiman ( ) MA(1).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 54. Semua faktor dapat dikalikan dan model umum dapat ditulis sebagai berikut:. (1  1B 4  1B  11B5 )(1  B 4  B  B5 )Yt  (1  1B 4  1B  11B5 )et (1  B 4  B  B 5  1 B 4  1 B 8  1 B 5  1 B 9  1 B  1 B 5  1 B 2  1 B 6 . 11 B 5  11 B 9  11 B 6  11 B10 )Yt  (1  1 B 4  1 B  11 B 5 )et Yt  ( B 4Yt  1 B 4Yt )  ( BYt  1 BYt )  ( B 5Yt  1 B 5Yt  1 B 5Yt  11 B 5Yt )  1 B 8Yt  (1 B 9Yt  11 B 9Yt )  1 B 2Yt  (1 B 6Yt  11 B 6Yt )  11 B10Yt . et  1B 4et  1Bet  11B5et. Yt  (1  1 )Yt 1  1Yt 2  (1  1 )Yt 4  (1  1  1  11 )Yt 5  (1  11 )Yt 6  1Yt 8  (1  11 )Yt 9  11Yt 10  et  1et 1  1et 4  11et 5 Jika koefisien dari 1 , 1 , 1 , dan 1 telah diperoleh, maka persamaan di atas dapat digunakan untuk peramalan (Makridakis, dkk. 1999).. J. Sifat-sifat Model ARIMA Berdasarkan ACF dan PACF Untuk menentukan model ARIMA, grafik ACF dan grafik PACF dapat dijadikan petunjuk. Perlu diingat bahwa untuk menentukan orde AR dapat dilihat dari grafik PACF dan untuk menentukan orde MA dapat dilihat dari grafik ACF. Berikut ini adalah rangkuman sifat-sifat sampel ACF, PACF, dan ordenya..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 55. Tabel 2.9.11 Rangkuman Plot Sampel ACF dan PACF Berdasarkan Proses Proses. Pola ACF. Pola PACF. Model ARIMA. AR (p). Meluruh menuju nol secara. Di atas batas interval. ARIMA. eksponensial/ gelombang. maksimum sampai lag ke p. (p, 0, 0). sinus teredam.. dan di bawah batas pada. lag  p. . MA (q). Di atas batas interval. Meluruh menuju nol secara. ARIMA. maksimum sampai lag ke q. eksponensial/ gelombang. (0, 0, q). dan di bawah batas pada. sinus teredam.. lag > q. ARMA (p,q). Meluruh menuju nol secara. Meluruh menuju nol secara. ARIMA. eksponensial/ gelombang. eksponensial/ gelombang. (p, 0, q). sinus teredam.. sinus teredam.. Tabel 2.9.12 Gambar Ilustrasi Sampel ACF dan PACF Berdasarkan Proses Proses. Pola ACF. Pola PACF. Model ARIMA. AR (p) untuk p=2. AR (p) untuk p=2. ARIMA AR (p). (2, 0, 0).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 56. MA (q) untuk q=2. MA (q) untuk q=2. MA (q). ARIMA (0, 0, 2). ARMA (p, q) untuk p=2 dan. ARMA (p, q) untuk p=2 dan. q=2. q=2. ARMA (p,q). ARIMA (2, 0, 2). Berdasarkan rangkuman tersebut, kita dapat memperkirakan model yang kemungkinan sesuai untuk data runtun waktu yang diberikan. Contoh 2.9.1 Diberikan data kuartalan yang dapat dilihat pada lampiran 2. Pada gambar 2.5.1.2 dan gambar 2.5.2.2 pada subbab sebelumnya jelas bahwa data tidak stasioner dalam rata-rata, sehingga perlu dilakukan differencing data. Setelah melalui proses differencing data, diperoleh plot grafik ACF dan PACF sebagai berikut:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 57. Gambar 2.9.1.1 Plot Grafik ACF Data Kuartalan Setelah Differencing. Gambar 2.9.1.2 Plot Grafik PACF Data Kuartalan Setelah Differencing Berdasarkan grafik ACF dan grafik PACF di atas terdapat musiman. Grafik PACF menunjukkan nilai yang signifikan pada lag 3 yang mengindikasikan bahwa model AR(3) nonmusiman dan nilai PACF tunggal yang signifikan pada lag 4 menunjukkan model AR(1) musiman. grafik ACF menunjukkan nilai yang signifikan pada lag 0 yang mengindikasikan bahwa model MA(0) nonmusiman dan nilai ACF yang signifikan pada lag 4, 8, dan 12 menunjukkan model MA(3) musiman. Oleh karena itu, dapat diperkirakan model yang kemungkinan sesuai untuk data runtun waktu yang diberikan adalah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 58. ARIMA (3,1,0)(0,0,3)4. Namun perlu dilakukan pemeriksaan diagnostik pada model terlebih dahulu dan model harus residual white noise, berdistribusi Normal, serta memiliki nilai AIC terkecil yang akan dibahas pada bab III.. K. Estimasi Model AR, MA, dan ARMA Salah satu langkah yang paling penting dalam peramalan yaitu estimasi atau pendugaan. Estimasi adalah proses yang menggunakan sampel statistik untuk menduga atau menaksir hubungan parameter populasi yang tidak diketahui. Berikut ini akan dibahas estimasi model AR, MA, dan ARMA. 1. Estimasi Model AR Pada persamaan. Yt    1Yt 1  2Yt 2  ...   pYt  p  et ,. model. umum AR(p) dinyatakan sebagai:. Yt  1Yt 1  2Yt 2  3Yt 3  ...   pYt  p  et .. (11-1). Apabila kedua sisi persamaan (11-1) dikalikan Yt k , dengan k  1, 2, 3,..., p, hasilnya adalah. Yt k Yt  1Yt k Yt 1  2Yt k Yt 2  3Yt k Yt 3  ...   pYt k Yt  p  Yt k et .. (11-2). Bila memasukkan nilai harapan pada kedua sisi persamaan di atas dan diasumsikan terdapat stasioneritas, persamaan tersebut akan menjadi.  k  1 k 1  2 k 2  3 k 3  ...   p k  p ,. (11-3). dengan  k adalah kovarians antara Yt dan Yt k . Hal ini dapat berlaku karena E (Yt k , Yt ), yaitu nilai harapan ruas kiri persamaan (11-2) didefinisikan sebagai kovarian antara variabel Yt k dan Yt , dengan variabel-variabel tersebut terpisah sejauh k periode waktu. Demikian pula. E (Yt k , Yt 1 ) adalah  k 1 , karena Yt k dan Yt 1 terpisah sejauh k  1 periode dan demikian seterusnya. Akhirnya E (Yt k et ) adalah nol, karena.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 59. nilai-nilai kesalahan bersifat acak dan tidak berkorelasi dengan nilai-nilai. Yt k sebelumnya. Kemudian, sistem persamaan Yule-Walker dari model AR(p) dapat diberikan sebagai berikut:.  k  1 k 1  2  k 2  3  k 3  ...   p  k  p ,. (11-4). Berdasarkan definisi 2.5.21. k . k . 0. Apabila pada (11-4) k  1, 2, 3,..., p, maka sistem persamaan berikut yang dikenal sebagai persamaan Yule-Walker akan didapat:. 1  1  2 1  3  2  ...   p  p 1  2  1 1  2  3 1  ...   p  p 2  3  1  2  2 1  3  ...   p  p 3   p  1  p 1  2  p 2  3  p 3  ...   p.       . (11-5). atau  1   1    2     p 1. 1. 2 1. 1. 1 . 1 .  p 2.  p 3.   p 1  1   1        p 2  2    2    p 3  3     3               1   p    p . (11-6). Jika elemen-elemen vektor dan matriks parameter disubstitusi dengan penduganya, maka diperoleh penduga Yule-Walker yaitu.  1   ˆ1  ˆ  2    ˆ  p1. ˆ1 1 ˆ1. ˆ 2 ˆ1. . 1 . ˆ p2. ˆ p3.  ˆ p1  ˆ1   ˆ1       ˆ p2  ˆ2   ˆ 2   ˆ p3  ˆ3    ˆ 3                1  ˆp   ˆ p . (11-7).