Metode Iterasi Dua Titik Berparameter Real
dengan Orde Konvergensi Optimal
Wartono
1,a), Ika Safitri
1,b)1Program Studi Matematika, Universitas Islam Negeri Sultan Syarif Kasim Riau
a) e-mail: [email protected] b) e-mail: [email protected]
Abstrak
Pada artikel ini, sebuah metode iterasi baru dikonstruksi menggunakan generalisasi metode iterasi dua titik dengan delapan parameter real A, B, C, D, E, F, G, dan H. Generalisasi bentuk metode iterasi dilakukan untuk menentukan orde konvergensi optimal dengan mengganti nilai-nilai parameter real. Hasil kajian menunjukkan bahwa metode iterasi mempunyai orde konvergensi tiga yang melibatkan delapan parameter real. Selanjutnya orde konvergensi metode iterasi meningkat dengan mengganti A = E dan B = F + 2 sehingga hanya melibatkan enam parameter real. Selain itu, metode iterasi memerlukan tiga evaluasi fungsi dan memiliki indeks efisiensi sebesar 41/3 1, 5874. Simulasi numerik diberikan untuk menguji performansi metode baru dengan menggunakan beberapa fungsi real. Performa metode iterasi baru tersebut adalah jumlah iterasi, orde konvergensi yang dihitung secara komputasi dan nilai mutlak fungsi. Selanjutnya, ukuran-ukuran performansi metode iterasi baru dibandingkan dengan Metode Newton, Metode Chun, Metode Newton Ganda dan Metode Noor. Hasil simulasi numerik menunjukkan bahwa metode iterasi baru mempunyai performa lebih baik dibandingkan dengan metode iterasi lainnya. Kata kunci: Indeks efisiensi, metode iterasi dua titik, orde konvergensi, persamaan nonlinier
Abstract
In this paper, a new iterative method was constructed by using a generalized two-point iterative method with eight real parameters A, B, C, D, E, F, G, and H. Generating form of the iterative method was done to find an optimal order of convergence by replacing the value of the real parameters. The result of the study shows that the iterative method has a third-order convergence involving eight real parameters. Furthermore, the convergence order of the iterative method increases by taking A = E and B = F + 2 so that it involves six real parameters. Besides that, the iterative method requires three evaluation functions and has an efficiency index equal to 41/3 1.5874. Numerical simulations are given to test the performance of the new method by using several test functions. The performances of the new iterative method are the number of iteration, computationally order of convergence, and the absolute value of the function. Furthermore, performance measures of the new method were compared with Newton’s method, Chun’s method, Double Newton’s method, and Noor’s method. Numerical simulation results show that the performance of the new method is better than other iterative methods.
Pendahuluan
Persamaan nonlinear merupakan representasi matematis dari persoalan-persoalan pada bidang sains dan teknologi [1, 2]. Salah satu masalah yang sering dijumpai adalah bagaimana menyelesaikan persamaan nonlinear tersebut dalam bentuk:
𝑓(𝑥) = 0 (1)
Pada umumnya hampir sebagian besar persamaan nonlinear yang terbentuk merupakan persamaan nonlinear yang rumit dan kompleks sehingga penyelesaian analitis sangat sulit untuk dilakukan. Oleh karena itu, penyelesaian Persamaan (1) dapat dilakukan dengan menggunakan perhitungan komputasi yang bersifat mengulang sebagai sebuah pendekatan hasil numerik. Penyelesaian persamaan nonlinear dengan menggunakan cara seperti tersebut biasa dikenal dengan nama metode iterasi.
Salah satu metode iterasi yang sering digunakan untuk menyelesaikan Persamaan (1) adalah metode Newton dengan orde konvergensi kuadratik dan indeks efisiensi sebesar 21/2 1, 4142 [3].Secara umum metode Newton memiliki bentuk sebagai berikut
)
(
'
)
(
1 n n n nx
f
x
f
x
x
, n0,1,2,3,..., (2) f '(xn) 0.Metode Newton di konstruksi dengan menggunakan polinomial Taylor orde satu, sedangkan metode iterasi yang dihasilkan oleh polinomial Taylor orde dua adalah metode Halley, metode Chebyshev dan metode Halley irasional (sebagian peneliti menyebutnya metode Euler). Metode-metode iterasi tersebut mempunyai orde konvergensi masing-masing tiga [4, 5, 6, 7]. Metode iterasi yang dikonstruksi menggunakan polinomial Taylor baik orde satu maupun orde dua adalah metode iterasi satu titik.
Pada saat ini, beberapa peneliti mengembangkan metode Newton menjadi metode iterasi dua titik dengan orde konvergensi lebih tinggi yang menghasilkan suatu metode iterasi dalam bentuk perkalian dengan f(yn)/f(xn). Berbagai pendekatan digunakan untuk menghasilkan bentuk metode iterasi tersebut,
seperti: metode analisis homotopi [8], modifikasi metode Euler [9], modifikasi metode Newton ganda [10,11, 12], modifikasi metode King [13], fungsi kuadratik [14], kombinasi linear tiga parameter [15], metode perturbasi homotopi [16].
Selanjutnya, Ghanbari [17] mengembangkan bentuk metode iterasi dua titik yang disebutkan di atas dengan melibatkan parameter real yang ditulis dalam bentuk
2 2 1 2 2 ( ) ( ) ( ) ( ) ( ) ( ) '( ) ( ) ( ) ( ) ( ) '( ) n n n n n n n n n n n n n n f x Af x Bf x f y Cf y f y x x f x Df x Ef x f y Ff y f x . (3)
Pada artikel ini, penulis membahas bagaimana mengkonstruksi metode iterasi dua titik dengan cara memperluas bentuk iterasi yang diberikan oleh persamaan (3) dengan melibatkan delapan parameter
real. Pemberian delapan parameter real ini akan memungkinkan munculnya varian-varian metode iterasi dua titik baik berorde tiga maupun berorde empat.
Simulasi numerik diberikan untuk menguji performa metode iterasi baru dengan menggunakan beberapa fungsi real. Ukuran-ukuran performa yang akan diuji meliputi: jumlah iterasi, komputasi orde konvergensi, dan nilai mutlak fungsi. Selanjutnya, performa metode iterasi baru dibandingkan dengan metode iterasi lainnya, yaitu: Newton [3], metode Chun [13], metode Newton Ganda [11], dan metode Noor [16].
Metode
Pada bagian ini, penulis menggunakan beberapa definisi yang digunakan pada proses mengkonstruksi metode iterasi, menentukan orde konvergensi, baik menggunakan ekspansi deret Taylor maupun komputasi (COC) dan simulasi numerik. Adapun definisi yang digunakan adalah sebagai berikut:
Definisi 1. Misalkan f (x) merupakan sebuah fungsi dengan akar persamaan dan {xn} adalah sebuah barisan
bilangan real untuk n 0 yang konvergen ke . Jika terdapat c 0 dan p 1 sedemikian hingga,
c
e
e
x
x
p n n n p n n n
|
|
|
|
lim
|
|
|
|
lim
1 1
, (4)maka p adalah orde konvergensi dari deret {xn}, dan c adalah konstanta galat asimtotik (asymptotic error constant).
Untuk p1, 2, 3,maka deret konvergen linear, kuadratik, dan kubik [1].
Definisi 2. Misalkan en = xn adalah galat pada iterasi ke n, maka galat pada iterasi ke-(n+1) didefinisikan oleh
1 1 ( ) p p n n n e ce e , (5)
dengan p adalah orde konvergensi dan
c
adalah konstanta asimtotik [1].Definisi 3. Misalkan r adalah jumlah dari evaluasi pada fungsi atau salah satu dari derivatifnya, maka efisiensi dari
suatu metode iterasi diukur dengan indeks efisiensi yang didefinisikan oleh [3]
IE p1r. (6)
Definisi 4. Misalkan adalah akar persamaan fungsi f (x) dan xn 1, xn dan xn + 1 adalah akar-akar pendekatan pada
iterasi ke- (n 1), n dan (n + 1) yang dekat dengan , maka orde konvergensi komputasi dihitung menggunakan formulasi [3] 1 1 ln ( ) / ( ) ln ( ) / ( ) n n n n x x x x . (7)
Selanjutnya untuk mengkonstruksi metode iterasi dua titik, penulis awali dengan menuliskan kembali bentuk umum metode iterasi dua langkah yang diberikan oleh
1 ( ) ( ), ( ) '( ) n n n n n n f y x y f x f y f x , (8)dengan
)
(
'
)
(
n n n nx
f
x
f
x
y
. (9)Misalkan ( f(xn), f(yn) ) suatu fungsi dalam f(xn) dan f(yn) yang melibatkan delapan parameter real A, B,
C, D, E, F, G, dan H yang ditulis dalam bentuk : 2 2 2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n n n n n f x Af x Bf y Cf y Df x f y f x Ef x Ff y Gf y Hf x f y , (10)
maka Persamaan (8) dapat ditulis kembali dalam bentuk
2 2 1 2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n n n n n n n f x Af x Bf y Cf y Df x f y x y f x Ef x Ff y Gf y Hf x f y
'
(
)
)
(
n nx
f
y
f
. (11)Persamaan (11) merupakan metode iterasi dua titik dengan parameter A, B, C, D, E, F, G, dan H dan melibatkan tiga evaluasi fungsi yaitu f(xn), f '(xn), dan f (yn).
Hasil dan Diskusi
1. Analisis Konvergensi
Salah satu ukuran performa suatu metode iterasi adalah orde konvergensi, baik yang dihitung secara analitis menggunakan ekspansi deret Taylor maupun secara numerik. Berikut ini diberikan orde konvergensi dari metode iterasi (11) menggunakan ekspansi deret Taylor.
Teorema 1. Misalkan D adalah sebuah akar dari fungsi f(x) yang terdiferensial f : DRR untuk interval buka D. Jika x0 cukup dekat ke maka Persamaan (11) memiliki orde konvergensi empat untuk A
= E, dan B = F + 2 yang memenuhi persamaan galat berikut
) ( )) 2 )( ( ' 2 5 ( 2 3 32 23 22 22 22 4 5 1 n n n c c c Fc f Ec Dc Hc e O e e
. (12)Bukti : Misalkan adalah sebuah akar sederhana dari f(x) = 0 maka f() = 0. Asumsikan bahwa f '() 0 dan xn = + en. Selanjutnya dengan menggunakan ekspansi deret Taylor, aproksimasi fungsi f(xn) di sekitar
diberikan oleh ( ) '( )( 4 ( 5)) 4 3 3 2 2 n n n n n n f e c e c e c e O e x f
. (13)Kemudian untuk fungsi f '(xn) diekspansi disekitar xn menggunakan deret Taylor sehingga diperoleh,
'( ) '( )(1 2 3 4 5 5 4 ( 5)) 3 4 2 3 2 n n n n n n f c e c e c e c e O e x f
. (14)Jika Persamaan (13) dibagi dengan Persamaan (14), kemudian dengan menggunakan deret geometri diperoleh ) ( ) 2 2 ( ) ( ' ) ( 3 5 3 2 2 2 2 n n n n n n e O e c c e c e x f x f , (15)
2( ) 3 ( 5). 3 2 2 2 2 n n n n c e c c e O e y
(16)Persamaan (16) juga dapat ditulis ke dalam bentuk:
y
n
s
n,
(17) dengan 2( 3) 3 ( 5) 2 2 2 2 n n n n c e c c e O e s . (18)Oleh karena f () = 0 dan yn= + sn, maka ekspansi deret Taylor terhadap f(yn) disekitar adalah
( ) '( )( 3 3 ( 5)) 2 2 n n n n n f s c s c s O e y f
. (19)Substitusi Persamaan (18) ke Persamaan (19), maka diperoleh,
f(yn) f'(
)(c2en2 (2c22 2c3)en3 (5c23 7c2c3 3c4)en4 O(en5)). (20)Selanjutnya dengan menggunakan Persamaan (13) dan (19), maka kuadrat dari f (xn) dan f (yn)
masing-masing diberikan oleh
f(xn)2 f'(
)2(en2 2c2en3 (2c3 c22)en4 O(en5)), (21) dan ( ) '( ) ( (4 2 3 4 32) 5 ( 6)) 4 2 2 2 2 n n n n f c e c c c e O e y f
. (22)Penjumlahan f(xn) dan f(xn)2, serta penjumlahan f(yn) dan f(yn)2 masing-masing diberikan oleh
3 2 3 2 2 2 ) ) ( ' 2 ( )) ( ' ( )( ( ' ) ( ) (xn Af xn f en c Af en c Af c en f
)) ( ) ) ( ' ) ( ' 2 ( 4 4 5 2 2 3 Af c c en O en c Af
. (23) 3 2 3 2 2 2 ) ) ( ' 2 ( )) ( ' ( )( ( ' ) ( ) (xn Ef xn f en c Ef en c Ef c en f
)) ( ) ) ( ' ) ( ' 2 ( 4 5 4 2 2 3 Ef c c en O en c Ef
. (24) dan 3 2 2 3 2 2 2 ) 2 2 ( )( ( ' ) ( ) (yn Cf yn f Bc en Bc Bc en Bf
(3 7 5 '( ) 22) 4 ( 5)) 3 2 3 2 4 Bc c Bc Cf c en O en Bc
. (25) 2 3 2 3 2 2 2 ) 2 2 ( )( ( ' ) ( ) (yn Gf yn f Fc en Fc Fc en Ff
)) ( ) ) ( ' 5 7 3 ( 22 4 5 3 2 3 2 4 Fc c Fc Hf c en O en Fc
. (26)Sedangkan perkalian f(xn) dan f(yn), diberikan oleh
( ) ( ) '( ) ( (2 2) 4 ( 5)) 2 3 3 2 2 n n n n n f y f D c e c c e O e x Df
. (27) ( ) ( ) '( ) ( (2 3 22) 4 ( 5)) 3 2 2 n n n n n f y f H c e c c e O e x Hf
. (28)Selanjutnya, bagi Persamaan (20) terhadap Persamaan (13) maka diperoleh
)
(
)
4
2
(
)
(
'
)
(
2 3 5 2 3 2 2 n n n n ne
O
e
c
c
e
c
x
f
y
f
. (29)Berikutnya hasil dari
2 2 2 2 2 ( n) ( n) ( n) ( n) ( n) ( n) '( ) n ( '( ) ) n f x Af x Bf y Cf y Df x f y f e c Af Bc e
2 3 5 3 3 2 2 2 (c 2Bc 2Bc 2Af'( )c Df'( ) ) c en O e( )n . (30) dan f x( n)Ef x( n)2Ff y( n)Gf y( n)2Hf x( n) (f yn) f'( )
en(c2Ef'( ) Fc e2) n2
2 3 5 3 3 2 2 2 (c 2Fc 2Fc 2Ef'( ) c Hf'( ) ) c en O e( )n . (31)Gunakan Persamaan (30) dan (31), maka diperoleh
2 2 2 2 2 2 ( ) ( ) ( ) ( ) ( ) ( ) 1 '( )( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n n n n n n f x Af x Bf y Cf y Df x f y f A E Bc Fc e f x Ef x Ff y Gf y Hf x f y
2(B F c) 3 ( '( )(f A D E H AF BE 2EF c) 2
2 2 2 2 2 2 5 2 2 (F BF 3(F B c)) f'( ) ( E AE c) ) en O e( )n . (32)Kemudian substitusi Persamaan (16), (29) dan (32) ke Persamaan (11) dan dengan menggunakan manipulasi aljabar, maka diperoleh orde konvergensi metode iterasi (11) dalam bentuk
2
3 1 '( )( ) 2 (2 ) 2 n n x f EA c B F c e
2 3 2 3 2 3 2 '( ) ( ) '( )( )2 (7 4 4 ) (( 7) (7 9)) f A E Ec f E A c B F c c B F F B c
2 4 5 2 '( )( ( )3 (2 ) ( )) n ( )n f E A E A F BE D H c e O e . (33)Akhirnya, oleh karena xn+1 = + en+1, Persamaan (33) menjadi
3 2 2 2 1 ( '( )( ) (2 ) ) n n f E A c B F c e e
3 2 3 2 3 2 2 )) 9 7 ( ) 7 (( ) 4 4 7 ( 2 ) )( ( ' ) ( ) ( ' A E Ec f E A c B F cc B F F B c f
( ) )) ( ) 2 ( 3 ) ( )( ( ' E A E A F BE D H c22 en4 O en5 f
. (34)Berdasarkan Persamaan (38) dapat dilihat bahwa orde konvergensi pada Persamaan (11) meningkat dengan menentukan A = E dan B = F + 2. Oleh karena itu, dengan mensubstitusikan kembali nilai A = E dan B = F + 2 ke Persamaan (34), maka diperoleh
3 2
4 51 2 3 (5 2 ) 2 '( )(2 ) 2 ( )
n n n
e c c F c f E D H c e O e (35)
Persamaan (35) memperlihatkan bahwa metode iterasi yang diberikan pada Persamaan (11) mempunyai orde konvergensi empat untuk A = E, B = F +1, dan D, E, F, H.
Bentuk Khusus
Adanya delapan parameter pada Persamaan (11), memberikan kemungkinan metode iterasi dapat membentuk metode iterasi lainnya dengan memberikan nilai-nilai sembarang parameter.
a. Selanjutnya dengan mengganti A = E dan B = F + 2 diperoleh metode iterasi berode konvergensi empat dengan enam parameter yang ditulis dalam bentuk
2 2 1 2 2 ( ) ( ) ( 2) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n n n n n n n n n n n n f x Ef x F f y Cf y Df x f y x y f x Ef x Ff y Gf y Hf x f y ( ) '( ) n n f y f x . (36)
Berikut ini beberapa metode iterasi yang dapat dibentuk.
Untuk kasus C = D = E = G = H = 0 dan F R memberikan beberapa kemungkinan metode iterasi: - Untuk F R, Persamaan (11) menjadi metode iterasi King [12].
- Untuk F =2, Persamaan (11) menjadi metode iterasi Chun [13].
- Untuk F = 1, Persamaan (14) menjadi metode iterasi dalam bentuk [16] 2 2 1 ( ) ( ) '( )( ( ) ( )) n n n n n n n f x f y x x f x f x f y . (37)
- Untuk F = 0, Persamaan (14) menjadi metode Alamsyah dan Wartono [9] untuk = 1 yang diberikan dalam bentuk
1 ( ) ( ) ( ) 1 2 '( ) ( ) '( ) n n n n n n n n f x f y f y x x f x f x f x . (38) - Untuk 5, 3, 7 2 2 2
F , Persamaan (11) menjadi metode Noor [16] yang masing-masing ditulis
'
(
)
)
(
)
(
5
)
(
2
)
(
)
(
2
)
(
'
)
(
1 n n n n n n n n n nx
f
y
f
y
f
x
f
y
f
x
f
x
f
x
f
x
x
, (39)'
(
)
)
(
)
(
3
)
(
2
)
(
)
(
2
)
(
'
)
(
1 n n n n n n n n n nx
f
y
f
y
f
x
f
y
f
x
f
x
f
x
f
x
x
, (40) dan'
(
)
)
(
)
(
7
)
(
2
)
(
3
)
(
2
)
(
'
)
(
1 n n n n n n n n n nx
f
y
f
y
f
x
f
y
f
x
f
x
f
x
f
x
x
. (41)b. Untuk A = B = C = D = E = F = G = H = 0, Persamaan (11) menjadi metode Potra-Ptak [18]. 2. Simulasi Numerik
Untuk menguji performa metode baru pada Persamaan (11) yang disingkat GMID, diberikan simulasi numerik menggunakan perangkat lunak Maple 13 dengan 850 digit arithmetic Selanjutnya performa yang diuji adalah jumlah iterasi dan nilai mutlak fungsi pada iterasi ke-n, sedangkan metode iterasi pembanding adalah metode Newton [3], metode Chun [13], metode Newton Ganda [10], dan metode Noor [16] yang masing-masing disingkat MN, MC, MND dan MNR.
Simulasi numerik dilakukan dengan mengambil tebakan awal x0 sedekat mungkin dengan akar persamaan dengan menampilkan 15 digit aritmetik. Adapun fungsi yang akan digunakan adalah sebagai berikut.
10 4 ) ( 3 2 1 x x x f , = 1,365230034140968, 2 2(x) e 4x f x , = 4,306584728220699,
1
)
1
(
)
(
6 3x
x
f
, = 2,000000000000000,5
)
ln(
)
(
4x
x
x
f
, = 8,309432694231571,1
)
1
cos(
)
(
2 3 5 2
x
x
e
x
f
x x , = 1,000000000000000, 1 , 0 ) ( 6 x xe x f , = 0,111832559158962,x
x
x
f
7(
)
cos(
)
, = 0,739085133215160, 1 ) ( sin ) ( 2 8 x x x f , = 1,4044916482153441.Banyaknya jumlah iterasi yang digunakan oleh metode iterasi (11) dan metode iterasi lainnya, dan penghentian program komputasi menggunakan kriteria berikut,
n nx
x
1 . (42)dengan
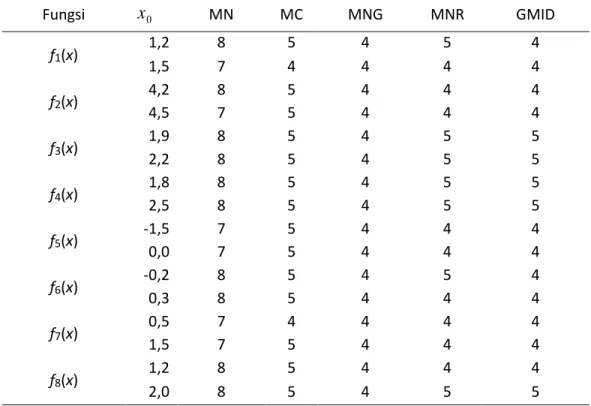
1095, seperti diperlihatkan dalam tabel berikut.Tabel 1 Perbandingan Jumlah Iterasi dengan
1095Fungsi
x
0 MN MC MNG MNR GMID f1(x) 1,2 8 5 4 5 4 1,5 7 4 4 4 4 f2(x) 4,2 8 5 4 4 4 4,5 7 5 4 4 4 f3(x) 1,9 8 5 4 5 5 2,2 8 5 4 5 5 f4(x) 1,8 8 5 4 5 5 2,5 8 5 4 5 5 f5(x) -1,5 7 5 4 4 4 0,0 7 5 4 4 4 f6(x) -0,2 8 5 4 5 4 0,3 8 5 4 4 4 f7(x) 0,5 7 4 4 4 4 1,5 7 5 4 4 4 f8(x) 1,2 8 5 4 4 4 2,0 8 5 4 5 5Berdasarkan Tabel 1 jumlah iterasi dari metode iterasi baru dan metode iterasi lainnya yang berorde empat lebih sedikit dibandingkan metode-metode lainnya.
Selain jumlah iterasi, ukuran lain performa suatu metode iterasi ditentukan oleh orde konvergensi yang dihitung secara komputasi yang diberikan oleh
1 1 ln ( ) / ( ) ln ( ) / ( ) n n n n x x x x . (43)
Orde konvergensi yang dihitung secara komputasi (computational order of convergence atau COC) dengan rumus yang diberikan oleh persamaan (43) dengan menggunakan ketelitian sebesar 10-95 ditunjukkan pada tabel berikut.
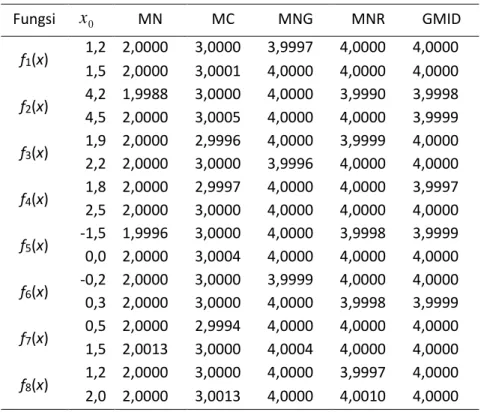
Tabel 2 Perbandingan COC dengan
1095Fungsi
x
0 MN MC MNG MNR GMID f1(x) 1,2 2,0000 3,0000 3,9997 4,0000 4,0000 1,5 2,0000 3,0001 4,0000 4,0000 4,0000 f2(x) 4,2 1,9988 3,0000 4,0000 3,9990 3,9998 4,5 2,0000 3,0005 4,0000 4,0000 3,9999 f3(x) 1,9 2,0000 2,9996 4,0000 3,9999 4,0000 2,2 2,0000 3,0000 3,9996 4,0000 4,0000 f4(x) 1,8 2,0000 2,9997 4,0000 4,0000 3,9997 2,5 2,0000 3,0000 4,0000 4,0000 4,0000 f5(x) -1,5 1,9996 3,0000 4,0000 3,9998 3,9999 0,0 2,0000 3,0004 4,0000 4,0000 4,0000 f6(x) -0,2 2,0000 3,0000 3,9999 4,0000 4,0000 0,3 2,0000 3,0000 4,0000 3,9998 3,9999 f7(x) 0,5 2,0000 2,9994 4,0000 4,0000 4,0000 1,5 2,0013 3,0000 4,0004 4,0000 4,0000 f8(x) 1,2 2,0000 3,0000 4,0000 3,9997 4,0000 2,0 2,0000 3,0013 4,0000 4,0010 4,0000Berdasarkan Tabel 2 dapat dilihat bahwa nilai COC pada setiap fungsi dari Persamaan (11) mendekati 4 (empat). Oleh karena itu dapat disimpulkan bahwa metode pada Persamaan (11) memiliki orde konvergensi 4 (empat).
Selanjutnya nilai nilai mutlak fungsi, |f(xn)| pada setiap metode iterasi dengan menggunakan Total Number of Functional Evaluation (TNFE) yang sama sebesar 12 evaluasi fungsi, seperti ditunjukkan dalam tabel berikut.
Tabel 3 Nilai |f(xn)| dengan TNFE=12
Fungsi
x
0 MN MC MNG MNR GMIDf1(x) 1,2 2,7417e – 35 8,0815e – 45 3,9823e – 43 3,4525e – 14 2,0486e – 124 1,5 4,5366e – 76 1,7344e – 96 4,5366e – 76 1,2273e – 62 4,5178e – 182 f2(x) 4,2 2,6996e – 45 1,4792e – 57 2,6996e – 45 2,1964e – 26 5,1992e – 121 4,5 3,1919e – 52 2,4261e – 66 3,1919e – 52 3,6357e – 40 1,7482e – 105 1,9 7,2278e – 36 3,4892e – 45 7,2274e – 36 3,8007e – 15 1,6019e – 33
Fungsi
x
0 MN MC MNG MNR GMIDf3(x) 2,2 2,7348e – 26 3,7378e – 33 2,7348 e-26 9,6064e – 18 1,0775e – 54 f4(x) 1,8 2,8660e – 41 4,2365e – 52 2,8660 e-41 2,8694e – 21 3,4640e – 50
2,5 3,8845e – 28 1,5951e – 35 4,6449 e-16 2,0875e – 19 1,4617e – 58 f5(x) -1,5 5,7389e – 66 5,1899e – 92 5,7389e – 66 1,4576e – 56 9,5119e – 131
0,0 1,9261e – 65 9,3636e – 73 1,9261e – 65 2,2067e – 47 5,7241e – 134 f6(x) -0,2 1,0735e – 42 9,0538e – 54 1,0735e – 42 4,5325e – 23 8,1694e – 136 0,3 3,0850e – 36 1,2725e – 45 3,0850e – 36 3,8010e – 26 8,5238e – 106 f7(x) 0,5 2,6328e – 78 6,3304e – 33 2,6328e – 78 8,6634e – 62 4,9531e – 250 1,5 3,7607e – 64 3,5077e – 80 3,7607e – 64 1,4098e – 52 6,9210e – 136 f8(x) 1,2 2,0864e – 47 7,4954e – 60 2,0864e – 47 2,8002e – 28 1,4071e – 167 2,0 2,2623e – 32 8,2994e – 41 2,2623e – 32 3,0978e – 23 4,6600e – 69 Berdasarkan Tabel 3 dapat dilihat bahwa nilai mutlak fungsi, |f(xn)| pada metode iterasi baru lebih kecil dibandingkan dengan metode lainnya. Hal ini menunjukkan bahwa metode iterasi pada Persamaan (11) mempunyai akurasi yang lebih baik dibandingkan metode lainnya.
Kesimpulan
Pada artikel ini, metode iterasi baru yang diberikan pada Persamaan (11) dikonstruksi dengan cara memperumum bentuk metode iterasi dua titik yang melibatkan delapan parameter real. Metode iterasi baru memiliki orde konvergensi 4 (empat) untuk A = E dan B = F + 2 dengan persamaan galat yang diberikan oleh ) ( ) ) 2 )( ( ' ) 2 5 ( ( 22 4 5 3 2 3 2 1 n n n c c F c f E D H c e O e e
. (44)Metode iterasi baru pada Persamaan (11) memerlukan tiga evaluasi fungsi untuk setiap iterasinya sehingga menghasilkan indeks efisiensi sebesar 41/3 1, 5874. Berdasarkan Tabel 1 dan 2 dapat dilihat bahwa Persamaan (11) memiliki nilai COC yang lebih tinggi dibandingkan metode iterasi lainnya. Selain itu, Persamaan (11) memiliki jumlah iterasi paling sedikit sehingga dapat dikatakan bahwa Persamaan (11) lebih efektif dalam menghampiri akar-akar suatu persamaan nonlinier, sedangkan Tabel 3 menunjukkan bahwa metode iterasi baru mempunyai akurasi yang lebih baik dibandingkan dengan metode iterasi pada proses menghampiri akar-akar persamaan nonlinear.
Ucapan Terima Kasih
Penulis mengucapkan terima kasih kepada seluruh pihak yang telah membantu baik moril maupun materil sehingga artikel ini dapat selesai tepat waktu.
Referensi
[1] J. H. Mathews, “Numerical Methods for Mathematics, Science, and Engineering”, Prentice-Hall Inc., New Jersey, 1993.
[2] S. C. Chapra dan R. P. Canale, “Numerical Methods for Engineers”, McGraw-Hill, New York, 2010. [3] J. F. Traub, “Iterative Method to Solution of Equations”, Chelsea Publishing Company, New York,
1964.
[4] S. Amat, S. Busquier, J. M. Gutierrez, dan M. A. Hernandez, “On the global convergence of Chebyshev’s method”, Journal of Computational and Applied Mathematics, 220: 17 – 21, 2008. [5] A. Melman, “Geometry and convergence of Euler’s and Halley’s methods”, SIAM Review, 39(4): 728
– 735, 1997.
[6] I. K. Argyros, “A note on the Halley Method in Banach spaces”. Mathematics and Computation, 58 : 215 - 224, 1993.
[7] V. Candela, dan A. Marquina., “Recurrence relations for rational cubic methods the Halley method”, Departamento de Analisis Matematico, 44 : 169 - 184, 1990.
[8] C. Chun, “Construction of Newton-like iteration methods for solving nonlinear equations”, Numerische Mathematik, 104: 297 – 315, 2006.
[9] Alamsyah dan Wartono, “Modifikasi metode Cauchy tanpa turunan kedua dengan orde konvergensi empat”, Jurnal Sains Matematika dan Statistika, 3(2): 59 – 66, 2017.
[10] C. Chun, dan Y. M. Ham, “Some fourth-order modifications of Newton’s method”, Applied Mathematics and Computation, 197: 654 - 658, 2008.
[11] C. Chun, “Some fourth order iterative method for solving nonlinear equation”, Applied Mathematics and Computation, 195 : 454 - 459, 2008.
[12] R. F. King, “A family of fourth order method for nonlinier equation”, Siam Journal on Numerical Analysis, 10: 876-879, 1973.
[13] C. Chun, “Some variants of King’s fourth order family of method nonlinear equation”. Applied Mathematics and Computation, 190 : 57 - 62, 2007.
[14] J. R. Sharma, R. K. Guha dan R. Sharma, “Some modified Newton’s method with fourth-order convergence”, Advances in Applied Science Research, 2(1): 240 - 247, 2011.
[15] A. Husni dan Wartono, “Modifikasi metode iterasi dua langkah menggunakan kombinasi linear tiga parameter real”, Euclid, 6(2): 157 – 166, 2019.
[16] M. A. Noor, “Some iterative methods for solving nonlinear equations using homotopy perturbation method”, International Journal of Computer Mathematics, 87(1): 141 – 149, 2010.
[17] B. Ghanbari, “A new general fourth-order family of methods for finding simple roots of nonlinear equations”, Journal of King Saud University, 23 : 395 - 398, 2011.
[18] F. A. Potra dan V. Ptak, “Non Discrete introduction and iterative processes”, In Research Notes in Mathematics, 103, Pitman, Boston, 1984.