Data input yang digunakan dalam penelitian ini adalah data (real) seismik post stack

BAB IV

PROSEDUR PENELITIAN

4.1. Data Penelitian

Data input yang digunakan dalam penelitian ini adalah data (real) seismik post stack time migration (PSTM) tiga dimensi (3-D). Data tersebut dimulai dari inline 1001 sampai dengan 1474, dengan spasi antar inline 25 meter. Dan Crossline 4923 sampai dengan 5437 dengan spasi antar crossline 12.5 meter. Serta dengan rangetime dari 0 sampai 3996 ms, dengan sampling rate 2.

4.2. Perangkat Penelitian

Dalam penelitian ini digunakan beberapa perangkat komputer. Perangkat keras yang digunakan adalah satu unit Workstation (Sun Blade 1000 / Solaris 8 / DELL PRECISION 390), dua buah monitor 24 inch, Server (Sun Enterprise 450 / Solaris 8, 4GB, 8 x 433 (64bit) MHz prosessor), dan Network: workgroupswitch 10-100 MB/s. Serta peralatan standar berupa satu unit Personal Computer.

4.3. Pemrograman Semblans dan Koherensi dengan Algoritma Struktur Eigen

Proses pemrograman dalam penelitian ini menggunakan MATLAB dan beberapa produk open sourceunder MATLAB untuk pengolahan data seismik, yaitu SEISLAB dan CREWES.

▸ Baca selengkapnya: dibawah ini yang bukan termasuk dalam menyimpan data adalah

4.3.1. Pembacaan dan Menampilkan Data Seismik (SEGY) 3D

Pembacaan data seismik 3D standard, yang tersimpan dalam file dengan ekstensi “.SEGY”, oleh MATLAB dapat dilakukan dengan modul SEISLAB atau CREWES.

Output pembacaan ini adalah berupa data matriks 2D (i x j), dimana komponen baris (i) adalah komponen time sampel dari data seismik dan komponen kolom (j) adalah komponen trace-nya.

Gambar 4.1. Workspace hasil pembacaan data SEGY

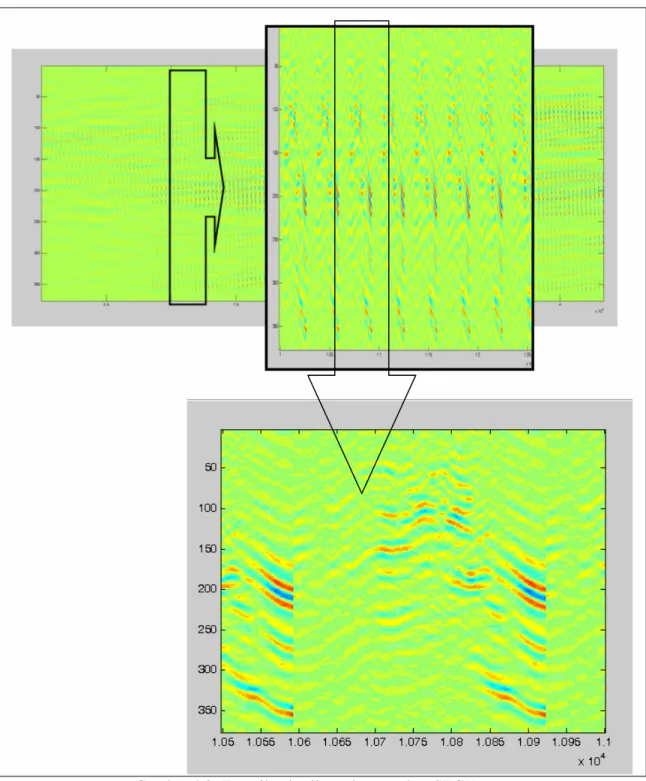
Tampilan di atas menunjukkan workspace hasil proses pembacaan awal data seismik ini. ‘dataout’ merupakan matriks data seismik yang telah dibaca. Jika trace seismik tersebut ditampilkan (Gambar 4.2), maka akan diketahui bahwa nilai 376 pada dataout tersebut adalah jumlah komponen time-sample, sedangkan nilai 43361 merupakan jumlah komponen trace data seismik.

Gambar 4.2. Tampilan hasil pembacaan data SEGY

Hasil pembacaan menunjukkan pola pengulangan ataupun putusnya data pada interval 331.

Langkah selanjutnya adalah bagaimana data di atas dapat diproses dalam 3D, maka akan dijelaskan pada sub-bab berikut.

4.3.2. Membaca dan menampilkan geometri header

Proses ini dilakukan agar didapatkan gambaran yang jelas tentang kondisi jumlah dan geometri dari data seismik yang akan digunakan dalam perhitungan. Dengan fasilitas dari SEISLAB, proses ini dapat dilakukan dengan perintah:

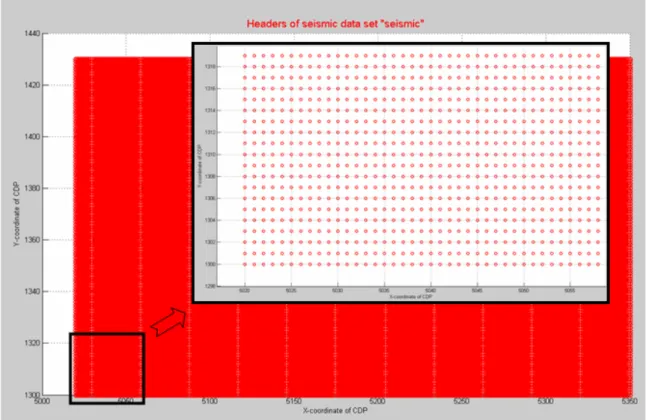
s_header_plot(seismic,{'cdp_x','cdp_y'},{'colors','ro'});

Gambar 4.3. Tampilan geometri header survey eismik dari hasil pembacaan data SEGY

Dari hasil di atas, maka dapat diketahui jumlah trace inline dan crossline dari data seismik terbaca. Dimana Inline data adalah dari 1300-1430, yaitu

sejumlah 131 trace, dan Xline adalah dari 5020-5350, yaitu sebanyak 331 trace. Maka, total keseluruhan trace data adalah jumlah trace inline dikali dengan jumlah trace xline; 131 x 331, yaitu sama dengan empat puluh tiga ribu tiga ratus enam puluh satu (43361).

Sehingga dapat diketahui pula, bahwa tampilan dua dimensi pada hasil pembacaan data seismik di atas pada hakikatnya merupakan tampilan penampang xline yang dijajarkan.

4.3.3. Membentuk matriks dan menampilkan penampang data 3D

Proses ini dilakukan dengan urutan program singkat ‘menampilkan data 3 dimensi’ sebagai berikut:

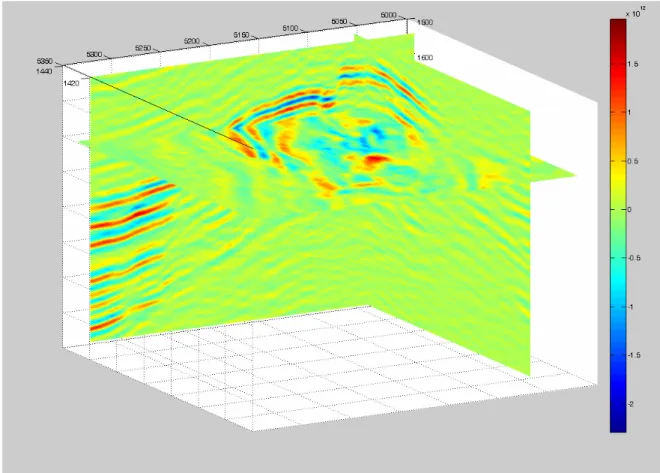
z=dataout’; data3D=reshape(z,[331,131,376]); treal = (1500:2:2250); xreal = (1300:1:1430); yreal = (5020:1:5350); [x,y,z] = meshgrid(xreal,yreal,treal);

figure;slice(x,y,z,data3D,1420,5068,1700);set(gca,’ydir’,’reverse’); shading interp

Gambar 4.4. Program ‘menampilkan data 3 dimensi’

Urutan program di atas meliputi proses mengembalikan matriks 2D menjadi matriks 3D (i x j x k). Hal ini dapat dilakukan dengan perintah reshape dan dengan pengetahuan yang jelas akan jumlah dan posisi inline dan xline dari data. Hasilnya, didapatkan matriks data tiga dimensi yang mewakili 331 xline, 131 inline, dan 376 timesample.

Gambar 4.5. Workspace hasil program ‘menampilkan data 3 dimensi’

Selanjutnya adalah menampilkan image slice dari masing-masing komponen, dengan terlebih dahulu mendefinisikan koordinat inline, xline, dan time yang sebenarnya dari data.

Gambar 4.6. Penampang seismik dengan tampilan crossing pada xline 5068, inline 1420, dan time 1700

4.3.4. Program Semblans dan Koherensi Struktur Eigen

Berdasarkan penjelasan algoritma koherensi pada bab III, maka dibuatlah bahasa programming pada MATLAB sebagai berikut;

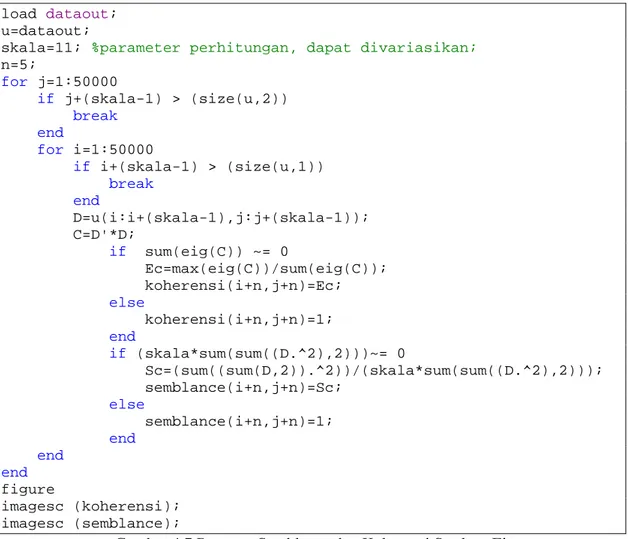
load dataout; u=dataout;

skala=11; %parameter perhitungan, dapat divariasikan;

n=5; for j=1:50000 if j+(skala-1) > (size(u,2)) break end for i=1:50000 if i+(skala-1) > (size(u,1)) break end D=u(i:i+(skala-1),j:j+(skala-1)); C=D'*D; if sum(eig(C)) ~= 0 Ec=max(eig(C))/sum(eig(C)); koherensi(i+n,j+n)=Ec; else koherensi(i+n,j+n)=1; end if (skala*sum(sum((D.^2),2)))~= 0 Sc=(sum((sum(D,2)).^2))/(skala*sum(sum((D.^2),2))); semblance(i+n,j+n)=Sc; else semblance(i+n,j+n)=1; end end end figure imagesc (koherensi); imagesc (semblance);

Gambar 4.7 Program Semblance dan Koherensi Struktur Eigen

Sebagai input dari program ini adalah data matriks hasil pembacaan data seismik ‘.SEGY’, yang masih berupa data matriks dua dimensi. Selanjutnya, dilakukan penentuan parameter perhitungan yaitu skala data yang akan dilibatkan dalam satu kali perhitungan algoritma koherensi. Dalam penelitian ini, ditentukan beberapa parameter/skala yang berbeda untuk kemudian dilihat tingkat skala terbaik dalam memberikan tampilan koherensi dari data

yang bersangkutan untuk dapat diinterpretasi. Adapun skala yang digunakan adalah skala 3, 5, 9 dan 11.

4.4. Pengolahan Data menggunakan Software 4.4.1. Operasi Coherence Cube

Pada operasi Coherence Cube dilakukan kuantifikasi dari pengukuran similaritas/kesamaan bentuk gelombang dari lokalisasi data seismik pada aperture “global”, dengan memanfaatkan perhitungan dip dan azimuth. Kualitas hasil coherence cube bergantung pada pemilihan parameter prosessing, terutama aperture temporal dan spasial dalam algoritma perhitungannya.

ƒ Input

Dalam prosesi ini dapat dilakukan pengaturan range data seismik yang akan dilibatkan dalam perhitungan. Hal ini biasa disesuaikan dengan zona interest yang ingin diteliti, termasuk dalam rangka efektifitas penggunaan space hardware. Maka untuk penelitian ini, range yang dipilih (dari data input awal) sebagai berikut:

o Inline: 1002-1468 o Xline: 4924-5438

o Time(slice Z): 1500-2250

ƒ Parameter

Sebagaimana telah disebutkan di depan, pemilihan parameter dalam mengeksekusi program coherence cube ini merupakan hal yang paling

menentukan kualitas output yang akan dihasilkan. Parameter-parameter tersebut antara lain:

9 Temporal aperture

Aperture temporal atau lebar window merupakan parameter yang paling kritis/penting. Secara umum, aperture yang lebih pendek/kecil digunakan ketika akan melihat komponen-komponen stratigrafi atau sesar dengan sudut yang sangat kecil. Sedangkan aperture yang lebih lebar digunakan untuk mendeteksi komponen struktur yang lebih nyata secara vertikal, seperti sesar dengan sudut yang besar

Aperture yang lebih lebar dapat dipakai untuk mengurangi efek noise pada hasil koherensi, namun dapat berefek pada tidak jelasnya suatu event-event yang pendek/kecil seperti channel.

Dalam proses ini, nilai aperture yang dimasukkan merupakan setengah dari aperture itu sendiri; nilai n mengindikasikan bahwa yang dilibatkan dalam satu kali perhitungan terdiri atas n sample yang berada di atas dan nsample yang berada di bawah suatu titik tengah perhitungan.

9 Spatial aperture

Aperture ini menentukan pilihan berupa jumlah dan jauhnya trace yang akan dilibatkan dalam satu kali perhitungan. Dalam prakteknya, jika dipilih n sebagai nilai aperturenya, berarti trace ke n pada setiap sisi yang bersebelahan dengan trace yang akan dihitung akan dilibatkan

dalam perhitungaannya (jika tipe aperture spasialnya berbentuk persegi). Dalam hal ini, adapun nilai aperture yang dipilih adalah antara satu sampai dengan tiga, pada inline maupun xline.

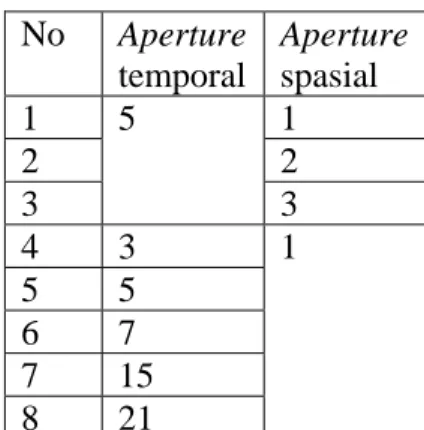
Dalam penelitian ini, ditentukan beberapa variasi parameter untuk melihat output yang paling optimal dalam memberikan tafsiran struktur yang diinginkan sebagai berikut:

No Aperture temporal Aperture spasial 1 1 2 2 3 5 3 4 3 5 5 6 7 7 15 8 21 1

Tabel 4.1. Variasi parameter Coherence Cube

4.4.2. Operasi Atribut Spectral Decomposition

Perhitungan Spectral Decomposition ini menggantikan input trace tunggal dengan trace gather yang menunujukkan pemisahan/pemecahan spektral dari atribut input. Input dari perhitungan ini sendiri adalah volum seismik, sedangkan outputnya terdiri atas beberapa volum yang masing-masing merepresentasikan data dengan pita frekuensi yang berbeda.

Dari hasil atribut spectral decomposition ini, dapat dilihat iluminasi struktur dari berbagai pita frekuensi yang berbeda; dapat dipilih pita frekuensi mana yang memberikan resolusi terbaik.

Selanjutnya, output dari spectral decomposition tersebut kembali dijadikan input coherence cube.

Adapun dalam penelitian ini, ditentukan output Spectral Decomposition untuk menghasilkan band atau banyaknya tampilan frekuensi sejumlah sepuluh volume. Range frekuensi yang digunakan adalah 10Hz sampai dengan 50Hz Dan increment atau jarak frekuensinya ditentukan dari rumus octave increment yaitu menggunakan filter Gabor-Morlet sebagai berikut:

dimana,

Fi = frekuensi ke-i

Flow = batas bawah freluensi Fhigh = batas atas frekuensi