BAB II LANDASAN TEORI

BAB II

LANDASAN TEORI

A. Segitiga Datar

1. Pengertian Segitiga

Diberikan tiga buah titik A, B, dan C yang tidak segaris. Titik A dihubungkan dengan titik B, titik B dihubungkan dengan titik C, dan titik C dihubungkan dengan titik A. Bangun yang terbentuk disebut segitiga.

AB , BC , dan AC disebut sisi segitiga ABC. Titik A, B, dan C disebut titik sudut. Ketiga sisi segitiga saling berpotongan dan membentuk sudut, yaitu A, B, dan C. Jadi, sebuah segitiga memiliki tiga titik sudut, tiga sisi dan tiga sudut.

2. Jenis Segitiga

Bentuk segitiga ditentukan oleh panjang sisi dan besar sudut yang dimiliki, sebagai berikut :

A B

C

a. Jenis segitiga ditinjau dari besar sudut-sudutnya

Ditinjau dari besar sudut-sudutnya, segitiga dibedakan menjadi tiga yaitu :

1) Segitiga lancip yaitu segitiga yang besar tiap sudutnya kurang dari 90º.

2) Segitiga tumpul yaitu segitiga yang besar salah satu sudutnya lebih dari 90º.

3) Segitiga siku-siku yaitu segitiga yang besar salah satu sudutnya 90º.

b. Jenis segitiga ditinjau dari panjang sisi-sisinya

Ditinjau dari panjang sisi-sisinya, segitiga dibedakan menjadi tiga yaitu :

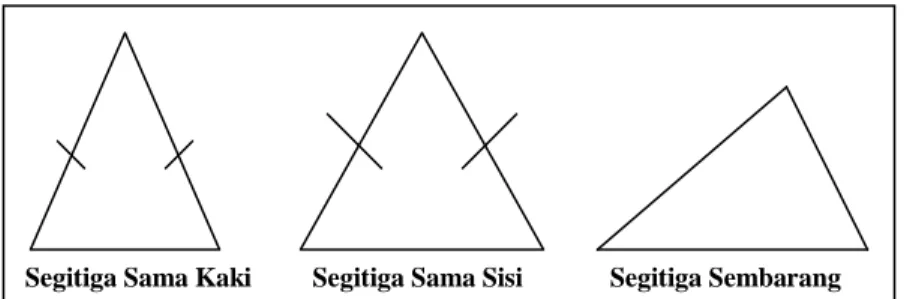
1) Segitiga sama sisi yaitu segitiga yang ketiga sisinya sama panjang.

2) Segitiga sama kaki yaitu segitiga yang mempunyai dua sisi sama panjang.

3) Segitiga sembarang yaitu segitiga yang ketiga sisinya tidak sama panjang satu sama lain.

Segitiga Lancip Segitiga Tumpul _{Segitiga Siku-Siku}

3. Aturan Cosinus

Aturan cosinus dalam trigonometri adalah aturan yang memberikan hubungan yang berlaku dalam suatu segitiga, yaitu antara panjang sisi-sisi segitiga dan cosinus dari salah satu sudut dalam segitiga tersebut. (Wikipedia, 2011)

Aturan kosinus menyatakan bahwa :

 cos . . 2 2 2 2 qp p q r   

dengan  adalah sudut yang dibentuk oleh sisi q dan sisi p, dan r adalah sisi yang berhadapan dengan sudut  .

Aturan yang sama berlaku pula untuk sisi q dan sisi p :

 cos . . 2 2 2 2 pr r p q     cos . . 2 2 2 2 qr r q p   

Dengan kata lain, bila panjang dua sisi sebuah segitiga dan sudut yang diapit oleh kedua sisi tersebut diketahui maka dapat

Gambar 3 : Jenis Segitiga menurut Panjang Sisi-sisinya

Gambar 4 : Segitiga Sembarang

Segitiga Sama Sisi Segitiga Sembarang Segitiga Sama Kaki

P R r q p α β γ Q

ditentukan panjang sisi yang lain. Jika panjang ketiga sisi diketahui, dapat ditentukan besar sudut dalam segitiga tersebut. Dari aturan kosinus dapat diperoleh :

i. r2 q2 p22.qp.cos 2.qp.cos q2 p2r2 qp r p q . 2 cos 2 2 2     ii. q2  p2 r2 2.pr.cos 2 2 2 cos . . 2 pr   p r q pr q r p . 2 cos 2 2 2     iii. p2 q2 r2 2.qr.cos 2.qr.cos q2r2 p2 qr p r q . 2 cos 2 2 2     Aturan kosinus :  cos . . 2 2 2 2 qr r q p     cos . . 2 2 2 2 pr r p q     cos . . 2 2 2 2 qp p q r   

B. Bola

Tempat kedudukan titik – titik yang berjarak r dari titik tetap P dinamakan permukaan bola atau bola. Lihat gambar 1, P adalah pusat bola dan r adalah jari – jari bola.

Misalkan titik A pada permukaan bola. Garis yang menghubungkan A dengan P, lanjutannya akan memotong permukaan bola pada titik A1. Titik A1 dinamakan titik lawan dari A, sebaliknya titik A dinamakan titik lawan dari A1.

• P

Gambar 5

P = Pusat bola ; r = jari – jari bola r A1 A • P Gambar 6 A1 = titik lawan A A = titik lawan A1

Irisan permukaan bola dengan bidang datar yang melalui pusat bola, dinamakan lingkaran besar.

Irisan permukaan bola dengan bidang yang berjarak dari pusat bola lebih kecil dari jari – jari bola, dinamakan lingkaran kecil.

C. Segitiga Bola

Segitiga bola terjadi jika tiga buah lingkaran besar pada permukaan sebuah bola saling berpotongan. Ketiga titik potong merupakan titik-titik sudut dengan sisinya yang berhadapan dengan sudut-sudut segitiga bola tersebut. Dari sudut-sudut dan sisi-sisi segitiga bola dapat

P • L Gambar 7 L = Lingkaran besar • P LI Gambar 8 LI = Lingkaran kecil

ditentukan penurunan rumus-rumus pokok untuk suatu segitiga bola yang menunjukkan unsur-unsur yang terdapat pada segitiga bola. (Ali, 1997)

Sisi-sisi p, q, r dan sudut – sudut P, Q, R satuannya adalah derajat. Dalam segitiga bola bila diketahui 3 hal maka 3 lainnya dapat dicari dengan rumus-rumus segitiga bola.

1. Aturan Sinus

Jika sebuah segitiga bola dengan sisi-sisi p, q, r dan sudut-sudut P, Q, R seperti pada gambar berikut :

P Q R O r q p P Q R p r q

Gambar 9 : Segitiga Bola r q R P

Q

p

Maka dalam segitiga bola PQR akan berlaku hubungan : r R q Q p P sin sin sin sin sin sin _{ }

Pada segitiga TUW :

TW = TU sin P ... (1) Pada segitiga TVW :

TW = TV sin Q ... (2) Dari persamaan (1) dan (2) diperoleh :

TU sin  = TV sin Q ... (3) Pada segitiga OTU :

TU = OT sin q ... (4) Pada segitiga TVO :

TV = OT sin p ... (5) Dari persamaan (3), (4) dan (5) diperoleh :

TU sin  = TV sin Q

OT sin q . sin P = OT sin p . sin Q sin q . sin P = sin p . sin Q

Gambar 10 : Segitiga Bola P R O U W T V p r q Q

q Q p P sin sin sin sin  ... (6)

Melalui cara yang sama, maka dapat dibuktikan : r R p P sin sin sin sin _ ... (7)

Dari persamaan (6) dan (7) terbukti bahwa : r R q Q p P sin sin sin sin sin sin _{ } (Hanafiah dkk, 1992) 2. Aturan Cosinus

Berikut ini ditunjukkan pembuktian rumus-rumus pokok untuk suatu segitiga bola PQR. Rumus-rumus ini menunjukkan hubungan antara unsur-unsur yang terdapat pada segitiga bola.

(1) Rumus Cosinus untuk sisi – sisi segitiga bola. cos p = cos q . cos r + sin q sin r . cos P cos q = cos p . cos r + sin p sin r . cos Q cos r = cos p . cos q + sin p sin q . cos R (2) Rumus Cosinus untuk sudut – sudut segitiga bola.

cos P = cos Q . cos R + sin Q sin R . cos p cos Q = cos P . cos R + sin P sin R . cos q cos R = cos P . cos Q + sin P sin Q . cos r (Smart, 1980)

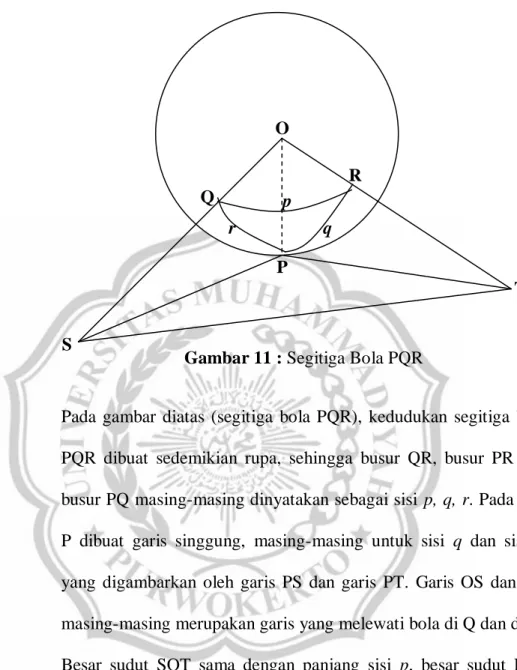
Pada gambar diatas (segitiga bola PQR), kedudukan segitiga bola PQR dibuat sedemikian rupa, sehingga busur QR, busur PR dan busur PQ masing-masing dinyatakan sebagai sisi p, q, r. Pada titik P dibuat garis singgung, masing-masing untuk sisi q dan sisi r, yang digambarkan oleh garis PS dan garis PT. Garis OS dan OT masing-masing merupakan garis yang melewati bola di Q dan di R. Besar sudut SOT sama dengan panjang sisi p, besar sudut POT sama dengan panjang sisi q dan besar sudut POS sama dengan panjang sisi r. Dari gambar segitiga bola diatas, diperoleh :

Gambar 11 : Segitiga Bola PQR O T S P R Q q p r

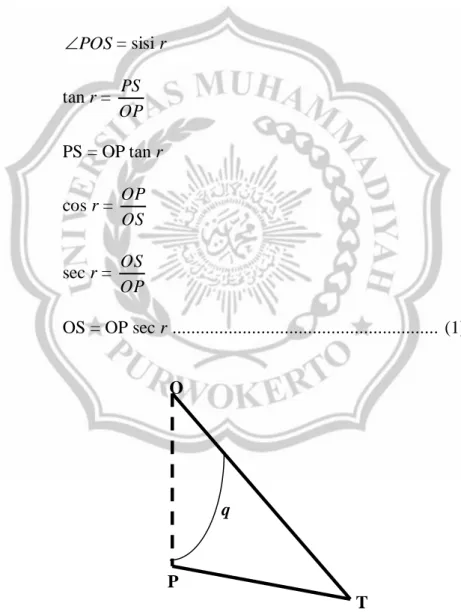
POS  = sisi r tan r = OP PS PS = OP tan r cos r = OS OP sec r = OP OS OS = OP sec r ... (1)

Gambar 12 :Segitiga SOP

Gambar 13 : Segitiga TOP O P S r O P T q

POT  = sisi q tan q = OP PT PT = OP tan q cos q = OT OP sec q = OP OT OT = OP sec q ... (1) Dari segitiga SPT diperoleh :

SPT PT PS PT PS ST2  2 22 . cos ... (3)

 ST2 (OPtanr)2 (OPtanq)22(OPtanr)(OPtanq)(cosP) ) )(cos tan )( tan ( 2 tan tan2 2 2 2 P q OP r OP q OP r OP   

OP2tan2r OP2tan2q2.OP2tanrtanq.cosP OP2(tan2rtan2q2.tanrtanq.cosP)

Dari segitiga SOT diperoleh :

SOT OT OS OT OS ST2  2 22 . cos ... (4)

 ST2 (OPsecr)2(OPsecq)22(OPsecr)(OPsecq)(cosp) OP2sec2rOP2sec2q2(OPsecr)(OPsecq)(cosp) OP2sec2rOP2sec2q2.OP2secrsecq.cosp OP2(sec2rsec2q2.secrsecq.cosp)

Maka dari persamaan (3) dan (4) diperoleh :

2

 OP2(tan2rtan2q2.tanrtanq.cosP) OP2(sec2rsec2q2.secrsecq.cosp)

 tan2rtan2q2.tanrtanq.cosP sec2rsec2q2.secrsecq.cosp

Karena sec2r= 1 + tan2r dan sec2q= 1 + tan2q, maka :  tan2rtan2q2.tanrtanq.cosP

(1+ tan2r)(1+ tan2q)2.secrsecq.cosp  (tan2rtan2q)2.tanrtanq.cosP

2( tan2r+ tan2q)2.secrsecq.cosp

 (tan2rtan2q)(tan2rtan2q)2.tanrtanq.cosP 22.secrsecq.cosp

 2.tanrtanq.cosP22.secrsecq.cosp  2.tanrtanq.cosP2(1secrsecq.cosp)  tanrtanq.cosP1secrsecq.cosp

 p q r P q q r r cos cos 1 cos 1 1 cos cos sin cos sin         q r p P q q r r cos . cos cos 1 cos cos sin cos sin       q r p q r q r q r P q r cos . cos cos cos . cos cos . cos cos . cos cos . sin . sin _{ }   q r p q r q r P q r cos . cos cos cos . cos cos . cos cos . sin . sin _  

 cospcosr.cosqsinr.sinq.cosP (Terbukti)

Langkah lebih lanjut dengan cara yang sama seperti yan diuraikan diatas dan menggilir kedudukan P,Q dan R. Sehingga diperoleh persamaan-persamaan serupa diatas.

D. Sistem Koordinat

Letak suatu benda pada suatu bidang datar dapat ditentukan dengan dua garis lurus yakni menggunakan kordinat x dan kordinat y. Akan tetapi pada permukaan yang tidak datar seperti pada bola langit tentu tidak dapat ditentukan dengan dua garis lurus, melainkan dengan garis lengkung (busur) sesuai dengan bentuk bola langit (Azhari, 2004). Dibawah ini akan diuraikan mengenai cara menentukan letak di bola langit, yakni :

1. Sistem Koordinat Ekuator

Gambar 14 : Sistem Koordinat Ekuator

Ekuator _b’’ γ

P

α

B

δ

KLU KLS

Jika khatulistiwa di bumi atau bidang ekuator bumi diperpanjang, maka akan memotong bola langit sehingga menjadi lingkaran khatulistiwa langit, yang bisa disebut ekuator langit. Setiap titik pada ekuator langit berjarak 90° dari kedua kutub langit (Salam, 2001).

Bola langit dengan ekuator langit dan bujur sehingga melalui  (titik Aries) disebut sistem koordinat ekuator. Titik Aries adalah titik perpotongan antara lingkaran ekliptika dengan lingkaran ekuator langit (Shadiq, 1994).

2. Sistem Koordinat Ekliptika

Dalam sistem koordinat ekliptika, lingkaran ekliptika menjadi lingkaran dasar utama, sedangkan titik asalnya adalah titik Aries seperti yang digunakan dalam sistem koordinat ekuator (Azhari, 2004).

Gambar 15 : Sistem Koordinat Ekliptika KLU KLS Ekliptika B b’

β

λ

γ

P

Lingkaran ekliptika adalah lingkaran semu tahunan matahari (Shadiq, 1994). Kemiringan sudut ekliptika terhadap bidang ekuator sebesar 23,5º (Ali, 1997). Titik Aries adalah titik perpotongan antara lingkaran ekliptika dengan lingkaran ekuator langit (Shadiq, 1994). 3. Sistem Koordinat Horizon

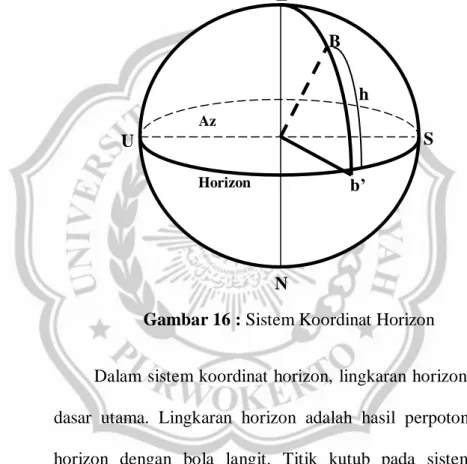
Dalam sistem koordinat horizon, lingkaran horizon merupakan dasar utama. Lingkaran horizon adalah hasil perpotongan bidang horizon dengan bola langit. Titik kutub pada sistem koordinat horizon adalah zenith (Z) dan nadir (N). Posisi benda langit pada sistem ini ditentukan oleh azimuth dan altitude/tinggi.

E. Deklinasi Matahari

Deklinasi matahari merupakan data yang cukup penting selain lintang dan bujur tempat. Deklinasi matahari adalah jarak matahari

Gambar 16 : Sistem Koordinat Horizon Z S N U B b’ h Horizon Az

dengan equator langit diukur sepanjang lingkaran deklinasi. Lingkaran waktu deklinasi biasanya diberi tanda huruf Yunani δ (delta). Deklinasi sebelah utara equator diberi tanda positif ( + ) dan sebelah selatan equator diberi tanda negatif ( + ).

Harga deklinasi Titik Kutub Langit Selatan adalah – 90o dan titik Kutub Langit Utara adalah 90o. Lambang deklinasi adalah :  (baca

:delta) (Salam, 2001: 9). Deklinasi matahari berubah sewaktu – waktu selama satu tahun, tetapi pada tanggal – tanggal yang sama, bilangan deklinasi itu kira – kira sama pula. (Ali, 1997)

F. Edaran Harian Matahari

Matahari merupakan sebuah bintang putih kekuning-kuningan dengan diameter 1.390.000 km dan berada pada jarak 150.000.000 km dari bumi (Anonim, 2007)

Edaran harian matahari terdiri dari gerak harian dan tempuan harian, yang dijelaskan sebagai berikut :

1. Gerak harian

Setiap hari matahari terbit di sebelah timur, lalu bergerak semakin lama semakin tinggi, hingga akhirnya tengah hari mencapai tempat kedudukannya yang paling tinggi pada hari itu.Titik tertinggi yang dicapai matahari dalam perjalanannya dinamakan titik kulminasi. Waktu itu matahari sedang berkulminasi (Ali, 1997).

2. Tempuan harian

Perjalanan matahari menurut arah timur barat bukanlah suatu gerak yang sesungguhnya, tetapi disebabkan oleh perputaran bumi sekeliling porosnya yang berlaku dalam waktu 24 jam menurut arah barat – timur. Karena perputaran sekeliling poros itu, gerak setiap titik diatas bumi berlaku didalam suatu bidang yang tegak lurus pada poros bumi (Ali,1997).

3. Tinggi Matahari

Yang dimaksud tinggi matahari adalah ketinggian posisi ”matahari yang terlihat” pada awal atau akhir waktu shalat diukur dari horizon. Tinggi matahari biasanya diberi tanda “hΘ ” atau hanya ditulis “h” saja, singkatan dari “high”, yang berarti ketinggian, sedangkan “Θ” adalah tanda matahari (Shadiq, 1994)

Selisih antar ketinggian yang tampak oleh pengamat dan ketinggian yang sebenarnya disebut “sudut refraksi”.Besarnya refraksi itu tergantung pada ketinggian benda langit, keadaan suhu dan tekanan udara. Pada ketinggan yang lebih kecil (makin dekat horizon) harga refraksi makin besar (Depag RI, 1983). Nilai yang terbesar adalah 34,5 menit busur, yakni pada saat benda langit itu berada pada garis horizon, sedang nilai yang terkecil adalah nol, yakni pada saat benda langit itu berada pada titik zenit (Depag RI, 1983).

Berikut ini disajikan gambaran mengenai edaran harian matahari.

Keterangan :

A : Posisi matahari terbit

B : Posisi matahari berkulminasi (berada di titik zenith) C : Posisi matahari terbenam

Gambar 17 : perjalanan matahari dari terbit

hingga terbenam tepat di equator langit ( = 0) KLS KLU Timur Barat Lingkaran ufuk Matahari berkulminasi Zenith Nadir A B C

G. Posisi Matahari dengan Segitiga Bola Keterangan : M = Matahari m = Bayangan matahari Ts = Timur sesungguhnya Bs = Barat sesungguhnya t = Sudut Waktu h = Tinggi δ = Deklinasi φ = Lintang

Gambar 18 : Gambar Posisi Matahari

dengan Segitiga Bola Z N S U KLU KLS Horizon Ekuator Bs m Ts M 90º - φ 90º - h 90º - δ

t

h

H. Aplikasi Rumus Segitiga Bola dalam Edaran Harian Matahari

Dari turunan rumus segitiga bola maka akan diperoleh aplikasi rumus segitiga bola dalam edaran harian matahari, yaitu : 1. Sudut waktu benda langit

Bahwa yang dimaksud dengan sudut waktu benda langit adalah jarak antara suatu benda langit dengan titik kulminasinya .

(Shadiq, 1994)

Rumus sudut waktu benda langit :

    cos . cos sin tan . tan cost   h

Gambar 19 : Aplikasi rumus segitiga Bola

dalam Edaran harian matahari

U S Q E Z N KLU KLS P Horizon Bs Ts Edaran Harian Matahari M Θ



p

hΘ



p

tΘ M' M'' Sudut waktu matahari

2. Tinggi benda langit

Bahwa yang dimaksud dengan tinggi benda langit adalah busur pada lingkaran vertikal yang diukur dari titik perpotongan antara lingkaran horizon dengan lingkaran vertikal ke arah objek (benda langit). (Azhari,2004)

Rumus tinggi benda langit :

t h