SIFAT-SIFAT INTEGRAL LIPAT

(1)

TUGAS KALKULUS LANJUT

SIFAT-SIFAT INTEGRAL LIPAT

Oleh:

KAMELIANI

1211041016

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS NEGERI MAKASSAR

(2)

Universitas Negeri Makassar Page 2

SIFAT-SIFAT INTEGRAL LIPAT

A. SIFAT-SIFAT INTEGRAL LIPAT

Integral lipat dua dan integral lipat tiga mewarisi hampir semua sifat-sifat integral tunggal. Berikut adalah sifat-sifat integral lipat dua (yang juga dimiliki integral sifat tiga).

(1) Integral lipat dua bersifat linear, yaitu

∬[𝑓(𝑥, 𝑦) + 𝑔(𝑥, 𝑦)]𝑑𝐴 𝑅 = ∬ 𝑓(𝑥, 𝑦)𝑑𝐴 𝑅 + ∬ 𝑔(𝑥, 𝑦)𝑑𝐴 𝑅 ∬ 𝑘𝑓(𝑥, 𝑦)𝑑𝐴 𝑅 = 𝑘 ∬ 𝑓(𝑥, 𝑦) 𝑅 𝑑𝐴, 𝑑𝑖𝑚𝑎𝑛𝑎 𝑘 𝑎𝑑𝑎𝑙𝑎ℎ 𝑘𝑜𝑛𝑠𝑡𝑎𝑛𝑡𝑎 (2) . 𝐽𝑖𝑘𝑎 𝑓(𝑥, 𝑦) ≤ 𝑔(𝑥, 𝑦) 𝑢𝑛𝑡𝑢𝑘 𝑠𝑒𝑡𝑖𝑎𝑝 (𝑥, 𝑦)𝑑𝑖 𝑅, 𝑚𝑎𝑘𝑎 𝑏𝑒𝑟𝑙𝑎𝑘𝑢 ∬ 𝑓(𝑥, 𝑦)𝑑𝐴 𝑅 ≤ ∬ 𝑔(𝑥, 𝑦) 𝑅 𝑑𝐴 (3) . 𝑗𝑖𝑘𝑎 𝑓(𝑥, 𝑦) ≥ 0 𝑢𝑛𝑡𝑢𝑘 𝑠𝑒𝑚𝑢𝑎 (𝑥, 𝑦)𝑑𝑖 𝑅, 𝑑𝑎𝑛 𝑆 ⊂ 𝑅 𝑚𝑎𝑘𝑎 𝑏𝑒𝑟𝑙𝑎𝑘𝑢 ∬ 𝑘𝑓(𝑥, 𝑦)𝑑𝐴 𝑆 ≤ 𝑘 ∬ 𝑓(𝑥, 𝑦) 𝑅 𝑑𝐴,

(4). Integral lipat dua bersifat aditif (dapat dijumlahkan) pada daerah yang saling

berimpit pada hanya sebuah sisi atau ruas garis.

∬ 𝑓(𝑥, 𝑦)𝑑𝐴 𝑅∪𝑆 = ∬ 𝑓(𝑥, 𝑦) 𝑅 𝑑𝐴 + ∬ 𝑓(𝑥, 𝑦) 𝑆 𝑑𝐴

(3)

Universitas Negeri Makassar Page 3 Sifat-sifat integral tersebut membawa beberapa akibat yang perlu dikemukakan di sini. Misalkan 𝑚 ≤ 𝑓(𝑥, 𝑦) ≤ 𝑀 untuk semua (𝑥, 𝑦) di 𝑅 maka

𝑚 (luas R)

= ∬ 𝑚 𝑑𝑥𝑑𝑦 ≤ ∬ 𝑓(𝑥, 𝑦)𝑑𝑥 𝑑𝑦 ≤ ∬ 𝑀 𝑑𝑥𝑑𝑦 = 𝑀

_𝑅 (luas R) Satu sifat lainnya yang perlu dikemukakan adalah akibat dari sifat

−|𝑓(𝑥, 𝑦)| ≤ 𝑓(𝑥, 𝑦) ≤ |𝑓(𝑥, 𝑦)| Berdasarkan sifat integral nomor 2, maka berlaku

− ∬ |𝑓(𝑥, 𝑦)|𝑑𝑥𝑑𝑦 ≤ ∬ 𝑓(𝑥, 𝑦) 𝑑𝑥𝑑𝑦 ≤ ∬ |𝑓(𝑥, 𝑦)| 𝑑𝑥𝑑𝑦 𝑅 𝑅 Atau ∬ 𝑓(𝑥, 𝑦) 𝑑𝑥𝑑𝑦 ≤ ∬ |𝑓(𝑥, 𝑦)| 𝑑𝑥𝑑𝑦 𝑅

Untuk fungsi 𝑓 yang kontinu, ternyata urutan pengintegralan tidak menjadi masalah. Hal ini dituliskan dalam teorema berikut.

Teorema urutan integral (Teorema Fubini)

∬ 𝑓(𝑥, 𝑦) 𝑑𝑥𝑑𝑦 = ∫ [∫ 𝑓(𝑥, 𝑦)𝑑𝑦𝑑 𝑐 ] 𝑑𝑥 𝑏 𝑎 𝑅 = ∫ [∫ 𝑓(𝑥, 𝑦)𝑑𝑥𝑏 𝑎 ] 𝑑𝑦 𝑑 𝑐

(4)

B. PENERAPAN SIFAF-SIFAT INTEGRAL DALAM

MENYELESAIKAN MASALAH

.

Soal dan Pembahasan

1. Hitunglah integral berikut berdasarkan daerah D yang diberikan! ∬ 𝑒𝑥𝑦_𝑑𝐴

𝐷

, 𝐷 = {(𝑥, 𝑦)|1 ≤ 𝑦 ≤ 2 , 𝑦 ≤ 𝑥 ≤ 𝑦3_} Penyelesaian:

Dengan menerapkan sifat (1) dan (2), maka ∬ 𝑒𝑥𝑦_𝑑𝐴 𝐷 = ∫ ∫ 𝑒𝑥𝑦_{𝑑𝑥 𝑑𝑦} 𝑦3 𝑦 2 1 = ∫ 𝑦𝑒 𝑦𝑥_{| 𝑦}3 𝑦𝑑𝑦 2 1 = ∫ (𝑦𝑒 𝑦2_{− 𝑦𝑒)𝑑𝑦} 2 1 = ∫ (𝑦𝑒 𝑦2 )𝑑𝑦 2 1 − ∫ (𝑦𝑒)𝑑𝑦 2 1 = [1₂𝑒 𝑦2₋1 2𝑒𝑦2] 2₁ = (1 2𝑒 4− 1 24𝑒) − ( 1 2𝑒 − 1 2𝑒) = 1 2𝑒 4− 2𝑒

2. Hitunglah integral berikut berdasarkan daerah D yang diberikan! ∬ 6𝑥2_{− 40𝑦 𝑑𝐴}

𝐷

,

D adalah segitiga dengan titik puncak (0,3) , (1,1), dan (5,3)

Penyelesaian:

Pertama-tama harus dibuat persamaan garis yang melalui titik-titik puncak tersebut, agar bisa diketahui batas-batas daerahnya.

Kita dapat membuat persamaan garis berdasarkan dua titik puncak yang diketahui.  Persamaan garis yang melalui titik (0,3) dan (1,1)

𝑦 − 𝑦₁ 𝑦₂− 𝑦_`1=

𝑥 − 𝑥₁ 𝑥₂− 𝑥_`1

(5)

Universitas Negeri Makassar Page 5 𝑦 − 3 1 − 3= 𝑥 − 0 1 − 0 𝑦 − 3 = −2𝑥 𝑦 = −2𝑥 + 3

 Persamaan garis yang melalui titik (0,3) dan (5,3) 𝑦 − 𝑦₁ 𝑦₂− 𝑦_`1= 𝑥 − 𝑥₁ 𝑥₂− 𝑥_`1 𝑦 − 3 3 − 3= 𝑥 − 0 5 − 0 5𝑦 = 15 𝑦 = 3

 Persamaan garis yang melalui titik (1,1) dan (5,3) 𝑦 − 𝑦₁ 𝑦₂− 𝑦_`1= 𝑥 − 𝑥₁ 𝑥₂− 𝑥_`1 𝑦−1 3−1= 𝑥−1 5−1 4𝑦 − 4 = 2𝑥 − 2 𝑦 =1 2𝑥 + 1 2

(6)

Universitas Negeri Makassar Page 6 Ada dua cara untuk mendeskripsikan daerah yang diarsir.

 Cara I

Jika kita menggunakan fungsi x, maka daerah D akan dibagi menjadi dua daerah karena fungsi yang berada di bawah berbeda bergantung pada nilai x. Pada kasus ini, daerah D diberikan sebagai 𝐷 = 𝐷₁∪ 𝐷₂, dimana 𝐷₁= {(𝑥, 𝑦)|0 ≤ 𝑥 ≤ 1 , −2𝑥 + 3 ≤ 𝑦 ≤ 3} 𝐷₂= {(𝑥, 𝑦)|1 ≤ 𝑥 ≤ 5 ,1

2𝑥 + 1

2≤ 𝑦 ≤ 3} Dengan menggunakan sifat (6), maka ∬ 6𝑥2_{− 40𝑦 𝑑𝐴} 𝐷 = ∬ 6𝑥2_{− 40𝑦 𝑑𝐴} 𝐷1 + ∬ 6𝑥2_{− 40𝑦 𝑑𝐴} 𝐷2 = ∫ ∫3 6𝑥2− 40𝑦 −2𝑥+3 𝑑𝑦𝑑𝑥 1 0 +∫ ∫ 6𝑥 2_{− 40𝑦} 3 1 2𝑥+12 𝑑𝑦𝑑𝑥 5 1 = ∫ (6𝑥2_{𝑦 − 20𝑦}2_)| −2𝑥+3 3 _𝑑𝑥 1 0 + ∫ (6𝑥 2_{𝑦 − 20𝑦}2_)|1 2𝑥+12 3 _𝑑𝑥 5 1 = ∫ [12𝑥1 3_{− 180 + 20(−2𝑥 + 3)}2_]𝑑𝑥 0 + ∫ [−3𝑥 3_{+ 15𝑥}2_{− 180 + 20 (}1 2𝑥 + 1 2) 2 ] 𝑑𝑥 5 1 = [3𝑥4_{− 180𝑥 −}10 3 (−2𝑥 + 3)3] 10+ [− 3 4𝑥4+ 5𝑥3− 180𝑥 + 40 3 ( 1 2𝑥 + 1 2) 3 ] 5 1 = −935 3

Perhatikan bahwa menyelesaikan integral pada fungsi berbentuk kuadrat tidak perlu dikalikan satu persatu. Lebih mudah diintegralkan dengan integral subsitusi yang telah dipelajari di Calculus I.

(7)

Universitas Negeri Makassar Page 7  Cara II

Jika kita menggunakan fungsi y, maka daerah D tidak perlu dibagi menjadi dua bagian.

Batas-batas untuk x adalah 𝑦 = −2𝑥 + 3 → 𝑥 = −1 2𝑦 + 3 2 𝑦 =1 2𝑥 + 1 2 → 𝑥 = 2𝑦 − 1 𝐷 = {(𝑥, 𝑦)| −1₂𝑦 +3 2≤ 𝑥 ≤ 2𝑦 − 1 , 1 ≤ 𝑦 ≤ 3 } Sehingga ∬ 6𝑥2_{− 40𝑦 𝑑𝐴} 𝐷 = ∫ ∫2𝑦−1(6𝑥2_{− 40𝑦)𝑑𝑥𝑑𝑦} −12𝑦+32 3 1 = ∫ 2𝑥3_{− 40𝑥𝑦 |} 2𝑦 − 1 −1 2𝑦 + 3 2 3 1 𝑑𝑦 = ∫ 100𝑦 − 100𝑦3 2_{+ 2(2𝑦 − 1)}3_{− 2} 1 (−1 2𝑦 + 3 2) 3 dy = [50y2₋100 3 y3+ 1 4(2y − 1)4+ (− 1 2y + 3 2) 4 ] 3₁ = −935 3

3. Hitunglah nilai integral berikut dengan membalikkan urutan dari integralnya. ! ∫ ∫ 𝑥9 3_𝑒𝑦3_{𝑑𝑦𝑑𝑥}

𝑥2

3 0 Penyelesaian:

Perhatikan bahwa kita tidak bisa melakukan integral terhdap 𝑦 karena kita membutuhkan 𝑦2 di depan eksponensial untuk melakukan integral terhadap 𝑦. Akan tetapi, jika urutan integral dibalik, maka kita bisa menghitung nilai integral di atas.

(8)

Universitas Negeri Makassar Page 8 Membalik urutan integral artinya kita akan melakukan integral terhadap 𝑥 terlebih dahulu kemudian terhadap 𝑦. Ketika membalik urutan integral, maka batas-batsanya juga akan berubah.

Agar memudahkan mencari batas-batasnya, maka pertama-tama kita gambarkan daerah yang diberikan berdasarkan batas-batas yang telah diketahui. Berdasarkan integral di atas, batas-batas daerahnya adalah

0 ≤ 𝑥 ≤ 3 𝑥2_{≤ 𝑦 ≤ 9}

Berdasarkan pertidaksamaan di atas, batas bawah pada sumbu y adalah 𝑦 = 𝑥^2 dan batas atas pada sumbu y adalah 𝑦 = 9 dengan batas pada sumbu 𝑥 yaitu antara 𝑥 = 0 dan 𝑥 = 3.

Berikut ini adalah gambar daerah yang dimaksud

Karena kita ingin mengintegralkan terhadap 𝑥 terlebih dahulu,maka kita perlu menentukan batas-batas untuk 𝑥 terlebih dahulu, kemudian batas-batas untuk 𝑦 . Batas pada sumbu 𝑥 adalah 0 ≤ 𝑥 ≤ √𝑦

Batas pada sumbu 𝑦 adalah 0 ≤ 𝑦 ≤ 9

Sehingga bentuk integralnya sekarang adalah sebagai berikut ∫ ∫ 𝑥9 3_𝑒𝑦3_{𝑑𝑦𝑑𝑥} 𝑥2 3 0 = ∫ ∫ 𝑥√𝑦 3_𝑒𝑦3_{𝑑𝑥𝑑𝑦} 0 9 0

(9)

Universitas Negeri Makassar Page 9 Berikut adalah penyelesaian untuk bentuk integral yang baru

∫ ∫ 𝑥√𝑦 3𝑒𝑦3_{𝑑𝑥𝑑𝑦} 0 9 0 = ∫ 𝑒𝑦3∫ 𝑥3 𝑑𝑥𝑑𝑦 √𝑦 0 9 0 = ∫ 𝑒𝑦3_{∫ 𝑥}√𝑦 3_{𝑑𝑥𝑑𝑦} 0 9 0 = ∫ 𝑒𝑦3_[1 4𝑥4] 9 0 √𝑦 0 𝑑𝑦 = ∫ 𝑒𝑦3_[1 4𝑥4] 9 0 √𝑦 0 𝑑𝑦 = ∫ 1 4𝑦2𝑒𝑦 3 9 0 𝑑𝑦 =1 4𝑒𝑦3|90 =1 4(𝑒729− 1)

C.

Menerapkan Sifat-Sifat Integral untuk Menyelesaikan Soal Integral pada Daerah Persegi Panjang dan Bukan Persegi Panjang

Contoh Soal!

 Daerah Persegi Panjang

1. Tentukan Volume benda pejal di bawah bidang 𝑧 = 𝑥 + 𝑦 + 1 pada 𝑅 = {(𝑥, 𝑦): 0 ≤ 𝑥 ≤ 1, 1 ≤ 𝑦 ≤ 3 Penyelesaian: ∫ ∫ (𝑥 + 𝑦 + 1)1 0 3 1 𝑑𝑥𝑑𝑦 = ∫ [ 1 2𝑥2+ 𝑦𝑥 + 𝑥] 3 1 1 0 𝑑𝑦 = ∫ (1 2+ 𝑦 + 1) 𝑑𝑦 3 1 = [1₂𝑦 +1 2𝑦2+ 𝑦] 31 = (3 2+ 9 2+ 3) − ( 1 2+ 1 2+ 1) = 7

(karena di integralkan terhadap 𝑥, maka 𝑦 dianggap konstanta, sehingga berlaku sifat linear integral

(10)

Universitas Negeri Makassar Page 10 daerah 𝑧 = 𝑥 + 𝑦 + 1 pada 𝑅 = {(𝑥, 𝑦): 0 ≤ 𝑥 ≤ 1, 1 ≤ 𝑦 ≤ 3

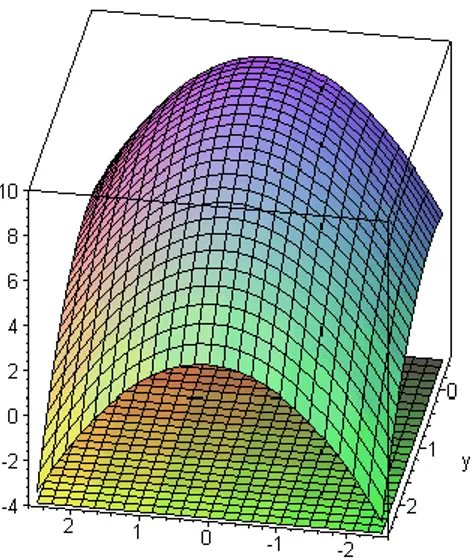
2. Carilah Volume benda pejal yang berada di atas fungsi g(x,y) dan berada di bawah fungsi f(x,y) dengan batas-batas x dan y sebagai berikut.

𝑔(𝑥, 𝑦) = −4 𝑓(𝑥, 𝑦) = 9 − 𝑥2_{− 𝑦}2 −2,5 ≤ 𝑥 ≤ 2,5 − 0,5 ≤ 𝑦 ≤ 2,5 Penyelesaian: Volume = ∫ ∫ [9 − 𝑥2,5 2_{− 𝑦}2_{− (−4)]𝑑𝑦𝑑𝑥} −0,5 2,5 −2,5 = ∫ [13𝑦 − 𝑥2_{𝑦 −}1 3𝑦3] 2,5 −2,5 2,5 −0,5 𝑑𝑥 = ∫ {[655 24 − 2,5𝑥2] − [− 155 24 + 0,5𝑥2]} 𝑑𝑥 2,5 −2,5 = ∫ [135 4 − 3𝑥2] 𝑑𝑥 2,5 −2,5 = [135₄ 𝑥 − 𝑥3_] 2,5 −2,5 =275 4 + 275 4 = 137,5 satuan volume

(11)

 Daerah bukan Persegi Panjang

1. Carilah volume benda yang dibatasi oleh persamaan bola 𝑥2+ 𝑦2+ 𝑧2 = 6 dan Paraboloida 𝑧 = 𝑥2+ 𝑦2

Penyelesaian:

Bentuk daerahnya adalah sebagai berikut

Gambar di atas adalah daerah yang dimaksud yakni irisan antara bola dan paraboloida.

Subsitusi 𝑧 = 𝑥2+ 𝑦2 ke persamaan 𝑥2+ 𝑦2+ 𝑧2 = 6 sehingga diperoleh

(12)

𝑥2_{+ 𝑦}2_{+ (𝑥}2_{+ 𝑦}2₎2_{= 6} 𝑥2_{+ 𝑦}2_{+ (𝑥}2_{+ 𝑦}2₎2_{− 6 = 0} (𝑥2_{+ 𝑦}2_{− 2)(𝑥}2_{+ 𝑦}2_{+ 3) = 0}

Untuk (𝑥2+ 𝑦2− 2) = 0 maka 𝑦 = ±√2 − 𝑥2 untuk (𝑥2+ 𝑦2+ 3) = 0 tidak ada solusi

Batas-batas untuk y adalah −√2 − 𝑥2 ≤ 𝑦 ≤ √2 − 𝑥2 sedangkan untuk x adalah −√2 ≤ 𝑥 ≤ √2

Sehingga dengan menggunakan maple, volume benda yang diperoleh adalah diperoleh

∫ ∫√2−𝑥 √6 − 𝑥2_{− 𝑦}2 2 −√2−𝑥2 − (𝑥 2_{+ 𝑦}2₎ √2 −√2 𝑑𝑦𝑑𝑥 = 4√6 𝜋 − 22 3 𝜋 = 7,74

Perhitungan dengan Maple

(13)

D.

Menerapkan Sifat-Sifat Integral untuk Menyelesaikan Soal Integral dalam Koordinat Polar

Soal Dan Pembahasan

1. Hitunglah nilai integral berikut dengan mengubahnya ke dalam koordinat polar terlebih dahulu.

∬ 2𝑥𝑦 𝑑𝐴 𝐷

D adalah daerah di antara lingkaran dnegan jari-jari 2 dan jari-jari 5 . lingkaran-lingkaran tersebut berpusat pada titik asal. Daerahnya berada pada kuadran I.

Penyelesaian:

Pertama-tama kita harus mengubah daerah D dalam koordinat polar. Lingkaran dengan jari-jari 2 berarti 𝑟 = 2 , dan lingkaran dengan jari-jari 5 berarti 𝑟 = 5 . Karena daerah yang dimaksud berada di antara jari-jari tersebut, maka dapat dituliskan 2 ≤ 𝑟 ≤ 5

Sedangkan daerah yang dimaksud berada pada kuadran I, sehingga dapat dituliskan 0 ≤ 𝜃 ≤𝜋₂

Diketahui bahwa dalam koordinat polar, 𝑥 = 𝑟 cos 𝜃 dan 𝑦 = 𝑟 sin 𝜃, 𝑑𝐴 = 𝑟𝑑𝑟𝑑 𝜃 Sehingga, ∬ 2𝑥𝑦 𝑑𝐴 𝐷 = ∫ ∫ 2(5 2 𝜋 2 0 𝑟 cos 𝜃)( 𝑟 sin 𝜃)𝑟𝑑𝑟𝑑 𝜃 = ∫ ∫ 𝑟5 3_{(sin 2𝜃)} 2 𝜋 2 0 𝑑𝑟𝑑 𝜃 = ∫ [1₄𝑟4_{(sin 2𝜃)] 5} 2 𝜋 2 0 𝑑 𝜃 =1 4∫ [𝑟 4_{(sin 2𝜃)]5} 2 𝜋 2

0 𝑑 𝜃 (menggunakan sifat kelinearan integral) =609

4 ∫ (sin 2𝜃)

𝜋 2

(14)

Universitas Negeri Makassar Page 14 = −609 4 ( 1 2) cos 2𝜃 | 𝜋 2 0 =609 4

2. Tentukan luas daerah yang dibatasi oleh 𝑟 = 3 + 2 sin 𝜃 dan 𝑟 = 2 Penyelesaian:

Daerah yang dimaksud adalah sebagai berikut.

Untuk mengetahui luas daerah di atas, maka terlebih dahulu perlu diketahui batas-batas untuk nilai 𝜃 dimana kurva saling berpotongan.

Untuk mengetahui nilai 𝜃 bisa dilakukan dengan cara sebagai berikut. Diketahui 𝑟 = 3 + 2 sin 𝜃 dan 𝑟 = 2

Dapat dituliskan 3 + 2 sin 𝜃 = 2 sin 𝜃 = −1 2 𝑚𝑎𝑘𝑎 𝜃 = 7𝜋 6 , 11𝜋 6

(15)

Universitas Negeri Makassar Page 15 Berikut ini adalah gambar daerah 𝜃

Kita tahu bahwa −𝜋₆ adalah bentuk lain dari 11𝜋₆

Jika kita gunakan 7𝜋₆ ≤ 𝜃 ≤11𝜋₆ maka kita akan menghitung daerah yang tidak di arsir. Oleh karena itu batas yang digunakan adalah −𝜋₆≤ 𝜃 ≤7𝜋₆

Untuk menentukan nilai 𝑟, fungsi yang terdekat dengan titik asal merupakan batas bawah, dan fungsi yang terjauh merupakan batas atas.

Sehingga luas daerah D adalah 𝐴 = ∬ 𝑑𝐴 𝐷 = ∫ ∫ 𝑟𝑑𝑟𝑑𝜃 3+2 sin 𝜃 2 7𝜋 6 −𝜋₆ = ∫ 1 2𝑟2|₂ 3+2 sin 𝜃 7𝜋 6 −𝜋₆ 𝑑𝜃 = ∫ (5 2+ 6 𝑠𝑖𝑛𝜃 + 2 sin2𝜃 ) 𝑑𝜃 7𝜋 6 −𝜋₆ = ∫ (7 2+ 6 𝑠𝑖𝑛𝜃 − cos (2𝜃)) 𝑑𝜃 7𝜋 6 −𝜋₆

(16)

Universitas Negeri Makassar Page 16 =7 2𝜃 − 6 cos 𝜃 − 1 2sin 2𝜃|_−𝜋 6 7𝜋 6 =11√3 2 + 14𝜋 3 = 24,187

3. Tentukan volume benda yang berada di bawah bola 𝑥2+ 𝑦2+ 𝑧2 = 9, di atas bidang 𝑧 = 0, dan berada pada silinder 𝑥2+ 𝑦2= 5

Penyelesaian:

Kita tahu bahwa rumus untuk menentukan volume adalah 𝑉 = ∬ 𝑓(𝑥, 𝑦)𝑑𝐴

𝐷

Ubah fungsi 𝑥2+ 𝑦2+ 𝑧2= 9 ke bentuk 𝑧 = √9 − 𝑥2+ 𝑦2. Kita mengambil nilai yang positif karena kita akan menghitung di atas bidang 𝑥𝑦 (𝑧 = 0)

Kini kita mempunyai dua fungsi yaitu 𝑧 = 0 dan 𝑧 = √9 − 𝑥2+ 𝑦2

Kita ingin menghitung daerah yang berada di bawah bola tetapi berada pada silinder 𝑥2+ 𝑦2= 5.

Untuk lebih jelasnya perhatikan gambar berikut.

Jadi, daerah yang akan dicari volumenya adalah sebuah cilinder yang penutupnya merupakan sebuah bola.

(17)

Universitas Negeri Makassar Page 17 Sebelumnya kita ubah terlebih dahulu batas-batasnya dalam koordinat polar.

0 ≤ 𝜃 ≤ 2𝜋

0 ≤ 𝑟 ≤ √5 (jari-jari silinder)

Sehingga volume daerah yang dimaksud adalah 𝑉 = ∬ √9 − 𝑥2_{− 𝑦}2 𝐷 𝑑𝐴 = ∫ ∫ √9 − 𝑟√5 2_{𝑟 𝑑𝑟 𝑑𝜃} 0 2𝜋 0 (𝑟2_{= 𝑥}2_{+ 𝑦}2₎ = ∫ −1 3(9 − 𝑟2) 3 2| 0 √5 2𝜋 0 𝑑𝜃 = −1 3∫ (9 − 𝑟2) 3 2_| 0 √5 2𝜋 0 𝑑𝜃 = ∫ 19 3 2𝜋 0 𝑑𝜃 =38𝜋 3

4. Hitunglah volume benda yang berada di antara fungsi 𝑧 = 𝑥2+ 𝑦2 dan bidang 𝑧 = 16.

Penyelesaian:

(18)

Universitas Negeri Makassar Page 18 Volume yang dicari adalah daerah selisih antara kedua kurva tersebut, yakni

𝑉 = ∬ 16 𝐷

𝑑𝐴 − ∬ 𝑥2_{+ 𝑦}2_{𝑑𝐴 = ∬ 16 − (𝑥}2_{+ 𝑦}2_)𝑑𝐴 𝐷

𝐷

Agar memudahkan dalam mencari nilai volume, fungsi di atas di ubah dalam koordinat polar. Demikian pula batas-batas daerahnya.

Berikut ini adalah batas-batas daerahnya

0 ≤ 𝜃 ≤ 2𝜋 0 ≤ 𝑟 ≤ 4 𝑧 = 16 − 𝑟2 Sehingga, 𝑉 = ∬ 16 − (𝑥2_{+ 𝑦}2_)𝑑𝐴 𝐷 = ∫ ∫(16 − 𝑟2₎ 4 0 2𝜋 0 𝑟 𝑑𝑟 𝑑𝜃 = ∫ (8𝑟2₋1 4𝑟4)|₀ 4 2𝜋 0 𝑑𝜃 = ∫ 64 2𝜋 0 𝑑𝜃 = 128𝜋

(19)

Universitas Negeri Makassar Page 19 DAFTAR PUSTAKA

Purcell,dkk.2011.Kalkulus Edisi Kesembilan Jilid 2. Jakarta: Erlangga

Budi Wono Setya.2001.Kalkulus Peubah Banyak dan Penggunannya.Bandung:ITB.

http://www.math24.net/definition-and-properties-of-double-integrals.html (di akses

24 Desember 2014)

http://tutorial.math.lamar.edu/Classes/CalcIII/DIGeneralRegion.aspx (di akses 24

Desember 2014)

http://ltcconline.net/greenl/courses/202/multipleintegration/Volume.htm (di akses 29

Desember 2014)

http://www2.seminolestate.edu/lvosbury/CalculusIII_Folder/ExamplesForExam4.ht m (di akses 5 Januari 2015)

http://tutorial.math.lamar.edu/Classes/CalcIII/DIPolarCoords.aspx (di akses 5