Lecture 12: Penerapan Integral Lipat Dua

(1)

Kalkulus Multivariabel I

Penerapan Integral Lipat-Dua

Atina Ahdika, S.Si, M.Si

Statistika FMIPA Universitas Islam Indonesia

(2)

Penerapan Integral Lipat-Dua Penerapan Integral Lipat-Dua

Penerapan Integral Lipat-Dua

Penerapan lain dari integral lipat-dua antara lain adalah menghitung pusat massa, momen inersia, dan luas permukaan. Tinjaulah sebuah lembaran tipis yang sedemikian tipisnya sehingga kita dapat memandangnya sebagai

objek berdimensi dua, kita menyebut lembaran ini lamina_{. Di sini, kita}

(3)

Andaikan sebuah lamina menutupi sebuah daerah S pada bidangxy, dan

misalkan kerapatan (massa per satuan luas) di (x,y) disimbolkan dengan

δ(x,y). Daerah S dipartisi menjadi persegi panjang-persegi panjang kecil

R1,R2, . . . ,Rk seperti ditunjukkan pada gambar. Ambil sebuah titik

(4)

Maka massa Rk secara hampiran adalahδ(¯xk,y¯k)A(Rk), dan massa total

lamina tersebut secara hampiran adalah

m_≈

n X

k=1

δ(¯xk,y¯k)A(Rk)

Massa sebenarnya, m diperoleh dengan mengambil limit rumus di atas

sebagai norma partisi mendekati nol, yang tentu saja merupakan sebuah integral lipat dua

m=

Z Z

S

(5)

Contoh 1:

Sebuah lamina dengan kerapatanδ(x,y) =xy dibatasi oleh sumbu x, garis

(6)

(7)

Penerapan Integral Lipat-Dua Pusat Massa

Pusat Massa

Jika m1,m2, . . . ,mn berturut-turut adalah kumpulan titik-titik massa yang

masing-masing terletak di (x1,y1),(x2,y2), . . . ,(xn,yn), maka momen total

terhadap sumbu y dan sumbux dapat dinyatakan dengan

My =

Lebih lanjut, koordinat (¯x,¯y) dari pusat massa (titik keseimbangan) adalah

(8)

Sekarang perhatikan sebuah lamina dengan kerapatan berupa peubah

δ(x,y) yang melingkupi daerah S pada bidang xy. Buat partisi seperti

pada gambar dan asumsikan sebagai sebuah hampiran bahwa suatu massa dari setiap Rk terpusat di (¯xk,y¯k),k = 1,2, . . . ,n. Gunakan limitnya

sebagai suatu aturan pembagian partisi yang mendekati nol. Cara ini menghasilkan rumus umum,

¯

x= My

m =

RR

S

xδ(x,y)dA

RR

S

δ(x,y)dA ¯y= Mx

m =

RR

S

yδ(x,y)dA

RR

S

(9)

Contoh 2:

Tentukan pusat massa dari lamina pada Contoh 1. Penyelesaian:

Pada Contoh 1, kita telah mendapatkan massa mdari lamina yaitu 768₅ .

Momen My danMx yang mengacu pada sumbu y dan sumbu x adalah

My = Z Z

S

xδ(x,y)dA=

8

Z

0

x2/3 Z

0

x2y dy dx

= 1

2

8

Z

0

x10/3dx = 12288

(10)

(11)

Penerapan Integral Lipat-Dua Momen Inersia

Momen Inersia

Dari pelajaran fisika kita pelajari bahwa energi kinetik, KE, dari sebuah

partikel dengan massa m, dan kecepatan v, yang bergerak dalam sebuah

garis lurus dirumuskan dengan

KE = 1

2mv

2 ₍₁₎

Jika suatu partikel tidak bergerak dalam sebuah garis lurus tetapi berputar

dalam sebuah sumbu dengan kecepatan sudut sebesar ω radian per satuan

waktu, maka kecepatan linearnya adalah v=rω, di manar adalah jari-jari

dari lintasan perputarannya. Ketika kita mensubstitusikan ini ke dalam (1), maka kita akan memperoleh

KE = 1 2(r

(12)

Suku r2m disebutmomen inersia _{dari suatu partikel dan dilambangkan}

dengan I. Jadi, untuk sebuah partikel yang berputar

KE = 1 2Iω

2 ₍₂₎

(13)

Untuk sebuah sistem dengann partikel pada suatu bidang dengan massa

m1,m2, . . . ,mn dan pada jarak-jarak r1,r2, . . . ,rn dari garis L, maka

momen inersia sistem terhadap Ldidefinisikan sebagai

I =m1r12+m2r22+. . .+mnrn2 = n X

k=1

mkrk2

(14)

Misalkan sebuah lamina dengan kerapatan δ(x,y) yang melingkupi daerah

S pada bidang xy. Jika kita mempunyai partisiS, membuat hampiran

untuk momen inersia dari setiap bagian Rk, menjumlahkan dan

menentukan limitnya, maka akan diperoleh rumus-rumus berikut. Momen

inersia _{(disebut juga momen kedua) dari suatu lamina terhadap sumbu} _x_,

sumbuy, dan sumbuz dinyatakan dengan

Ix = Z Z

S

y2δ(x,y)dA Iy = Z Z

S

x2δ(x,y)dA

Iz = Z Z

S

(15)

Contoh 3:

Tentukan momen inersia terhadap sumbu x,y, dan z dari lamina pada

(16)

Penerapan Integral Lipat-Dua Luas Permukaan

Luas Permukaan

Pada materi ini, kita akan membahas mengenai luas permukaan yang didefinisikan dengan z =f(x,y) atas sebuah daerah spesifik.

Andaikan G adalah permukaan atas sebuah daerahS yang tertutup dan

terbatas pada bidang xy. Asumsikan bahwaf mempunyai

turunan-turunan parsial pertama kontinu fx danfy. Kita akan mulai

dengan membuat partisi P pada daerahS dengan garis-garis sejajar

(17)

Misalkan Rm,m= 1,2, . . . ,n, menyatakan persegi panjang-persegi

panjang yang dihasilkan dan terletak sepenuhnya di dalam S. Untuk setiap

m, misalkanGm adalah bagian dari permukaan yang diproyeksikan keRm,

dan misalkan Pm adalah suatu titik dariGm yang diproyeksikan ke sudut

Rm dengan koordinat x dan koordinaty yang terkecil. MisalkanTm

menyatakan suatu jajaran genjang dari bidang singgung di Pm yang

diproyeksikan ke Rm, seperti ditunjukkan pada Gambar kiri, dan perincian

(18)

Selanjutnya, kita mencari luas jajaran genjang Tm yang proyeksinya adalah

Rm. Misalkanum dan vm menyatakan vektor-vektor yang membentuk

sisi-sisi Tm. Maka,

um = ∆xmi+fx(xm,ym)∆xmk

(19)

Dengan demikian, luas Tm adalah

A(Tm) =|um×vm|=A(Rm) q

(20)

Kemudian, jumlahkan luas dari bidang-bidang singgung jajaran genjang Tm

ini, m= 1,2, . . . ,n, dan ambil limitnya agar diperoleh luas permukaan G.

A(G) = lim

|P_|→0

n X

m=1

A(Tm)

= lim

|P_|→0

q

[fx(xm,ym)]2+ [fy(xm,ym)]2+ 1A(Rm)

=

Z Z

S q

[fx(xm,ym)]2+ [fy(xm,ym)]2+ 1dA

Singkatnya,

A(G) =

Z Z

S q

f2

(21)

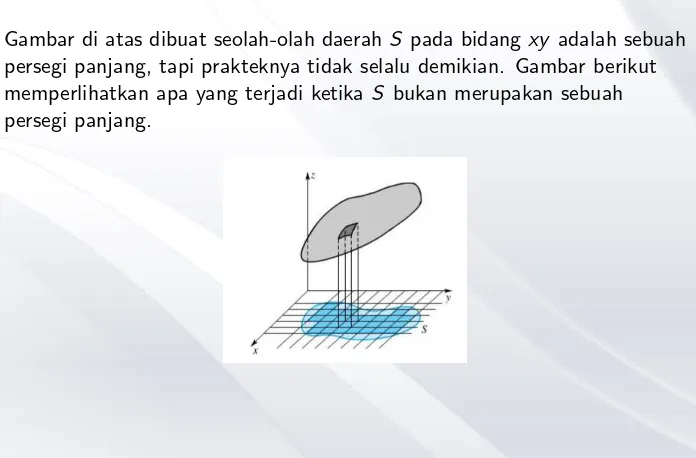
Gambar di atas dibuat seolah-olah daerahS pada bidangxy adalah sebuah

persegi panjang, tapi prakteknya tidak selalu demikian. Gambar berikut

memperlihatkan apa yang terjadi ketika S bukan merupakan sebuah

(22)

Contoh 1:

Jika S adalah daerah persegi panjang pada bidang xy yang dibatasi oleh

garis x = 0,x = 1,y = 0, dan y = 2, tentukan luas dari bagian

(23)

(24)

Contoh 2:

(25)

Penyelesaian:

Bagian G (yang diarsir) dari permukaan tersebut diproyeksikan ke daerah

melingkar S di dalam lingkaranx2+y2= 9. Misalkan f(x,y) =x2+y2. Makafx = 2x,fy = 2y, dan

A(G) =

Z Z

S p

(26)

Bentuk S menyarankan kita untuk menggunakan koordinat kutub.

(27)

Penerapan Integral Lipat-Dua Latihan

Latihan

1. Tentukan massa m dan pusat massa (¯x,¯y) dari lamina yang dibatasi

kurva-kurva berikut dengan kerapatan yang diberikan.

a. x= 0,x = 4,y = 0,y = 3;δ(x,y) =y+ 1 b. y=ex_,_y _{= 0}_,_x_{= 0}_,_x _{= 1;}_δ₍_x_,_y_{) = 2}₋_x₊_y

2. Tunjukkan bahwa momen inersia dari sebuah lamina persegi panjang

homogen dengan panjang sisia danb terhadap sumbu tegak lurus

melalui pusat massanya adalah

I = k 12(a

3_b₊_ab3₎

(28)

Penerapan Integral Lipat-Dua Latihan

3. Sketsalah daerah-daerah berikut dan hitung luas permukaannya.

a. Bagian dari permukaanz =p

4−y2 _{yang tepat berada di atas} bujursangkar pada bidangxy dengan verteks-verteks

(1,0),(2,0),(2,1),dan (1,1).

b. Bagian dari permukaanz =p4−y2 _{pada oktan pertama yang tepat} berada di atas lingkaranx2₊_y2_{= 4 pada bidang} _xy_.

c. Bagian dari bolax2+y2+z2=a2di dalam silinder lingkaran

(29)

Penerapan Integral Lipat-Dua Pustaka

Pustaka

Purcell, E. J & D. Vanberg, 1999. Terjemahan, Kalkulus dan

Geometri Analitis, Jilid 1 dan 2. Jakarta : Erlangga.

Spiegel. M. & Wrede R.C. 2002. Theory and Problem of Advanced

Calculus. Schaum Outline Series. New York: Mc Graw-Hill.

Purcell, E. J & D. Vanberg, 2003. Terjemahan, Kalkulus , Jilid 2.

Jakarta : Erlangga.

Mendelson, Elliot, 1988. Schaum’s Outlines, 3000 Solved Problems in